Array Optimization for a Wave Energy Converter with Adaptive Resonance Using Dual Bayesian Optimization
Abstract
1. Introduction
2. Dual Bayesian Optimization for Array Layout Optimization
2.1. Power Performance Optimization of Single Unit SR-WEC
2.2. Dual Bayesian Optimization Strategy
2.3. Step 1—Annual Excitation Maximization of WEC Array
2.4. Step 2—Power Performance Optimization of WEC Array
3. SR-WEC Array Layout and Performance Optimization
3.1. Identification of Optimal Array Layout
3.2. Power Performance Maximization for Optimal Array Layout
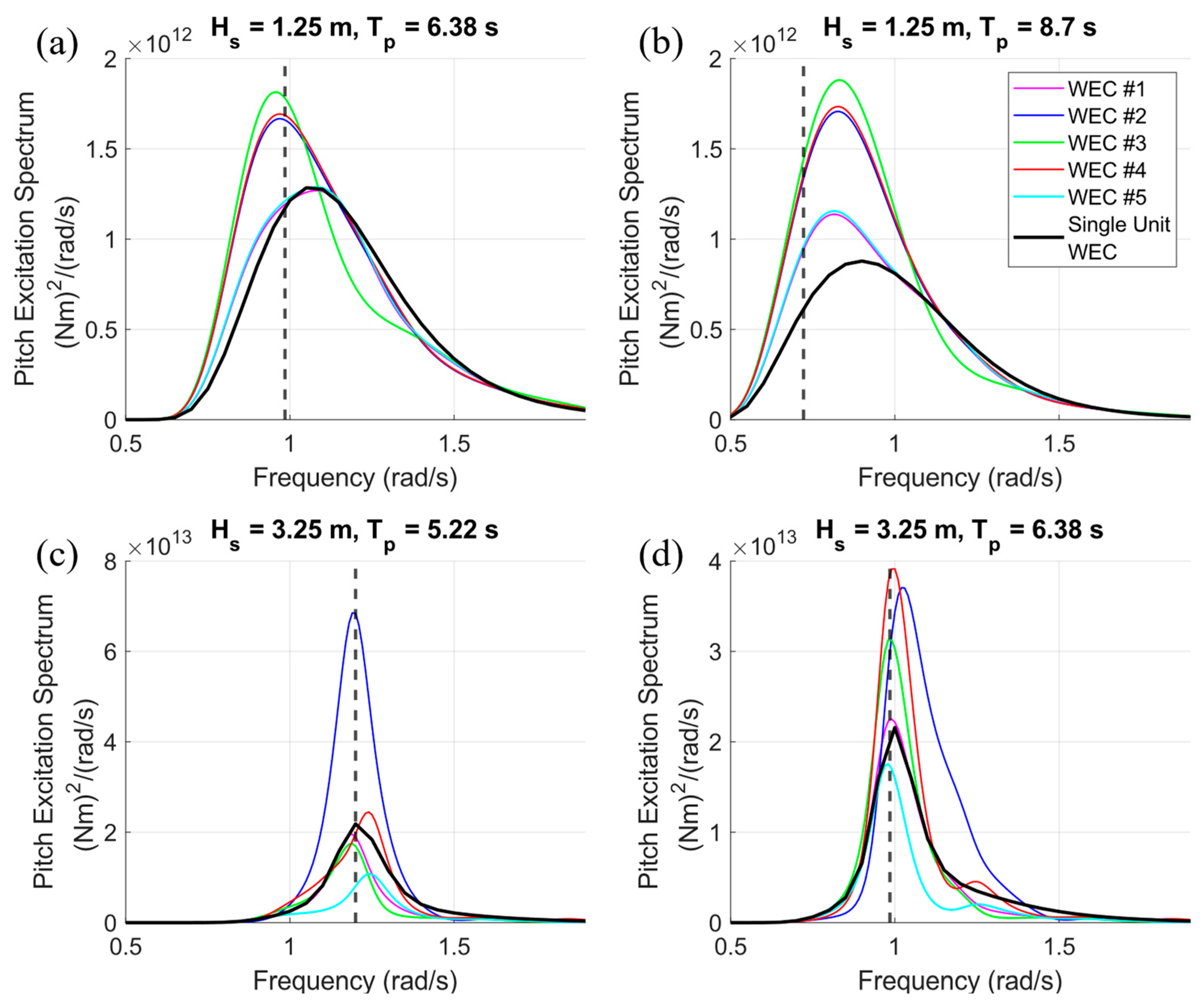
3.3. Power Performance and Adaptive Resonance in Time Domain for Optimal Array Layouts
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| WEC | = 1.25 m | 4.06 s | 5.22 s | 6.38 s | 7.54 s | 8.70 s |
|---|---|---|---|---|---|---|
| SR-WEC 1 | 45.86 | 27.23 | 34.14 | 32.80 | 31.04 | |
| 14.15 | 18.35 | 19.37 | 25.39 | 16.83 | ||
| SR-WEC 2 | 45.86 | 27.23 | 34.14 | 32.80 | 31.04 | |
| 14.15 | 18.35 | 19.37 | 25.39 | 16.83 | ||
| SR-WEC 3 | 39.47 | 14.71 | 44.01 | 35.51 | 32.54 | |
| 12.15 | 17.37 | 11.97 | 44.21 | 19.14 | ||
| SR-WEC 4 | 41.71 | 25.28 | 34.53 | 31.32 | 30.41 | |
| 8.67 | 16.86 | 24.99 | 14.33 | 19.23 | ||
| SR-WEC 5 | 41.71 | 25.28 | 34.53 | 31.32 | 30.41 | |
| 8.67 | 16.86 | 24.99 | 14.33 | 19.23 |
| WEC | = 1.25 m | 4.06 s | 5.22 s | 6.38 s | 7.54 s | 8.70 s |
|---|---|---|---|---|---|---|
| SR-WEC 1 | 39.85 | 14.55 | 36.3 | 9.55 | 9.63 | |
| 22.59 | 16.31 | 28.3 | 56 | 57.48 | ||
| SR-WEC 2 | 34.8 | 22.84 | 22.86 | 32.16 | 35.36 | |
| 10.37 | 19.23 | 11.14 | 26.94 | 25.08 | ||
| SR-WEC 3 | 50.02 | 29.53 | 37.74 | 21.61 | 22.17 | |
| 41.02 | 25.68 | 44.48 | 24.42 | 26.36 | ||
| SR-WEC 4 | 50.26 | 26.13 | 34.82 | 41.2 | 40.6 | |
| 28.42 | 12.22 | 21.62 | 40.36 | 39.69 | ||
| SR-WEC 5 | 49.48 | 12.41 | 15.87 | 46.67 | 41.58 | |
| 22.47 | 10.25 | 50.39 | 38.76 | 37.12 |
| WEC | = 2.25 m | 4.06 s | 5.22 s | 6.38 s | 7.54 s | 8.70 s |
|---|---|---|---|---|---|---|
| SR-WEC 1 | 35.95 | 4.77 | 52.94 | 25.16 | 33.51 | |
| 23.14 | 31.66 | 52.23 | 24.62 | 8.3 | ||
| SR-WEC 2 | 14.31 | 26.76 | 3.36 | 11.47 | 15.05 | |
| 34.72 | 47.41 | 31.87 | 30.74 | 17.81 | ||
| SR-WEC 3 | 44.27 | 33.74 | 28.57 | 21.07 | 3.92 | |
| 34.02 | 20.04 | 37.69 | 27.53 | 23.28 | ||
| SR-WEC 4 | 27.91 | 9.98 | 27.86 | 63.06 | 18.89 | |
| 29.66 | 15.87 | 39.1 | 55.43 | 23.4 | ||
| SR-WEC 5 | 42.25 | 22.9 | 59.82 | 41.17 | 33.18 | |
| 4.6 | 9.34 | 70.74 | 18.15 | 21.05 |
| WEC | = 3.25 m | 4.06 s | 5.22 s | 6.38 s | 7.54 s | 8.70 s |
|---|---|---|---|---|---|---|
| SR-WEC 1 | 52.1 | 5.11 | 35.16 | 15.92 | 31.25 | |
| 19.04 | 26.21 | 26.58 | 28.7 | 50.01 | ||
| SR-WEC 2 | 27.44 | 11.85 | 22.75 | 4.46 | 11.77 | |
| 35.08 | 32 | 44.99 | 42.58 | 20.76 | ||
| SR-WEC 3 | 49.41 | 10.73 | 27.33 | 30.23 | 16.01 | |
| 39.2 | 22.2 | 48.42 | 36.74 | 55.09 | ||
| SR-WEC 4 | 29.87 | 15.8 | 44.47 | 39.05 | 29.64 | |
| 16.33 | 32.32 | 32.74 | 31.63 | 24.51 | ||
| SR-WEC 5 | 45.17 | 4.88 | 13.99 | 40.51 | 23.61 | |
| 9.36 | 74.05 | 52.77 | 49.4 | 37.97 |
References
- Zhang, Y.; Zhao, Y.; Sun, W.; Li, J. Ocean wave energy converters: Technical principle, device realization, and performance evaluation. Renew. Sustain. Energy Rev. 2021, 141, 110764. [Google Scholar] [CrossRef]
- Guo, B.; Ringwood, J.V. A review of wave energy technology from a research and commercial perspective. IET Renew. Power Gener. 2021, 15, 3065–3090. [Google Scholar] [CrossRef]
- Shields, M.; Beiter, P.; Nunemaker, J.; Cooperman, A.; Duffy, P. Impacts of turbine and plant upsizing on the levelized cost of energy for offshore wind. Appl. Energy 2021, 298, 117189. [Google Scholar] [CrossRef]
- Yang, B.; Wu, S.; Zhang, H.; Liu, B.; Shu, H.; Shan, J.; Ren, Y.; Yao, W. Wave energy converter array layout optimization: A critical and comprehensive overview. Renew. Sustain. Energy Rev. 2022, 167, 112668. [Google Scholar] [CrossRef]
- Bailey, H.; Robertson, B.; Buckham, B. Variability and stochastic simulation of power from wave energy converter arrays. Renew. Energy 2018, 115, 721–733. [Google Scholar] [CrossRef]
- Martić, I.; Degiuli, N.; Grlj, C.G. Scaling of wave energy converters for optimum performance in the Adriatic Sea. Energy 2024, 294, 130922. [Google Scholar] [CrossRef]
- Budal, K. Theory for absorption of wave power by a system of interacting bodies. J. Ship Res. 1977, 21, 248–254. [Google Scholar] [CrossRef]
- Tay, Z.Y.; Venugopal, V. The impact of energy extraction of wave energy converter arrays on wave climate under multi-directional seas. J. Ocean Eng. Mar. Energy 2019, 5, 51–72. [Google Scholar] [CrossRef]
- Hantoro, R.; Septyaningrum, E.; Hudaya, Y.R.; Utama, I. Stability analysis for trimaran pontoon array in wave energy converter–pendulum system (WEC-PS). Brodogr. Int. J. Nav. Archit. Ocean Eng. Res. Dev. 2022, 73, 59–68. [Google Scholar] [CrossRef]
- Cheng, Y.; Xi, C.; Dai, S.; Ji, C.; Cocard, M. Wave energy extraction for an array of dual-oscillating wave surge converter with different layouts. Appl. Energy 2021, 292, 116899. [Google Scholar] [CrossRef]
- Giassi, M.; Göteman, M. Layout design of wave energy parks by a genetic algorithm. Ocean Eng. 2018, 154, 252–261. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Hua, X. Proposal of a novel analytical wake model and array optimization of oscillating wave surge converter using differential evolution algorithm. Ocean Eng. 2021, 219, 108380. [Google Scholar] [CrossRef]
- Jeong, H.-J.; Koo, W. Analysis of various algorithms for optimizing the wave energy converters associated with a sloped wall-type breakwater. Ocean. Eng. 2023, 276, 114199. [Google Scholar] [CrossRef]
- Neshat, M.; Alexander, B.; Wagner, M. A hybrid cooperative co-evolution algorithm framework for optimising power take off and placements of wave energy converters. Inf. Sci. 2020, 534, 218–244. [Google Scholar] [CrossRef]
- Babarit, A. On the park effect in arrays of oscillating wave energy converters. Renew. Energy 2013, 58, 68–78. [Google Scholar] [CrossRef]
- Sarkar, D.; Contal, E.; Vayatis, N.; Dias, F. Prediction and optimization of wave energy converter arrays using a machine learning approach. Renew. Energy 2016, 97, 504–517. [Google Scholar] [CrossRef]
- Atan, R.; Finnegan, W.; Nash, S.; Goggins, J. The effect of arrays of wave energy converters on the nearshore wave climate. Ocean Eng. 2019, 172, 373–384. [Google Scholar] [CrossRef]
- Child, B.; Venugopal, V. Optimal configurations of wave energy device arrays. Ocean Eng. 2010, 37, 1402–1417. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, Q.; Kang, Y.; Yu, F. Hydrodynamic interactions among wave energy converter array and a hierarchical genetic algorithm for layout optimization. Ocean Eng. 2022, 256, 111521. [Google Scholar] [CrossRef]
- Sharp, C.; DuPont, B. Wave energy converter array optimization: A genetic algorithm approach and minimum separation distance study. Ocean Eng. 2018, 163, 148–156. [Google Scholar] [CrossRef]
- Bozzi, S.; Giassi, M.; Miquel, A.M.; Antonini, A.; Bizzozero, F.; Gruosso, G.; Archetti, R.; Passoni, G. Wave energy farm design in real wave climates: The Italian offshore. Energy 2017, 122, 378–389. [Google Scholar] [CrossRef]
- Payne, G.S.; Taylor, J.R.; Bruce, T.; Parkin, P. Assessment of boundary-element method for modelling a free-floating sloped wave energy device. Part 2: Experimental validation. Ocean Eng. 2008, 35, 342–357. [Google Scholar] [CrossRef]
- Cruz, J.M.B.P.; Salter, S.H. Numerical and experimental modelling of a modified version of the Edinburgh Duck wave energy device. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2006, 220, 129–147. [Google Scholar] [CrossRef]
- So, R.; Michelen, C.; Bosma, B.; Lenee-Bluhm, P.; Brekken, T.K.A. Statistical analysis of a 1: 7 scale field test wave energy converter using WEC-sim. IEEE Trans. Sustain. Energy 2017, 8, 1118–1126. [Google Scholar] [CrossRef]
- Jin, C.; Meduri, A.; Kang, H. Multivariable design optimization for adaptive resonance of a surface riding wave energy converter. Ocean Eng. 2023, 286, 115576. [Google Scholar] [CrossRef]
- Penalba, M.; Ringwood, J.V. A review of wave-to-wire models for wave energy converters. Energies 2016, 9, 506. [Google Scholar] [CrossRef]
- Shan, S.; Wang, G.G. Survey of modeling and optimization strategies to solve high-dimensional design problems with computationally-expensive black-box functions. Struct. Multidiscip. Optim. 2010, 41, 219–241. [Google Scholar] [CrossRef]
- Lei, B.; Kirk, T.Q.; Bhattacharya, A.; Pati, D.; Qian, X.; Arroyave, R.; Mallick, B.K. Bayesian optimization with adaptive surrogate models for automated experimental design. Npj Comput. Mater. 2021, 7, 194. [Google Scholar] [CrossRef]
- Lim, J.; Choi, M.; Lee, S. A Bayesian optimization algorithm for the optimization of mooring system design using time-domain analysis. J. Mar. Sci. Eng. 2023, 11, 507. [Google Scholar] [CrossRef]
- Elsas, J.; Casaprima, N.; Cardoso, P.; Menezes, I. Bayesian optimization of riser configurations. Ocean Eng. 2021, 236, 109402. [Google Scholar] [CrossRef]
- Baheri, A.; Ramaprabhu, P.; Vermillion, C. Iterative 3d layout optimization and parametric trade study for a reconfigurable ocean current turbine array using bayesian optimization. Renew. Energy 2018, 127, 1052–1063. [Google Scholar] [CrossRef]
- Garnett, R. Bayesian Ooptimization; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Veritas, N. Environmental Conditions and Environmental Loads; Det Norske Veritas: Oslo, Norway, 2000. [Google Scholar]
- Cummins, W. The Impulse Response Function and Ship Motion. Report 1661. Department of the Navy, David W. Taylor Model Basin, Hydromechanics Laboratory, Research and Development Report. October 1962. Available online: https://dome.mit.edu/bitstream/handle/1721.3/49049/DTMB_1962_1661.pdf (accessed on 1 October 2024).
- Meyer, J.; Windt, C.; Hildebrandt, A.; Schlurmann, T. Mechanically coupled wave farms: On the accuracy of a mid-fidelity hydrodynamic model under consideration of varying calibration approaches. Ocean Eng. 2024, 305, 117874. [Google Scholar] [CrossRef]
- Wood, G.D.; Kennedy, D.C. Simulating Mechanical Systems in Simulink with SimMechanics; The Mathworks Report; Mathworks: Natick, MA, USA, 2003; Volume 210. [Google Scholar]
- Sheshaprasad, S.; Naghavi, F.; Hasanpour, S.; Albader, M.; Gardner, M.C.; Kang, H.; Toliyat, H.A. Optimal Electric Power Take-off Strategy for Surface Riding Wave Energy Converter. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–7. [Google Scholar]
- Meduri, A.; Kang, H. Synergistic Integration of Multiple Wave Energy Converters with Adaptive Resonance and Offshore Floating Wind Turbines through Bayesian Optimization. J. Mar. Sci. Eng. 2024, 12, 1455. [Google Scholar] [CrossRef]
- Ancellin, M.; Dias, F. Capytaine: A Python-based linear potential flow solver. J. Open Source Softw. 2019, 4, 1341. [Google Scholar] [CrossRef]
- Astariz, S.; Iglesias, G. Enhancing wave energy competitiveness through co-located wind and wave energy farms. A review on the shadow effect. Energies 2015, 8, 7344–7366. [Google Scholar] [CrossRef]
- Short, W.; Packey, D.; Holt, T. A Manual for the Economic Evaluation of Energy Efficiency and Renewable Energy Technologies; National Renewable Energy Lab (NREL): Golden, CO, USA, 1995. [Google Scholar]



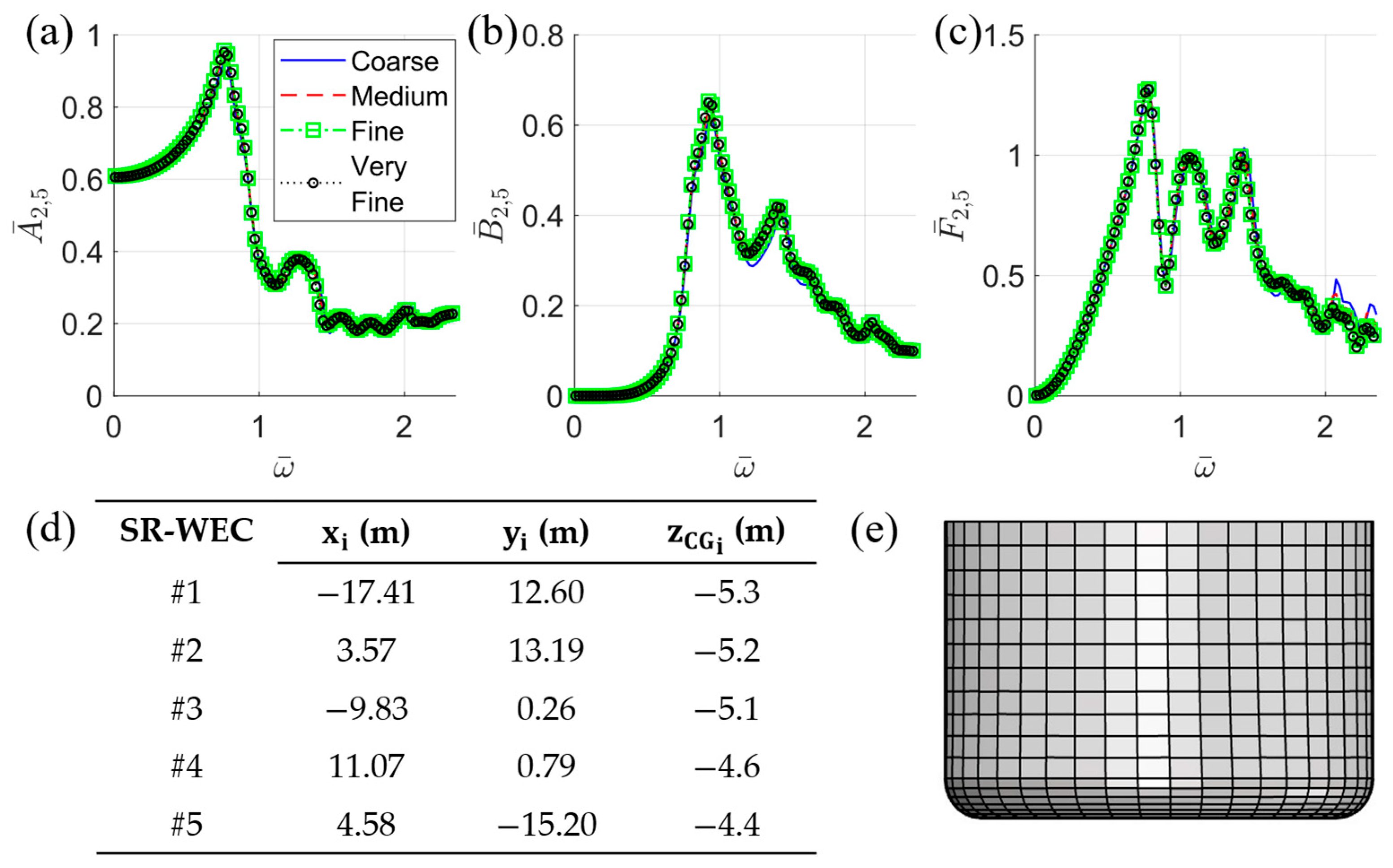









| Parameter | Description | Value | Parameter | Description | Value |
|---|---|---|---|---|---|
| D | Diameter | 12 m | Stator Length | 12 m | |
| d | Draft | 7.5 m | Translator Length (m) | 1.905 m | |
| Radius of Smoothed Edge | 1 m | Translator Mass (kg) | 24,300 kg | ||
| Center of Gravity (below MWL) | −5.4 m | Total Displaced Mass (kg) | 861,451.9 kg |
| Type | Description | Linear Layout | Description | Random Layout |
|---|---|---|---|---|
| BEM | Frequency | [0.01, 3.01] rad/s | Frequency | [0.01, 3.01] rad/s |
| Wave Heading | 0 | Wave Heading | 0 | |
| Variable | Array Spacing | 1 [13 m, 18 m] | Array Coordinates | 5 [−20 m, 20 m] |
| Center of Gravity | 3 [−5.4 m, −4 m] | Center of Gravity | 5 [−5.4 m, −4 m] | |
| Bayesian optimization | Objective Function | Objective Function | ||
| Variables | 4 | Variables | 15 | |
| Constraint | None | Constrain | ||
| Number of Iterations | 200 | Number of Iterations | 200 | |
| Exploration Ratio | 0.8 | Exploration Ratio | 0.8 |
| Type | Description | Optimal Linear Layout | Optimal Random Layout |
|---|---|---|---|
| WEC-Sim v6.0 | Simulation Length | 3600 s | 3600 s |
| ) | 5 ( = 1.25 m) ( = 4.06 s, 5.22 s, 6.38 s, 7.54 s, 8.7 s) | 15 ( = 1.25 m, 2.25 m, 3.25 m) ( = 4.06 s, 5.22 s, 6.38 s, 7.54 s, 8.7 s) | |
| Wave Spectrum and Heading | JONSWAP, Unidirectional, | JONSWAP, Unidirectional, | |
| Variables | [0.5, 78] kN/(m/s) | 5 [0.5, 78] kN/(m/s) | |
| PTO Stiffness | 3 [1, 90] kN/m | 5 [1, 90] kN/m | |
| Bayesian optimization | Objective Function | ( ) | () |
| Number of Iterations | 50 | 100 | |
| Exploration Ratio | 0.8 | 0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meduri, A.; Kang, H. Array Optimization for a Wave Energy Converter with Adaptive Resonance Using Dual Bayesian Optimization. J. Mar. Sci. Eng. 2024, 12, 2143. https://doi.org/10.3390/jmse12122143
Meduri A, Kang H. Array Optimization for a Wave Energy Converter with Adaptive Resonance Using Dual Bayesian Optimization. Journal of Marine Science and Engineering. 2024; 12(12):2143. https://doi.org/10.3390/jmse12122143
Chicago/Turabian StyleMeduri, Aghamarshana, and HeonYong Kang. 2024. "Array Optimization for a Wave Energy Converter with Adaptive Resonance Using Dual Bayesian Optimization" Journal of Marine Science and Engineering 12, no. 12: 2143. https://doi.org/10.3390/jmse12122143
APA StyleMeduri, A., & Kang, H. (2024). Array Optimization for a Wave Energy Converter with Adaptive Resonance Using Dual Bayesian Optimization. Journal of Marine Science and Engineering, 12(12), 2143. https://doi.org/10.3390/jmse12122143







