Dynamic Response Assessment of Floating Offshore Wind Turbine Mooring Systems with Different In-Line Tensioner Configurations Based on Fully Coupled Load Calculations

Abstract

In-line tensioning technology has significantly reduced the cost barriers that previously hindered the expansion of the floating offshore wind industry. However, assessing the impact of in-line tensioners on the dynamic response of floating offshore wind turbines (FOWTs) lacks effectiveness, and the relevant mooring configuration specifications are not complete. Thus, a fully coupled calculation method is introduced in this paper to solve the relevant issues in mooring systems with in-line tensioners using a classic spar platform model. Three distinct design scenarios were selected to study the variation in mooring configurations of in-line tensioners along different mooring lines and at varied positions within each line. The potential occurrence of reverse tension phenomena was deliberated and assessed. We identified the varying tension patterns at the fairlead and in-line tensioner locations in mooring systems with in-line tensioners, and the influence of such variations on platform dynamics. The findings also demonstrate that the appropriate configuration of in-line tensioners should be selected to avoid the risk of reverse tension. This research has potential to contribute to the security and economy of the deployment of this emerging in-line mooring method.

1. Introduction

In-line tensioning technology has gained prominence in the floating offshore industry due to its notable cost-effectiveness. Wind energy, as an enduring and eco-friendly source of clean energy, is increasingly being adopted globally because of its vast potential and diverse technological applications. By 2030, the total capacity of offshore wind power is projected to reach 380 GW, escalating to 2000 GW by 2050 [1]. However, the high costs associated with FOWTs pose substantial barriers to their large-scale development. Mooring tensioning systems, a primary cost component for both capital expenditures (CAPEX) and operational expenditures (OPEX), facilitate the deployment of FOWTs far from shorelines and are not limited by water depth [2,3]. Furthermore, Yang et al. [4] highlighted that, compared to traditional marine petroleum exploitation, the equipment used in floating wind power platforms entails lower risks post-failure and reduced requirements for equipment redundancy, thus supporting the potential application of in-line tensioning technology.

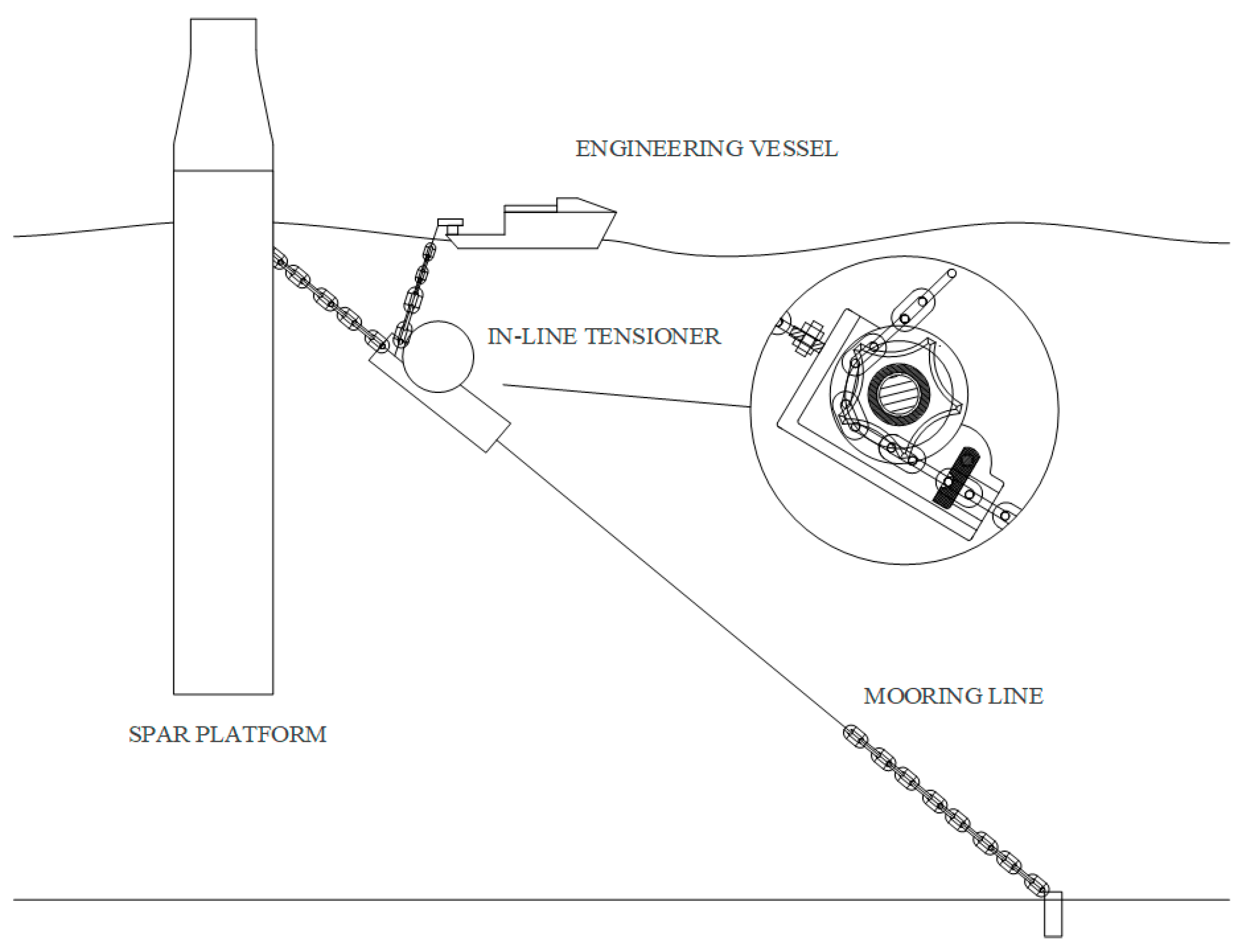
The concept of in-line tensioning was initially introduced in a 2006 patent application by Dove et al. [5], representing a breakthrough in mooring system design. As shown in Figure 1, this new type of mooring tensioning equipment can replace traditional systems on mooring platforms, offering a more convenient tensioning operation while significantly improving cost-effectiveness, with the ability to achieve required tensioning capabilities. Characterized by a sprocket and a retaining device within a frame structure, in-line tensioners function through an engineering ship’s lifting system, which pulls the chain’s free end to achieve tension. This method, enhanced by the significant envelope angle of the chain around the sprocket, not only reduces the operational load, but also mitigates issues related to chain storage on platforms, conserves deck space, and positions the chain guide device underwater to minimize damage. The practical application of this concept was first realized in Shell’s FPSO project in the Stones area, marking a significant advancement in the use of in-line tensioners, which eliminate the need for power units on the platform [6]. Financial constraints in the Vito project led Johnson et al. [7] to adopt this technology, which notably reduced costs and decreased the transportation and installation time of the equipment.

The fully coupled method is a frequently utilized analytical technique for calculating dynamic response in FOWTs. Ormberg et al. [8] affirmed that coupling analysis yields robust results when juxtaposed with experimental tests. Unlike traditional floating structures, the mooring systems of offshore wind equipment must actively integrate wind load with the motions of the ship and mooring, necessitating a fully coupled response analysis. Masciola et al. [9] compared the fully coupled and uncoupled analysis results, and it was found that the responses to changes in loads were different. Instead, a comprehensive fully coupled response calculation and analysis should be carried out. Withee et al. [10] introduced a program for the fully coupled dynamic calculation of offshore wind platforms that can assess the time-domain consequence when the FOWT is subject to combined irregular wind and wave impacts. Wayman et al. [11] investigated the 5 MW wind turbine and developed a computational program to examine the interconnected dynamic reaction within the frequency spectrum. Kvittem et al. [12] used a numerical tool obtained by combining two types of fluid dynamics software, SIMO-RIFLEX and Aerodyn, to study a catenary model with a nonlinear geometric recovery force applied to a semi-submersible platform, and the contribution of dynamic tension to the fatigue problem was evaluated. Wang et al. [13] adopted two different fully coupled computing processes to analyze the numerical properties of a floating vertical-axis wind turbine and a horizontal-axis wind turbine and compared time-domain results, such as the global motion of the turbine in freedom, the bending moment, and the tension at the fairlead. Ma et al. [14] developed a numerical method for the OC4 project with three catenary lines. They validated the reasons and conditions leading to mooring line fractures, determined the maximum tension levels, and pinpointed areas at risk.

Research into mooring configurations reveals their significant impact on the dynamic responses of platform motion and mooring tension. The in-line tensioner is typically positioned in the middle of a mooring line within a multi-point mooring system, and any changes to the mooring configuration will have an impact on its dynamic response. Giorgi et al. [15] developed a mesh-free nonlinear computational method and analyzed the mooring lines of spar-structured wave energy converters. They conducted a sensitivity analysis and compared the dynamic response results of five different mooring configurations. Jiang et al. [16] used the Navier–Stokes method to investigate the mooring-induced damping of platform movements under various mooring parameter alterations. Additionally, they analyzed factors such as decaying oscillatory motions and concluded that mooring configurations should be tailored to the specific characteristics of the floating concepts. These configurations must be designed to optimize performance, and their physical parameters need to be customized to the unique features of each concept. Amaechi et al. [17] conducted a computational investigation to examine various mooring configurations for a paired-column semi-submersible platform. Specifically, they observed significant variations in surge displacements among different mooring configurations, while the amplitudes of rotational motions remained relatively consistent. Neisi et al. [18] proposed a multi-segment mooring system for the OC4 project, utilizing buoys and clump weights. They compared the platform’s responses under both regular and irregular waves with those of classical models. The results indicated that variations in the natural period significantly altered the low-frequency resonance phenomenon. Bruschi et al. [19] studied the influence of clump weights on the response of SPAR platforms and the tension in the mooring lines. They utilized the FAST numerical simulation program to investigate the dynamic response under the wave effect. Their results indicated that the position arrangement of the clump weight has a far greater impact than the variation in weight. Lopez et al. [20] conducted experimental research on a SPAR platform, focusing on a mooring system that included weighted clumps. They compared their findings with the results from OpenFAST. The results indicated that this configuration reduced the maximum tension in the mooring lines under extreme conditions. While most research concentrates on the responses of various balanced mooring configurations, the in-line tensioner often results in an unbalanced arrangement.

Under varying mooring configurations, reverse tensions are observed during changes in mooring tension. However, the in-line tensioner is a new technology that works as a compression-sensitive component. It is necessary to evaluate and study its dynamic response fully. Azcona et al. [21] tested mooring dynamic results under different settings through an analytical procedure based on the lumped mass formula. Experimental activities were carried out and compared to numerical prediction. Excitation response was compared under different periods of horizontal harmonic motion. Cao et al. [22] examined the impact of various configurations of the spar platform mooring system on sudden load through a model experiment using a 3 m depth wave flume, took the sinusoidal displacement as the top excitation, and summarized the influencing factors and changes. Qiao et al. [23] studied the possible slack–taut phenomenon of mooring lines and found that this large tension change is influenced by changes in axial excitation. Li et al. [24] studied the reverse tension on a subsea mooring connector and analyzed its response characteristics. The platform motion data were monitored by GPS equipment on FPSO. The abilities of the lumped mass model and nonlinear finite element model in dealing with rigid–flexible coupling problems were compared, and it was found that there is a risk of reverse force after the change in vertical displacement.

Addressing the current gaps in evaluating in-line tensioner applications, this study proposes a modeling method that integrates fully coupled calculations of FOWT systems with in-line tensioners. Utilizing SIMO-RIFLEX v4.3 software, this study scrutinizes the tension and motion alterations in a mooring system equipped with an in-line tensioner on a classical OC3-Hywind spar platform, examining the dynamic tension variations resulting from the placement of an in-line tensioner at various locations along different mooring lines, and subsequently evaluates their effects on platform movement. Additionally, this study explores the phenomenon of potential reverse tension in in-line tensioners across different mooring configurations and outlines governing principles. This study seeks to assess emerging in-line tensioning technology to facilitate the widespread advancement of the floating wind power industry.

2. Methodology and System Parameters

2.1. In-Line Tensioner Parameters

The in-line tensioner used in this study consists of a main frame that provides a one-way passage of the chain in the working state and an anchor sprocket wheel set in the frame for guidance. It can be permanently present on the mooring line during the wind turbine operation period.

Table 1. The main parameters of the in-line tensioner.

Item	Value	Unit
Chain diameter	0.09	m
Axial length	2.46	m
Total mass	12,793	kg
Frame mass	6472	kg
Sprocket wheel mass	6318	kg
Minimum breaking load	9801	kN

and Figure 2 report the main characteristics and a 3D-rendered graph of the in-line tensioner.

2.2. Wind Turbine and Platform Parameters

The 5 MW wind turbine component employed in this study was designed by the National Renewable Energy Laboratory (NREL) as an example of a three-blade upwind variable-speed variable-pitch wind turbine. It has been widely used to analyze dynamics and has been validated on various floating platform types. Its detailed parameters are described in

Table 2. Main parameters of the NREL 5 MW wind turbine [26].

Item	Value	Unit
Rating	5	MW
Rotor mass	110,000	kg
Rotor diameter	126	m
Hub height	90	m
Tower mass	347,460	kg
Nacelle mass	240,000	kg

[25,26].

The classical spar platform was adopted, which has substantial research foundations, and was studied with an NREL 5 MW offshore turbine in the stage IV study of the OC3 project [26]. Its detailed parameters are described in

Table 3. Main parameters of the OC3-Hywind spar platform [27].

Item	Value	Unit
Depth to platform	120	m
Depth to the top of the taper	4	m
Depth to bottom of taper	12	m
Roll inertia	4,229,230	t·m2
Pitch inertia	4,229,230	t·m2
Yaw inertia	164,230	t·m2
Platform mass	746,633	t
Platform diameter	6.5	m
Elevation to the tower base	10	m

.

2.3. Mooring System Parameters

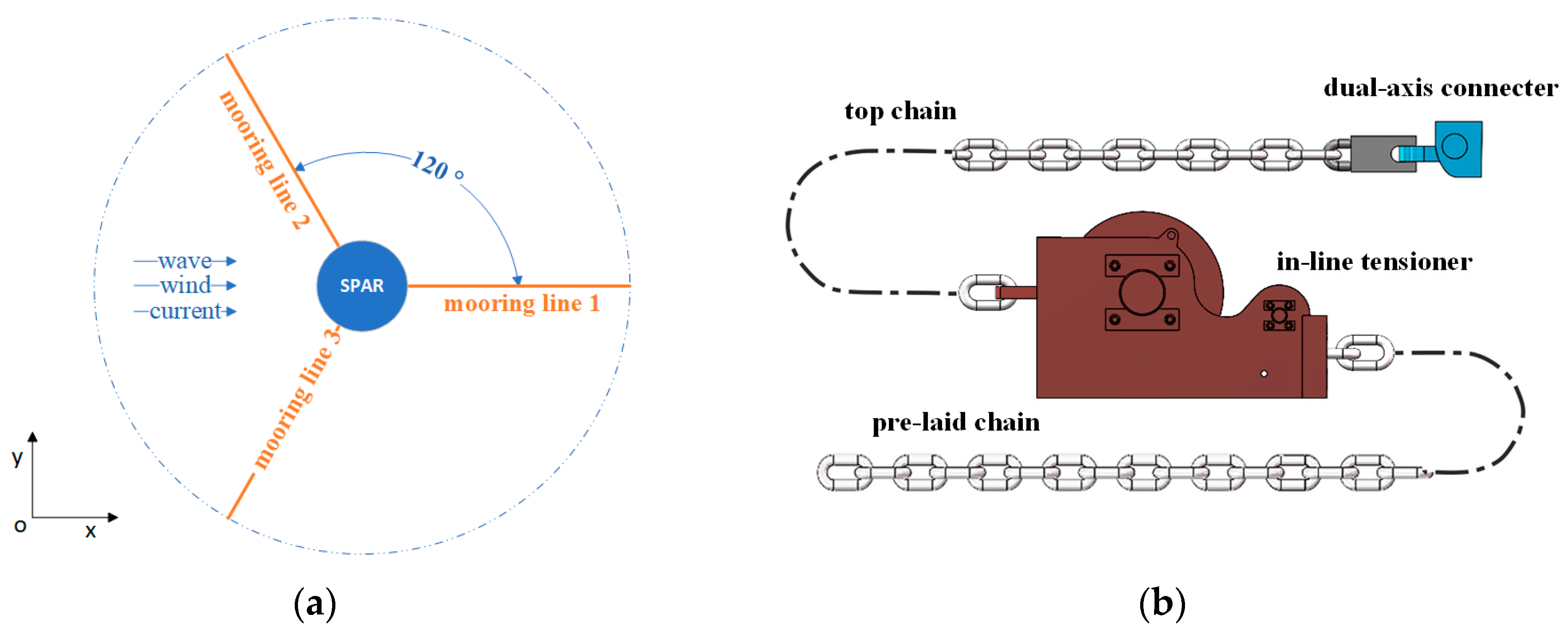
This study focuses on the mooring system of the Equinor Hywind offshore structure. The triangular connection between chain lines and the offshore platform is eliminated, and the commonly used three-line catenary mooring method is simplified. The system also includes yaw damping to describe the platform yaw stiffness of the current scenario accurately, and detailed information on the mooring parameters can be found in

Table 4. Mooring system parameters [27].

Item	Value	Unit
Angle Between Mooring Lines	120	deg
Mooring Line Diameter	0.09	m
Radius to Anchors from Platform Centerline	853.87	m
Radius to Fairleads from Platform Centerline	5.2	m
Depth to Anchors Below SWL	320	m
Depth to Fairleads Below SWL	70	m
Equivalent Mooring Line Mass Density	77.7066	kg/m
Additional Yaw Spring Stiffness	98,340	kN·m/rad

.

As shown in Figure 3a, one mooring line aligns with the X axis, whereas the other two are symmetrically positioned on either side of the X axis, thereby securing the spar platform in a central position. From a top–down perspective, each mooring line is precisely spaced 120° apart from the others. In this study, the initial arrangement scheme of the in-line tensioner is similar to that planned for the floating offshore wind farm in Lannion, but only set on one mooring line in the three-line mooring system [28].

Figure 3b expounds the initial arrangement of the mooring line with the in-line tensioner, consisting of a top chain part, connected to the spar structure by the dual-axis connecter to avoid out-of-plane bending on the first connecting link, and a pre-laid chain connected to the anchor. The in-line tensioner connects the two parts and forms a 902.2 m mooring line of the same length as the OC3 project for subsequent analytical studies.

2.4. Fully Coupled Analytical Calculation Method

The research employed fully coupled load calculations utilizing the dynamic response calculation programs SIMO and RIFLEX [29,30]. 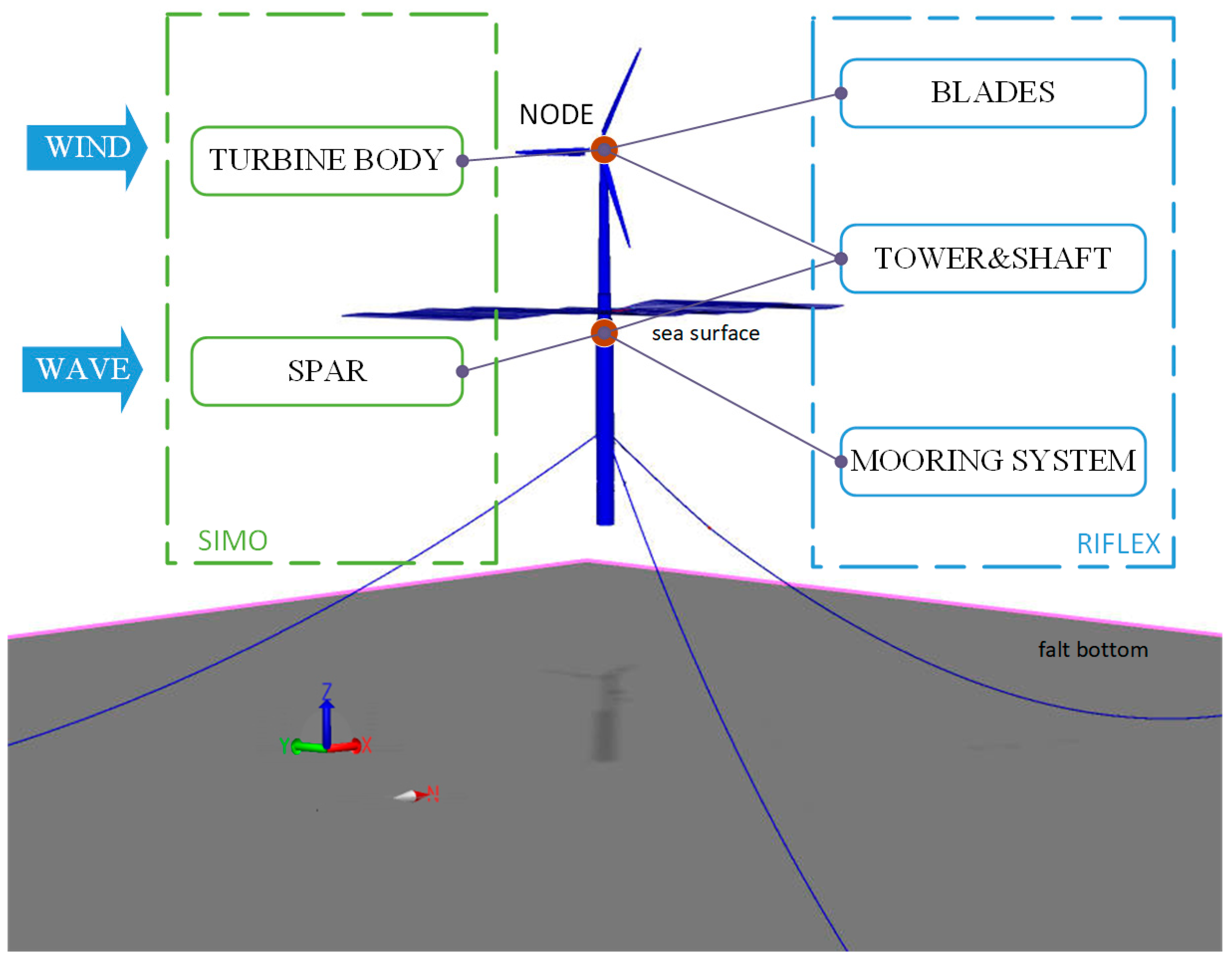The modeling and simulation coordination occurred within the established SIMA workbench v.4.3, demonstrating its computational proficiency for OC3-Hywind by delivering dependable outcomes when juxtaposed with a range of numerical tools during the fourth-phase evaluation of the OC3 project [27]. In the fully coupled simulation, it is essential to describe the mechanical dynamic response behavior of the aerodynamics, hydrodynamics, and structural dynamics of the system. The components that need to be described include the turbine, blades, shaft, tower, SPAR structure, and the mooring system. The fully coupled model used for the calculations is illustrated in Figure 4.

The SPAR structure is described in the SIMO as a rigid body with specific mass properties and hydrostatic stiffness data. The calculation of linear radiation forces is achieved through the convolution of a delay function combined with infinite-frequency additional mass. Low-frequency damping for horizontal motion is represented using a quadratic damping coefficient. The determination of linear wave excitation forces relies on the potential flow coefficient, while the assessment of the averaged wave drift force coefficient relies on the potential flow coefficient. Additionally, a portion of the turbine is also described as a rigid body in the SIMO, possessing wind coefficients and mass properties.

RIFLEX has the advantage of describing slender structures that are small in comparison to diameter and wavelength. In the FOWT system, components such as blades, shafts, towers, and mooring lines fall under this category of slender flexible structures. For the wind turbine structural model, the blades and shaft line are described in terms of refluxate blade lines and are defined using flexible beam elements, with external blade lines and internal eccentricity lines. The shaft line, incorporating flex–joint connections, is represented by axisymmetric beam elements, facilitating the definition of torsional stiffness. The modeling of the tower is conducted using linear elastic beam elements to describe the mechanical behavior of the tower structure under wind loads. The mooring line is discretized into finite elements and simplified into a uniform circular cross-section homogeneous element with equivalent mass. The mechanical properties of the mooring line are described by defining cross-sectional parameters, allowing for an analysis of its behavior under various loads, thereby accurately capturing its response characteristics.

The coupling connection between SIMO and REFLEX is defined by a common node, where the mooring lines are connected to the SPAR structure by a fairlead point, realized by establishing a leader–follower relationship to achieve the common node. The tower is flexibly connected to the top of the spar and shaft line to form a common node. The turbine body, blade lines, and shaft lines are connected by defining common nodes on the hub, forming a coupled analytical model that describes the kinematic and mechanical properties of the FOWT.

The rotor loads for turbine blades are computed using the blade element momentum theory. This method considers dynamic wake and stall effects, blade tip and hub loss corrections, and yawed inflow corrections. The aerodynamic loads are shown as secondary drag loads, with integrated structural damping as stiffness-proportional Rayleigh damping. As shown in Equations (1) and (2), the hydrodynamic loads are calculated according to Morison’s generalized equation, where the total fluid force acting on each element is tangent to the structure, which includes inertial and viscous drag loads and considers the Froude–Krylov force acting in a normal direction to the structure. Inertial effects are considered by accounting for linear mass acceleration and a hydrodynamic additional mass term, which accounts for water scattering pressure due to object acceleration in a fluid medium.

$$d{F}_N=(f_N^{FK}\rho A{\dot{u}}_N+m_a^N{\dot{u}}_N-m_a^N{\ddot{x}}_N+{\displaystyle \frac{1}{2}}\rho C_d^N(u_N-{\dot{x}}_N)\left|u_N-{\dot{x}}_N\right|dl)$$

(1)

$$d{F}_T=(f_T^{FK}\rho A{\dot{u}}_T+m_a^N{\dot{u}}_T-m_a^T{\ddot{x}}_T+{\displaystyle \frac{1}{2}}\rho C_d^T(u_T-{\dot{x}}_T)\left|u_T-{\dot{x}}_T\right|dl)$$

(2)

In the coupled computational model, the accurate description of the dynamic behavior of the mooring lines is achieved through the precise definition of the position and orientation of each node in space. To accomplish this, each node of the unit has six degrees of freedom, described using base vectors and orthogonal rotation matrices. This enables the computation of forces and moments on the mooring line model, considering the relative motion and orientation of each node. This approach enables modeling complex interactions between the mooring line and its surroundings, facilitating the precise analysis of its dynamic behavior.

Finite rigid bodies are added at the finite element node to simulate the eccentricities of the finite rigid bodies at the node. As shown in Equation (3), the rigid body surface point P is described as the current state of a rigid element, and its primitive state is defined by the vector $e_j^0$; when deformation occurs, its position is represented by the position vector with the rotation matrix component T_ij of the node added.

$$x_p=x+e=(X_i+v_i+e_j^0{T}_{ij})I_i$$

(3)

3. Fully Coupled Analytical Calculation of System with In-Line Tensioner

3.1. Fully Coupled Analytical Calculation Program Validation

To verify the accuracy of the spar structure platform model of the OC3 project in this study, the platform’s fairlead tension results are compared and verified with the results of other numerical simulations.

The numerical results for comparison are, respectively, from the modeling and calculation results from POSTECH using FAST software and the modeling and calculation results from LUH using ADAMS software [31]. Among them, the dynamic stall method is used for the treatment of aerodynamics, the finite element method is used for the treatment of turbines, and the calculation of mooring lines is based on quasi-static catenary equations. The wind condition for verification is uniform and stable, and there is no shear constant wind. The wave condition is a regular Airy wave with a significant wave height of 6 m and a period of 10 s. This is to assess the fully coupled numerical response results under the action of regular waves. Figure 5 presents the numerical results of the platform’s tension response within two periods, with an average tension of 680 kN, which is the same as that of the verified numerical results. This result is consistent with the verification case, confirming the accuracy of the model setup employed in this study.

3.2. Comparison of Computational Models for Mooring Line with In-Line Tensioner

There is no numerical modeling specification for the mooring line with the in-line tensioner. This study is based on the working characteristics of the in-line tensioner, comparing the different model description methods, and selecting the appropriate numerical modeling method to describe the mooring line with the in-line tensioner. During the normal service period of the platform, the in-line tensioner exists in the mooring line as a permanent mooring accessory. The chain segment where the in-line tensioner exists during the service process is different from the ordinary chain structure. As shown in Figure 6, on one side of the tensioner is a chain link and connector with freely rotatable connections. On the other side, the chain link is restricted by the stopper, thus restricting the free-sliding connection relationship between the two chain links. There is only slight sliding between the ring chain link and the stopper. The part of the in-line tensioner that withstands mooring loads is mainly in the frame structure. The bending stiffness of the frame takes the place of the contribution of the original mooring chain segment. In terms of mass distribution, it is different from the uniformly distributed mass of the anchor chain segment. Due to the presence of the sprocket wheel, there is a concentration of mass on one side.

This study focuses on the impact of in-line tensioners as permanent accessories on floating offshore wind platforms and considers their influence under different layout scenarios. The mooring line, as a slender flexible body, is described in RIFLX using the finite element method. The key lies in accurately representing the different element structures and cross-sectional shape parameters, as well as specifying the system boundary conditions with external loads or displacements. The frame structure containing a chain stopper contributes mechanical characteristics during the movement of the mooring line. It is simplified into a series of segments with uniform cross-sectional properties and connected to the chain segment through nodes. The sprocket wheel does not contribute to the mooring dynamic response and can be simplified as an external mass for the purpose of description and mass properties. The description of the elements for the in-line tensioner segment will primarily focus on bar elements that are subjected to axial force, as well as beam elements that can define torsional and bending properties.

When the mooring line with an in-line tensioner is described using bar elements, it is defined using the total Lagrangian equation and subsequently transformed into an equation based on cross-sectional forces and small strain theory. As shown in Figure 7, the main frame of the tensioner in the line is described as a uniform element with a constant cross-sectional area along its extension direction. The initial length is referred to as $L_0$, while the length after deformation is precisely determined using the total Lagrangian equation and the linear displacement equation. The Green strain formula in Equation (4) captures both stretching and shearing effects, making it a reliable measure of material deformation. The small strain theory states that the axial force $N$ of nodes can be determined using Equation (5).

$$E_f={\displaystyle \frac{1}{2}}{\displaystyle \frac{L^2-L_0^2}{L_0^2}}={\displaystyle \frac{1}{2L_0^2}}(△x^2+△y^2+△z^2-L_0^2)$$

(4)

$$N={\displaystyle \frac{L-L_0}{L_0}}(EA)$$

(5)

When a mooring line containing an in-line tensioner is described using beam elements, it is based on the co-rotated ghost reference in the framework of basic continuum mechanics theory [32]. As shown in Figure 8, the beam element has three translational degrees of freedom and three rotational degrees of freedom at each node, and its position parameters are defined by its nodal coordinate system. The X-axis passes through the cross-section centroid along the element node. The beam element’s X-axis is defined as the line that connects the centroids of each section of the node. The Y-axis is defined by the mean direction of the node end, and the Z-axis is defined as perpendicular to both the X-axis and Y-axis. This defines a node coordinate system, where C₀ is on the X-axis and the YZ-axis defines the node section.

For the beam element, the initial element is configured as C0, and after deformation, it is Cn. In the process of deformation calculation, through the node transformation of the coordinate system deformed with the beam section, the internal axial force and bending moment and the torque center of the element are determined by the shape of the section. Under the assumption of small strains, higher-order terms beyond the second order may be disregarded, and the quadratic axial strain term can be omitted. The Green strain can be represented by Equation (6).

$$E_{xx}=u_{(0,xx)}-y{v}_{(0,xx)}-z{w}_{(0,xx)}+{\displaystyle \frac{1}{2}}(v_{(0,x)}^2+w_{(0,x)}^2)$$

(6)

The torsional behavior of the beam is based on the relationship represented by Equation (7):

$$M_{\theta }=G{I}_t{\theta }_{\mathrm{x}}$$

(7)

where $M_{\theta }$ is the twisting moment and $G{I}_t$ is the torsional stiffness.

Equation (8) represents the geometric stiffness matrix expression using the internal virtual work equation. The component of the internal load vector of the equilibrium projection is decomposed into the combined action of the force and moment at the nodes of the element. The load distribution of the element is determined by the stiffness matrix $k_e$ and the node transformation matrix $u_p$, and can be expressed as Equation (8):

$$k_e=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& {\displaystyle {\int }_{L0}{N}_{xx}{N}_{v,x}^{T}dx}& 0& 0\\ 0& 0& {\displaystyle {\int }_{L0}{N}_{xx}{N}_{w,x}^{T}dx}& 0\\ 0& 0& 0& 0\end{array}\right]$$

(8)

$$k_e{u}_p=F^e$$

(9)

The tensioner part, compared by using the total Lagrangian description, the description of the bar element, and the co-rotated ghost reference description of the beam element are included in the calculation results. Due to the sprocket wheel parts not directly participating in the mooring force, an evenly distributed wrapping weight can be determined according to the actual layout position. The mooring system is calculated using the continuous mass formulation. Because in this study we mainly focus on the change in the axial force at the tensioner, in this comparison process, the mooring tension at the tensioner is selected as the evaluation index. In the process of comparison, the calculation model is established by using the model parameters introduced above. To confirm the difference between the responses of two different elements, we chose a wind-free environment and defined the wave input according to the Jonswap spectrum, where Hs is 6 m and Tp is 10 s. Mooring line 1 on the leeward side is selected as the comparative mooring line, and the tension response at the position of the tensioner is compared. Figure 9 shows the computed results with various element descriptions, and we can observe that the two different element descriptions have similar results in the dynamic and static analyses. This demonstrates that the tensioner’s bending and torsional stiffness do not significantly impact the mooring tension fluctuation. In follow-up studies, the mooring line with the tensioner will be described as a bar element.

3.3. Definition of Environment Load for Mooring Line with In-Line Tensioner

Various environmental conditions were selected to compare the influence of the in-line tensioner at different placement positions on the changes in tension and platform movement. Studies on the arrangement of the tensioner on different mooring lines and in different positions on the lines were, respectively, set up. In this study, according to the actual use of the in-line tensioner, different positions of the tensioner and different sea conditions are considered, respectively, based on the environmental parameters of the OC3 project and the requirements of DNV for the design of the sea state [33]. Three different design load cases are selected for subsequent research and verification. This is to evaluate the influence of the arrangement of the in-line tensioner within the FOWT mooring system under different wave conditions and wind speeds. Wind and waves are assumed to be collinear and incident to the wind turbines. Irregular wave trains are ocean waves whose energy distribution can be defined by the Jonswap spectrum. This spectrum is a common tool used in ocean engineering to analyze and model irregular wave trains, considering factors such as wave height, period, and direction.

Table 5. Design load condition parameters.

Item	Wave Condition	Wind Condition
Dlc1	Hs = 6 m, Tp = 10 s, (γ = 2.2)	steady, uniform, no shear V = 6 m/s
Dlc2	Hs = 6 m, Tp = 10 s, (γ = 2.2)	steady, uniform, no shear V = 8 m/s
Dlc3	Hs = 10.5 m, Tp = 14.3 s, (γ = 3.0)	steady, uniform, no shear V = 8 m/s

summarizes the specific parameter conditions of different sea states in detail.

4. Results and Discussion

4.1. Discussion on the Results of Arrangements on Different Mooring Lines

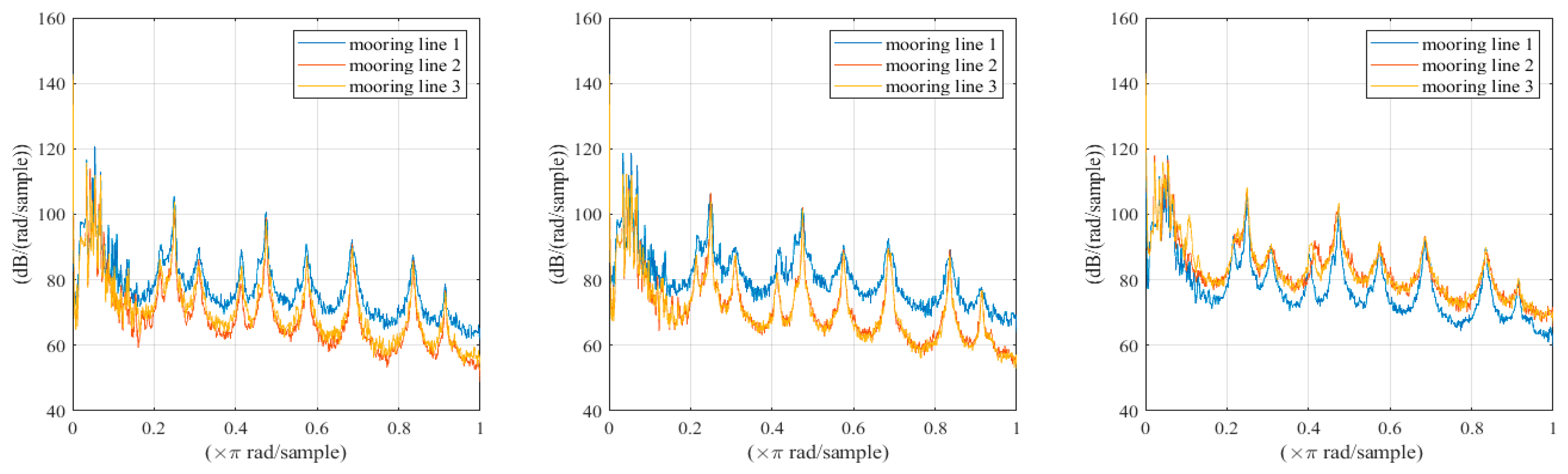
In this study, using the model-building method discussed above, adequate calculations were implemented in the time-domain computer program SIMO-RIFLEX through fully coupled load calculations. We accurately compared the dynamic response of the in-line tensioner when the in-line tensioner was not included and when the tensioner was arranged on three different mooring lines. All mooring lines are divided into three parts: the top chain segment, the in-line tensioner segment, and the pre-laid chain segment. To evaluate the impact when the in-line tensioner is arranged on different mooring lines, a case where the tensioner is arranged 50 m from the fairlead along the mooring line length on different mooring lines is selected for comparison. Based on the time-domain data of the dynamic tension response of the tensioners on the mooring lines, in the case of DCL1, the average tension when arranging the in-line tensioners on mooring lines 1, 2, and 3 is 10% of the minimum break strength of the in-line tensioners. The results shown in Figure 10 indicate that, based on the time-domain data of the dynamic tension response of tensioners on three different mooring lines, the power spectral density reveals a significant change in lines 2 and 3 compared to line 1, characterized by a noticeable difference between the troughs of waves and troughs in the wave frequency range. This suggests that mooring line 1 is more significantly affected by the wave frequency range. Based on the results, it is evident that the dynamic tension response is similar when the in-line tensioner is arranged on mooring line 2 or mooring line 3. However, the dynamic tension of the in-line tensioner arranged on mooring line 1 has unique response characteristics. This is related to the symmetrical arrangement of mooring line 2 and mooring line 3, while mooring line 1 is located on the lee side so it has different response characteristics.

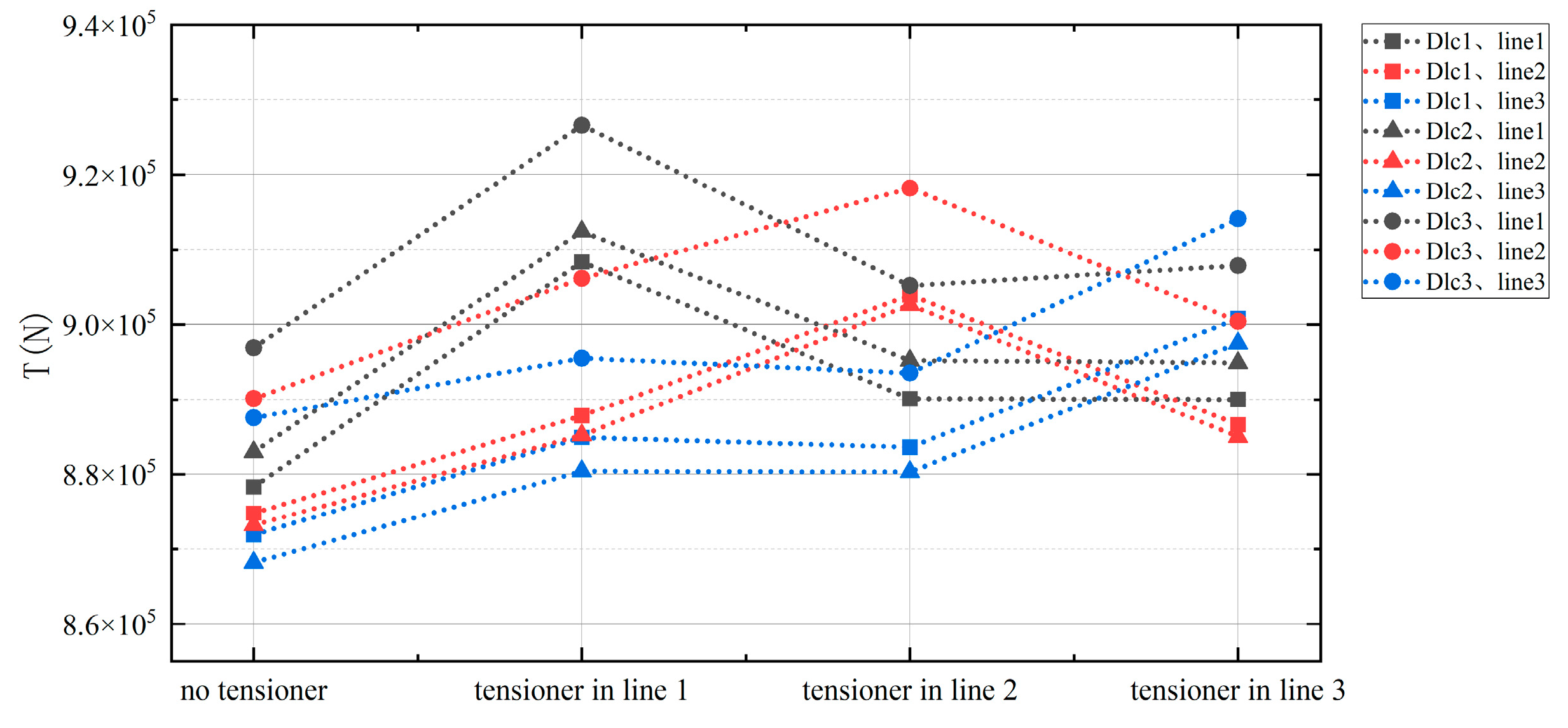
In this case, the mean tension of all mooring lines is compared between different arrangements of the in-line tensioner and the classical catenary mooring without an in-line tensioner. The comparison of this change is shown in

Table 6. Comparison of the average tension change at in-line tensioner.

Item	Average Tension Change (KN)
	dlc1			dlc2			dlc3
	Line 1	Line 2	Line 3	Line 1	Line 2	Line 3	Line 1	Line 2	Line 3
Tensioner in line 1	30.1	11.8	11.7	29.4	12.2	11.9	29.7	8.3	11
Tensioner in line 2	13	29.1	11.8	12	29.4	11.9	16.1	28.1	10.3
Tensioner in line 2	13	11.7	28. 9	12.2	12.1	29.3	8	6	26. 6

and Figure 11. When the in-line tensioner is used on a mooring line under different sea conditions, the average tension in each of the three mooring lines increases. It is worth noting that the line with average mooring tension increased the most with the in-line tensioner, which also changed the maximum average mooring tension line from the previous mooring line on the lee side to the mooring line with the in-line tensioner. Attention should be paid to the transformation of the maximum average tension line to avoid the underestimation of average mooring tension. The amplitude of this increase did not increase with the severity of the sea state and wind speed, but was kept at a relatively close value.

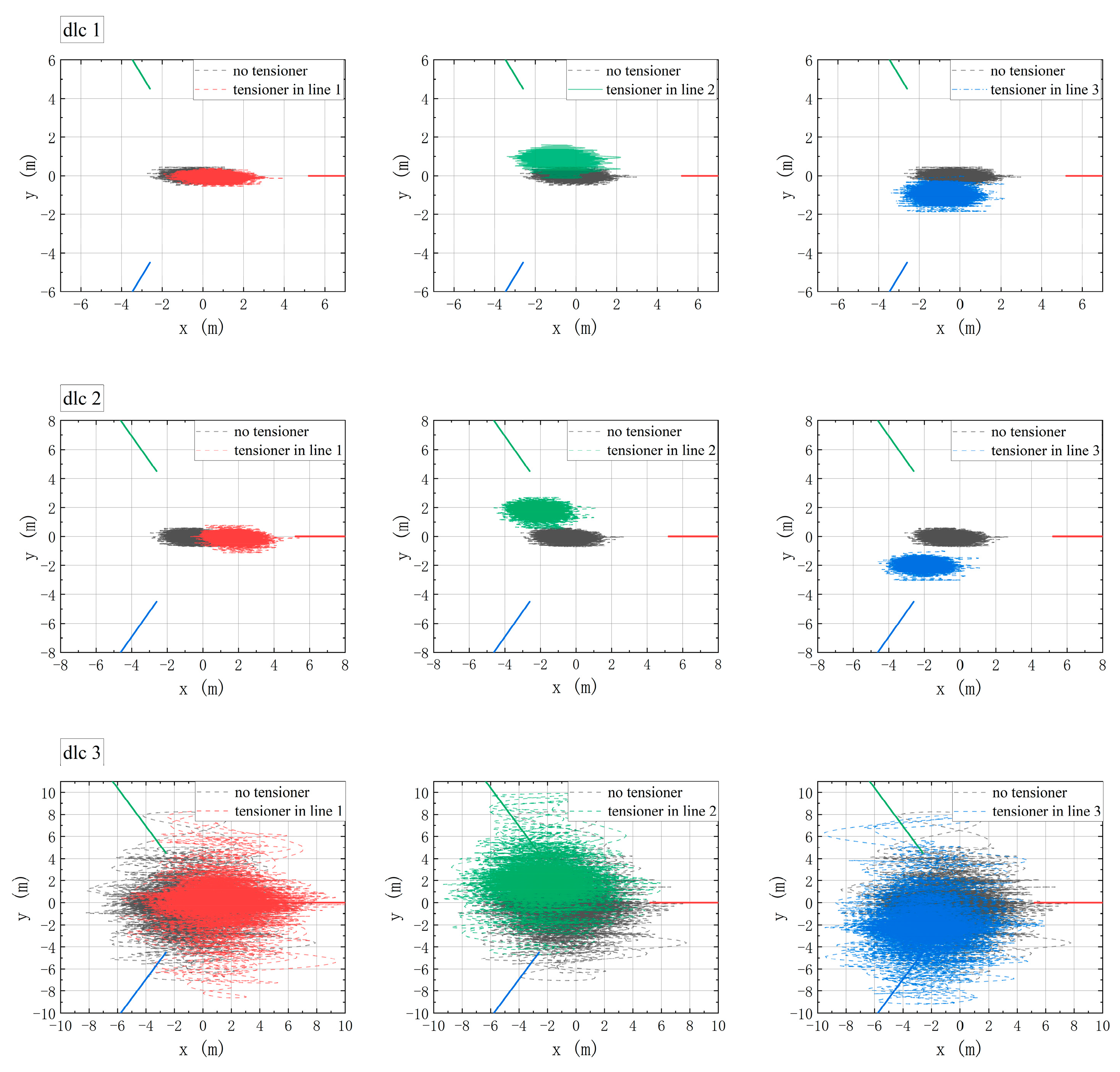
This study also compares the displacement changes of floating offshore wind platforms over time and finds that the in-line tensioner arrangement on different mooring lines will affect the platform movement. It can be seen from Figure 12 that in different sea states, the movement trajectory of the platform on the XOY plane is offset to the side of the in-line tensioner, but it has no obvious influence on the overall movement trajectory. Among them, when the in-line tensioner is arranged on mooring line 1, the motion of the platform does not change in the y direction, but only shifts in the x direction, while when the tensioner is arranged on mooring lines 2 and 3, the platform movement trajectory shifts to the position where the in-line tensioner is arranged, and the deviation degree is higher when the tensioner is arranged on mooring line 1. However, this degree of position deviation is within an acceptable range and will not pose a threat to the operation of the wind turbine.

The influence of the position of the in-line tensioner on the change in heave motion can be seen in Figure 13. When the in-line tensioner is used in the mooring system, no matter which mooring line is arranged, the mean value of displacement change in the heave direction decreases, but the variation amplitude of heave motion does not change. Moreover, the change in the platform motion amplitude is mainly affected by the sea state, and the in-line tensioner only causes deviation, and does not increase the amplitude change. This degree of position deviation is acceptable for wind platforms, which are less sensitive to mooring motion changes than oil platforms. This is also related to the stability of the spar structure. Spar structures always have good stability in deep water.

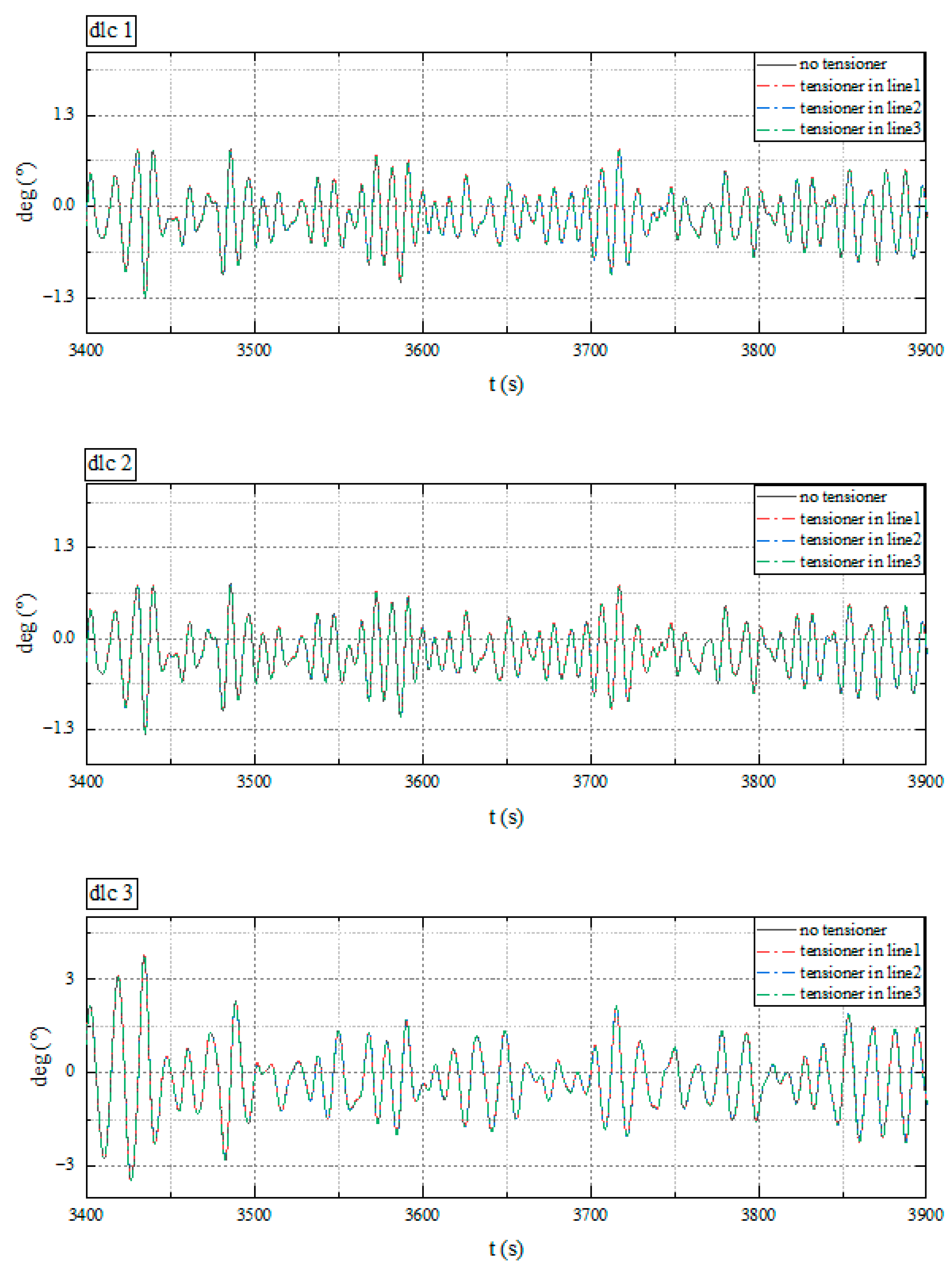
It can be seen in Figure 14 that when the in-line tensioner is arranged on different mooring lines, the X-axis rotation motion of the floating offshore wind platform is influenced. Because mooring line 1 is in the incident wind direction, in the same direction as the X-axis, and has good symmetry, it has the least influence on the rotation of the X-axis. In addition, the influence of the arrangement of the tensioner on the rotational motion of the X-axis does not change the period and frequency of the change and has no obvious effect on the amplitude. Generally, the influence of the change of X-axis rotation motion caused by the use of a tensioner is limited.

It can be seen in Figure 15 that when the in-line tensioner is arranged under different mooring lines, it has no effect on the rotational motion of the Y-axis of the floating offshore wind platform, and the calculated results demonstrate strong consistency across varying sea conditions.

4.2. Discussion on the Results of Different In-Line Position Configurations

To study how various configurations of in-line tensioners on a single mooring cable affect the change in mooring tension, the upwind line with the maximum load is taken as the research object. The in-line tensioner was installed on line 1 at different distances from the fairlead. These distances included 50 m, 100 m, 200 m, 300 m, 400 m, 500 m, and 550 m for the purpose of conducting a comparative study.

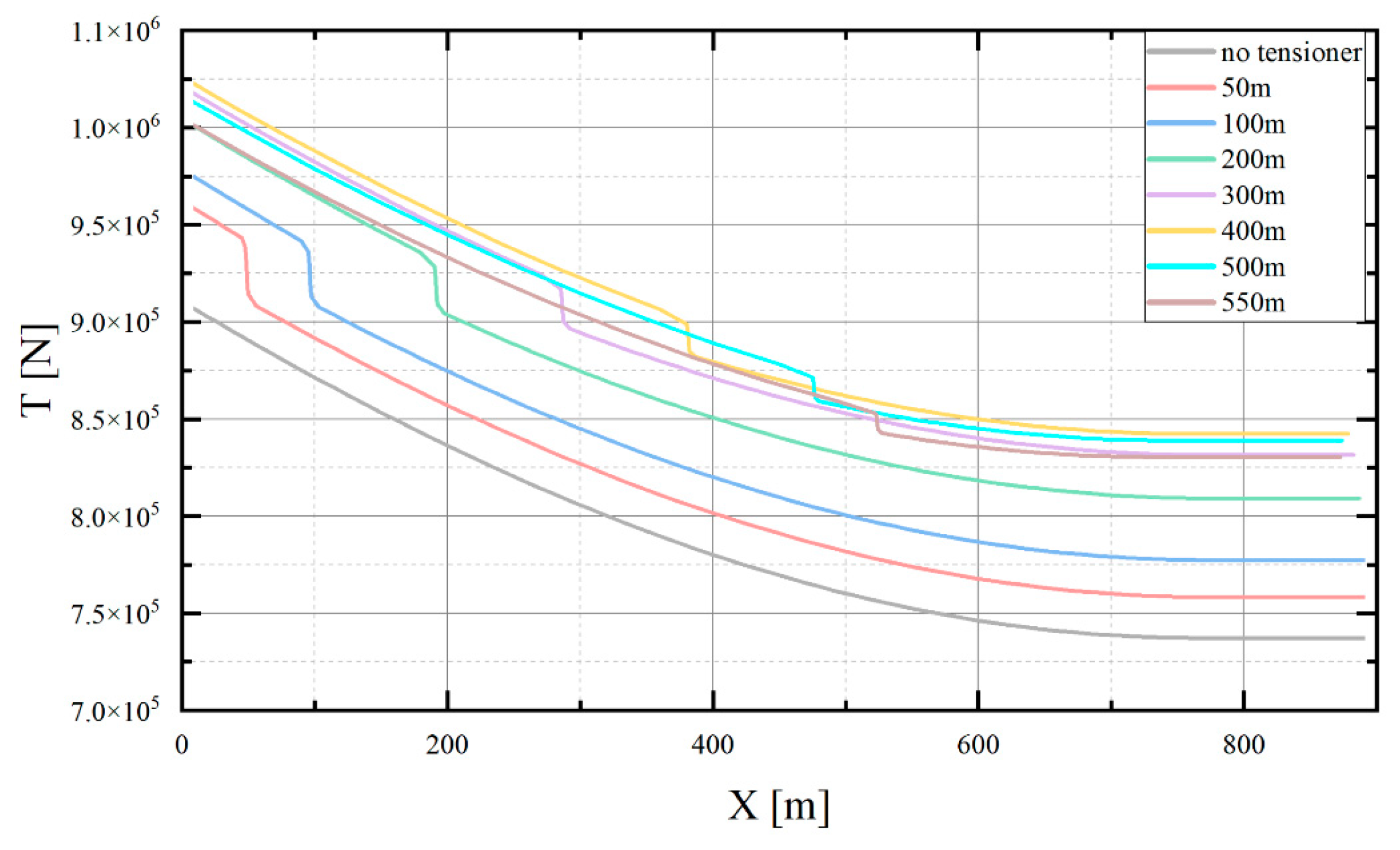
Figure 16 shows the mooring tension results of the static analysis under different arrangement conditions of the tensioner on mooring line 1. There is a significant sudden change in static analysis results at the in-line tensioner, producing a tension change of about 28 kN at 50 m, and this tension change decreases as the in-line tensioner moves away from the fairlead, producing a tension change of about 17 kN at 550 m. This change in tension results in the presence of a high-tension section in the tension distribution of the mooring line, which is in the top chain section between the in-line tensioner and the fairlead, and increases in distance as the tensioner moves away from the fairlead. The maximum and minimum values of the mooring static tension of the mooring line show a parabola trend correlated with the change in the position of the in-line tensioner on the mooring line. This may be because the chain segment of the in-line tensioner has changed the mooring damping, which results in a large amount of energy dissipation in the middle of the mooring line, and the motion characteristics of the mooring line with the in-line tensioner are changed. When the position of the tensioner changes between 0 m and 100 m, the tension changes faster and reaches an extreme value at about 400 m, which increases by about 112 kN compared with the mooring line without the tensioner.

Based on the findings presented in Figure 17, it appears that the in-line tensioner does not have a significant impact on the geometry of the mooring line at various positions. However, there is a noticeable partial change in the shape of the mooring line due to the concentration of mass at the tensioner location.

Figure 18 shows the results of the average value of the time-domain data of the dynamic tension response when the in-line tensioner is arranged at different positions on the mooring line. The average tension value from 2000 s to 8000 s after a wave is fully developed in the time-domain results. It can be seen from the results that as the arrangement of the tensioner is farther away from the fairlead, the mean tension value at the in-line tensioner decreases. From 50 m to 550 m, the tension at the fairlead decreases by about 130 kN, and this degree of change is not affected by different wave and wind conditions. This is consistent with the tension variation law of the mooring line without a tensioner as it is farther away from the fairlead. However, it is worth noting that different arrangement positions of the tensioner within the line cause changes in the average value of the dynamic tension at the fairlead. As shown in Figure 19, as the distance between the in-line tensioner and the fairlead changes; under the conditions of dlc1 and dlc2, the maximum value at 300 m is 17 kN smaller than that at 50 m. Under the conditions of dlc3, the gap is 12 kN. This is a point worthy of attention when arranging the tensioner. The tensioner should not be arranged in the middle of the chain segment but should be close to the position of the fairlead or the touchdown point of the catenary.

It can be seen from Figure 20 that, under different arrangements of the in-line tensioner on the mooring line, the changes in the displacement and rotational movements of the platform in various directions can be observed. Among them, the platform movement position in the X-axis direction is the most obviously affected. This is because the in-line tensioner will cause the platform’s movement to shift to the side where the in-line tensioner is located. When the in-line tensioner is on the middle part of the mooring line, it has a more significant impact on the movement of the platform. As can be seen from Figure 21, the change in the position of the in-line tensioner on the line has minimal impact on the rotational movement of the platform.

4.3. Discussion on Reverse Tension at the In-Line Tensioner

In the DNV specification [34], it is stated that if a mooring connection device must be used, its operation performance must meet the requirements of the long-term stable operation of the mooring system. Reverse tension happens in the process of changing equipment in a short period from a tension state into a compression state. Reverse load will cause extreme tension and sudden change, threatening the safety of the mooring system.

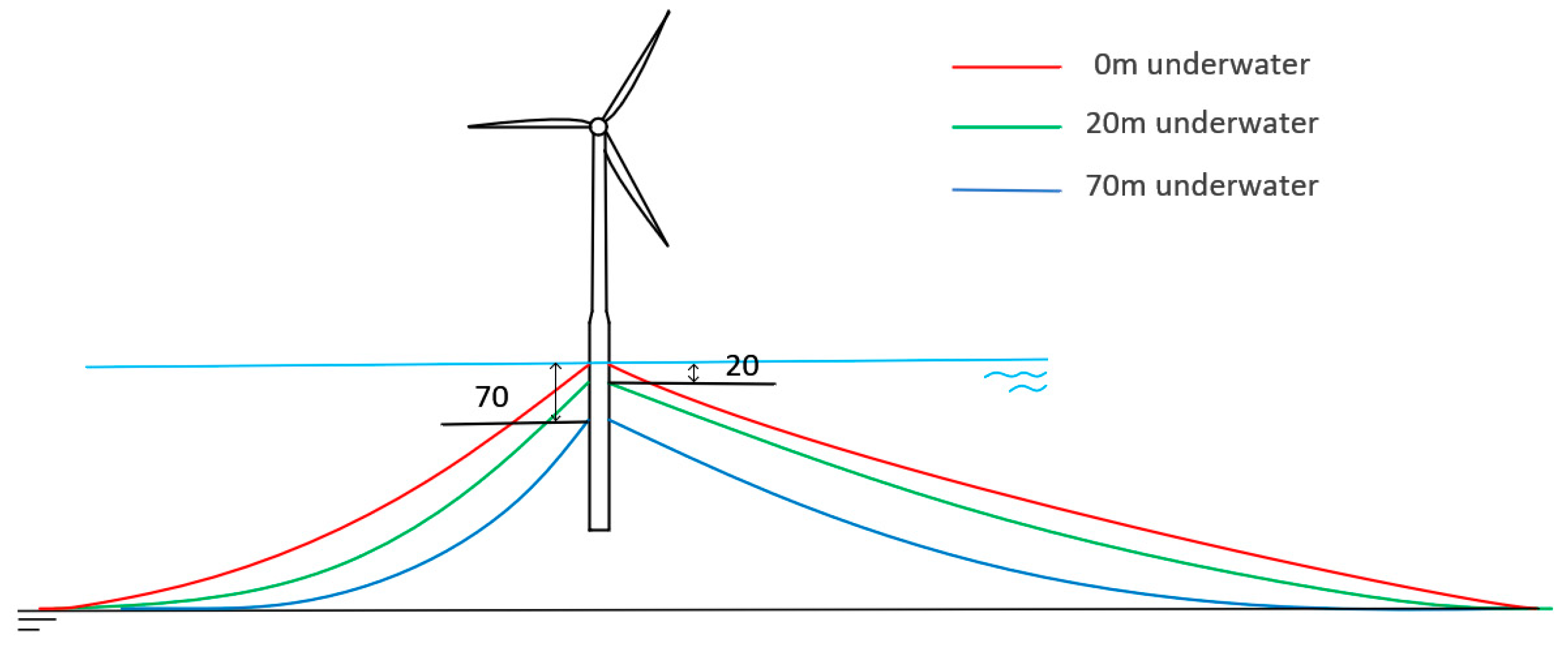
As a piece of special connection operation equipment, the special tension response of the in-line tensioner should be fully studied. The main design intention of the in-line tensioner is a one-way braking device, although there will be additional locking measures after tensioning is in place; it will be completely locked in both directions, but in terms of the design intention, reverse tension presents an abnormal working state. In general, reverse tension occurs more frequently at the fairlead; reverse tension in the fairlead has been confirmed to exist, and most previous studies have focused on this. However, during the research process, we also found that changes in the configuration of the mooring line with the in-line tensioner will affect the occurrence of reverse tension. The movement of the platform is influenced by changes in fairlead position, which in turn affect the tension response of the mooring line. To study the most intense condition of dlc3, three situations were set, respectively, in which the fairlead was located under the water at 0 m, −20 m, and −70 m, and the in-line tensioner was arranged on mooring line 1 in the direction of wave and wind incidence. A setup diagram of the analysis model is shown in Figure 22.

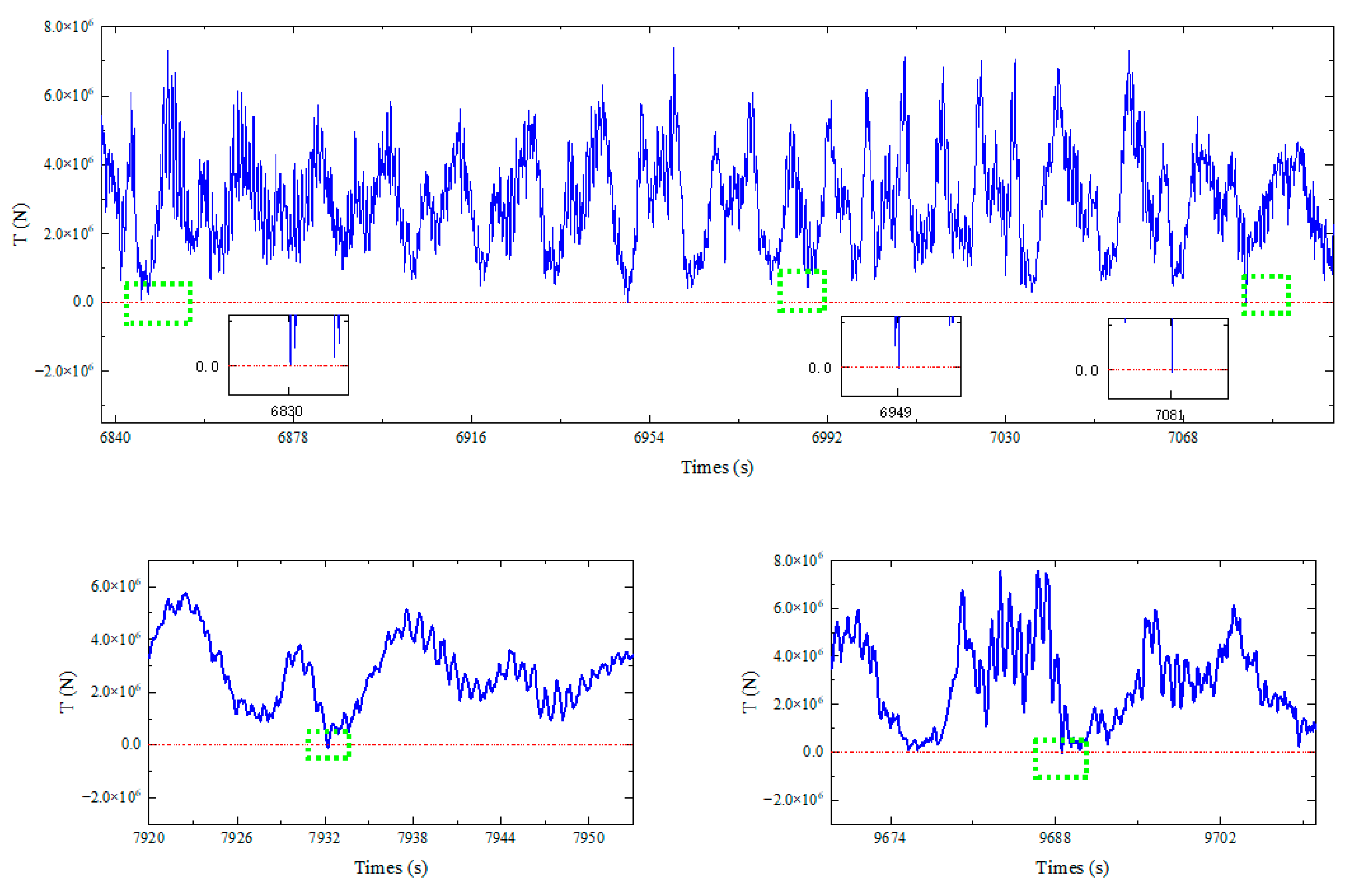
As the fairlead approaches the water surface, the fluctuation amplitude of the mooring tension and the average mooring tension increase significantly. When the fairlead is located 20 m and 0 m underwater, the phenomenon of reverse tension appears in the process of tension response. As shown in Figure 23, when the fairlead is located 0 m underwater, five times the amount of reverse tension appears at the in-line tensioner, respectively, at 6830 s, 6949 s, 7081 s, 7932 s, and 9688 s, and the reverse tension is 17.312 kN, 17.256 kN, 34.858 kN, 86.371 kN, and 53.090 kN. 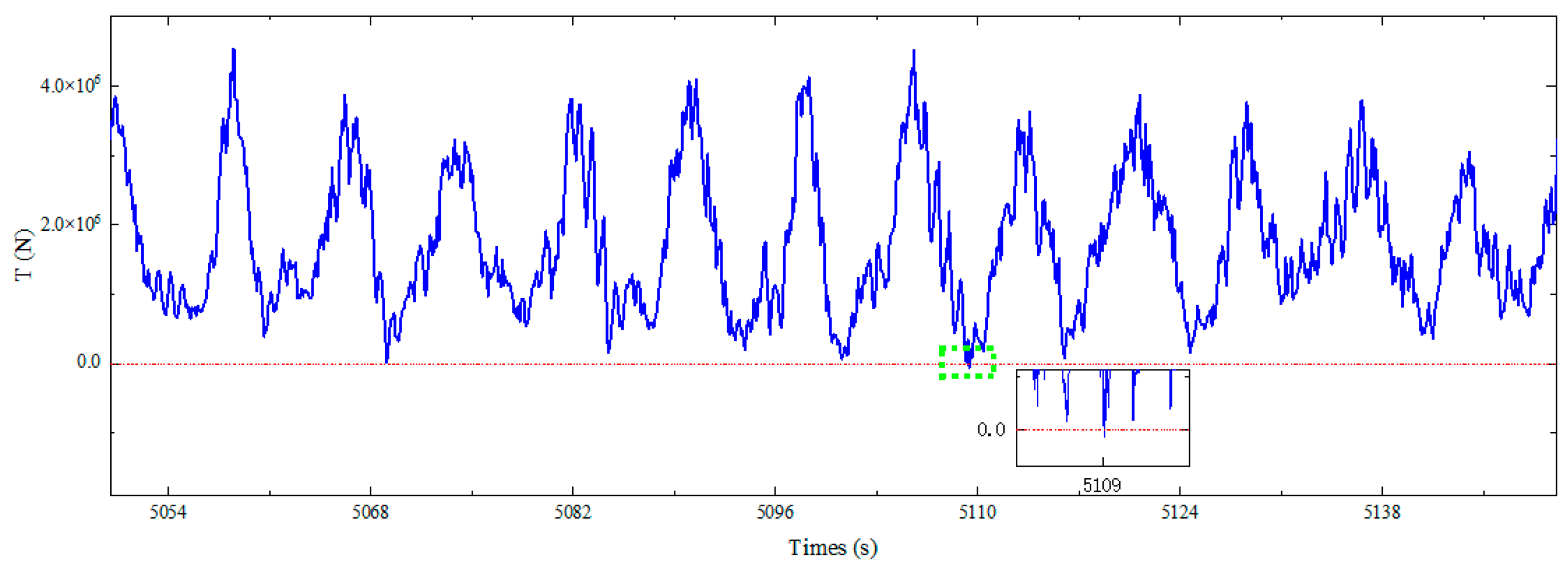As shown in Figure 24, when the fairlead is located 20 m underwater, there is reverse tension at the in-line tensioner, which occurs at 5109 s at a value of 60.379 kN. However, when the fairlead is 70 m underwater, there is no reverse tension at the in-line tensioner. 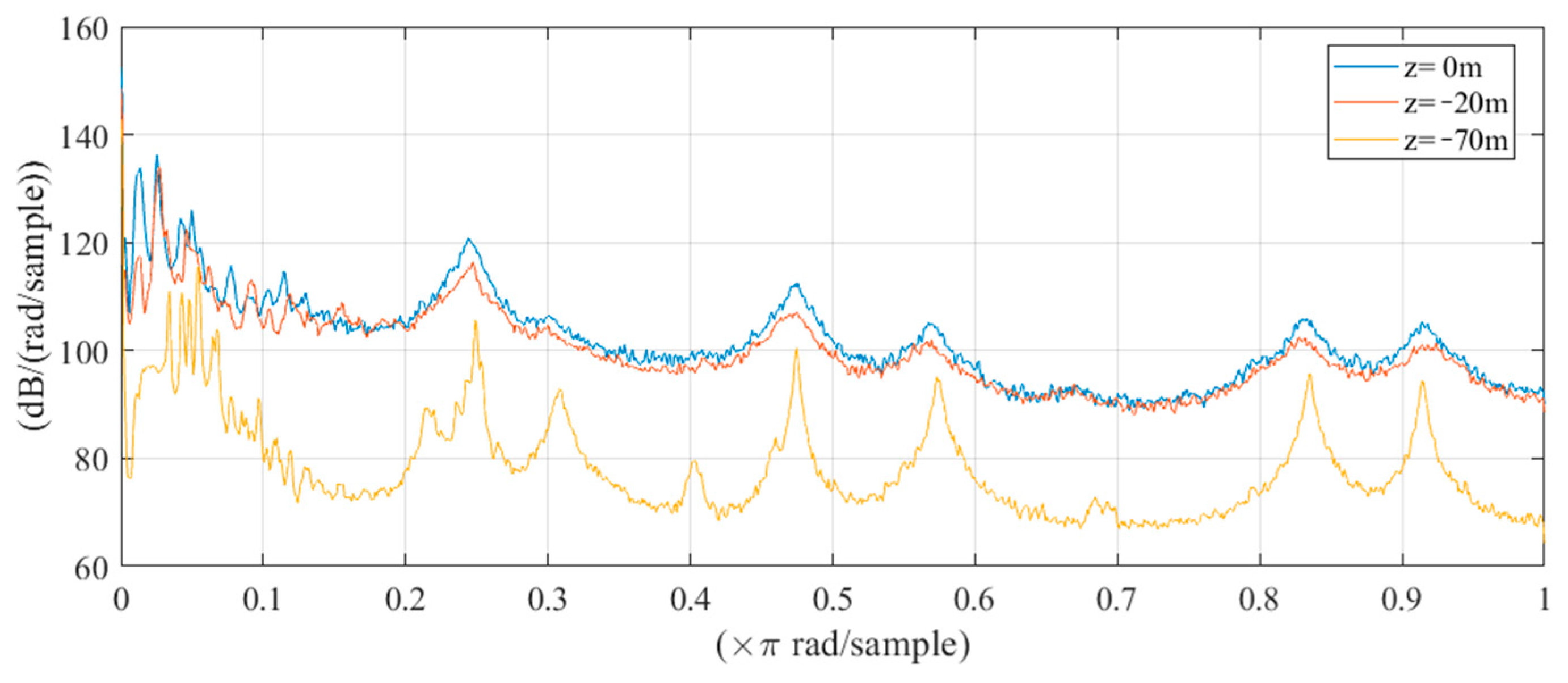Figure 25 shows that when the mooring line is positioned close to the sea surface, configurations with reverse tension exhibit similar responses in the frequency domain, all of which are greater than those cases without reverse tension. The changes in the layout of the mooring line significantly intensify the dynamic responses of the mooring lines across various frequency bands, leading to reverse tension at the tensioner. This situation is detrimental to the operation of the equipment and poses a threat to the safety of the mooring system. As a new type of compression-sensitive component, the in-line tensioner should be designed to avoid reverse tension.

4.4. Suggestions for Mooring Systems with In-Line Tensioners

From the above analysis, it can be found that when the in-line tensioner is adopted in the mooring system, the maximum average mooring tension position changes from the original lee side to the mooring line with the in-line tensioner. This change necessitates close attention to changes in hazardous positions during the design and inspection process. Placing the tensioner on different lines causes deviation in the platform’s displacement trajectory and reduces its heave motion. This deviation can be ignored in single arrangements; however, its impact on grouped arrangements must be considered. To avoid a high-tension section on the mooring line, the location of the tensioner should be arranged close to the fairlead or touchdown point, instead of in the middle section of the mooring line. It is a significant concern that after using the in-line tensioner, the top chain will have a higher tension load. Therefore, a higher specification of the top chain can be considered to meet the safety requirements.

It is important to consider using an in-line tensioner throughout the preliminary scheme phase of FOWT mooring systems. The position of the fairlead and anchor point should also be comprehensively evaluated to minimize the amplitude of tension change and prevent the mooring line from experiencing reverse tension or relaxation to near-zero tension values. Since the existence of reverse tension is confirmed, higher requirements should be put forward not only for the mooring configuration, but also for the in-line tensioner design. A reverse locking device should be required in the design specification to achieve two-way locking, and the structure should be able to withstand a certain range of reverse tension. Considering the presence of higher tension amplitude phenomena, there should also be more detailed specifications for fatigue problems.

According to the research results, in-line tensioning is a new technology worthy of promotion in the FOWT industry. Under conditions considering wave effects, the use of an in-line tensioner for FOWTs will result in changes in response; however, this will not compromise the operational safety of the platform. Given its significant economic advantages, this approach also offers considerable technical benefits. It can be concluded that the utilization of an in-line tensioner can effectively fulfill the requirements of safety and reliability. However, it is crucial to carefully monitor the alterations in dynamic response resulting from changes in layout position.

5. Conclusions

This study focused on in-line tensioner within mooring systems to establish a fully coupled analysis model. It analyzes platform posture alterations and the in-line tensioner tension response under varying sea conditions and at multiple configurations of the mooring system. The potential for reverse tension is also examined, leading to the following conclusions:

• Considering the distinct quality and stiffness properties of the in-line tensioner and chain segment, a comparison is made between the total Lagrangian formulation of bar elements and the co-rotational ghost reference description method of beam elements. This study introduces a fully coupled computational approach to effectively characterize the behavior of mooring lines using in-line tensioners for FOWTs.
• The placement of the in-line tensioner will make the mooring maximum average force change from the original lee side mooring line to the mooring line with the in-line tensioner and make the displacement trajectory of the platform deviate to the position of the in-line tensioner on the XOY plane and influence platform motion. The impact of the heave and rotation movements of the platform is small, and tension change is minimally affected by sea conditions.
• When the arrangement position of the in-line tensioner is far away from the fairlead on the mooring line, the change in the dynamic tension at the fairlead shows a parabolic trend with the change in position. The tension at the in-line tensioner decreases with the arrangement position, but there will be a high-tension section. To avoid this, the in-line tensioner should be arranged close to the fairlead or touchdown point, instead of in the middle section of the mooring line. A higher specification of the top chain can be considered to meet safety requirements.
• When the fairlead is positioned near the sea surface, the in-line tensioner experiences a phenomenon known as reverse tension. The frequency of this reverse tension increases as the span between the fairlead and the sea level decreases. This necessitates careful consideration of the fairlead location during the platform design phase. The minimum tension requirement for the in-line tensioner should be specified in the design specification, and a locking device capable of withstanding a specific level of tension is necessary for the in-line tensioner design.

This study is confined to the dynamic response assessment of mooring systems of a SPAR structure using in-line tensioners. The response of various floating wind turbine platforms is not extensively covered. Future research will explore the application of in-line tensioners across different platform structures and under varying wave angle disturbances to assess the viability of this emerging in-line tension technology. And, substantial research focused on optimizing FOWT systems is underway [35,36]. It is anticipated that integrating in-line tensioning technology into the objective cost function during the early design stages, while also considering mooring response constraints, could enhance the feasibility of scaling up FOWTs.