Research on the Give-Way Ships Determination Based on Field Theory
Abstract
1. Introduction
1.1. Related Works
- (1)
- Algorithms Based on Mathematical Models
- (2)
- Artificial Intelligence Algorithms
1.2. Reflection
2. Theoretical Foundations
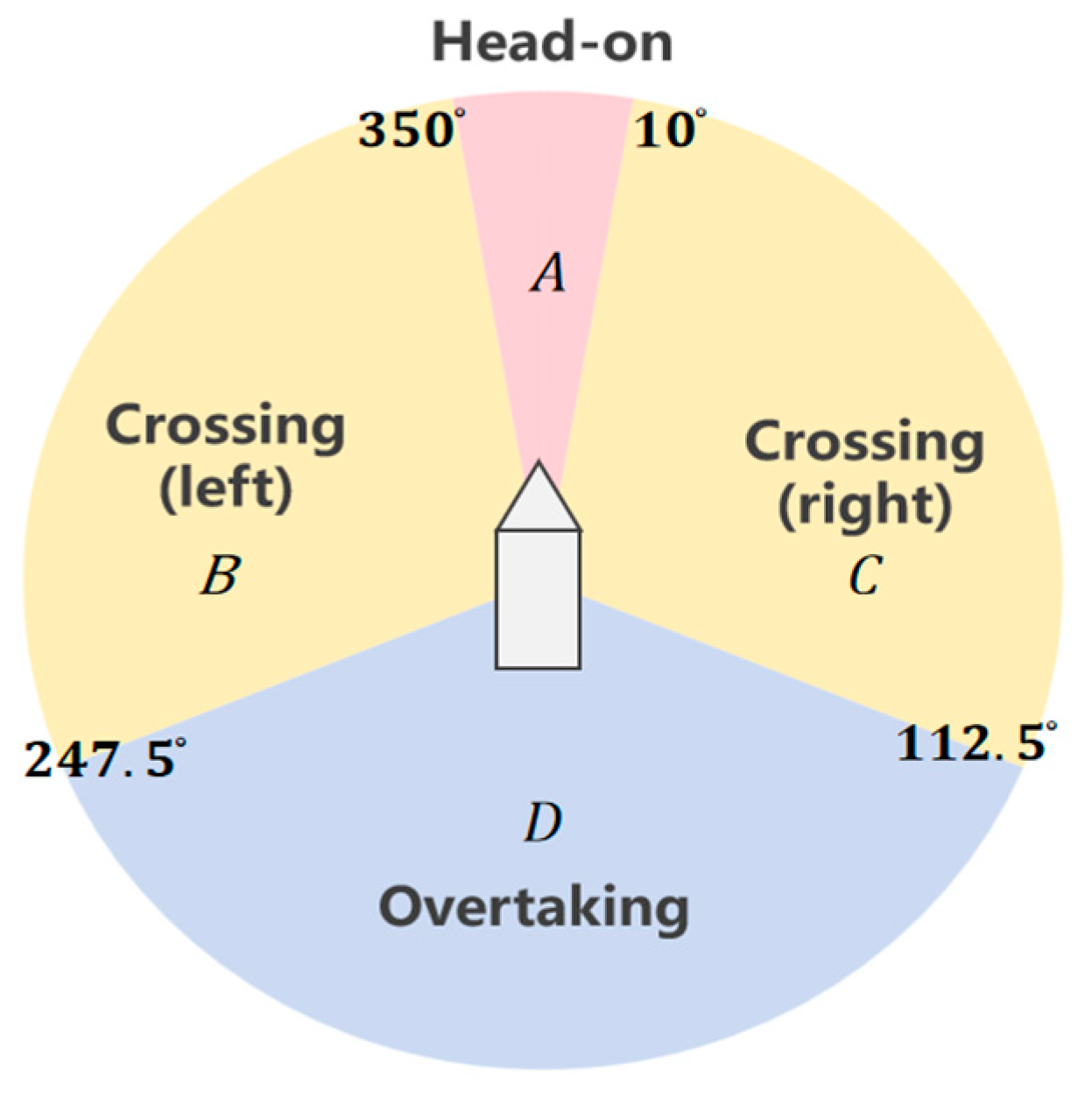
2.1. Encounter Situation Classification
2.2. Field Theory
- (a)
- Acceleration exists when the ship is sailing, so the ship will be subject to a wider range of ship collision risk along the direction of speed than in the opposite direction, which is equivalent to the risk of collision extending to the bow orientation.
- (b)
- In the view of the give-way ship, the direct ship’s bearing towards itself is more dangerous compared to the bearing away itself, which is equivalent to the risk of collision extended to the give-way ship’s bearing.
2.3. Relative Motion Parameters
3. Modeling Methodology
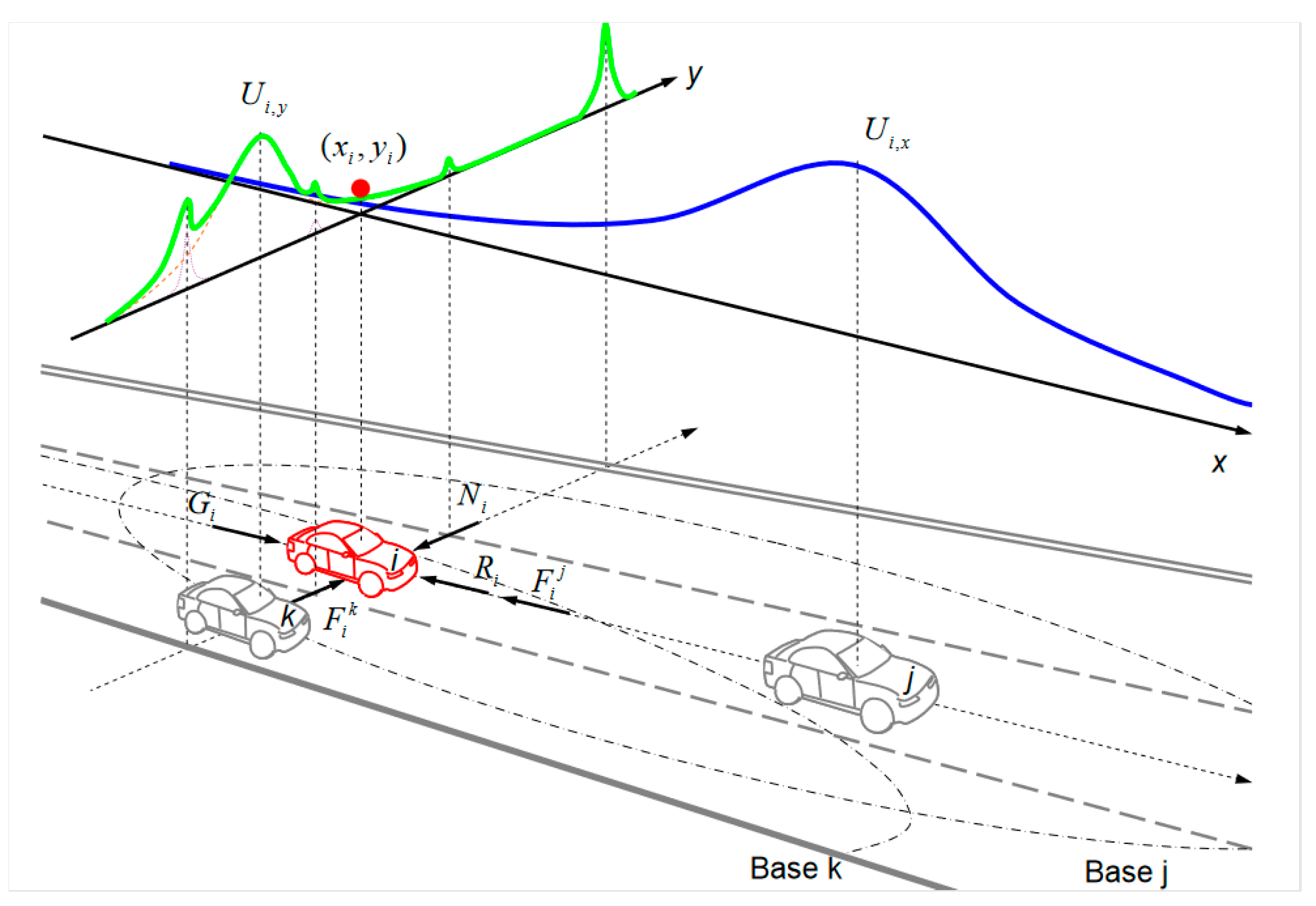
3.1. Collision Risk Field
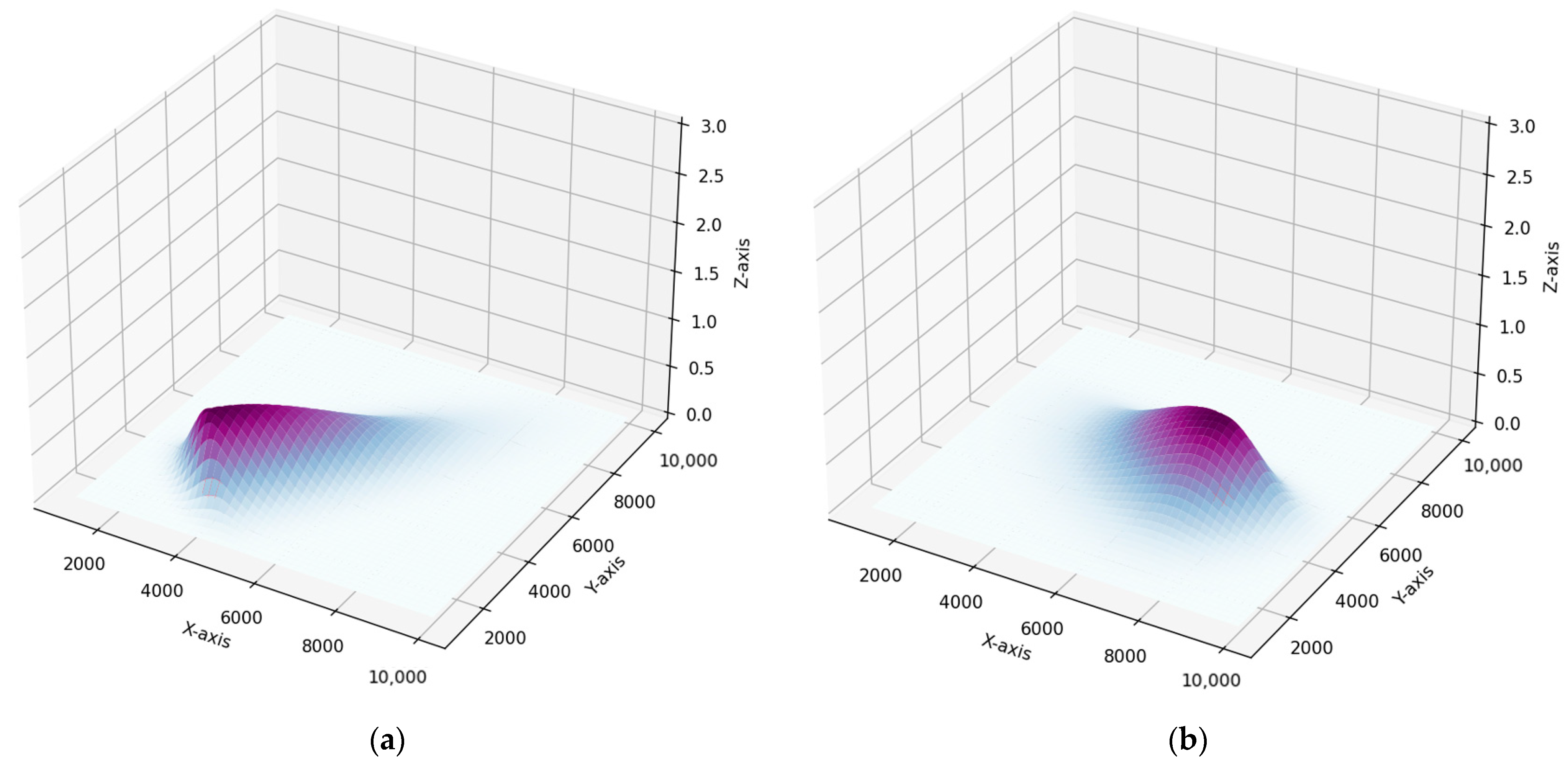
3.1.1. Asymmetric Gaussian Functions
3.1.2. Impact Factors
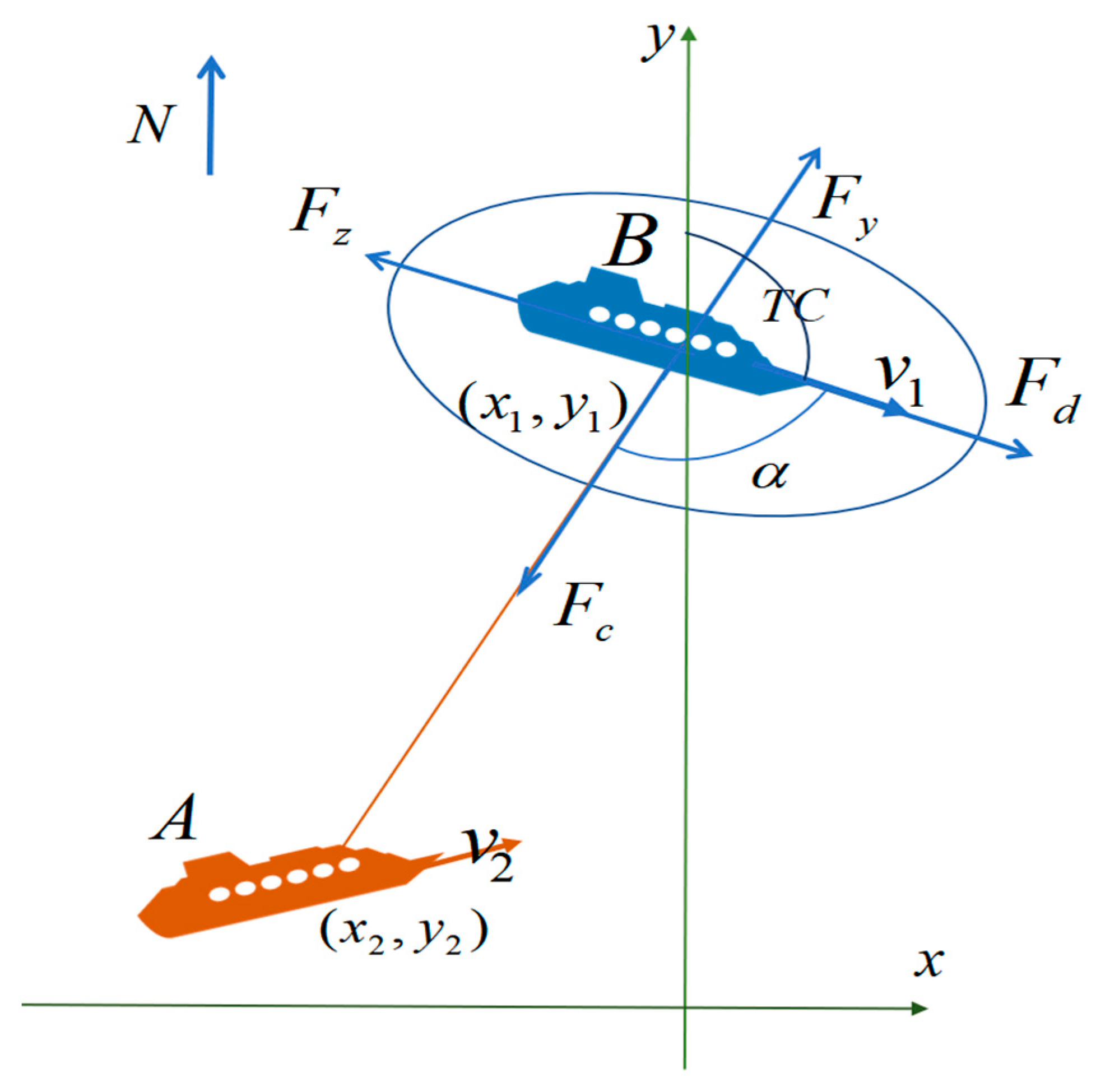
- The four psychological forces (, , , ) are decomposed according to the relative azimuthal into a coordinate system built with the course of the stand-on ship as the coordinate axis:
- According to the decomposed psychological forces to get the impact factor corresponding to the axis, the larger the impact factor, the wider the range of collision risk.
- The minimum encounter distance between the two ships in the AIS data is calculated according to Equation (10), which is combined with the parameters in the least square method calibration as , .
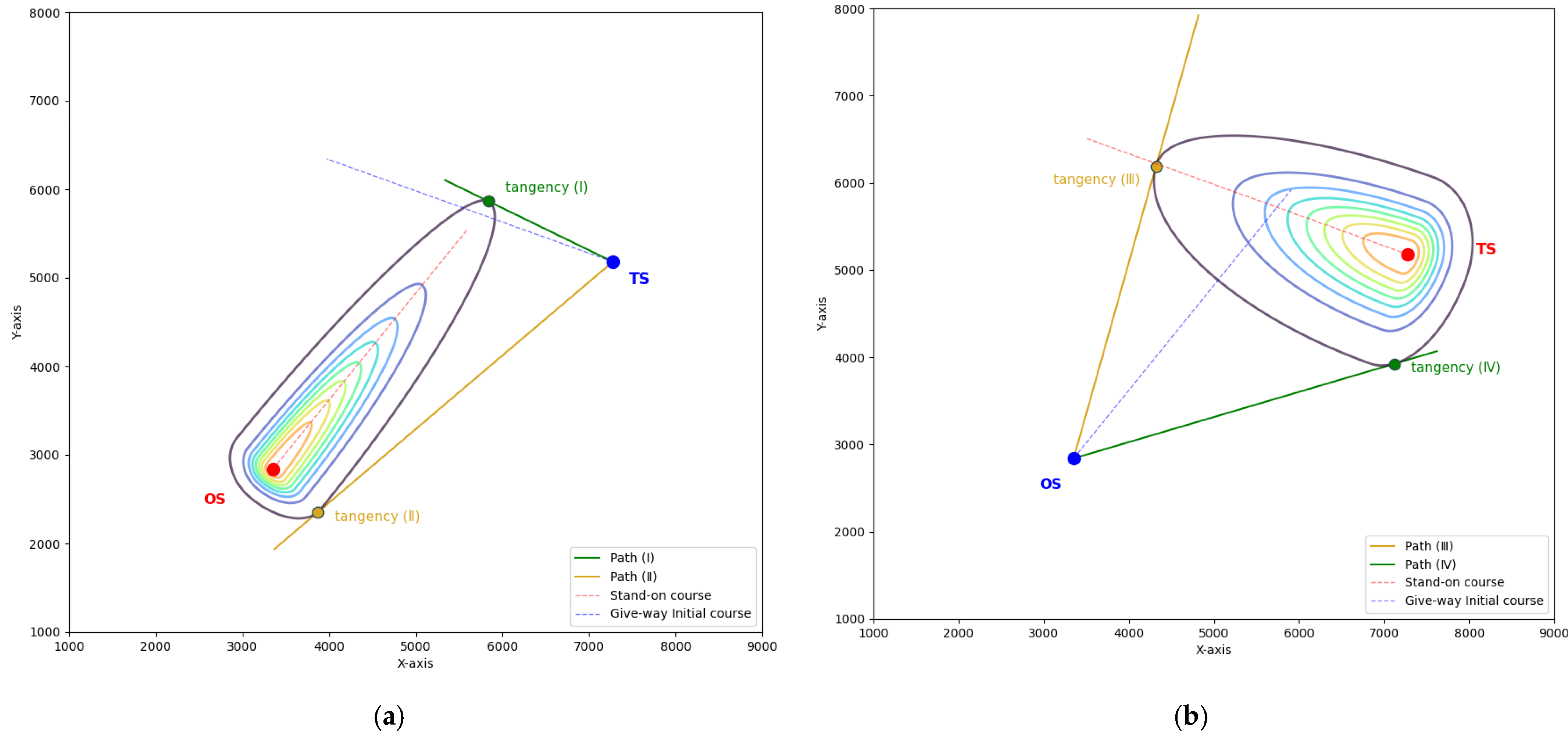
3.2. Cost Function
4. Experimental Analysis
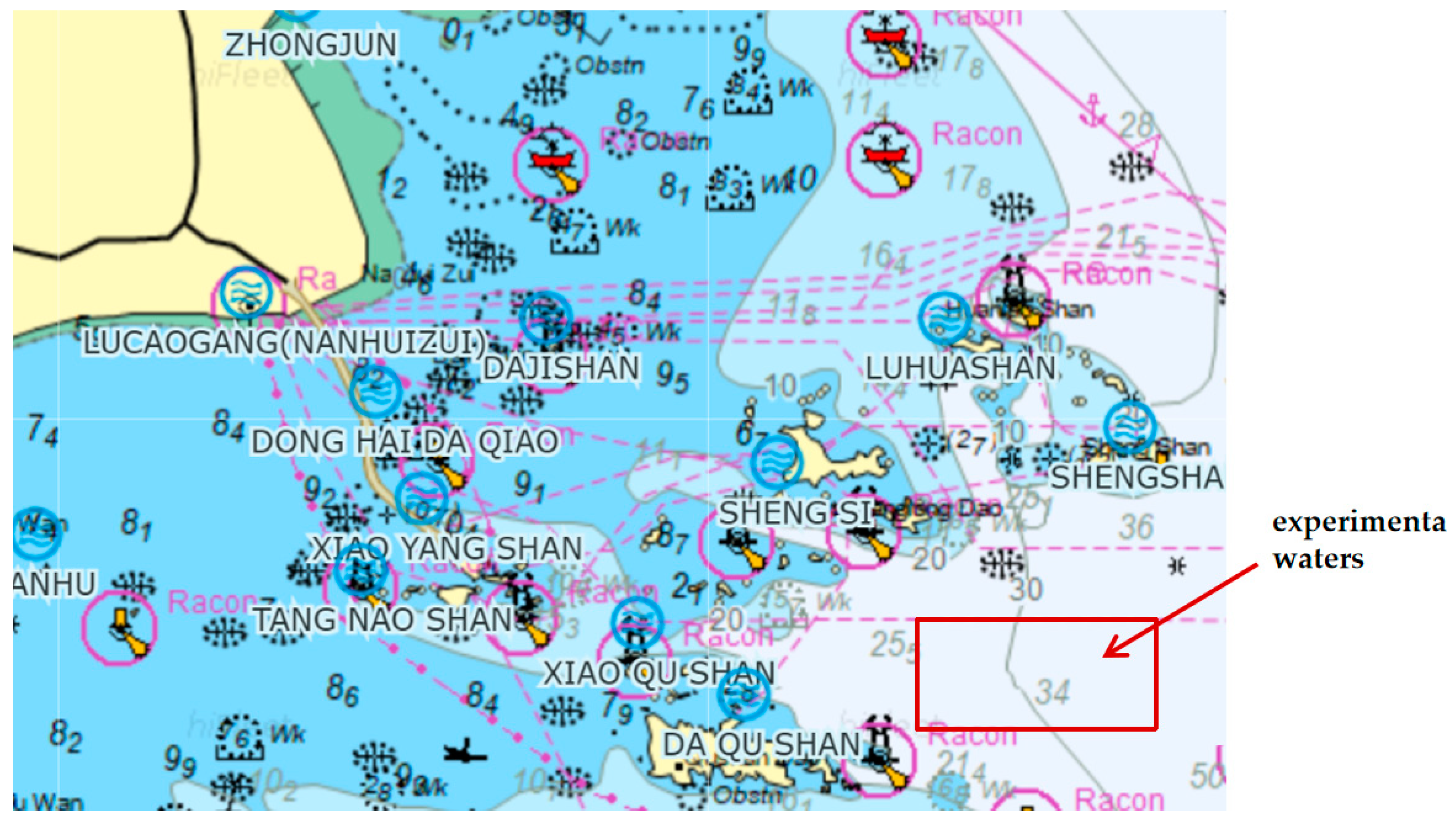
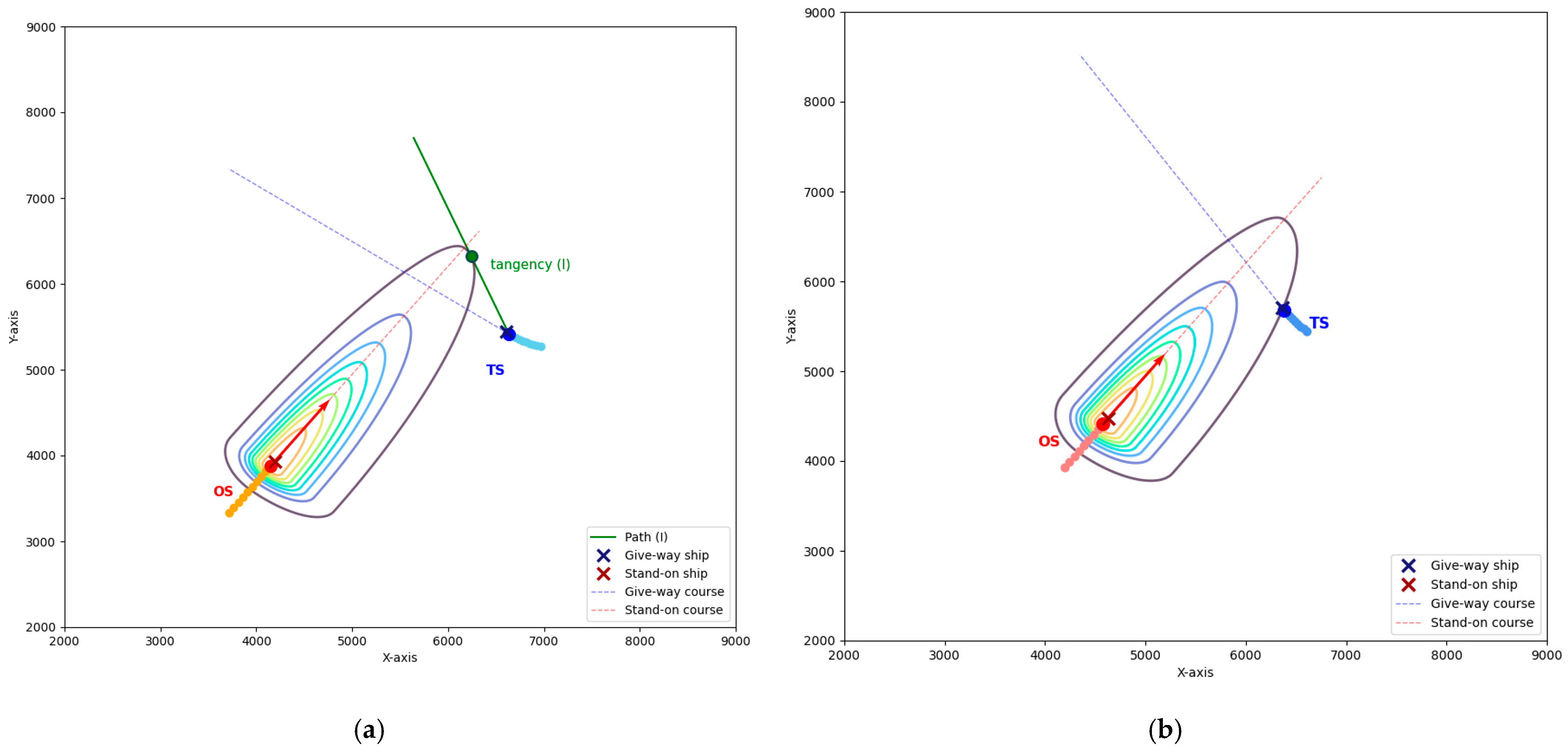
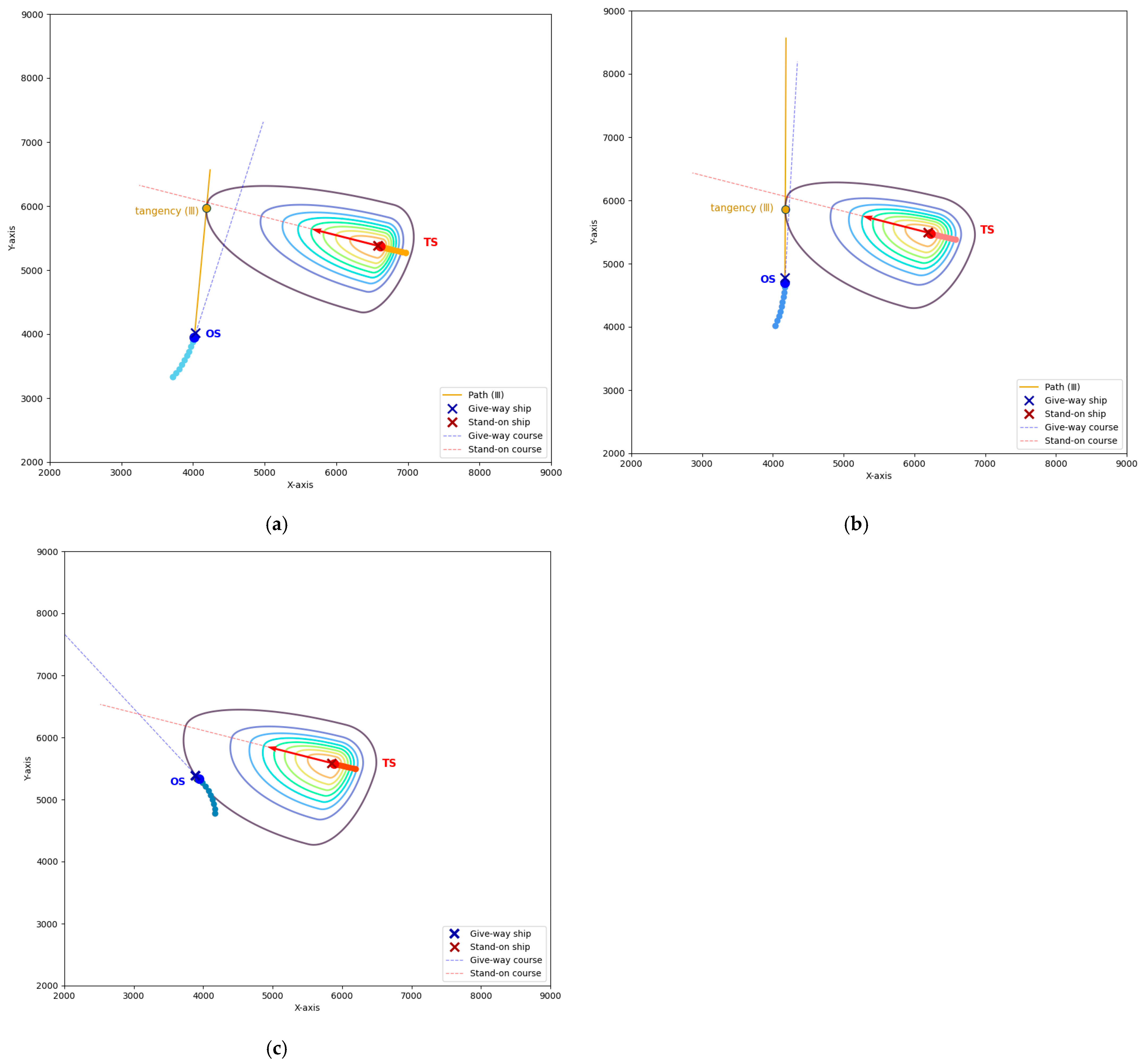
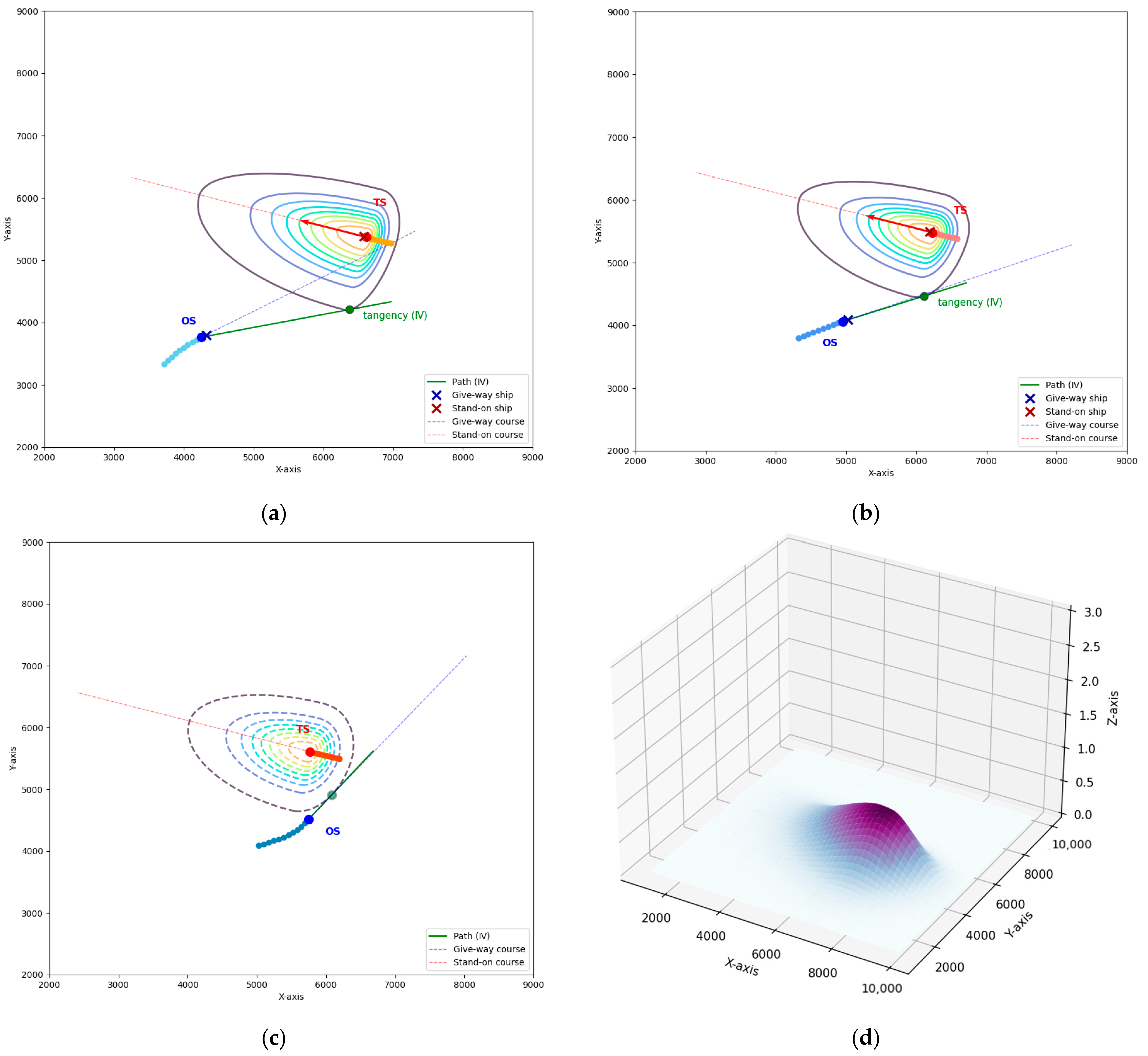
4.1. Experiment Presentation
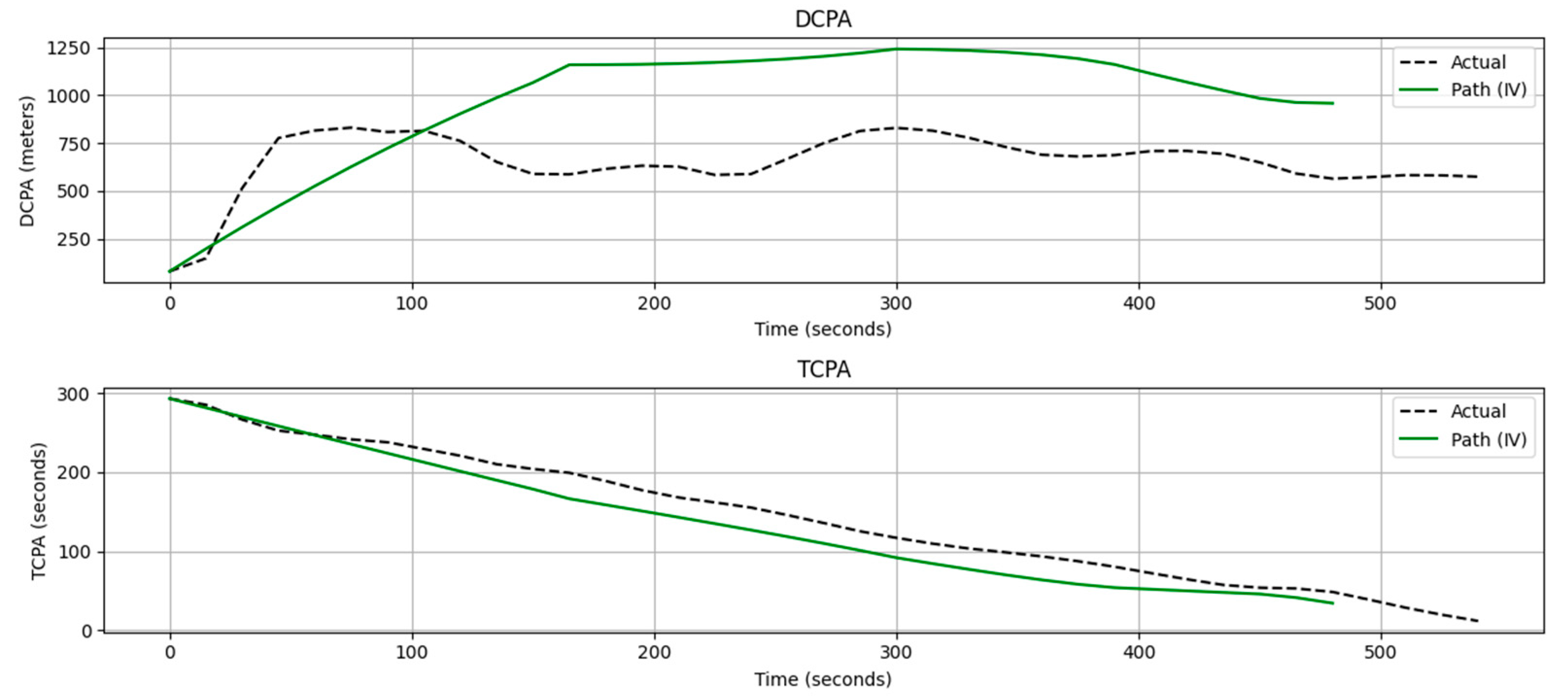
4.2. Results and Discussion
4.2.1. Results and Evaluation
4.2.2. Limitations of the Research
5. Conclusions
- Introducing the concept of field theory, this research realizes real-time dynamic changes according to the distance and state of the two ships, and taking into account the length, width and other factors, constructing a dynamic collision hazard field based on the speed direction, and integrating the danger of the spatial orientation of the give-way ship. In addition, calibrating the boundary of the collision hazard field according to the actual data is more in line with the actual navigational environment and meets people’s psychological feelings.
- Considering the comfort of path traveling and the keeping ability of global sailing, the cost function is used to quantitatively determine the give-way ship, the ship with the lowest cost is identified as the give-way ship, which is easy to understand and apply to practice.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- European Maritime Safety Agency. Annual Overview of Marine Casualties and Incidents 2023; European Maritime Safety Agency: Lisbon, Portugal, 2023. [Google Scholar]
- Ahmed, Y.A.; Hannan, M.A.; Oraby, M.Y.; Maimun, A. European Maritime Safety Agency. Mar. Sci. Eng. 2021, 9, 790. [Google Scholar] [CrossRef]
- Li, X.; Yuen, K.F. A Human-Centred Review on Maritime Autonomous Surfaces Ships: Impacts, Responses, and Future Directions. Transp. Rev. 2024, 44, 791–810. [Google Scholar] [CrossRef]
- Namgung, H. Local Route Planning for Collision Avoidance of Maritime Autonomous Surface Ships in Compliance with COLREGs Rules. Sustainability 2021, 14, 198. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, L.; Negenborn, R.R.; van Gelder, P.H.A.J.M. A Ship Collision Avoidance System for Human-Machine Cooperation during Collision Avoidance. Ocean. Eng. 2020, 217, 107913. [Google Scholar] [CrossRef]
- Ventikos, N.P.; Chmurski, A.; Louzis, K. A Systems-Based Application for Autonomous Vessels Safety: Hazard Identification as a Function of Increasing Autonomy Levels. Saf. Sci. 2020, 131, 104919. [Google Scholar] [CrossRef]
- Hagen, I.B.; Knutsen, K.S.; Johansen, T.A.; Brekke, E. Exploration of COLREG-Relevant Parameters from Historical AIS-Data. J. Navig. 2024, 1–19. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Song, F.; Mao, W. A Collaborative Collision Avoidance Strategy for Autonomous Ships under Mixed Scenarios. J. Navig. 2023, 76, 200–224. [Google Scholar] [CrossRef]
- Ohn, S.-W.; Namgung, H. Requirements for Optimal Local Route Planning of Autonomous Ships. J. Mar. Sci. Eng. 2022, 11, 17. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.; Jiang, L.; An, L.; Yang, R. Collision-Avoidance Navigation Systems for Maritime Autonomous Surface Ships: A State of the Art Survey. Ocean. Eng. 2021, 235, 109380. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, D.; Yan, X.; Haugen, S.; Guedes Soares, C. A Distributed Anti-Collision Decision Support Formulation in Multi-Ship Encounter Situations under COLREGs. Ocean. Eng. 2015, 105, 336–348. [Google Scholar] [CrossRef]
- Vagale, A.; Bye, R.T.; Oucheikh, R.; Osen, O.L.; Fossen, T.I. Path Planning and Collision Avoidance for Autonomous Surface Vehicles II: A Comparative Study of Algorithms. J. Mar. Sci. Technol. 2021, 26, 1307–1323. [Google Scholar] [CrossRef]
- Öztürk, Ü.; Akdağ, M.; Ayabakan, T. A Review of Path Planning Algorithms in Maritime Autonomous Surface Ships: Navigation Safety Perspective. Ocean. Eng. 2022, 251, 111010. [Google Scholar] [CrossRef]
- Statheros, T.; Howells, G.; Maier, K.M. Autonomous Ship Collision Avoidance Navigation Concepts, Technologies and Techniques. J. Navig. 2008, 61, 129–142. [Google Scholar] [CrossRef]
- Xue, Y.; Clelland, D.; Lee, B.S.; Han, D. Automatic Simulation of Ship Navigation. Ocean. Eng. 2011, 38, 2290–2305. [Google Scholar] [CrossRef]
- Lyu, H.; Hao, Z.; Li, J.; Li, G.; Sun, X.; Zhang, G.; Yin, Y.; Zhao, Y.; Zhang, L. Ship Autonomous Collision-Avoidance Strategies—A Comprehensive Review. J. Mar. Sci. Eng. 2023, 11, 830. [Google Scholar] [CrossRef]
- IMAZU, H.; KOYAMA, T. The Determination of Collision Avoidance Action. J. Jpn. Inst. Navig. 1984, 70, 31–37. [Google Scholar] [CrossRef][Green Version]
- Kang, L.; Lu, Z.; Meng, Q.; Gao, S.; Wang, F. Maritime Simulator Based Determination of Minimum DCPA and TCPA in Head-on Ship-to-Ship Collision Avoidance in Confined Waters. Transp. A: Transp. Sci. 2019, 15, 1124–1144. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Cai, Y. The Ship Maneuverability Based Collision Avoidance Dynamic Support System in Close-Quarters Situation. Ocean. Eng. 2017, 146, 486–497. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, N. A Survey on Ship Collision Risk Evaluation. Promet Traffic Transp. 2014, 26, 475–486. [Google Scholar] [CrossRef]
- Zhu, Z.; Lyu, H.; Zhang, J.; Yin, Y. An Efficient Ship Automatic Collision Avoidance Method Based on Modified Artificial Potential Field. J. Mar. Sci. Eng. 2021, 10, 3. [Google Scholar] [CrossRef]
- Mohanan, M.G.; Salgoankar, A. A Survey of Robotic Motion Planning in Dynamic Environments. Rob. Auton. Syst. 2018, 100, 171–185. [Google Scholar] [CrossRef]
- Abdelaal, M.; Fränzle, M.; Hahn, A. Nonlinear Model Predictive Control for Trajectory Tracking and Collision Avoidance of Underactuated Vessels with Disturbances. Ocean. Eng. 2018, 160, 168–180. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Zhao, R.; Liang, X.; Wei, Q. Collision Avoidance Strategies for Unmanned Surface Vehicles Based on Probabilistic Game Theory Framework. In Proceedings of the OCEANS 2022—Chennai, Chennai, India, 21–24 February 2022; IEEE: New York, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Cho, Y.; Han, J.; Kim, J. Efficient COLREG-Compliant Collision Avoidance in Multi-Ship Encounter Situations. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1899–1911. [Google Scholar] [CrossRef]
- Zheng, M.; Zhang, K.; Han, B.; Lin, B.; Zhou, H.; Ding, S.; Zou, T.; Yang, Y. An Improved VO Method for Collision Avoidance of Ships in Open Sea. J. Mar. Sci. Eng. 2024, 12, 402. [Google Scholar] [CrossRef]
- Zhang, K.; Huang, L.; He, Y.; Zhang, L.; Huang, W.; Xie, C.; Hao, G. Collision Avoidance Method for Autonomous Ships Based on Modified Velocity Obstacle and Collision Risk Index. J. Adv. Transp. 2022, 2022, 1534815. [Google Scholar] [CrossRef]
- Tsou, M.-C.; Hsueh, C.-K. The Study of Ship Collision Avoidance Route Planning by Ant Colony Algorithm. J. Mar. Sci. Technol. 2010, 18, 16. [Google Scholar] [CrossRef]
- Tsou, M.-C.; Kao, S.-L.; Su, C.-M. Decision Support from Genetic Algorithms for Ship Collision Avoidance Route Planning and Alerts. J. Navig. 2010, 63, 167–182. [Google Scholar] [CrossRef]
- Xu, Q. Collision Avoidance Strategy Optimization Based on Danger Immune Algorithm. Comput. Ind. Eng. 2014, 76, 268–279. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, C.; Wang, N. Multiobjective Optimization Based Vessel Collision Avoidance Strategy Optimization. Math. Probl. Eng. 2014, 2014, 914689. [Google Scholar] [CrossRef]
- Liang, Z.; Li, F.; Zhou, S. An Improved NSGA-II Algorithm for MASS Autonomous Collision Avoidance under COLREGs. J. Mar. Sci. Eng. 2024, 12, 1224. [Google Scholar] [CrossRef]
- Zhao, L.; Bai, Y.; Paik, J.K. Achieving Optimal-Dynamic Path Planning for Unmanned Surface Vehicles: A Rational Multi-Objective Approach and a Sensory-Vector Re-Planner. Ocean. Eng. 2023, 286, 115433. [Google Scholar] [CrossRef]
- Lee, S.-M.; Kwon, K.-Y.; Joh, J. A Fuzzy Logic for Autonomous Navigation of Marine Vehicles Satisfying COLREG Guidelines. Int. J. Control Autom. Syst. 2004, 2, 171–181. [Google Scholar]
- Chen, Y.F.; Liu, M.; Everett, M.; How, J.P. Decentralized Non-Communicating Multiagent Collision Avoidance with Deep Reinforcement Learning. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; IEEE: New York, NY, USA, 2017; pp. 285–292. [Google Scholar]
- Namgung, H.; Kim, J.-S. Collision Risk Inference System for Maritime Autonomous Surface Ships Using COLREGs Rules Compliant Collision Avoidance. IEEE Access 2021, 9, 7823–7835. [Google Scholar] [CrossRef]
- Wróbel, K.; Gil, M.; Huang, Y.; Wawruch, R. The Vagueness of COLREG versus Collision Avoidance Techniques—A Discussion on the Current State and Future Challenges Concerning the Operation of Autonomous Ships. Sustainability 2022, 14, 16516. [Google Scholar] [CrossRef]
- Stępień, B. Towards a New Horizon: 1972 COLREG in the Era of Autonomous Ships. Ocean. Dev. Int. Law. 2024, 55, 170–184. [Google Scholar] [CrossRef]
- Akdağ, M.; Solnør, P.; Johansen, T.A. Collaborative Collision Avoidance for Maritime Autonomous Surface Ships: A Review. Ocean. Eng. 2022, 250, 110920. [Google Scholar] [CrossRef]
- García Maza, J.A.; Argüelles, R.P. COLREGs and Their Application in Collision Avoidance Algorithms: A Critical Analysis. Ocean. Eng. 2022, 261, 112029. [Google Scholar] [CrossRef]
- Chang, C.-H.; Wijeratne, I.B.; Kontovas, C.; Yang, Z. COLREG and MASS: Analytical Review to Identify Research Trends and Gaps in the Development of Autonomous Collision Avoidance. Ocean. Eng. 2024, 302, 117652. [Google Scholar] [CrossRef]
- Zhou, X.-Y.; Huang, J.-J.; Wang, F.-W.; Wu, Z.-L.; Liu, Z.-J. A Study of the Application Barriers to the Use of Autonomous Ships Posed by the Good Seamanship Requirement of COLREGs. J. Navig. 2020, 73, 710–725. [Google Scholar] [CrossRef]
- Kuwata, Y.; Wolf, M.T.; Zarzhitsky, D.; Huntsberger, T.L. Safe Maritime Autonomous Navigation With COLREGS, Using Velocity Obstacles. IEEE J. Ocean. Eng. 2014, 39, 110–119. [Google Scholar] [CrossRef]
- Namgung, H.; Ohn, S.-W. Fuzzy Inference and Sequence Model-Based Collision Risk Prediction System for Stand-On Vessel. Sensors 2022, 22, 4983. [Google Scholar] [CrossRef] [PubMed]
- Ni, D. A Unified Perspective on Traffic Flow Theory, Part I: The Field Theory. In Proceedings of the ICCTP 2011, Nanjing, China, 14–17 August 2011; American Society of Civil Engineers: Reston, VA, USA; pp. 4227–4243. [Google Scholar]
- Rødseth, Ø.J.; Wennersberg, L.A.L.; Nordahl, H. Improving Safety of Interactions between Conventional and Autonomous Ships. Ocean. Eng. 2023, 284, 115206. [Google Scholar] [CrossRef]
- Elguebaly, T.; Bouguila, N. Finite Asymmetric Generalized Gaussian Mixture Models Learning for Infrared Object Detection. Comput. Vision. Image Underst. 2013, 117, 1659–1671. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Du, W.-K.; Hu, X.-Y.; Bai, G.-Q.; Zhang, J.-B. USV Collision Hazard Assessment and Track Planning Algorithm. Ocean. Eng. 2022, 261, 112149. [Google Scholar] [CrossRef]
- Coldwell, T.G. Marine Traffic Behaviour in Restricted Waters. J. Navig. 1983, 36, 430–444. [Google Scholar] [CrossRef]


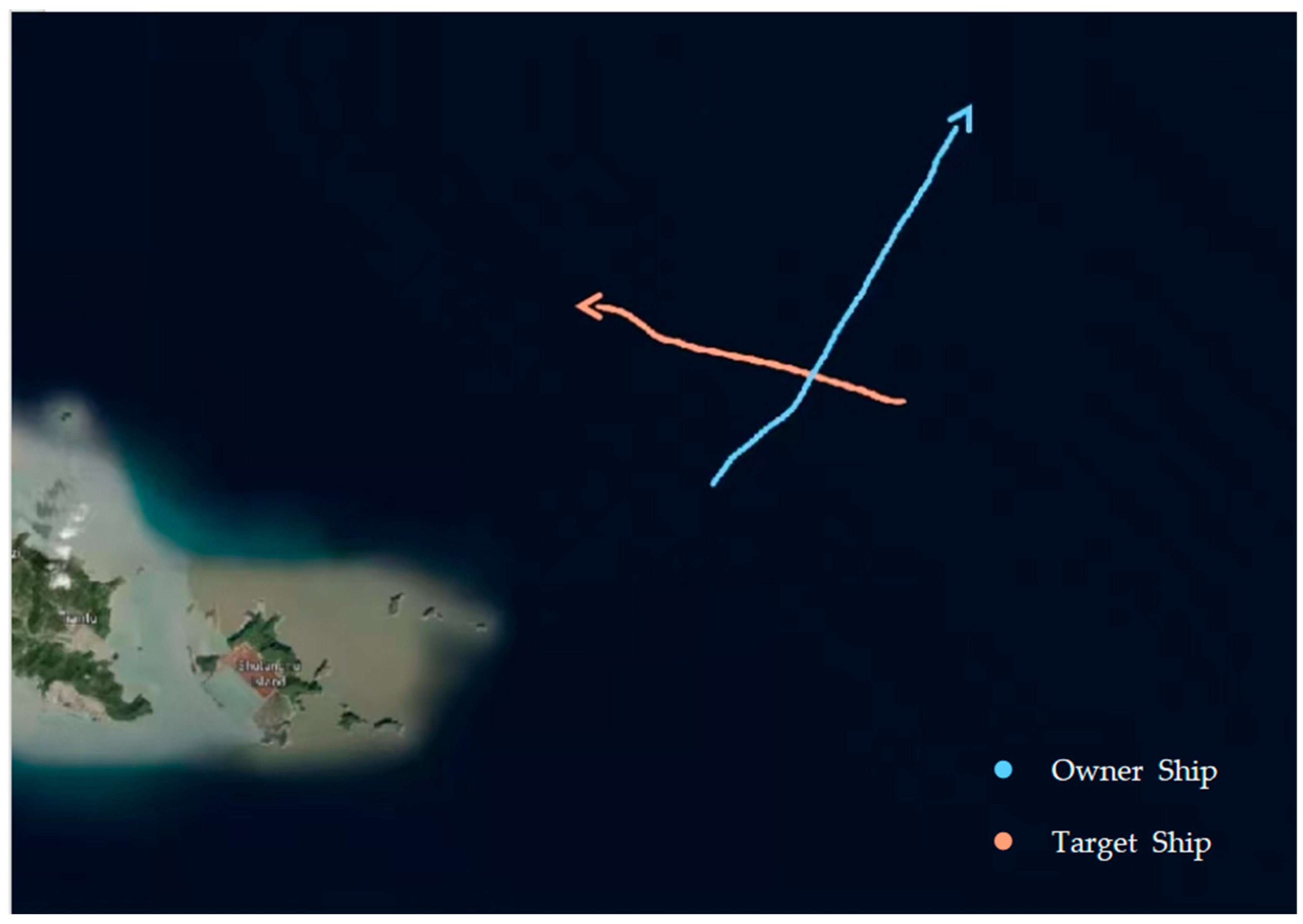
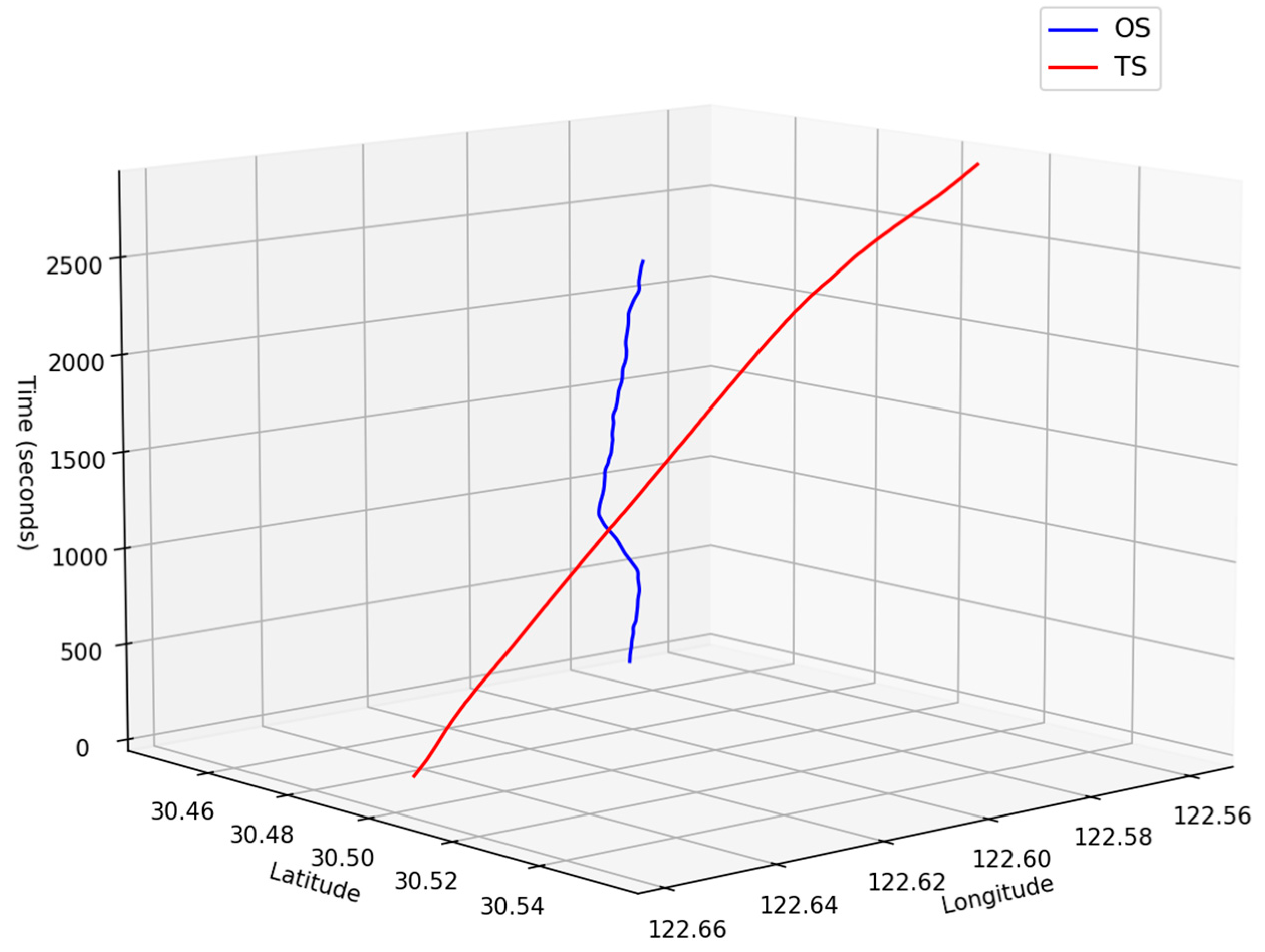




| MMSI | OS: 412750950 | TS: 477726100 |
|---|---|---|
| Length (m) | 140 | 292 |
| Width (m) | 20 | 45 |
| Speed (kn) | 10 | 5.2 |
| Course (deg) | 36.07 | 285.97 |
| Displacement (kg) | 18,468,268.5 | 82,023,165 |
| Ship type | Cargo | Cargo |
| Give-Way Ship | Path | Stand-On Ship | ||||
|---|---|---|---|---|---|---|
| TS | 231.19 | 20.77 | 4.25 | 8.43 | ||
| Path | 258.93 | 27.45 | 6.44 | 10.15 | ||
| 236.14 | 33.86 | 6.39 | 10.68 | |||
| Path | 249.55 | 27.18 | 6.97 | 8.59 | ||
| 244.19 | 24.41 | 5.38 | 9.01 | |||
| 225.16 | 44.10 | 5.89 | 8.72 | |||
| OS | 338.80 | 48.42 | 18.61 | 9.25 | ||
| Path | 349.73 | 62.08 | 22.89 | 14.54 | ||
| 294.06 | 87.76 | 26.16 | 12.56 | |||
| 309.44 | 84.84 | 29.00 | 13.94 | |||
| Path | 346.80 | 60.98 | 25.91 | 17.05 | ||
| 274.71 | 71.38 | 22.81 | 13.52 | |||
| 252.07 | 85.91 | 21.25 | 17.20 | |||
| TS | OS | |||
|---|---|---|---|---|
| 804.09 | 1364.76 | 2750.84 | 2456.04 | |
| 626.31 | 174.91 | 1252.69 | 2394.95 | |
| 46.50 | 66.04 | 88.09 | 30.05 | |
| \ | 510 | \ | 480 | |
| cost | \ | 33.46 | \ | 15.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Shen, Y.; Xie, Z.; Liu, Y. Research on the Give-Way Ships Determination Based on Field Theory. J. Mar. Sci. Eng. 2024, 12, 1973. https://doi.org/10.3390/jmse12111973
Zhang Y, Shen Y, Xie Z, Liu Y. Research on the Give-Way Ships Determination Based on Field Theory. Journal of Marine Science and Engineering. 2024; 12(11):1973. https://doi.org/10.3390/jmse12111973
Chicago/Turabian StyleZhang, Yunfeng, Yong Shen, Zhexue Xie, and Yihua Liu. 2024. "Research on the Give-Way Ships Determination Based on Field Theory" Journal of Marine Science and Engineering 12, no. 11: 1973. https://doi.org/10.3390/jmse12111973
APA StyleZhang, Y., Shen, Y., Xie, Z., & Liu, Y. (2024). Research on the Give-Way Ships Determination Based on Field Theory. Journal of Marine Science and Engineering, 12(11), 1973. https://doi.org/10.3390/jmse12111973






