Numerical Investigation of Flow and Scour around Complex Bridge Piers in Wind–Wave–Current Conditions
Abstract
:1. Introduction
2. Numerical Model
2.1. Hydrodynamic Model
2.2. Free Surface Model and Wave Generation
2.3. Wind Generation
2.4. Sediment Transport and Morphological Models
3. Model Validation
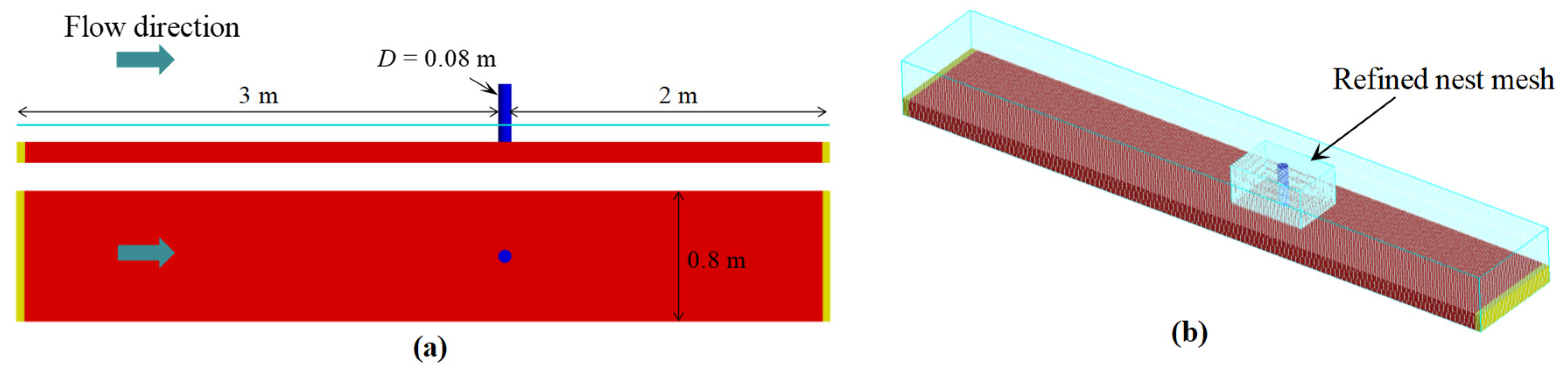
3.1. Numerical Setup
3.2. Comparison with Experimental Results
4. Results and Discussion
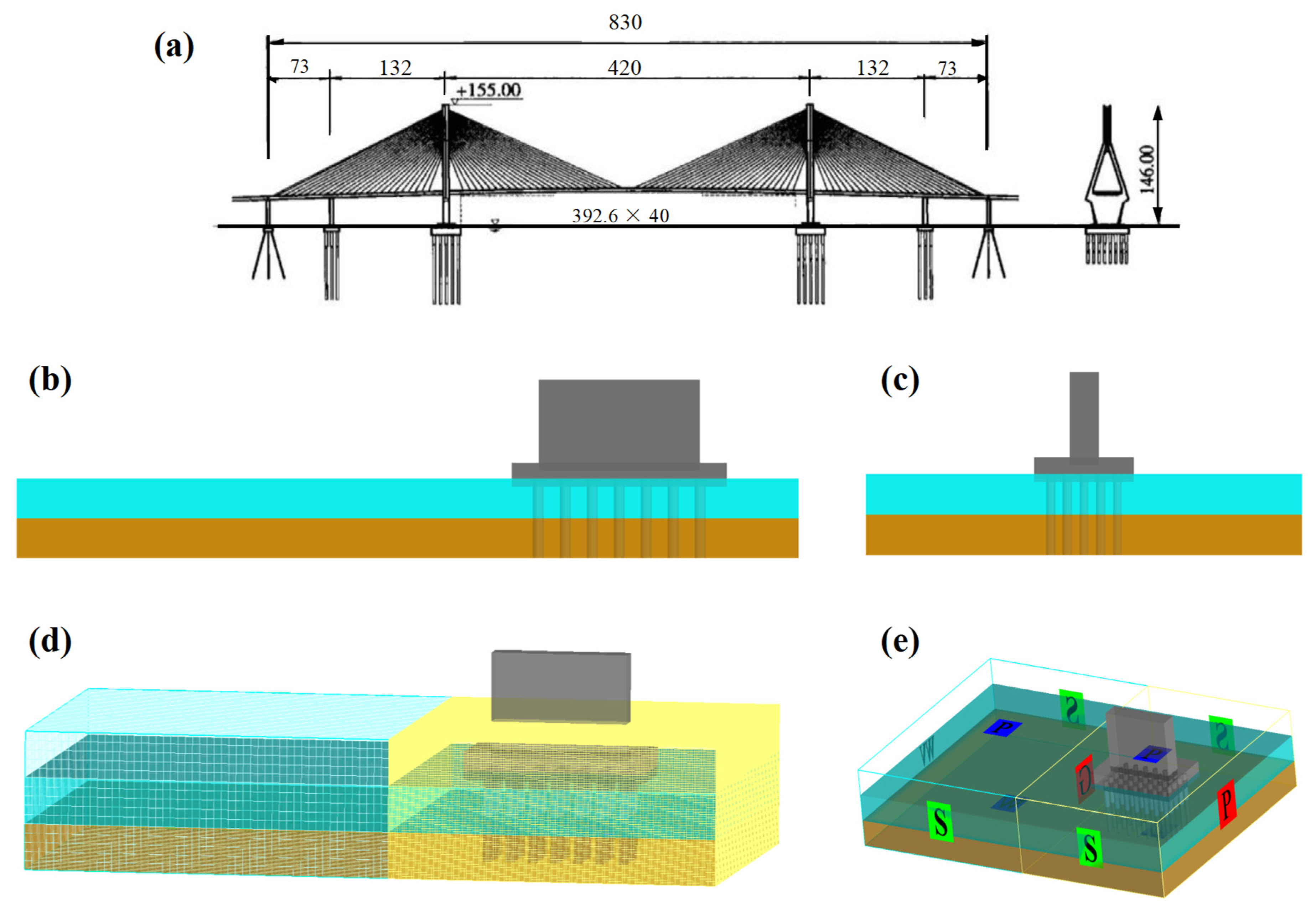
4.1. Description of the Full-Scale Model Setup
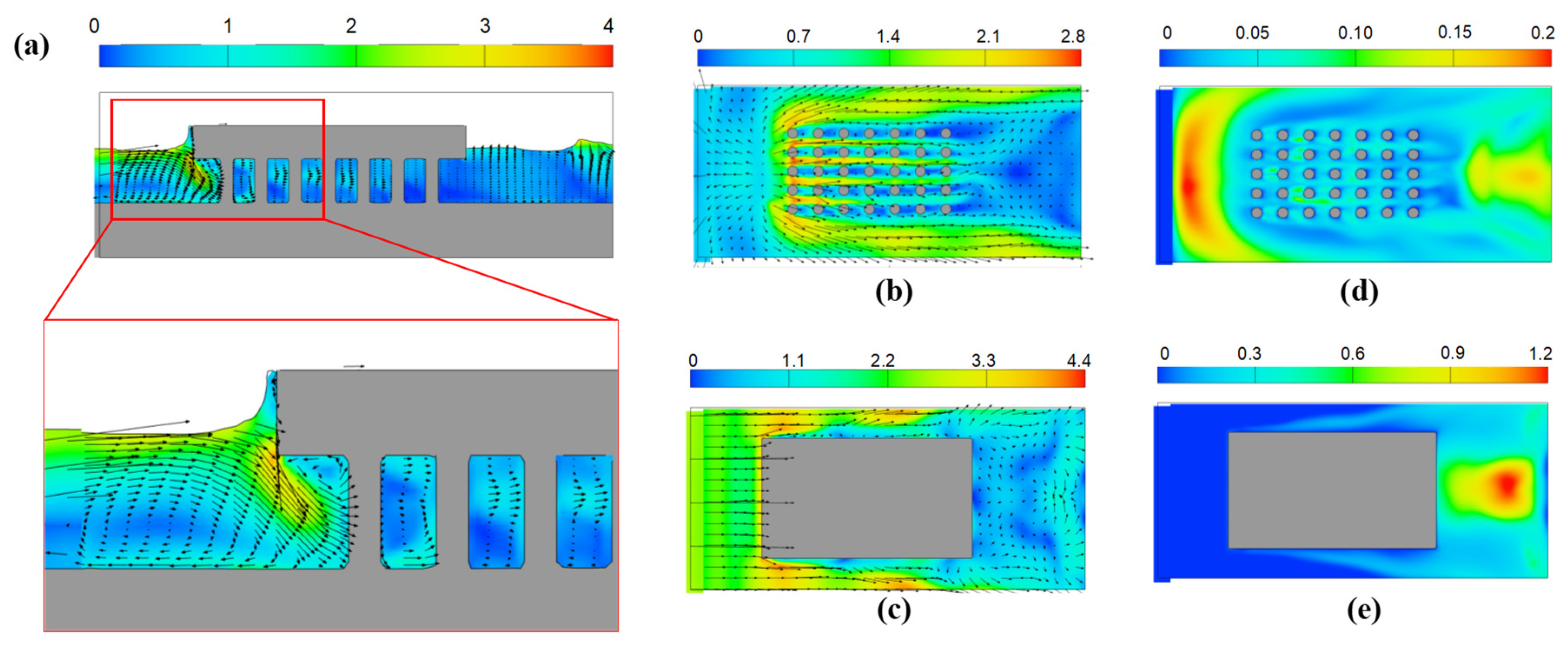
4.2. Flow Field Analysis
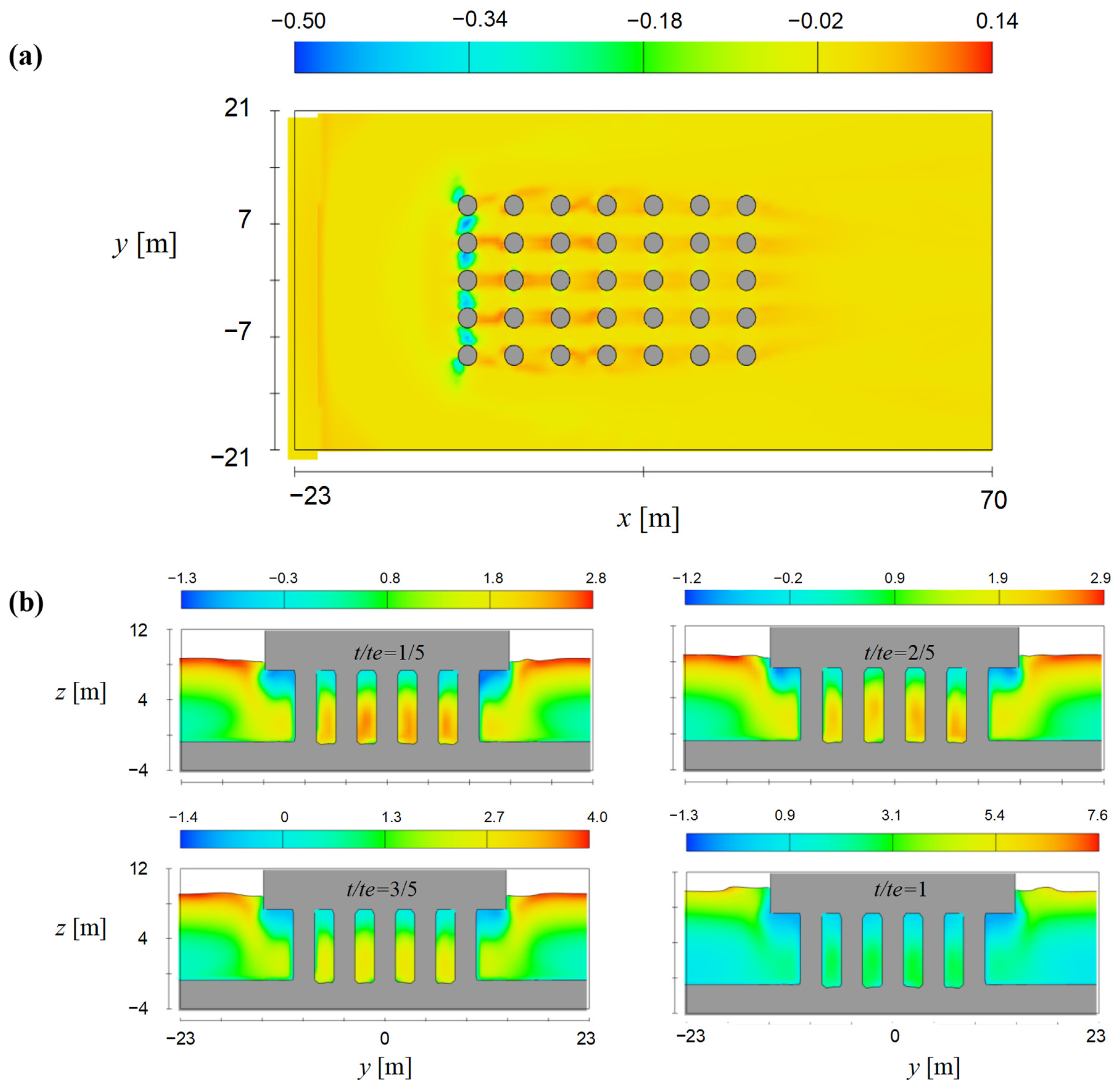
4.3. Scour Analysis
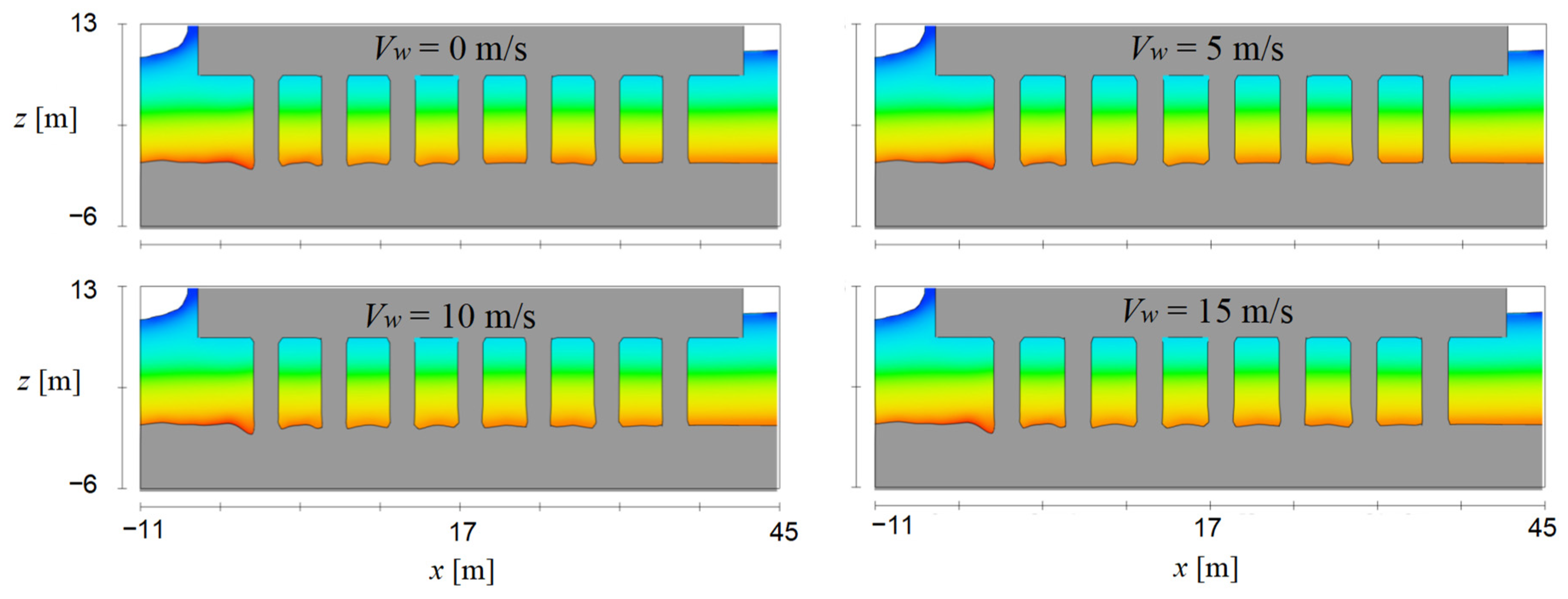
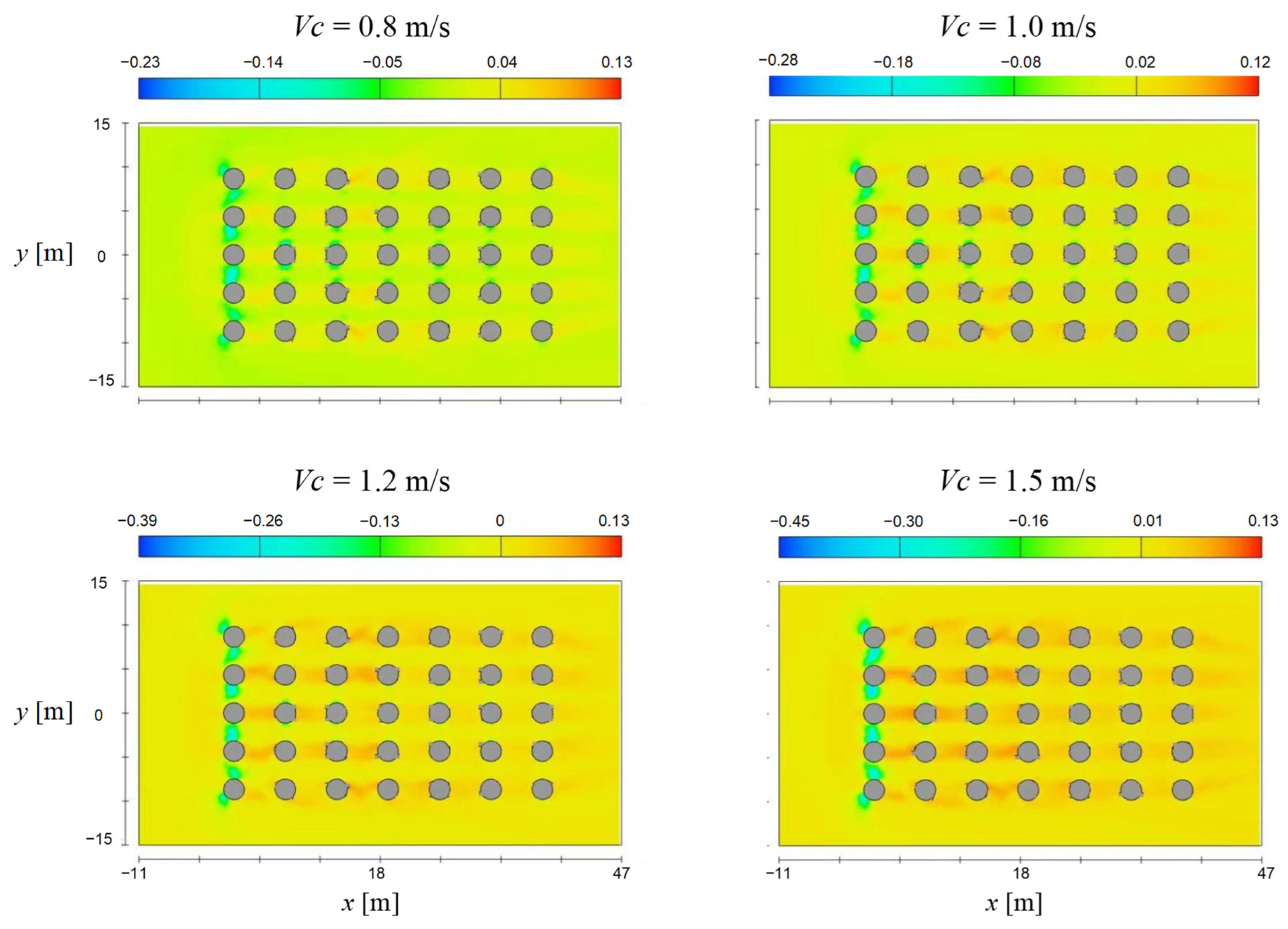
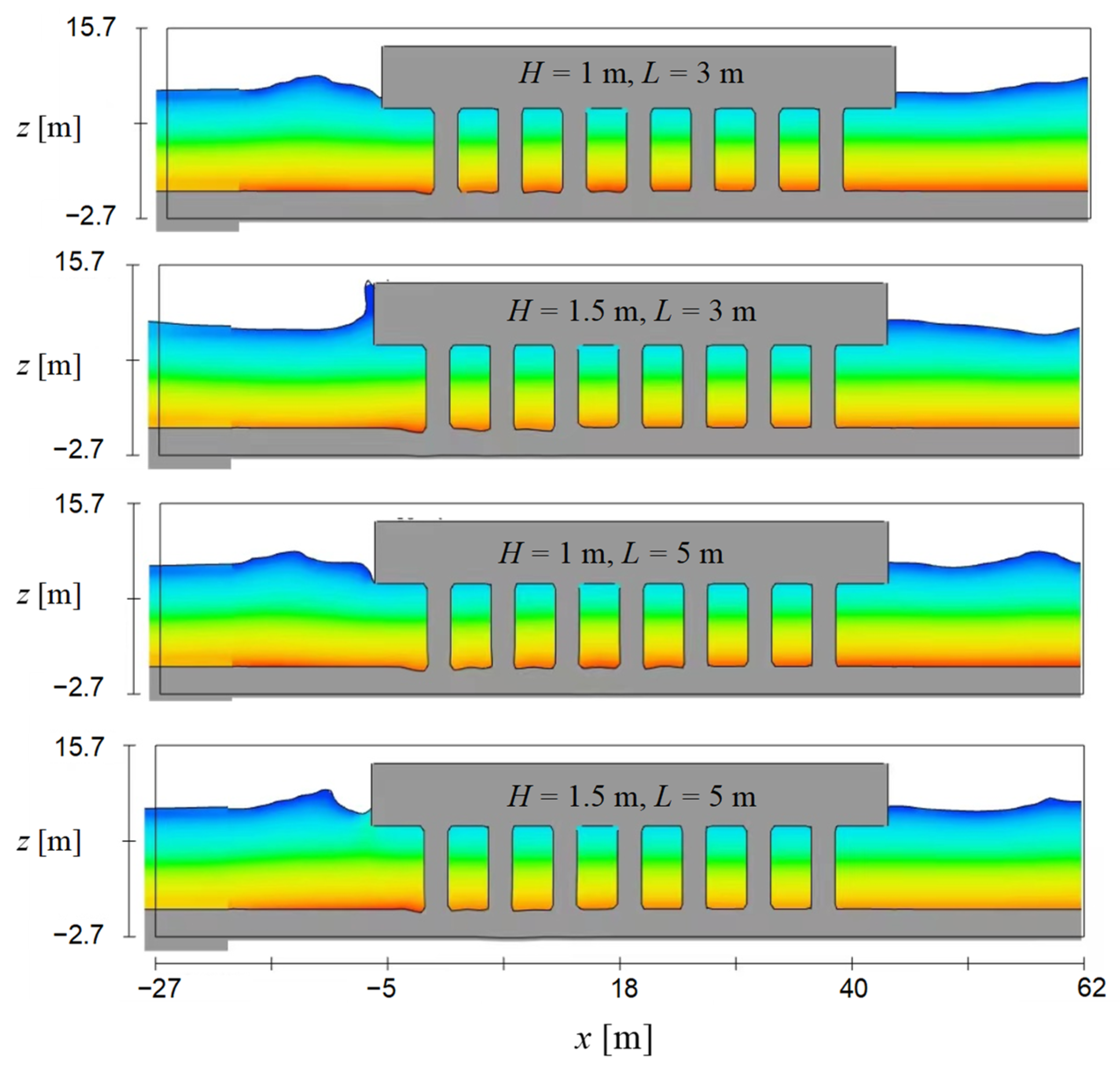
4.4. Influencing Parameter Analysis
5. Conclusions
- (1)
- Compared to the single pier with a uniform cross-sectional shape, the flow field around a complex pier is much more complicated. A flow-sheltering phenomenon is significant within the pile group area, and the regions with high TKE are observed in front of the pile group and downstream of the pile cap.
- (2)
- Scour predominantly occurs around the first row of piles, while the downstream piles experience a less significant impact from scour due to the sheltered position behind the first row, consequently reducing flow inundation on the downstream piles and resulting in a reduced bed scour depth.
- (3)
- The effect of the current velocity on bridge scour is more pronounced compared to that exerted by waves or wind. The wind or wave effect primarily manifests through its impact force on the superstructure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
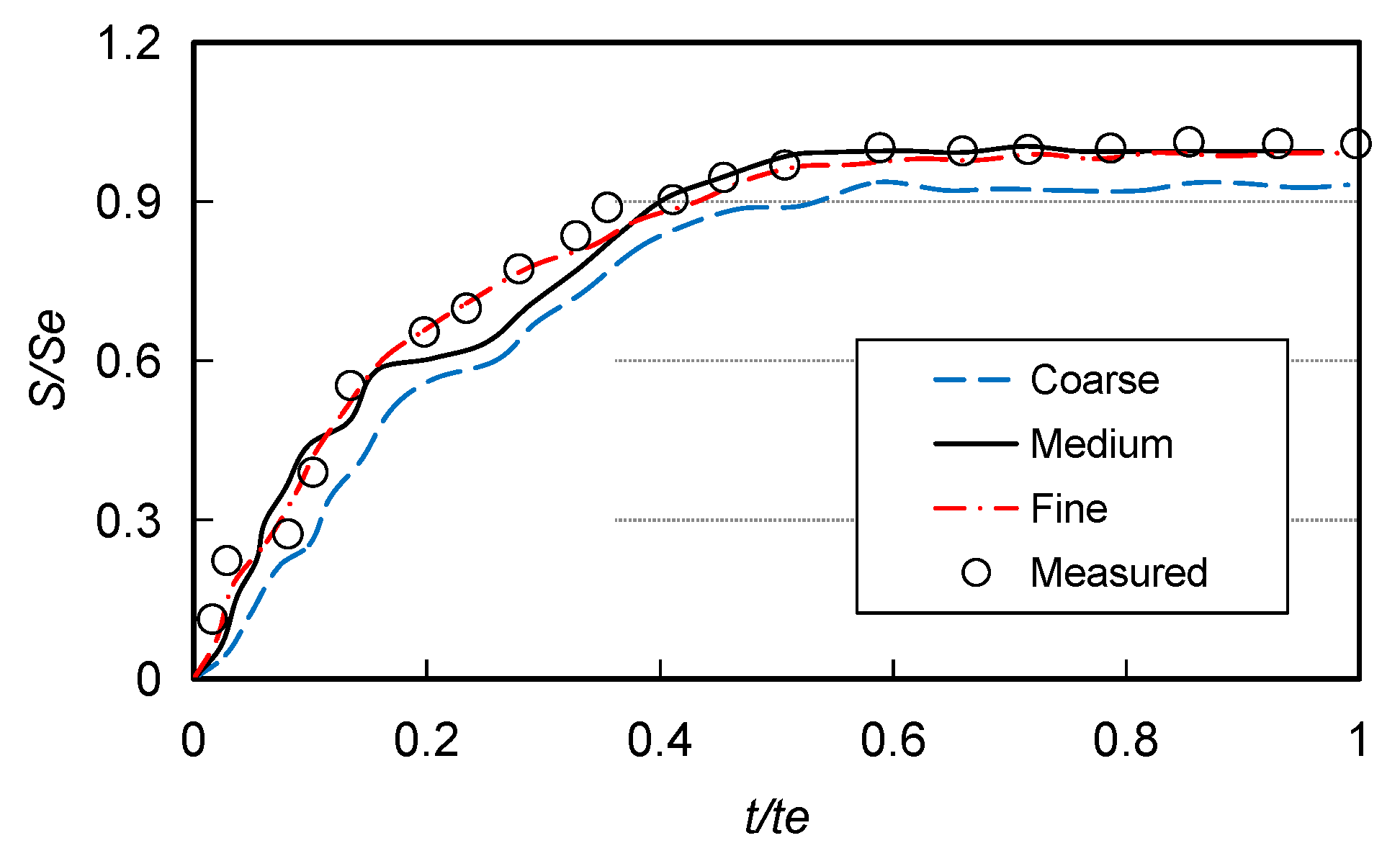
Appendix A. Mesh Convergence
References
- Xu, J.; Xia, J.; Wang, L.; Zhu, H.; Avital, E.J. Direct numerical simulation on local scour around the cylinder induced by internal solitary waves propagating over a slope. Ocean. Eng. 2022, 247, 110525. [Google Scholar] [CrossRef]
- Li, J.; Kong, X.; Yang, Y.; Yang, Z.; Hu, J. Computer vision-based measurement of wave force on the rectangular structure. Ocean. Eng. 2023, 270, 113624. [Google Scholar] [CrossRef]
- Tonkin, S.; Yeh, H.; Kato, F.; Sato, S. Tsunami scour around a cylinder. J. Fluid Mech. 2003, 496, 165–192. [Google Scholar] [CrossRef]
- Bricker, J.D.; Francis, M.; Nakayama, A. Scour depths near coastal structures due to the 2011 Tohoku tsunami. J. Hydraul. Res. 2012, 50, 637–641. [Google Scholar] [CrossRef]
- McGovern, D.J.; Todd, D.; Robinson, T.; Whitehouse, R.J.S.; Monaghan, J.; Gomes, E. Experimental observations of tsunami induced scour at onshore structures. Coast. Eng. 2019, 152, 103505. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. The Mechanics of Scour in the Marine Environment; World Scientific: Singapore, 2002. [Google Scholar]
- Melville, B.W.; Coleman, S.E. Bridge Scour; Water Resources Publications: Highlands Ranch, CO, USA, 2000. [Google Scholar]
- Coleman, S.E. Clearwater local scour at complex piers. J. Hydraul. Eng. 2005, 131, 330–334. [Google Scholar] [CrossRef]
- Moreno, M.; Maia, R.; Couto, L. Prediction of equilibrium local scour depth at complex bridge piers. J. Hydraul. Eng. 2016, 142, 04016045. [Google Scholar] [CrossRef]
- Yang, Y.; Melville, B.W.; Sheppard, D.M.; Shamseldin, A.Y. Clear-water local scour at skewed complex bridge piers. J. Hydraul. Eng. 2018, 144, 0001458. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Jing, H. Experimental study of flow field and sediment suspension in the gap area of tandem piles under oscillatory flows. Ocean. Eng. 2022, 266, 113124. [Google Scholar] [CrossRef]
- Ramos, P.X.; Bento, A.M.; Maia, R.; Pego, J.P. Characterization of the scour cavity evolution around a complex bridge pier. J. Appl. Water Eng. Res. 2015, 4, 128–137. [Google Scholar] [CrossRef]
- Ettema, R.; Constantinescu, G.; Melville, B.W. Flow-Field Complexity and Design Estimation of Pier-Scour Depth: Sixty Years since Laursen and Toch. J. Hydraul. Eng. 2017, 143, 03117006. [Google Scholar] [CrossRef]
- Afzal, M.S.; Bihs, H.; Kamath, A.; Arntsen, Ø.A. Three-dimensional numerical modeling of pier scour under current and waves using level-set method. J. Offshore Mech. Arct. Eng. 2015, 137, V002T08A030. [Google Scholar]
- Baykal, C.; Sumer, B.M.; Fuhrman, D.R.; Jacobsen, N.G.; Fredosøe, J. Numerical simulation of scour and backfilling processes around a circular pile in waves. Coast. Eng. 2017, 122, 87–107. [Google Scholar] [CrossRef]
- Ahmad, N.; Bihs, H.; Myrhaug, D.; Kamath, A.; Arntsen, Ø.A. Three-dimensional numerical modelling of wave-induced scour around piles in a side-by-side arrangement. Coast. Eng. 2018, 138, 132–151. [Google Scholar] [CrossRef]
- Li, J.; Fuhrman, D.R.; Kong, X.; Xie, M.; Yang, Y. Three-dimensional numerical simulation of wave-induced scour around a pile on a sloping beach. Ocean. Eng. 2021, 233C, 109174. [Google Scholar] [CrossRef]
- Li, J.; Kong, X.; Yang, Y.; Deng, L.; Xiong, W. CFD investigations of tsunami-induced scour around bridge piers. Ocean. Eng. 2022, 244, 110373. [Google Scholar] [CrossRef]
- Gautam, S.; Dutta, D.; Bihs, H.; Afzal, M.S. Three-dimensional Computational Fluid Dynamics modelling of scour around a single pile due to combined action of the waves and current using Level-Set method. Coast. Eng. 2021, 170, 104002. [Google Scholar] [CrossRef]
- Hu, R.; Wang, X.; Liu, H.; Chen, D. Numerical study of local scour around tripod foundation in random waves. J. Mar. Sci. Eng. 2022, 10, 475. [Google Scholar] [CrossRef]
- Lai, Y.G.; Liu, X.F.; Bombardelli, F.A.; Song, Y. Three-dimensional numerical modeling of local scour: A state-of-the-art review and perspective. J. Hydraul. Eng. 2022, 148, 0312202. [Google Scholar] [CrossRef]
- Zhao, M. A Review on recent development of numerical modelling of local scour around hydraulic and marine structures. J. Mar. Sci. Eng. 2022, 10, 1139. [Google Scholar] [CrossRef]
- Qu, K.; Wen, B.H.; Ren, X.Y.; Kraatz, S.; Sun, W.Y.; Deng, B.; Jiang, C.B. Numerical investigation on hydrodynamic force of coastal bridge deck under joint action of solitary wave and wind. Ocean. Eng. 2020, 217, 108037. [Google Scholar] [CrossRef]
- Qu, K.; Wang, Y.; Tang, H.S.; Agrawal, A.; Shields, G.; Chien, S.I.; Gurung, S.; Imam, Y.; Chiodi, I. Extreme storms surge and waves and vulnerability of coastal bridges in New York city metropolitan region: An assessment based on hurricane sandy. Nat. Hazards 2021, 105, 2697–2734. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD, 3rd ed.; DCW Industries, Inc.: La Canada, CA, USA, 2006. [Google Scholar]
- Hirt, C.W. Volume-fraction techniques: Power tools for wind engineering. In Proceedings of the 1st International Symposium on Computational Wind Engineering (CWE 92), Tokyo, Japan, 21–23 August 1992; pp. 327–338. [Google Scholar]
- Kuai, Y.; Qi, M.; Li, J. Numerical study on the propagation of solitary waves in the near-shore. Ocean. Eng. 2018, 165, 155–163. [Google Scholar] [CrossRef]
- Amorocho, J.; Devries, J.J. A new evaluation of the wind stress coefficient over water surfaces. J. Geophys. Res. 1980, 85, 433–442. [Google Scholar] [CrossRef]
- van Rijn, L. Sediment transport, Part I: Bed load transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef]
- Soulsby, R.L.; Whitehouse, R.J.S. Threshold of sediment motion in coastal environments. In Pacific Coasts and Ports ’97: Proceedings of the 13th Australasian Coastal and Ocean Engineering Conference and the 6th Australasian Port and Harbour Conference, Christchurch, New Zealand, 7–11 September 1997; Centre for Advanced Engineering, University of Canterbury: Christchurch, New Zealand, 1997; Volume 1, p. 1. [Google Scholar]
- Paola, C.; Voller, V.R. A generalized Exner equation for sediment mass balance. J. Geophys. Res. 2005, 110, F04014. [Google Scholar] [CrossRef]
- Li, J.; Kong, X.; Yang, Y.; Yang, Z.; Hu, J. Numerical modeling of solitary wave-induced flow and scour around a square onshore structure. J. Mar. Sci. Eng. 2023, 11, 198. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; Yang, Z. Influence of scour development on turbulent flow field in front of a bridge pier. Water 2020, 12, 2370. [Google Scholar] [CrossRef]
- Yang, Z.; Li, J.; Zhang, H.; Yuan, C.; Yang, H. Experimental study on 2D motion characteristics of submerged floating tunnel in waves. J. Mar. Sci. Eng. 2020, 8, 123. [Google Scholar] [CrossRef]
- Xie, M.; Zhang, C.; Li, J.; Li, S.; Zhang, H.; Yang, Z. Flow structure and bottom friction on the non-linear turbulent boundary layer under stormy waves. Coast. Eng. 2021, 164, 103811. [Google Scholar] [CrossRef]
- Alemi, M.; Maia, R. Numerical simulation of the flow and local scour process around single and complex bridge piers. Int. J. Civ. Eng. 2016, 16, 475–487. [Google Scholar] [CrossRef]
- Bento, A.M.; Pêgo, J.P.; Viseu, T.; Couto, L. Scour development around an oblong bridge pier: A numerical and experimental study. Water 2023, 15, 2867. [Google Scholar] [CrossRef]
- Simarro, G.; Fael, C.M.S.; Cardoso, A.H. Estimating equilibrium scour depth at cylindrical piers in experimental studies. J. Hydraul. Eng. 2011, 137, 1089–1093. [Google Scholar] [CrossRef]
- Simarro, G.; Martín, J.P. Exponential expression for time evolution in local scour. J. Hydraul. Res. 2004, 42, 663–665. [Google Scholar] [CrossRef]
- Xu, B.; Wei, K.; Qin, S.; Hong, J. Experimental study of wave loads on elevated pile cap of pile group foundation for sea-crossing bridges. Ocean. Eng. 2020, 197, 106896. [Google Scholar] [CrossRef]

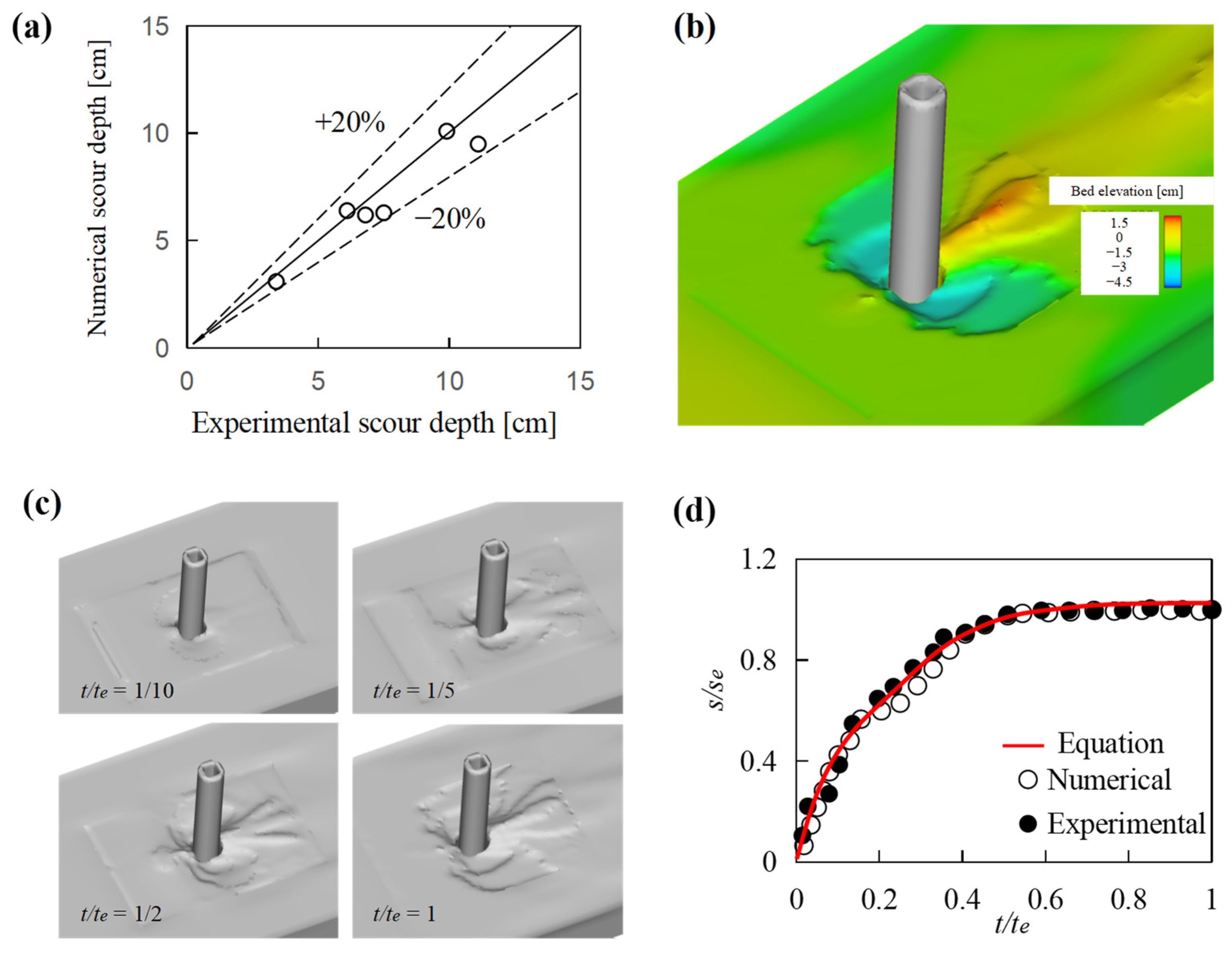
| Case No. | Vc [m/s] | d50 [mm] | Se [cm] | Sn [cm] | Error [−] |
|---|---|---|---|---|---|
| 1 | 0.16 | 1.65 | 3.4 | 3.1 | 8.8% |
| 2 | 0.16 | 0.62 | 6.8 | 6.2 | 8.8% |
| 3 | 0.16 | 0.14 | 6.1 | 6.4 | 4.9% |
| 4 | 0.21 | 1.65 | 7.5 | 6.3 | 16% |
| 5 | 0.21 | 0.62 | 11.1 | 9.5 | 14% |
| 6 | 0.21 | 0.14 | 9.9 | 10.1 | 2% |
| Case No. | Vw [m/s] | Vc [m/s] | H [m] | L [m] | Se [m] |
|---|---|---|---|---|---|
| 1 | 0 | 1.0 | 1.0 | 3.0 | 0.28 |
| 2 | 5 | 1.0 | 1.0 | 3.0 | 0.28 |
| 3 | 10 | 1.0 | 1.0 | 3.0 | 0.30 |
| 4 | 15 | 1.0 | 1.0 | 3.0 | 0.30 |
| 5 | 5 | 0.8 | 1.0 | 3.0 | 0.23 |
| 6 | 5 | 1.2 | 1.0 | 3.0 | 0.38 |
| 7 | 5 | 1.5 | 1.0 | 3.0 | 0.45 |
| 8 | 5 | 1.0 | 1.5 | 3.0 | 0.31 |
| 9 | 5 | 1.0 | 1.0 | 5.0 | 0.29 |
| 10 | 5 | 1.0 | 1.5 | 5.0 | 0.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Li, J.; Zou, W.; Chen, B. Numerical Investigation of Flow and Scour around Complex Bridge Piers in Wind–Wave–Current Conditions. J. Mar. Sci. Eng. 2024, 12, 23. https://doi.org/10.3390/jmse12010023
Yang Y, Li J, Zou W, Chen B. Numerical Investigation of Flow and Scour around Complex Bridge Piers in Wind–Wave–Current Conditions. Journal of Marine Science and Engineering. 2024; 12(1):23. https://doi.org/10.3390/jmse12010023
Chicago/Turabian StyleYang, Yilin, Jinzhao Li, Waner Zou, and Benshuang Chen. 2024. "Numerical Investigation of Flow and Scour around Complex Bridge Piers in Wind–Wave–Current Conditions" Journal of Marine Science and Engineering 12, no. 1: 23. https://doi.org/10.3390/jmse12010023
APA StyleYang, Y., Li, J., Zou, W., & Chen, B. (2024). Numerical Investigation of Flow and Scour around Complex Bridge Piers in Wind–Wave–Current Conditions. Journal of Marine Science and Engineering, 12(1), 23. https://doi.org/10.3390/jmse12010023






