A Wetting and Drying Approach for a Mode-Nonsplit Discontinuous Galerkin Hydrodynamic Model with Application to Laizhou Bay
Abstract
1. Introduction
2. Three-Dimensional Model of the DG Method
2.1. Governing Equations and Boundary Conditions
2.2. Discontinuous Galerkin Discretization
3. Wetting and Drying Treatments
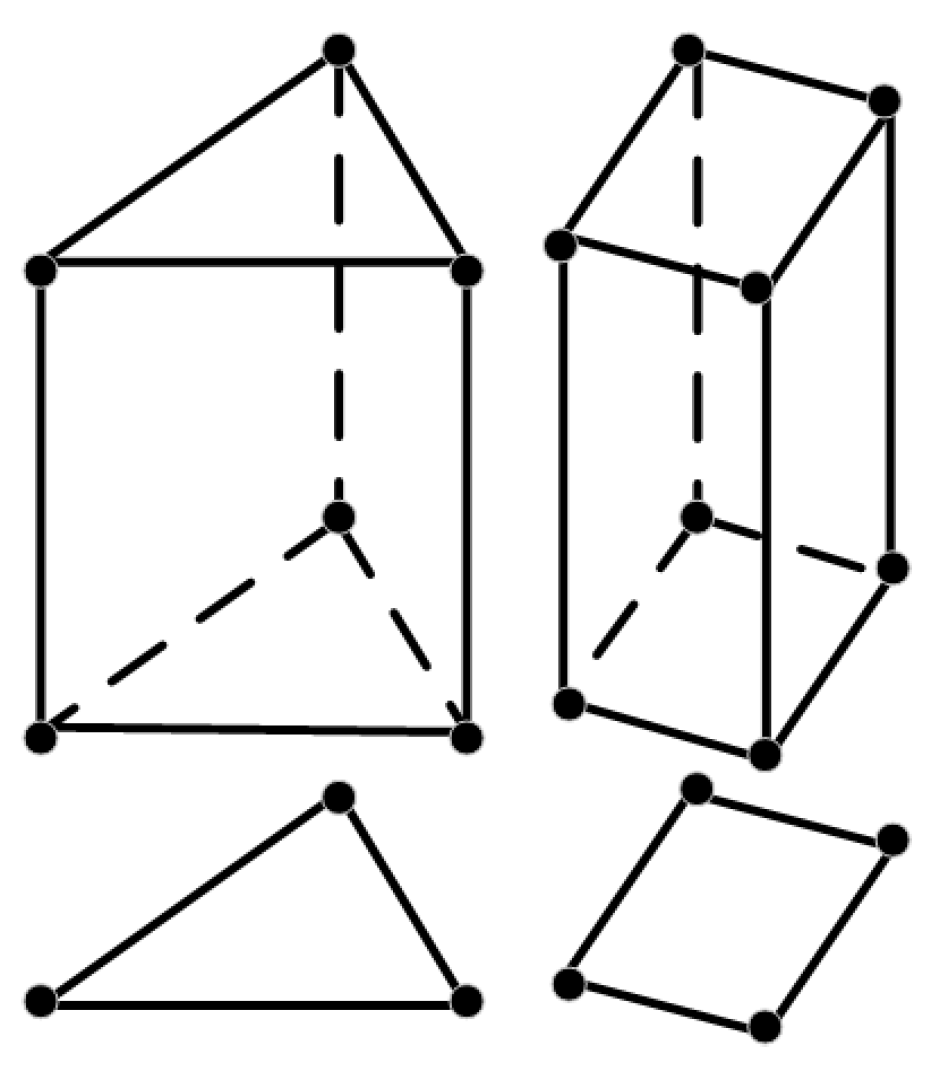
3.1. Wet–Dry Nodes and Elements
- wet nodes, for ;
- dry nodes, for .
- wet elements, for ;
- dry elements, for ;
- semidry elements for .

3.2. Calculation of Elements in the Model
3.3. Combined 2D and 3D Limiters
4. Tests and Analysis of the Wet–Dry Approach
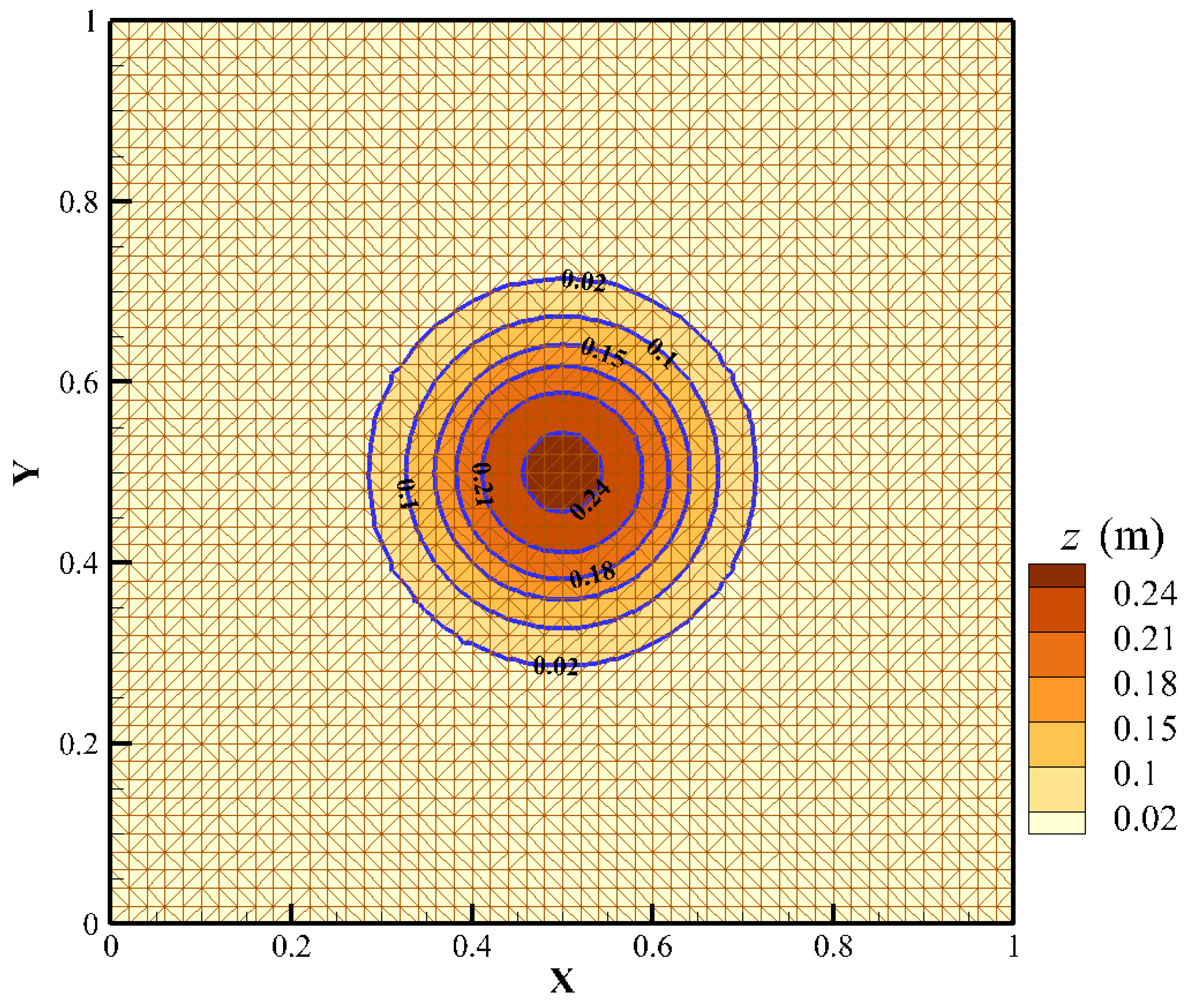
4.1. Well-Balanced Test
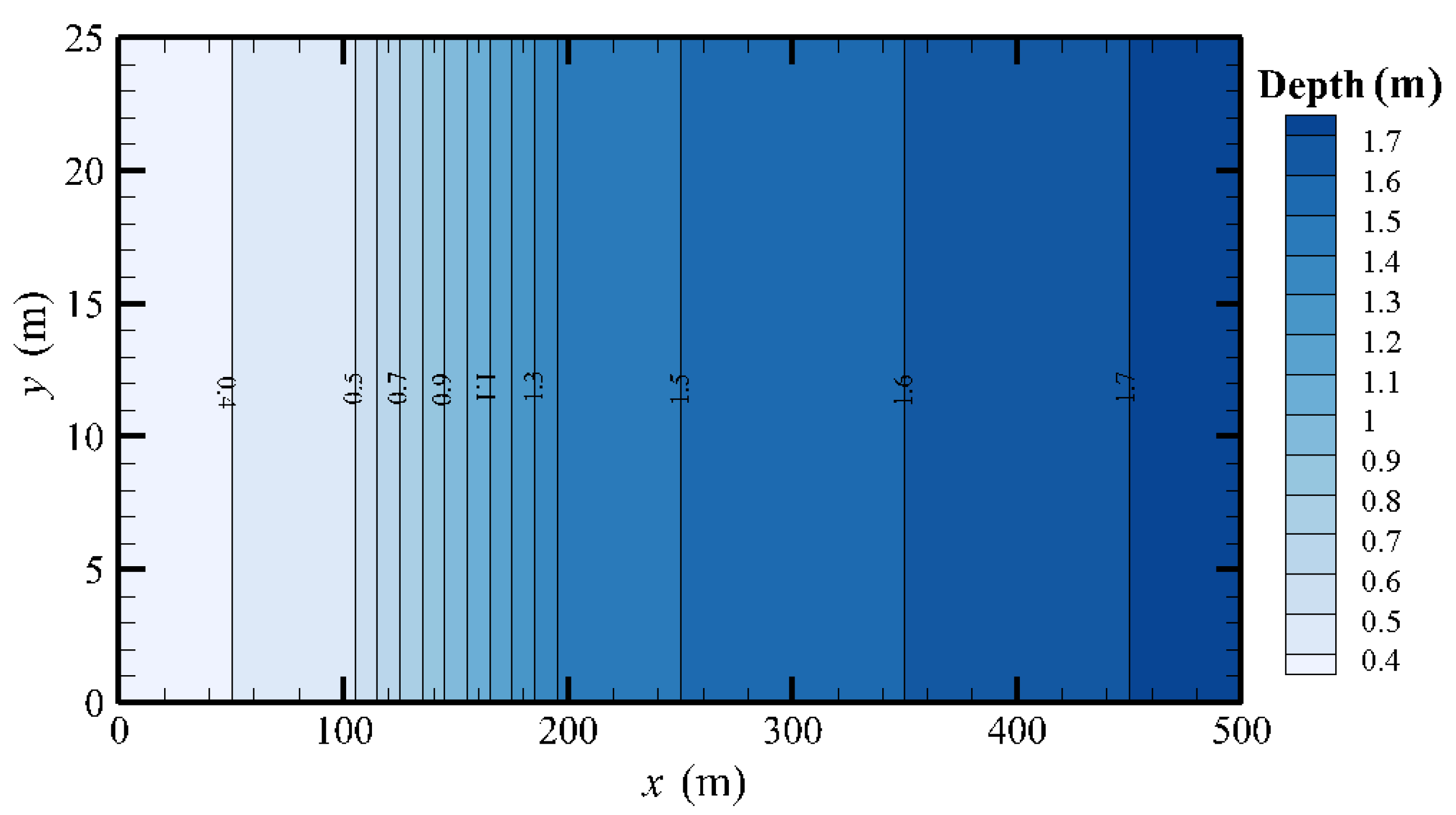
4.2. Long Waves Climbing a Sloping Beach
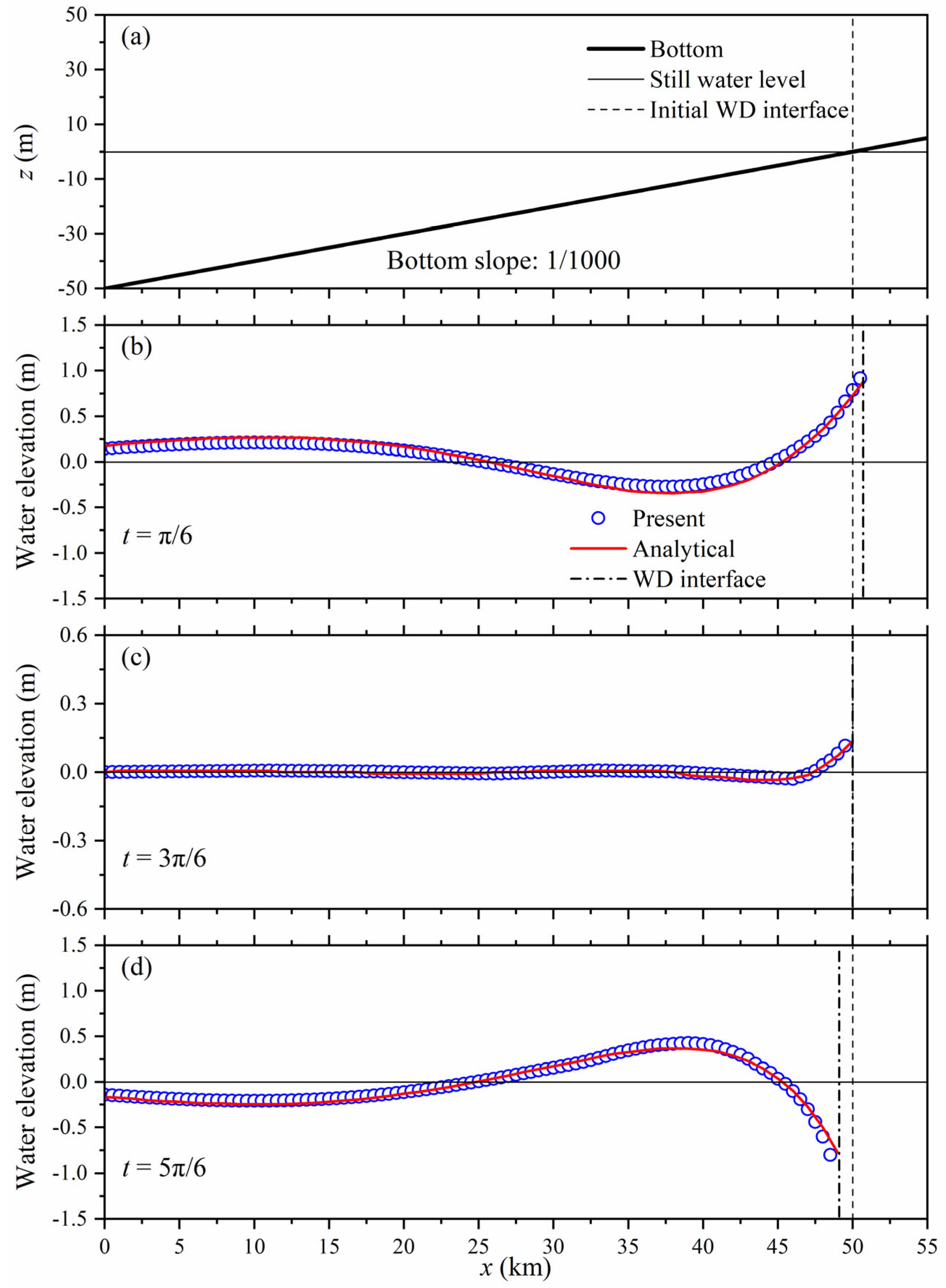
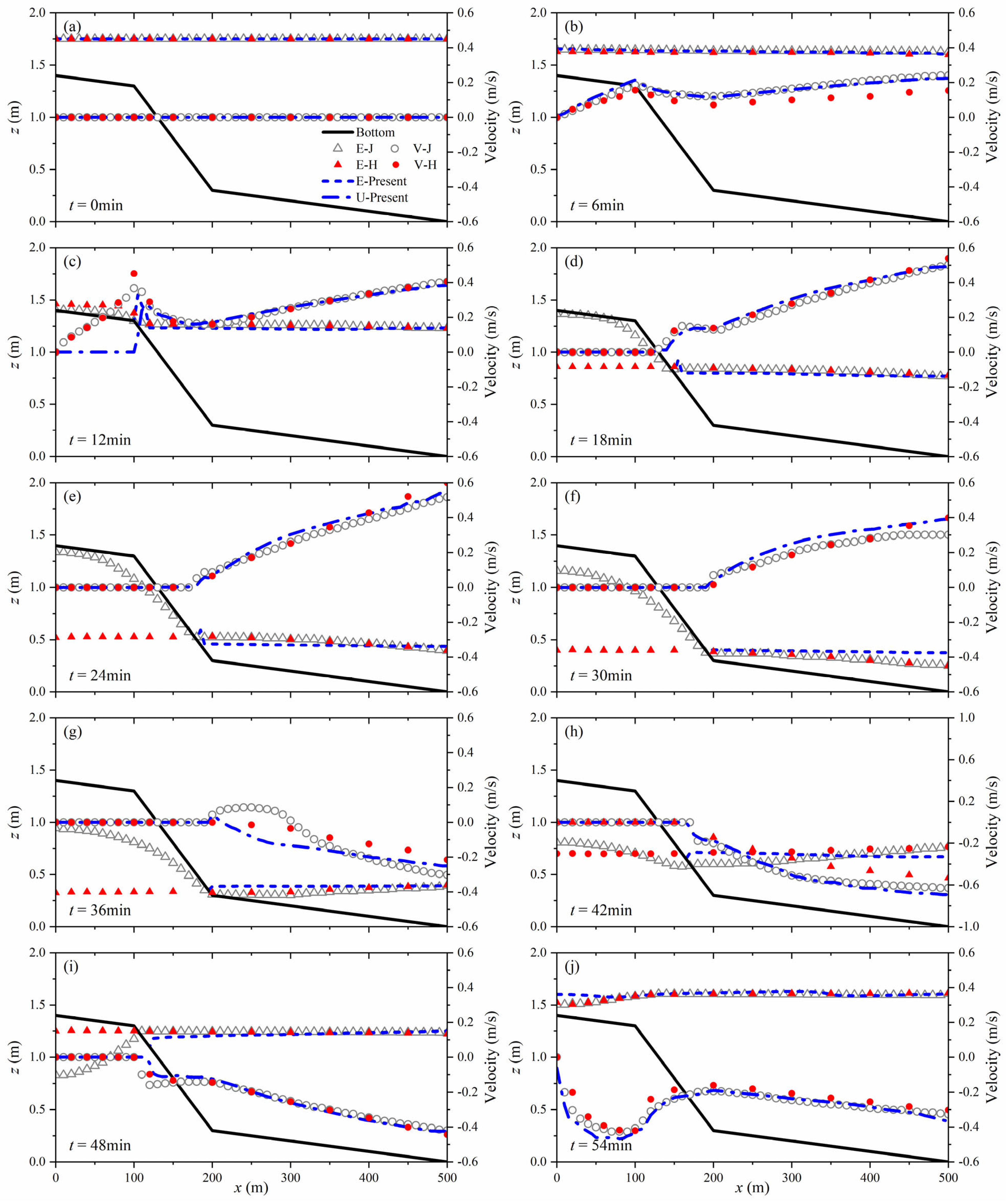
4.3. Basin with Variable Slope under a Tidal Cycle
4.4. Discussion on the Use of 2D and 3D Limiters
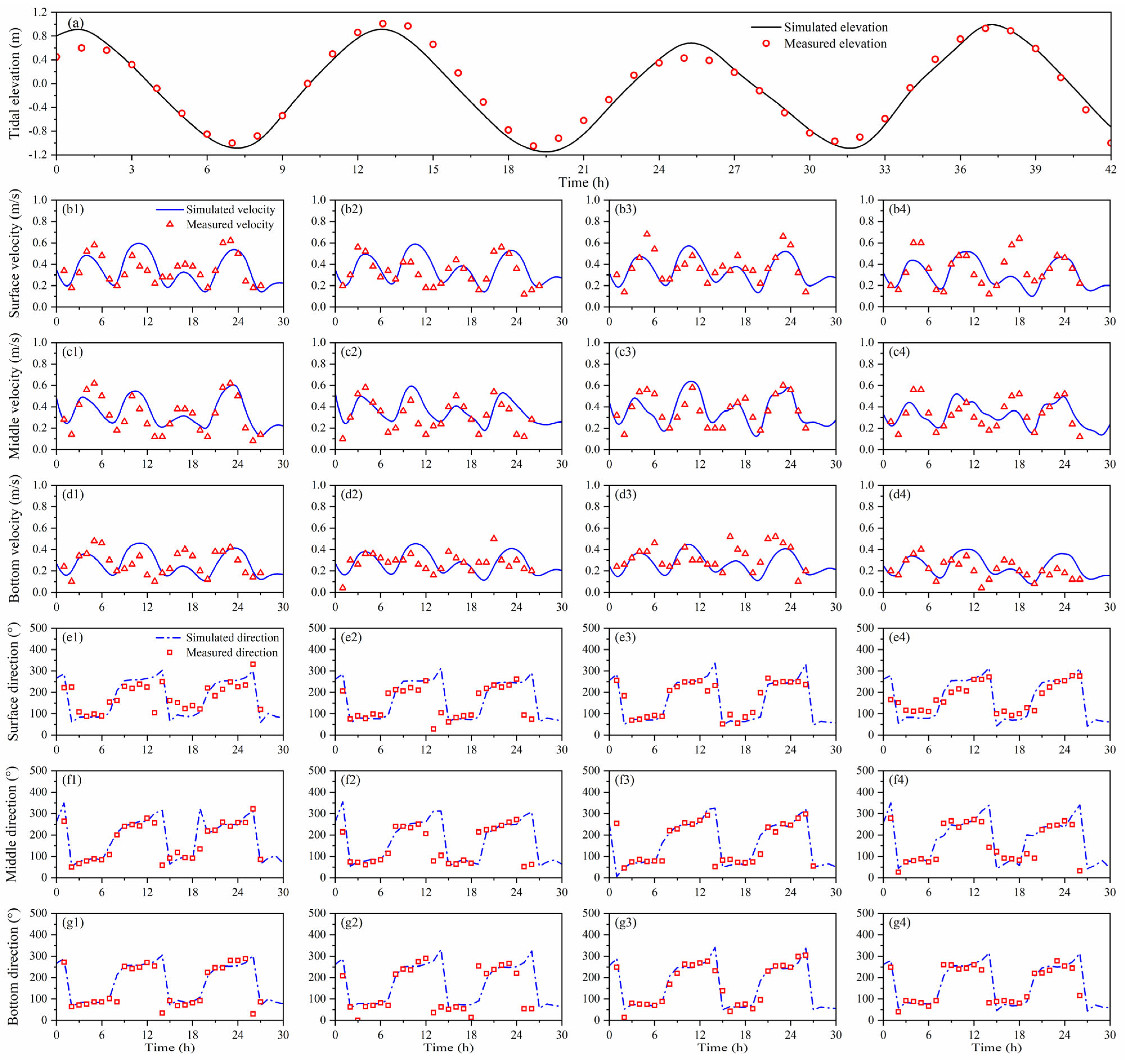
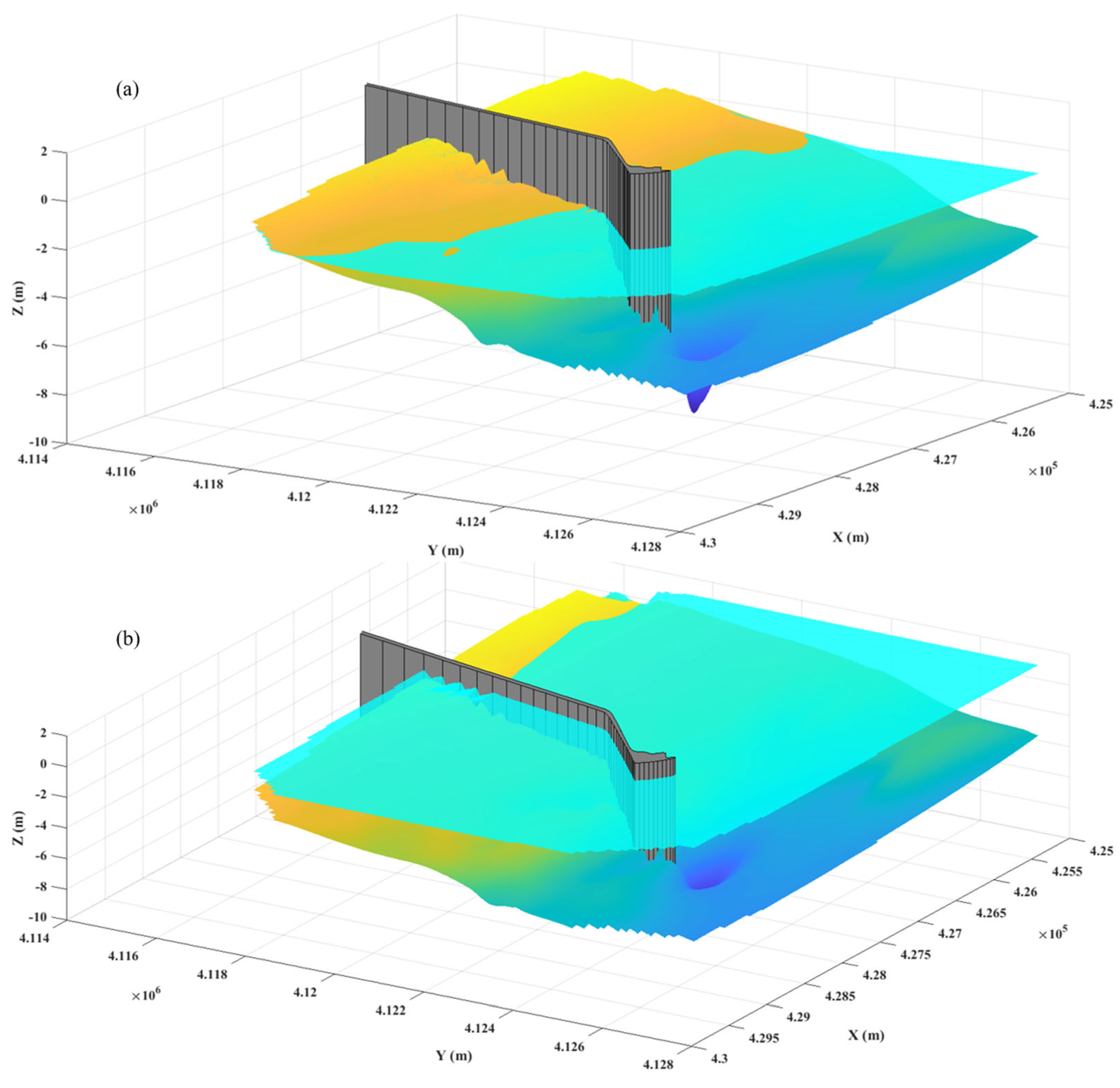
5. Application of the Model for Tidal Flow in Laizhou Bay
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marsooli, R.; Orton, P.M.; Georgas, N.; Blumberg, A.F. Three-dimensional hydrodynamic modeling of coastal flood mitigation by wetlands. Coast. Eng. 2016, 111, 83–94. [Google Scholar] [CrossRef]
- Safak, I.; List, J.H.; Warner, J.C.; Kumar, N. Observations and 3D hydrodynamics-based modeling of decadal-scale shoreline change along the outer banks, North Carolina. Coast. Eng. 2017, 120, 78–92. [Google Scholar] [CrossRef]
- Stansby, P.; Chini, N.; Lloyd, P. Oscillatory flows around a headland by 3D modelling with hydrostatic pressure and implicit bed shear stress comparing with experiment and depth-averaged modelling. Coast. Eng. 2016, 116, 1–14. [Google Scholar] [CrossRef]
- Delandmeter, P.; Lambrechts, J.; Legat, V.; Vallaeys, V.; Naithani, J.; Thiery, W.; Remacle, J.-F.; Deleersnijder, E. A fully consistent and conservative vertically adaptive coordinate system for SLIM 3D v0.4 with an application to the thermocline oscillations of Lake Tanganyika. Geosci. Model. Dev. 2018, 11, 1161–1179. [Google Scholar] [CrossRef]
- Kärnä, T.; Kramer, S.C.; Mitchell, L.; Ham, D.A.; Piggott, M.D.; Baptista, A.M. Thetis coastal ocean model: Discontinuous Galerkin discretization for the three-dimensional hydrostatic equations. Geosci. Model. Dev. 2018, 11, 4359–4382. [Google Scholar] [CrossRef]
- Vallaeys, V.; Lambrechts, J.; Delandmeter, P.; Pätsch, J.; Spitzy, A.; Hanert, E.; Deleersnijder, E. Understanding the circulation in the deep, micro-tidal and strongly stratified Congo River Estuary. Ocean. Model. 2021, 167, 101890. [Google Scholar] [CrossRef]
- Le, H.A.; Lambrechts, J.; Ortleb, S.; Gratiot, N.; Deleersnijder, E.; Soares-Frazão, S. An implicit wetting–drying algorithm for the discontinuous Galerkin method: Application to the Tonle Sap, Mekong River Basin. Environ. Fluid. Mech. 2020, 20, 923–951. [Google Scholar] [CrossRef]
- Medeiros, S.C.; Hagen, S.C. Review of wetting and drying algorithms for numerical tidal flow models. Int. J. Numer. Meth. Fl. 2013, 71, 473–487. [Google Scholar] [CrossRef]
- Ji, Z.G.; Morton, M.R.; Hamrick, J.M. Wetting and drying simulation of estuarine processes. Estuar. Coast. Shelf. Sci. 2001, 53, 683–700. [Google Scholar] [CrossRef]
- Martins, R.; Leandro, J.; Djordjević, S. Wetting and drying numerical treatments for the Roe Riemann scheme. J. Hydraul. Res. 2018, 56, 256–267. [Google Scholar] [CrossRef]
- Dietrich, J.C.; Kolar, R.L.; Luettich, R.A. Assessment of ADCIRC’s wetting and drying algorithm. Dev. Water. Sci. 2004, 55, 1767–1778. [Google Scholar] [CrossRef]
- Oey, L.Y. A wetting and drying scheme for POM. Ocean. Model. 2005, 9, 133–150. [Google Scholar] [CrossRef]
- Chen, C.; Qi, J.; Li, C.; Beardsley, R.C.; Lin, H.; Walker, R.; Gates, K. Complexity of the flooding/drying process in an estuarine tidal-creek salt-marsh system: An application of FVCOM. J. Geophys. Res. Oceans 2008, 113, 1–21. [Google Scholar] [CrossRef]
- Aureli, F.; Maranzoni, A.; Mignosa, P.; Ziveri, C. A weighted surface-depth gradient method for the numerical integration of the 2D shallow water equations with topography. Adv. Water. Resour. 2008, 31, 962–974. [Google Scholar] [CrossRef]
- Jiang, Y.W.; Wai, O.W.H. Drying–wetting approach for 3D finite element sigma coordinate model for estuaries with large tidal flats. Adv. Water Resour. 2005, 28, 779–792. [Google Scholar] [CrossRef]
- Heniche, M.; Secretan, Y.; Boudreau, P.; Leclerc, M. A two-dimensional finite element drying-wetting shallow water model for rivers and estuaries. Adv. Water Resour. 1999, 23, 359–372. [Google Scholar] [CrossRef]
- Bokhove, O. Flooding and drying in discontinuous Galerkin finite-element discretizations of shallow-water equations. Part 1: One dimension. J. Sci. Comput. 2005, 22–23, 47–82. [Google Scholar] [CrossRef]
- Ern, A.; Piperno, S.; Djadel, K. A well-balanced Runge-Kutta discontinuous Galerkin method for the shallow-water equations with flooding and drying. Int. J. Numer. Meth. Fl. 2008, 58, 1–25. [Google Scholar] [CrossRef]
- Bunya, S.; Kubatko, E.J.; Westerink, J.J.; Dawson, C. A wetting and drying treatment for the Runge–Kutta discontinuous Galerkin solution to the shallow water equations. Comput. Method. Appl. M. 2009, 198, 1548–1562. [Google Scholar] [CrossRef]
- Kesserwani, G.; Liang, Q. Well-balanced RKDG2 solutions to the shallow water equations over irregular domains with wetting and drying. Comput. Fluids. 2010, 39, 2040–2050. [Google Scholar] [CrossRef]
- Kärnä, T.; De Brye, B.; Gourgue, O.; Lambrechts, J.; Comblen, R.; Legat, V.; Deleersnijder, E. A fully implicit wetting–drying method for DG–FEM shallow water models, with an application to the Scheldt estuary. Comput. Method. Appl. M. 2011, 200, 509–524. [Google Scholar] [CrossRef]
- Meister, A.; Ortleb, S. A positivity preserving and well-balanced DG scheme using finite volume subcells in almost dry regions. Appl. Math. Comput. 2016, 272, 259–273. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, X. Positivity-preserving well-balanced discontinuous Galerkin methods for the shallow water equations on unstructured triangular meshes. J. Sci. Comput. 2013, 57, 19–41. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, X.; Shu, C.-W. Positivity-preserving high order well-balanced discontinuous Galerkin methods for the shallow water equations. Adv. Water Resour. 2010, 33, 1476–1493. [Google Scholar] [CrossRef]
- Vater, S.; Beisiegel, N.; Behrens, J. A limiter-based well-balanced discontinuous Galerkin method for shallow-water flows with wetting and drying: One-dimensional case. Adv. Water Resour. 2015, 85, 1–13. [Google Scholar] [CrossRef]
- Vater, S.; Beisiegel, N.; Behrens, J. A limiter-based well-balanced discontinuous Galerkin method for shallow-water flows with wetting and drying: Triangular grids. Int. J. Numer. Meth. Fl. 2019, 91, 395–418. [Google Scholar] [CrossRef]
- Li, L.X.; Zhang, Q.H. A new vertex-based limiting approach for nodal discontinuous Galerkin methods on arbitrary unstructured meshes. Comput. Fluids. 2017, 159, 316–326. [Google Scholar] [CrossRef]
- Vallaeys, V. Discontinuous Galerkin Finite Element Modelling of Estuarine and Plume Dynamics. Ph.D. Thesis, UCL-Université Catholique de Louvain, Ottignies-Louvain-la-Neuve, Belgium, 2018. [Google Scholar]
- Kowalik, Z.; Murty, T.S. Numerical Modeling of Ocean Dynamics; World Scientific: Singapore, 1993. [Google Scholar] [CrossRef]
- Chen, C.; Qi, J.; Liu, H.; Beardsley, R.C.; Lin, H.; Cowles, G. A wet/dry point treatment method of FVCOM, part I: Stability experiments. J. Mar. Sci. Eng. 2022, 10, 896. [Google Scholar] [CrossRef]
- Dawson, C.; Aizinger, V. A discontinuous Galerkin method for three- dimensional shallow water equations. J. Sci. Comput. 2005, 22–23, 245–267. [Google Scholar] [CrossRef]
- Conroy, C.J.; Kubatko, E.J. hp discontinuous Galerkin methods for the vertical extent of the water column in coastal settings part I: Barotropic forcing. J. Comput. Phys. 2016, 305, 1147–1171. [Google Scholar] [CrossRef]
- Hesthaven, J.S.; Warburton, T. Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications; Springer Science & Business Media: Berlin, Germany, 2007. [Google Scholar]
- Duran, A.; Marche, F. Recent advances on the discontinuous Galerkin method for shallow water equations with topography source terms. Comput. Fluids. 2014, 101, 88–104. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. the basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Burchard, H.; Bolding, K.; Villarreal, M.R. GOTM, a General Ocean Turbulence Model: Theory, Implementation and Test Cases; Technical Report EUR 18745 EN; European Commission: Brussels, Belgium, 1999. [Google Scholar]
- Faghih-Naini, S.; Kuckuk, S.; Aizinger, V.; Zint, D.; Grosso, R.; Köstler, H. Quadrature-free discontinuous Galerkin method with code generation features for shallow water equations on automatically generated block-structured meshes. Adv. Water Resour. 2020, 138, 103552. [Google Scholar] [CrossRef]
- Li, W. Quadrature-free forms of discontinuous Galerkin methods in solving compressible flows on triangular and tetrahedral grids. Math. Comput. Simulat. 2024, 218, 149–173. [Google Scholar] [CrossRef]
- Toro, E.F. Shock-Capturing Methods for Free-Surface Shallow Flows; Wiley-Blackwell: Hoboken, NJ, USA, 2001. [Google Scholar]
- Ran, G.Q.; Zhang, Q.H.; Chen, Z.R. Development of a three-dimensional hydrodynamic model based on the discontinuous Galerkin method. Water 2022, 15, 156. [Google Scholar] [CrossRef]
- Bates, P.D.; Hervouet, J.M. A new method for moving–boundary hydrodynamic problems in shallow water. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1999, 455, 3107–3128. [Google Scholar] [CrossRef]
- Li, L.X.; Zhang, Q.H. Development of an efficient wetting and drying treatment for shallow-water modelling using the quadrature-free Runge–Kutta discontinuous Galerkin method. Int. J. Numer. Meth. Fl. 2020, 93, 314–338. [Google Scholar] [CrossRef]
- Lu, X.; Mao, B.; Zhang, X.; Ren, S. Well-balanced and shock-capturing solving of 3D shallow-water equations involving rapid wetting and drying with a local 2D transition approach. Comput. Method. Appl. M. 2020, 364, 112897. [Google Scholar] [CrossRef]
- Delandmeter, P. Discontinuous Galerkin Finite Element Modelling of Geophysical and Environmental Flows. Ph.D. Thesis, Universite Catholique de Louvain, Ottignies-Louvain-la-Neuve, Belgium, 2017. [Google Scholar]
- Brufau, P.; García-Navarro, P. Unsteady free surface flow simulation over complex topography with a multidimensional upwind technique. J. Comput. Phys. 2003, 186, 503–526. [Google Scholar] [CrossRef]
- Carrier, G.F.; Greenspan, H.P. Water waves of finite amplitude on a sloping beach. J. Fluid. Mech. 1958, 4, 97–109. [Google Scholar] [CrossRef]
- Leclerc, M.; Bellemare, J.F.; Dumas, G.; Dhatt, G. A finite element model of estuarian and river flows with moving boundaries. Adv. Water Resour. 1990, 13, 158–168. [Google Scholar] [CrossRef]
- Li, M.; Zheng, J. Introduction to Chinatide software for tide prediction in China seas. J. Waterw. Harb. 2007, 28, 65–68. (In Chinese) [Google Scholar]
- Le, H.P.; Cayocca, F.; Waeles, B. Dynamics of sand and mud mixtures: A multiprocess-based modelling strategy. Cont. Shelf. Res. 2011, 31, S135–S149. [Google Scholar] [CrossRef]




| L1 error | L∞ error | ||||
|---|---|---|---|---|---|
| D | Du | Dv | D | Du | Dv |
| 3.52 × 10−12 | 3.77 × 10−13 | 3.79 × 10−13 | 7.48 × 10−11 | 3.76 × 10−11 | 3.74 × 10−11 |
| Limiters in Model | No Limiter | 2D Limiter | 3D Limiter | Combined 2D and 3D Limiters |
|---|---|---|---|---|
| Status | Breakdown | Breakdown | Breakdown | Normal |
| Running time (s) | 3070.5 | 3104.0 | 3074.0 | 7200.0 (end) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Zhang, Q.; Ran, G.; Nie, Y. A Wetting and Drying Approach for a Mode-Nonsplit Discontinuous Galerkin Hydrodynamic Model with Application to Laizhou Bay. J. Mar. Sci. Eng. 2024, 12, 147. https://doi.org/10.3390/jmse12010147
Chen Z, Zhang Q, Ran G, Nie Y. A Wetting and Drying Approach for a Mode-Nonsplit Discontinuous Galerkin Hydrodynamic Model with Application to Laizhou Bay. Journal of Marine Science and Engineering. 2024; 12(1):147. https://doi.org/10.3390/jmse12010147
Chicago/Turabian StyleChen, Zereng, Qinghe Zhang, Guoquan Ran, and Yang Nie. 2024. "A Wetting and Drying Approach for a Mode-Nonsplit Discontinuous Galerkin Hydrodynamic Model with Application to Laizhou Bay" Journal of Marine Science and Engineering 12, no. 1: 147. https://doi.org/10.3390/jmse12010147
APA StyleChen, Z., Zhang, Q., Ran, G., & Nie, Y. (2024). A Wetting and Drying Approach for a Mode-Nonsplit Discontinuous Galerkin Hydrodynamic Model with Application to Laizhou Bay. Journal of Marine Science and Engineering, 12(1), 147. https://doi.org/10.3390/jmse12010147







