Experimental Evaluation and Validation of Pressure Distributions in Ice–Structure Collisions Using a Pendulum Apparatus
Abstract
:1. Introduction
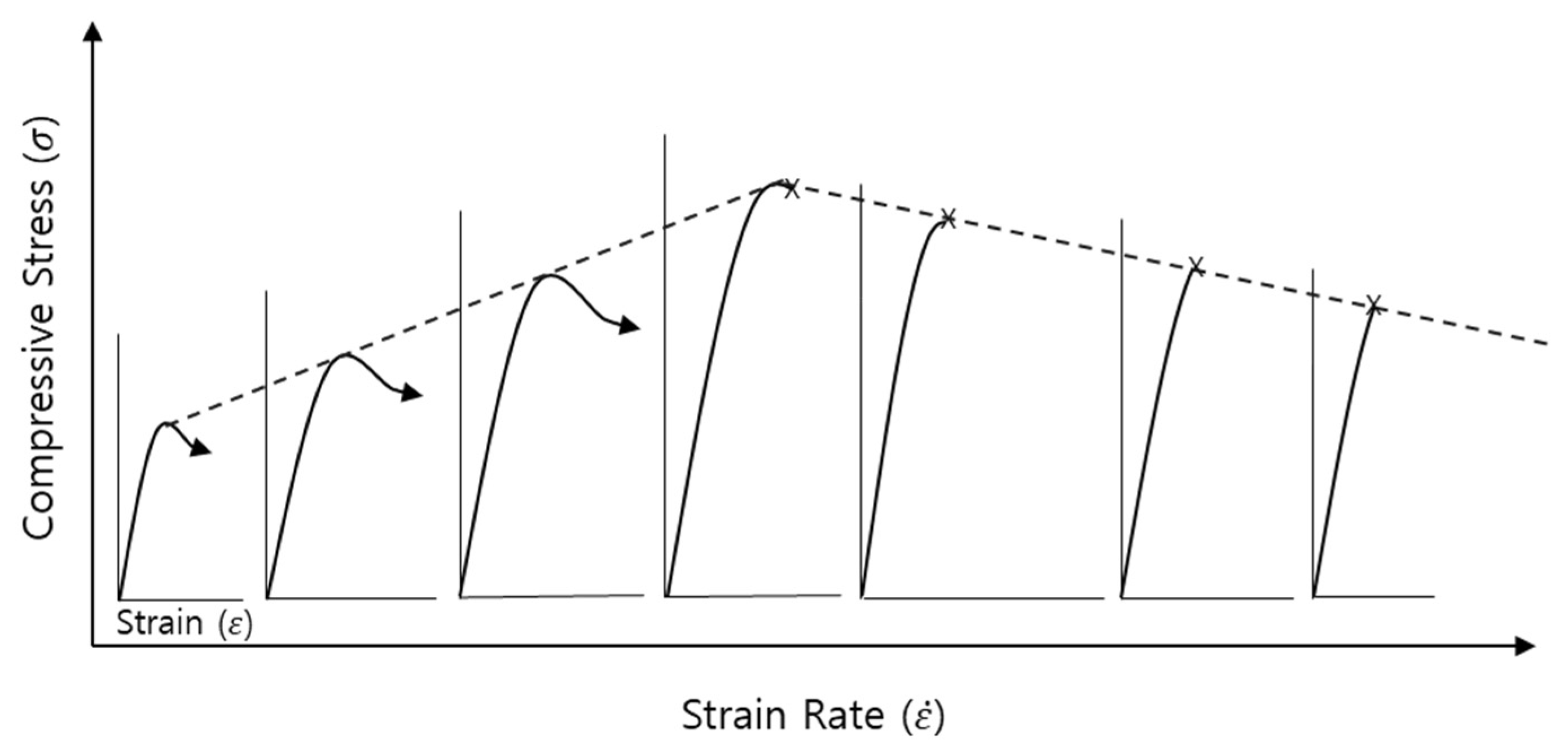
2. Ice Collision Interactions and Problem Definition
3. Configuration of the Ice-Collision-Pendulum Tests
3.1. Overview of Ice-Collision-Pendulum Apparatus
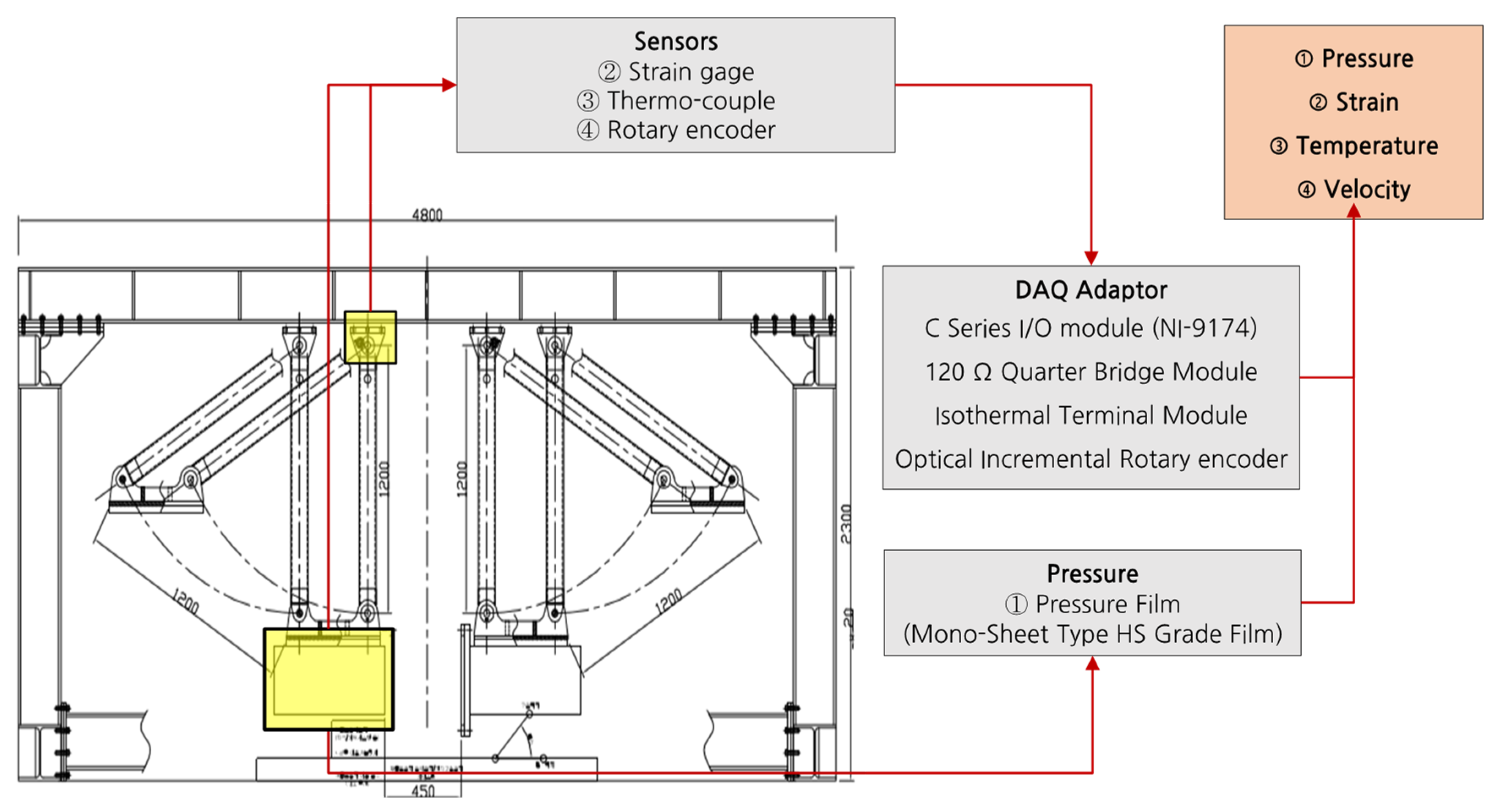
3.2. Experimental Measurement System Configuration
- The time-dependent strain on the plate specimen was measured by a strain gauge.
- The angular velocity of the pendulum was captured by a rotary encoder.
- The ambient temperature in the laboratory was recorded by a K-type thermocouple.

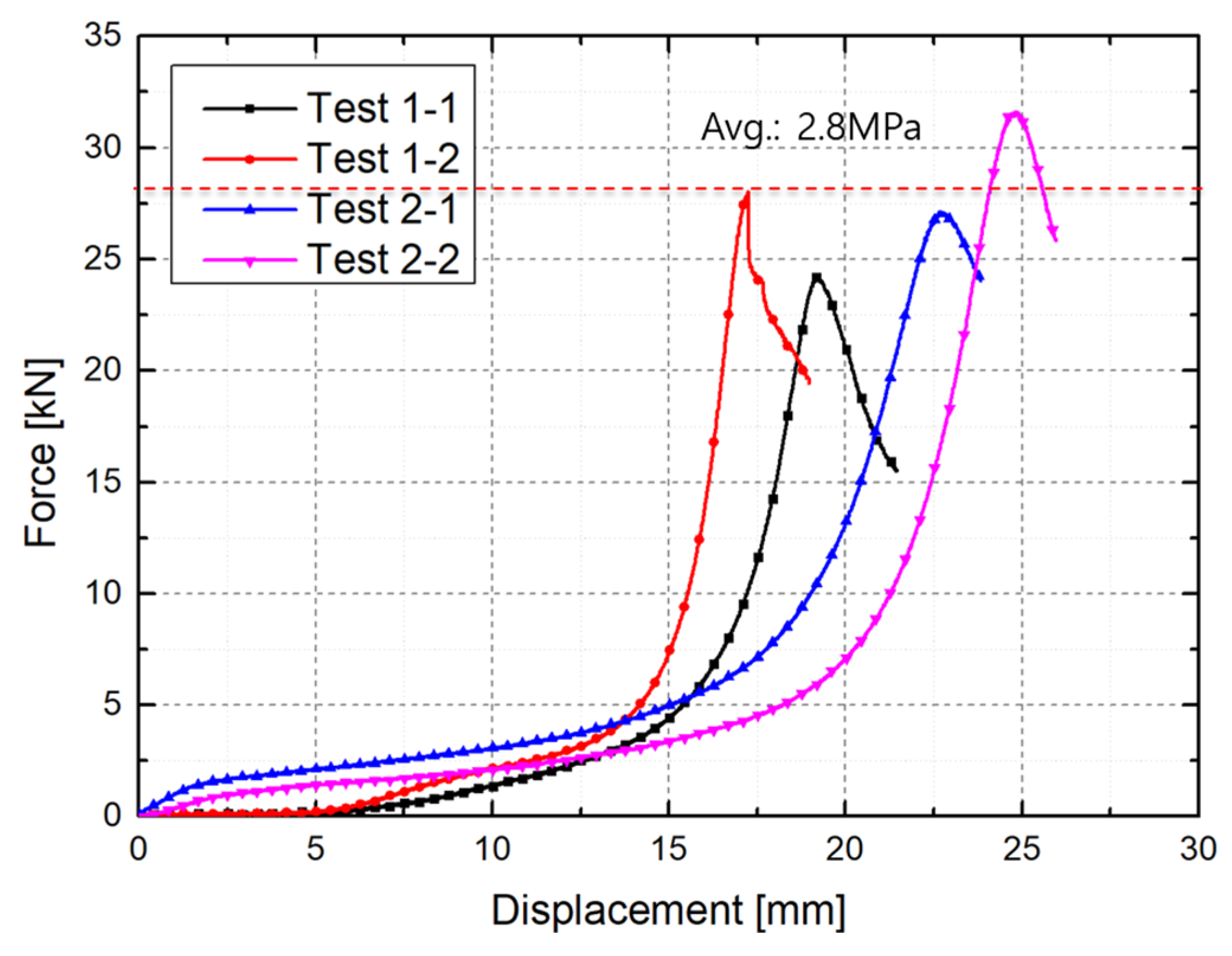
3.3. Ice Specimen Fabrication and Strength Measurement
4. Ice-Collision-Experiment Results
4.1. Experimental Conditions
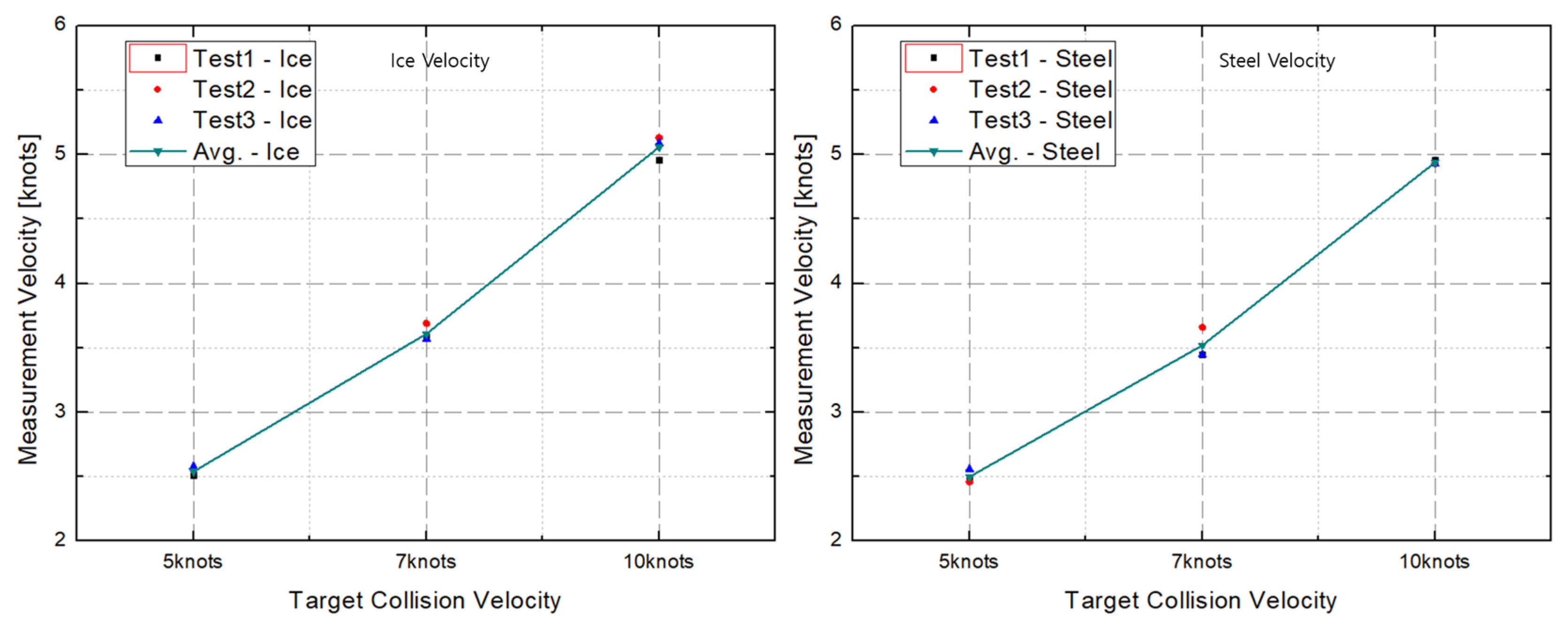
4.2. Measurement of Collision Velocity
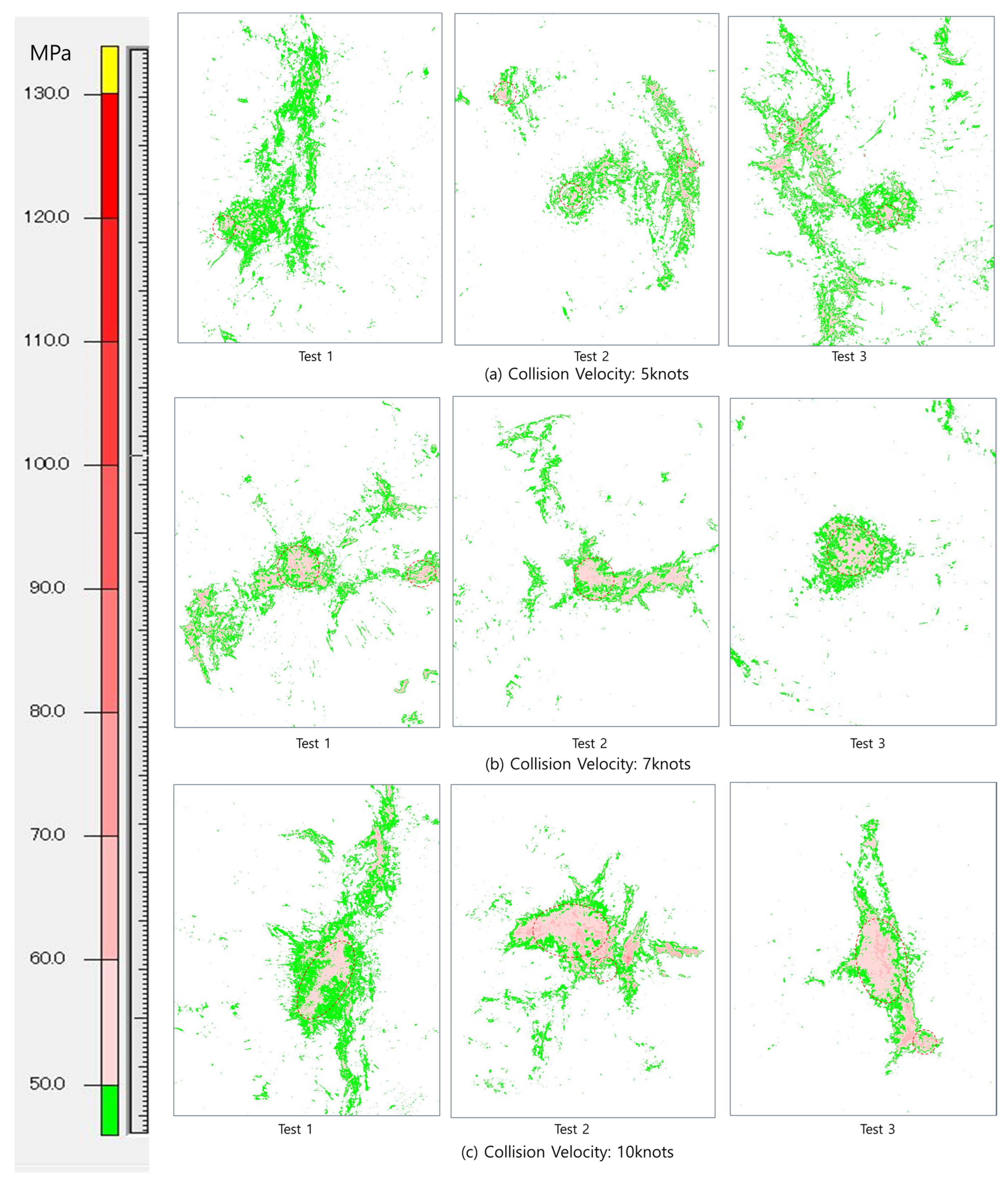
4.3. Fracture Patterns and Pressure Distribution in the Ice Specimens Post-Collision
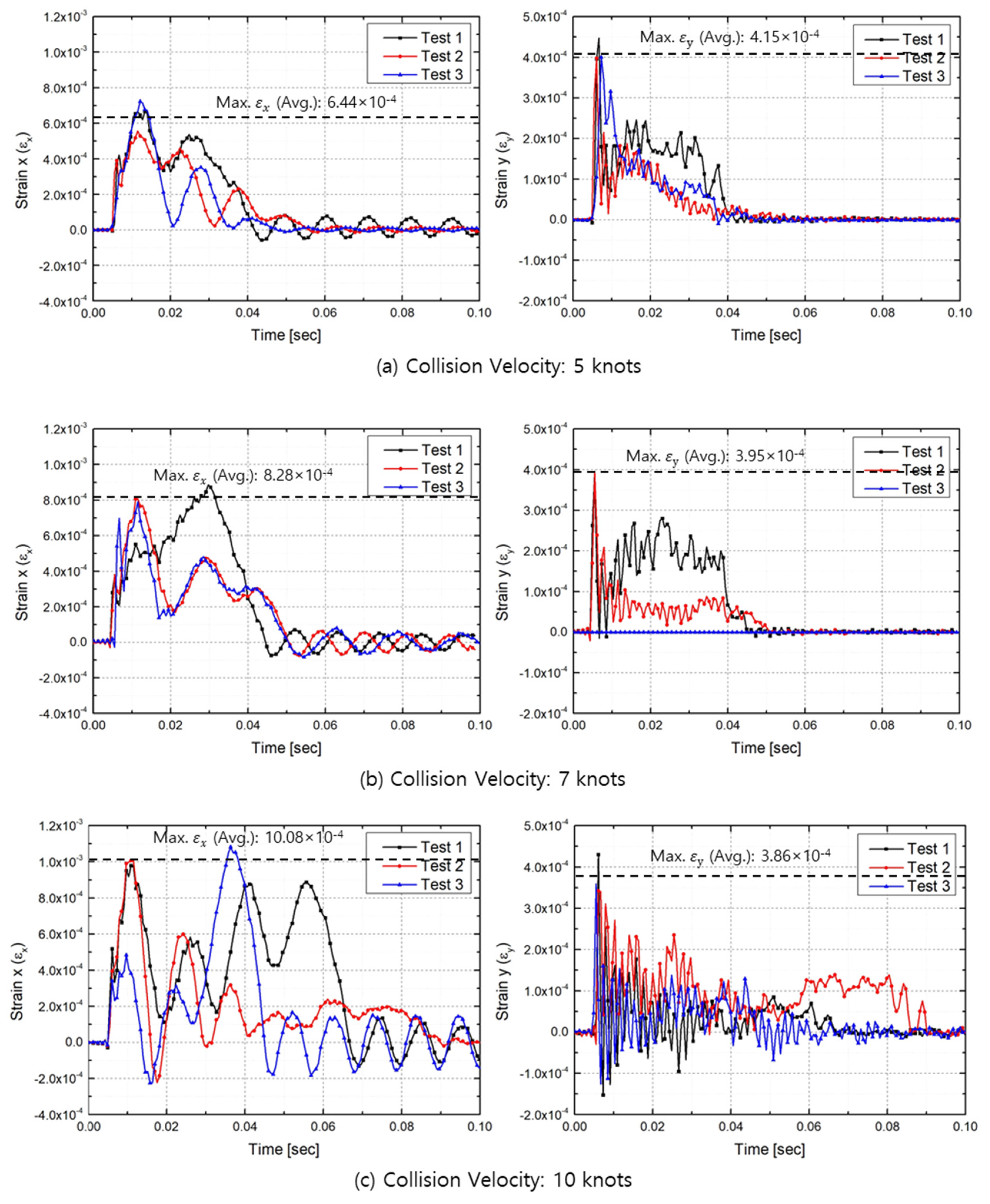
4.4. Strain History of Steel Specimen
4.5. Simplified Numerical Model to Simulate Experiments
4.6. Analysis of Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FSICR. Ice Class Regulations 2010: Finnish-Swedish Ice Class Rules 2010; Finnish Transport Safety Agency: Helsinki, Finland, 2010; p. 48. [Google Scholar]
- Hill, B.T. Ship collision with iceberg database. In Proceedings of the 7th International Conference and Exhibition on Performance of Ships and Structures in Ice, Banff, AB, Canada, 16–19 July 2006; pp. 16–19. [Google Scholar]
- Kärnä, T.; Kamesaki, K.; Tsukuda, H. A numerical model for dynamic ice-structure interaction. Comput. Struct. 1999, 72, 645–658. [Google Scholar] [CrossRef]
- Leira, B.; Børsheim, L.; Espeland, O.; Amdahl, J. Ice-Load Estimation for a Ship Hull Based on Continuous Response Monitoring. J. Eng. Marit. Environ. 2009, 223, 529–540. [Google Scholar] [CrossRef]
- Suyuthi, A.; Leira, B.J.; Riska, K. Fatigue damage of ship hulls due to local ice-induced stresses. Appl. Ocean. Res. 2013, 42, 87–104. [Google Scholar] [CrossRef]
- Suyuthi, A.; Leira, B.J.; Riska, K. Statistics of local ice load peaks on ship hulls. Struct. Saf. 2013, 40, 1–10. [Google Scholar] [CrossRef]
- Suominen, M.; Li, F.; Lu, L.; Kujala, P.; Bekker, A.; Lehtiranta, J. Effect of maneuvering on ice-induced loading on ship hull: Dedicated full-scale tests in the Baltic Sea. J. Mar. Sci. Eng. 2020, 8, 759. [Google Scholar] [CrossRef]
- Hu, J.; Zhou, L. Experimental and numerical study on ice resistance for icebreaking vessels. Int. J. Nav. Arch. Ocean. Eng. 2015, 7, 626–639. [Google Scholar] [CrossRef]
- Zhou, L.; Chuang, Z.; Ji, C. Ice forces acting on towed ship in level ice with straight drift. Part I: Analysis of model test data. Int. J. Nav. Archit. Ocean. Eng. 2018, 10, 60–68. [Google Scholar] [CrossRef]
- Choi, Y.H.; Choi, H.Y.; Lee, C.S.; Kim, M.H.; Lee, J.M. Suggestion of a design load equation for ice-ship impacts. Int. J. Nav. Arch. Ocean. 2012, 4, 386–402. [Google Scholar] [CrossRef]
- Yu, T.Q.; Wang, J.X.; Liu, J.J.; Liu, K. Experimental and Numerical Simulation of the Dynamic Response of a Stiffened Panel Suffering the Impact of an Ice Indenter. Metals 2022, 12, 505. [Google Scholar] [CrossRef]
- Quinton, B.W. Progressive Damage to a Ship’s Structure Due to Ice Loading. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2008. [Google Scholar]
- Zhu, L.; Qiu, X.; Chen, M.; Yu, T.X. Simplified ship-ice collision numerical simulations. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–1 July 2016. [Google Scholar]
- Zhu, L.; Cai, W.; Chen, M.; Tian, Y.; Bi, L. Experimental and numerical analyses of elastic-plastic responses of ship plates under ice floe impacts. Ocean. Eng. 2020, 218, 108174. [Google Scholar] [CrossRef]
- Cai, W.; Zhu, L.; Yu, T.X.; Li, Y.G. Numerical simulations for plates under ice impact based on a concrete constitutive ice model. Int. J. Impact Eng. 2020, 143, 103594. [Google Scholar] [CrossRef]
- Glen, I.; Comfort, G. Ice Impact Pressure and Load: Investigation by Laboratory Experiments and Ship Trials. In Proceedings of the Seventh International Conference on Port and Ocean Engineering Under Arctic Conditions, Helsinki, Finland, 5–9 April 1983. [Google Scholar]
- Gagnon, R.; Daley, C.; Colbourne, B. A large double-pendulum device to study load, pressure distribution and structure damage during ice impact tests in the lab. In Proceedings of the International Conference on Port and Ocean Engineering Under Arctic Conditions, Trondheim, Norway, 14–18 June 2015. [Google Scholar]
- Gagnon, R.; Andrade, S.; Quinton, B.; Daley, C.; Colbourne, B. Pressure distribution data from large double-pendulum ice impact tests. Cold Reg. Sci. Technol. 2020, 175, 103033. [Google Scholar] [CrossRef]
- Clarke, G.S. Ice Collision Experiments with a Pendulum Impact Apparatus. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2012. [Google Scholar]
- Lande Andrade, S.; Elruby, A.Y.; Hipditch, E.; Daley, C.G.; Quinton, B.W. Full-scale ship-structure ice impact laboratory experiments: Experimental apparatus and initial results. Ships Offshore Struct. 2023, 18, 500–514. [Google Scholar] [CrossRef]
- Zhang, M. Ice Load Prediction for Design of Ice-Going Ships for Inland Waterways. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2019. [Google Scholar]
- Zhang, N.; Zheng, X.; Ma, Q. Updated smoothed particle hydrodynamics for simulating bending and compression failure progress of ice. Water 2017, 9, 882. [Google Scholar] [CrossRef]
- Gao, Y.; Hu, Z.; Wang, J. Sensitivity analysis for iceberg geometry shape in ship-iceberg collision in view of different material models. Math. Probl. Eng. 2014, 2014, 414362. [Google Scholar] [CrossRef]
- Kubat, I.; Timco, G. Vessel damage in the Canadian Arctic. In Proceedings of the International Conference on Port and Ocean Engineering Under Arctic Conditions, Trondheim, Norway, 16–19 June 2003. [Google Scholar]
- Zhou, L.; Gao, J.; Li, D. An engineering method for simulating dynamic interaction of moored ship with first-year ice ridge. Ocean. Eng. 2019, 171, 417–428. [Google Scholar] [CrossRef]
- Arakawa, M.; Maeno, N.; Higa, M.; Iijima, Y.-I.; Kato, M. Ejection velocity of ice impact fragments. Icarus 1995, 118, 341–354. [Google Scholar] [CrossRef]
- Kim, H.; Welch, D.A.; Kedward, K.T. Experimental investigation of high velocity ice impacts on woven carbon/epoxy composite panels. Compos. Part. A Appl. Sci. Manuf. 2003, 34, 25–41. [Google Scholar] [CrossRef]
- Tippmann, J.D. Development of a Strain Rate Sensitive Ice Material Model for Hail Ice Impact Simulation; University of California: San Diego, CA, USA, 2011. [Google Scholar]
- Tippmann, J.D.; Kim, H.; Rhymer, J.D. Experimentally validated strain rate dependent material model for spherical ice impact simulation. Int. J. Impact Eng. 2013, 57, 43–54. [Google Scholar] [CrossRef]
- Combescure, A.; Chuzel-Marmot, Y.; Fabis, J. Experimental study of high-velocity impact and fracture of ice. Int. J. Solids Struct. 2011, 48, 2779–2790. [Google Scholar]
- Chai, W.; Leira, B.J.; Høyland, K.V.; Sinsabvarodom, C.; Yu, Z. Statistics of thickness and strength of first-year ice along the Northern Sea Route. J. Mar. Sci. Technol. 2021, 26, 331–343. [Google Scholar] [CrossRef]
- Kim, S.-Y.; Choi, K. Standardization of laboratory experimental techniques with a cold room in Korea. In Proceedings of the 18th IAHR International Symposium on Ice, Sapporo, Japan, 28 August–1 September 2006. [Google Scholar]
- Kim, J.-H.; Choi, K.-S.; Seo, Y.-K. Standardization of Ice Mechanics Experimental Procedures in a Cold Room. J. Ocean. Eng. Technol. 2007, 21, 60–66. [Google Scholar]
- Kim, J.-H.; Choi, K.-S. Comparison of EG/AD/S and EG/AD model ice properties. Int. J. Ocean. Syst. Eng. 2011, 1, 32–36. [Google Scholar] [CrossRef]
- Kim, H.; Daley, C.; Colbourne, B. Comparison of Ice Load Development on Non-Planar Surface. Int. J. Offshore Polar Eng. 2015, 25, 194–204. [Google Scholar] [CrossRef]
- Choi, K.; Kim, J.; Seo, Y. An experiment for the mechanical properties of model ice grown in a cold room. In Proceedings of the 19th IAHR Ice Symposium, Vancouver, BC, Canada, 6–11 July 2008; pp. 985–992. [Google Scholar]
- Cho, S.-R.; Jeong, S.-Y.; Ha, J.-S.; Kang, K.-J. An experimental study on generation and measurement method of EG/AD model ice at cold room for improvement of its properties. J. Soc. Nav. Archit. Korea 2013, 50, 414–420. [Google Scholar] [CrossRef]
- Bruneau, S.E.; Dillenburg, A.K.; Ritter, S. Ice sample production techniques and indentation tests for laboratory experiments simulating ship collisions with ice. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Anchorage, AK, USA, 30 June–5 July 2013. [Google Scholar]
- Do, Y.; Kim, Y. Basic Experimental Study for Ice-Concrete Friction Behavior. J. Soc. Nav. Archit. Korea 2020, 57, 365–372. [Google Scholar] [CrossRef]
- Batto, R.A.; Schulson, E.M. On the Ductile-to-Brittle Transition in Ice under Compression. Acta Met. Mater. 1993, 41, 2219–2225. [Google Scholar] [CrossRef]
- Schulson, E.M. Brittle failure of ice. Eng. Fract. Mech. 2001, 68, 1839–1887. [Google Scholar] [CrossRef]
- Carney, K.S.; Benson, D.J.; DuBois, P.; Lee, R. A phenomenological high strain rate model with failure for ice. Int. J. Solids Struct. 2006, 43, 7820–7839. [Google Scholar] [CrossRef]
- Kim, H.; Daley, C. Characteristics of ice crushing pressure on non-planar surface. In Proceedings of the SNAME Maritime Convention, Bellevue, WA, USA, 6–8 November 2013. [Google Scholar] [CrossRef]
- Kim, H.; Daley, C.; Colbourne, B. A numerical model for ice crushing on concave surfaces. Ocean. Eng. 2015, 106, 289–297. [Google Scholar] [CrossRef]
- Kim, H.; Quinton, B. Evaluation of moving ice loads on an elastic plate. Mar. Struct. 2016, 50, 127–142. [Google Scholar] [CrossRef]
- Wells, J.; Jordaan, I.; Derradji-Aouat, A.; Taylor, R. Small-scale laboratory experiments on the indentation failure of polycrystalline ice in compression: Main results and pressure distribution. Cold Reg. Sci. Technol. 2011, 65, 314–325. [Google Scholar] [CrossRef]
- Gagnon, R.E. A numerical model of ice crushing using a foam analogue. Cold Reg. Sci. Technol. 2011, 65, 335–350. [Google Scholar] [CrossRef]
- Kajaste-Rudnitski, J.; Kujala, P. Ship propagation through ice field. J. Struct. Mech. 2014, 47, 34–49. [Google Scholar]
- Han, D.; Lee, H.; Choung, J.; Kim, H.; Daley, C. Cone ice crushing tests and simulations associated with various yield and fracture criteria. Ships Offshore Struc. 2017, 12, S88–S99. [Google Scholar] [CrossRef]
- Kim, H. Simulation of compressive ‘cone-shaped’ ice specimen experiments using LS-DYNA. In Proceedings of the 13th International LS-DYNA Users Conference, Dearborn, MI, USA, 8–10 June 2014. [Google Scholar]
- Daley, C. Energy based ice collision forces. In Proceedings of the Proceedings of the 15th International Conference on Port and Ocean Engineering under Arctic Conditions (POAC), Espoo, Finland, 23–27 August 1999; pp. 674–686. [Google Scholar]
- Daley, C.; Kim, H. Ice collision forces considering structural deformation. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Nantes, France, 16–17 February 2010; pp. 817–825. [Google Scholar]
- Zhang, M.; Garme, K.; Burman, M.; Zhou, L. A numerical ice load prediction model based on ice-hull collision mechanism. Appl. Sci. 2020, 10, 692. [Google Scholar] [CrossRef]
- Cai, W.; Zhu, L.; Gudmestad, O.T.; Guo, K.L. Application of rigid-plastic theory method in ship-ice collision. Ocean. Eng. 2022, 253, 111237. [Google Scholar] [CrossRef]









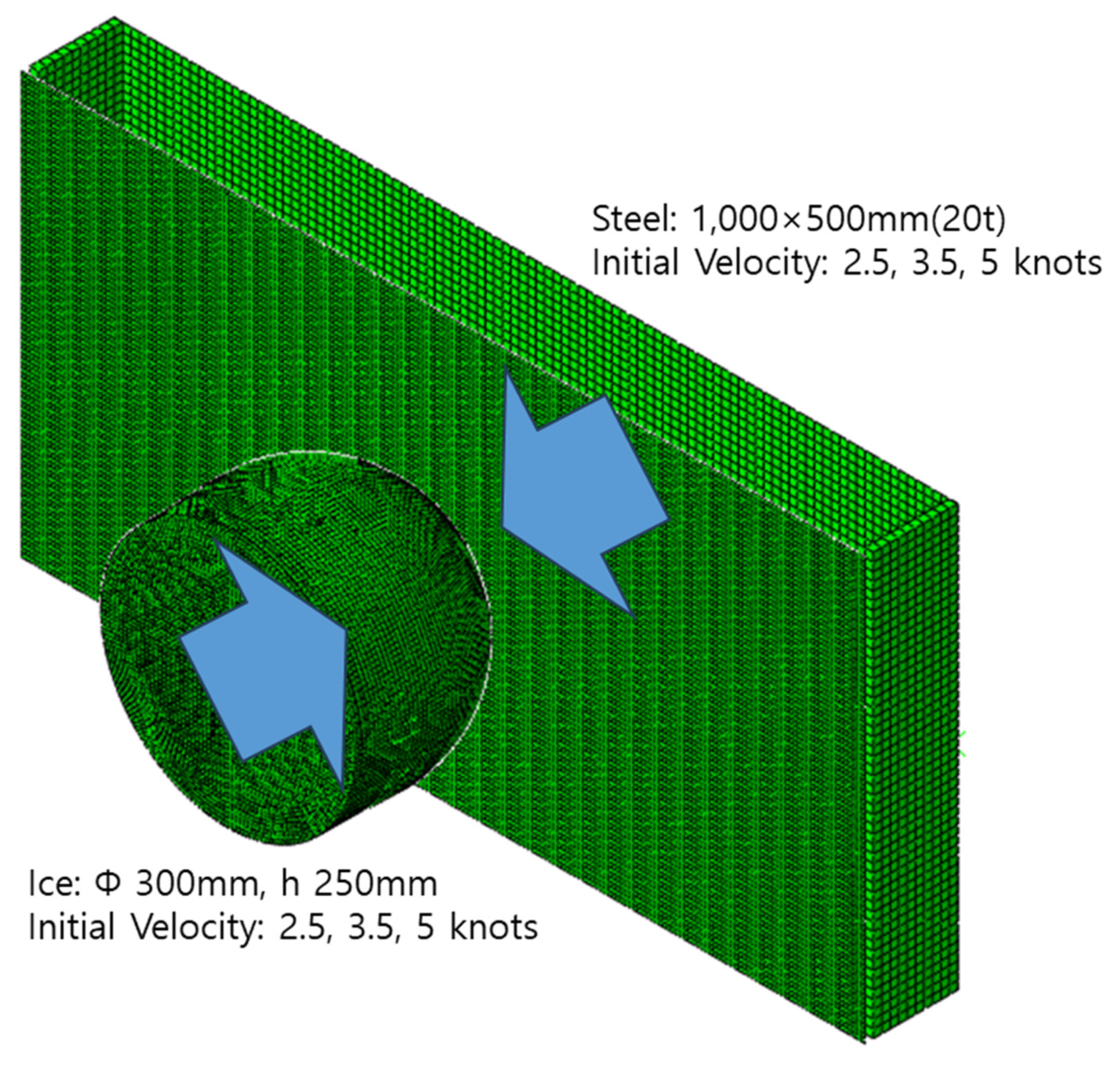


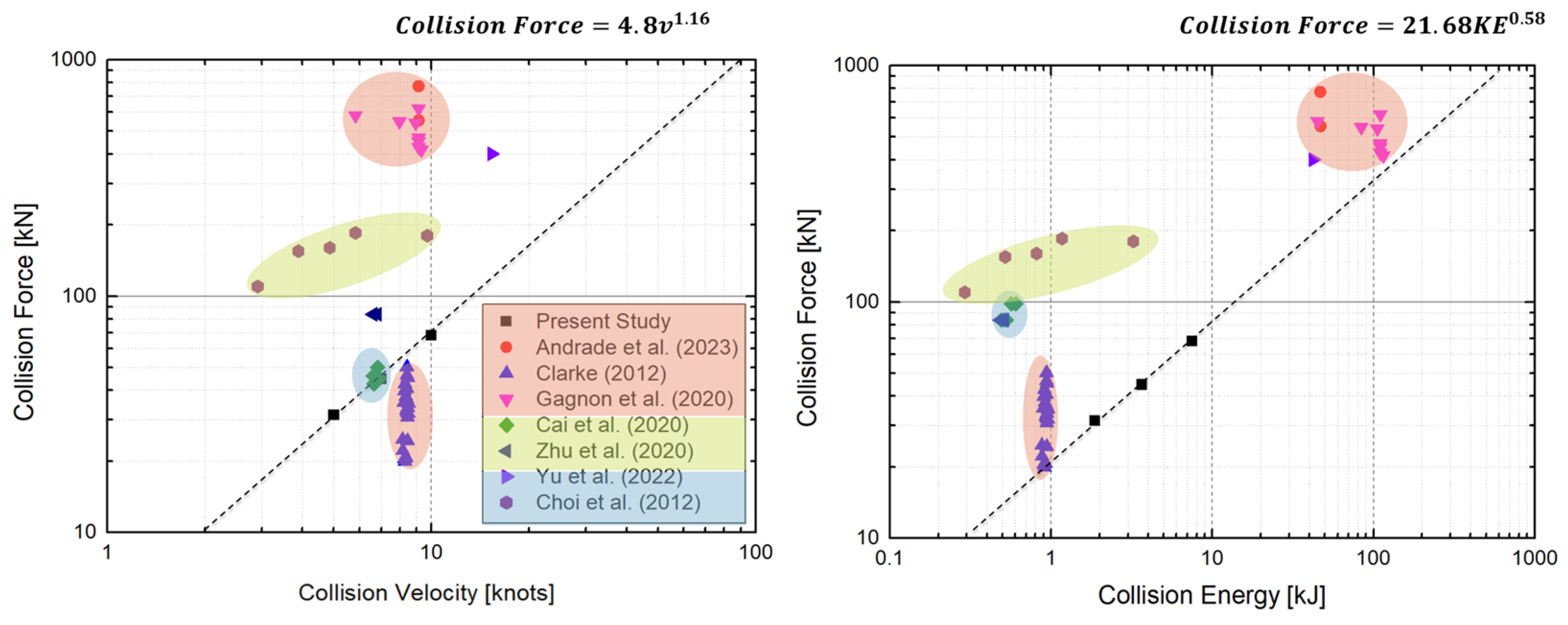
| Collision Speed | Collision Type | Collision Velocity | Ice Mass () | Reference |
|---|---|---|---|---|
| High speed (aerospace) | Droplet | 30~530 m/s | 3.2 g | Arakawa et al. [26] |
| Projectile | 30~200 m/s | 60~500 g | Kim et al. [27] Tippmann [28] Tippmann et al. [29] | |
| Projectile | 62.5 and 127.5 m/s | 7.3 g | Combescure et al. [30] | |
| Low speed (marine) | Free drop | 1.5~5.0 m/s | 260~300 kg | Choi et al. [10] |
| 7.9 m/s | 1340 kg | Yu et al. [11] | ||
| Trolley | 2.0~3.5 m/s | 80~90 kg | Zhu et al. [13,14] | |
| Cai et al. [15] | ||||
| Pendulum | 5.32 m/s | 1000 kg (ice + carriage) | Clarke [19] | |
| 4.7 m/s | 4650 kg (ice + carriage) | Andrade [20] Gagnon et al. [18] |
| Specification | Attribute | Value |
|---|---|---|
| Collision speed | Normal collision speed | 3–10 kts |
| Max collision speed | 11 (kts) (5.8 (m/s)) | |
| Collision energy | Max kinetic energy | 7000 (J) (20t) |
| Dimensions | Chamber size (LBH) | 5 × 2 × 2.3 (m) |
| Arm length () | 1.2 (m) | |
| Max angle | 45 (degree) | |
| Max height () | 0.4 (m) | |
| Specimen | Steel specimen (Plain plate) | 1 × 0.5 (m) (20t) |
| 79.8 kg | ||
| Ice specimen (Hemi-spherical shape) | D: 300 mm, h: 250 mm | |
| 25.7 kg |
| Test | Size (mm) | Temperature (°C) |
|---|---|---|
| Test 1 (2 ea.) | 100 × 100 × 300 | −20 |
| Test 2 (2 ea.) | 100 × 100 × 250 | −20 |
| Test Condition | Value | |
|---|---|---|
| Ice specimens (hemispherical) | Size | D = 300, h = 250 |
| Weight | 35 kg | |
| Steel plate (thickness = 20 mm) | Size (mm) | 1000 × 500 |
| Weight | 78 kg | |
| Ice holder | Weight | 8 kg |
| Pendulum | Weight | 120 kg |
| Steel-plate jig | Weight | 208 kg |
| Temperature | Room | −20 °C |
| Collision velocity | Relative velocity | 5, 7, and 10 knots |
| Target Speed | Test 1 | Test 2 | Test 3 | Average |
|---|---|---|---|---|
| 5 Knots | 4.99 | 5.01 | 5.14 | 5.04 |
| 7 Knots | 7.04 | 7.25 | 7.02 | 7.10 |
| 10 Knots | 9.92 | 10.06 | 10.02 | 10.00 |
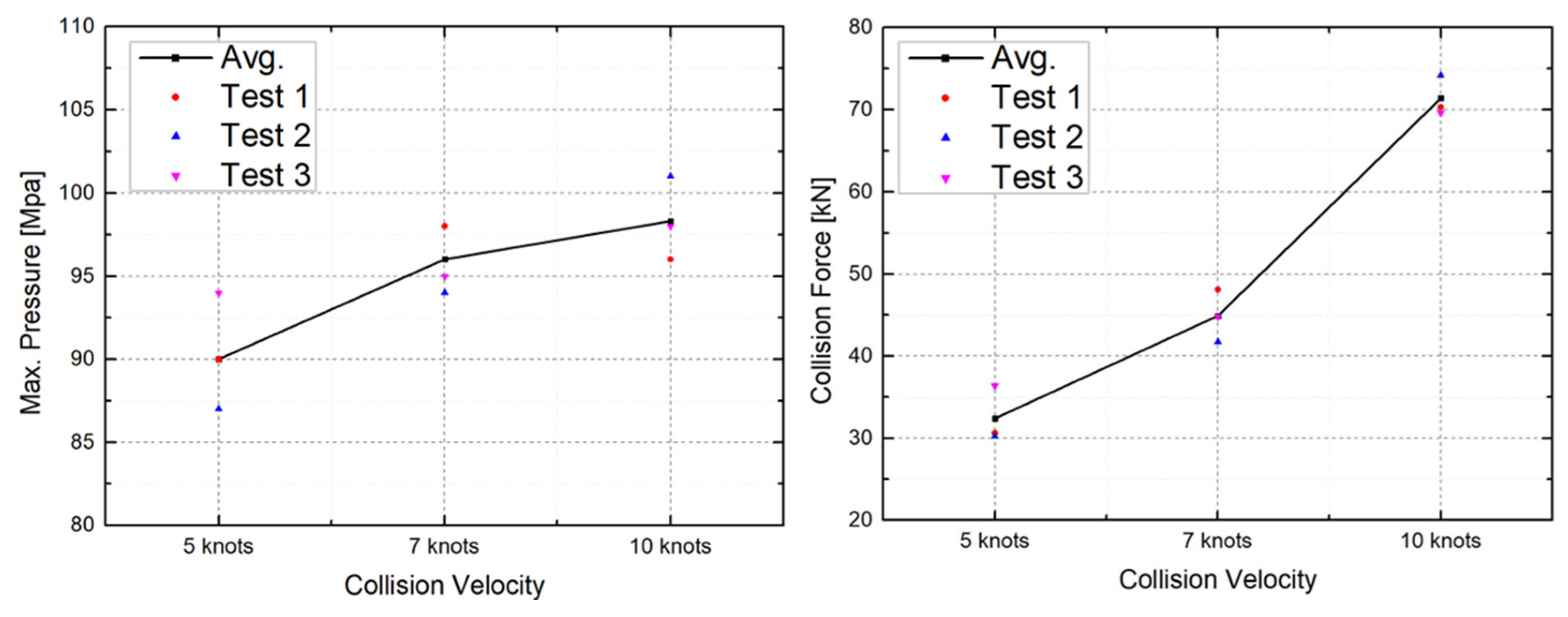
| Measured Variables | Collision Velocity | Test 1 | Test 2 | Test 3 |
|---|---|---|---|---|
| Max pressure (MPa) | 5 knots | 90 | 87 | 94 |
| 7 knots | 98 | 94 | 95 | |
| 10 knots | 96 | 101 | 98 | |
| Avg. pressure () | 5 knots | 77 | 78 | 74 |
| 7 knots | 79 | 77 | 90 | |
| 10 knots | 83 | 84 | 80 | |
| Pressure area () | 5 knots | 3.5 | 3.9 | 4.4 |
| 7 knots | 5.8 | 5.1 | 5.0 | |
| 10 knots | 7.5 | 6.9 | 7.1 | |
| Collision force () | 5 knots | 30.6 | 30.2 | 36.4 |
| 7 knots | 48.1 | 41.7 | 44.8 | |
| 10 knots | 70.3 | 74.2 | 69.6 |
| Measurement | 5 Knots | 7 Knots | 10 Knots |
|---|---|---|---|
| Max pressure () | 90.3 | 95.7 | 98.3 |
| Avg. pressure () | 76.3 | 78.5 | 82.2 |
| Pressure area () | 3.9 | 5.3 | 7.2 |
| Collision force () | 32.4 | 44.9 | 71.4 |
| Collision Velocity | Strain | Test 1 | Test 2 | Test 3 |
|---|---|---|---|---|
| 5 knots | Max | 6.36 × 10−4 | 5.84 × 10−4 | 7.13 × 10−4 |
| Max | 4.47 × 10−4 | 3.96 × 10−4 | 4.45 × 10−4 | |
| 7 knots | Max | 8.85 × 10−4 | 8.08 × 10−4 | 7.92 × 10−4 |
| Max | 3.96 × 10−4 | 3.93 × 10−4 | N/A | |
| 10 knots | Max | 1.04 × 10−4 | 1.07 × 10−4 | 1.15 × 10−4 |
| Max | 4.45 × 10−4 | 3.49 × 10−4 | 3.64 × 10−4 |
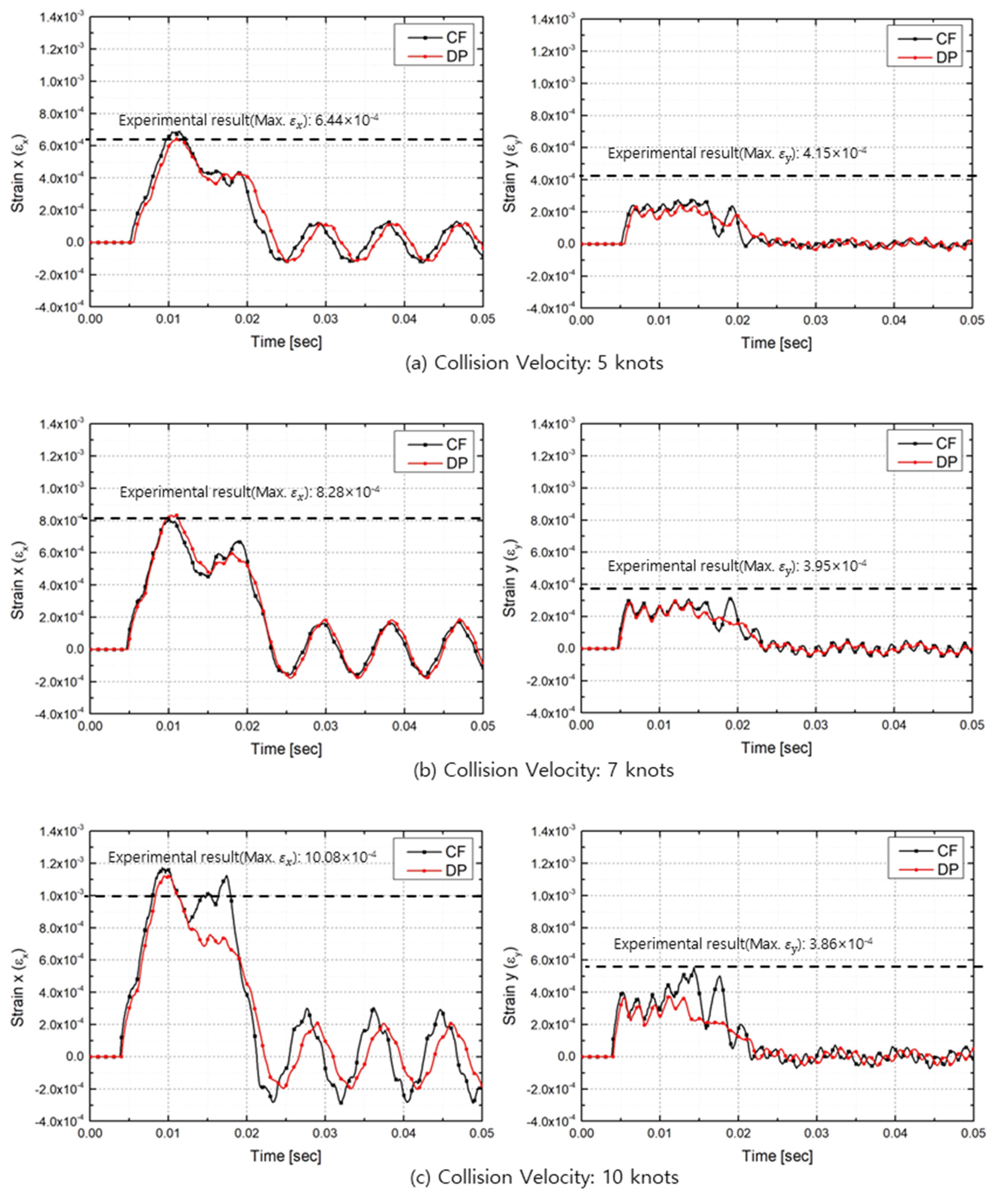
| Strain | Collision Velocity | Exp. (Avg.) | FEA with CF | FEA with DP |
|---|---|---|---|---|
| Max (Difference %) | 5 knots | 6.44 × 10−4 | 6.90 × 10−4 (7.1%) | 6.43 × 10−4 (0.2%) |
| 7 knots | 8.85 × 10−4 | 8.06 × 10−4 (8.9%) | 8.63 × 10−4 (2.2%) | |
| 10 knots | 10.80 × 10−4 | 11.71 × 10−4 (8.3%) | 11.08 × 10−4 (2.8%) | |
| Avg. Difference | – | 8.1% | 1.7% | |
| Max (Difference %) | 5 knots | 4.10 × 10−4 | 2.80 × 10−4 (31.7%) | 2.40 × 10−4 (41.5%) |
| 7 knots | 3.96 × 10−4 | 3.12 × 10−4 (21.2%) | 2.99 × 10−4 (24.5%) | |
| 10 knots | 3.74 × 10−4 | 5.53 × 10−4 (47.9%) | 3.76 × 10−4 (0.5%) | |
| Avg. Difference | – | 33.6% | 22.2% |
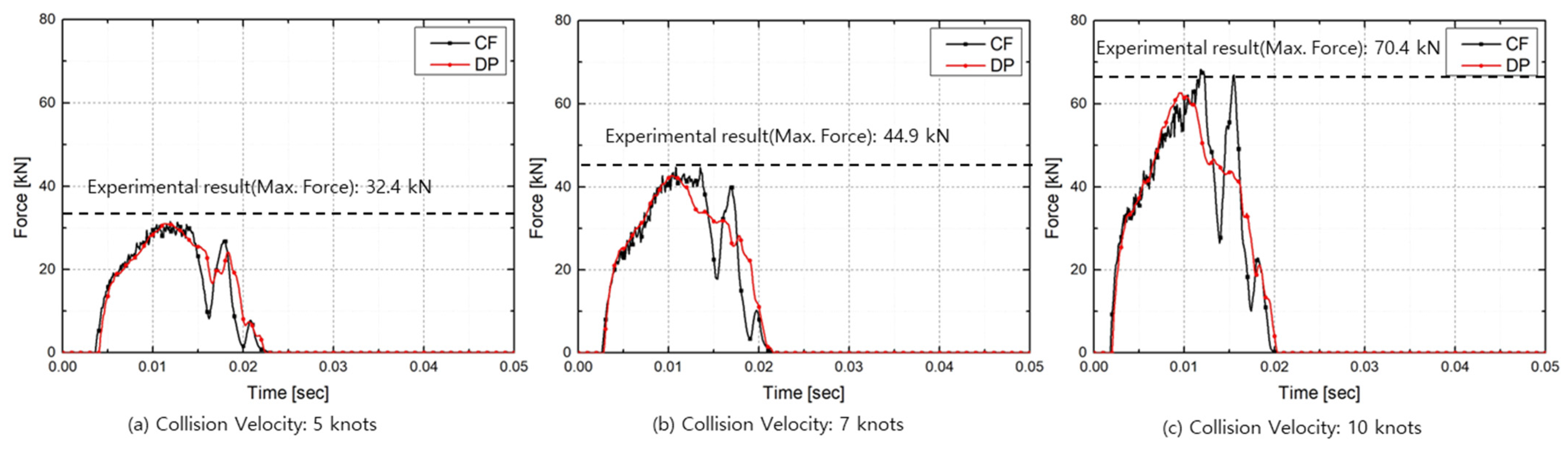
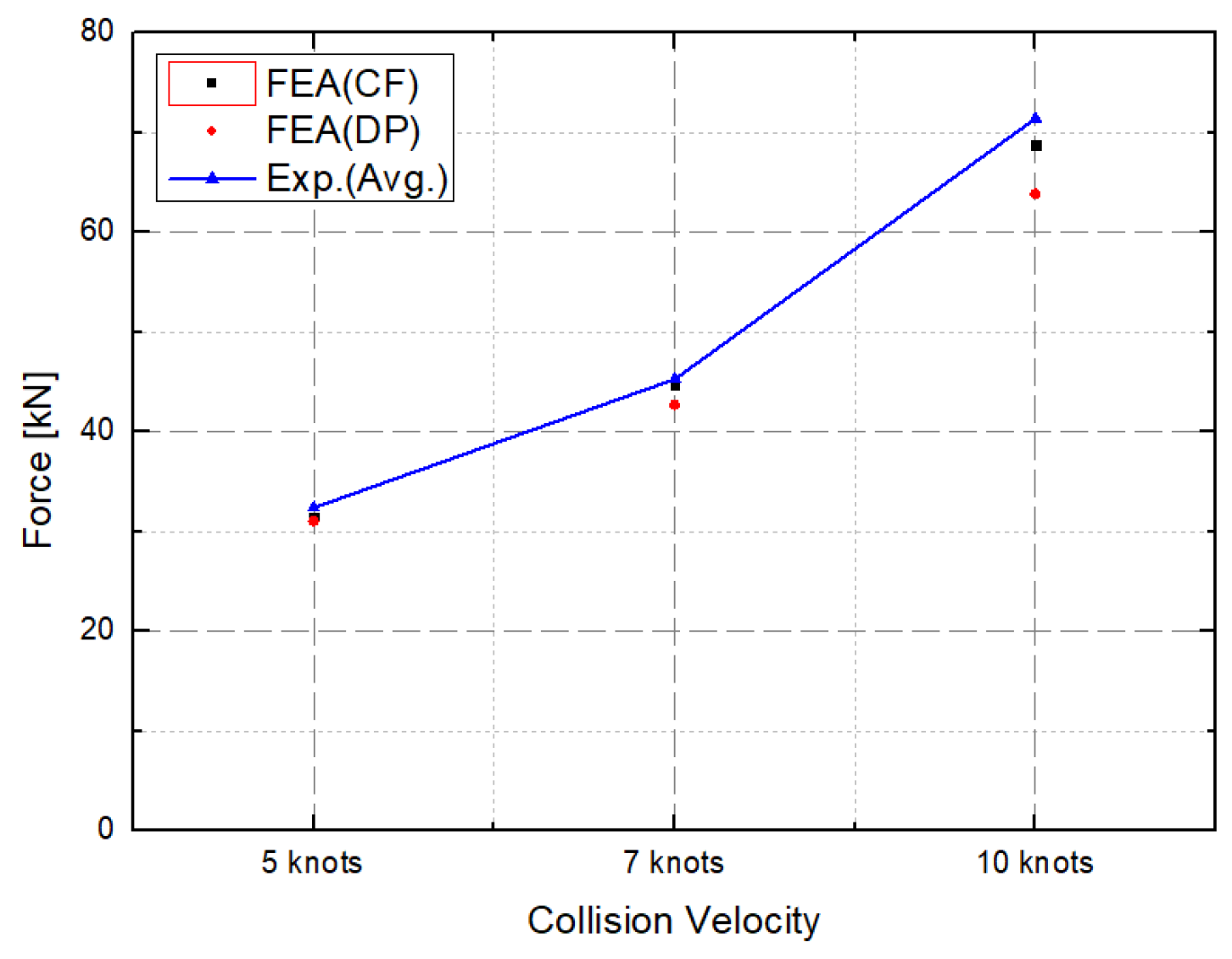
| Collision Velocity | Experiment (kN) | FEA with CF (kN) (Difference (%)) | FEA with DP (kN) (Difference (%)) |
|---|---|---|---|
| 5 knots | 32.4 | 31.47 (2.9%) | 31.05 (4.2%) |
| 7 knots | 45.3 | 44.7 (1.3%) | 42.7 (5.7%) |
| 10 knots | 71.4 | 68.79 (3.6%) | 63.87 (10.5%) |
| Avg. Difference | - | 2.6 % | 6.8 % |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, H.-S.; Hwang, S.-Y.; Lee, J.H. Experimental Evaluation and Validation of Pressure Distributions in Ice–Structure Collisions Using a Pendulum Apparatus. J. Mar. Sci. Eng. 2023, 11, 1761. https://doi.org/10.3390/jmse11091761
Jang H-S, Hwang S-Y, Lee JH. Experimental Evaluation and Validation of Pressure Distributions in Ice–Structure Collisions Using a Pendulum Apparatus. Journal of Marine Science and Engineering. 2023; 11(9):1761. https://doi.org/10.3390/jmse11091761
Chicago/Turabian StyleJang, Ho-Sang, Se-Yun Hwang, and Jang Hyun Lee. 2023. "Experimental Evaluation and Validation of Pressure Distributions in Ice–Structure Collisions Using a Pendulum Apparatus" Journal of Marine Science and Engineering 11, no. 9: 1761. https://doi.org/10.3390/jmse11091761
APA StyleJang, H.-S., Hwang, S.-Y., & Lee, J. H. (2023). Experimental Evaluation and Validation of Pressure Distributions in Ice–Structure Collisions Using a Pendulum Apparatus. Journal of Marine Science and Engineering, 11(9), 1761. https://doi.org/10.3390/jmse11091761








