Transient Translational–Rotational Motion of an Ocean Current Converter Mooring System with Initial Conditions
Abstract
:1. Introduction
2. Mathematical Model
2.1. Dynamic Governing Equations
2.2. Integration of Two Ropes with Different Lengths in Parallel
2.2.1. Relation between Tension and Elongation
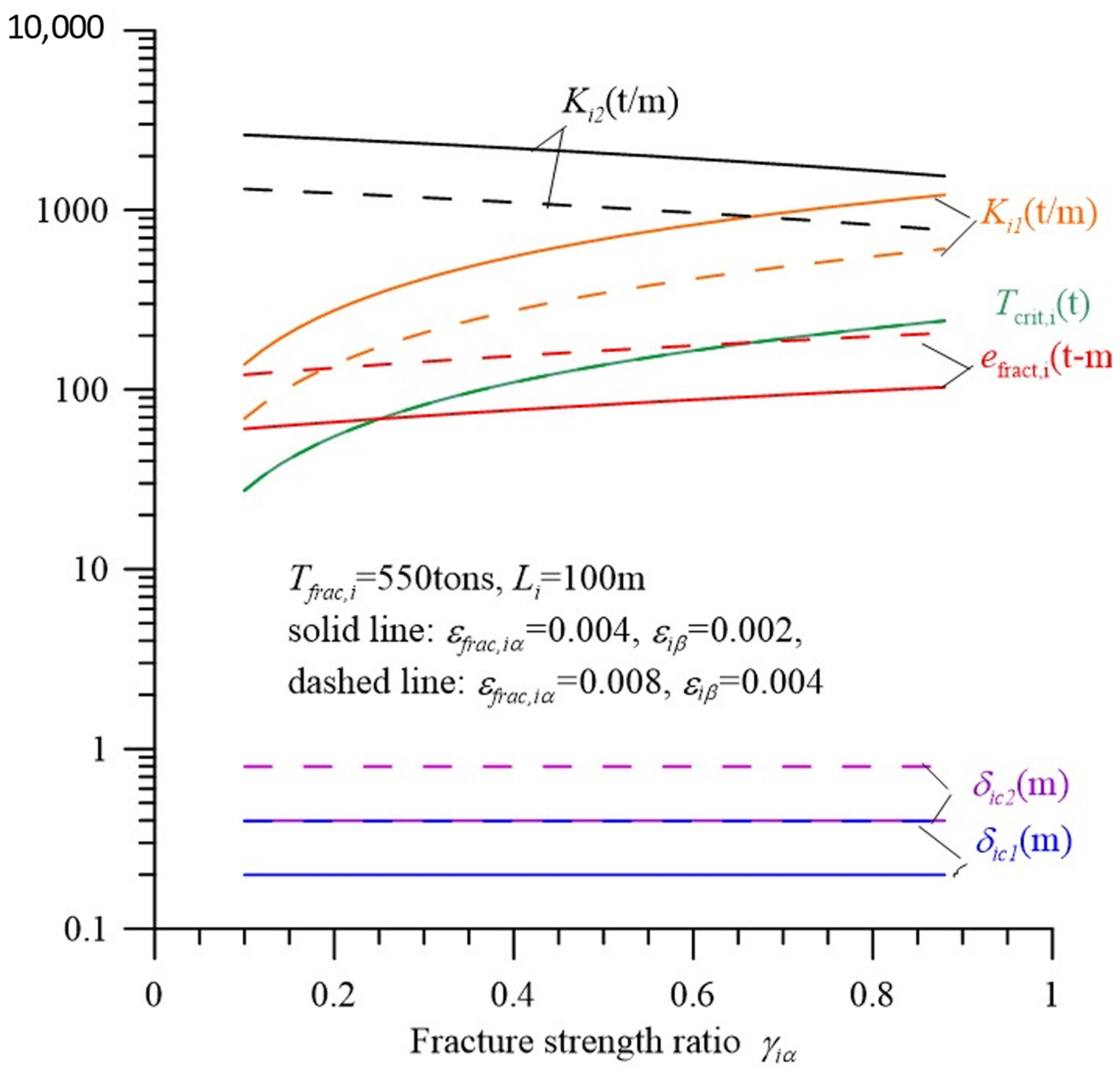
2.2.2. Strain Energy, Effective Spring Constant, and Fracture Strength
2.3. Examples of Integrated Ropes
3. Solution Method
3.1. Transient Response
3.2. Derivation of a Fundamental Solution
4. Numerical Results and Discussion
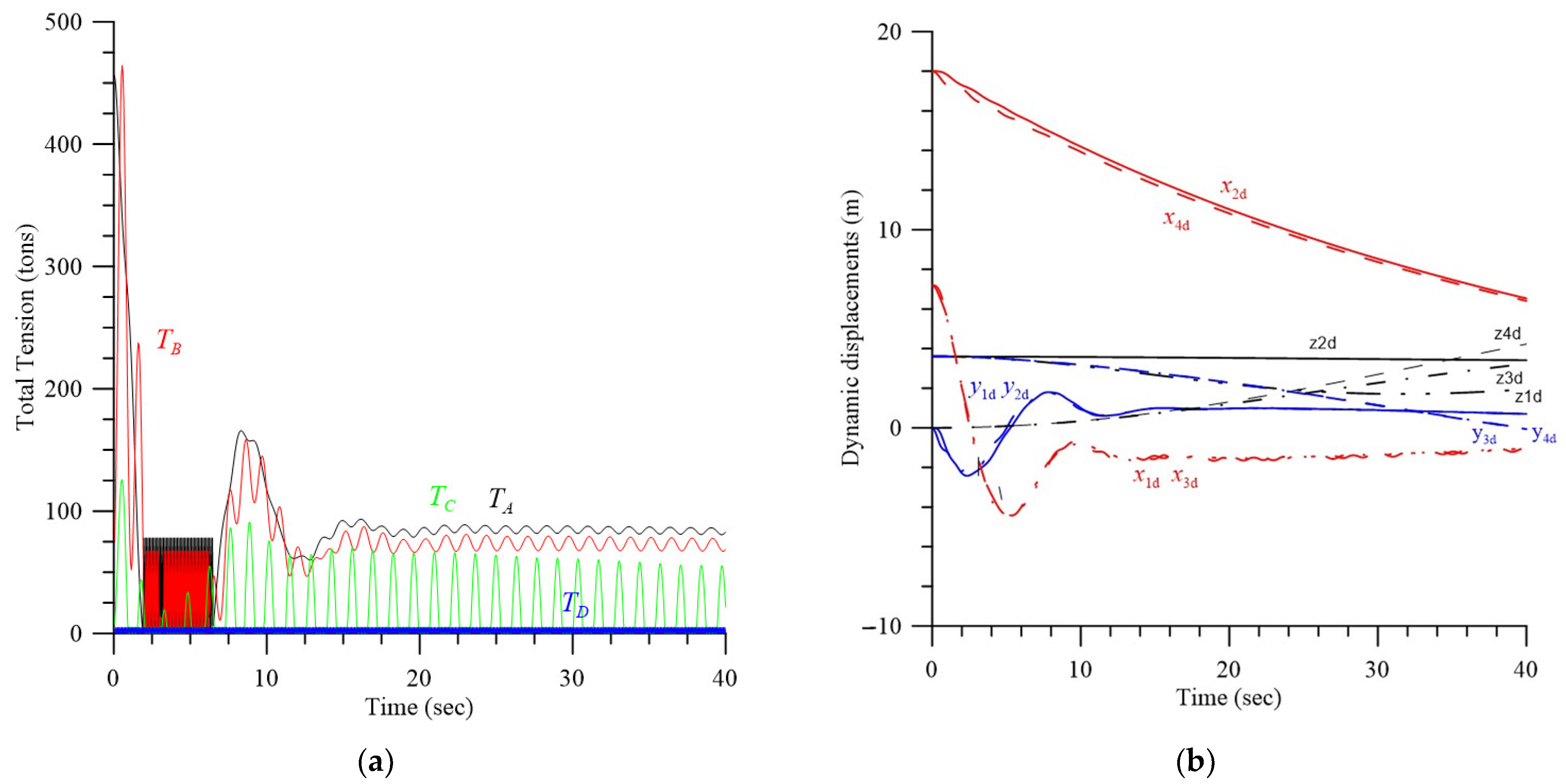
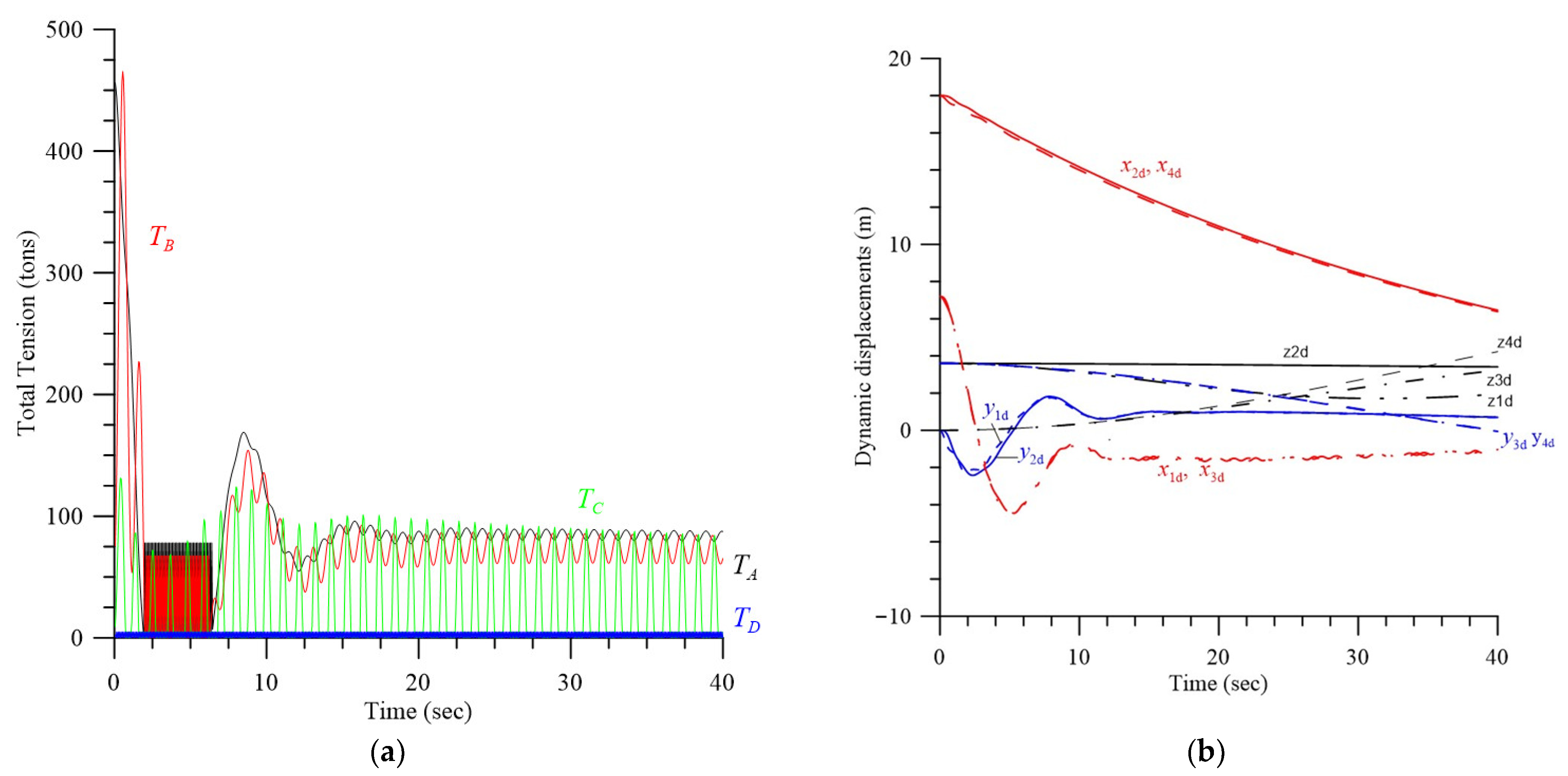
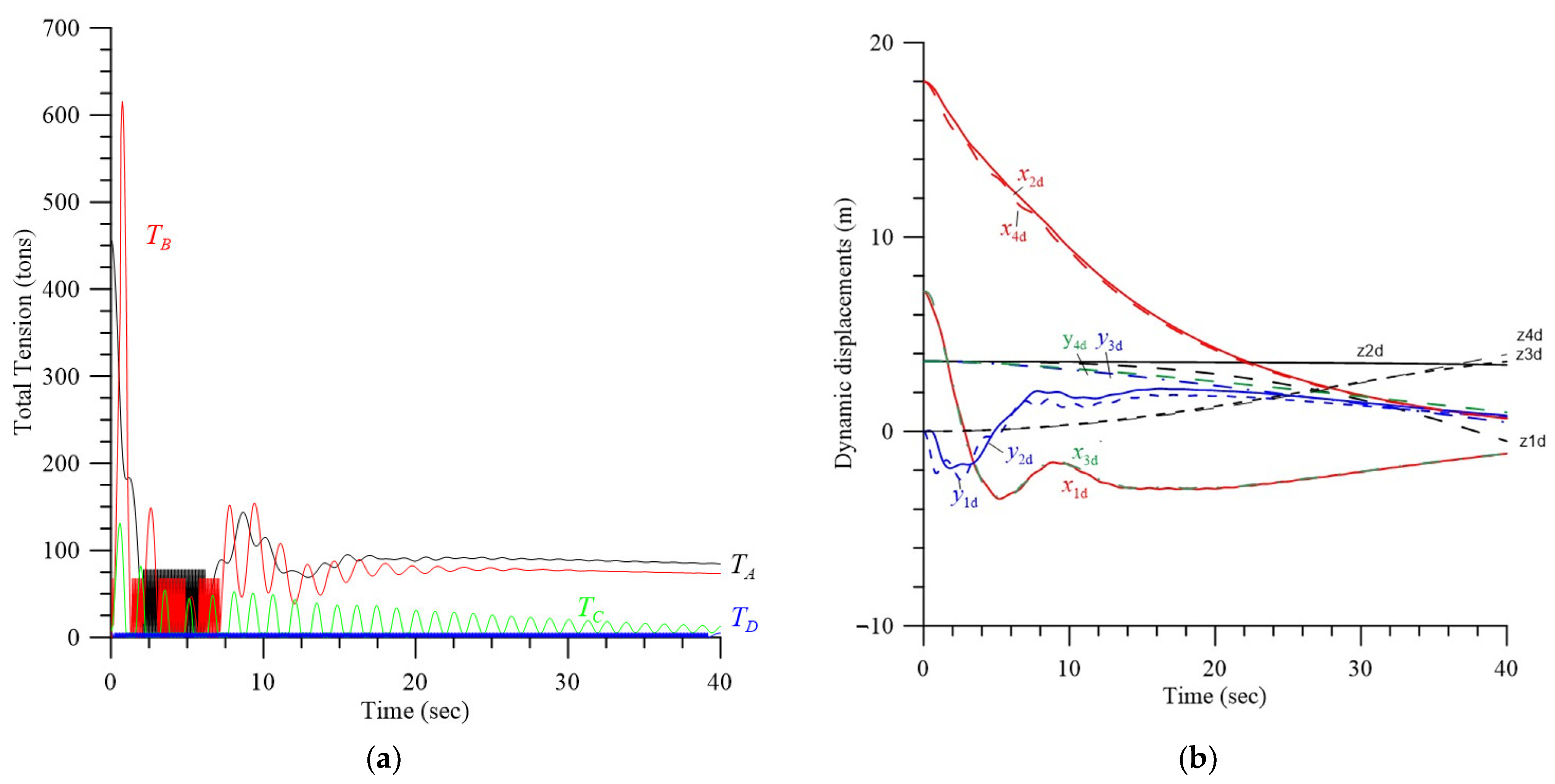
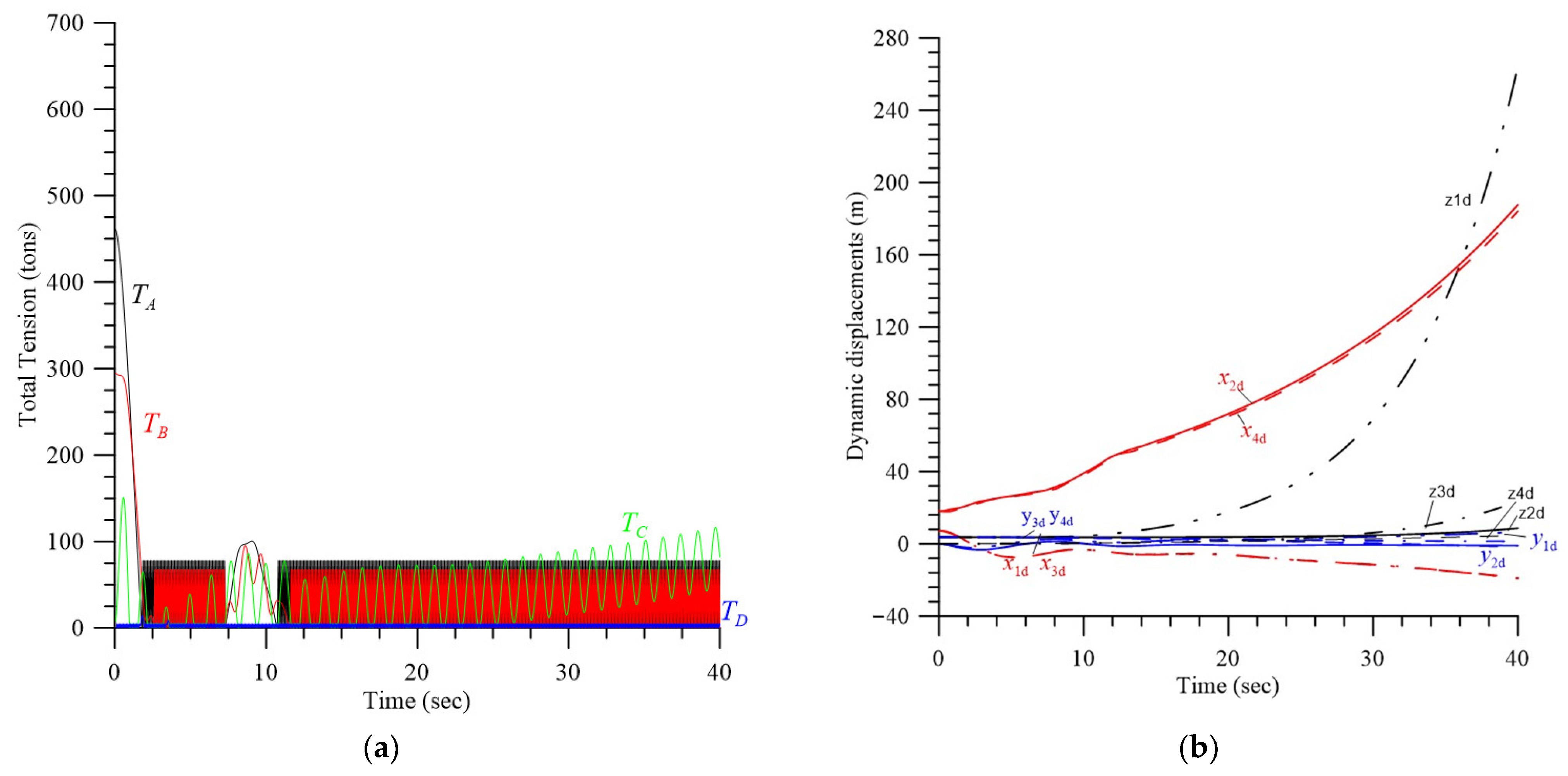
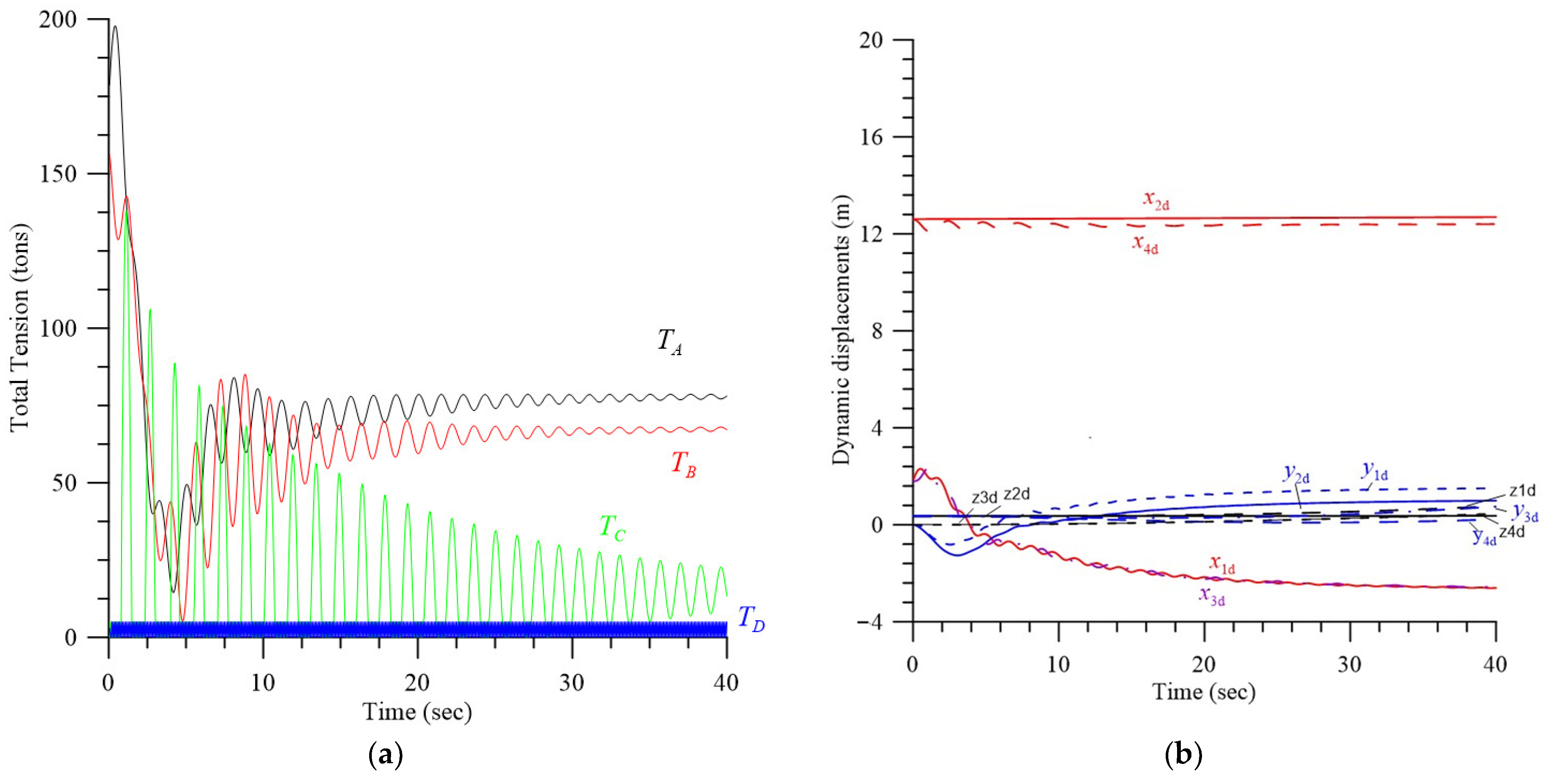
4.1. Effects of Initial Displacements, Effective Spring Constant, and Double-Rope Parallel Mode
4.2. Effects of the Length of Rope and Hydrodynamic Heaving Damping
4.2.1. Transient Response and Improvement of Stability and Safety, LC = 100 m, LD = 110 m
4.2.2. Transient Response and Improvement of Stability and Safety, LC = 110 m, LD = 100 m
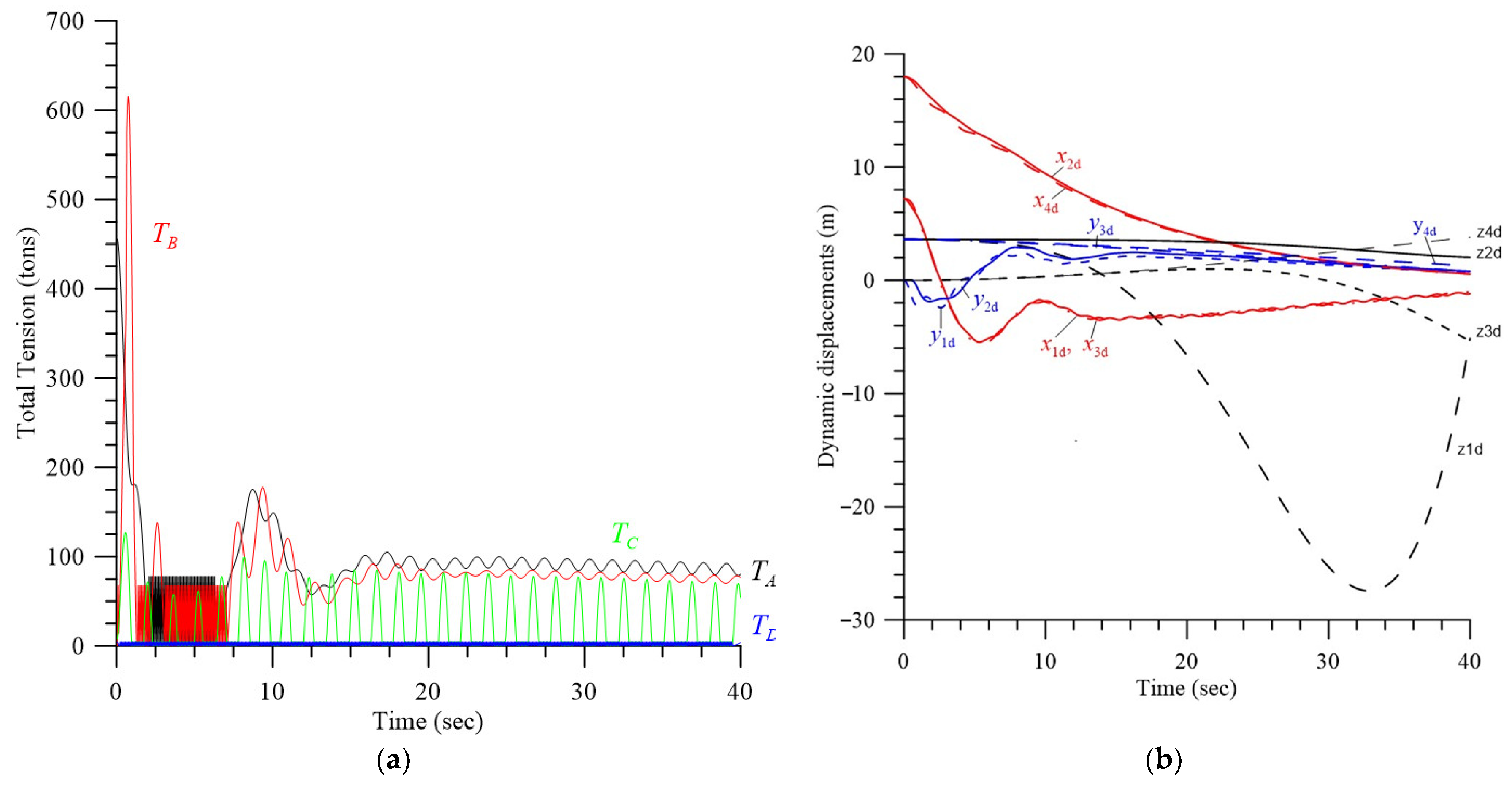
4.3. Effect of Initial Velocities
5. Conclusions
- The lower the effective spring constants of the ropes are, the higher the buffering feature of the mooring system will be.
- The higher the effective spring constants of the ropes are, the higher the momentary tension of the ropes will be.
- In traditional setups, the lower the effective spring constants of single-rope mode are, the lower the fracture strength of the rope will be. This disadvantage can be overcome by using the double-rope parallel mode.
- The effect of the lengths of ropes C and D on the transient response is significant.
- The larger the hydrodynamic damping coefficients are, the stabler the mooring system will be.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ABX: ABT | cross-sectional area of surfaced cylinder of pontoons 3 and 4, respectively |
| ABY, ATY | damping area of platform and convertor under current, respectively |
| C | matrix of damping |
| damping coefficient of floating platform and convertor | |
| Ei | Young’s modulus of rope i, i = A, B, C, D |
| efrac | fracture energy of rope |
| FB | buoyance |
| the drag of the floating platform and the convertor under steady current | |
| Hbed | depth of seabed |
| mass moment of inertia of the convertor and the platform about the j-axis. | |
| g | gravity |
| K | matrix of stiffness |
| Kid | |
| Li, | length of rope i, i = A, B, C, D |
| LE, | |
| M | matrix of mass |
| Mi | mass of element i |
| effective mass of rope A in the i-direction | |
| hydrodynamic moment of convertor or platform about the i-axis | |
| coordinate | |
| Ti | tension force of rope i |
| t | time variable |
| V | ocean current velocity |
| Wi | weight of component i |
| wPE | weight per unit length of HSPE |
| xi, yi, zi | displacements of component i |
| ε | strain |
| ρ | density of sea water |
| angular displacement of convertor or platform about the j-axis | |
| θi | angles of rope i |
| δi | elongation of rope i |
| Subscript: | |
| 0~4 | mooring foundation, floating platform, convertor, and two pontoons, respectively |
| A, B, C, D | Ropes A, B, C, and D, respectively |
| crit | critical |
| iα, iβ | component α, β of rope i = A, B, C, and D |
| frac | fracture |
| s, d | static and dynamic, respectively |
| PE | PE dyneema rope |
| P | platform |
| T | convertor |
Appendix A. Elements of the Mass Matrix
Appendix B. Elements of the Hydrodynamic Damping Matrix
Appendix C. Elements of the Stiffness Matrix
References
- Chen, Y.Y.; Hsu, H.C.; Bai, C.Y.; Yang, Y.; Lee, C.W.; Cheng, H.K.; Shyue, S.W.; Li, M.S. Evaluation of test platform in the open sea and mounting test of KW Kuroshio power-generating pilot facilities. In Proceedings of the 2016 Taiwan Wind Energy Conference, Keelung, Taiwan, 24–25 November 2016. [Google Scholar]
- IHI; NEDO. The Demonstrtion Experiment of the IHI Ocean Current Turbine Located Off the Coast of Kuchinoshima Island, Kagoshima Prefecture, Japan, 14 August 2017. Available online: https://tethys.pnnl.gov/project-sites/ihi-ocean-current-turbine (accessed on 28 August 2021).
- Nobel, D.R.; O’Shea, M.; Judge, F.; Robles, E.; Martinez, R.F.; Thies, P.R.; Johanning, L.; Corlay, R.; Davey, T.A.D.; Vejayan, N.; et al. Standardising Marine Renewable Energy Testing: Gap Analysis and Recommendations for Development of Standards. J. Mar. Sci. Eng. 2021, 9, 971. [Google Scholar] [CrossRef]
- Lin, S.M.; Chen, Y.Y.; Hsu, H.C.; Li, M.S. Dynamic Stability of an Ocean Current Turbine System. J. Mar. Sci. Eng. 2020, 8, 687. [Google Scholar] [CrossRef]
- Lin, S.M.; Chen, Y.Y. Dynamic stability and protection design of a submarined floater platform avoiding Typhoon wave impact. J. Mar. Sci. Eng. 2021, 9, 977. [Google Scholar] [CrossRef]
- Lin, S.M.; Chen, Y.Y.; Liauh, C.T. Dynamic stability of the coupled pontoon-ocean turbine-floater platform-rope system under harmonic wave excitation and steady ocean current. J. Mar. Sci. Eng. 2021, 9, 1425. [Google Scholar] [CrossRef]
- Lin, S.M.; Liauh, C.T.; Utama, D.W. Design and dynamic stability analysis of a submersible ocean current generator-platform mooring system under typhoon irregular wave. J. Mar. Sci. Eng. 2022, 10, 538. [Google Scholar] [CrossRef]
- Lin, S.M.; Utama, D.W.; Liauh, C.T. Coupled translational-rotational stability analysis of a submersible ocean current converter-platform mooring system under typhoon wave. J. Mar. Sci. Eng. 2023, 11, 518. [Google Scholar] [CrossRef]
- Anagnostopoulos, S.A. Dynamic response of offshore platforms to extreme waves including fluid-structure interaction. Eng. Struct. 1982, 4, 179–185. [Google Scholar] [CrossRef]
- Geuzaine, P.; Farhat, C.; Brown, G. Application of a three-field nonlinear fluid-structure formulation to the prediction of the aeroelastic parameters of an f-16 fighter. Comput. Fluids 2003, 32, 3–29. [Google Scholar]
- Bathe, K.J.; Nitikitpaiboon, C.; Wang, X. A mixed discplacement-based finite element formulation for acoustic fluid-structure interaction. Comput. Struct. 1995, 56, 225–237. [Google Scholar] [CrossRef]
- Lin, S.M.; Lee, S.Y.; Tsai, C.C.; Chen, C.W.; Wang, W.R.; Lee, J.F. Wave modes of an elastic tube conveying blood. CMES Comput. Model. Eng. Sci. 2008, 34, 33–54. [Google Scholar]
- Lin, S.M.; Wang, W.R.; Lee, S.Y.; Chen, C.W.; Hsiao, Y.C.; Teng, M.J. Wave modes of a pre-stressed thick tube conveying blood on the viscoelastic foundation. Appl. Math. Model. 2015, 39, 466–482. [Google Scholar] [CrossRef]
- Belibassakis, K.A. A boundary element method for the hydrodynamic analysis of floating bodies in variable bathymetry regions. Eng. Anal. Bound. Elem. 2008, 32, 796–810. [Google Scholar] [CrossRef]
- Tsui, Y.Y.; Huang, Y.C.; Huang, C.L.; Lin, S.W. A finite-volume-based approach for dynamic fluid-structure interaction. Numer. Heat Transf. Part B Fundam. 2013, 64, 326–349. [Google Scholar] [CrossRef]
- Hasanpour, A.; Istrati, D.; Buckle, I. Coupled SPH–FEM Modeling of Tsunami-Borne Large Debris Flow and Impact on Coastal Structures. J. Mar. Sci. Eng. 2021, 9, 1068. [Google Scholar] [CrossRef]






| Parameter | Dimension | Parameter | Dimension | |
|---|---|---|---|---|
| depth of seabed Hbed | 1000 m | length of rope C, LC | 100 m | |
| length of rope D, LD | 100 m | horizontal distance between the inverter and platform LE | 300 m | |
| inclined angle of rope A, | mass moment of inertia of the convertor | / (kg-m2) | ||
| cross-sectional area of surfaced cylinder of pontoon 3, ABX | 4 m2 | mass moment of inertia of the platform | (kg-m2) | |
| cross-sectional area of surfaced cylinder of pontoon 4, ABT | 4 m2 | distance from the gravity of invertor to rope B, D, RTB/RTD | 16.5/12.82 m | |
| HSPE rope | Young’s modulus EPE | 100 GPa, | current velocity V | 1.6 m/s |
| weight per unit length wPE | 16.22 kg/m | mass of the platform M1 | 300 tons | |
| diameter DPE | 154 mm | mass of the invertor M2 | 538 tons | |
| cross-sectional area APE | 0.0186 m2 | mass of the pontoon 3, M3 | 250 tons | |
| fracture strength Tfrac | 759 tons | mass of the pontoon 4, M4 | 250 tons | |
| distance from the gravity of platform to ropes A, B, C, RPA/RPB/RPC | 5/5.8/2.5 m | static tension of ropes A, B, C, D, TAs/TBs/TCs/TDs | 78.07/67.53/5/5 tons | |
| static drag of the invertor FDT | 67.53 tons | net buoyance of invertor and platform FBNT/FBNB | 533/320.77 tons | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, S.-M.; Wang, W.-R.; Yuan, H. Transient Translational–Rotational Motion of an Ocean Current Converter Mooring System with Initial Conditions. J. Mar. Sci. Eng. 2023, 11, 1533. https://doi.org/10.3390/jmse11081533
Lin S-M, Wang W-R, Yuan H. Transient Translational–Rotational Motion of an Ocean Current Converter Mooring System with Initial Conditions. Journal of Marine Science and Engineering. 2023; 11(8):1533. https://doi.org/10.3390/jmse11081533
Chicago/Turabian StyleLin, Shueei-Muh, Wen-Rong Wang, and Hsin Yuan. 2023. "Transient Translational–Rotational Motion of an Ocean Current Converter Mooring System with Initial Conditions" Journal of Marine Science and Engineering 11, no. 8: 1533. https://doi.org/10.3390/jmse11081533
APA StyleLin, S.-M., Wang, W.-R., & Yuan, H. (2023). Transient Translational–Rotational Motion of an Ocean Current Converter Mooring System with Initial Conditions. Journal of Marine Science and Engineering, 11(8), 1533. https://doi.org/10.3390/jmse11081533





