Research on Scale Effect of Resistance Components for Full-Formed Ship Based on Large-Scale Model Towing Test
Abstract
1. Introduction
2. Measurements and Methods
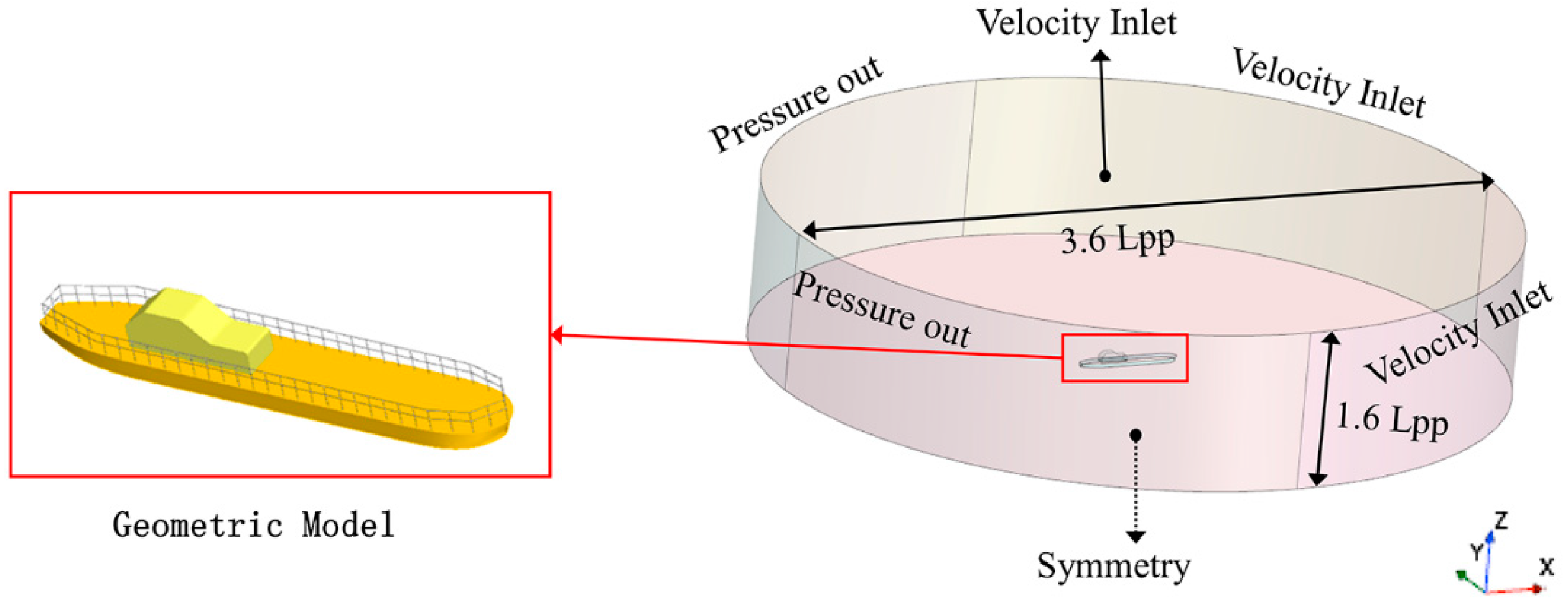
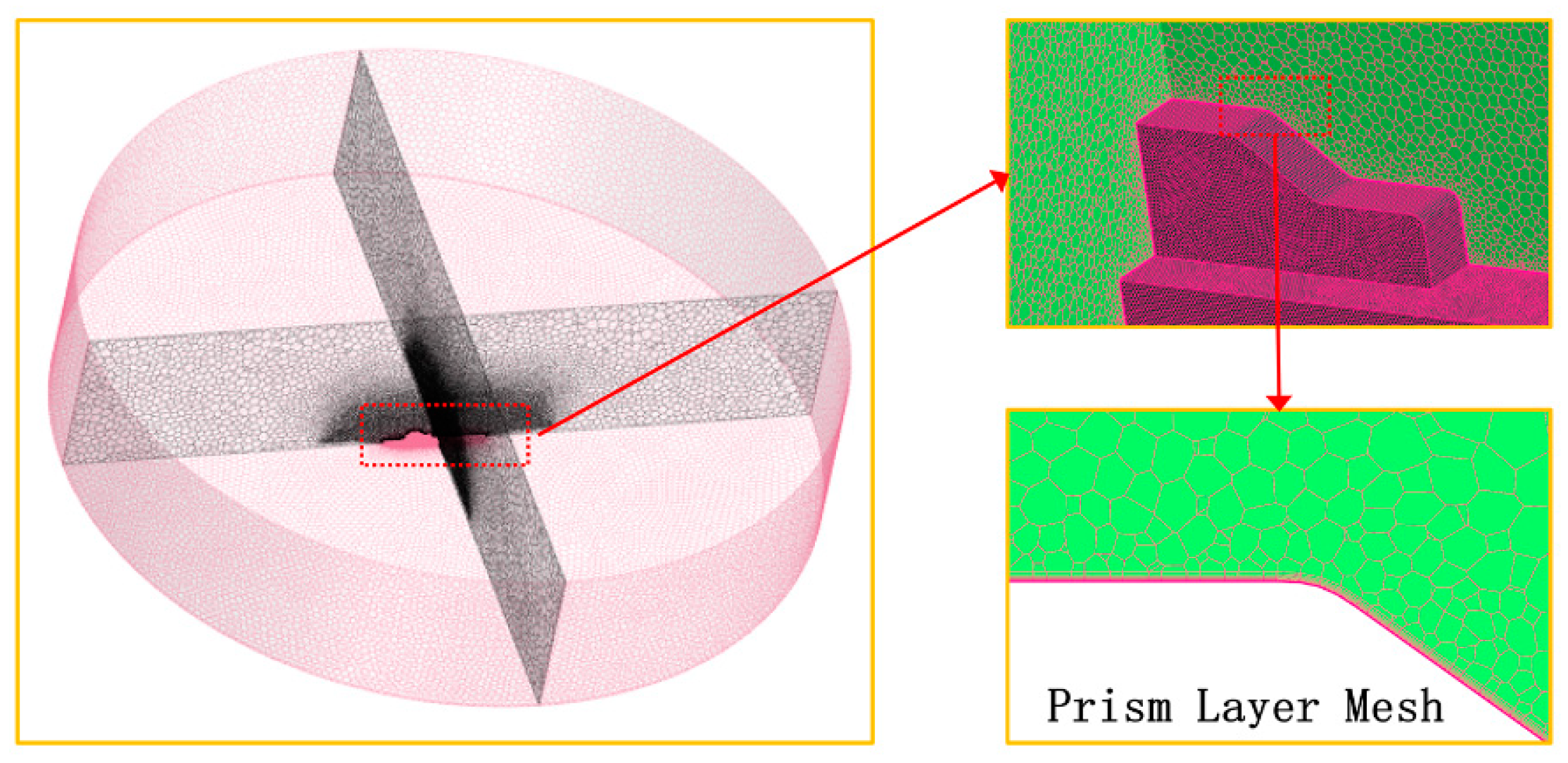
2.1. Geometric Model
2.2. Small-Scale Model Tests in the Towing Tank
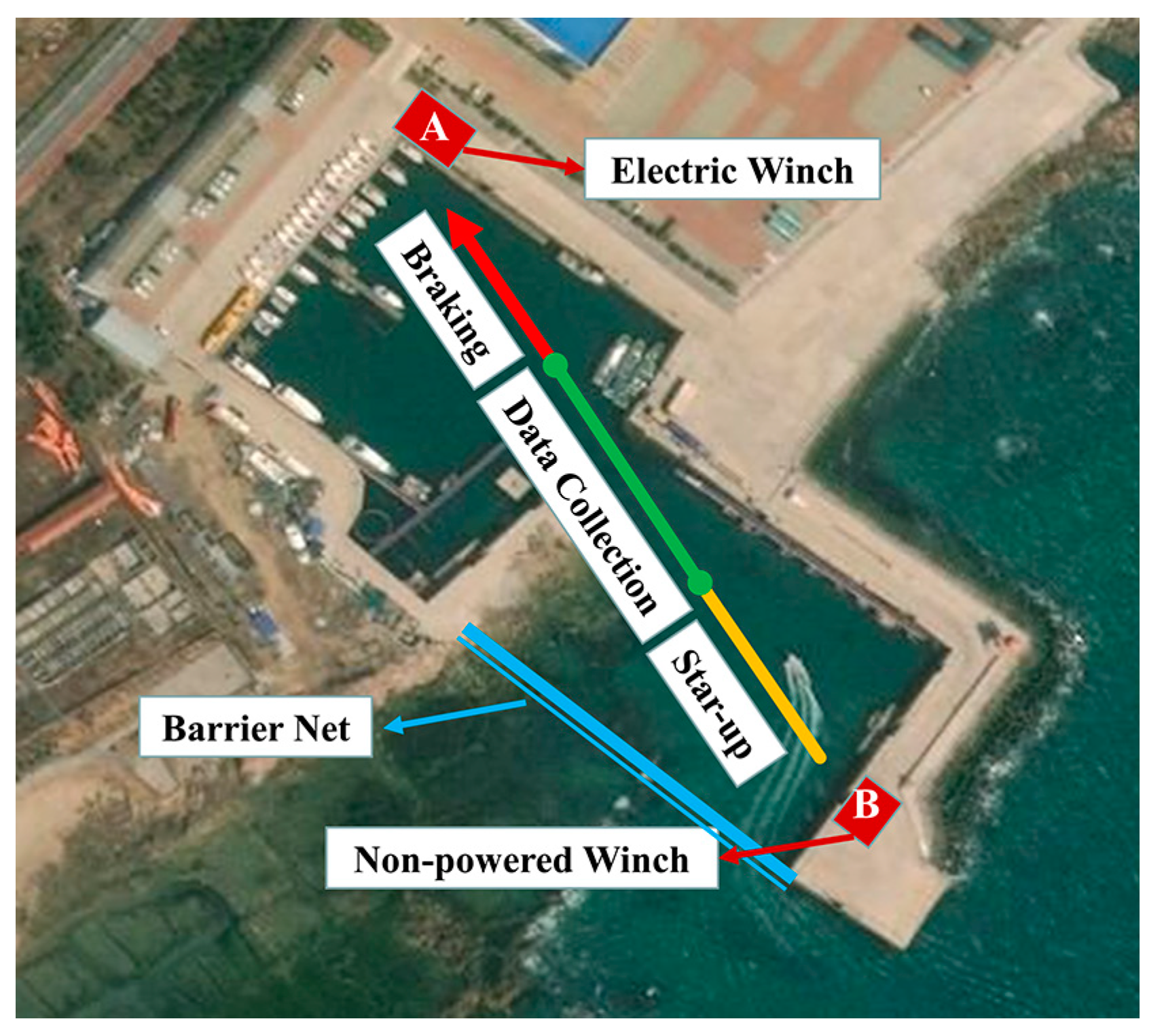
2.3. Experimental Plan and Procedure of Large-Scale Model Tests in the Port
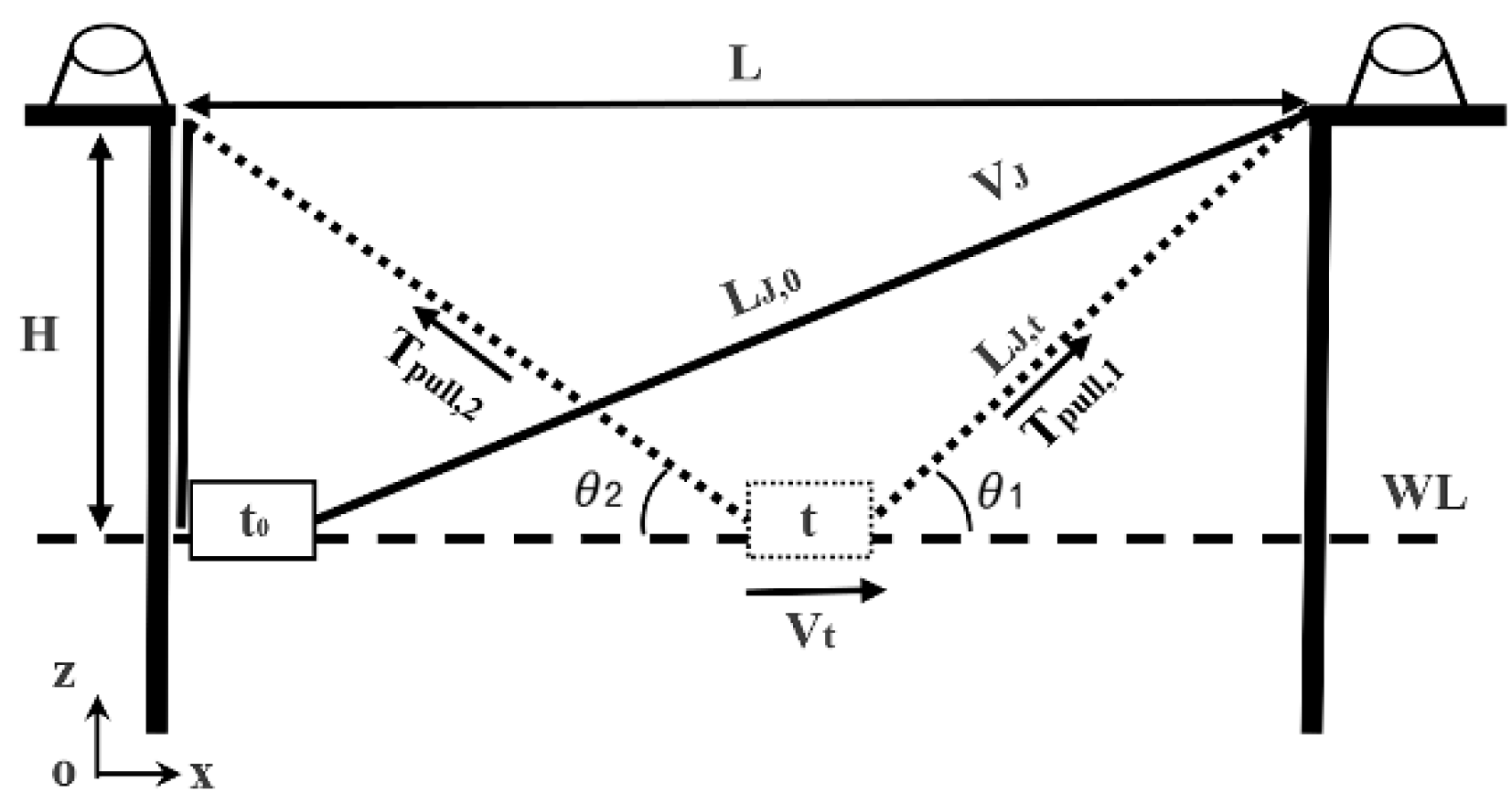
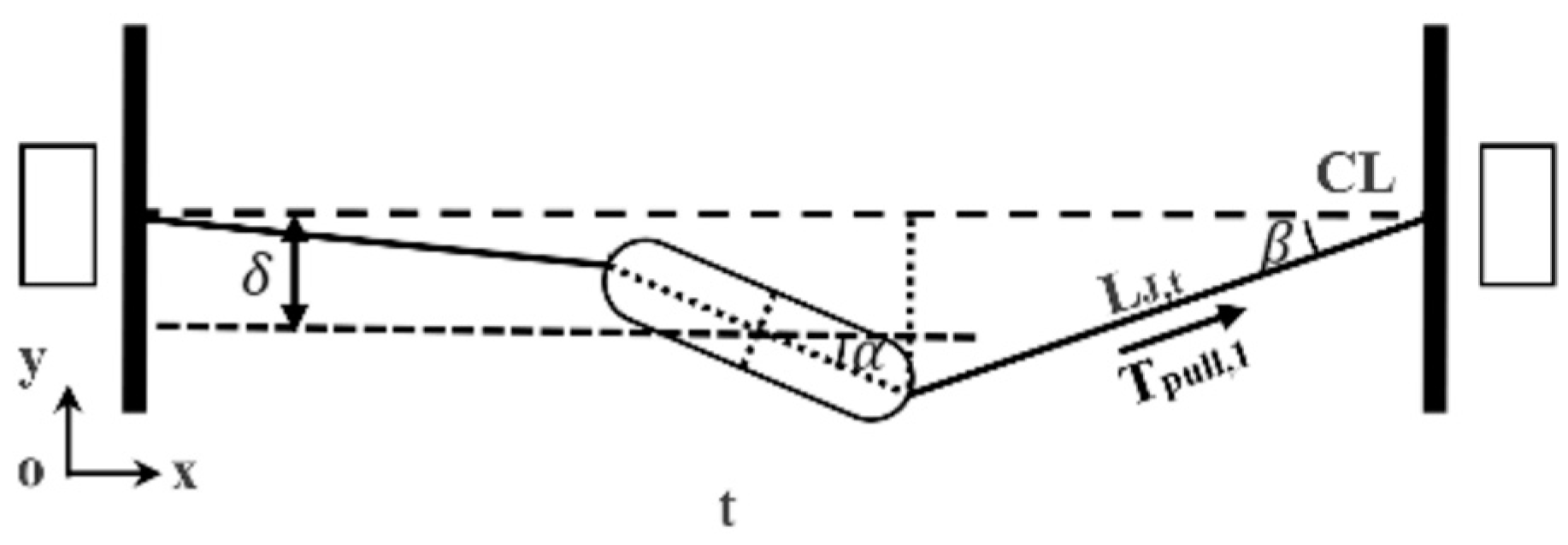
2.4. Data-Processing Methods for Large-Scale Model Test
2.4.1. Sensor Force Correction
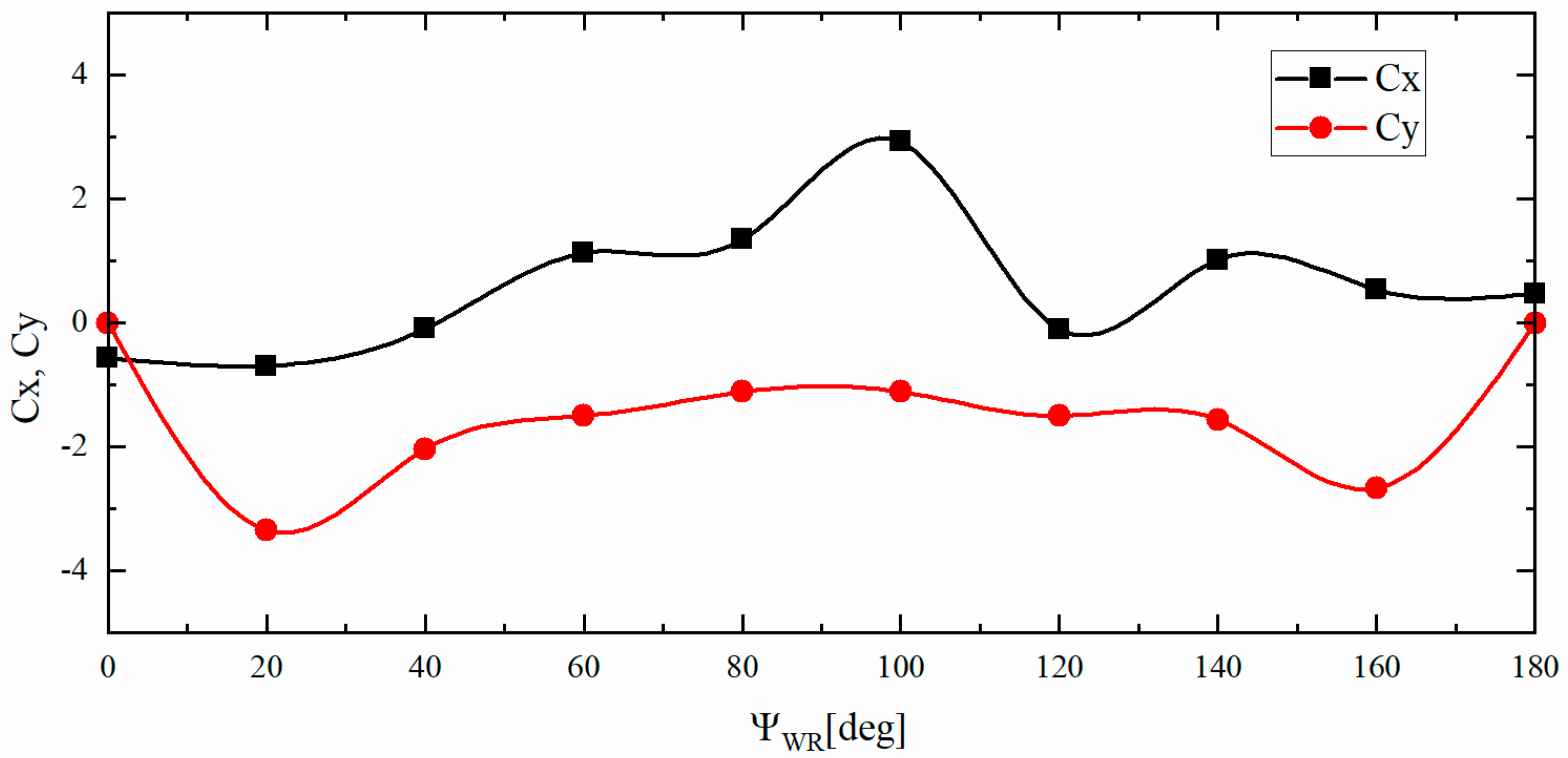
2.4.2. Wind-Resistance Correction
2.4.3. Blockage-Effect Correction
2.5. Uncertainty Analysis for Large-Scale Model Test
3. Results
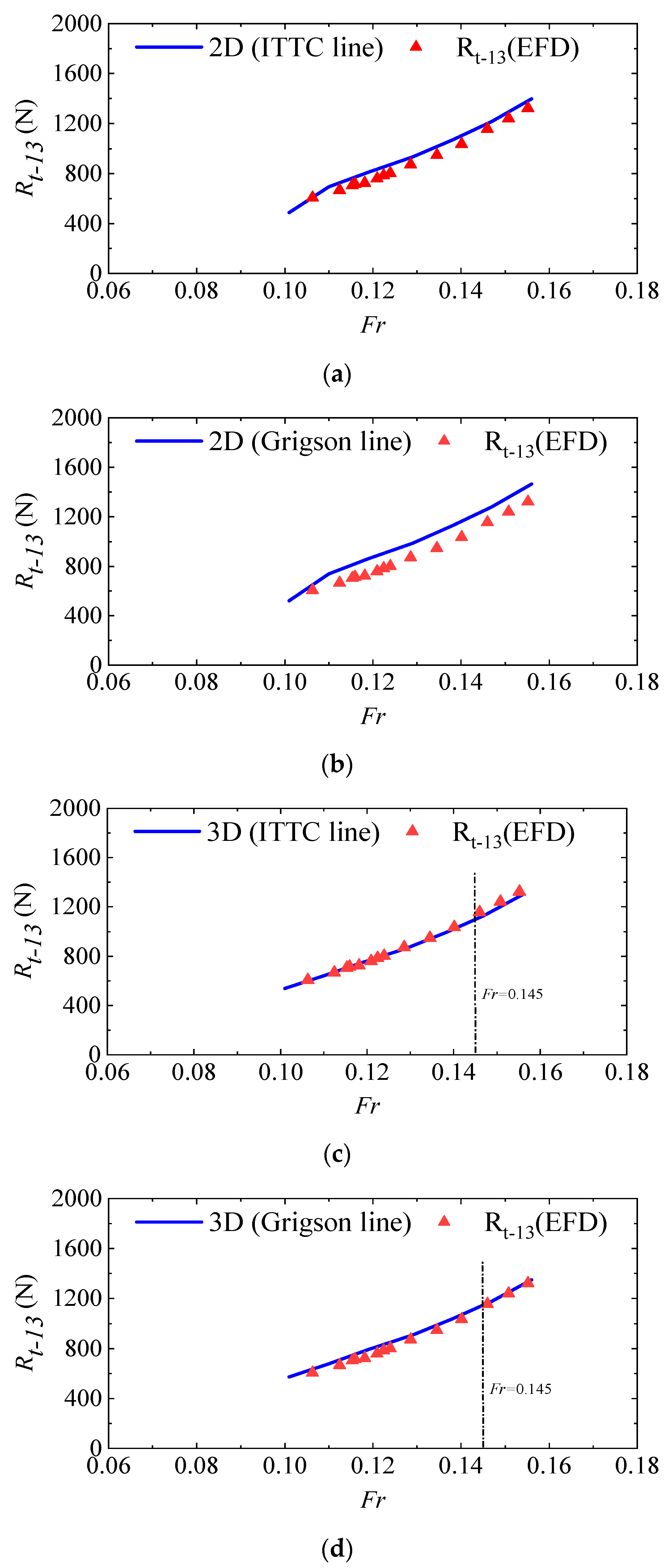
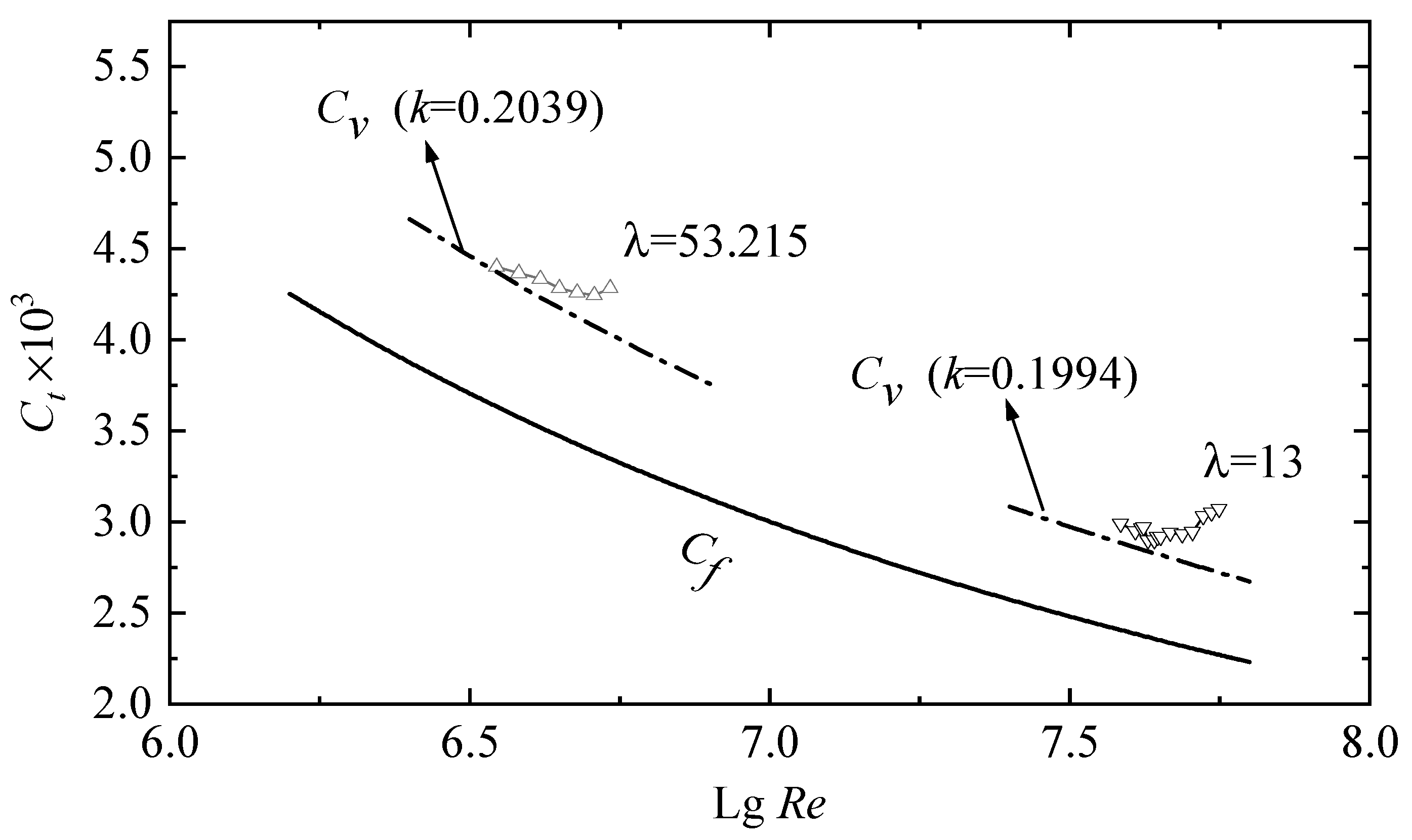
3.1. Analysis of Total Resistance
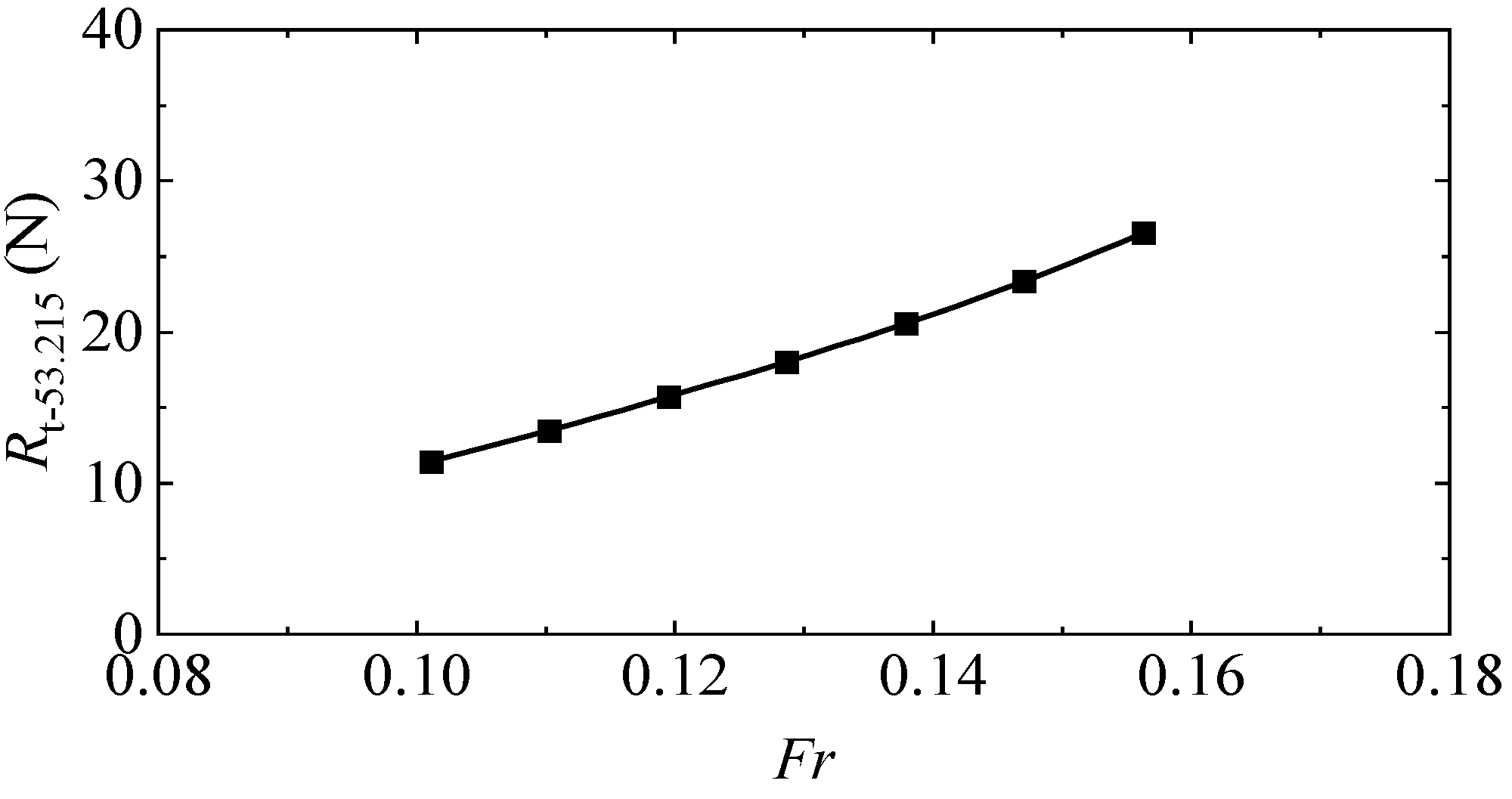
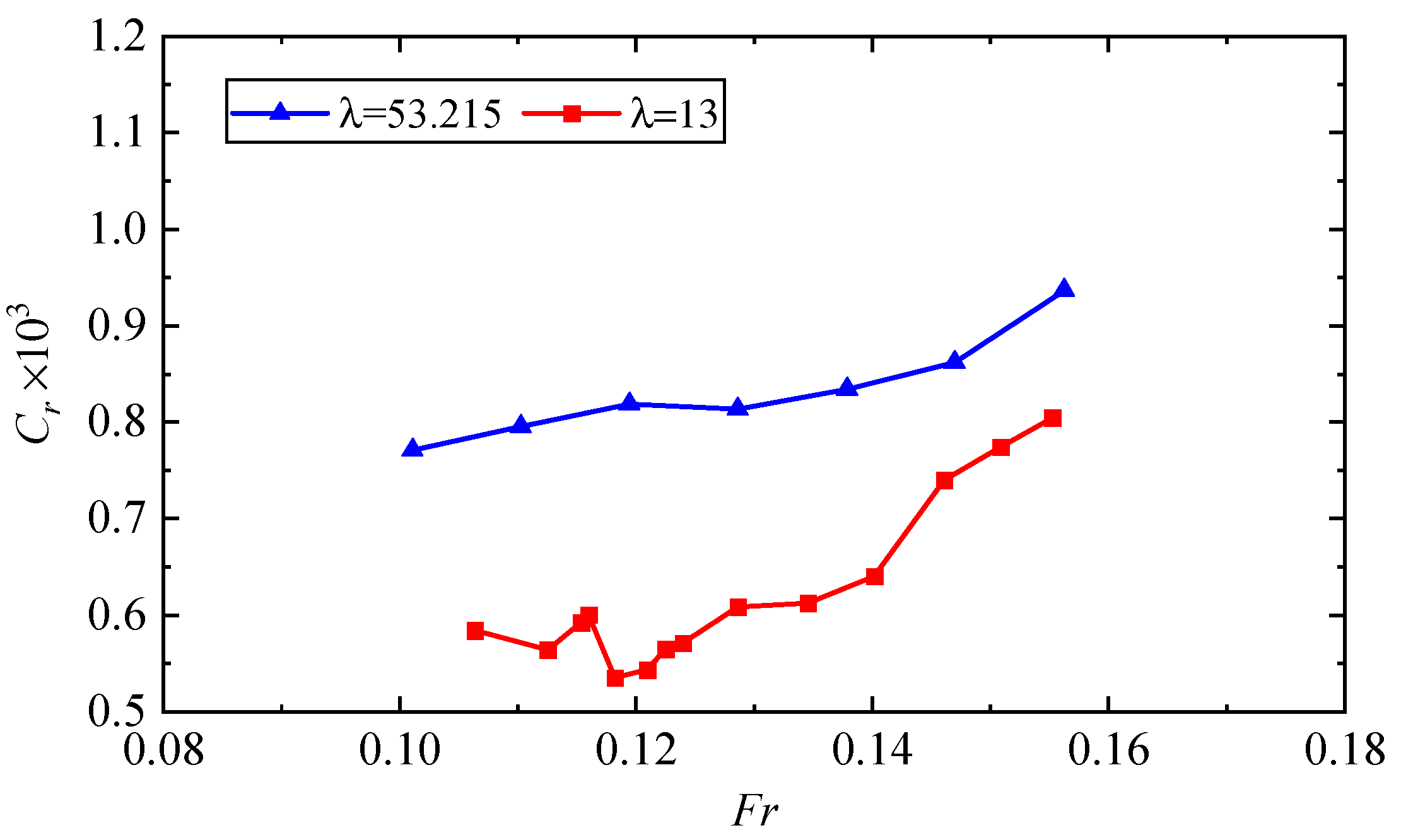
3.2. Scale Effect of Residual Resistance
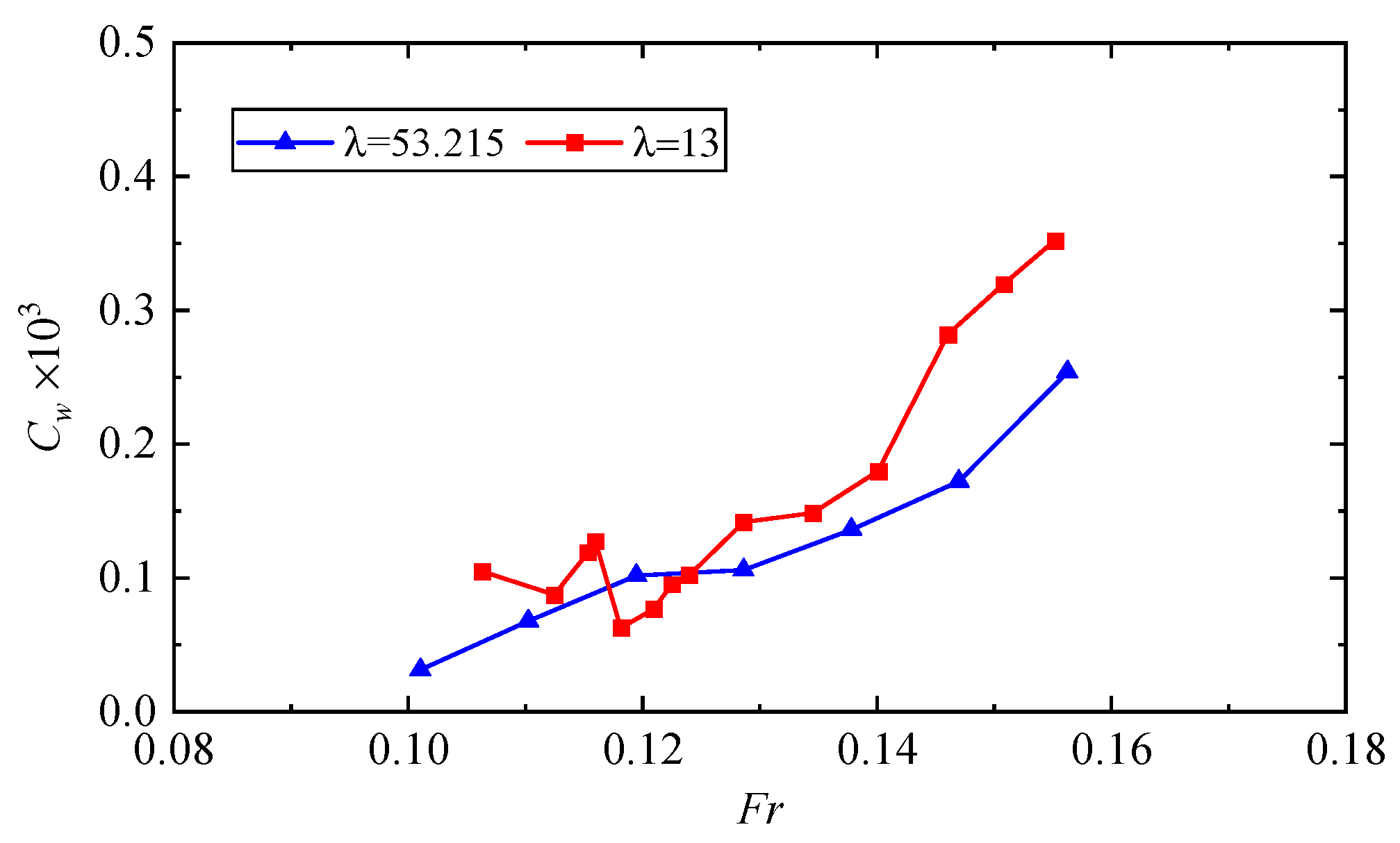
3.3. Scale Effect of Wave-Making Resistance
4. Conclusions and Discussions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, J.H.; Choi, J.E.; Choi, B.J.; Chung, S.H.; Seo, H. Development of energy-saving devices for a full slow-speed ship through improving propulsion performance. Ocean Eng. 2015, 7, 390–398. [Google Scholar] [CrossRef]
- Attah, E.E.; Bucknall, R. An analysis of the energy efficiency of LNG ships powering options using the EEDI. Ocean Eng. 2015, 110, 62–74. [Google Scholar] [CrossRef]
- Zaccone, R.; Ottaviani, E.; Figari, M.; Altosole, M. Ship voyage optimization for safe and energy-efficient navigation: A dynamic programming approach. Ocean Eng. 2018, 153, 215–224. [Google Scholar] [CrossRef]
- Wang, L.Z.; Guo, C.Y.; Su, Y.M.; Wu, T.C. A numerical study on the correlation between the evolution of propeller trailing vortex wake and skew of propellers. Ocean Eng. 2018, 10, 212–224. [Google Scholar] [CrossRef]
- Wang, L.; Guo, C.; Su, Y.; Xu, P.; Wu, T. Numerical analysis of a propeller during heave motion in cavitating flow. Appl. Ocean Res. 2017, 66, 131–145. [Google Scholar]
- Dogrul, A.; Song, S.; Demirel, Y.K. Scale effect on ship resistance components and form factor. Ocean Eng. 2020, 209, 107428. [Google Scholar] [CrossRef]
- Song, K.W.; Guo, C.Y.; Gong, J.; Li, P.; Wang, L.Z. Influence of interceptors, stern flaps, and their combinations on the hydrodynamic performance of a deep-vee ship. Ocean Eng. 2018, 170, 306–320. [Google Scholar] [CrossRef]
- Song, K.W.; Guo, C.Y.; Wang, C.; Sun, C.; Li, P.; Wang, W. Numerical analysis of the effects of stern flaps on ship resistance and propulsion performance. Ocean Eng. 2019, 193, 106621. [Google Scholar] [CrossRef]
- Zeng, Q.; Hekkenberg, R.; Thill, C.; Hopman, H. Scale effects on the wave-making resistance of ships sailing in shallow water. Ocean Eng. 2020, 212, 107654. [Google Scholar] [CrossRef]
- Shen, H.L.; Obwogi, E.O.; Su, Y.M. Scale effects for rudder bulb and rudder thrust fin on propulsive efficiency based on computational fluid dynamics. Ocean Eng. 2016, 117, 199–209. [Google Scholar]
- Kim, M.; Hizir, O.; Turan, O.; Incecik, A. Numerical studies on added resistance and motions of KVLCC2 in head seas for various ship speeds. Ocean Eng. 2017, 140, 466–476. [Google Scholar] [CrossRef]
- Song, S.; Demirel, Y.K.; Atlar, M. An investigation into the effect of biofouling on the ship hydrodynamic characteristics using CFD. Ocean Eng. 2019, 175, 122–137. [Google Scholar] [CrossRef]
- Farkas, A.; Degiuli, N.; Marti, I. Assessment of hydrodynamic characteristics of a full-scale ship at different draughts. Ocean Eng. 2018, 156, 135–152. [Google Scholar] [CrossRef]
- Shivachev, E.; Khorasanchi, M.; Day, S.; Turan, O. Impact of trim on added resistance of KRISO container ship (KCS) in head waves: An experimental and numerical study. Ocean Eng. 2020, 211, 107594. [Google Scholar] [CrossRef]
- Duan, W.Y.; Tang, S.X.; Chen, J.K. Power and speed prediction of KVLCC2 in head waves based on TEBEM. Ocean Eng. 2022, 249, 110811. [Google Scholar] [CrossRef]
- Yldz, B.; Sener, B.; Duman, S.; Datla, R. A numerical and experimental study on the outrigger positioning of a trimaran hull in terms of resistance. Ocean Eng. 2020, 198, 106938. [Google Scholar] [CrossRef]
- Sun, S.; Chang, X.; Guo, C.; Zhang, H.; Wang, C. Numerical investigation of scale effect of nominal wake of four-screw ship. Ocean Eng. 2019, 183, 208–223. [Google Scholar] [CrossRef]
- Niklas, K.; Pruszko, H. Full-scale CFD simulations for the determination of ship resistance as a rational, alternative method to towing tank experiments. Ocean Eng. 2019, 190, 106435. [Google Scholar] [CrossRef]
- Song, K.; Guo, C.; Sun, C.; Wang, C.; Gong, J.; Li, P.; Wang, L. Simulation strategy of the full-scale ship resistance and propulsion performance. Eng. Appl. Comp. Fluid Mech. 2021, 15, 1321–1342. [Google Scholar] [CrossRef]
- Jiao, J.; Ren, H.; Sun, S.; Liu, N.; Li, H.; Adenya, C.A. A state-of-the-art large scale model testing technique for ship hydrodynamics at sea. Ocean Eng. 2016, 123, 174–190. [Google Scholar] [CrossRef]
- Jiao, J.; Sun, S.; Li, J.; Adenya, C.A.; Ren, H.; Chen, C.; Wang, D. A comprehensive study on the seakeeping performance of high speed hybrid ships by 2.5D theoretical calculation and different scaled model experiments. Ocean Eng. 2018, 160, 197–223. [Google Scholar] [CrossRef]
- Jiao, J.; Ren, H.; Soares, C.G. A review of large-scale model at-sea measurements for ship hydrodynamics and structural loads. Ocean Eng. 2021, 227, 108863. [Google Scholar] [CrossRef]
- Grogan, G.R.; Borthen, J.L. Performing Detailed Design Reviews of a US Navy Surface Combatant within an Integrated Data Environment. J. Ship. Pro. 2010, 26, 66–75. [Google Scholar] [CrossRef]
- Grigoropoulos, G.J.; Politis, C.G. A Measuring System of the six Degrees of Motions of a Moving Body. J. Ship. Tech. Res. 1999, 45, 4–7. [Google Scholar]
- Coraddu, A.; Dubbioso, G.; Mauro, S.; Viviani, M. Analysis of twin screw ships’ asymmetric propeller behaviour by means of free running model tests. Ocean Eng. 2013, 68, 47–64. [Google Scholar] [CrossRef]
- Guo, C.Y.; Zhong, X.H.; Zhao, D.G.; Wang, C.; Lin, J.F.; Song, K.W. Propulsion performance of large-scale ship model in real sea environment. Ocean Eng. 2020, 210, 107440. [Google Scholar] [CrossRef]
- Su, Y.; Lin, J.; Zhao, D.; Guo, C.; Wang, C.; Guo, H. Real-time prediction of large-scale ship model vertical acceleration based on recurrent neural network. J. Mar. Sci. Eng. 2020, 8, 777. [Google Scholar] [CrossRef]
- Su, Y.-m.; Lin, J.-f.; Zhao, D.-g.; Guo, C.-y.; Guo, H. Influence of a pre-swirl stator and rudder bulb system on the propulsion performance of a large-scale ship model. Ocean Eng. 2020, 218, 108189. [Google Scholar] [CrossRef]
- Lin, J.F.; Zhao, D.G.; Guo, C.Y.; Su, Y.M.; Zhong, X.H. Comprehensive test system for ship-model resistance and propulsion performance in actual seas. Ocean Eng. 2020, 197, 106915. [Google Scholar] [CrossRef]
- Zhou, G.; Wang, Y.; Zhao, D.; Lin, J. Engineering. Uncertainty analysis of ship model propulsion test on actual seas based on Monte Carlo method. J. Mar. Sci. Eng. 2020, 8, 398. [Google Scholar] [CrossRef]



| Parameter | Small-Scale | Large-Scale | Full-Scale |
|---|---|---|---|
| λ | 53.215 | 13 | 1 |
| Lpp (m) | 5.912 | 24.58 | 319.56 |
| B (m) | 0.987 | 4.04 | 52.50 |
| T (m) | 0.340 | 1.39 | 18.10 |
| S (m2) | 8.638 | 144.75 | 24,462.37 |
| ▽ (m3) | 1.679 | 115.17 | 253,038.42 |
| CB | 0.847 | 0.847 | 0.847 |
| CM | 0.998 | 0.998 | 0.998 |
| CP | 0.848 | 0.848 | 0.848 |
| Fr | Ship Speed | |
|---|---|---|
| Full-Scale (kn) | Small-Scale (m/s) | |
| 0.101 | 11 | 0.776 |
| 0.110 | 12 | 0.846 |
| 0.119 | 13 | 0.917 |
| 0.129 | 14 | 0.987 |
| 0.139 | 15 | 1.058 |
| 0.147 | 16 | 1.128 |
| 0.156 | 17 | 1.199 |
| Single Measurement at 15.6 °C: V = 2.089 m/s, RT = 1033.78 N | |||
|---|---|---|---|
| Components | Symbol | Value (Relative) | Remark |
| Wetted area | 0.282% | negligible | |
| Dynamometer | 0.097% | negligible | |
| Speed | 0.957% | dominant | |
| Viscosity | 0.060% | negligible | |
| Yaw angle | 0.190% | negligible | |
| Combined uncertainty | 1.044% | Single | |
| Expanded uncertainty | 2.088% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, C.; Zhong, X.; Zhao, D. Research on Scale Effect of Resistance Components for Full-Formed Ship Based on Large-Scale Model Towing Test. J. Mar. Sci. Eng. 2023, 11, 1300. https://doi.org/10.3390/jmse11071300
Guo C, Zhong X, Zhao D. Research on Scale Effect of Resistance Components for Full-Formed Ship Based on Large-Scale Model Towing Test. Journal of Marine Science and Engineering. 2023; 11(7):1300. https://doi.org/10.3390/jmse11071300
Chicago/Turabian StyleGuo, Chunyu, Xianghai Zhong, and Dagang Zhao. 2023. "Research on Scale Effect of Resistance Components for Full-Formed Ship Based on Large-Scale Model Towing Test" Journal of Marine Science and Engineering 11, no. 7: 1300. https://doi.org/10.3390/jmse11071300
APA StyleGuo, C., Zhong, X., & Zhao, D. (2023). Research on Scale Effect of Resistance Components for Full-Formed Ship Based on Large-Scale Model Towing Test. Journal of Marine Science and Engineering, 11(7), 1300. https://doi.org/10.3390/jmse11071300






