On the Stability of Rubble Mound Structures under Oblique Wave Attack
Abstract
1. Introduction
2. Methodology
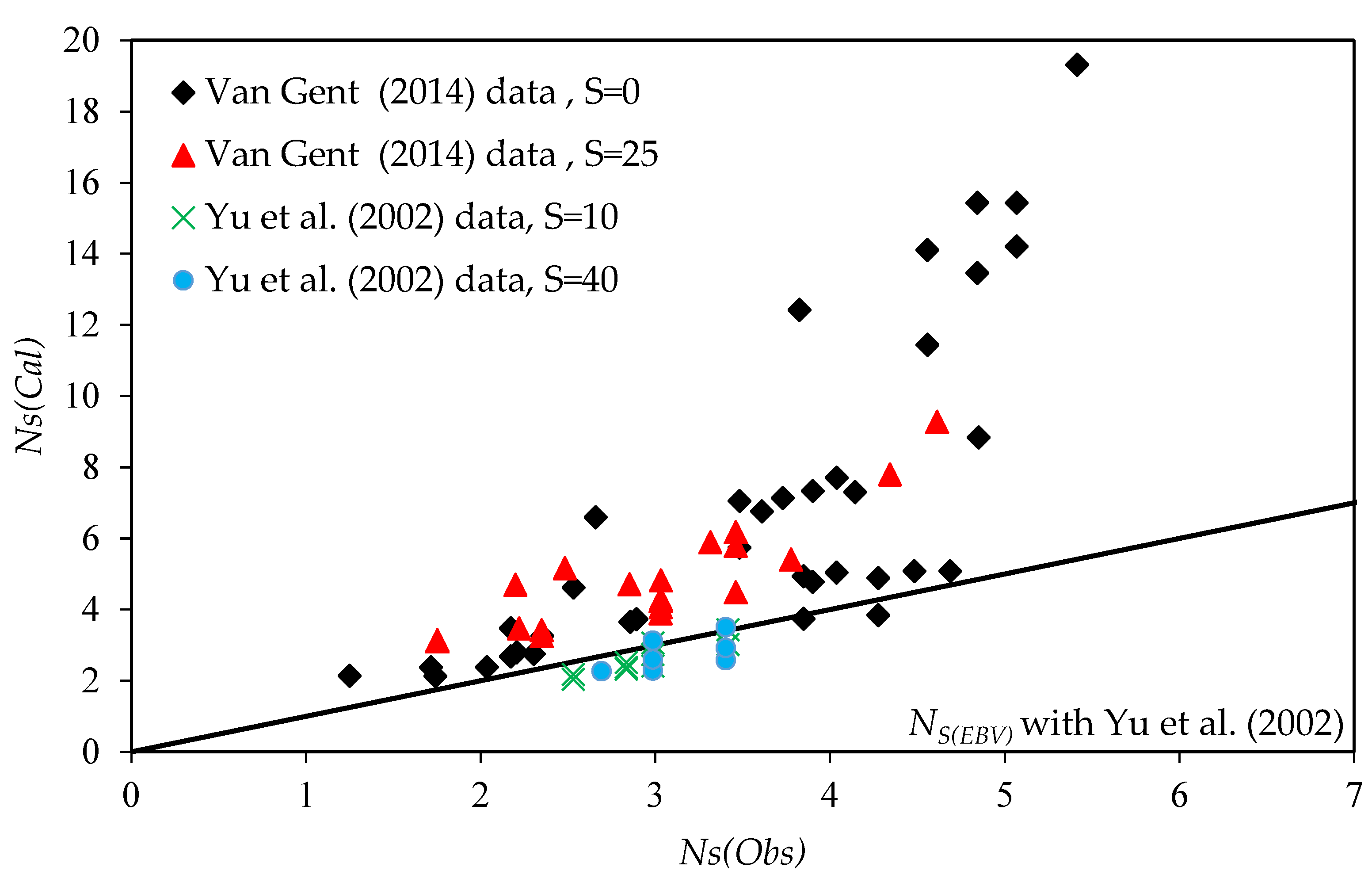
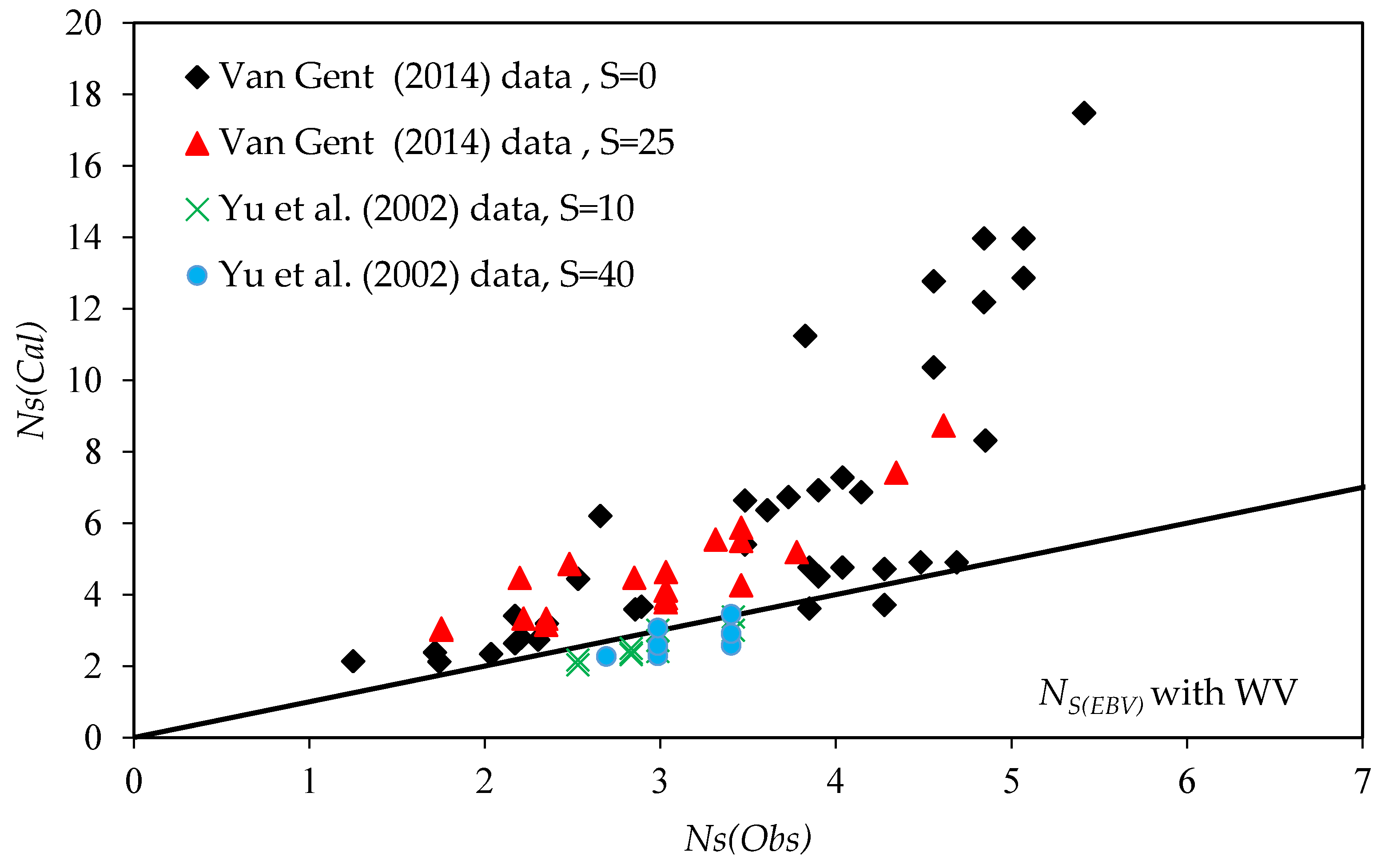
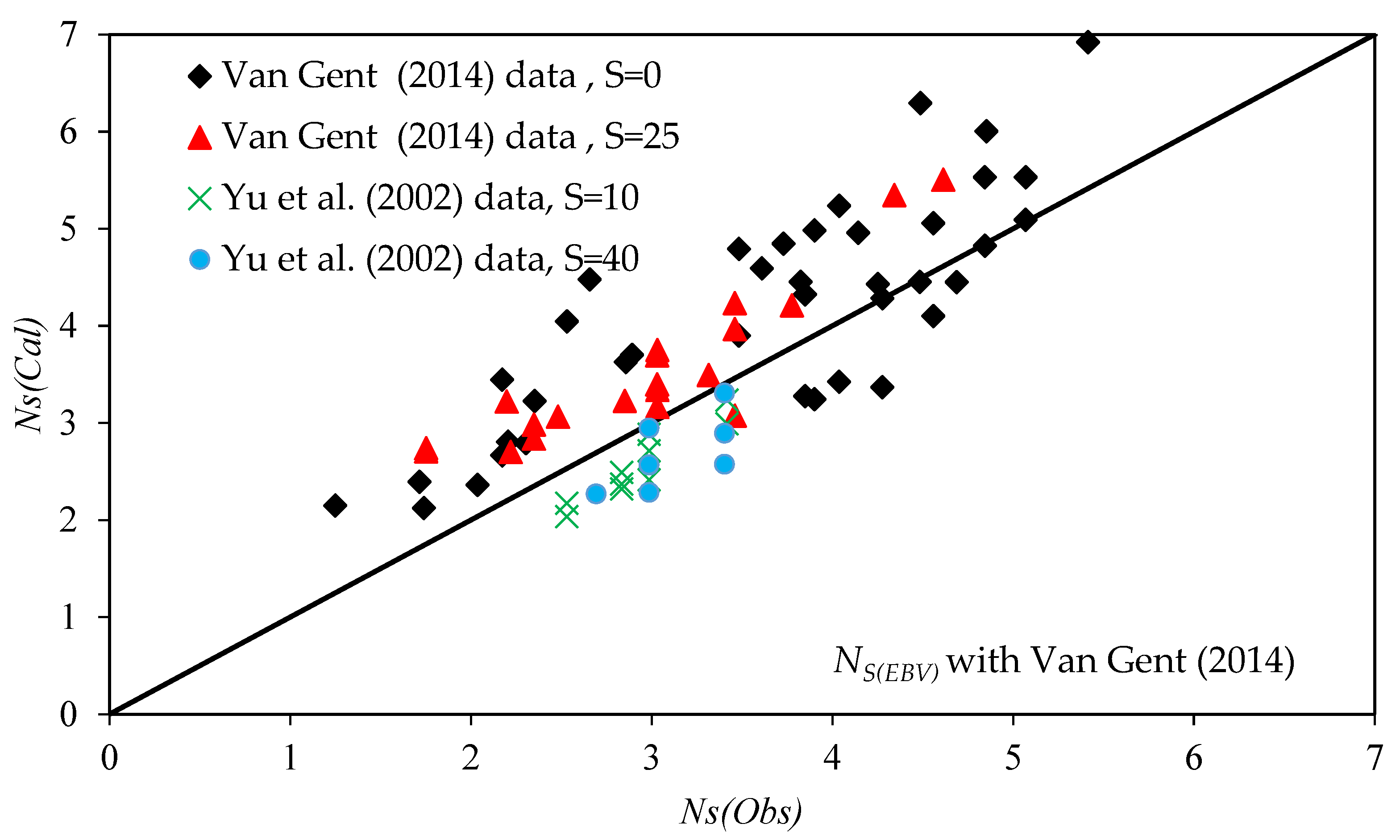
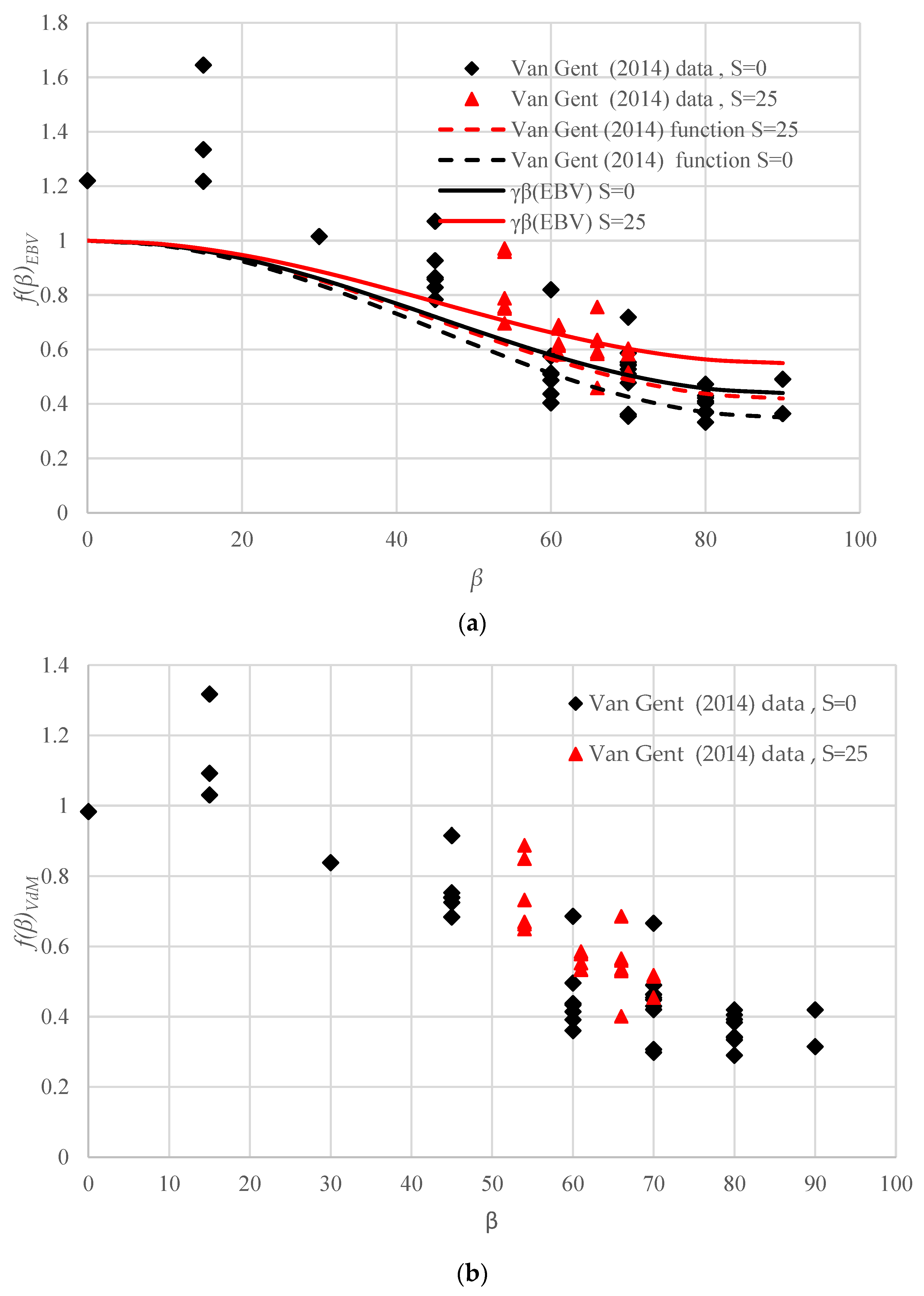
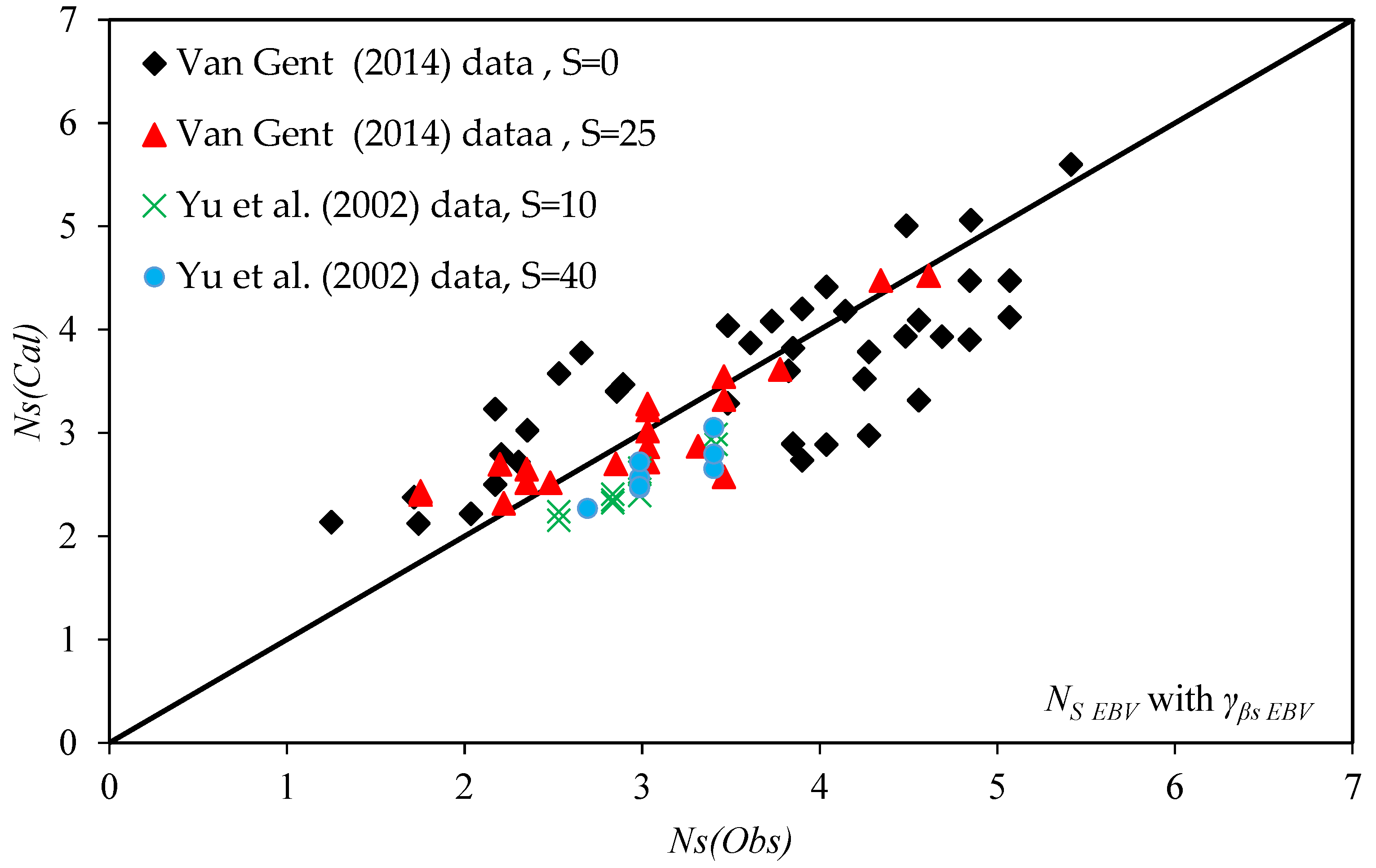
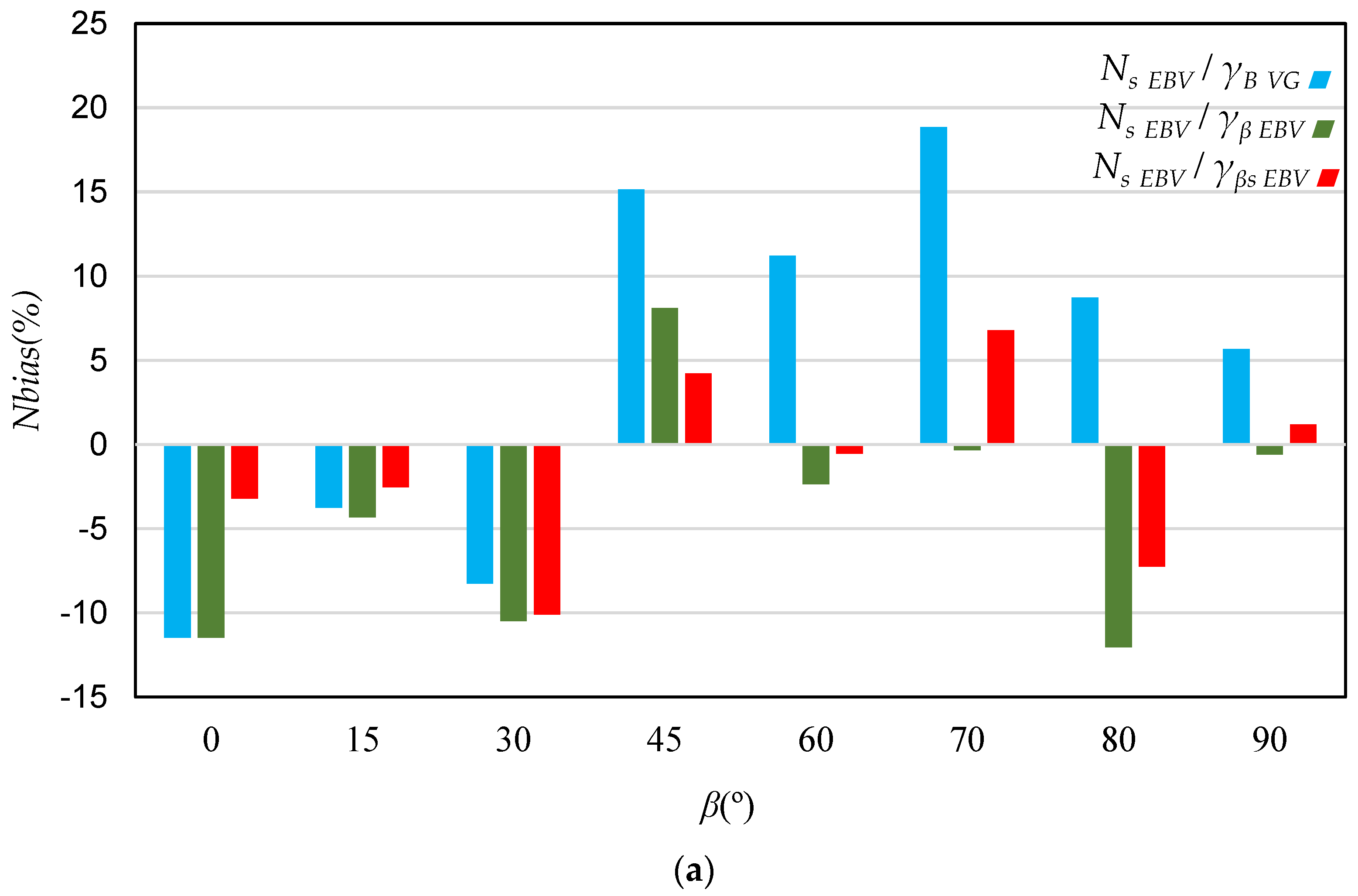
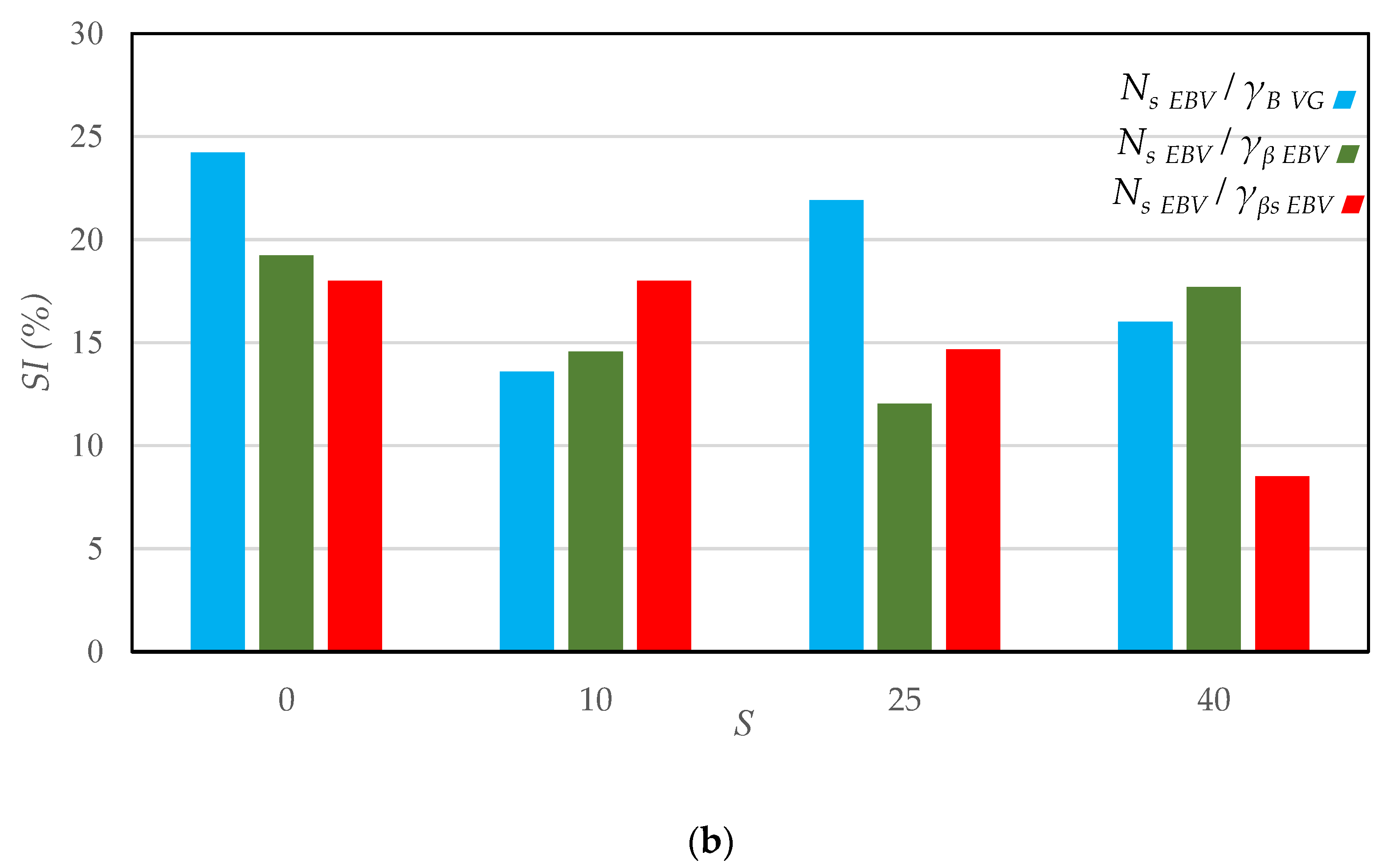
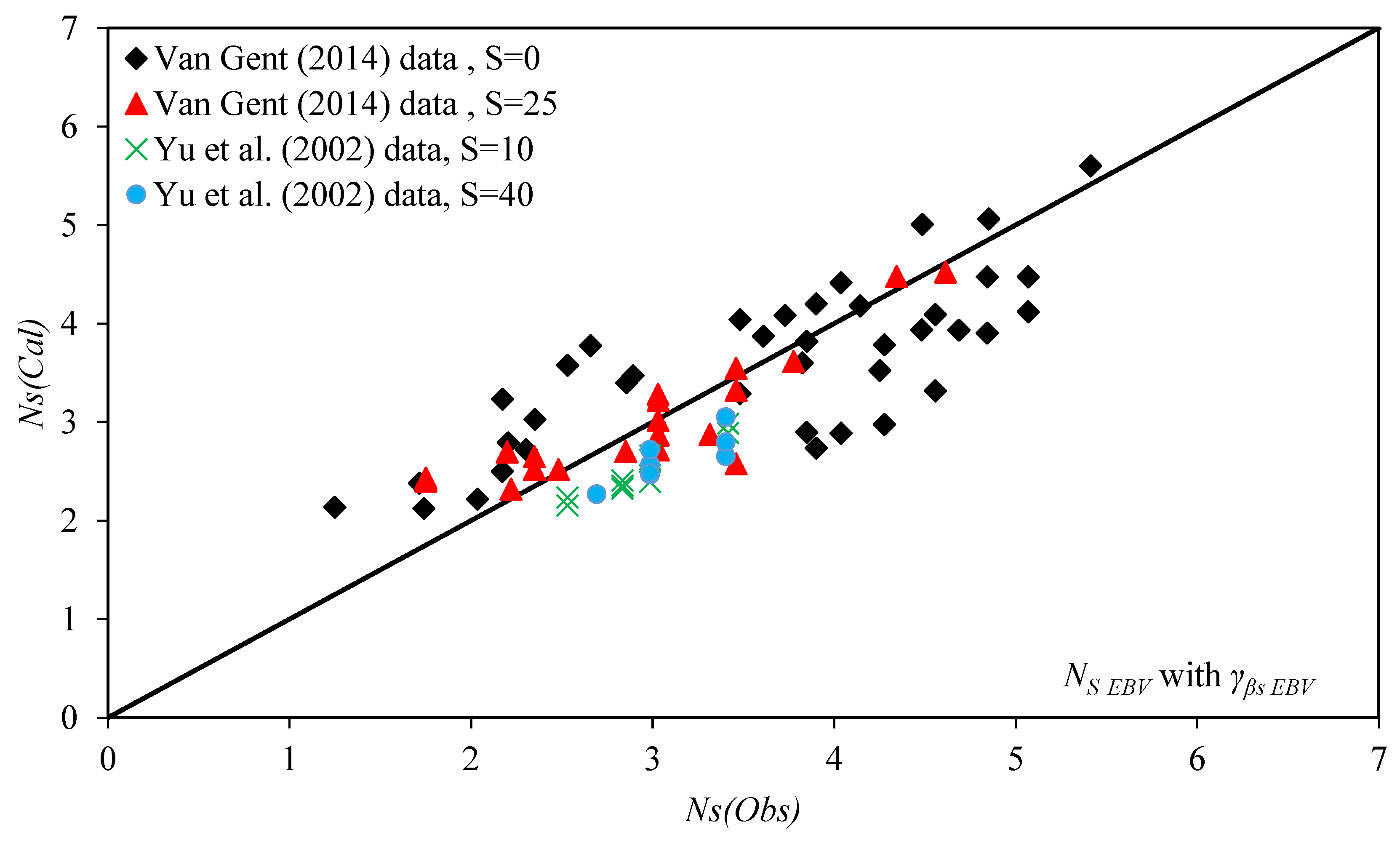
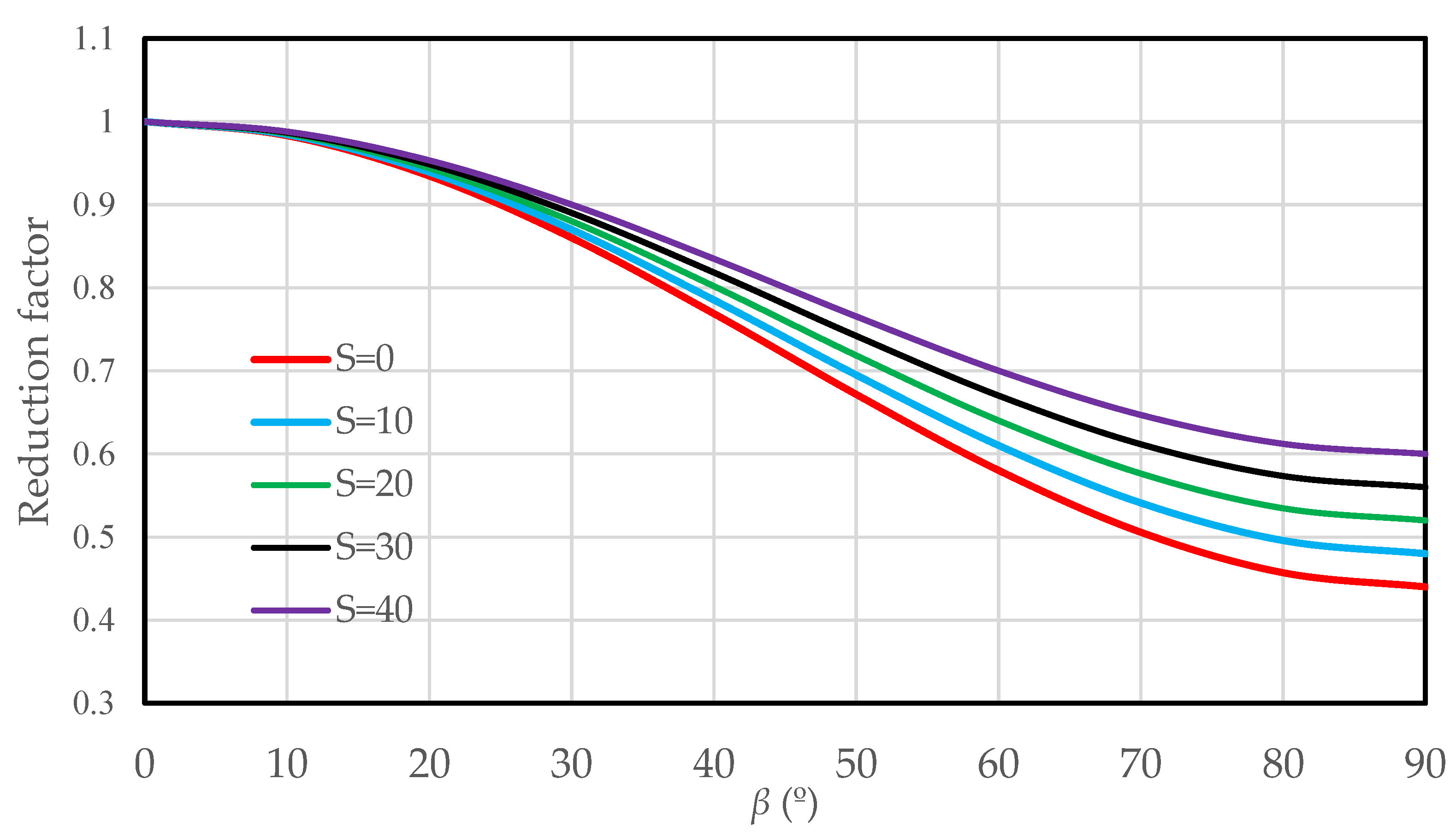
3. Results and Discussion
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Name | Unit |
| α | Structure slope angle | [°] |
| β | Wave angle | [°] |
| CP | Permeability coefficient | [-] |
| CC | Correlation coefficient | [-] |
| ∆ = (ρs/ρw) − 1 | Relative buoyant mass density | [-] |
| Dn50 = (M50/ρa)1/3 | Armour equivalent cube length exceeded by 50% of a sample by weight | [m] |
| D50 | Equivalent spherical diameter | [m] |
| Dn50c | Core equivalent cube length exceeded by 50% of a sample by weight | [m] |
| EBV | Etemad-Shahidi et al. [1] | [-] |
| γβ EBV | New wave angle and spreading reduction factor which is a function of β (quantitatively) and S (qualitatively) for EBV formula | [-] |
| γβS EBV | New wave angle and spreading reduction factor which is a function of β (quantitatively) and S (quantitatively) for EBV formula | [-] |
| γBVG | Wave angle and spreading reduction factor suggested by Van Gent [19] | [-] |
| Hm0 | Significant wave height based on frequency domain analysis | [m] |
| H2% | Average of the highest 2% of incident waves | [m] |
| H50 | Average of the 50 highest waves | [m] |
| Hs | Significant wave height at toe of the structure | [m] |
| h | Water depth | |
| KD | Hudson stability coefficient | [-] |
| Irm−1,0 | Iribarrn number based on Tm−1,0. | [-] |
| Irc | Transition Iribarrn number in VSK formula | [-] |
| mi | Measured values | [-] |
| Average of the measured values | [-] | |
| M50 | Median rock mass | [kg] |
| n | The number of observations | [-] |
| Nw | Number of wave attack | [-] |
| Ns | Stability number using Hs | [-] |
| NS EBV | Stability number calculated by EBV formula | [-] |
| NS VSK | Stability number calculated by VSK formula | [-] |
| Ns Measured | Measured stability number | |
| N50 | Stability number using H50 | [-] |
| P | Nominal permeability | [-] |
| Pi | Predicted values | [-] |
| Rc | Crest freeboard | [m] |
| ρs | Rock density | [kg/m3] |
| ρw | Water density | [kg/m3] |
| Som = 2πHmo/gTom2 | Deep water wave steepness using Tom | [-] |
| Som−1,0 | Deep water mean wave steepness using T−1,0 | [-] |
| Sd | Damage level | [-] |
| SI | Scatter index | [-] |
| Tm−1,0 = m−1/m0 | Mean energy wave period based on frequency domain | [s] |
| TP | Peak wave period | [s] |
| Tm | Mean wave period | [s] |
| Tm−1,0,deep | Mean energy wave period based on frequency domain analysis in deep water | [s] |
| VSK | Van Gent et al. [22] | [-] |
| VG | Van Gent [19] | |
| WV | Wolters and Van Gent [18] | [-] |
References
- Etemad-Shahidi, A.; Bali, M.; van Gent, M.R.A. On the stability of rock armored rubble mound structures. Coast. Eng. 2020, 158, 103655. [Google Scholar]
- Kolahdoozan, M.; Bali, M.; Rezaee, M.; Moeini, M.H. Wave-transmission prediction of π-type floating breakwaters in intermediate waters. J. Coast. Res. 2017, 33, 1460–1466. [Google Scholar] [CrossRef]
- Han, M.; Wang, C. Hydrodynamics study on rectangular porous breakwater with horizontal internal water channels. J. Ocean Eng. Mar. Energy 2020, 6, 377–398. [Google Scholar] [CrossRef]
- Wang, C.M.; Han, M.M.; Lyu, J.; Duan, W.H.; Jung, K.H.; Kang An, S. Floating forest: A novel concept of floating breakwater-windbreak structure. In WCFS2019: Proceedings of the World Conference on Floating Solutions; Springer: Singapore, 2020; pp. 219–234. [Google Scholar]
- Rahman, S.; Baeda, A.; Achmad, A.; Jamal, R. Performance of a New Floating Breakwater. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; p. 012081. [Google Scholar]
- Zhu, Y.; Tang, H. Automatic Damage Detection and Diagnosis for Hydraulic Structures Using Drones and Artificial Intelligence Techniques. Remote Sens. 2023, 15, 615. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Dong, G.; Chen, H.; Liu, Q.; Zang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Karimaei Tabarestani, M.; Feizi, A.; Bali, M. Reliability-based design and sensitivity analysis of rock armors for rubble-mound breakwater. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 136. [Google Scholar] [CrossRef]
- Etemad-Shahidi, A.; Bali, M.; van Gent, M.R.A. On the toe stability of rubble mound structures. Coast. Eng. 2021, 164, 103835. [Google Scholar] [CrossRef]
- Etemad-Shahidi, A.; Koosheh, A.; van Gent, M.R.A. On the mean overtopping rate of rubble mound structures. Coast. Eng. 2022, 177, 104150. [Google Scholar] [CrossRef]
- Houtzager, D.; Hofland, B.; Caldera, G.; van der Lem, C.; van Gent, M.; Bakker, P.; Antonini, A. Embedded rocking measurement of single layer armour units: Development and first results. In Proceedings of the ICE Breakwaters 2023: Coasts, Marine Structures and Breakwaters, Portsmouth, UK, 25–27 April 2023. [Google Scholar]
- De Waal, J.; Van der Meer, J. Wave runup and overtopping on coastal structures. In Proceedings of the 23rd International Conference on Coastal Engineering, Venice, Italy, 4–9 October 1992; pp. 1758–1771. [Google Scholar]
- Galland, J.-C. Rubble mound breakwater stability under oblique waves: An experimental study. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, 23–28 October 1994; pp. 1061–1074. [Google Scholar]
- Hebsgaard, M.; Sloth, P.; Juhl, J. Wave overtopping of rubble mound breakwaters. In Proceedings of the 26th International Conference on Coastal Engineering, Copenhagen, Denmark, 22–26 June 1998; pp. 2235–2248. [Google Scholar]
- Andersen, T.L.; Burcharth, H.F. Three-dimensional investigations of wave overtopping on rubble mound structures. Coast. Eng. 2009, 56, 180–189. [Google Scholar] [CrossRef]
- Nørgaard, J.Q.H.; Andersen, T.L.; Burcharth, H.F.; Steendam, G.J. Analysis of overtopping flow on sea dikes in oblique and short-crested waves. Coast. Eng. 2013, 76, 43–54. [Google Scholar] [CrossRef]
- Yu, Y.-X.; Liu, S.-X.; Zhu, C.-H. Stability of armour units on rubble mound breakwater under multi-directional waves. Coast. Eng. J. 2002, 44, 179–201. [Google Scholar] [CrossRef]
- Wolters, G.; Van Gent, M. Oblique wave attack on cube and rock armoured rubble mound breakwaters. Coast. Eng. Proc. 2011, 32, 34. [Google Scholar] [CrossRef]
- Van Gent, M.R.A. Oblique wave attack on rubble mound breakwaters. Coast. Eng. 2014, 88, 43–54. [Google Scholar] [CrossRef]
- Hudson, R. Design of Quarry-Stone Cover Layers for Rubble-Mound Breakwaters; Coastal Engineering Research Centre: Vicksburg, MS, USA, 1958. [Google Scholar]
- Van der Meer, J.W. Deterministic and probabilistic design of breakwater armor layers. J. Waterw. Port Coast. Ocean Eng. 1988, 114, 66–80. [Google Scholar] [CrossRef]
- Van Gent, M.R.A.; Smale, A.J.; Kuiper, C. Stability of rock slopes with shallow foreshores. In Proceedings of the Coastal Structures 2003, Portland, OR, USA, 26–30 August 2003; pp. 100–112. [Google Scholar]
- Etemad-Shahidi, A.; Bali, M. Stability of rubble-mound breakwater using H50 wave height parameter. Coast. Eng. 2012, 59, 38–45. [Google Scholar] [CrossRef]
- Van der Meer, J. Stability of rubble mound revetments and breakwaters. In Developments in Breakwaters; ICE Publishing: London, UK, 1985; pp. 191–202. [Google Scholar]
- The Rock Manual. The Use of Rock in Hydraulic Engineering. CIRIA-CUR, Publication C683. 2007. Available online: https://www.kennisbank-waterbouw.nl/DesignCodes/rockmanual/introduction.pdf (accessed on 31 May 2023).
- Sigurdarson, S.; van der Meer, J. Design and Construction Aspects of Berm Breakwaters. In Coastal Structures and Solutions to Coastal Disasters 2015: Resilient Coastal Communities; American Society of Civil Engineers: Reston, VA, USA, 2017; pp. 864–875. [Google Scholar]
- U.S. Army Corps of Engineers. Coastal Engineering Manual (CEM), Engineer Manual 1110-2-1100, 2002, Washington, DC (6 volumes) 2011: US. Chapter VI, Part 5. Available online: https://www.publications.usace.army.mil/USACE-Publications/Engineer-Manuals/u43544q/636F617374616C20656E67696E656572696E67206D616E75616C/ (accessed on 30 April 2023).




| Reference | Formula | Equation No | |
|---|---|---|---|
| Galland [13] | cos0.25 β | (1) | |
| Yu et al. [17] | cos1.157 β | (2) | |
| Wolters and Van Gent [18] | cos1.1 β | (3) | |
| Van Gent [19] | (1 − cβ) cos2β + cβ | cβ = 0.42 for short-crested | (4) |
| cβ = 0.35 for long-crested | |||
| k | 1.10 | 1.15 | 1.20 | 1.25 | 1.30 |
| Nw1–2/Nw1 (%) | 39 | 25 | 16 | 11 | 7 |
| ΔSd (%) | 21.6 | 14.3 | 9.3 | 6.5 | 4 |
| Parameter | β | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 15 | 30 | 45 | 60 | 70 | 80 | 90 | |
| Nw | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 |
| cotα | 1.5 | 1.5 | 1.5 | 1.5 | 1.5, 2 | 1.5, 2 | 1.5, 2 | 1.5 |
| D | 1.7 | 1.7 | 1.7 | 1.7 | 1.7 | 1.7 | 1.7 | 1.7 |
| S | 0–40 | 0–40 | 0–40 | 0–40 | 0–40 | 0–25 | 0–25 | 0–25 |
| P | 0.4, 0.5 | 0.4, 0.5 | 0.4, 0.5 | 0.1–0.5 | 0.1–0.5 | 0.1–0.5 | 0.1–0.5 | 0.1–0.5 |
| som−1,0 (×10−2) | 3–6 | 3–6 | 3–6 | 3–6 | 3–6 | 3–6 | 3–6 | 3–6 |
| Irm−1,0 | 2.7–3.6 | 2.6–3.6 | 2.6–3.5 | 2.6–3.6 | 2.2–3.7 | 2.3- 4.0 | 2.2–3.0 | 3.1–3.5 |
| h/Hs | 3.4–10.5 | 3.0–14.7 | 3–8.0 | 2.6–11.0 | 2.4–14.5 | 2.7–11.3 | 4.6–6.5 | 5.5–5.9 |
| Dn50c /Dn50 | 0.4–0.43 | 0.4–0.43 | 0.4–0.43 | 0–0.43 | 0–0.43 | 0–0.43 | 0–0.43 | 0.0–0.43 |
| Sd | 2–7.1 | 2.2–11.5 | 2.3–6.5 | 2.0–7.0 | 2.0–8.8 | 2–12 | 2.2–9.2 | 3.4–3.7 |
| Ns | 1.7–3.0 | 1.2–3.4 | 2.3–3.42 | 2.0–3.4 | 1.7–4.7 | 2.2–4.8 | 3.8–5.4 | 4.2–4.5 |
| Parameter | S | |||
|---|---|---|---|---|
| 0 | 10 | 25 | 40 | |
| Nw | 1000 | 1000 | 1000 | 1000 |
| cotα | 1.5, 2 | 1.5 | 1.5, 2 | 1.5 |
| D | 1.7 | 1.7 | 1.7 | 1.6 |
| β | 0–90 | 0–45 | 50–70 | 0–45 |
| P | 0.1–0.5 | 0.4 | 0.1–0.5 | 0.4 |
| som−1,0 (×10−2) | 3–6 | 3–6 | 3–6 | 3–6 |
| Irm−1,0 | 2.2–4.0 | 2.6–2.7 | 2.2–3.3 | 2.6–2.7 |
| h/Hs | 2.4–14.7 | 3.0–4.0 | 5.3–14.1 | 3–3.76 |
| Dn50c /Dn50 | 0.0–0.43 | 0.40 | 0.0–0.43 | 0.40 |
| Sd | 2–11.5 | 2–6.5 | 2.3–6.5 | 2.1–7.2 |
| Ns | 1.2–5.4 | 2.5–3.4 | 2.5–3.4 | 2.7–3.4 |
| Ns EBV/γB VG | Ns EBV/γβ EBV | Ns EBV/γβs EBV | |
|---|---|---|---|
| NBias | 16.4 | −0.05 | −0.05 |
| SI | 24 | 17.7 | 17.70 |
| CC | 0.83 | 0.80 | 0.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bali, M.; Etemad-Shahidi, A.; van Gent, M.R.A. On the Stability of Rubble Mound Structures under Oblique Wave Attack. J. Mar. Sci. Eng. 2023, 11, 1261. https://doi.org/10.3390/jmse11071261
Bali M, Etemad-Shahidi A, van Gent MRA. On the Stability of Rubble Mound Structures under Oblique Wave Attack. Journal of Marine Science and Engineering. 2023; 11(7):1261. https://doi.org/10.3390/jmse11071261
Chicago/Turabian StyleBali, Meysam, Amir Etemad-Shahidi, and Marcel R. A. van Gent. 2023. "On the Stability of Rubble Mound Structures under Oblique Wave Attack" Journal of Marine Science and Engineering 11, no. 7: 1261. https://doi.org/10.3390/jmse11071261
APA StyleBali, M., Etemad-Shahidi, A., & van Gent, M. R. A. (2023). On the Stability of Rubble Mound Structures under Oblique Wave Attack. Journal of Marine Science and Engineering, 11(7), 1261. https://doi.org/10.3390/jmse11071261











