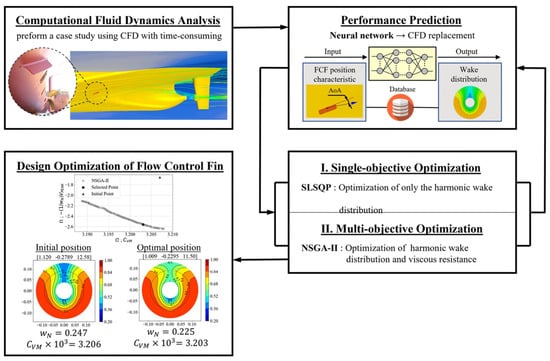
Optimal Design of Flow Control Fins for a Small Container Ship Based on Machine Learning
Abstract
1. Introduction
1.1. Importance of Flow Control Fins (FCFs) in Ship Energy Efficiency
1.2. Contributions
2. Theoretical Backgrounds
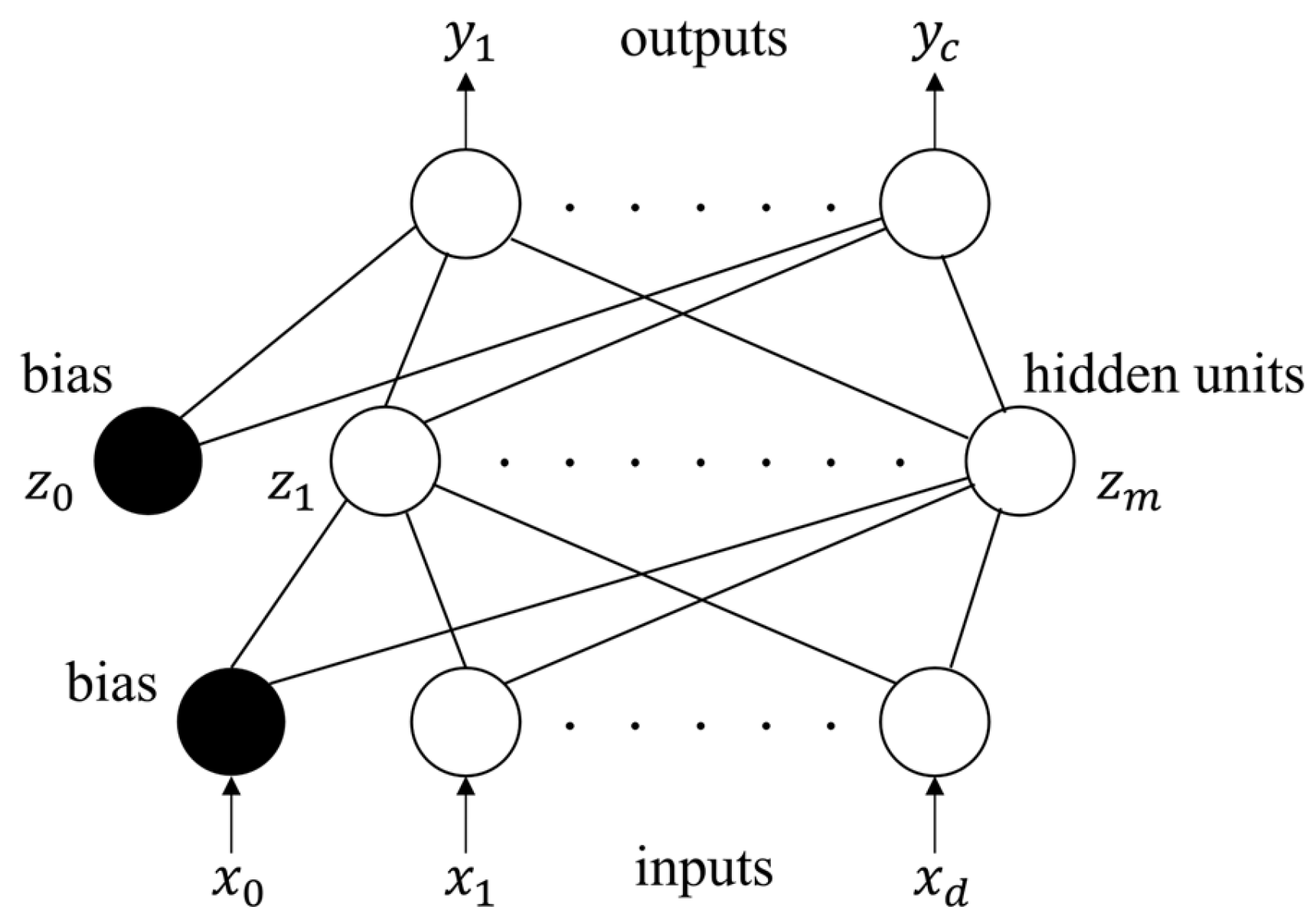
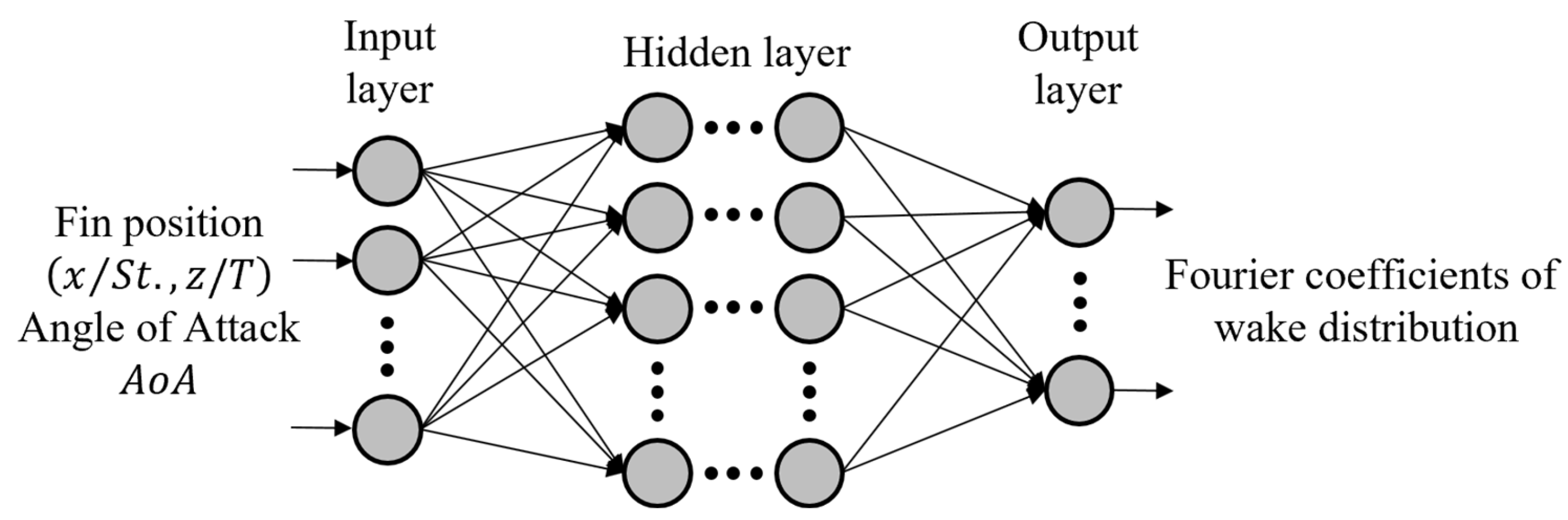
2.1. Artificial Neural Network (ANN)
2.2. Optimization Algorithms
2.2.1. Sequential Least Squares Programming (SLSQP)
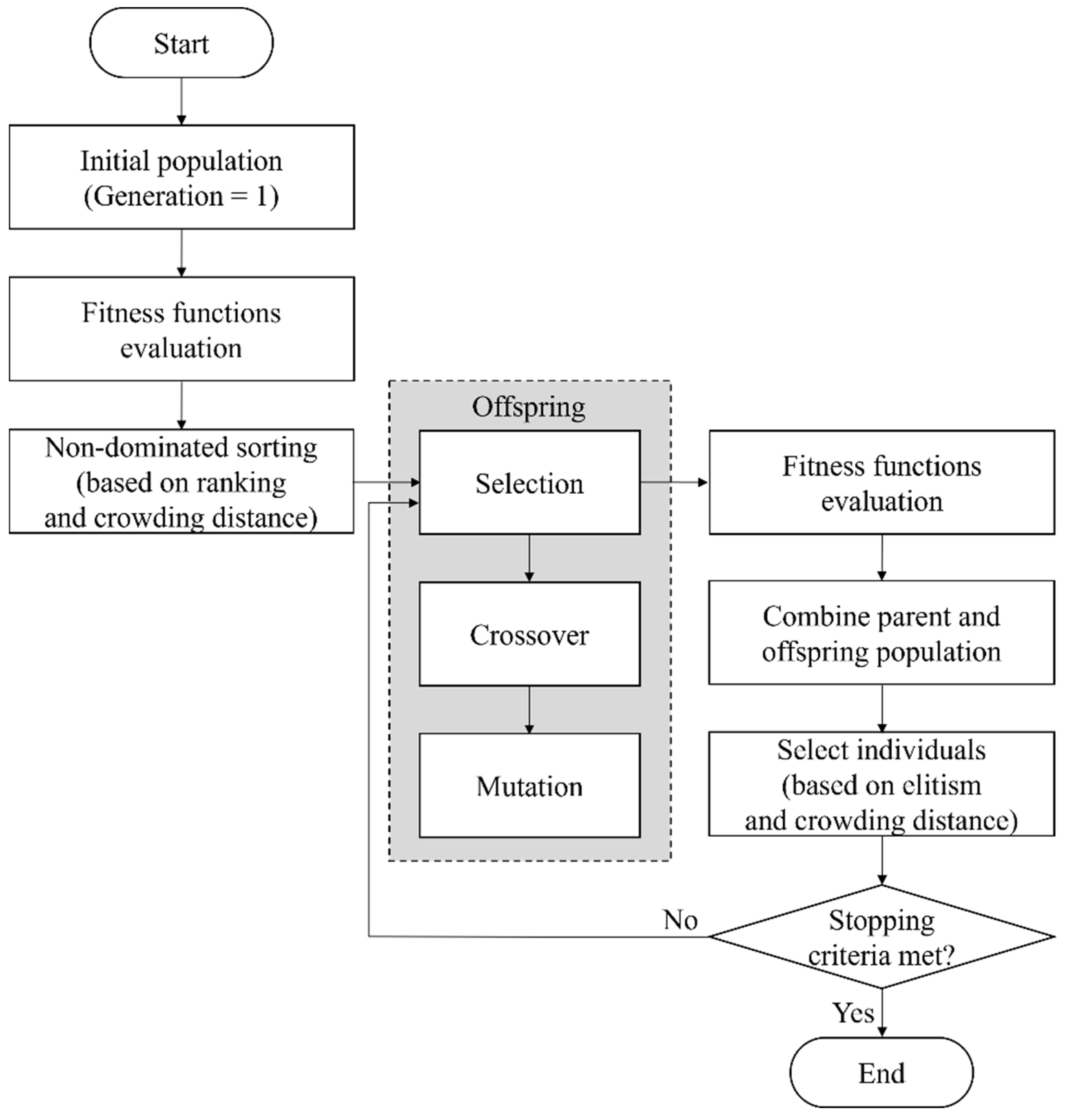
2.2.2. Non-Dominated Sorting Genetic Algorithm-II (NSGA-II)
3. Problem Description
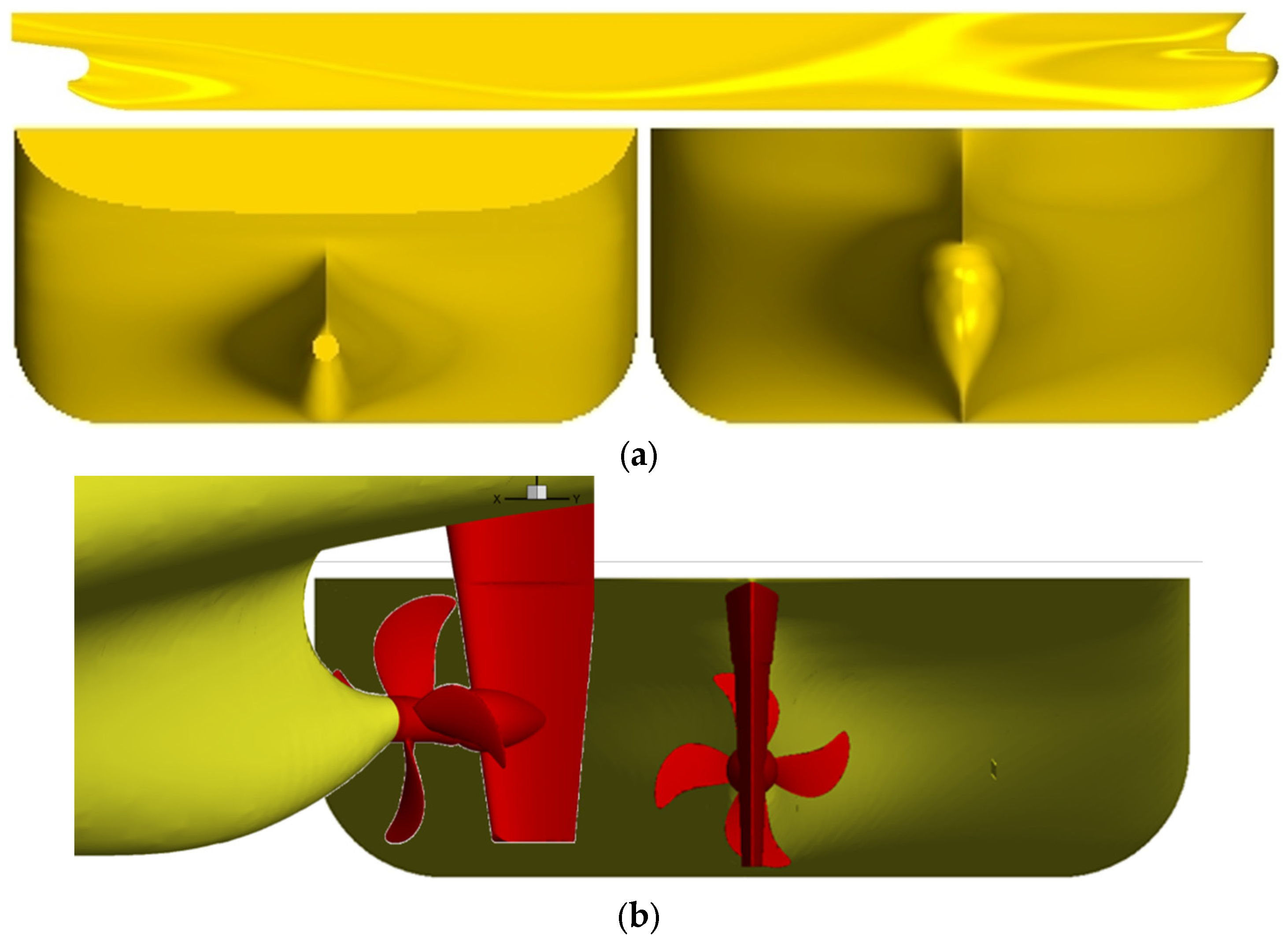
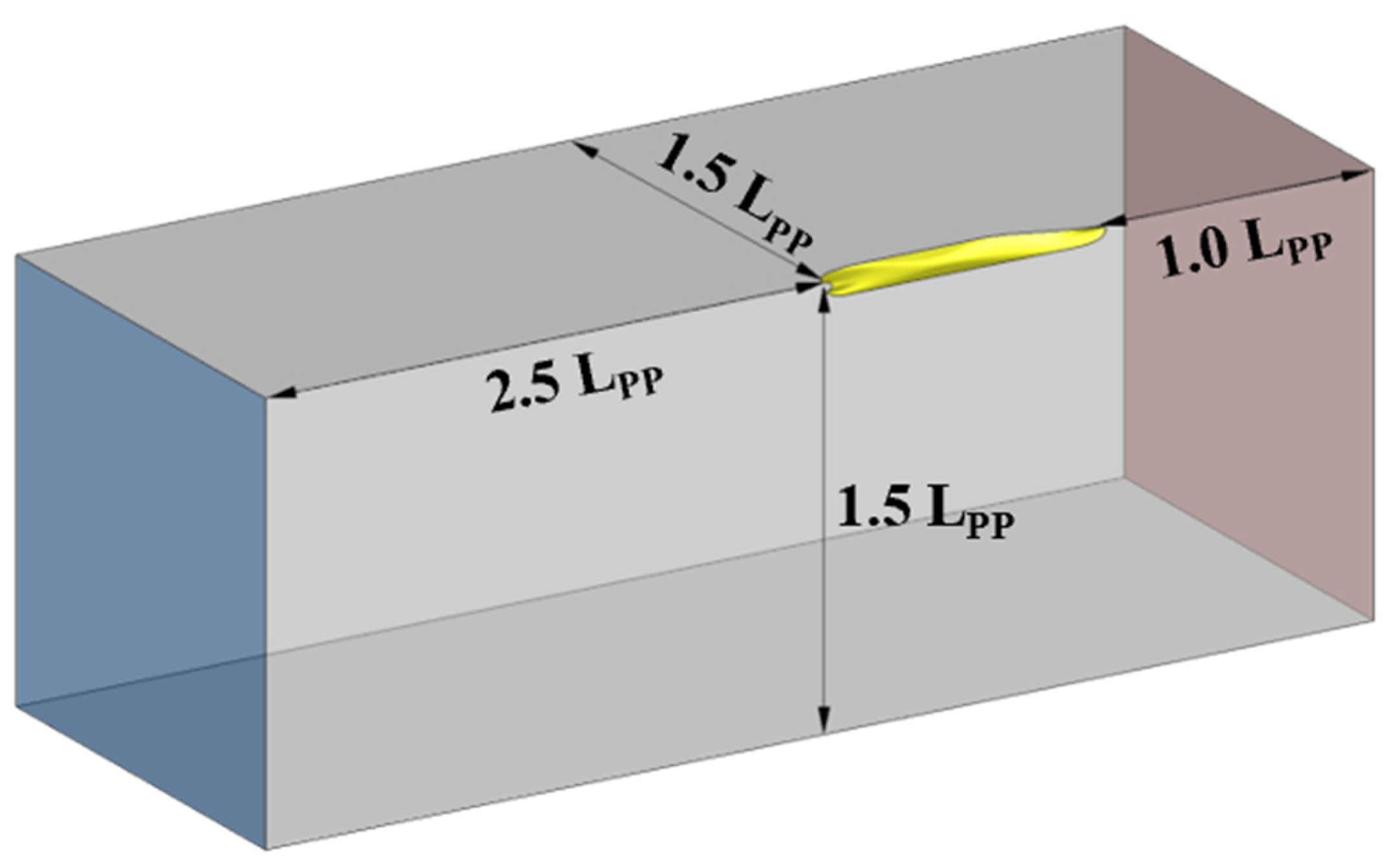
3.1. Geometry of Target Ship and Flow Control Fins
3.2. CFD Simulation for Training Data
4. Methodologies
4.1. ANN-Based Prediction of Wake Distribution
4.2. Selection of the Optimal Fin Position
4.2.1. Single-Objective Optimization Using SLSQP
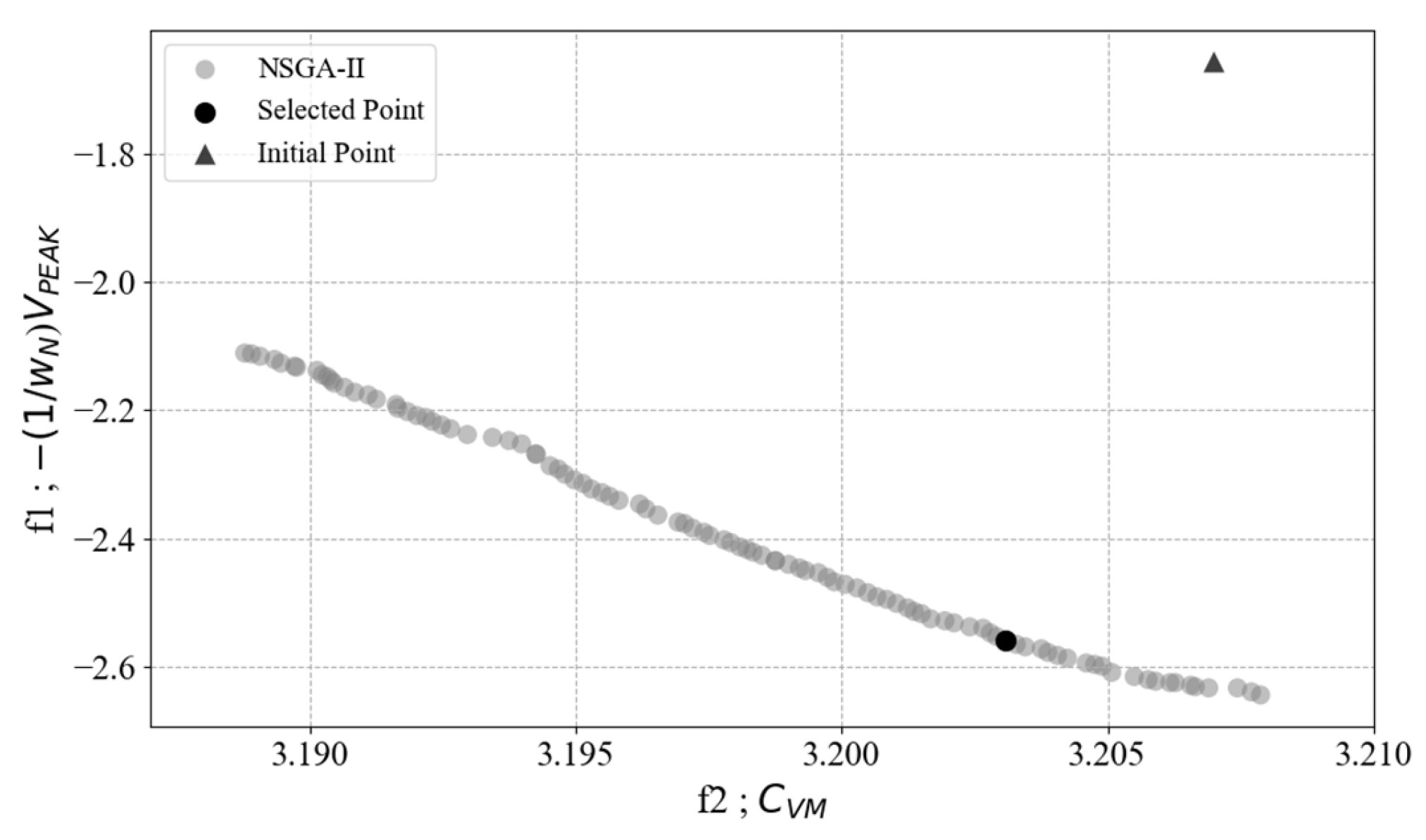
4.2.2. Multi-Objective Optimization Using NSGA-II
5. Results
5.1. Validation of CFD Analysis
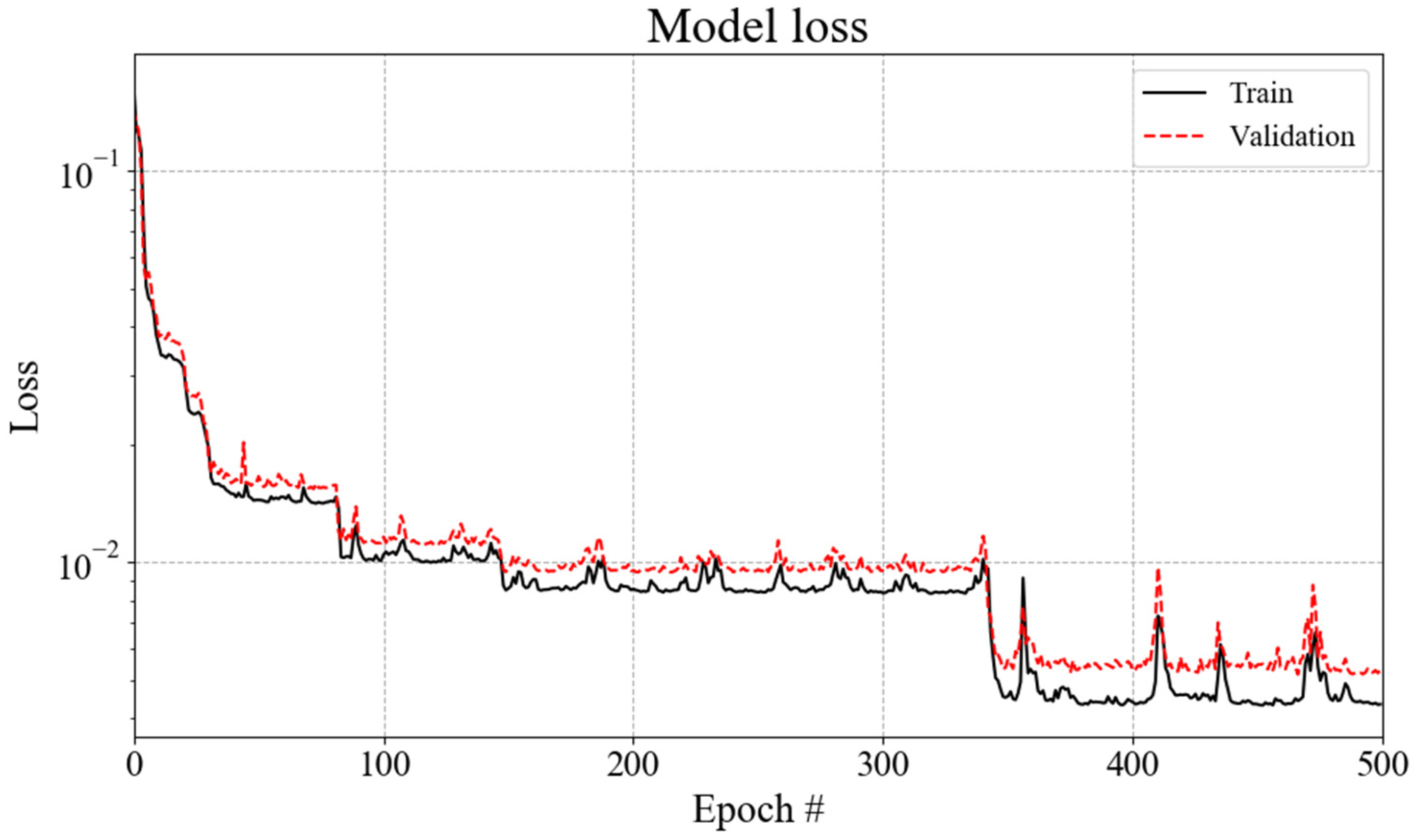
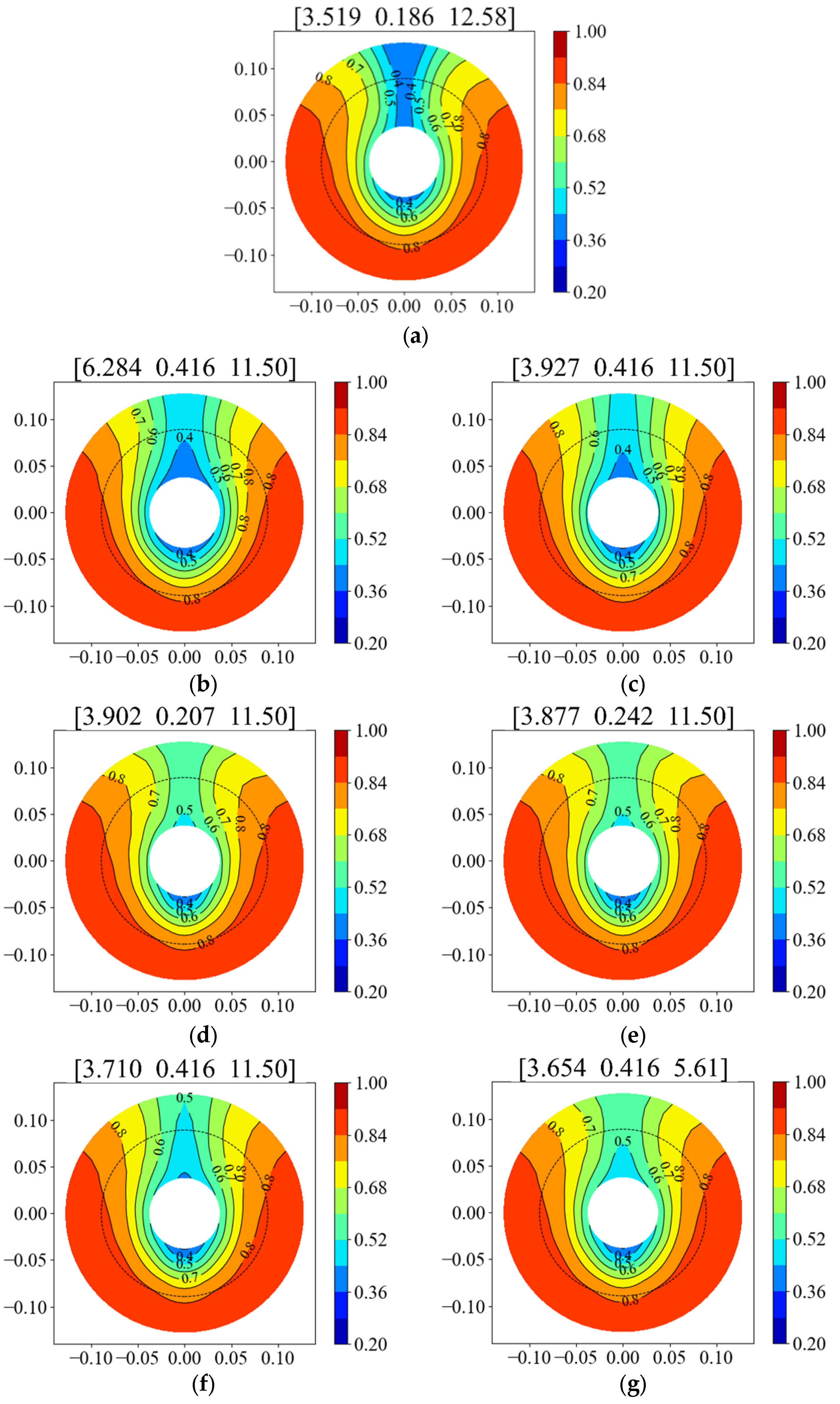
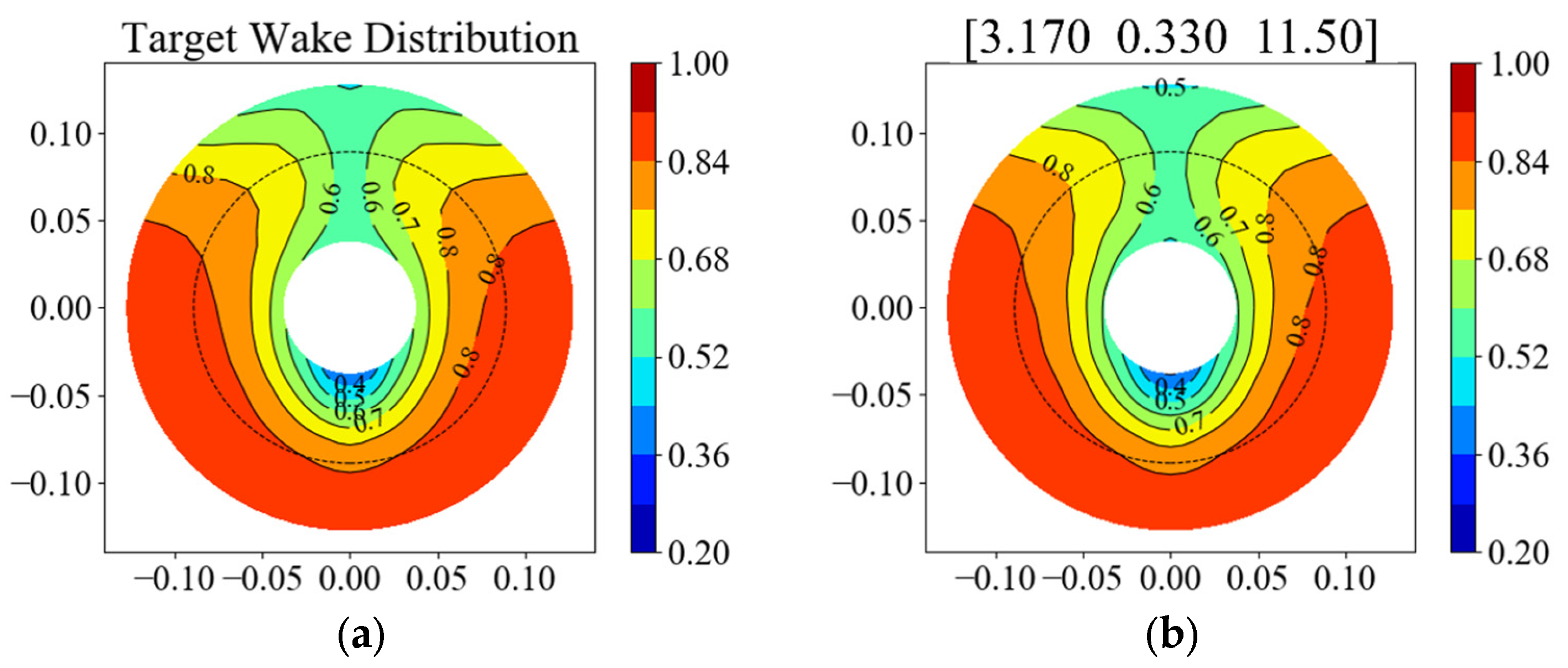
5.2. The ANN-Based Prediction
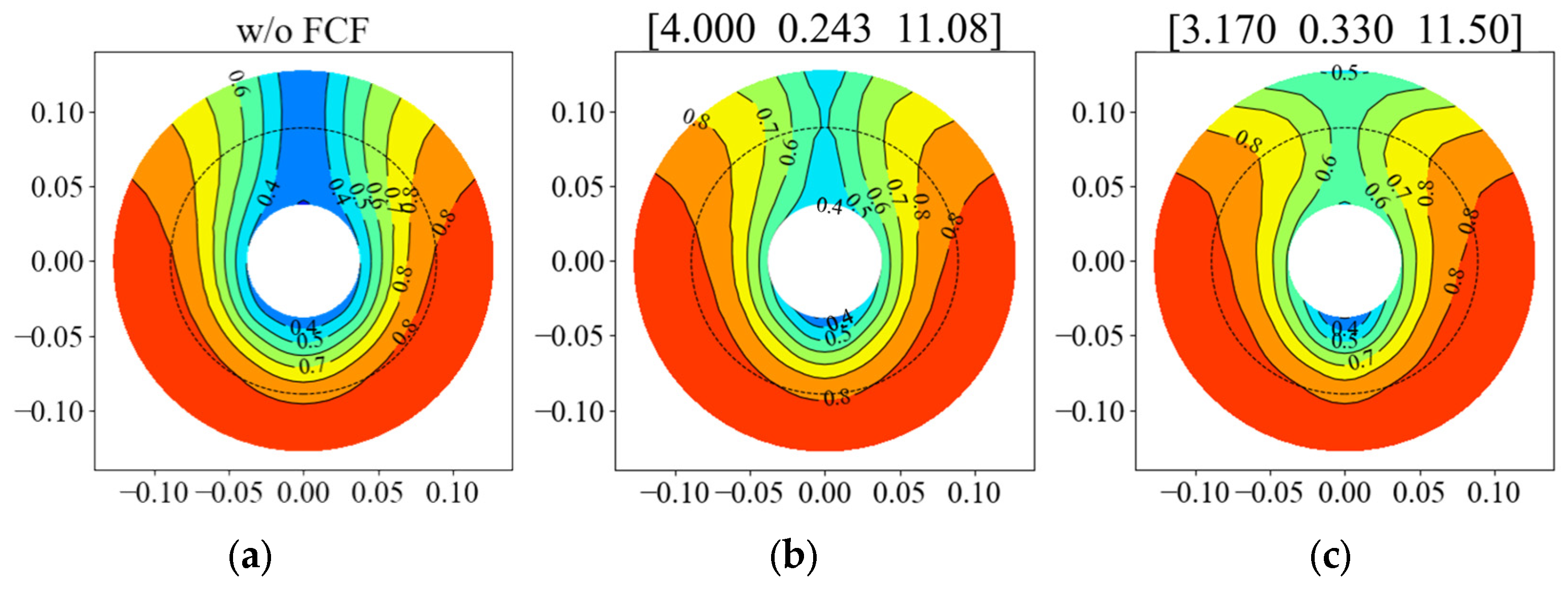
5.3. Optimization of the Design Variables of FCFs
5.3.1. Single-Objective Optimization Results
5.3.2. Multi-Objective Optimization Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Joung, T.-H.; Kang, S.-G.; Lee, J.-K.; Ahn, J. The IMO initial strategy for reducing Greenhouse Gas (GHG) emissions, and its follow-up actions towards 2050. J. Int. Marit. Saf. Environ. Aff. Shipp. 2020, 4, 1–7. [Google Scholar] [CrossRef]
- Lee, H.D.; Hong, C.B.; Kim, H.T.; Choi, S.H.; Han, J.M.; Kim, B.; Lee, J.H. Development and application of energy saving devices to improve resistance and propulsion performance. In Proceedings of the Twenty-fifth International Ocean and Polar Engineering Conference, Kona, HI, USA, 21–26 June 2015. [Google Scholar]
- Inoue, T.; Saito, Y. A Study on the Principle and Energy Saving Effect of Multi ALV-Fin. In Proceedings of the 2nd Hull Performance & Insights Conference, Ulrichshusen, Germany, 27–29 March 2017. [Google Scholar]
- Park, Y.; Hwangbo, S.M.; Yu, J.-W.; Cho, Y.; Lee, J.H.; Lee, I. Development of a small-sized tanker with reduced greenhouse gas emission under in-service condition based on CFD simulation. Ocean. Eng. 2022, submitted.
- Hwangbo, S.; Shin, H. Statistical prediction of wake fields on propeller plane by neural network using back-propagation. J. Ship Ocean. Technol. 2000, 4, 1–12. [Google Scholar]
- Kim, S.-Y.; Moon, B. Wake distribution prediction on the propeller plane in ship design using artificial intelligence. Ships Offshore Struct. 2006, 1, 89–98. [Google Scholar] [CrossRef]
- Wie, D.-E.; Kim, D.-J. The Design Optimization of a Flow Control Fin Using CFD. J. Soc. Nav. Archit. Korea 2012, 49, 174–181. [Google Scholar] [CrossRef]
- Pache, R.; Rung, T. Data-driven surrogate modeling of aerodynamic forces on the superstructure of container vessels. Eng. Appl. Comput. Fluid Mech. 2022, 16, 746–763. [Google Scholar] [CrossRef]
- Sun, T.; Chen, G.; Yang, S.; Wang, Y.; Wang, Y.; Tan, H.; Zhang, L. Design and optimization of a bio-inspired hull shape for AUV by surrogate model technology. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1057–1074. [Google Scholar] [CrossRef]
- Zhang, S.; Tezdogan, T.; Zhang, B.; Lin, L. Research on the hull form optimization using the surrogate models. Eng. Appl. Comput. Fluid Mech. 2021, 15, 747–761. [Google Scholar] [CrossRef]
- Alexiou, K.; Pariotis, E.G.; Zannis, T.C.; Leligou, H.C. Prediction of a ship’s operational parameters using artificial intelligence techniques. J. Mar. Sci. Eng. 2021, 9, 681. [Google Scholar] [CrossRef]
- Lin, J.; Han, Y.; Guo, C.; Su, Y.; Zhong, R. Intelligent ship anti-rolling control system based on a deep deterministic policy gradient algorithm and the Magnus effect. Phys. Fluids 2022, 34, 057102. [Google Scholar] [CrossRef]
- Yang, Z.R.; Yang, Z. Artificial Neural Networks. In Comprehensive Biomedical Physics, 1st ed.; Brahme, A., Ed.; Elsevier: Amsterdam, The Netherlands, 2014; Volume 6, pp. 1–17. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural networks and their applications. Rev. Sci. Instrum. 1994, 65, 1803–1832. [Google Scholar] [CrossRef]
- Kraft, D. A Software Package for Sequential Quadratic Programming; DFVLR-FB 88-28 Technical Report; DLR German Aerospace Center–Institute for Flight Mechanics: Koln, Germany, 1988; Available online: http://www.opengrey.eu/item/display/10068/ (accessed on 10 April 2023).
- Parkinson, A.R.; Balling, R.; Hedengren, J.D. Optimization Methods for Engineering Design: Applications and Theory, 5th ed.; Brigham Young University: Provo, UT, USA, 2013. [Google Scholar]
- Nayak, S. Multiobjective optimization. In Fundamentals of Optimization Techniques with Algorithms; Academic Press: Cambridge, MA, USA, 2020; pp. 253–270. [Google Scholar] [CrossRef]
- Andersson, J. A Survey of Multiobjective Optimization in Engineering Design; LiTH-IKP-R-1097 Technical Report; Department of Mechanical Engineering, Linköping University: Linköping, Sweden, 2000. [Google Scholar]
- Srinivas, N.; Deb, K. Muiltiobjective optimization using nondominated sorting in genetic algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Hino, T. Proceedings of CFD Workshop Tokyo 2005; National Maritime Research Institute: Tokyo, Japan, 2005. [Google Scholar]
- Farkas, A.; Degiuli, N.; Martić, I. Assessment of hydrodynamic characteristics of a full-scale ship at different draughts. Ocean Eng. 2018, 156, 135–152. [Google Scholar] [CrossRef]
- Farkas, A.; Degiuli, N.; Martić, I.; Dejhalla, R. Numerical and experimental assessment of nominal wake for a bulk carrier. J. Mar. Sci. Technol. 2019, 24, 1092–1104. [Google Scholar] [CrossRef]
- Dogrul, A. Numerical prediction of scale effects on the propulsion performance of Joubert BB2 submarine. Brodogr. Teor. Praksa Brodogr. Pomor. Teh. 2022, 73, 17–42. [Google Scholar] [CrossRef]










| Designation | Symbol (Unit) | Full-Scale Ship |
|---|---|---|
| Length bet. perpendiculars | (m) | 137.5 |
| Breadth | (m) | 23.6 |
| Draft | (m) | 7.4 |
| Block coefficient | 0.595 | |
| Propeller diameter | (m) | 5.5 |
| Boundary Surface | Type |
|---|---|
| Inlet | Velocity inlet |
| Outlet | Pressure outlet |
| Top, bottom, side, centerplane | Symmetry |
| Ship | Wall |
| Item | Value |
|---|---|
| # of Nodes of Hidden layer—1 | 11 |
| # of Nodes of Hidden layer—2 | 22 |
| # of Nodes of Hidden layer—3 | 44 |
| # of Nodes of Hidden layer—4 | 66 |
| # of Nodes of Hidden layer—5 | 89 |
| Vs [kn] | ||||||
|---|---|---|---|---|---|---|
| EXP | CFD | Difference | EXP | CFD | Difference | |
| 17.0 | 3.929 | 3.870 | −1.50% | 0.741 | 0.678 | −0.06 |
| 18.0 | 3.999 | 3.993 | −0.15% | 0.843 | 0.834 | −0.01 |
| 19.0 | 4.199 | 4.178 | −0.50% | 1.073 | 1.049 | −0.02 |
| Bare Hull | Optimal Fin | |
|---|---|---|
| 3.206 | 3.207 | |
| [N] | 52.37 | 52.41 |
| Bare Hull | Optimal Fin | |
|---|---|---|
| 3.206 | 3.203 | |
| [N] | 52.37 | 52.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, M.-K.; Lee, I. Optimal Design of Flow Control Fins for a Small Container Ship Based on Machine Learning. J. Mar. Sci. Eng. 2023, 11, 1149. https://doi.org/10.3390/jmse11061149
Lee M-K, Lee I. Optimal Design of Flow Control Fins for a Small Container Ship Based on Machine Learning. Journal of Marine Science and Engineering. 2023; 11(6):1149. https://doi.org/10.3390/jmse11061149
Chicago/Turabian StyleLee, Min-Kyung, and Inwon Lee. 2023. "Optimal Design of Flow Control Fins for a Small Container Ship Based on Machine Learning" Journal of Marine Science and Engineering 11, no. 6: 1149. https://doi.org/10.3390/jmse11061149
APA StyleLee, M.-K., & Lee, I. (2023). Optimal Design of Flow Control Fins for a Small Container Ship Based on Machine Learning. Journal of Marine Science and Engineering, 11(6), 1149. https://doi.org/10.3390/jmse11061149