Abstract
Geoacoustic inversion is a challenging task in marine research due to the complex environment and acoustic propagation mechanisms. With the rapid development of deep learning, various designs of neural networks have been proposed to solve this issue with satisfactory results. As a data-driven method, deep learning networks aim to approximate the inverse function of acoustic propagation by extracting knowledge from multiple replicas, outperforming conventional inversion methods. However, existing deep learning networks, mainly incorporating stacked convolution and fully connected neural networks, are simple and may neglect some meaningful information. To extend the network backbone for geoacoustic inversion, this paper proposes a transformer-based geoacoustic inversion model with additional frequency and sensor 2-D positional embedding to perceive more information from the acoustic input. The simulation experimental results indicate that our proposed model achieves comparable inversion results with the existing inversion networks, demonstrating its effectiveness in marine research.
1. Introduction
Acoustic wave propagation in shallow water is highly susceptible to the geoacoustic characteristics of the seabed that play a crucial role in sound transmission processes. The influence of seafloor properties on acoustic propagation mechanisms has been widely studied [1], with particular attention given to shallow sea environments characterized by complex and variable ocean conditions. In such environments, the reflection and absorption processes of the seabed significantly affect acoustic signal propagation [2]. Understanding the acoustic parameters of the seafloor is vital for both sonar equipment performance evaluation and acoustic field modelling. However, obtaining these geoacoustic characteristics efficiently remains challenging and has, hence, garnered much attention within the marine science community [3].
There are two primary approaches used for determining underwater acoustic parameters: experimental measurements, including in situ measurements during sea trials [4,5], and acoustic inversion techniques. The first approach can only obtain the local bottom characteristics of the target area, making it impractical and resource-intensive to acquire a large range of seafloor acoustic parameters. In contrast, acoustic inversion techniques process data received from sonar systems and are an efficient means of measuring bottom characteristics. These methods enable a quick and cost-effective acquisition of geoacoustic parameters from measured acoustic data, and have made significant contributions to marine research, such as matched-field inversion (MFI) [6], time-of-arrival analysis [7], and modal dispersion techniques [8]. Among these techniques, matched-field inversion (MFI) is the most widely used method. Vertical linear arrays (VLA), towed linear arrays, bottom horizontal linear arrays (HLA) or distributed sensor networks (DSN) are developed for source localization by comparing the energy of the measured signal with that generated by an acoustic forward model simulation. Bayesian approaches [9] that use posterior probability density estimates to infer parameters have also gained attention in uncertain ocean environments. While no single geoacoustic inversion system is superior to others, the efficiency of these methods is usually their most appealing feature.
Motivated by the development of deep learning, its excellent techniques have been increasingly applied in marine acoustics, leading to remarkable achievements and superior performance compared to traditional approaches [10,11]. Various neural networks have been adopted for geoacoustic inversion. This is a functional approximation problem that estimates objective geoacoustic characteristics, such as the sound speed profile, layer thickness, and density of sediments, efficiently.
Liu et al. [12] proposed a deep convolutional neural network architecture for multi-range vertical array processing, demonstrating its efficacy in geoacoustic inversion. Zhu et al. [13] developed a deep-reinforcement-learning-based inversion method to estimate the shear wave velocity, exhibiting better efficiency and accuracy compared to heuristic algorithms. Shen et al. [14] introduced a radial basis function neural network (RBFNN) to MFI, achieving comparable performance to conventional methods. Alfarraj and AlRegib [15] proposed a semi-supervised framework based on a mixed convolutional and recurrent neural network for acoustic impedance inversion, delivering satisfactory results. Yang and Ma [16] investigated a supervised deep fully convolutional neural network (FCN) for marine seismic velocity, which performed better than conventional methods. These studies have demonstrated the superior performance of deep-learning-based inversion methods in geoacoustic inversion. However, such methods have primarily utilized traditional neural network backbones, including convolutional neural networks (CNNs) and fully convolutional networks (FCNs).
While these networks are effective, they possess certain limitations that result in practical bottlenecks. For example, CNNs are biased towards local information due to their use of kernel sliding, and, hence, potentially discard global information for an acoustic signal [17]. Considering these limitations, our research aims to enhance the architecture of deep learning models for geoacoustic inversion.
The present study presents a novel geoacoustic inversion model known as the geoacoustic inversion transformer (GIT). The transformer architecture, originally designed for natural language processing (NLP) [18], has been shown to outperform convolutional neural networks (CNNs) in various domains [19,20]. By leveraging the multi-head self-attention mechanism (MHSA) intrinsic to transformers, the proposed model can process sonar received signals from a more comprehensive global perspective, thus improving its performance in acoustic input analysis [17]. Furthermore, this study proposes a 2-D frequency and sensor positional embedding that captures the position information from both the sensor and frequency domains. It is expected that the proposed GIT can achieve satisfactory inversion performance due to its strong feature representation ability. This study showcases the potential of utilizing transformer architecture in the field of geoacoustic inversion, which remains an underexplored area of research.
The remainder of this paper is organized as follows: Section 2 outlines the problem formulation of geoacoustic inversion. Section 3 presents the proposed inversion framework. The numerical simulation environment and experimental results are presented in Section 4. This section includes a comparison of the proposed model performance with another inversion model. Section 5 gives the study conclusions.
2. Problem Formulation
Equation (1) gives the mathematical representation of a true acoustic observation:
where y represents the measured signal at the receiver array, x is a vector that represents the model parameters, M is the nonlinear physical model that maps x to y, and e is the measurement noise. Due to the complicated propagation mechanism, the true physical model is unknown in most marine scenarios. In this case, an alternative method is to use an approximate accurate model that can be expressed as:
The forward acoustic propagation model that represents a numerical model of the true function M is a well-known approach to simulate the acoustic environment in geoacoustic inversion. Both the geoacoustic properties of the ocean floor and the geometrical parameters are contained in the input vector x. The problem of geoacoustic inversion can be expressed as follows: Given an observation of the system output and the forward model , find the geoacoustic parameters .
In this approach, the task of geoacoustic inversion can be accomplished if suitable exists. Because the mapping is extremely complex, finding such an approximation of is difficult. However, deep learning neural networks and data-based methods can be adapted to approximate successfully.
3. Methodology
In this section, data preprocessing of the received acoustic signal is presented, followed by a description of the proposed inversion transformer with FS positional embedding.
3.1. Data Preprocessing for Tokenization
Due to multiple reflections of sound waves between the seafloor and surface, the acoustic data received by the sonar system in shallow water contains rich information about the geoacoustic characteristics of the ocean bottom. To extract this implicit information, conventional fast Fourier transform (FFT) analysis is first used on the time-domain to obtain the complex pressure . The complex pressure at the specific frequency f can be formulated as:
where represents the source term, means the Green function, and is the noise. In practice, the magnitudes of the source frequency spectrum between the simulation data and the real data may be different such that the source magnitudes used to generate the synthetic data are flat across the frequency band. For this reason, the complex pressure is normalized by the L2-norm to reduce the influence of mismatch caused by the source terms [21].
If the acoustic data is clean without noise (i.e., , the normalization Equation (5) can eliminate the effect of the source magnitude. In this case, the above equation can be rewritten as:
In Equation (6), the complex pressure is independent of the source term . The influence of the source magnitude can also be effectively suppressed in the case of acoustic data with a reasonably high SNR. Multiplying the complex pressure with its conjugate transposition gives the normalized sample covariance matrix (SCM), expressed by Equation (6) [22].
The SCM is complex in the frequency domain, but the neural network usually receives real numerical values such that the input must be transformed to allow the real-valued model input. For each frequency point, the SCM can be separated into the real and imaginary parts, which are used as two channels of the input feature of size .
Consider a broadband signal which has numbers of frequency points, the SCMs at different frequency points are stacked along the first dimension, and the input is a matrix of size and can be expressed as:
where F represents the number of frequency points in a broad signal. To eliminate the effect of unit and scale differences between individual features, to treat each dimensional feature equally, min-max normalization is both applied on the data and the ground-truth. Equation (10) expresses the normalization.
where x is the feature or the ground-truth label and z is the normalized item.
The CNNs and transformers are two major classes of deep learning models that have been used extensively in various domains. Unlike CNNs, which process the normalized input directly using kernel sliding, transformers employ a tokenization procedure to preprocess and obtain feature tokens that serve as the basic units in transformer models. To exploit both the frequency and sensor domain information simultaneously, a simple convolutional kernel with a kernel size of (2, L) and stride of (2, L) is deployed before the transformer layers. The first dimension of the convolution kernel is set to 2 to integrate the information on the real and imaginary parts of the . As a result, the input is transformed into tokens with a preset embedding size that encapsulates all useful information pertaining to the frequency and sensor.
3.2. Frequency and Sensor 2-D Positional Embedding
In standard transformers, a positional embedding is added to each token embedding to enable the model to perceive sequential information. However, in geoacoustic inversion, both the distribution of frequency points and the sonar sensor position affect the energy and phase of the acoustic signal, making it imperative to jointly consider both factors. In this case, this study proposes an incorporation of 2-D positional embeddings in both the frequency and sensor domains to simultaneously capture the position and frequency information.
For each domain, a learnable positional embedding is attached to each token that is initialized as follows:
where means the order of the frequency or sensor, , and is the embedding dimension. For broad signals with F frequency points and L sonar receivers, the token embedding is attached with an (F, ) frequency positional embedding in the first dimension, and an (L, ) sensor positional embedding in the second dimension. As a result, meaningful feature tokens with 2-D order information are obtained as input that would be fed into the transformer.
3.3. Transformer Model Based on MHSA
The transformer architecture comprises of multiple encoder and decoder blocks. To reduce the complexity of the model, only the encoder blocks are utilized in the proposed GIT model shown in Figure 1. The model employs N transformer encoders that incorporate the MHSA mechanism to compute the correlation between tokens. To facilitate the regression task of geoacoustic inversion, a regression token is inserted at the beginning of the token sequence following the [CLS] token similar to vision transformers [19]. The first encoder receives feature tokens of size (, ). Then the MHSA layer in the N transformer encoder generates three attention matrices, a query matrix , a key matrix , and the corresponding value matrix , to extract features from .
where , , and are both learnable matrices to measure the attention weights, represents which self-attention head is to be calculated, and the embedding dimension of the attention weight is .
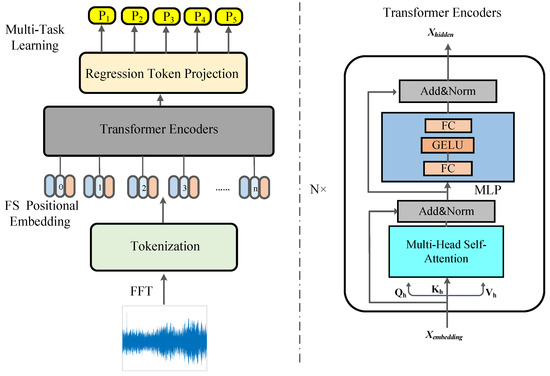
Figure 1.
The architecture of the proposed GIT for goacoustic inversion.
The Softmax activation and division operation would not change the feature dimension, after the MHSA layers, and the feature maps remain the shape of (, ). A multi-layer perceptron (MLP) layer is utilized following the MHSA calculation. This MLP layer is primarily composed of a fully connected layer that is enhanced with a GELU activation function, benefiting the transformer training process. A dropout layer is employed to mitigate the risk of overfitting during model training. In this case, we have the final feature map with rich information to describe the token relations from the perspectives of both the frequency and receiver domains.
As mentioned above, the regression token is preset at the beginning of the token sequences. It serves as a representative of all the tokens in the set and efficiently integrates information from other items in the token sequence. This integration allows for the projection of embeddings into the number of inverted parameters that play an essential role in the GIT. By training with the optimizer, the model assigns appropriate values to all parameters through multi-task learning.
3.4. Multi-Task Learning with Transformer
The task of geoacoustic inversion consists of various parameters with distinct metric spaces and scales. As a result, using one GIT to independently invert each parameter is unsuitable and costly. To address this challenge, we adopt the multi-task learning approach [23] in our model training. The aim is to employ one GIT network to invert all objective parameters simultaneously.
In this case, the multi-task learning method treats the inversion of each parameter as a subtask. By using adaptive loss weights, we compute the mean squared error (MSE) loss between the predicted values for all parameters and their true values. After gradient descent, the task loss weights are automatically adjusted based on the uncertainty of each task’s homoskedasticity. This approach takes advantage of the similarities and dissimilarities between tasks, resulting in enhanced accuracy and prediction performance.
To automatically balance the weight of each regression loss, we formulate the total loss as follows:
where i represents the number of subtasks, and is the adaptive weight on the corresponding task . This approach enables us to converge inverted parameters with differing scales using one GIT for greater efficiency.
4. Experiments and Analysis
In this section, the objective inversion parameters are first listed, and the simulation environment is described, which is based on the Kraken acoustic model [24]. Furthermore, the experimental setup is given for reproducibility. Finally, we provide a comprehensive analysis of the experimental results to demonstrate the effectiveness of our proposed GIT for geoacoustic inversion.
4.1. Numerical Simulations
Following the SwellEx96 S5 experiment [25], the environment is modeled as a range-independent waveguide shown in Figure 2, which consists of the waveguide, a sediment layer, a mudstone layer, and the halfspace ocean bottom. To generate a large number of replicas for GIT model training, the boundaries between these layers are treated as discontinuities in parameter values, which allows for an accurate representation of real-world underwater environments. Specifically, the shallow point source, located 54 m below the sea surface, emits white noise with the frequency band –3300 Hz; the acoustic signal is received by a 21-element vertical line array (VLA), which is placed in the shallow water. For comprehensive analysis, 13 frequencies are selected from the range of [49, 388] Hz for inversion. The deterministic parameters are the seawater density 1.0 g/cm, the seawater depth 220 m, the sediment layer attenuation 0.2 dB/kmHz, the mudstone layer depth 800 m with the density of 2.06 g/cm, the mudstone layer attenuation 0.06 dB/kmHz, the halfspace compressional speed 5200 m/s with density of 2.66 g/cm, and the halfspace attenuation 0.02 dB/kmHz. In particular, the objective parameters for inversion are the sediment layer depth , the sediment density , the top and bottom sound speed of the sediment layer , , and the top sound speed of the mudstone layer .
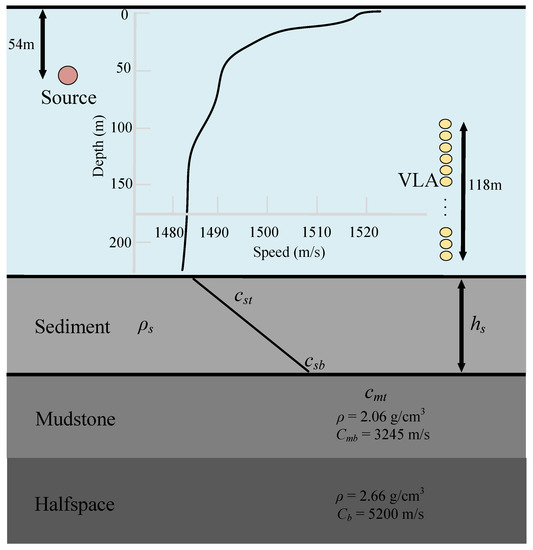
Figure 2.
Simulation environment generated by Kraken.
4.2. Inversion Procedure
Starting with generating the synthetic data, our inversion procedure contains the following steps: training and testing, followed by performance comparison with the CNN-based methods, and parameter sensitivity assessment to determine the most influential factors in achieving high inversion performance. The simulated signal waveform selected from one replica and its corresponding spectrum can be seen in Figure 3.
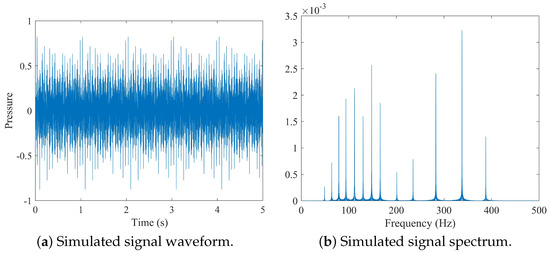
Figure 3.
Simulated signal waveform and spectrum based on the ocean environment shown in Figure 2.
- 1.
- The proposed GIT model is trained using replicas, sampled for a uniform distribution for each parameter in the interval, which is shown in Table 1.
 Table 1. Intervals of objective parameters for inversion.Due to the large data size, the inversion parameters of the training data are believed to cover the whole parameter interval.
Table 1. Intervals of objective parameters for inversion.Due to the large data size, the inversion parameters of the training data are believed to cover the whole parameter interval. - 2.
- Multi-task learning is used to optimize the neural network for multiple objective losses, along the direction of minimizing the MSE loss function for each subtask i, which is expressed as:where y is the network prediction on the geoacoustic parameters, contains the true values of the candidate parameter, while the other parameters vary randomly in the training procedure. Convergence can be achieved when reaches a certain level, or would not decrease any more.
- 3.
- To improve the robustness, Gaussian white noise is added to the training data with signal-to-noise-ratios (SNRs) randomly from 10 to 50 dB, which can be formulated as:
- 4.
- For the testing data, it consists of samples (SNR = 20 dB), which is also generated using the parameters in Table 1.
4.3. Experimental Setup
In our work, all the experiments were conducted on a workstation with the detailed test platform and environment shown in Table 2.

Table 2.
The test platform and environment.
During training, the batch size is set to 128 for efficiency. A total of 400 epochs with a learning rate 0.001 is given for GIT training, and is optimized by the Adam algorithm [26]. For the transformer configurations, the embedding dimension is 384, the number of Encoders N is 3, and the number of attention heads is 12. From Figure 4, which shows the loss curves, it is demonstrated that our model is not over-fitted and can successfully work for geoacoustic inversion.
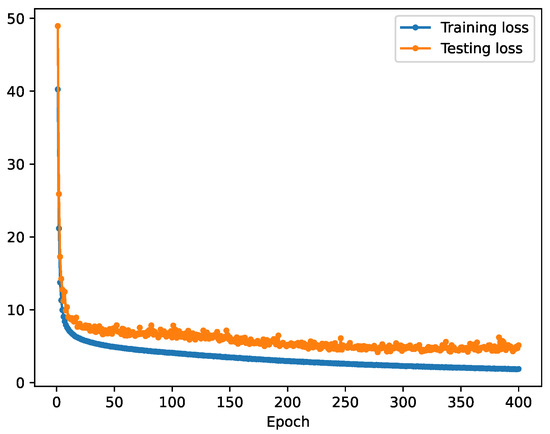
Figure 4.
The training and testing loss curves.
4.4. Experimental Results
In this section, we evaluate the performance of our proposed GIT in comparison with the current state-of-the-art neural networks for acoustic inversion. Additionally, we conduct a comparative study between the 2-D FS positional embedding model and the original positional embedding model to demonstrate its effectiveness. Moreover, we investigate the parameter sensitivity concerning the number of transformer Encoders N and the number of attention heads H to analyze their influence on the inversion performance.
4.4.1. Performance Comparison with CNNs
Owing to the powerful feature extraction ability with convolution kernels, the existing inversion methods mainly make use of the CNNs and their variants. Specifically, a convolutional and recurrent neural networks mixed model (CRNN) [15] and a deep fully convolutional neural network (FCN) [16], which has been widely used in the area of acoustic inversion, are chosen for the comparison experiments. Moreover, it is noted that these networks are modified to accept the input and trained from scratch in a supervised manner. The mean absolute error (MAE) is selected as the evaluation metric.
The results shown in Table 3 demonstrate that the proposed method, GIT, outperforms the other two methods, CRNN and FCN, in terms of the MAE for all six objective parameters. Specifically, CRNN had the highest MAE values of all methods for most of the objective parameters, indicating its lower accuracy compared to FCN and GIT. However, it still outperformed the other methods in terms of . FCN showed better performance than CRNN by achieving lower MAE values for all the objective parameters except . It achieved a significant improvement in MAE values compared to CRNN with a relatively simpler network architecture. However, its values were still higher than GIT. GIT (proposed) was the best performing method among all the methods presented in the table. It obtained the lowest MAE values for all the objective parameters, indicating its high accuracy compared to CRNN and FCN. Thus, GIT has strong potential as an effective method for inverting the objective parameters. GIT achieved an MAE of 56.7, which was lower than the MAEs of CRNN (93.2) and FCN (64.2). Moreover, when considering the individual objective parameters, GIT consistently achieved lower MAEs than the other two methods. This suggests that GIT was more accurate in estimating the objective parameter values than CRNN and FCN.

Table 3.
Inversion performance comparisons with CNNs on the objective parameters.
In summary, CRNN performed the worst among the inversion methods, while FCN and GIT showed better performance in terms of lower MAE values. FCN outperformed CRNN for most of the objective parameters except for , while GIT provided the best performance in terms of lower MAE values for all the objective parameters.
4.4.2. Performance Impact on the FS Positional Embedding
As mentioned in Section 3.2, a 2-D Frequency and sensor positional embedding approach to jointly capture the information on the frequency and sensor domain is used. We compare it with a randomly initialized 1-D positional embedding transformer with the same experimental configuration. As can be seen in Table 4, we find the proposed FS positional embedding can describe more useful information, and, thus, it performs better than 1-D positional embedding.

Table 4.
Effect of positional embedding methods on the objective parameters.
Specifically, based on the results presented in Table 4, it can be seen that using the FS positional embedding method resulted in lower MAE across all parameters when compared to the 1-D method. For example, the MAE value for the first parameter decreased from 66.8 to 56.7 when switching from the 1-D to the FS method. Similarly, for the second parameter , the MAE value decreased from 0.129 to 0.101. This trend continued for the remaining parameters as well. This suggests that the proposed FS positional embedding can capture both the frequency and sensor position information to benefit the geoacoustic inversion. Overall, these results suggest that the FS positional embedding method may be a more effective approach for improving the accuracy of the inversion for the various parameters tested in this study.
4.5. Parameter Sensitivity
As major parameters for the GIT, we further analyzed the parameter sensitivity of the embedding dimension , the number of heads H, and the number of transformer encoders N.
As shown in Table 5, increasing the number of encoders generally improved the accuracy of inversion, which indicates a deeper GIT has better generalization performance. For example, the MAE value decreased from 67.8 to 52.6 as the number of encoders increased from two to five. However, using six encoders led to a significant increase in MAE values, indicating that too many encoders may not be optimal.

Table 5.
Inversion performance varying with the number of encoders N on the objective parameters.
Table 6 demonstrates the variation in inversion performance concerning the number of attention heads H. It is clear from the table that the number of attention heads had a significant impact on the inversion performance. Specifically, when using only three attention heads, the MAE values were relatively high, indicating poor performance. However, as the number of attention heads increased to 6, 12 and 24, the MAE values decreased, which suggests better inversion performance. Notably, by increasing the number of attention heads from 3 to 12, there was a significant decrease in the MAE values for all parameters. However, using 24 attention heads, although the values remained low, there seemed to be no significant improvement over 12 attention heads.

Table 6.
Inversion performance varying with the number of attention heads on the objective parameters.
Overall, the results suggest that using more attention heads to capture more perspectives of the sample data can improve the inversion performance, but there may be a saturation point beyond which any further increase in the number of attention heads might not result in a significant improvement in inversion performance.
We also conducted experiments on the inversion performance varying with the embedding dimension . Table 7 demonstrates that the inversion performance varied significantly with different objective parameters and embedding dimensions. For instance, the best performance in terms of the MAE was obtained when the embedding dimension was 384, whereas the worst score was observed at an embedding dimension of 192. Similarly, the highest score for MAE_ was seen at an embedding dimension of 96, and the lowest value was observed at 384.

Table 7.
Inversion performance varying with the embedding dimension on the objective parameters.
In all, the embedding dimension and the number of encoders parameter were more sensitive to the GIT than the number of attention heads H, which indicates the depth and width of GIT greatly influence the inversion performance.
4.6. Model Complexity
To show the real-time prediction performance of the GIT, besides MAE, we report the total number of parameters (No. Params), the average prediction time (Avg. time) with the standard deviation, and the frames per second (FPS) to evaluate the time-space complexity, which is shown in Table 8.

Table 8.
Time-space complexity comparison of the models.
It is evident from the table that the proposed GIT model outperformed both CRNN and FCN in terms of the average inference time and FPS. In particular, the GIT model showed significantly faster average inference time at 1.804 ± 0.246 ms, compared to CRNN (1341.944 ± 33.171 ms and FCN (8.805 ± 0.102 ms). Moreover, the GIT model was able to process 554.46 frames per second, which was considerably higher than both CRNN (0.75 FPS) and FCN (113.57 FPS).
The GIT model also strikes a balance between the parameter size and efficiency as it has fewer parameters than the FCN model but more than the CRNN model. This suggests that the GIT model can perform well while avoiding excessive computational costs associated with using larger models, such as FCN.
5. Conclusions
In this study, we propose the GIT, a transformer-based geoacoustic inversion model. By leveraging the multi-head self-attention (MHSA) mechanism, our model can effectively capture global information from the acoustic signals. Additionally, to incorporate positional information from both frequency and sonar sensors, we utilize a 2-D FS positional embedding on the tokens for MHSA calculation. Our experimental results demonstrate the effectiveness of the GIT in geoacoustic inversion by outperforming CNN-based models. However, there is still significant potential for further research based on our work. Due to the complexity of real-world data, we intend to apply domain-adaptive techniques to bridge the gap between simulated and real data. This will serve as the primary direction for future work.
Author Contributions
Conceptualization, S.F. and S.M.; data curation, S.F. and Q.L.; formal analysis, S.F. and X.Z.; investigation, S.M.; methodology, S.M. and Q.L.; project administration, S.M.; resources, Q.L.; software, Q.L.; supervision, S.M. and Q.L.; validation, S.F., S.M. and Q.L.; visualization, S.F.; writing—original draft, S.F. and Q.L.; writing—review and editing, S.F., S.M., X.Z. and Q.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Defense Fundamental Scientific Research Program (Grant No. JCKY2020550C011), and the Postgraduate Scientific Research Innovation Project of Hunan Province (Grant No. CX20220054).
Institutional Review Board Statement
This study did not require ethical approval.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bonnel, J.; Pecknold, S.P.; Hines, P.C.; Chapman, N.R. An Experimental Benchmark for Geoacoustic Inversion Methods. IEEE J. Ocean. Eng. 2021, 46, 261–282. [Google Scholar] [CrossRef]
- Xue, Y.; Lei, F.; Zhu, H.; Xiao, R.; Chen, C.; Cui, Z. An Inversion Method for Geoacoustic Parameters of Multilayer Seabed in Shallow Water. J. Phys. Conf. Ser. 2021, 1739, 012019. [Google Scholar] [CrossRef]
- Dumaz, L.; Garnier, J.; Lepoultier, G. Acoustic and geoacoustic inverse problems in randomly perturbed shallow-water environments. J. Acoust. Soc. Am. 2019, 146, 458–469. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Yang, K.; Ma, Y.; Yang, Q.; Huang, C. Synchrosqueezing transform for geoacoustic inversion with air-gun source in the East China Sea. Appl. Acoust. 2020, 169, 107460. [Google Scholar] [CrossRef]
- Lu, L.; Ren, Q.; Ma, L. Geoacoustic inversion base on modeling ocean-bottom reflection wave. J. Acoust. Soc. Am. 2016, 140, 3067. [Google Scholar] [CrossRef]
- Wang, P.; Song, W. Matched-field geoacoustic inversion using propagation invariant in a range-dependent waveguide. J. Acoust. Soc. Am. 2020, 147, EL491–EL497. [Google Scholar] [CrossRef]
- Dahl, P.H.; Dall’Osto, D.R. Vector Acoustic Analysis of Time-Separated Modal Arrivals From Explosive Sound Sources during the 2017 Seabed Characterization Experiment. IEEE J. Ocean. Eng. 2020, 45, 131–143. [Google Scholar] [CrossRef]
- Bonnel, J.; Dall’Osto, D.R.; Dahl, P.H. Geoacoustic inversion using vector acoustic modal dispersion. J. Acoust. Soc. Am. 2019, 146, 2930. [Google Scholar] [CrossRef]
- Zheng, G.; Zhu, H.; Wang, X.; Khan, S.; Li, N.; Xue, Y. Bayesian Inversion for Geoacoustic Parameters in Shallow Sea. Sensors 2020, 20, 2150. [Google Scholar] [CrossRef]
- Yang, H.; Lee, K.; Choo, Y.; Kim, K. Underwater Acoustic Research Trends with Machine Learning: Passive SONAR Applications. J. Ocean Eng. Technol. 2020, 34, 227–236. [Google Scholar] [CrossRef]
- Yang, H.; Lee, K.; Choo, Y.; Kim, K. Underwater Acoustic Research Trends with Machine Learning: Ocean Parameter Inversion Applications. J. Ocean Eng. Technol. 2020, 34, 371–376. [Google Scholar] [CrossRef]
- Liu, M.; Niu, H.; Li, Z.; Liu, Y.; Zhang, Q. Deep-learning geoacoustic inversion using multi-range vertical array data in shallow water. J. Acoust. Soc. Am. 2022, 151, 2101–2116. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Dong, H. Shear Wave Velocity Estimation Based on Deep-Q Network. Appl. Sci. 2022, 12, 8919. [Google Scholar] [CrossRef]
- Shen, Y.; Pan, X.; Zheng, Z.; Gerstoft, P. Matched-field geoacoustic inversion based on radial basis function neural network. J. Acoust. Soc. Am. 2020, 148, 3279–3290. [Google Scholar] [CrossRef]
- Alfarraj, M.; AlRegib, G. Semi-supervised Learning for Acoustic Impedance Inversion. arXiv 2019, arXiv:1905.13412. [Google Scholar]
- Yang, F.; Ma, J. Deep-learning inversion: A next-generation seismic velocity model building methodDL for velocity model building. Geophysics 2019, 84, R583–R599. [Google Scholar] [CrossRef]
- Feng, S.; Zhu, X. A Transformer-Based Deep Learning Network for Underwater Acoustic Target Recognition. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1505805. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Gong, Y.; Chung, Y.A.; Glass, J. Ast: Audio spectrogram transformer. arXiv 2021, arXiv:2104.01778. [Google Scholar]
- Niu, H.; Ozanich, E.; Gerstoft, P. Ship localization in Santa Barbara Channel using machine learning classifiers. J. Acoust. Soc. Am. 2017, 142, EL455–EL460. [Google Scholar] [CrossRef]
- Niu, H.; Reeves, E.; Gerstoft, P. Source localization in an ocean waveguide using supervised machine learning. J. Acoust. Soc. Am. 2017, 142, 1176–1188. [Google Scholar] [CrossRef] [PubMed]
- Kendall, A.; Gal, Y.; Cipolla, R. Multi-task learning using uncertainty to weigh losses for scene geometry and semantics. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7482–7491. [Google Scholar]
- Monteiro, N.M.; Oliveira, T.C. Mesh generation for underwater acoustic modeling with KRAKEN. Adv. Eng. Softw. 2023, 180, 103455. [Google Scholar] [CrossRef]
- Murray, J.; Ensberg, D. The Swellex-96 Experiment 1996. 1996. Available online: http://swellex96.ucsd.edu/index.html (accessed on 12 March 2023).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).