Calculation Model of Vertical Bearing Capacity of Rock-Embedded Piles Based on the Softening of Pile Side Friction Resistance

Abstract

Rock-socketed pile is widely used in coastal wharf, Marine bridge, and Marine power engineering, and the end bearing function is considered more in the design process. However, the lateral friction resistance of rock-socketed piles is an important bearing part, and the load transfer mechanism of the pile–soft rock interface is an important research focus. In this paper, a comparative analysis was adopted in the test, and ten groups of test specimens were made, including five groups of natural and saturated mudstone specimens, respectively. The characteristics of interfacial load transfer were analyzed through the shear test of a pile–mudstone interface. A calculation model for the vertical bearing capacity of rock-socketed piles based on the softening of lateral friction resistance was established, and the effects of interface relative displacement, lateral positive pressure, pile length, and pile stiffness on the vertical bearing capacity of rock-socketed piles were analyzed. The results show that the shear strength of the pile–rock interface is lower than that of the mudstone interface, and the interfacial shear strength shows the characteristics of “first increasing, then decreasing, and finally flattening with the increase of shear displacement”. The vertical ultimate bearing capacity and residual bearing capacity under saturation were 89.49% and 89.73% of the natural state, respectively. With the increase of pile side pressure, the proportion of pile side friction resistance increased by 39.96%, and the pile side friction resistance was fully exerted. With the increase of pile length, the vertical ultimate bearing capacity of pile foundation increased, and the residual bearing capacity change value increased from 6.80% to 16.97%. However, the increase in pile stiffness had little effect on the vertical bearing capacity. The calculation model can provide a certain reference for the design and calculation of rock-socketed piles in soft rock areas.

1. Introduction

Pile foundation is the most widely used infrastructure in ports, offshore bridges, and offshore wind power generation projects, among which rock-socketed piles have drawn significant attention because of their difficulty in construction and high bearing capacity. At present, only the end bearing capacity is considered in the project, and the effect of side friction resistance of rock-socketed pile is ignored. Therefore, the understanding and evaluation of pile bearing capacity are insufficient, which leads to the increase of depth or pile interface in the design of rock-socketed piles, resulting in great waste and increased construction difficulty. Therefore, it is necessary to study the coupling between the end of a rock-socketed pile and the side friction.

In recent decades, scholars and engineers have carried out preliminary research on the load transfer characteristics of rock-socketed piles and the influencing factors of pile side friction. Serrano et al. established a method to calculate the ultimate bearing capacity of the end of a rock-socketed pile based on the plasticity theory [1]. Vipulanandan et al. believed that pile end bearing capacity was controlled by rock cohesion and the friction angle and established the load-displacement (Q-W) relationship at the unit end [2]. Cui et al. studied the variation of the pile’s tip bearing capacity in rock-socketed pile using buried depth ratio and intermediate stress parameters. They found that pile tip bearing capacity decreased nonlinearly with the buried depth ratio and increased with the intermediate stress parameters [3]. Chong et al. conducted a comprehensive numerical simulation of rock-socketed piles by using 3DEC and found that the number of joint sets in rock mass has a significant impact on pile’s tip bearing capacity [4]. Kordjazi et al. found that pile tip bearing capacity is related to pile cone penetration, established a SVM model, and found that it was better than the traditional CPT-based method for determining a pile’s ultimate bearing capacity [5]. Lee et al. carried out a study on the influence of the time factor on pile tip bearing capacity and found that pile side friction increases with time [6]. Akguner et al. calculated and compared the bearing capacity of rock-socketed piles and found that a pile’s lateral friction plays a leading role in the bearing capacity of rock-socketed piles [7]. Manandhar et al. studied the influence of conical angle on pile tip bearing capacity and found that pile lateral friction increases with the increase of the pile tip conical angle [8]. Based on the pile–soil interaction analysis model of pile cap jackets, El-Din et al. found that the relationship between pile shear and pile top displacement increased first and then decreased [9]. Loukidis et al. found that the ultimate pile lateral friction is positively proportional to the initial horizontal effective stress and the tangent of the friction angle, and proposed a simple formula for calculating pile lateral resistance in non-expansive soil [10].

The above investigations on the load transfer characteristics of pile foundations and pile side friction mainly focused on the influence of buried depth ratio, initial stress, and soil type on pile bearing capacity and pile side friction. However, previous research results cannot explain the bearing and settlement characteristics of the pile foundation. Therefore, in recent years, some scholars have studied the pile–rock interface shear expansion effect, bearing capacity factor analysis, and pile foundation settlement characteristics. Li et al. proposed a load transfer method based on elastic theory in combination with the bearing characteristics and settlement characteristics of single piles [11]. Singh et al. found that the vertical and lateral bearing capacity of rock-socketed piles was unrelated to the depth of soil cover and considered that lateral friction resistance need not be considered [12]. Armaghani et al. established a hybrid model based on particle swarm optimization (PSO) and ANN, finding that the hybrid model had high accuracy in predicting the ultimate bearing capacity of rock-socketed piles [13]. Bawadi et al. proposed a calculation method for pile end bearing capacity using the SASW method [14]. Zhang et al. studied the size effect of large-diameter rock-socketed piles and found that the ultimate bearing capacity of the pile tip increased with the increase of rock-socketed depth and decreased with the increase of pile diameter [15]. Based on the physical parameters of large-diameter drilled piles, Bai et al. investigated the influence of the length–diameter ratio and rock-socketed depth on the bearing capacity and deformation characteristics of piles. They concluded that the influence of the length–diameter ratio and rock-socketed depth on the friction resistance ratio of rock-socketed sections and pile side resistance ratio was small [16]. Zhang et al. proposed a bilinear shear model to describe the relationship between shear stress and concrete–rock’s relative displacement for rock-socketed bored piles in soft rock, elucidating the critical shear displacement at the concrete–rock interface and establishing a load transfer method for soft rock-socketed piles [17]. Based on the indoor shear test, Liu et al. showed that the peak SCI shear load increased exponentially with the increase of directional stress and decreased logarithmically with the increase of cyclic shear time [18]. Lei et al. found that the shear expansion effect existed in the interface sliding of rock-socketed piles. Therefore, considering the shear expansion effect of the pile–rock interface, a pile side friction resistance expression suitable for soft rock-socketed piles, was established [19]. Yamin et al. tested the pile lateral friction resistance of a rock-socketed section of a rock-socketed pile and found that the pile lateral friction resistance increased first and then tended to be stable with the increase of relative displacement of pile–rock interface [20]. Arioglu et al. believed that the rock mass shear ability index (RMCI) was positively correlated with pile lateral friction and established a prediction formula for pile lateral friction based on the RMCI [21]. Suloshini et al. carried out a pile resistance test of bored pile in intact rock and found that pile lateral friction remained unchanged when the confining pressure ranged from 0 kPa to 400 kPa [22]. Based on the theoretical and experimental analysis of the load transfer law of rock-socketed piles in a Karst region, He et al. proposed a calculation method for the vertical bearing capacity of rock-socketed piles in a Karst region based on the load transfer method [23]. Wang et al. studied the load transfer mechanism of rock-socketed piles and found that pile side friction is related to the mechanical properties of the soil beside the pile [24]. Wang et al. carried out the study of the friction resistance transfer characteristics of rock-socketed piles on thick sediment, and derived the complete constitutive model function of the pile–rock interface. They concluded that the smaller the rock-socketed thickness, the greater the settlement and lateral friction resistance, the relatively small rock-socketed thickness and rock strength, with the lower peak was higher than the upper peak [25]. Liu et al. carried out a study on the lateral response of vertical loads to piles, and conducted a comparative analysis of the lateral response of vertical loads to rock-socketed piles in normal consolidated clay and over-consolidated clay, concluding that, with the application of vertical load, the initial lateral stiffness and ultimate bearing capacity of the normal consolidated clay increased by 10.0% and 49.4%, respectively. The initial lateral stiffness and ultimate bearing capacity of the over-consolidated clay decreased by 12.6% and 32.4%, respectively. It is shown that vertical load can either have positive effects on the lateral response of piles or can have a weakening effect depending on the soil stress ratio around the pile. [26].

Although the above studies have provided some insights on the ultimate bearing capacity of pile foundations, lateral friction resistance of piles, failure criterion of pile–rock interfaces and load transfer law, etc., previous studies have mainly focused on pile tip bearing capacity and did not include pile lateral friction resistance as an important part of pile bearing capacity. In particular, there is little research on the construction of the calculation model of the ultimate bearing capacity of soft rock-socketed piles under the consideration of pile lateral friction, the evolution law of vertical ultimate bearing capacity under the influence of various factors, and the failure criterion of the pile–rock interface in ocean engineering.

Therefore, the main purpose of this study is to carry out a pile–mudstone interface shear test of rock-socketed pile under natural and saturated conditions by making a “pile–mudstone” interface shear specimen, analyzing the following: the strength weakening characteristic of the pile–mudstone interface; establishing the weakening interface model and considering the influence of the pile–rock interface weakening on the load transfer of rock-socketed pile; and establishing the calculation model of the vertical bearing capacity of rock-socketed pile. The influence of pile length and elastic modulus on the vertical bearing capacity of pile foundation is discussed, which provides theoretical support for engineering application.

2. Shear Test of the Pile–Mudstone Interface

2.1. Testing System

The RMT-301 rock and concrete shear testing system (Figure 1) was utilized in this study to investigate the mechanical shear properties of the concrete–mudstone interface. This apparatus consists of three parts: a lower shear box, an upper shear box, and top cover; the servo control is employed for both vertical and horizontal loading processes. The device for reducing friction is attached between the shearing device and other equipment. The test error meets the requirements of the specifications.

2.2. Shear Sample Preparations

According to the sizes and specifications of upper and lower shear boxes in the shear test system, and considering various factors comprehensively, the sizes of the “pile–mudstone” bond specimens in this test were designed as rectangular specimens, in which:

(1)

The size of the mudstone specimen is 20 × 20 × 9.5 cm, and the error is within ±0.1 cm. The mechanical properties of mudstone are shown in

Table 1. Mechanical properties of mudstone.

Natural Density (g/cm3)	Saturation Density (g/cm3)	Natural Moisture Content (%)	Cohesion (MPa)		Internal Friction Angle (°)
			Natural State	Saturation State	Natural State	Saturation State
2.44	2.72	3.46	5.17	3.84	39.97	37.78

.

(2)

The size of the concrete specimen is 18 × 18 × 10.5 cm, and the error is within ±0.5 cm.

We first processed the mudstone specimen according to the size requirements, then closed the formwork on the mudstone specimen surface according to the size of the concrete specimen, and cast-in situ a C30 concrete specimen, as shown in Figure 2. The “pile–mudstone interface” is formed between the early mudstone specimen and the cast-in situ C30 concrete specimen, as shown in Figure 3.

2.3. Loading Schemes

Due to the relevant provisions of the rock test code for Hydraulic and Hydro-Power Engineering (DL/T5368-2007), normal stress can be applied to mudstone–concrete specimens at a certain loading rate after vertical and horizontal preloading is completed [27]. After the normal stress is applied, the horizontal shear force can be applied to the lower shear box. The relative displacement between the upper and lower shear boxes (that is, the shear displacement of the pile–mudstone contact interface) was used as the judging standard. When the displacement exceeded 70 mm, the interface of the pile–mudstone specimen could be judged to have been damaged, and the loading stopped. Figure 4 is the test photo of a specimen after interface failure and disconnection in the natural state.

3. Experimental Results

3.1. Effects of Water Content of Sample on Load-Carrying Capability

(1)

Shear stress–shear displacement curves of the pile–mudstone interface under natural and saturated conditions.

Under the action of all levels of normal pressure, the shear stress shear displacement relationship curve of the natural and saturated mudstone concrete interface test can be obtained, as shown in Figure 5. It can be seen from Figure 5 that in the natural and saturated state, the shear stress first increases rapidly to the peak, then decreases gradually after the peak, and finally remains stable with the increase of shear displacement. In the curve corresponding to the same level of normal stress, there is a very significant peak point of shear stress, and the peak shear stress and residual shear stress in the natural state are greater than those in the saturated state. When the interfacial shear stress exceeds the peak point, its value will gradually decrease and finally tend to be stable.

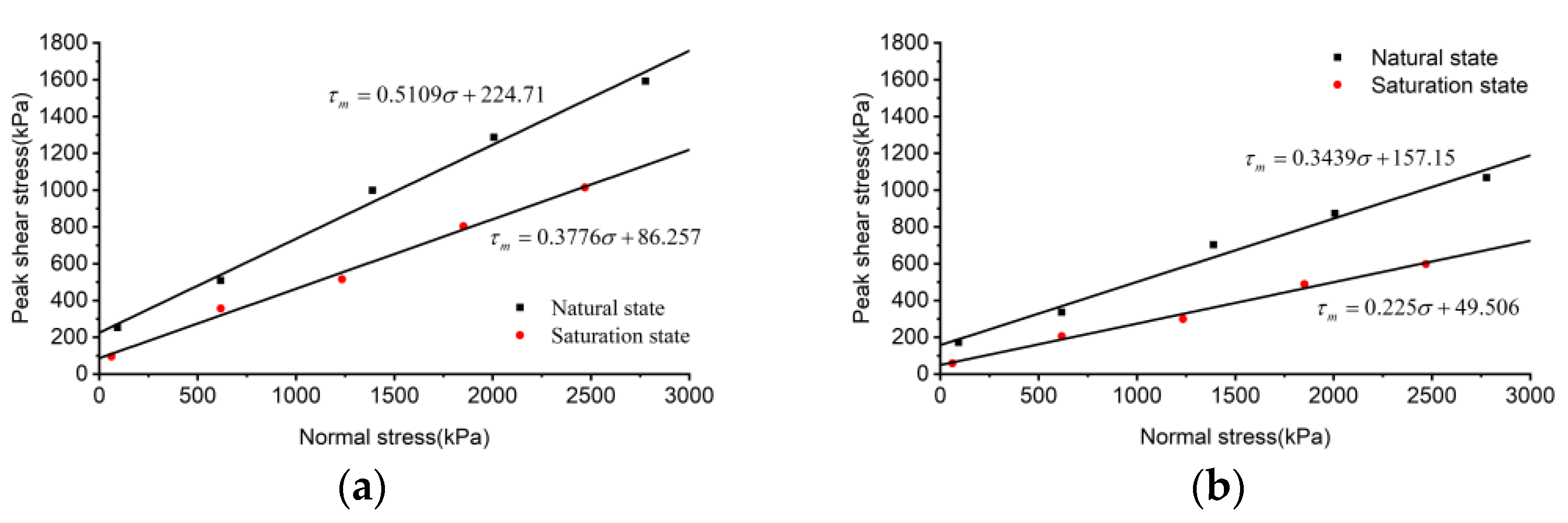
(2)

Shear strength of the mudstone–concrete interface.

In terms of the interfacial shear stress–shear displacement relation curve, the maximum shear stress ${\tau }_{max}$ of the mudstone–concrete interface in the natural and saturated state can be extracted respectively, and the variation relation between ${\tau }_{max}$-$\sigma$ can be obtained, as shown in Figure 6.

According to the relationship in the Figure, the maximum shear stress–normal stress of the pile–mudstone interface meets the Mohr strength criterion, the cohesion of the pile–mudstone interface is 86~224 kPa, and the internal friction Angle is 20–27°. When a large shear deformation occurs at the pile–mudstone interface, the shear stress tends to be stable, and the interface has been de-bonded. The shear stress at the interface is residual sliding friction, and the residual shear strength is 68.75% of the peak strength. The strength parameters (cohesion, internal friction Angle, sliding friction coefficient) of the pile–mudstone contact surface in the natural state are obviously larger than that in the saturated state, and the strength indexes are lower than that of the mudstone itself.

3.2. Analysis of Interface Failure Modes

It can be clearly seen from the failure form of mudstone–concrete interface:

(1)

The failure occurred at the mudstone–concrete interface, indicating that the contact interface should be the weak surface of the mudstone–concrete bonding member.

(2)

Regular observation can be found in Figure 7; after the destruction of the mudstone and concrete interface, there were some small holes or cracks, and this could fully account for the mudstone and concrete contact interface in the process of external horizontal shear; mudstone and concrete occur between the relatively large displacement, resulting in the destruction and the holes or cracks appearing.

4. Evolution of Vertical Bearing Capacity of the Rock-Socketed Pile

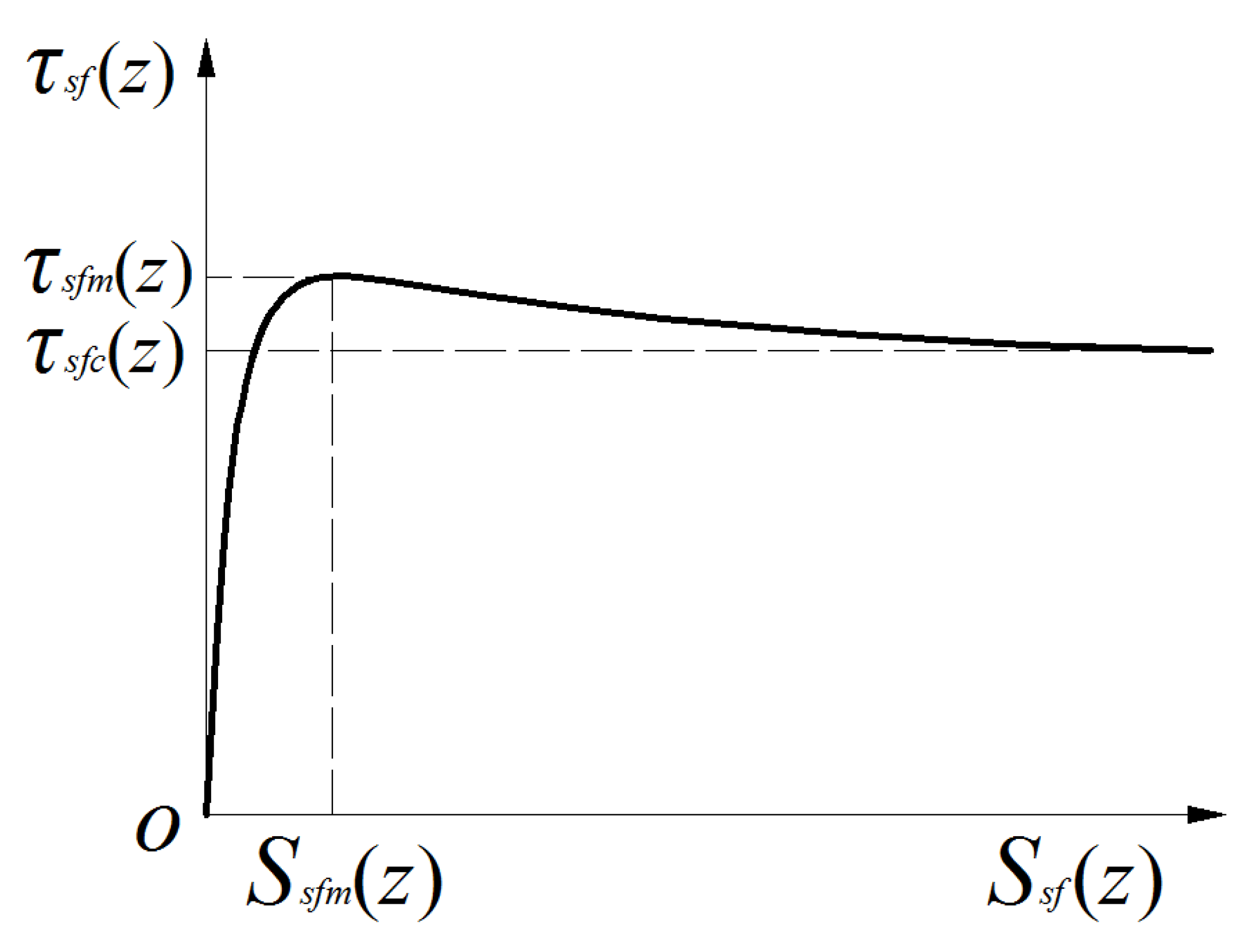
4.1. Lateral Friction Softening Model of Pile

Through the pile–mudstone interface shear test, the shear stress–shear displacement relationship curve of the contact interface is obtained, as shown in Figure 8. As can be seen from the Figure, under the action of normal stress at all levels, the shear stress at the contact interface (the lateral friction resistance of the pile) firstly increases to the peak point of shear stress with the increase of shear displacement. When the shear stress at the contact interface exceeds the peak point, its value gradually decreases and finally becomes stable.

According to the results of interfacial shear tests and the literature [28], it can be seen that the functional variation characteristic between pile side friction and pile rock relative displacement meets the softening model of pile side friction:

$${\tau }_i\left(z\right)=\frac{S_i\left(z\right)\left[\alpha +\gamma ·S_i\left(z\right)\right]}{{\left[\alpha +\beta ·S_i\left(z\right)\right]}^2}$$

(1)

where $\tau$ is the side friction of concrete rock-socketed pile at depth $z$ (kPa); $S_i$ is the relative displacement of rock stratum and concrete rock-socketed pile at depth $z$ (mm); ${\tau }_m$ is the ultimate side friction resistance of concrete rock-socketed pile at depth $z$ (kPa); $S_m$ is the relative displacement corresponding to the ultimate side friction at depth $z$ (mm); ${\tau }_c$ is the residual value of pile side friction at depth $z$ (kPa). $\alpha$, $\beta$, and $\gamma$ are calculated in mm·kPa⁻¹, kPa⁻¹, and kPa⁻¹, respectively. The calculated parameters $\alpha$, $\beta$, and $\gamma$ can be determined by the boundary conditions.

When the relative displacement of the interface is $S_m\left(z\right)$, the pile side friction resistance reaches the limit ${\tau }_m\left(z\right)$, and then:

$$\frac{\partial \left[{\tau }_i\left(z\right)\right]}{\partial \left[S_i\left(z\right)\right]}=\frac{\left[\alpha +2\gamma S_i\left(z\right)\right]·\left[\alpha +\beta S_i\left(z\right)\right]-2\beta \left[\alpha S_i\left(z\right)+\gamma S_i^2\left(z\right)\right]}{{\left[\alpha +\beta ·S_i\left(z\right)\right]}^3}=0$$

(2)

$S_m\left(z\right)$:

$$S_m\left(z\right)=\frac{\alpha }{\beta -2\gamma }$$

(3)

Substituting Equation (3) into Equation (1), we find ${\tau }_m\left(z\right)$:

$${\tau }_m\left(z\right)=\frac{1}{4\left(\beta -\gamma \right)}$$

(4)

In addition, when the relative displacement of the pile–rock interface is large enough, the lateral friction resistance of the contact interface is the residual ${\tau }_c\left(z\right)$:

$${\tau }_c\left(z\right)=\underset{S_i\to \infty }{\lim }\frac{S_i\left(z\right)\left[\alpha +\gamma ·S_i\left(z\right)\right]}{{\left[\alpha +\beta ·S_i\left(z\right)\right]}^2}=\frac{\gamma }{{\beta }^2}$$

(5)

The interfacial residual strength ratio $\eta ={\tau }_c\left(z\right)/{\tau }_m\left(z\right)$, parallel vertical (4), and Equation (5) can be used to calculate the calculation parameter β:

$$\beta =\frac{1\pm \sqrt{1-\frac{{\tau }_c}{{\tau }_m}}}{2·{\tau }_c}=\frac{1\pm \sqrt{1-\eta }}{2·\eta ·{\tau }_m}$$

(6)

Substituting Equation (6) into Equation (4), we can find $\gamma$:

$$\gamma =\frac{2-\eta \pm 2·\sqrt{1-\eta }}{4·{\tau }_c}=\frac{2-\eta \pm 2·\sqrt{1-\eta }}{4·\eta ·{\tau }_m}$$

(7)

Meanwhile, in conjunction with (3), (6), and (7), the calculation parameter $\alpha$ can be solved:

$$\alpha =\frac{\eta -1\mp \sqrt{1-\eta }}{2}·\frac{S_m}{{\tau }_c}=\frac{\eta -1\mp \sqrt{1-\eta }}{2·\eta }·\frac{S_m}{{\tau }_m}$$

(8)

From the above, all calculated coefficients should be positive, so the positive solution should be taken from Equations (6)–(8), then the calculation expressions of $\alpha$, $\beta$, and $\gamma$ are as follows:

$$\left\{\begin{array}{c}\begin{array}{c}\alpha =\frac{\eta -1+\sqrt{1-\eta }}{2·\eta }·\frac{S_m}{{\tau }_m}\\ \beta =\frac{1-\sqrt{1-\eta }}{2·\eta }·\frac{1}{{\tau }_m}\end{array}\\ \gamma =\frac{{\left(1-\sqrt{1-\eta }\right)}^2}{4·\eta }·\frac{1}{{\tau }_m}\end{array}\right\}$$

(9)

It can be seen from Equation (9) that the calculated parameters in the pile–rock lateral friction softening model are related to the maximum lateral friction ${\tau }_m$ and its corresponding displacement $S_m$, and the residual value ${\tau }_c$ of lateral friction.

The lateral friction softening model of the pile can also be normalized:

$$\frac{{\tau }_i}{{\tau }_m}=\frac{\frac{S_i}{S_m}\left({\alpha }_g+{\gamma }_g·\frac{S_i}{S_m}\right)}{{\left({\alpha }_g+{\beta }_g·\frac{S_i}{S_m}\right)}^2}$$

(10)

In the formula, ${\alpha }_g$, ${\beta }_g$, and ${\gamma }_g$ are the calculation parameters of normalization, respectively, and their expressions can be obtained similarly:

$$\left\{\begin{array}{c}\begin{array}{c}{\alpha }_g=\frac{\eta -1+\sqrt{1-\eta }}{2·\eta }\\ {\beta }_g=\frac{1-\sqrt{1-\eta }}{2·\eta }\end{array}\\ {\gamma }_g=\frac{{\left(1-\sqrt{1-\eta }\right)}^2}{4·\eta }\end{array}\right\}$$

(11)

Table 2. Selection of interface calculation parameters $\alpha$, $\beta$ and $\gamma$ under different normal pressures.

Interfacial State	Pile Side Positive Pressure σ (KPa)	α (m kPa−1)	β (kPa−1)	γ (kPa−1)	$${\mathit{\alpha }}_{\mathit{g}}/{10}^{-1}$$	$${\mathit{\beta }}_{\mathit{g}}/{10}^{-1}$$	$${\mathit{\gamma }}_{\mathit{g}}/{10}^{-1}$$
Native state	93	1.40 × 10−9	1.26 × 10−6	2.80 × 10−7	1.79	3.21	0.71
	617	7.54 × 10−10	6.25 × 10−7	1.33 × 10−7	1.82	3.18	0.68
	1389	3.97 × 10−10	3.21 × 10−7	7.28 × 10−7	1.77	3.23	0.73
	2006	3.52 × 10−10	2.48 × 10−7	5.36 × 10−8	1.81	3.19	0.69
	2778	3.18 × 10−10	1.99 × 10−7	4.25 × 10−8	1.82	3.18	0.68
Saturation State	62	3.41 × 10−9	3.08 × 10−6	5.42 × 10−7	1.96	3.04	0.54
	617	1.11 × 10−9	8.69 × 10−7	1.56 × 10−7	1.95	3.05	0.55
	1235	8.78 × 10−10	5.89 × 10−7	1.04 × 10−7	1.97	3.03	0.53
	1852	6.12 × 10−10	3.84 × 10−7	7.22 × 10−8	1.92	3.08	0.58
	2469	5.17 × 10−10	2.99 × 10−7	5.38 × 10−8	1.95	3.05	0.55

lists the calculation parameters of the natural mudstone–concrete interface softening model under different normal pressures. The residual strength ratio $\eta$ at the interface was between 0.67 and 0.70, and the residual strength ratio $\eta$ at the mudstone–concrete interface under a saturated state was between 0.58 and 0.61. The peak shear stress, peak displacement, and residual shear stress increased with the increase of pile positive pressure. The calculated parameters $\alpha$, $\beta$, and $\gamma$ decrease with the increase of pile positive pressure, but the normalized parameters ${\alpha }_g$, ${\beta }_g$, and ${\gamma }_g$ keep basically stable. In the natural state, ${\alpha }_g$, ${\beta }_g$, and ${\gamma }_g$ were in the range of (1.77–1.82) × 10⁻¹, (3.18–3.23) × 10⁻¹, and (0.67~0.73) × 10⁻¹, respectively. In the saturated state, ${\alpha }_g$, ${\beta }_g$, and ${\gamma }_g$ were in the range of (1.92~1.97) × 10⁻¹, (3.03~3.08) × 10⁻¹, and (0.53~0.58) × 10⁻¹, respectively. With the increase in water content, ${\alpha }_g$ increased, ${\beta }_g$ and ${\gamma }_g$ decreased.

4.2. Calculation Method of Vertical Bearing Capacity of the Rock-Socketed Pile Based on Lateral Friction Softening

The vertical bearing capacity of a soft rock-socketed pile includes the pile tip bearing capacity and pile side friction resistance. The diagram of rock-socketed load transfer is shown in Figure 9. As long as the calculation parameters $\alpha$, $\beta$, and $\gamma$ of the softening model of pile lateral friction resistance are known, the lateral friction resistance and vertical bearing capacity of rock-socketed pile can be calculated according to the functional relationship between the pile lateral friction resistance and the relative displacement of the pile–rock in each rock layer.

Based on the relationship between the axial compression deformation and vertical load balance, it can be concluded that:

$$\frac{d{S}_i}{dz}=\frac{F_i}{A·E}$$

(12)

$$d{F}_i=C\tau dz=C\frac{S_i\left[\alpha +\gamma ·S_i\right]}{{\left[\alpha +\beta ·S_i\right]}^2}dz=C\frac{{\tau }_m\frac{S_i}{S_m}\left[{\alpha }_g+{\gamma }_g·\frac{S_i}{S_m}\right]}{{\left[{\alpha }_g+{\beta }_g·\frac{S_i}{S_m}\right]}^2}dz$$

(13)

where $z$ is positive from the bottom upwards, $F_i$ and $S_i$ are the vertical loads and vertical displacement of the pile foundation at $z$, $E$ is the elastic modulus of the concrete pile foundation, and $A$ and $C$ are the area and perimeter of the pile section, respectively. According to Equation (12) above, it can be concluded that the pile body of a rock-socketed pile is regarded as an elastomer, and it is assumed that the displacement $S_T$ and $S_0$ of the pile top and bottom meet Equation (14):

$$S_T-S_0=\frac{F_T+F_0}{2·A·E}l=kl$$

(14)

where $F_T$ and $F_0$ are vertical loads and pile tip resistance, respectively, then the relative displacement $S_i$ at section $i$ is:

$$S_i=S_0+kz$$

(15)

$$d{S}_i=kdz$$

(16)

Substituting Equation (16) into Equation (13), the differential relation between $F_i$ and $S_i$ is:

$$d{F}_i=C\frac{S_i\left[\alpha +\gamma ·S_i\right]}{{\left[\alpha +\beta ·S_i\right]}^2}dz=\frac{1}{k}C\frac{S_i\left[\alpha +\gamma ·S_i\right]}{{\left[\alpha +\beta ·S_i\right]}^2}d{S}_i$$

(17)

By integrating Equation (17), the relation between vertical load $F_T$ and pile top displacement $S_T$ can be obtained:

$$F_T=C\frac{\gamma }{k{\beta }^2}\left[\left(\frac{\alpha }{\gamma }-\frac{2\alpha }{\beta }\right)ln\left(\frac{S_T+\frac{\alpha }{\beta }}{S_0+\frac{\alpha }{\beta }}\right)+\left(\frac{{\alpha }^2}{{\beta }^2}-\frac{{\alpha }^2}{\gamma \beta }\right)\frac{S_T-S_0}{\left(S_T+\frac{\alpha }{\beta }\right)\left(S_0+\frac{\alpha }{\beta }\right)}+S_T-S_0\right]+F_0$$

(18)

where $F_0$ is the pile tip resistance, $C$ is the sectional perimeter of the pile (m), $\alpha$ is the calculated parameter value (m∙kPa⁻¹), $\beta$ and $\gamma$ are calculated as parameters (kPa⁻¹), $S_T$ is pile top settlement (m), and $S_0$ is the settlement of the pile bottom (m).

4.3. Evolution Characteristic of Vertical Bearing Capacity of Rock-Socketed Pile

According to Equation (18), the vertical bearing capacity of the rock-socketed pile is mainly related to the relative displacement of pile–rock interface, positive pressure of the pile side, pile length, and elastic modulus. In order to analyze the evolution of the vertical bearing capacity of the rock-socketed pile, the evolution characteristics of the vertical bearing capacity of the rock-socketed pile under different pile lateral pressures, pile lengths and elastic modulus were analyzed, respectively.

(1)

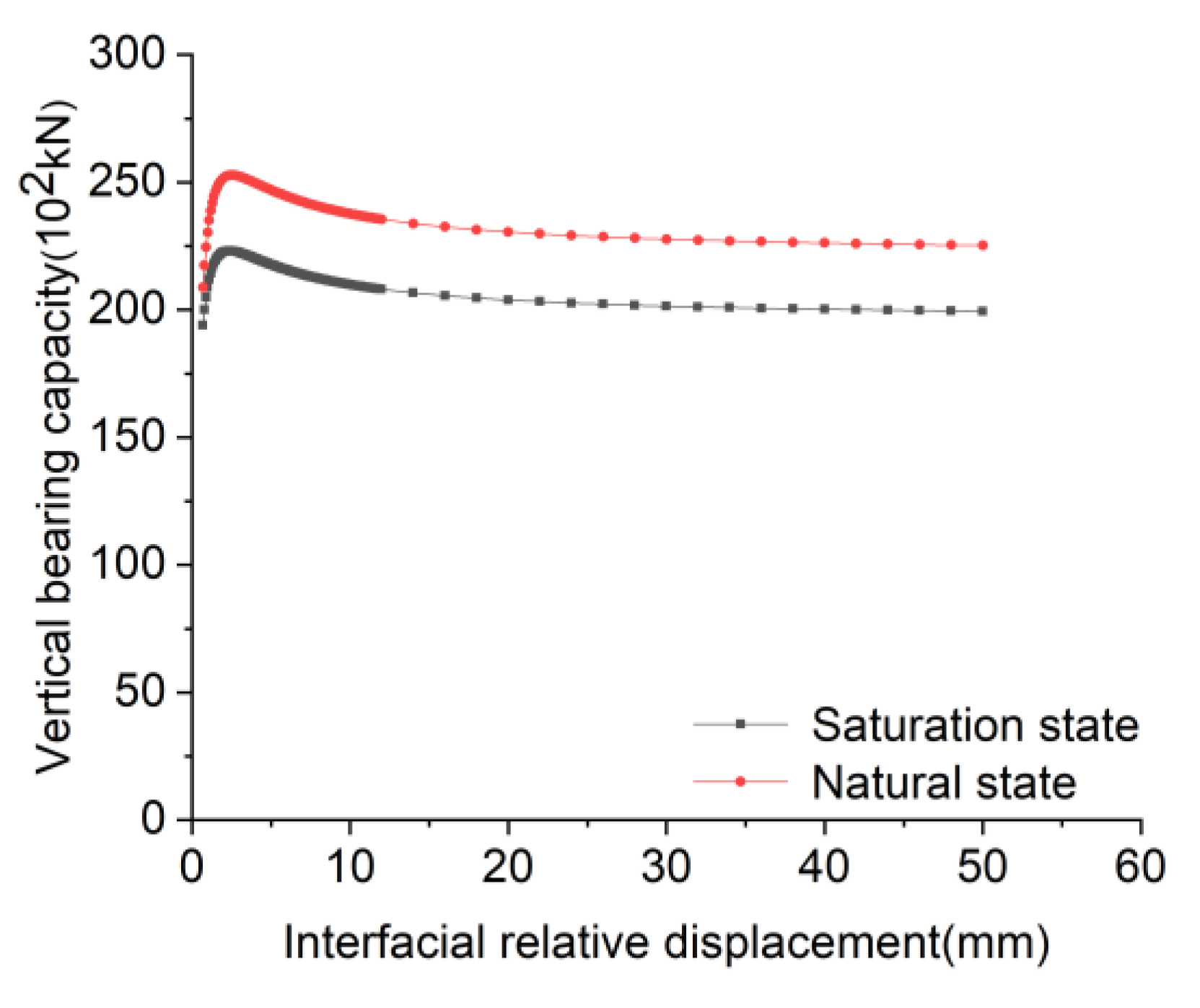
Influence of interface relative displacement on bearing capacity.

Taking a group of typical parameters as an example, the variation rule of vertical bearing capacity was analyzed, as shown in Figure 10. The vertical bearing capacity of rock-socketed pile in the natural mudstone condition increased rapidly with the increase of interface relative displacement. When the interface error momentum was 2.5 mm, the vertical bearing capacity reached the ultimate bearing value of 2.53 × 10⁴ kN. While the interface displacement continued to increase, the vertical bearing capacity gradually decreased and finally reached a stable value, showing a changing mechanism of “first increasing, then decreasing, and finally leveling”. In the natural state, the lateral friction resistance and tip resistance of rock-socketed pile accounted for 38% and 62% of the vertical ultimate bearing capacity, respectively, while the residual bearing capacity was 88.35% of the peak ultimate bearing capacity. The vertical ultimate bearing capacity and residual bearing capacity in the saturated state were 89.49% and 89.73% of those in the natural state, respectively.

(2)

Evolution characteristic of pile bearing capacity under positive lateral pressure.

Under different pile side positive pressures, the values of $\alpha$, $\beta$, and $\gamma$ were different. The five groups of interface softening model parameters obtained from experimental analysis under positive pressures were selected, and the specific parameter values are shown in Table 2. The evolution process of vertical bearing capacity of pile foundation under different lateral positive pressures is shown in Figure 11, through iterative calculation:

According to the figure, the vertical bearing capacity of the pile foundation increased gradually with the increase of the pile side positive pressure. Under the natural state, the proportion of lateral friction resistance in the vertical bearing capacity of the pile foundation increased from 18.17% to 58.13%, and the residual bearing capacity decreased from 93.63% to 82.03%. Under the saturated state, the proportion of lateral friction resistance in the vertical bearing capacity of the pile foundation increased from 10.55% to 54.99%, and the residual bearing capacity decreased from 96.12% to 81.23%. It can be seen that the greater the lateral positive pressure of the pile foundation is, the more fully the lateral friction resistance is exerted, and the vertical bearing capacity of the pile foundation increases linearly. However, when the interface fault momentum is larger, the residual bearing capacity decreases more. The vertical bearing capacity of the pile foundation under a natural state increases with the lateral positive pressure faster than that under a saturated state.

(3)

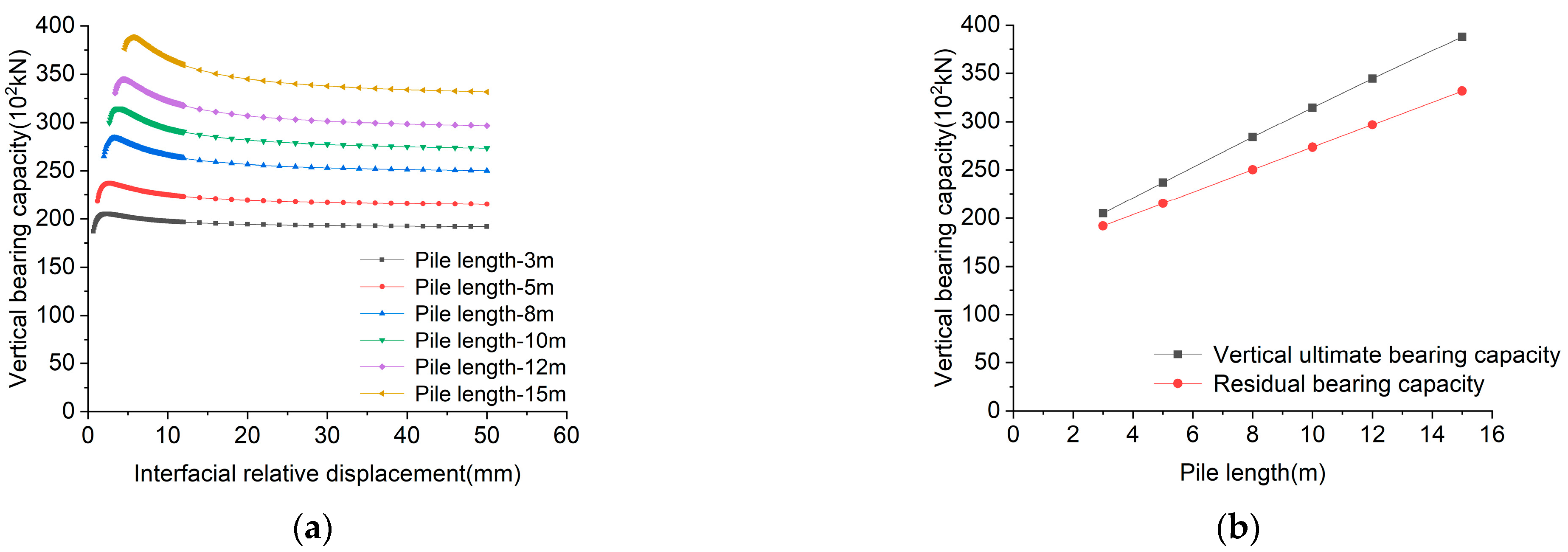
Influence of pile length on pile side friction.

In order to consider the various characteristics of lateral friction resistance under different pile lengths, this test designed five pile lengths of 3 m, 5 m, 8 m, 10 m, 12 m, and 15 m, respectively. The variation characteristic curves are shown in the Figure 12:

According to the analysis in Figure 12, under the condition that elastic modulus, parameters, and other factors remain unchanged, the pile lateral friction increases linearly with the increase of pile length, and residual strength also increases.

(4)

Influence of elastic modulus of the pile on bearing capacity

The pile body material of a rock-socketed pile is concrete, and the compression amount of the rock-socketed pile body under a vertical load is different with different concrete grades, resulting in a different wrong momentum at the pile–rock interface and affecting the vertical bearing capacity of the rock-socketed pile. Therefore, the influence of the pile body stiffness on the vertical bearing capacity is analyzed. Assuming that the pile stiffness is infinite, a rock-socketed pile can be regarded as a rigid body, and the calculation formula of the vertical bearing capacity of the pile can be simplified as:

$$F_T=C\frac{S_T\left[\alpha +\gamma ·S_T\right]}{{\left[\alpha +\beta ·S_T\right]}^2}l+F_0$$

(19)

The calculation results of vertical bearing capacity under different pile stiffness are shown in Figure 13:

It can be seen from Figure 13 that when the pile length and parameter value are certain, the elastic modulus has little influence on the peak value of the pile side friction and residual strength, and the difference in vertical bearing capacity between the elastic pile and rigid pile was only 0.106%. It can be seen that the stiffness of the pile body was much greater than that of the pile rock interface, so the pile body can be regarded as a rigid body, and the influence of elastic deformation of the pile body on vertical bearing capacity can be ignored.

(5)

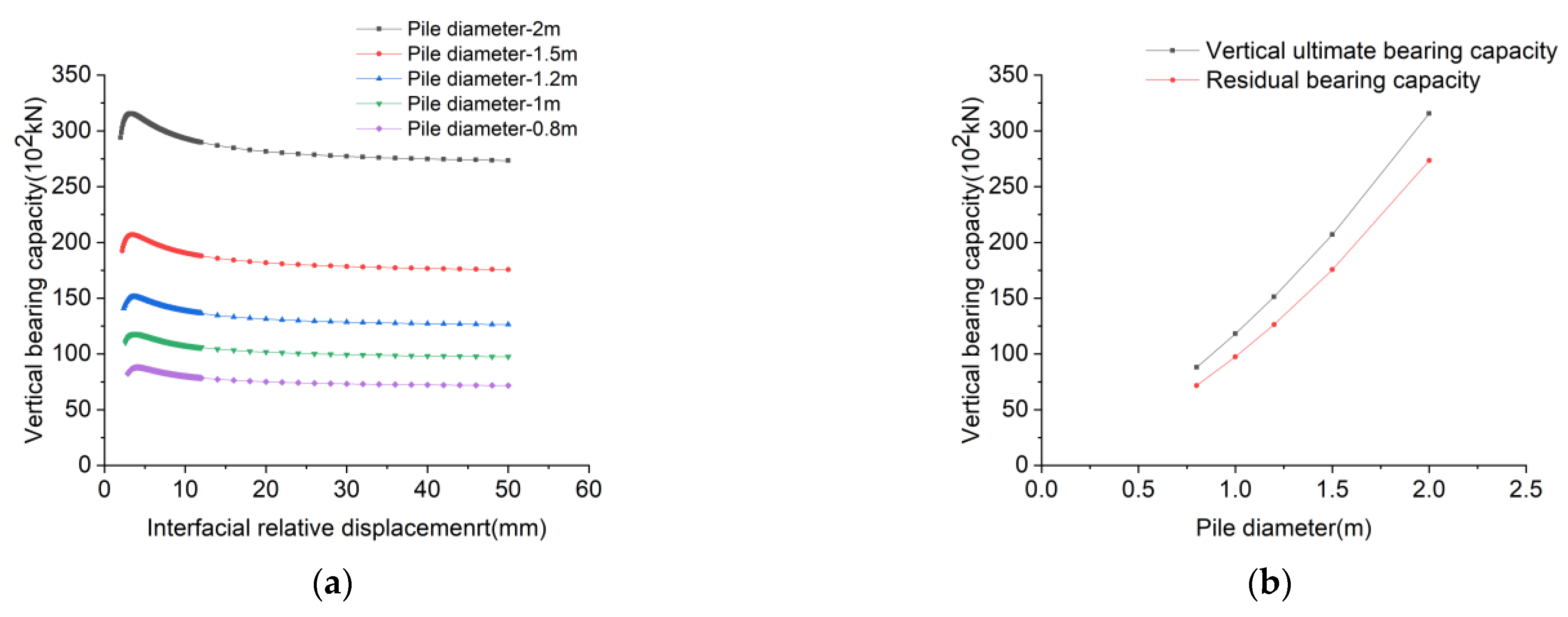
Influence characteristics of pile diameter on bearing capacity

In order to study the variation characteristics of vertical bearing capacity and lateral friction resistance of rock-socketed pile under different pile diameters, five working conditions with pile diameters of 0.8 m, 1 m, 1.2 m, 1.5 m, and 2 m were designed in this paper. The variation curve is shown in Figure 14:

According to the analysis in Figure 14, under the condition that the pile length, parameters, elastic modulus, and other factors remain unchanged, the vertical bearing capacity of the rock-socketed pile increases with the increase of pile diameter, and so does the residual strength value. The proportion of pile side friction increased from 28.58% to 49.78%, indicating that the pile side friction played more fully with the increase in the pile diameter.

5. Conclusions

(1)

Through laboratory shear tests of the pile–mudstone interface, it is concluded that the relationship curve between shear stress and shear displacement in the natural and saturated state first increases, then decreases, and then tends to be stable. The normal stress in the natural and saturated state has a linear relationship with the peak shear stress. Based on indoor experiments and theoretical formulas, a pile side friction resistance softening model considering the weakening of the pile–rock interface is established, and it is concluded that the shear stress at the pile–rock interface is the residual shear stress, and its value is 68.75% of the peak shear stress.

(2)

A calculation method of the vertical bearing capacity of the rock-socketed pile based on lateral friction softening was established, and the effects of interface relative displacement, lateral positive pressure, pile diameter, pile length, and pile stiffness on vertical bearing capacity were analyzed. The results show that the vertical bearing capacity of the rock-socketed pile shows softening characteristics of “first increase, then decrease, and finally flat” with the interface displacement. The ultimate bearing capacity and residual bearing capacity of the saturated condition are 88.27% and 88.56% of that of the natural condition, respectively.

(3)

According to the analysis of the factors affecting the vertical bearing capacity of the rock-socketed pile, the results show that the greater the positive pressure on the side of the rock-socketed pile foundation, the greater the proportion of the pile lateral friction increases by 39.96%, and the more fully the pile lateral friction is exerted. With the increase in pile diameter, the ratio of lateral friction increases from 28.58% to 49.78%. The greater the vertical ultimate bearing capacity of the pile foundation, the greater the decline of the residual bearing capacity. There is a linear relationship between vertical bearing capacity and pile length. Because the pile stiffness is much larger than the pile rock interface stiffness, the influence of pile elastic deformation on the vertical bearing capacity can be ignored.

Based on laboratory tests and the derivation of theoretical formulas, some qualitative and useful conclusions are drawn in this study. However, it should be noted that further studies are needed for finite element numerical simulation analysis considering the socket roughness factor. The action process based on super-large loads is short, and the creep phenomenon of actual engineering rock-socketed piles and soil/rock mass is not fully simulated. In the follow-up work, we will focus on these important problems to provide useful guidance for practical engineering applications.