Risk Estimation of Typhoon Disaster Based on Three-Dimensional Information Diffusion Method
Abstract
1. Introduction
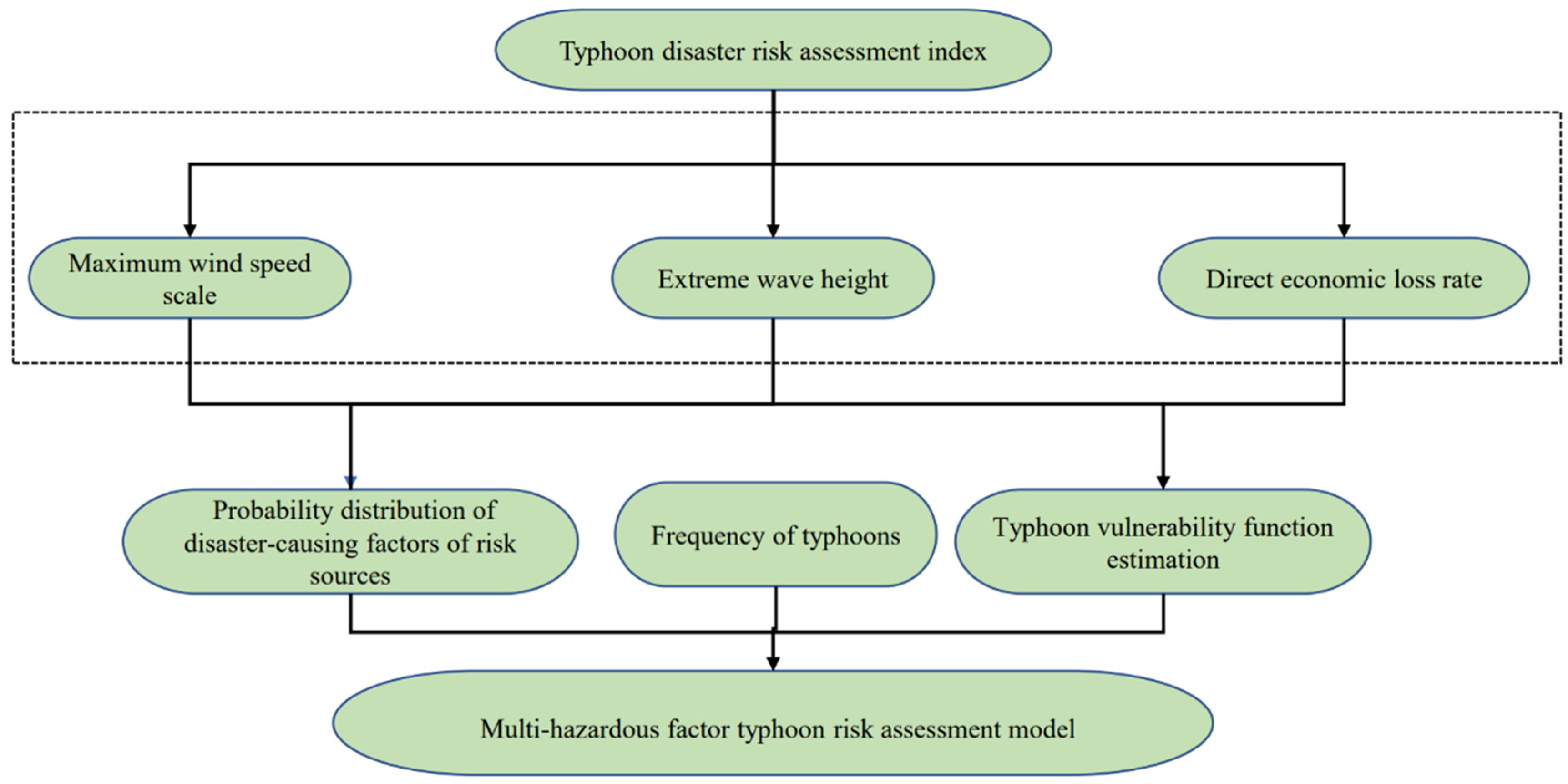
2. Theoretical Model
2.1. Construction of Probability Distribution of Disaster-Causing Factors of Risk Sources
2.2. Typhoon Vulnerability Function Estimation
2.3. Risk Assessment Model
3. Engineering Calculation Example
3.1. Data Source
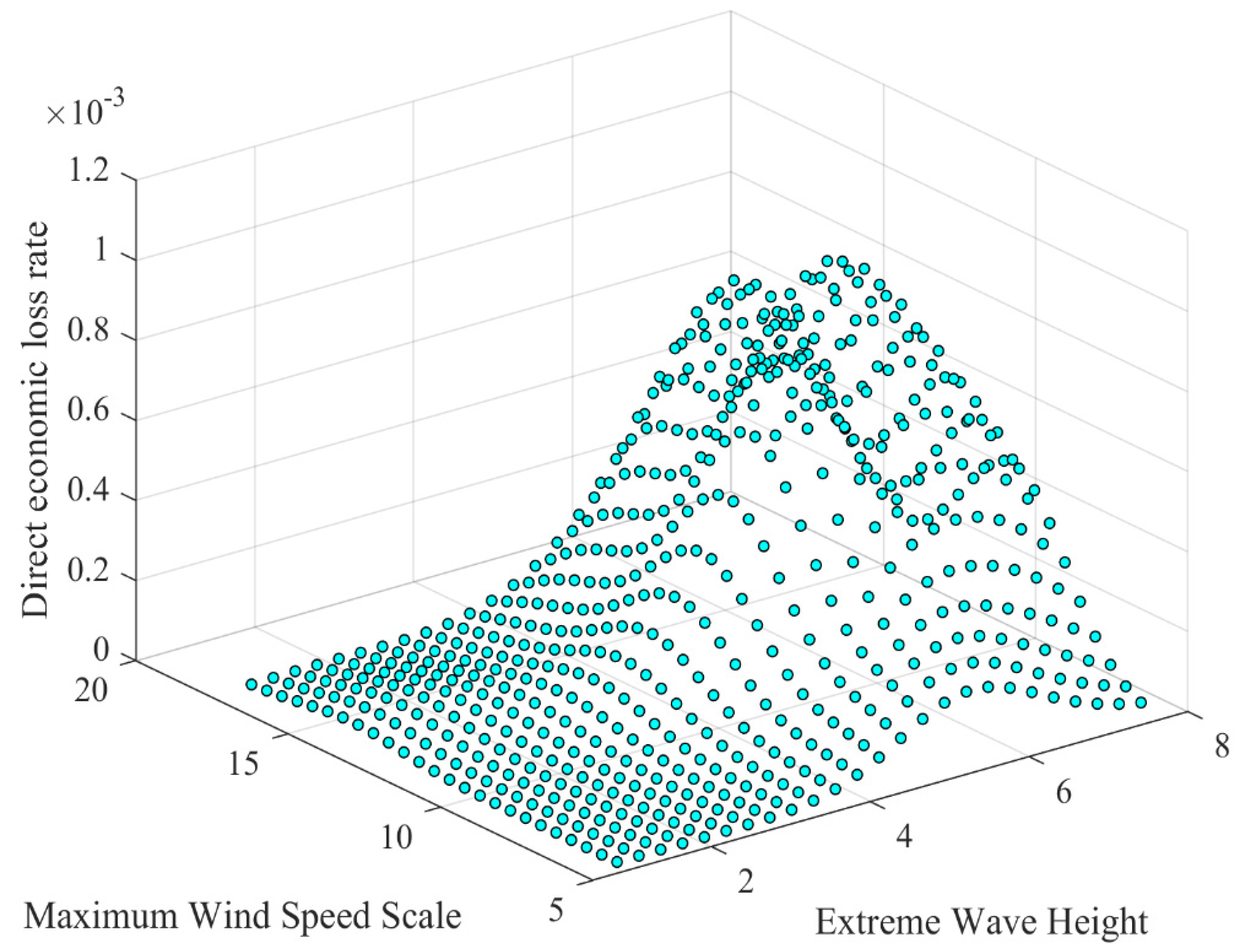
3.2. Model Calculation
3.2.1. Estimation of Probability Distribution
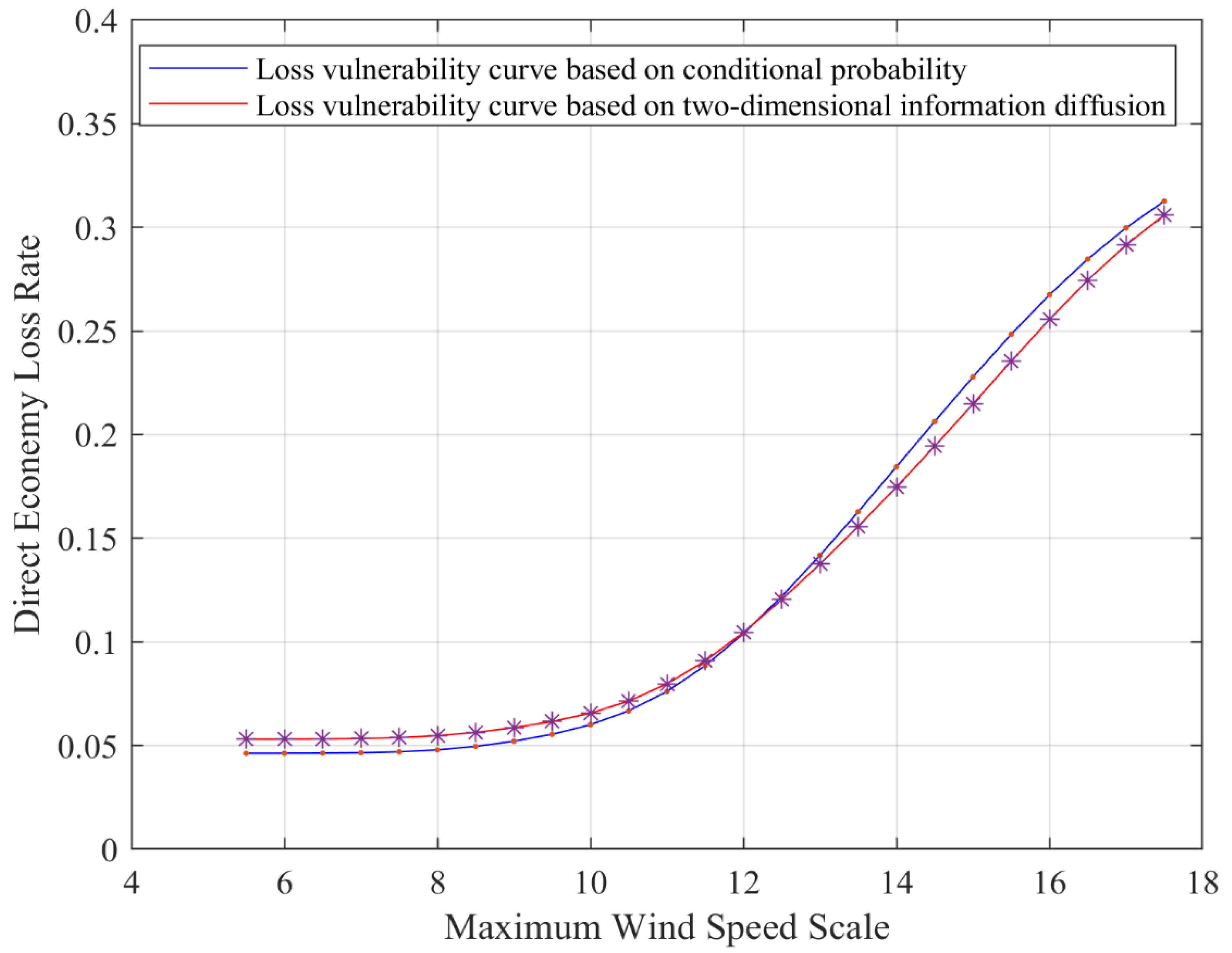
3.2.2. Estimation of Typhoon Disaster Losses at Different Levels of Risk-Causing Factors
3.2.3. Typhoon Risk Coupling
4. Conclusions
- (1)
- This paper transforms the formal expected loss model into a computable typhoon risk model based on the three-dimensional information diffusion method. It obtains the typhoon probability distribution and direct economic loss rate distribution under different wind speed scales and extreme wave heights. Additionally, the results are basically consistent with reality, which can provide a reference for the practical application of worldwide typhoon disaster risk assessment engineering.
- (2)
- The maximum wind speed scale and extreme wave height of the typhoon at landfall are considered, which reduces the limitation of risk assessment by a single uniform disaster factor and improves the efficiency of using small sample data. For example, the estimated direct economic loss rate of Typhoon Hagupit “0814” is 0.2167%, which is closer to the real value of 0.2109%.
- (3)
- The risk value of the multi-causal factor typhoon risk assessment model with expected loss is slightly higher than the traditional model, and the annual expected loss risk value is 12.33% higher than that of the traditional model, which reduces the limitations of the low-dimensional information diffusion model and makes the evaluation results more reasonable and reliable.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiang, C.Y.; Gao, S.Z.; Liu, D. Overview of typhoon activity in the Northwest Pacific and South China Sea in 2021. J. Mar. Meteorol. 2022, 42, 39–49. [Google Scholar] [CrossRef]
- Liu, G.; Chen, B.; Gao, Z.; Fu, H.; Jiang, S.; Wang, L.; Yi, K. Calculation of Joint Return Period for Connected Edge Data. Water 2019, 11, 300. [Google Scholar] [CrossRef]
- Liu, G.; Chen, B.; Jiang, S.; Fu, H.; Wang, L.; Jiang, W. Double Entropy Joint Distribution Function and its Application in Calculation of Design Wave Height. Entropy 2019, 21, 64. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Chen, B.; Wang, L.; Zhang, S.; Zhang, K.; Lei, X. Wave Height Statistical Characteristic Analysis. Limnology 2019, 37, 448–460. [Google Scholar] [CrossRef]
- Xu, J.C.; Ren, Q.W.; Shen, Z.Z. Low strain pile testing based on synchrosqueezing wavelet transformation analysis. J. Vibroeng. 2016, 18, 813–825. [Google Scholar] [CrossRef]
- Chen, B.; Kou, Y.; Wang, Y.; Zhao, D.; Liu, S.; Liu, G.; Wang, L.; Han, X. Analysis of storm surge characteristics based on stochastic process. AIMS Math. 2021, 6, 1177–1190. [Google Scholar] [CrossRef]
- Chen, B.; Kou, Y.; Wu, F.; Wang, L.; Liu, G. Study on evaluation standard of uncertainty of design wave height calculation model. J. Oceanol. Limnol. 2021, 39, 1188–1197. [Google Scholar] [CrossRef]
- Chen, B.Y.; Kou, Y.; Zhao, D.; Wu, F.; Wang, L.P.; Liu, G.L. Maximum Entropy Distribution Function and Uncertainty Evaluation Criteria. China Ocean Eng. 2021, 35, 238–249. [Google Scholar] [CrossRef]
- Zhou, X.; Cai, X.; Zhang, H.; Zhang, Z.; Jin, T.; Chen, H.; Deng, W. Multi-strategy competitive-cooperative co-evolutionary algorithm and its application. Inf. Sci. 2023, 635, 328–344. [Google Scholar] [CrossRef]
- Deng, W.; Xu, J.J.; Gao, X.Z.; Zhao, H.M. An enhanced MSIQDE algorithm with novel multiple strategies for global optimi-za-tion problems. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1578–1587. [Google Scholar] [CrossRef]
- Wang, L.P.; Chen, B.Y.; Chen, C.; Chen, Z.; Liu, G. Application of Linear Mean-Square Estimation in Ocean Engineering. China Ocean Eng. 2016, 30, 149–160. [Google Scholar] [CrossRef]
- Wang, L.P.; Chen, B.; Zhang, J.; Chen, Z. A New Model for Calculating the Design Wave Height in Typhoon-Affected Sea Areas. Nat. Hazards 2013, 67, 129–143. [Google Scholar] [CrossRef]
- Wang, L.; Xu, X.; Liu, G.; Chen, B.; Chen, Z. A New Method to Estimate Wave Height of Specified Return Period. Chin. J. Oceanol. Limnol. 2017, 35, 1002–1009. [Google Scholar] [CrossRef]
- Rakwatin, P.; Sansena, T.; Marjang, N.; Rungsipanich, A. Using Multi-Temporal Remote Sensing Data to Estimate 2011 Flood Area and Volume Over Chao Phraya River Basin, Thailand. Remote Sens. Lett. 2013, 4, 243–250. [Google Scholar] [CrossRef]
- Aye, Z.C.; Jaboyedoff, M.; Derron, M.H. An Interactive Web-GIS Tool for Risk Analysis: A Case Study in the Fella River Basin, Italy. Nat. Hazards Earth Syst. Sci. 2016, 16, 85–101. [Google Scholar] [CrossRef]
- Karbassi, A.R.; Maghrebi, M.; Lak, R.; Noori, R.; Sadrinasab, M. Application of sediment cores in reconstruction of long-term temperature and metal contents at the northern region of the Persian Gulf. Desert 2019, 24, 109–118. [Google Scholar]
- Chen, K.J.; Chen, Y.Y.; Chen, J.J. Assessment and analysis of typhoon hazard risk in the recent 30 years in eastern Guangdong. Soil Water Conserv. Res. 2019, 26, 362–366+372. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Y.J.; Wang, J.; Lv, Y.Y.; Luan, K.F. Typhoon disaster risk assessment of Chinese coastal cities based on the last 20 a historical data. Ocean Forecast. 2021, 38, 24–30. [Google Scholar]
- Zhao, J.T.; Dong, L.; Chu, S.H.; Zhang, H. Socio-economic sensitivity analysis of typhoon disaster--An example of Zhejiang Province. J. Langfang Norm. Coll. (Nat. Sci. Ed.) 2022, 22, 69–72+100. [Google Scholar]
- Shang, Z.H.; Zhou, M.Y.; Liang, Q.S.; Yang, S.H.; Zhang, R.L.; Zheng, K.H. Risk assessment of rice typhoon hazard in Zhanjiang City, Guangdong Province. Disaster Sci. 2021, 36, 85–90. [Google Scholar]
- Liu, B.; Siu, Y.L.; Mitchell, G.; Xu, W. Exceedance probability of multiple natural hazards: Risk assessment in China’s Yangtze River Delta. Nat. Hazards 2013, 69, 2039–2055. [Google Scholar] [CrossRef]
- Huang, C.F. A computer simulation method to evaluate the reliability of typhoon risk models. J. Nat. Hazards 2020, 29, 24–35. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, J.; Cai, W.; Tong, Z. Information diffusion-based spatio-temporal risk analysis of grassland fire disaster in northern China. Knowl.-Based Syst. 2010, 23, 53–60. [Google Scholar] [CrossRef]
- Zhong, L.; Liu, L.; Liu, Y. Natural Disaster Risk Assessment of Grain Production in Dongting Lake Area, China. Agric. Agric. Sci. Procedia 2010, 1, 24–32. [Google Scholar] [CrossRef]
- Wang, J.Y.; Chen, J.J.; Lin, J.; Yang, K.; Ma, Z.G.; Huang, R.C.; Xu, Z.H. Agricultural flood risk assessment in Fujian Province based on information diffusion theory. J. Nat. Resour. 2012, 27, 53–62. [Google Scholar]
- Xu, L.F.; Xu, X.G.; Meng, X.G. Risk assessment of soil erosion in different rainfall scenarios by RUSLE model coupled with Information Diffusion Model: A case study of Bohai Rim, China. Catena 2012, 100, 74–82. [Google Scholar] [CrossRef]
- Liu, G.L.; Li, Y.X.; Li, X.; Han, L.Z. Risk analysis of typhoon disaster in Guangdong Province based on information diffusion technology. J. Saf. Environ. 2021, 21, 1684–1692. [Google Scholar] [CrossRef]
- Liu, H.X.; Lu, Y.J.; Wang, M.L.; Guang, T. Risk assessment of extreme typhoon hazard in South China based on information diffusion technique. J. Trop. Oceanogr. 2020, 39, 31–41. [Google Scholar]
- Yu, S.B.; Yu, H.R.; Ji, C.H.; Lu, Y.Q. Risk assessment of typhoons along the southeast coast based on information diffusion. Disaster Sci. 2019, 34, 73–77. [Google Scholar]
- Huang, C.F. A formal model for dynamic risk analysis of natural hazards. Disaster Sci. 2015, 30, 4–5. [Google Scholar]
- Huang, C.F.; Guo, J.; Ai, F.L.; Wu, T. The basic paradigm of flood hazard risk analysis and its application. J. Nat. Hazards 2013, 22, 11–23. [Google Scholar] [CrossRef]
- Xu, Q.J.; Pan, J.L.; Liu, H.X. Typhoon disaster risk estimation based on three-dimensional information diffusion and stochastic process. J. Nanning Norm. Univ. (Nat. Sci. Ed.) 2020, 37, 54–69. [Google Scholar]
- Huang, C.F. A virtual case of dynamic risk analysis of natural disasters. Disaster Sci. 2015, 30, 1–11. [Google Scholar]
- Guo, J.; Zhao, S.J.; Huang, C.F. Research on systematic error and correction of probabilistic risk of natural disasters. Syst. Eng. Theory Pract. 2017, 37, 523–534. [Google Scholar]
- Shang, Z.H.; Li, X.Y. Typhoon disaster risk assessment in coastal areas of Guangdong Province. J. Lingnan Norm. Univ. 2015, 36, 136–142. [Google Scholar]




| Distribution | Extreme Wave Height | Maximum Wind Speed Scale |
|---|---|---|
| Normal distribution | 0.1279 (0.8768) | 0.1632 (0.6342) |
| Maximum Wind Speed Scale | Extreme Wave Height (m) | |||||
|---|---|---|---|---|---|---|
| 2.1 | 3.2 | 4.3 | 5.4 | 6.5 | 7.6 | |
| 12 | 0.0018 | 0.0036 | 0.0046 | 0.0029 | 0.0020 | 0.0008 |
| 13 | 0.0026 | 0.0044 | 0.0052 | 0.0036 | 0.0026 | 0.0012 |
| 14 | 0.0027 | 0.0044 | 0.0051 | 0.0034 | 0.0030 | 0.0015 |
| 15 | 0.0022 | 0.0037 | 0.0043 | 0.0032 | 0.0031 | 0.0017 |
| 16 | 0.0014 | 0.0027 | 0.0029 | 0.0023 | 0.0027 | 0.0016 |
| 17 | 0.0009 | 0.0018 | 0.0016 | 0.0012 | 0.0017 | 0.0011 |
| Maximum Wind Speed Scale | Extreme Wave Height (m) | |||||
|---|---|---|---|---|---|---|
| 2.1 | 3.2 | 4.3 | 5.4 | 6.5 | 7.6 | |
| 12 | 0.0964 | 0.1009 | 0.1081 | 0.1054 | 0.1086 | 0.1195 |
| 13 | 0.1124 | 0.1342 | 0.1499 | 0.1426 | 0.1448 | 0.1627 |
| 14 | 0.1351 | 0.1739 | 0.1905 | 0.1786 | 0.1892 | 0.2157 |
| 15 | 0.1730 | 0.2187 | 0.2238 | 0.2094 | 0.2348 | 0.2654 |
| 16 | 0.2322 | 0.2685 | 0.2541 | 0.2351 | 0.2702 | 0.2993 |
| 17 | 0.2950 | 0.3131 | 0.2868 | 0.2460 | 0.2913 | 0.3174 |
| Maximum Wind Speed Scale | Extreme Wave Height (m) | |||||
|---|---|---|---|---|---|---|
| 2.1 | 3.2 | 4.3 | 5.4 | 6.5 | 7.6 | |
| 12 | 0.0279 | 0.0550 | 0.0704 | 0.0452 | 0.0301 | 0.0176 |
| 13 | 0.0319 | 0.0546 | 0.0643 | 0.0421 | 0.0322 | 0.0201 |
| 14 | 0.0319 | 0.0522 | 0.0610 | 0.0424 | 0.0361 | 0.0241 |
| 15 | 0.0219 | 0.0501 | 0.0582 | 0.0431 | 0.0423 | 0.0303 |
| 16 | 0.0264 | 0.0507 | 0.0539 | 0.0417 | 0.0494 | 0.0376 |
| 17 | 0.0264 | 0.0559 | 0.0485 | 0.0371 | 0.0536 | 0.0427 |
| Maximum Wind Speed Scale | 12 | 13 | 14 | 15 | 16 | 17 |
|---|---|---|---|---|---|---|
| Direct econemy loss rate (%) | 0.1046 | 0.1376 | 0.1747 | 0.2148 | 0.2556 | 0.2915 |
| Number | Name | Three-Dimensional Information Diffusion | Two-Dimensional Information Diffusion | Number | Name | Three-Dimensional Information Diffusion | Two-Dimensional Information Diffusion |
|---|---|---|---|---|---|---|---|
| 0518 | Damrey | 0.1069 | 0.0797 | 1306 | Rumbia | 0.1281 | 0.1251 |
| 0601 | Chanchu | 0.2119 | 0.2314 | 1311 | Utor | 0.2238 | 0.2314 |
| 0606 | Prapiroon | 0.1891 | 0.1780 | 1319 | Usagi | 0.3131 | 0.3170 |
| 0801 | Neoguri | 0.0532 | 0.0507 | 1409 | Rammasun | 0.2702 | 0.2799 |
| 0809 | Kammuri | 0.0780 | 0.0527 | 1415 | Kalmaegi | 0.1965 | 0.1780 |
| 0812 | Nuri | 0.1259 | 0.1780 | 1510 | Linfa | 0.1447 | 0.1251 |
| 0814 | Hagupit | 0.2167 | 0.2314 | 1522 | Mujigae | 0.2869 | 0.2799 |
| 0907 | Goni | 0.0780 | 0.0527 | 1621 | Sarika | 0.1037 | 0.0797 |
| 1003 | Chanthu | 0.1779 | 0.1780 | 1622 | Haima | 0.1031 | 0.1251 |
| 1213 | Kai-tak | 0.1500 | 0.1251 |
| Risk Value (%) | 0.2542 | 0.2263 | 0.2011 | 12.33 | 26.40 | 12.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Yin, J.; Song, S.; Yang, W.; Tian, Y.; Wang, L.; Xu, Y. Risk Estimation of Typhoon Disaster Based on Three-Dimensional Information Diffusion Method. J. Mar. Sci. Eng. 2023, 11, 1080. https://doi.org/10.3390/jmse11051080
Liu G, Yin J, Song S, Yang W, Tian Y, Wang L, Xu Y. Risk Estimation of Typhoon Disaster Based on Three-Dimensional Information Diffusion Method. Journal of Marine Science and Engineering. 2023; 11(5):1080. https://doi.org/10.3390/jmse11051080
Chicago/Turabian StyleLiu, Guilin, Jingyi Yin, Shichun Song, Wenjin Yang, Yuhang Tian, Liping Wang, and Yu Xu. 2023. "Risk Estimation of Typhoon Disaster Based on Three-Dimensional Information Diffusion Method" Journal of Marine Science and Engineering 11, no. 5: 1080. https://doi.org/10.3390/jmse11051080
APA StyleLiu, G., Yin, J., Song, S., Yang, W., Tian, Y., Wang, L., & Xu, Y. (2023). Risk Estimation of Typhoon Disaster Based on Three-Dimensional Information Diffusion Method. Journal of Marine Science and Engineering, 11(5), 1080. https://doi.org/10.3390/jmse11051080




