Structural Design of the Substructure of a 10 MW Floating Offshore Wind Turbine System Using Dominant Load Parameters

Abstract

Fully coupled integrated load analyses (ILAs) to evaluate not only the load response but also the structural integrity are required to design a floating offshore wind turbine, since there has been no firmly established approach for obtaining the structural responses of a FOWT substructure in the time domain. This study aimed to explore if a direct strength analysis (DSA) technique that has been widely used for ships and offshore structures can adequately evaluate the FOWT substructure. In this study, acceleration and nacelle thrust were used for the dominant load parameters for DSA. The turbine thrust corresponding to the 50-year return period was taken from the literature. The acceleration response amplitude operator (RAO) was obtained through frequency response hydrodynamic analysis. The short-term sea states defined by the wave scatter diagram (WSD) of the expected installation area was represented by the JONSWAP wave spectrum. To account for the multi-directionality of the short-crested waves, the 0th order moments of the wave spectrum were corrected. The probabilities of each short-term sea state and each wave incidence angle were applied to derive the long-term acceleration for each return period. DSA cases were generated by combining the long-term acceleration and nacelle thrust to maximize the forces in the surge, sway, and heave directions. Linear spring elements were placed under the three outer columns of the substructure to provide soft constraints for hive, roll, and pitch motions. Nonlinear spring elements with initial tension were placed on the three fairlead chain stoppers (FCSs) to simulate the station-keeping ability of the mooring lines; they provided initial tension in the slacked position and an increased tension in the taut position. The structural strength evaluation of the coarse mesh finite element model with an element size same as the stiffener spacing showed that high stresses exceeding the permissible stresses occurred in the unstable members of the substructure. The high stress areas were re-evaluated using a fine mesh finite element model with an element size of 50 mm × 50 mm. The scope of structural reinforcement was identified from the fine mesh analyses. It was found that the DSA can be properly utilized for the substructure strength assessment of a FOWT.

1. Introduction

The design of floating offshore wind turbines (FOWTs) must be validated for structural safety through integrated load analyses (ILAs). ILAs should consider the combined loads generated by wind, waves, and currents and should be performed based on industry standards such as DNV-ST-0119 [1] or international standards such as IEC 61400-1 [2].

These standards recommend performing ILAs by categorizing design load cases (DLCs) into turbine startup, power production, turbine shutdown, and emergency shutdown based on environmental conditions. Even for a DLC corresponding to power production, a large number of power production DLCs are derived from wind speed, wave height, wind speed–wave height correlation, and wind–wave directionality correlation. These DLCs are also categorized into ultimate limit state (ULS), fatigue limit state (FLS), and accidental limit state (ALS) depending on the extremity and occurrence frequency of the environmental loads.

Many researchers have evaluated dynamic loadings and dynamic responses by performing ILAs of FOWTs. The most representative software for ILAs is the open code FAST (acronym of fatigue, aerodynamics, structures, and turbulence) [3]. FAST v4.0 was first released in 2002 and is currently updated as OpenFAST [4]. Yu and Shin [5] used OpenFAST to obtain the dynamic response of a FOWT with a 5 MW turbine as proposed by the National Renewable Energy Laboratory (NREL). The dynamic behavior of a fixed offshore wind turbine was analyzed using OpenFAST [6]. Zhao et al. [7] used OpenFAST to evaluate the fatigue damage of a 10 MW FOWT with a semi-submersible substructure where the substructure was replaced with the equivalent stiffnesses. For this reason, local stresses including stress concentration effects could not be captured in the study. Ha et al. [8] assessed the structural integrity of a spar-type FOWT with the NREL 5 MW turbine. They used the maximum loads captured at each structural locations: tower base moments, fairlead tensions, and accelerations at the centre of mass (CoM) that were obtained from the ILAs under an extreme environment. Devin et al. [9] performed the ILAs for a vertical axis wind turbine using OWENS [10] coupled with OpenFAST. Li et al. [11] investigated the motion and structural loads of the NREL 5 MW FOWT under a typhoon condition. Ahn et al. [12] used OpenFAST to investigate the variation of the tower base moment. The effect of second-order hydrodynamics was investigated using Wamit [13] and OpenFAST [14,15,16]. Yang et al. [17] developed a coupling technique of OpenFAST and Aqwa [18], where OpenFAST was responsible for turbine behavior and Aqwa for hydrodynamics. This approach was utilized to analyze a combined platform of floating wind and wave energy converters [19,20]. Aqwa was used to analyze the effects of secondary wave forcing on a wind–wave combined platform [21].

SIMA [22], developed by the classification society DNV, is known to be an alternative software. It is composed of a few modules: Simo for motion dynamics, Riflex for beam structural dynamics, Wasim for panel loads, and Sestra for shell structural dynamics. Chuang et al. [23] obtained the global responses to nonlinear waves of the NREL 5 MW turbine using SIMA. The main drawback of SIMA is that no technical explanation is given for the process of converting the motion response into pressures acting on the wet panels. There is a clear technical process for obtaining the kinematic responses from a given load. However, it is unlikely that the panel pressure and acceleration at CoM estimated from a given motion response is the unique solution.

Computational fluid dynamics (CFD) has also often been applied to the ILAs of FOWTs. Zhou et al. [24] investigated the effects of wave type and wave steepness on the NREL 5 MW FOWT through the CFD. Rezaeiha and Micallef [25] used the CFD to evaluate the wake interactions of two tandem FOWTs. Dong et al. [26] employed CFD to self-validate the aerodynamic performance of FOWTs in the vortex ring state. Clément et al. [27] adopted CFD to investigate the hydrodynamics of FOWTs by comparing the results of applying regular waves to a fixed cylinder with the coefficients of the Morison equation. Wang et al. [28] applied CFD to analyze the hydrodynamic responses of a FOWT under regular waves. However, CFD is known to be less appropriate for ILAs of FOWTs due to the relatively long computational time. In addition, it is very difficult to to generate turbulent wind fields and irregular wave fields using CFD modeling technique. CFD is an inappropriate method to use for representing the behavior of mooring lines, as it requires many grids to implement hydrodynamics on slender mooring lines.

Regardless of the software used, ILAs must be performed for more than 30 DLCs to design a single FOWT [29,30], and even a single DLC has many subDLCs derived from a DLC. In order to obtain stochastically stable responses, it is necessary to perform ILAs for wind and wave fields with various random phases, even for a single subDLC. The setting of the random phases is usually referred to as the ‘setting of seed’.

IEC 61400-3 [29] recommends 1 h ILAs for at least 6 seeds. However, a minimum of 3 h ILA is required to obtain a statistically stable response to a short-term sea state. As an example, the number of possible ILAs for the ULS equivalent of DLC 6.2 was estimated and summarized in Table 1.

Table 1. The estimated number of subDLCs for DLC 6.2.

Variables	Value	Case
Wind direction (degree)	−30, 0, +30	3
Wave direction (degree)	−30, 0, +30	3
Current direction (degree)	−30, 0, +30	3
Yaw misalignment angle	−180 to 150 (30° interval)	12
Wind speed	1 extreme wind speed	1
Sea state	Min 3 extreme sea states	3
Phases		6
The number of subDLCs	aligned wind, wave, and current dir	648
	misaligned wind, wave, and current dir	5832
Entire analysis period (hour)	aligned wind, wave, and current dir	1944
	misaligned wind, wave, and current dir	17,496

As shown in Table 1, the number of subDLCs can be up to 5832 depending on wind/wave directions, wind speeds, sea states, yaw alignments, and seeds. Assuming a 3 h subDLC analysis period, a total analysis period of 17,496 h (729 days) is required. The physical computation time for a 1 h analysis is dependent on the performance of the computer. For example, a 3 h subDLC ILA takes approximately 3 h to complete on a typical personal computer. Arithmetically, it would take about two years to complete all subDLCs for DLC 6.2 on a single personal computer.

The Life50+ [31], IEA wind [32], and Corewind [33] projects selected fewer than 10 representative DLCs and then performed ILAs. Balli and Zheng [34] proposed a pseudo-coupling approach to reduce the number of ILA simulations during the design development phase. While the pseudo-coupling approach is suitable for application to specific structural parts such as tower interfaces, ILAs for a large number of subDLCs are still required for structural strength assessment of the entire substructure.

ILAs for FOWTs typically do not include structural strength analyses for the substructure. Most ILA software considers the substructure as a single point mass [35], so the stresses in the substructure cannot be obtained through ILAs. It may be possible to derive the stresses and strains by discretizing the substructure as finite elements, but ILA for a single subDLC would require too long of an analysis period. For this reason, a separate process is required for the strength design of the substructure.

Direct strength analysis (DSA) is a widely used technique for the structural strength assessment of ships and floating offshore structures [36,37]. DSA is a technique that firstly obtains the load RAOs through frequency response hydrodynamic analysis, secondly derives long-term loads considering wave and wind conditions, thirdly generates a combination of long-term loads from a structural design perspective, and finally evaluates the structural integrity under the generated load combination. The loads that greatly affect the structural strength are defined as the dominant load parameters. In this study, DSA is applied to the 10 MW FOWT substructure.

2. Details of the Target Structure

This study applies DSA to the substructure of a 10 MW FOWT predicted to operate offshore of Ulsan, South Korea. It is assumed that the FOWT is equipped with the 10 MW rotor nacelle assembly (RNA) disclosed by Denmark Technical University [38]. Catenary mooring lines were connected from fairlead chain stoppers (FCSs) located on the substructure deck to seabed anchor points (see sketch in Figure 1).

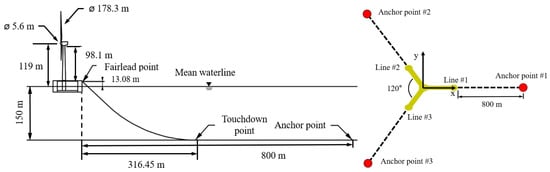
Figure 1. Floating offshore wind turbine and mooring line layout.

The dimensions and mass information of the turbine, including the tower and RNA, are presented in Table 2. The dimensions and material information of the mooring system are presented in Table 3. The dimensions and mass information of the floating body are summarized in Figure 2 and Table 4. The mass information of the FOWT system, including the turbine and floating body, is presented in Table 5.

Table 2. Properties of the wind turbine.

Property	Unit	Value
Output power	MW	10
Rotor diameter	m	178.3
Tower length	m	98.1
Hub height above mean waterline	m	119
Blade mass	ton	41.69
Hub mass	ton	105.52
Nacelle mass	ton	446.03
Tower mass	ton	654.70
Total mass	ton	1330

Table 3. Properties of mooring system.

Property	Unit	Value
Number of mooring lines	pcs	3
The angle between adjacent lines	deg	120
Chain diameter	mm	147
Chain grade		R5
Chain weight	ton	474
Initial tension	N	2.010 × 106
Minimum breaking load	N	2.229 × 107
Water depth	m	150
Fairlead position height above mean waterline	m	13.08
Horizontal dist. from FCS to touchdown point	m	316.45
Horizontal dist. from FCS to anchor point	m	800
Unstretched mooring length	m	850

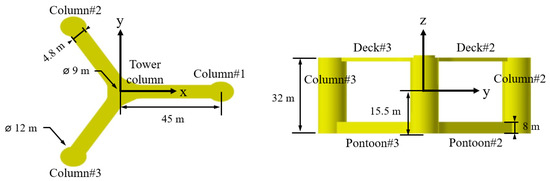
Figure 2. Sketches of floating body with principal dimensions.

Table 4. Properties of floating body.

Property	Unit	Value
Column span	m	45
Tower column diameter	m	9
Tower column height	m	33
Outer column diameter	m	12
Outer column height	m	32
Pontoon width	m	8
Pontoon height	m	4.8
Deck width	m	4
Deck height	m	1.6
Hull steel weight	ton	3400
Ballast water weight	ton	5185
Outfitting weight	ton	250
Fairlead chain stopper weight	ton	89
Draft	m	15.5

Table 5. Mass properties of the FOWT system without mooring lines.

Property	Unit	Target
Mass	ton	10,254
IXX wrt CoM	ton-mm2	1.954 × 1013
IYY wrt CoM	ton-mm2	1.948 × 1013
IZZ wrt CoM	ton-mm2	1.273 × 1013
CoM from mean waterline	m	(−0.94, 0, 4.19)

3. Technical Backgrounds for a DLP-Based Approach

3.1. Workflow of Direct Strength Analysis

The DNV [39] recommends using hull girder vertical bending moment/shear force and acceleration as DLPs for ships and offshore structures. The main loads acting on the floating body of the FOWT should be acceleration, just as on a ship. In addition, the thrust acting on the nacelle will be transmitted to the floating body through the tower, which will significantly affect the motion response. However, since semi-submersible floating bodies are not as long as ships, hull girder vertical bending moments are less likely to develop significantly, while hydrodynamic side shell pressure is expected to have a significant effect on the pontoon and column structures. The distribution of the wave-induced side shell pressure needs to be formalized using CFDs or experiments, and little research on it has been conducted to date. Therefore, in this study, the nacelle thrust acting on the superstructure and the acceleration acting on the entire FOWT system are selected as DLPs. The hydrodynamic side shell pressure should be considered in future studies.

As mentioned above, a combination of DLPs is required for the structural strength assessment of FOWT floating bodies. The magnitude of a DLP should be determined by considering the return period of the load, i.e., the load corresponding to the return period is the largest load that can occur during the design life of the FOWT.

In this study, the thrust released by the Technical University of Denmark is considered as the 50-year return period equivalent thrust [38]. To obtain the acceleration load, firstly the acceleration response (acceleration RAO) for a series of unit wave amplitudes and wave frequencies was derived through frequency response hydrodynamic analysis. Secondly, it was assumed that the short-term sea states indicated in the wave scatter diagram (WSD) of the Ulsan offshore area can be represented by the JONSWAP spectrum. Thirdly, the acceleration spectra and 0th order spectral moments were derived using this wave spectra and acceleration RAOs. The wave spreading function was used to correct the 0th moments of the acceleration spectra. Fourthly, since the corrected 0th order spectral moment is a parameter of the Weibull distribution, the long-term acceleration corresponding to a return period was derived.

After deriving the long-term accelerations corresponding to the return period, the load combinations for each component of the thrust and acceleration were generated. Based on the load combination cases, structural analyses were performed to check the structural integrity. The process is shown in Figure 3.

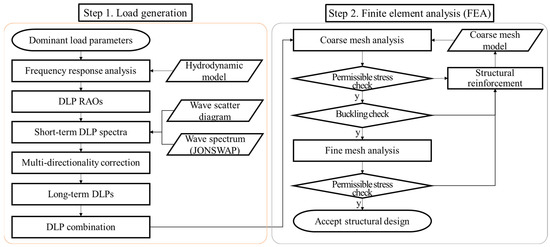
Figure 3. Flowchart for direct strength analysis.

3.2. Long-Term Load Assessment

A frequency response analysis should be performed to obtain the load response amplitude operator (load RAO) for a unit wave amplitude. The load RAO is combined with the short-term sea state defined in the WSD and converted to a load spectrum. Each short-term sea state is represented by a JONSWAP wave spectrum (see Equation (1)) known to derive more conservative long-term loads.

$$S_J\left(\omega \right)=\frac{5}{16}\frac{H_S^2{\omega }_P^4}{\omega }\exp \left[-\frac{5}{4}{\left(\frac{{\omega }_p}{\omega }\right)}^4\right]{\gamma }^a\left(1-0.287\ln \gamma \right)$$

(1)

$$a=\exp \left[-\frac{{\left(\omega -{\omega }_p\right)}^2}{2{\sigma }^2{\omega }_p^2}\right]$$

(2)

$$\sigma =\{\begin{array}{c}0.07 when \omega \le {\omega }_p\\ 0.09 when \omega >{\omega }_p\end{array}$$

(3)

$${\omega }_p=\frac{2\pi }{T_p}$$

(4)

$$\gamma =\exp \left(5.75-1.15\frac{T_p}{\sqrt{H_s}}\right)$$

(5)

$$S_R\left(\omega \right)={\left|{\overline{H}}_R\left(\omega \right)\right|}^2{S}_J\left(\omega \right)$$

(6)

In Equation (1), $H_s$ is the significant wave height, ${\omega }_p$ is the peak frequency, $T_p$ is the peak period, and $\gamma$ is the peak shape factor [40]. The coefficients used in the JONSWAP spectrum $S_J\left(\omega \right)$ are presented in Equations (2)–(5), respectively. From the load RAO ${\overline{H}}_R$ squared and the wave spectrum, the load spectrum $S_R\left(\omega \right)$ can be obtained (see Equation (6)).

$$f\left(\varphi \right)=K{\mathit{cos}}^n\left(\theta \right)$$

(7)

$${{\displaystyle \int }}_{\theta -0.5\pi }^{\theta +0.5\pi }f\left(\varphi \right)d\varphi =1.0$$

(8)

$$m_0={{\displaystyle \int }}_{\theta -0.5\pi }^{\theta +0.5\pi }f\left(\varphi \right)d\varphi {{\displaystyle \int }}_0^{\infty }{S}_R\left(\omega \right)d\omega$$

(9)

Wind-driven waves in reality are usually multi-directional and short-crested. Because the wave spectrum assumes that waves are unidirectional and long-crested, the 0th order spectral moment can be modified using the wave spreading function $f\left(\varphi \right)$ as shown in Equation (7). In Equation (7), $n$ is the spreading exponent, $\varphi$ is the wave incident direction of interest, and $\theta$ is the incident angle of a multi-directional wave. Using Equation (8), the coefficient $K$ in Equation (7) can be obtained. The modified 0th order moment is calculated using Equation (9).

$$p\left(x\ge x_0\right)=\exp \left(-\frac{x_0^2}{2m_0}\right)$$

(10)

$$p\left(x_0\right)=\frac{T_Z}{T_{RP}}$$

(11)

Assuming the long-term load distribution follows a Weibull probability density function, the probability that the load $x$ exceeds a specific load $x_0$ is given by Equation (10). The ratio of average zero-crossing period $T_Z$ to return period $T_{RP}$ is the probability that exceeds the return period [41] (see Equation (11)).

4. Long-Term Loads

4.1. Nacelle Thrust

A maximum thrust of 2080 kN was assumed as the 50-year return period thrust, based on a report [38] for the DTU 10 MW turbine. This maximum thrust is not driven by the extreme wind speed of the 50-year return period, but by the wind speed of 50 m/s. The 10 min mean extreme wind speed at the hub height in the Ulsan offshore area corresponding to the 50-year return period was 42.4 m/s, so a more conservative thrust was applied.

4.2. Acceleration

4.2.1. Acceleration RAO

Frequency response hydrodynamic analysis was performed to obtain the acceleration RAOs using a commercial potential flow code Ansys/Aqwa [18]. The coordinate system of the model with wave incident directions is shown in Figure 4a. The hydrodynamic model was composed of 21,055 diffraction elements. Even though the diffraction elements were used only for the wet part below the draft, the mass properties of the entire FOWT system were assigned to the hydrodynamic model. The frequency response analysis used six incident wave angles, ranging from 150 degrees to 210 degrees with even increment. A total of 50 frequencies were ranged between 0.1 and 3.5 rad/s with uniform spacing. The diffraction element-based displacement was compared with the original mass. It was proven from a negligible difference that the element size was acceptable enough to reproduce the original mass of the total FOWT (see Table 6).

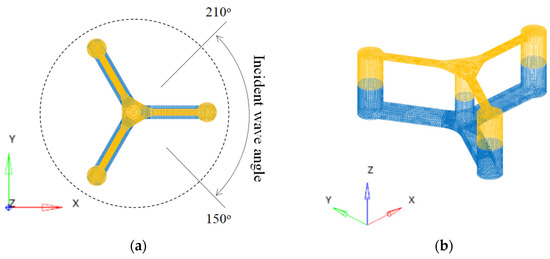
Figure 4. Hydrodynamic model: (a) Top view; (b) Isometric view.

Table 6. Comparison of displacements.

Item	Value
Original mass (ton)	10,727.96
Element-based displacement (ton)	10,717.20
Error (%)	−0.10

The motion RAOs and acceleration RAOs of heave and pitch directions developed significantly under the wave incident angle of 180 degrees. However, the roll motion RAO and roll acceleration RAO were barely developed under the same wave incident angle, as depicted in Figure 5.

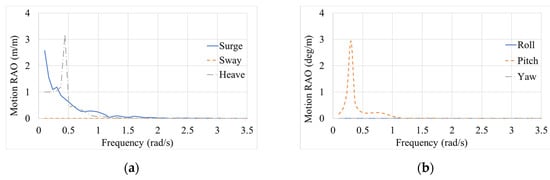
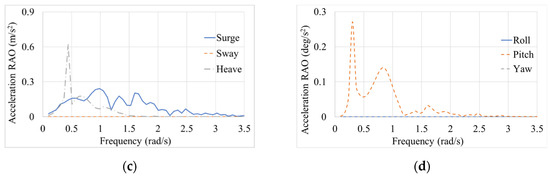
Figure 5. Response amplitude operators for a heading angle of 180 degrees: (a) Translational motion RAOs; (b) Rotational motion RAOs; (c) Translational acceleration RAOs; (d) Rotational acceleration RAOs.

4.2.2. Long-Term Prediction of Acceleration

Since it is assumed that the FOWT will be installed off the coast of Ulsan, the WSD corresponding to this area was used. This WSD, shown in Table 7, is based on 10 years of data from the Wangdolcho meteorological observation buoy, which is near Ulsan offshore.

Table 7. Wave scatter diagram.

		Tp (s)																					Prob. (%)
		0.5	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5	9.5	10.5	11.5	12.5	13.5	14.5	15.5	16.5	17.5	18.5	19.5	Sum
Hs (m)	0.5	0	7	1923	4811	5136	3357	1838	702	214	107	37	8	8	3	7	1	0	0	1	1	18161	22.76
	1	0	0	261	3844	6040	6328	6408	3074	1139	469	171	33	14	20	6	4	5	4	2	0	27822	34.87
	1.5	0	0	0	232	1513	2830	4977	4271	1439	621	265	48	7	7	4	3	4	3	5	0	16229	20.34
	2	0	0	0	2	105	704	2014	3536	1812	565	218	37	15	3	2	1	0	1	0	0	9015	11.30
	2.5	0	0	0	0	3	69	474	1378	1589	725	315	63	26	2	2	0	1	0	0	0	4647	5.82
	3	0	0	0	0	0	5	112	418	732	586	245	109	43	0	1	0	1	0	0	0	2252	2.82
	3.5	0	0	0	0	0	0	22	113	229	271	161	67	40	8	1	0	0	0	0	0	912	1.14
	4	0	0	0	0	0	0	2	42	105	123	84	30	35	7	0	0	0	0	0	0	428	0.54
	4.5	0	0	0	0	0	0	0	7	47	59	33	12	25	1	0	0	0	0	0	0	184	0.23
	5	0	0	0	0	0	0	0	1	19	26	27	6	4	0	0	0	0	0	0	0	83	0.10
	5.5	0	0	0	0	0	0	0	0	4	6	8	7	1	1	0	0	0	0	0	0	27	0.03
	6	0	0	0	0	0	0	0	0	0	0	6	3	0	0	0	0	0	0	0	0	9	0.01
	6.5	0	0	0	0	0	0	0	0	0	0	0	6	3	0	0	0	0	0	0	0	9	0.01
	7	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0.00
	Sum	0	7	2184	8889	12,797	13,293	15,847	13,542	7329	3558	1570	429	221	52	23	9	11	8	8	1	79,778	100.00
Prob. (%)		0.00	0.01	2.74	11.14	16.04	16.66	19.86	16.97	9.19	4.46	1.97	0.54	0.28	0.07	0.03	0.01	0.01	0.01	0.01	0.00	100.00

The long-term accelerations corresponding to 4 return periods of 1, 10, 50, and 100 years were calculated using Equations (1)-(11), with the assumption that 6 wave incident angles have the same probability of occurrence. The wave spreading exponent $n$ in Equation (7) was 8.0, which has been popularly used for the design of offshore structures. Even though the long-term accelerations are listed in Table 8, the acceleration components corresponding to the 50-year return period were only used for the direct strength assessment.

Table 8. Long-term accelerations.

${\mathit{T}}_{\mathit{R}\mathit{P}}$ (Year)	Surge (m/s2)	Sway (m/s2)	Heave (m/s2)	Roll (deg/s2)	Pitch (deg/s2)	Yaw (deg/s2)
1	0.871	0.409	2.340	0.395	0.790	0.674
10	0.973	0.460	2.661	0.460	0.920	0.755
50	1.063	0.496	2.840	0.505	1.009	0.817
100	1.080	0.505	2.947	0.522	1.045	0.835

4.3. DLP Combination

By combining the long-term acceleration component and nacelle thrust, 80 load combination cases were produced so that the resultant forces were maximized in the surge, sway, and heave directions, respectively (see Table 9, Table 10 and Table 11). The surge force-dominant cases consisted of surge and pitch acceleration components and nacelle thrust, as shown in Figure 6a. The sway force-dominant load cases were generated with similar combinations to the surge force-dominant cases.

Table 9. Surge force-dominant load cases.

Load Case	Acceleration					Thrust
	Surge (m/s2)	Sway (m/s2)	Heave (m/s2)	Roll (deg/s2)	Pitch (deg/s2)	Magnitude (kN)	Direction (Degree)
X1	+1.063	n/a	n/a	n/a	+1.009	2080	0
X2	+1.063	n/a	n/a	n/a	−1.009	2080	0
X3	−1.063	n/a	n/a	n/a	+1.009	2080	0
X4	−1.063	n/a	n/a	n/a	−1.009	2080	0
X5	+1.063	n/a	n/a	n/a	+1.009	2080	180
X6	+1.063	n/a	n/a	n/a	−1.009	2080	180
X7	−1.063	n/a	n/a	n/a	+1.009	2080	180
X8	−1.063	n/a	n/a	n/a	−1.009	2080	180

Table 10. Sway force-dominant load cases.

Load Case	Acceleration					Thrust
	Surge (m/s2)	Sway (m/s2)	Heave (m/s2)	Roll (deg/s2)	Pitch (deg/s2)	Magnitude (kN)	Direction (Degree)
Y1	n/a	+0.496	n/a	+0.505	n/a	2080	90
Y2	n/a	+0.496	n/a	−0.505	n/a	2080	90
Y3	n/a	−0.496	n/a	+0.505	n/a	2080	90
Y4	n/a	−0.496	n/a	−0.505	n/a	2080	90
Y5	n/a	+0.496	n/a	+0.505	n/a	2080	270
Y6	n/a	+0.496	n/a	−0.505	n/a	2080	270
Y7	n/a	−0.496	n/a	+0.505	n/a	2080	270
Y8	n/a	−0.496	n/a	−0.505	n/a	2080	270

Table 11. Heave force-dominant load cases.

Load Case	Acceleration					Thrust
	Surge (m/s2)	Sway (m/s2)	Heave (m/s2)	Roll (deg/s2)	Pitch (deg/s2)	Magnitude (kN)	Direction (degree)
Z1-1	n/a	n/a	+2.840	+0.505	+1.009	2080	0
Z1-2	n/a	n/a	+2.840	+0.505	+1.009	2080	45
Z1-3	n/a	n/a	+2.840	+0.505	+1.009	2080	90
Z1-4	n/a	n/a	+2.840	+0.505	+1.009	2080	135
Z1-5	n/a	n/a	+2.840	+0.505	+1.009	2080	180
Z1-6	n/a	n/a	+2.840	+0.505	+1.009	2080	225
Z1-7	n/a	n/a	+2.840	+0.505	+1.009	2080	270
Z1-8	n/a	n/a	+2.840	+0.505	+1.009	2080	315
Z2-1~Z2-8	n/a	n/a	+2.840	+0.505	−1.009	2080	8 directions
Z3-1~Z3-8	n/a	n/a	+2.840	−0.505	+1.009	2080	8 directions
Z4-1~Z4-8	n/a	n/a	+2.840	−0.505	−1.009	2080	8 directions
Z5-1~Z5-8	n/a	n/a	−2.840	+0.505	+1.009	2080	8 directions
Z6-1~Z6-8	n/a	n/a	−2.840	+0.505	−1.009	2080	8 directions
Z7-1~Z7-8	n/a	n/a	−2.840	−0.505	+1.009	2080	8 directions
Z8-1~Z8-8	n/a	n/a	−2.840	−0.505	−1.009	2080	8 directions

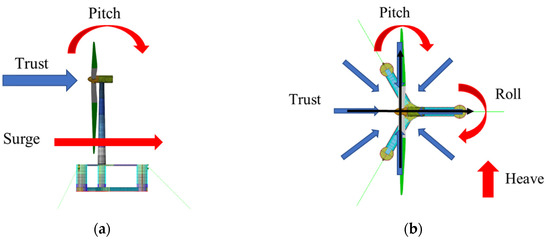
Figure 6. Load cases: (a) Surge force-dominant case; (b) Heave-force dominant case.

The heave force-dominant cases were generated using a slightly different principle than the surge-force dominant cases. In the surge-force dominant cases, the direction of the nacelle thrust could be matched to the surge direction to maximize the load in the surge direction. However, in the heave force-dominant cases, the direction of the nacelle thrust could not be matched with the heave direction, so the nacelle thrust directions were considered at every 45-degree interval. In other words, 8 nacelle thrust directions were considered for 1 heave force-dominant case, resulting in a total of 64 heave force-dominant cases (see Figure 6b).

5. Finite Element Analysis

5.1. Finite Element Model

5.1.1. Geometric Modeling

Internal members of the pontoon, deck, and column are shown in Figure 7. A single bulkhead and nine web frames were arranged in a pontoon. There were also four watertight bulkheads in an outer column to hold ballast water in the lower compartments. A deck included eight web frames without any bulkhead. Six web frames were in the tower column.

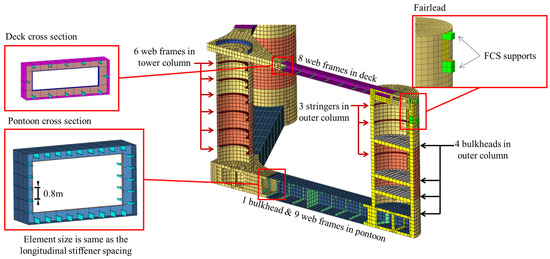
Figure 7. Structural components of the substructure.

A coarse mesh model included the floating body, tower, and RNA structures, but mooring lines were replaced with spring elements. Shell and beam elements with the element size same as the longitudinal stiffener spacing were used for the coarse mesh model. The number of elements used is shown in Table 12. The tower and RNA were modeled as shell elements only. Most of the floating body was modeled with shell elements, but the longitudinal stiffeners of the floating body were modeled with beam elements. At the fairlead positions, the supports of the FCS and stiffeners were modeled without FCS. Depending on the upwind directions, the RNA was rotated along the yaw angles.

Table 12. Finite element model properties of the substructure.

Item	Value
The number of shell elements	30,610
The number of beam elements	19,092

5.1.2. Loading and Boundary Conditions

Static and dynamic loads were required simultaneously to evaluate structural strength. Static loads included the self-weight of the FOWT and hydrostatic pressure acting on the side shells. Static loads were applied to all load cases presented in Table 9, Table 10 and Table 11. Dynamic loads include the acceleration components and nacelle thrusts shown in Table 9, Table 10 and Table 11. Finite element analysis (FEA), based on the implicit method, requires boundary conditions to adequately restrain the rigid body motions of six-degrees-of-freedom. In this study, spring elements with stiffness determined from the theoretical background were used instead of boundary conditions to avoid stress concentration at the nodes with boundary conditions.

A spring element with vertical stiffness was placed at the centre of the bottom plate of each column to constrain the heave motion under the static gravity-buoyancy loads and the dynamic heave acceleration load. This spring element is hereafter referred to as the heave spring element in this paper. To distribute the force applied to the heave spring element, the heave spring element was connected to all the nodes of each column bottom plate by a load coupling element. The stiffness of the heave spring, $k_h$, is determined by Equation (12). Where $\rho$, $g$, and $A$ are the seawater density, gravitational acceleration, and water plane area at the draft, respectively. The seawater density and gravitational acceleration applied were 1.025 ton/m³ and 9.81 m/s, respectively.

$$k_h=\rho gA$$

(12)

If the tensile force of the mooring line is implemented as a boundary condition on the FOWT, this boundary condition will cause a large stress concentration in the FCS support structures. It is also undesirable to represent the stiffness of the mooring line as a boundary condition because the mooring tension will only increase if the FOWT moves in the direction of the mooring line tensioning. In this study, a nonlinear spring was placed on each FCS support structure to solve these difficulties. Henceforth, this spring will be referred to as the mooring spring in this paper. Since the mooring spring has an initial tensile stiffness, an initial tensile force must remain even when the displacement is zero. Only when the mooring line is stretched, should the tensile force be increased.

However, the initial tensile force remains the same when the mooring line is slacked. For this reason, a nonlinear stiffness was assigned to the mooring spring, as shown in Figure 8 where the initial tension force of 2010 kN was theoretically obtained from a well-known elastic catenary equation. In addition, the tensile stiffness $k_m$ was assumed to be same as the initial tension per meter. The heave spring elements attached to the bottom plates of columns and the mooring spring elements connected to the FCS support structures are shown in Figure 9b.

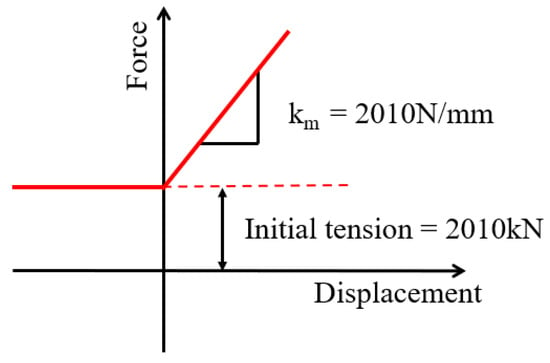
Figure 8. Nonlinear property of mooring springs.

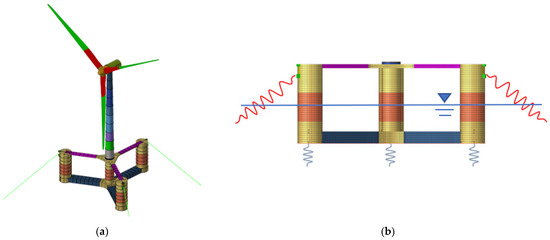
Figure 9. Coarse mesh finite element model: (a) Isometric view; (b) Side view with spring elements.

5.2. Permissible Stress

In this study, the permissible stresses given in DNV-OS-C102 [42] and DNV-RU-SHIP [43] are used. Based on the yield stress of 355 MPa for high-tensile steel AH36, the permissible stresses for the coarse and fine mesh models are shown in Table 13.

Table 13. Permissible stress.

Model	Permissible Stress (MPa)
Coarse mesh	355.0
Fine mesh (adjacent to weld)	532.5

5.3. Coarse Mesh Analysis Results

The structural analysis was performed using the commercial FEA code Abaqus/Standard [44]. In some load cases, the maximum von Mises stress exceeded the permissible stress of 355 MPa (see Figure 10). The maximum stresses occurred in the pontoon inner web frame, the column inner web frame, and the tower-floater body interface. The high stresses in the pontoon web frame occurred in most of the load cases; therefore, high stresses were induced by the static load (hydrostatic pressure) applied in all load cases. High stresses in the web frames inside the columns occurred in the surge force-dominant cases. The high stresses were caused by the seawater pressure and the forces transmitted from the pontoon connections. The surge force-dominant cases also caused high stresses at the tower-floater body interface. This is believed to be due to the tower’s overturning moment induced by the surge acceleration.

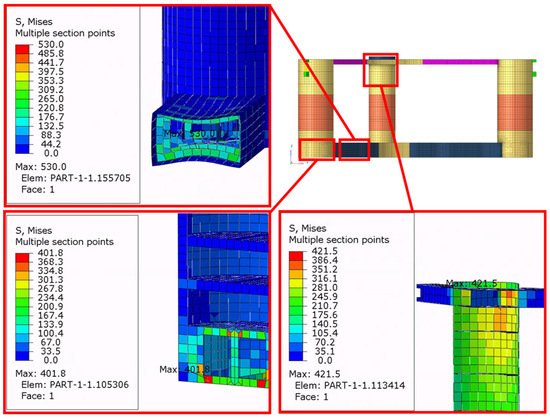
Figure 10. Structural parts with high stress.

5.4. Fine Mesh Analysis Results

For the three locations where high stresses occurred in the coarse mesh analysis, a fine mesh model with an element size of 50 mm × 50 mm was created (see Figure 11) [45]. The stiffeners that were modeled as beam elements were replaced with shell elements. The results of the fine mesh FEAs performed with the same loading conditions and boundary conditions are shown in Table 14. The stresses in the pontoon web frame did not exceed the allowable stresses, but the stresses in the column web frame and tower interface did exceed the criteria.

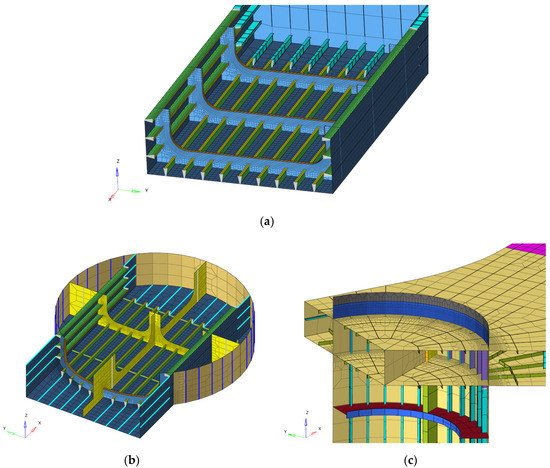
Figure 11. Fine mesh models: (a) Face plates of web frame in pontoon; (b) Web frame in outer column; (c) Tower interface.

Table 14. Refined mesh analysis results.

Location	Load Case	Maximum Stress (MPa)	Permissible Stress (MPa)	Result
Face plates of web frame in pontoon	Z1-5	441.8	532.5	Pass
Web frame in outer column	X3	889.5	532.5	Fail
Tower interface	X8	723.6	532.5	Fail

As mentioned above, there are few established techniques for evaluating the structural strength of the floating body of a FOWT. In this study, we verified the feasibility of applying DLP-based DSA to the FOWT floating body to detect structural weaknesses. Since the purpose of this study was sufficiently fulfilled, no further research on structural reinforcement was conducted, i.e., it is predicted that stresses that sufficiently meet the design criteria can be obtained by increasing the plate thicknesses and stiffener sizes.

6. Conclusions

In the design stage of the substructure of a FOWT using ILAs in the time domain, there exists a bottleneck in the structural integrity assessment. Very little software was available to do this, and some of the available software required too much time to practically verify structural integrity for all DLCs. The idea behind this study was to provide a practical solution to these problems.

An attempt was made to detect structural weaknesses and verify structural integrity by applying the DSA technique, which has been widely used in the hull structural design of ships and floating offshore oil/gas platforms, to the substructure of a 10 MW FOWT. The most essential parts of the DSA method are first, the selection of the DLPs, and second, the evaluation of structural integrity for the DSA cases with appropriate combinations of the selected DLPs. In this study, the acceleration generated by the entire FOWT system and the thrust acting on the nacelle were selected as the DLPs. In particular, the process and results for estimating the extreme values of the acceleration components by return periods are described in detail. The process of combining two DLPs to maximize the loads in the surge, sway, and heave directions is presented.

By applying the combined load cases to a coarse mesh finite element model with an element size of a representative longitudinal stiffener spacing and a fine mesh finite element model with an element size of 50 mm × 50 mm, it was possible to identify the causes of structural weaknesses and high stresses. The results show that the DSA can be very useful in the design of FOWT substructures as long as the DLPs are reasonably selected and combined.

The most important step in the ULS assessments is to verify structural stability against buckling. The evaluation of buckling stability should be carried out in future research. In addition, the hydrodynamic pressure is very likely to increase the stress in the substructure below mean water level. Future studies should be conducted to determine the hydrodynamic pressure profiles of the substructure of semi-submersible FOWTs using CFDs or basin tests.