Study on the Accessibility Impact of Anti-Rolling Tank on the Offshore Wind O&M Gangway
Abstract
1. Introduction
2. Mathematical Calculations
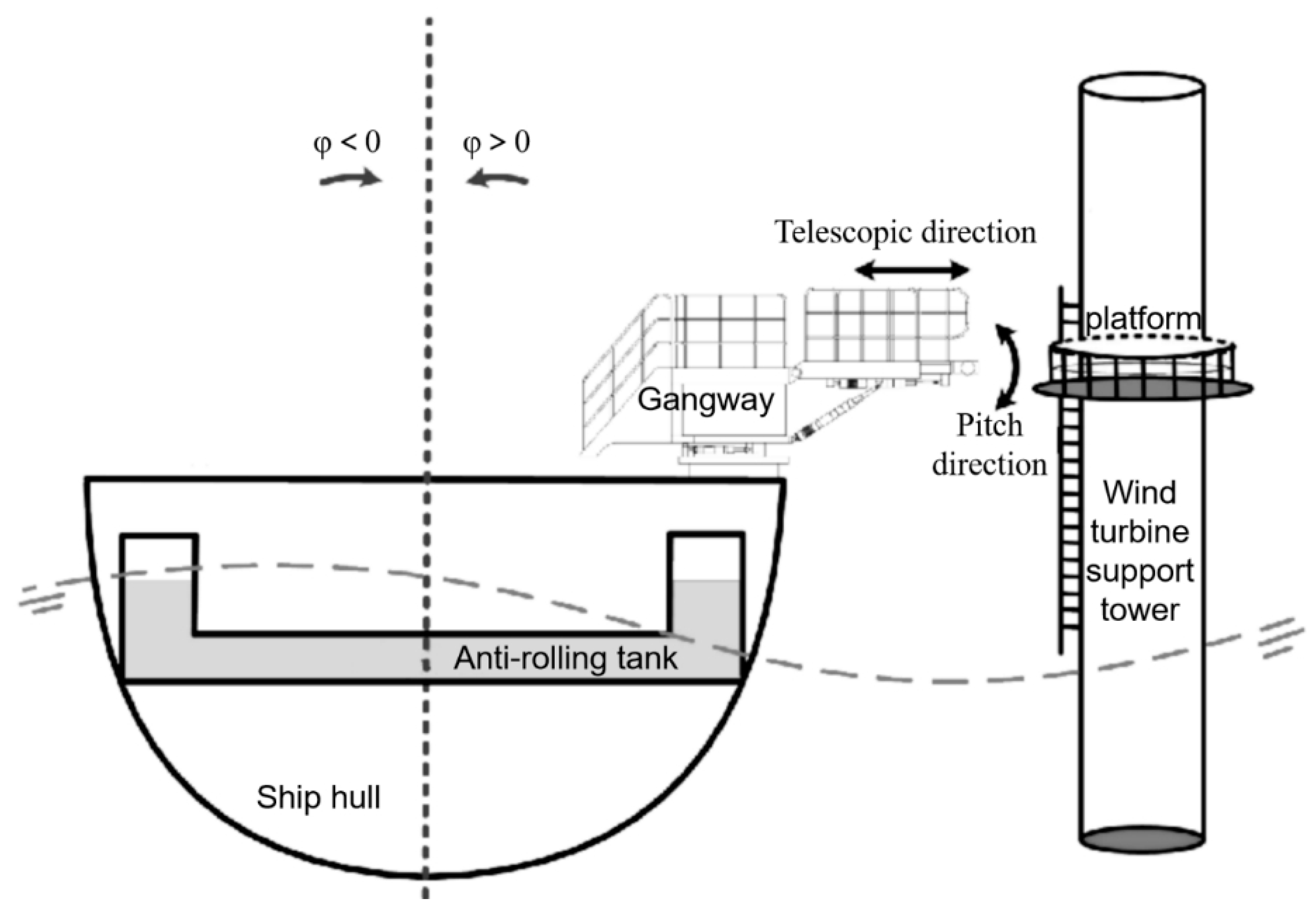
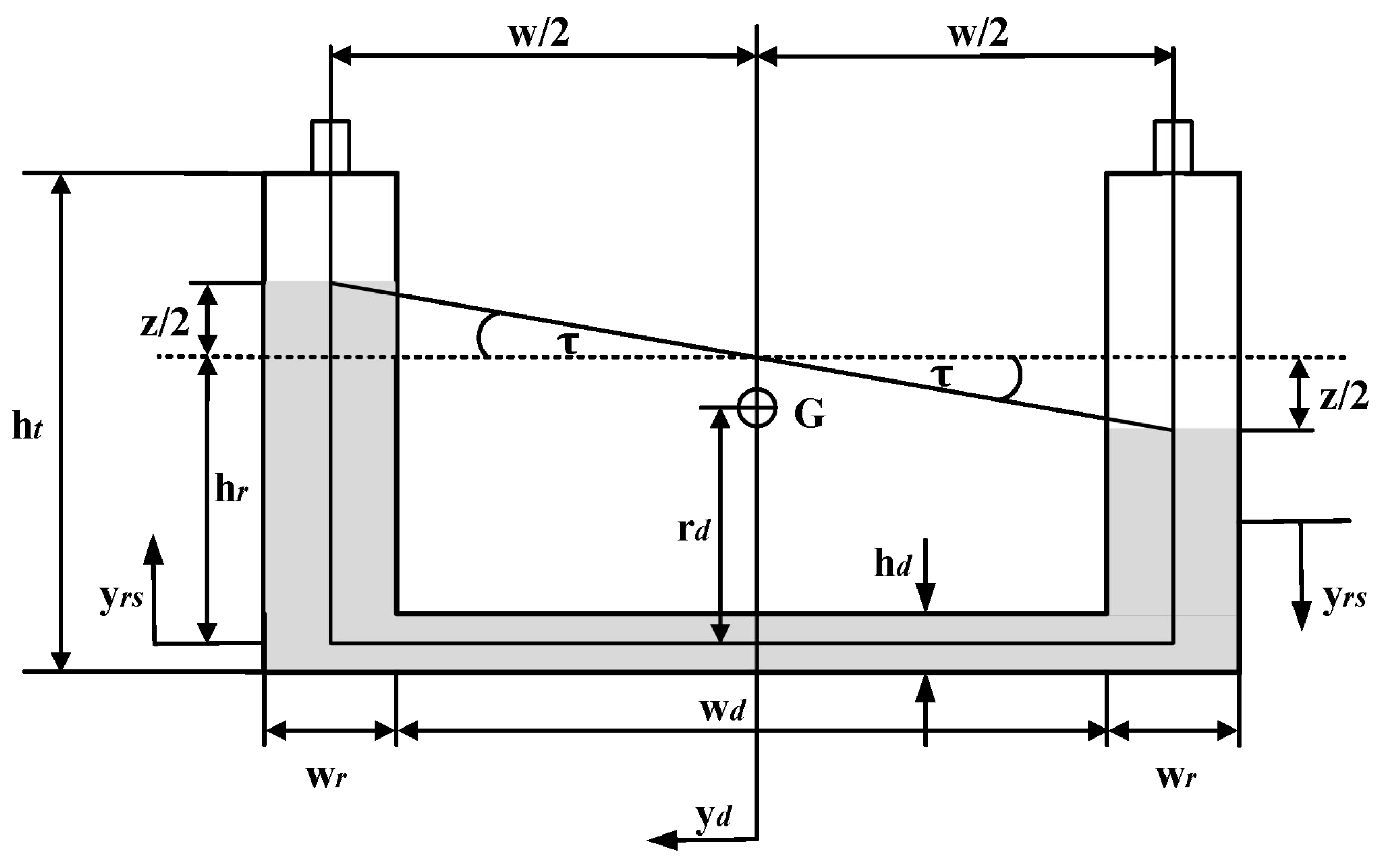
2.1. Ship Motion Model with Controllable Passive Anti-Rolling Tank
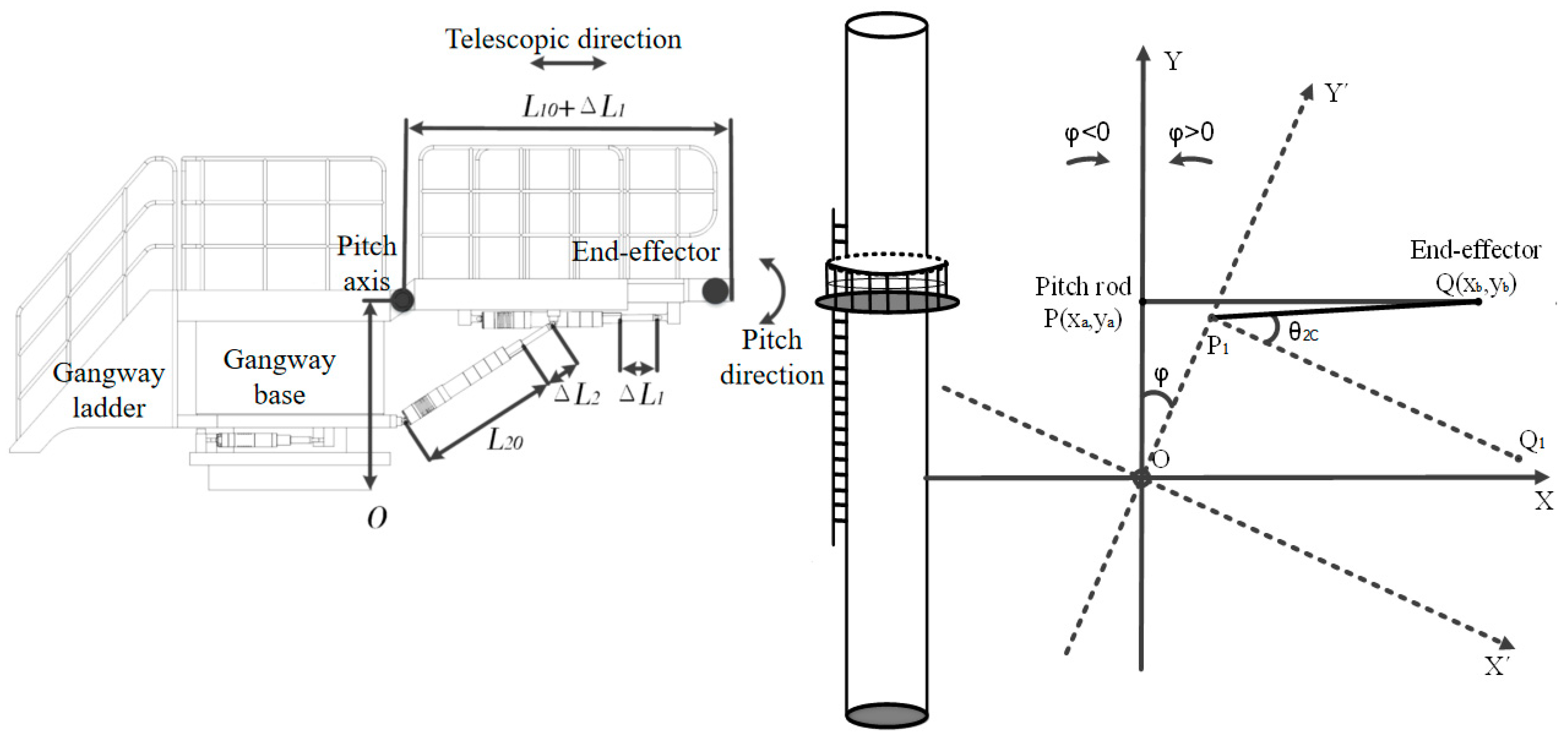
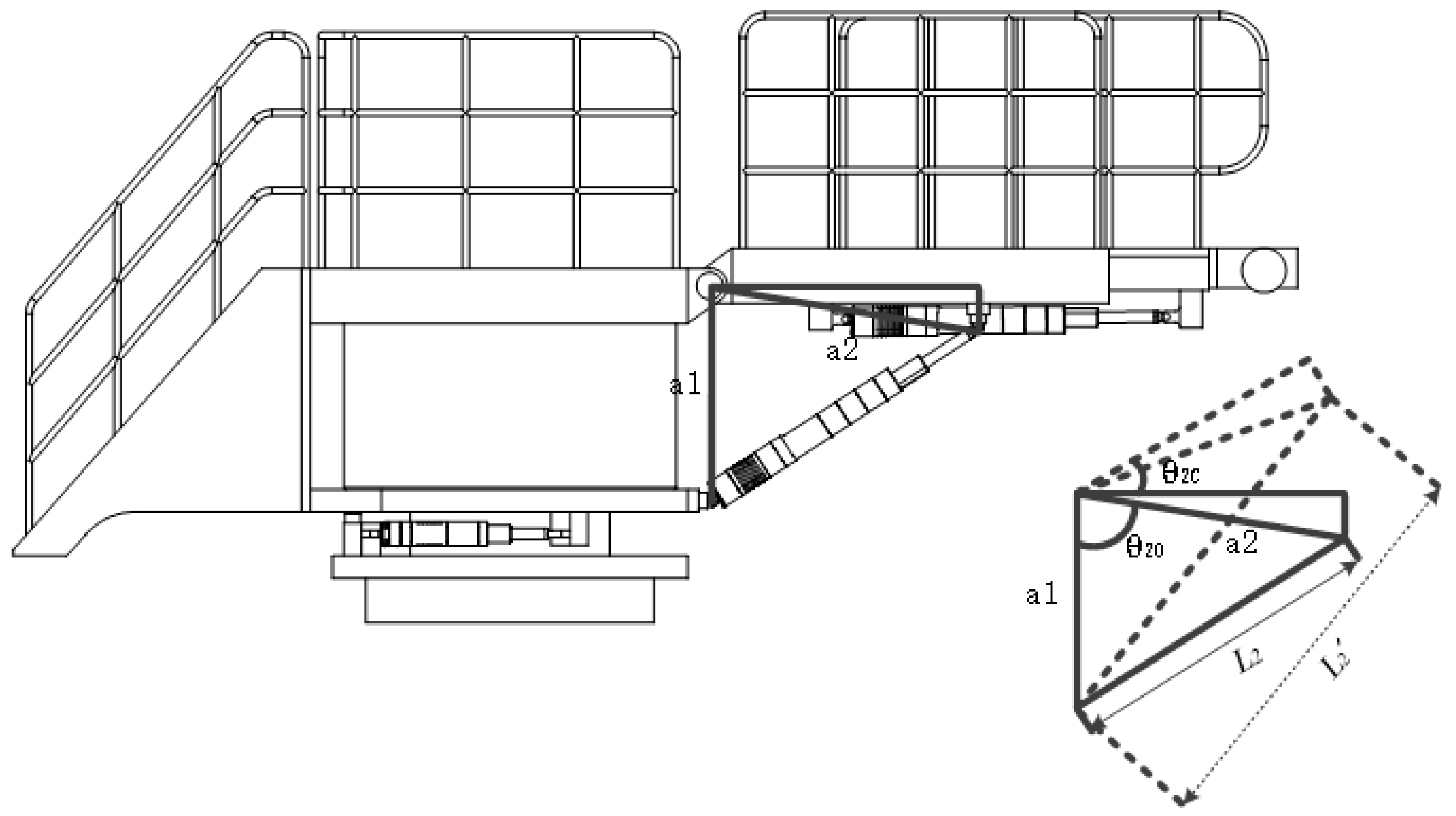
2.2. Inverse Kinematics of Gangway
2.3. Control of Air Valve
3. Simulation Analysis
3.1. Hydrodynamic Simulation
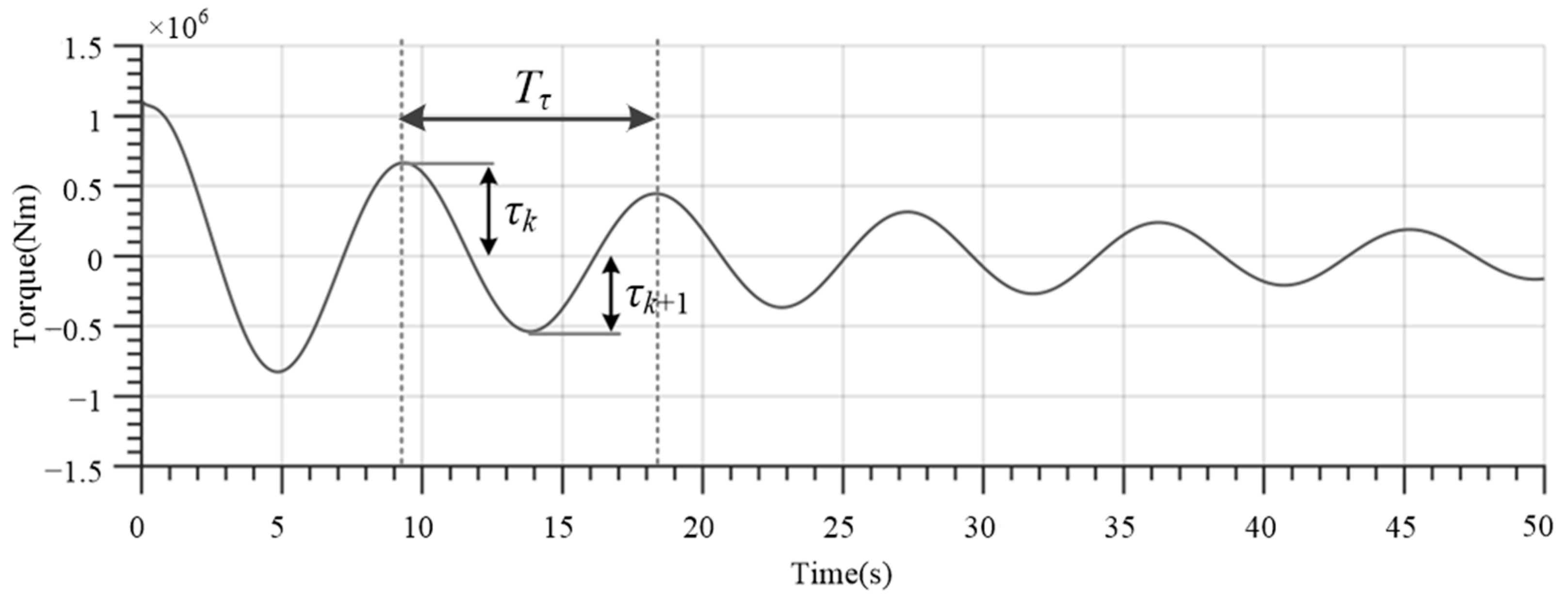
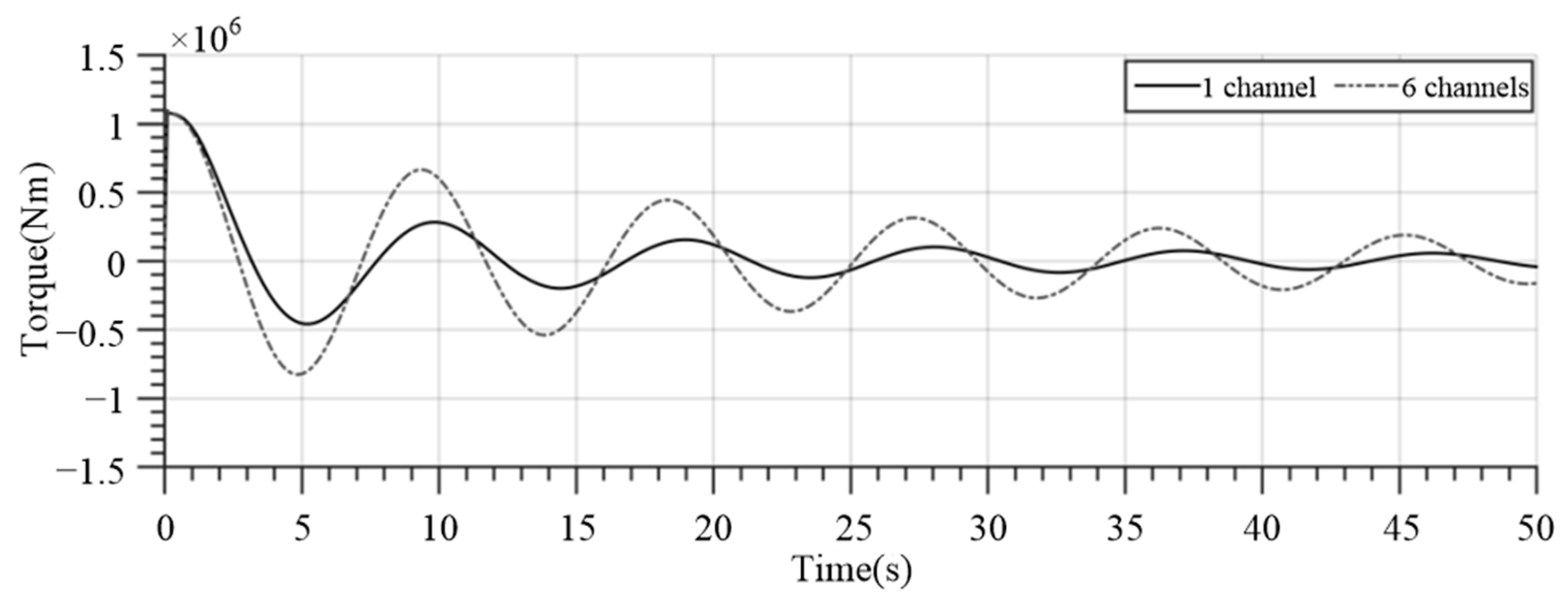
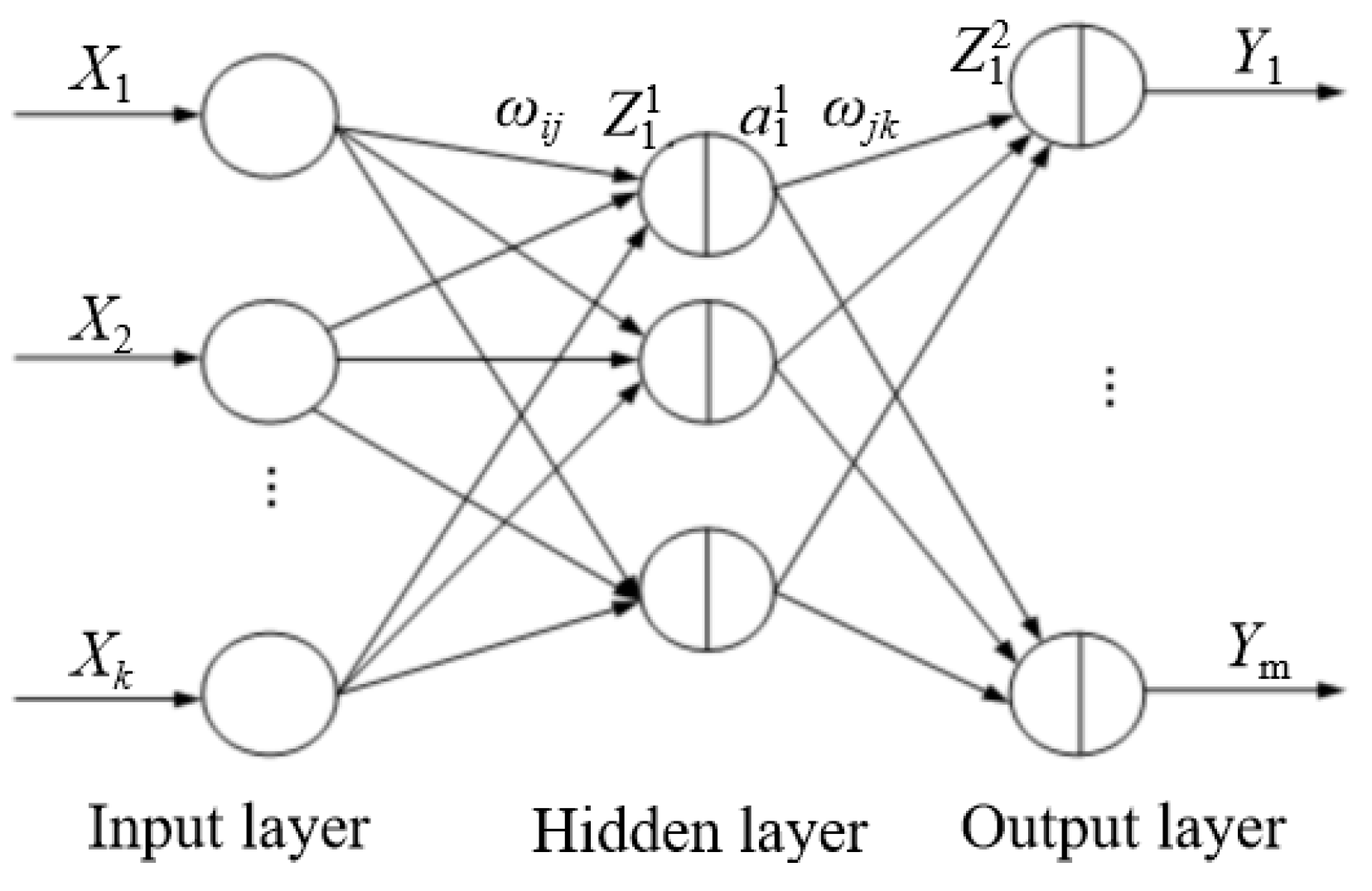
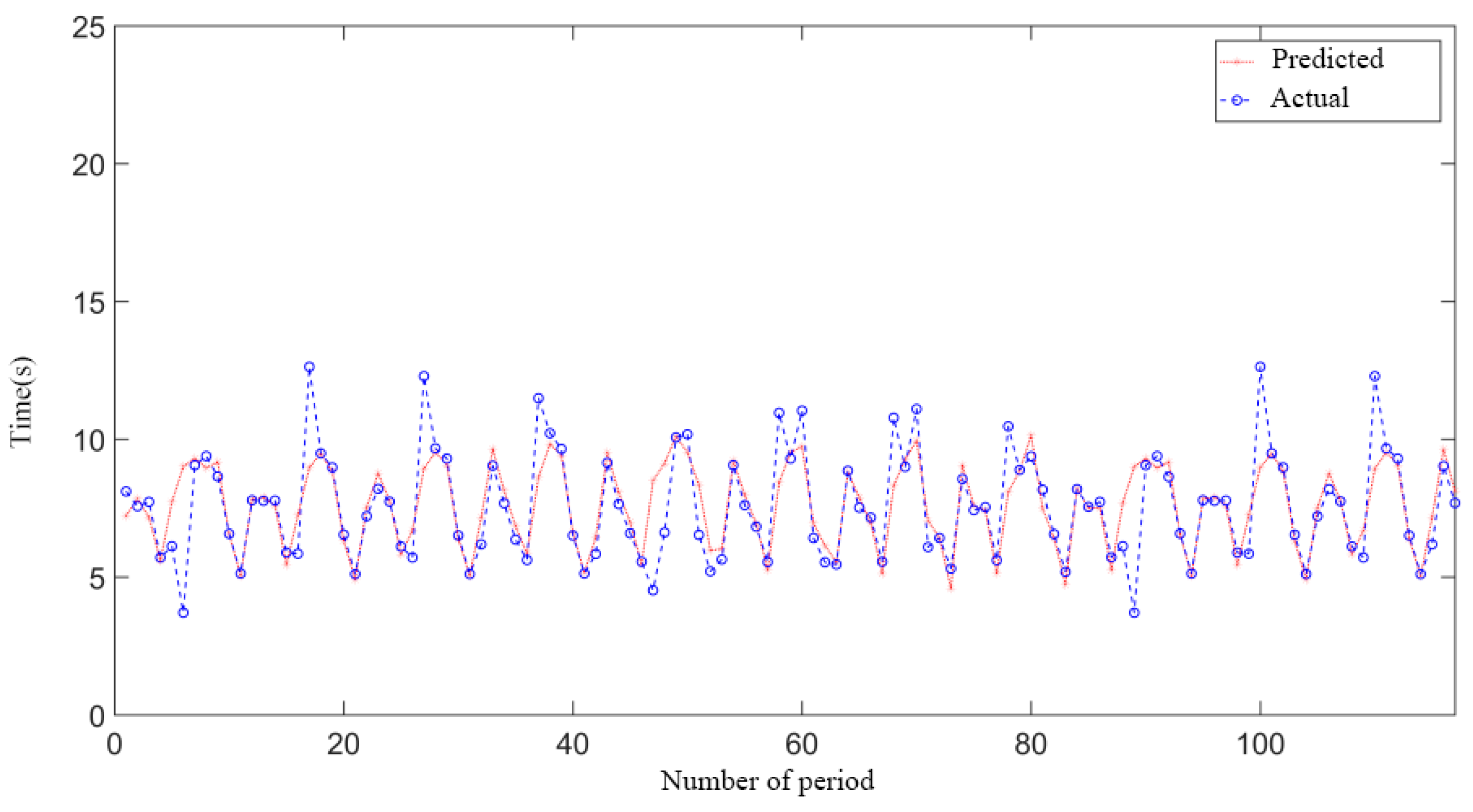
3.2. Roll Period Prediction Based on Wavelet Neural Network
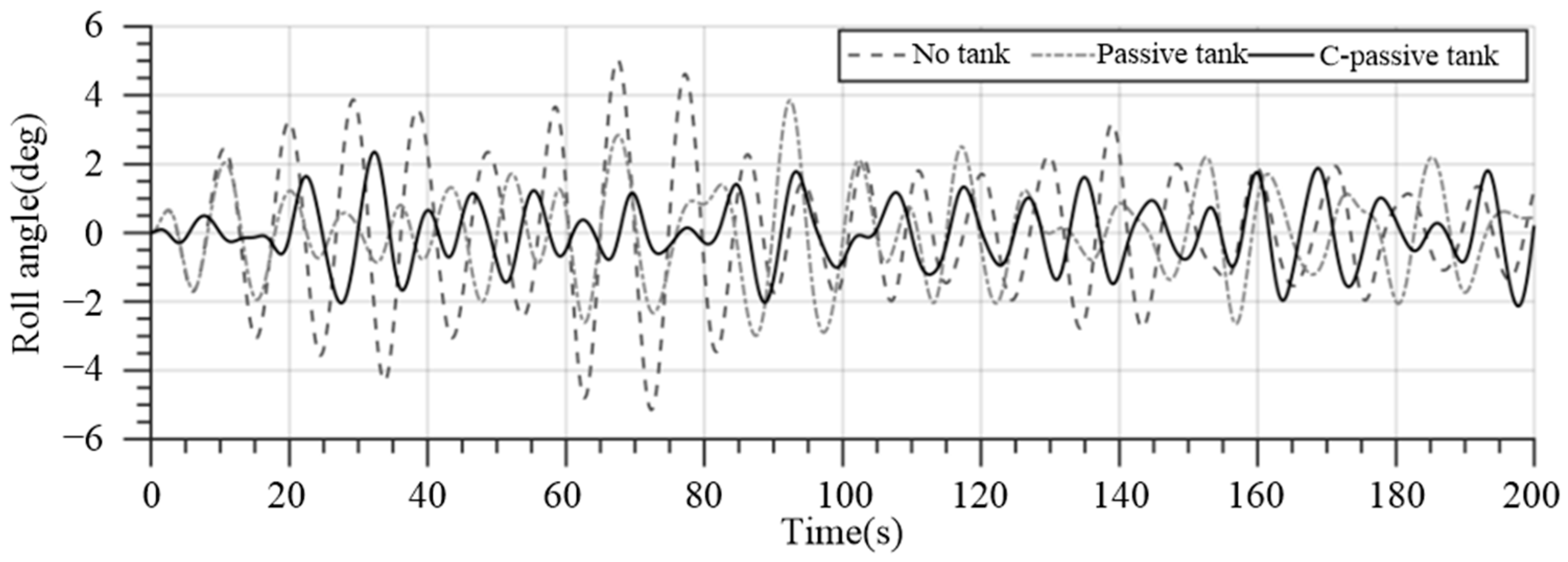
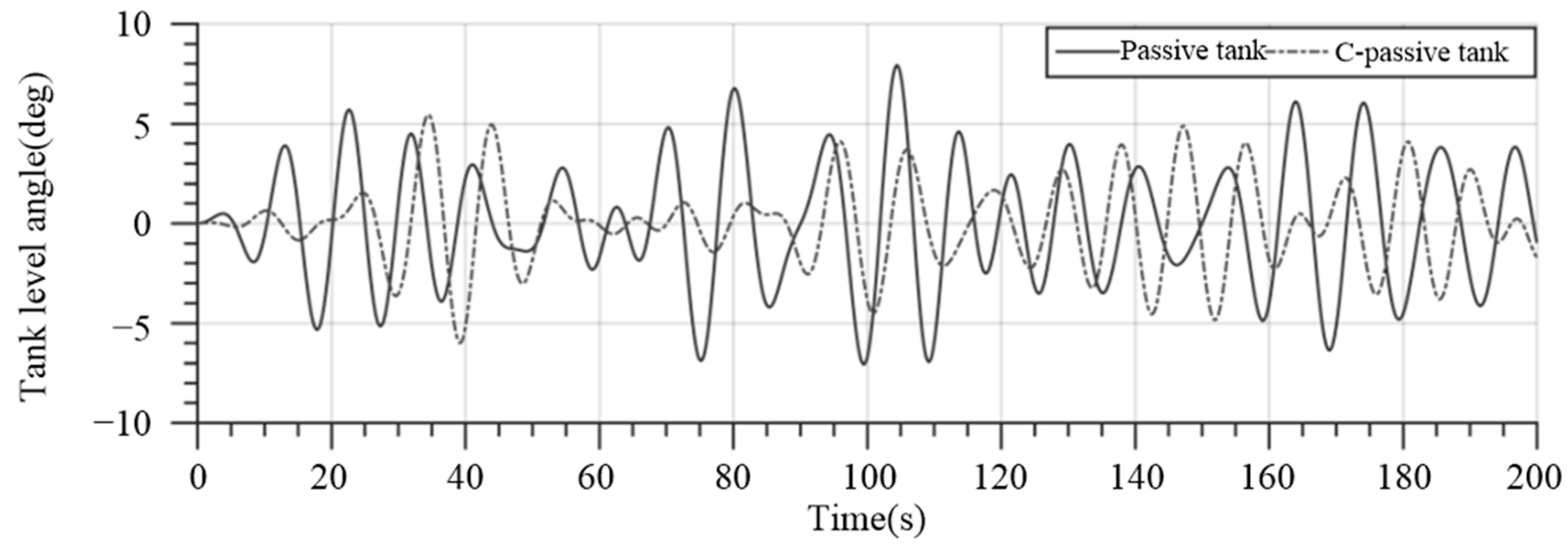
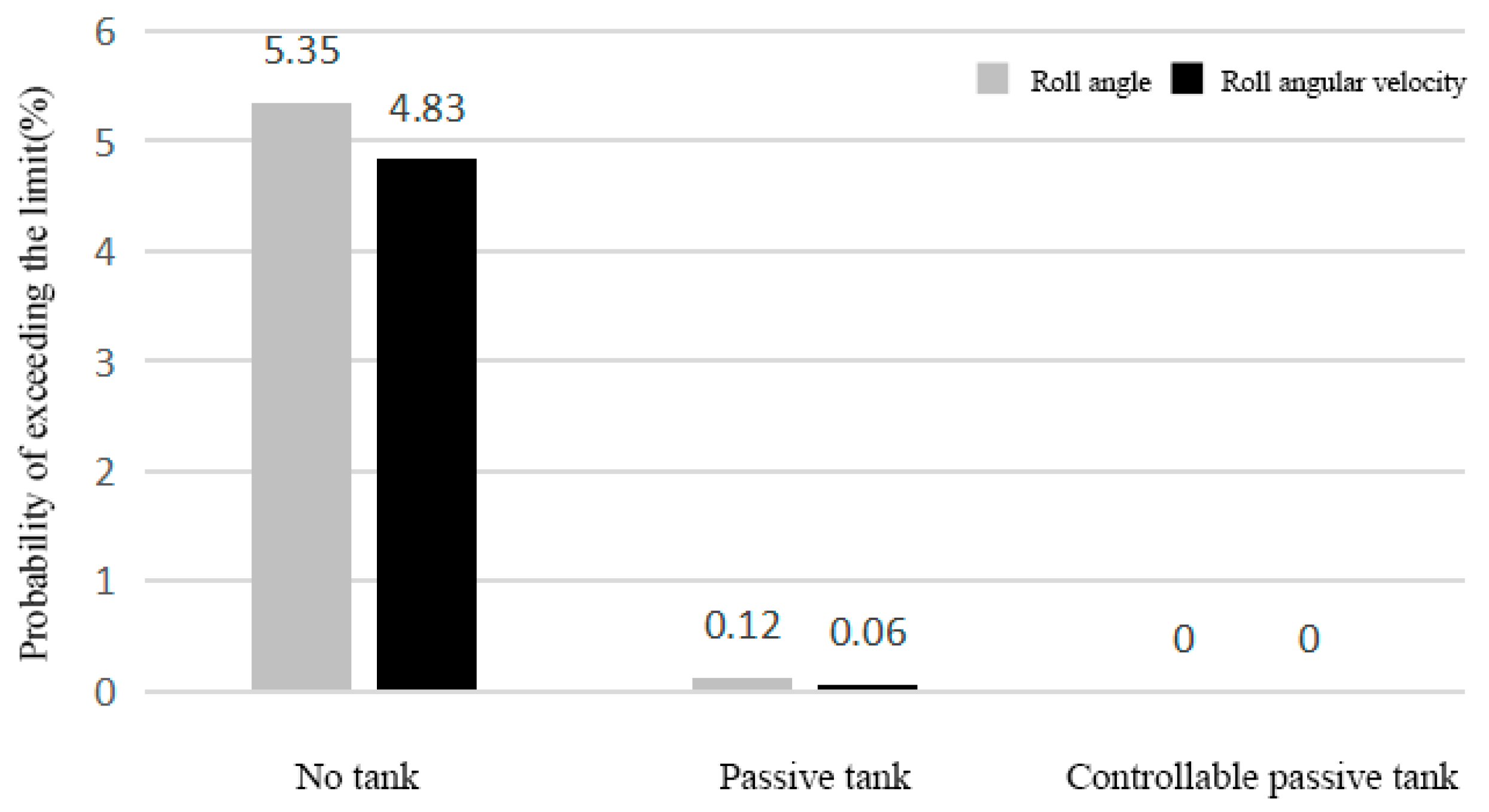
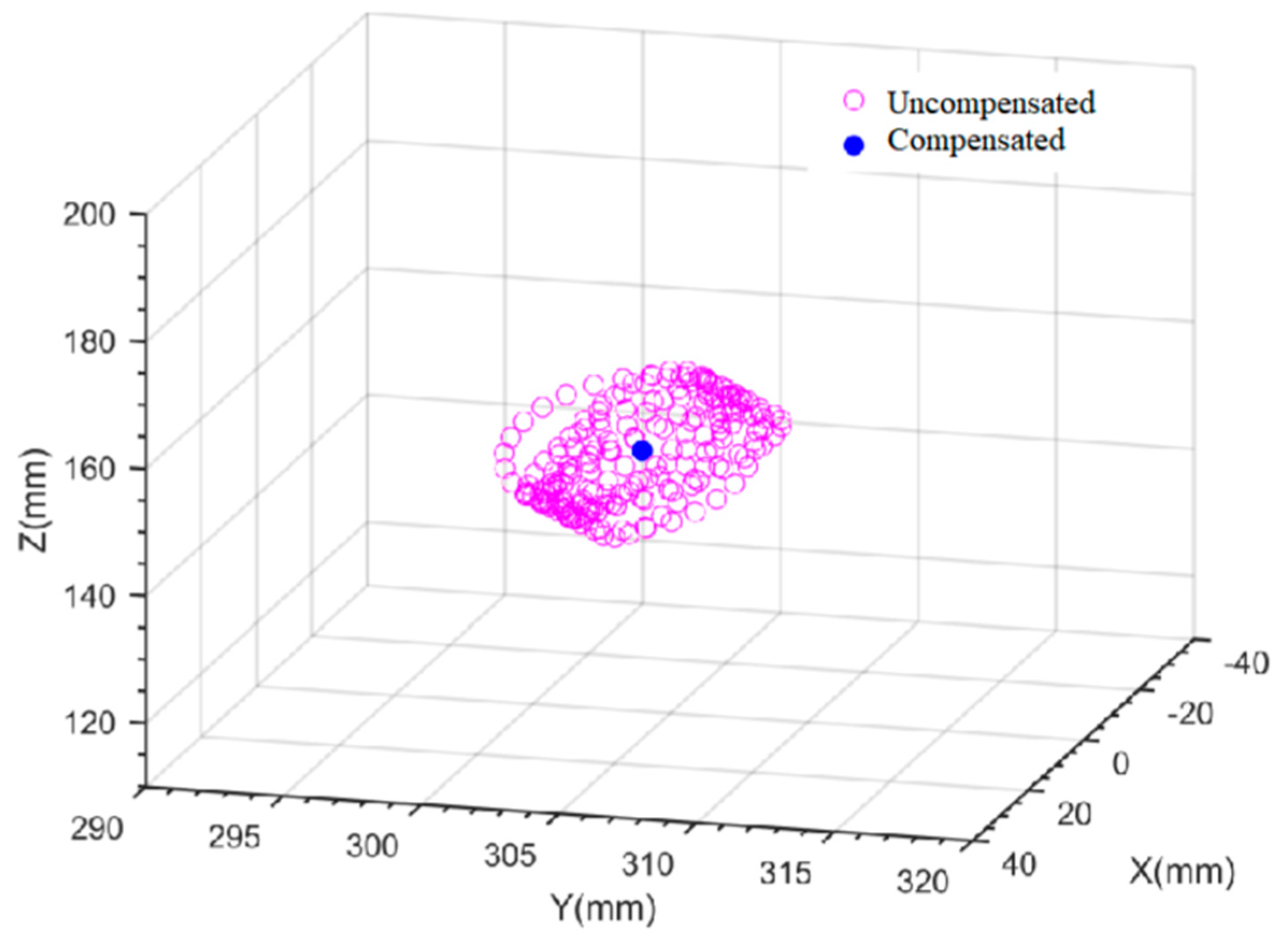
3.3. Impact of Anti-Rolling Tank on Gangway Accessibility
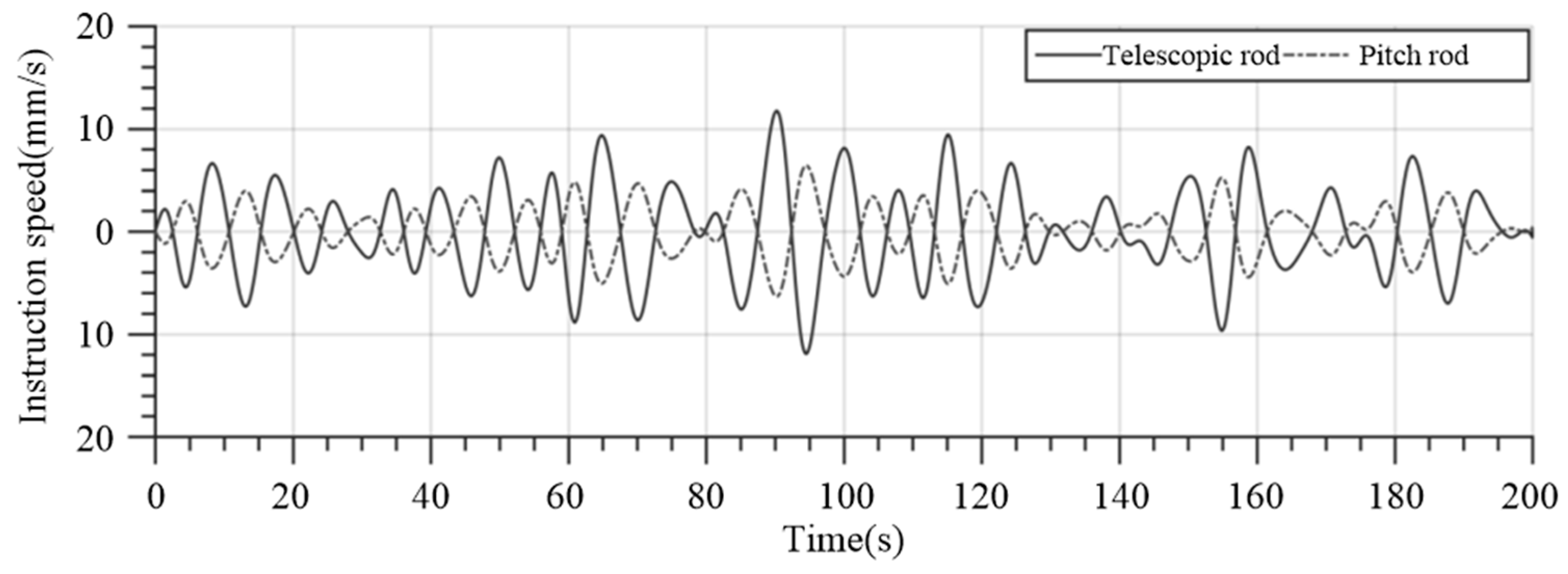
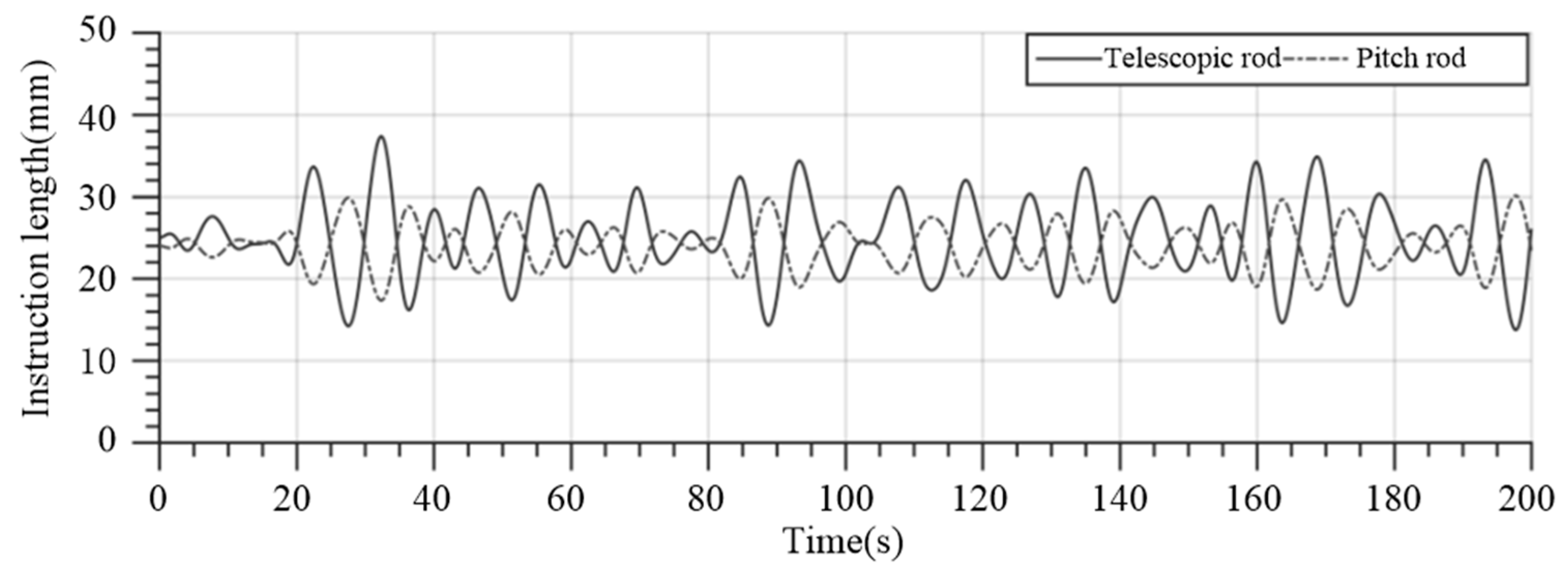
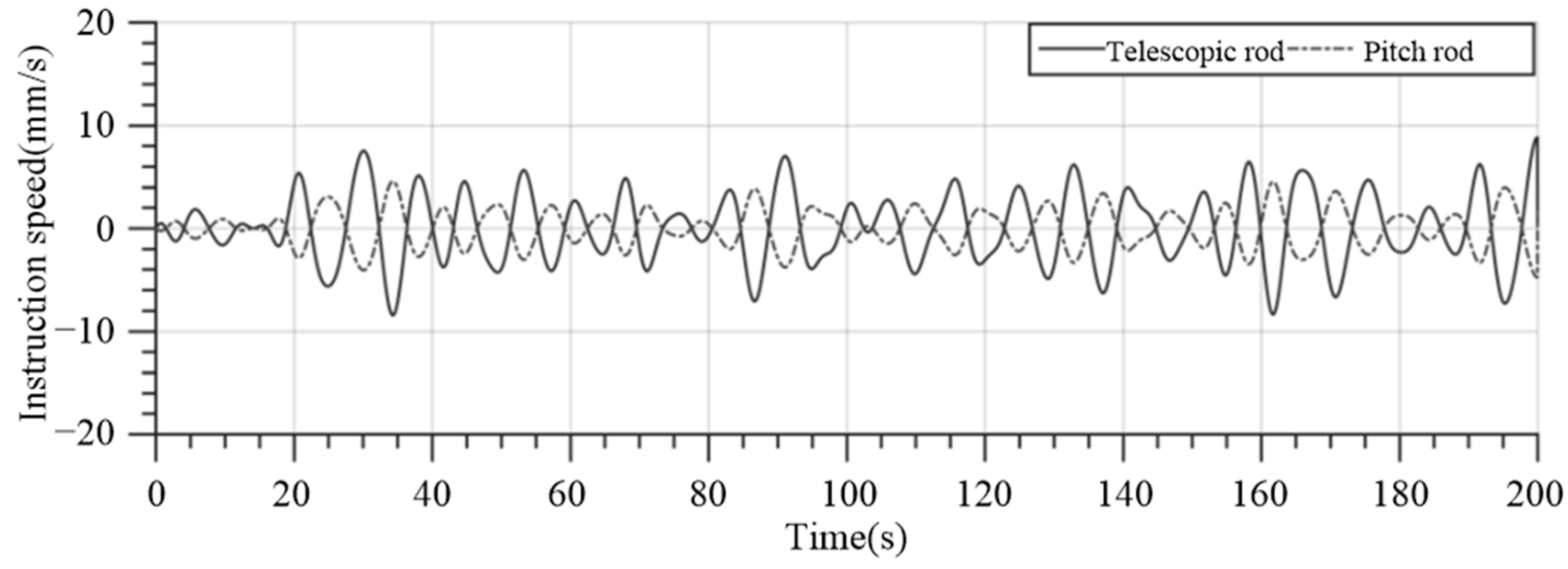
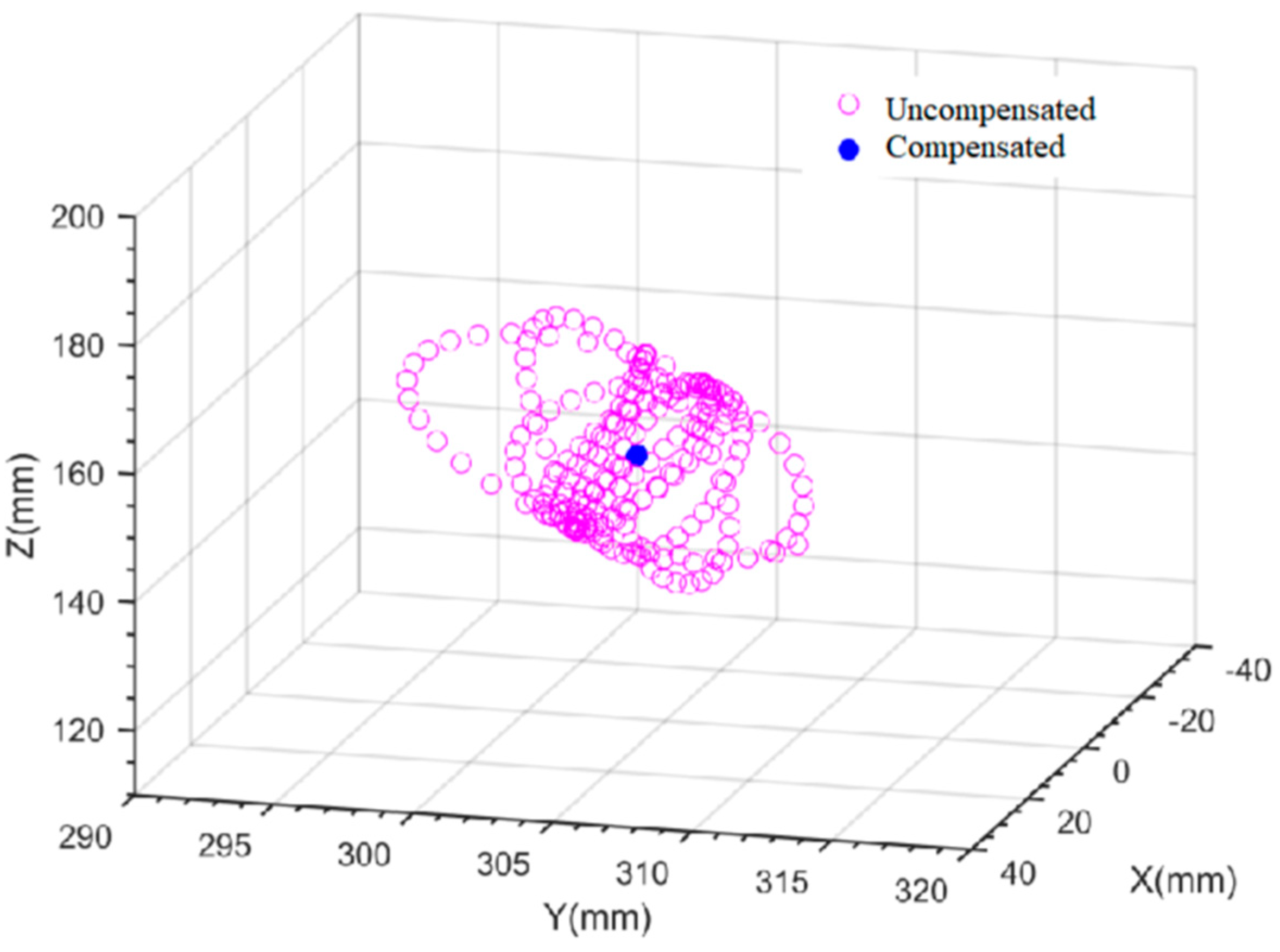
4. Hardware-in-the-Loop Simulation
4.1. Control Architecture
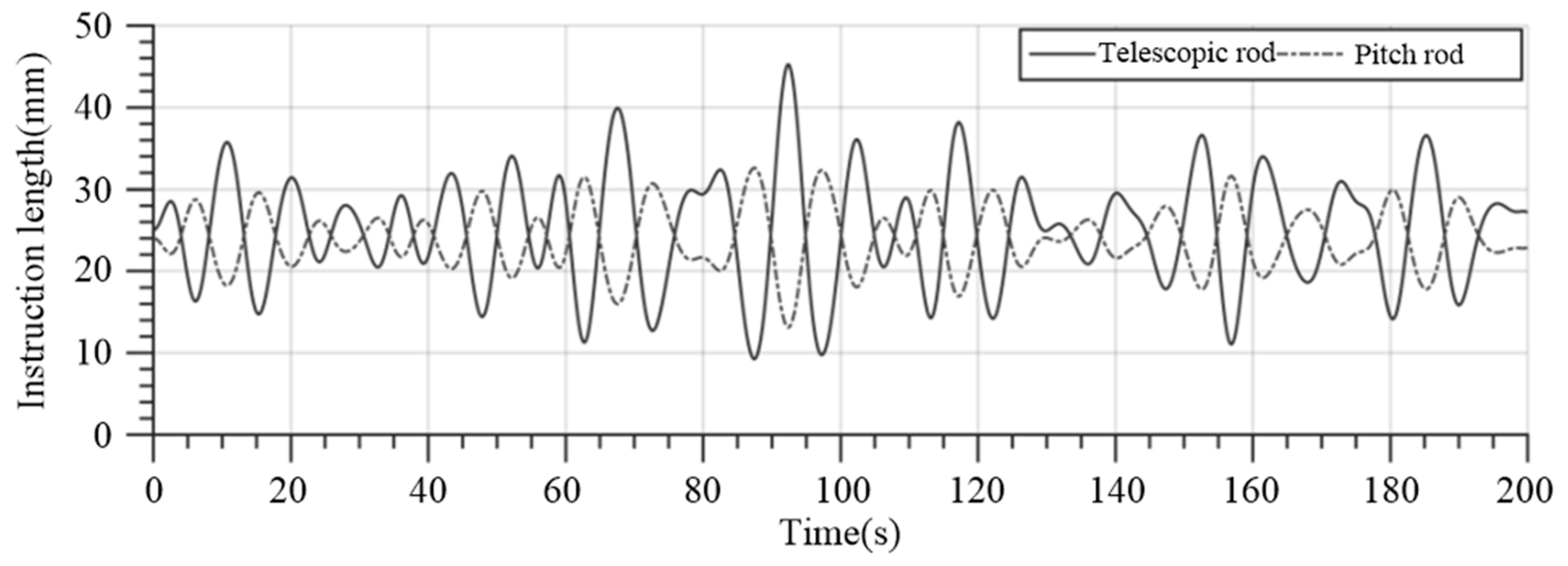
4.2. HIL Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Martin, J.; Atse, L. Technological Learning in the Transition to a Low-Carbon Energy System; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Matt, S.; Philipp, B.; Jake, N.; Aubryn, C.; Patrick, D. Impacts of turbine and plant upsizing on the levelized cost of energy for offshore wind. Appl. Energy 2021, 298, 117189. [Google Scholar]
- Perez, T. Ship Motion Control: Course Keeping and Roll Stabilisation Using Rudder and Fins; Springer: London, UK, 2005. [Google Scholar]
- Jin, H.; Yao, X. Ship Control Principle, 2nd ed.; Harbin Engineering University: Harbin, China, 2013. [Google Scholar]
- Zhang, S.; Liang, L.; Sun, M.; Zhao, P. Fluid motion and stabilization effect prediction of anti-rolling tank coupled ship rolling. Chin. J. Comput. Mech. 2016, 33, 252–256+262. [Google Scholar]
- Lewis, E. Principles of Naval Architecture, 2nd ed.; SNAME: New Jersey, NJ, USA, 1989; Volume 3. [Google Scholar]
- Liang, L.; Zhao, P.; Zhang, S.; Yuan, J.; Wen, Y. Simulation and analysis of Magnus rotating roll stabilizer at low speed. Ocean Eng. 2017, 142, 491–500. [Google Scholar] [CrossRef]
- Liang, L.; Jiang, Y.; Zhang, Q.; Le, Z. Aspect ratio effects on hydrodynamic characteristics of Magnus stabilizers. Ocean Eng. 2020, 216, 107699. [Google Scholar] [CrossRef]
- Perez, T.; Blanke, M. Ship roll damping control. Annu. Rev. 2012, 36, 129–147. [Google Scholar] [CrossRef]
- Fang, M.; Luo, J. On the track keeping and roll reduction of the ship in random waves using different sliding mode controllers. Ocean Eng. 2007, 34, 479–488. [Google Scholar] [CrossRef]
- Liu, Z.; Jin, H.; Katebi, R. Ship forward speed loss minimization using nonlinear course keeping and roll motion controllers. Ocean Eng. 2016, 113, 201–207. [Google Scholar] [CrossRef]
- Liang, L.; Wen, Y. Rudder roll stabilization with disturbance compensation model predictive control. J. Mar. Sci. Technol. 2018, 24, 249–259. [Google Scholar] [CrossRef]
- Liang, L.; Zhao, P.; Zhang, S.; Ji, M.; Yuan, J. Simulation analysis of rudder roll stabilization during ship turning motion. Ocean Eng. 2019, 189, 106322.1–106322.11. [Google Scholar]
- Zhang, Q.; Zhang, L.; Cao, K.; Xing, Y.; Wan, J. Design of u-type anti-rolling tank for Ultra-deepwater drillship. J. Wuhan Univ. Technol. 2019, 43, 271–350. [Google Scholar]
- Wen, X.; Wan, D. Numerical simulation of liquid sloshing in anti-roll tank by MPS method. Chin. J. Hydrodyn. 2019, 34, 489–493. [Google Scholar]
- Hu, J. Study on Control Strategy of Anti-Rolling Tanks under Parametric Roll; Harbin Engineering University: Harbin, China, 2019. [Google Scholar]
- Luo, H.; Wang, C.; Sheng, Q. Numerical and model test on eigen characters of rolling motion of anti-rolling tank. China Offshore Platf. 2020, 35, 1–6. [Google Scholar]
- Rahul, S.; Jyothish, P.; Anantha, S. Genetic Algorithm based design optimization of a passive anti-roll tank in a sea going vessel. Ocean Eng. 2020, 203, 107216. [Google Scholar]
- Liang, L.; Wang, J.; Song, J.; Li, Y. Design and simulation investigation of variable period passive anti-rolling tank. Chin. J. Ship Res. 2021, 16, 147–154. [Google Scholar]
- Immink, L. Feed forward Control of U Anti-Roll Tanks; University Science: Mill Valley, CA, USA, 2021. [Google Scholar]
- Lloyd, A. Seakeeping: Ship Behaviour in Rough Weather; Ellis Horwood: Chichester, UK, 1989. [Google Scholar]
- Gawad, A.; Ragab, S.; Nayfeh, A.; Mook, D. Roll stabilization by anti-roll passive tanks. Ocean Eng. 2001, 28, 457–469. [Google Scholar] [CrossRef]
- Jin, H.; Zhang, H. Research on pneumatical-passively-controlled tank stabilizers based on GPC strategy. Shipbuild. China 2010, 51, 67–75. [Google Scholar]
- Zhao, Y.; Yang, Q.; Su, D.; Zou, L.; Wang, A. Rogue wave prediction based on wavelet neural network. J. Harbin Inst. Technol. 2021, 53, 112–117. [Google Scholar]
- Zhang, S. Characteristics Research and Experimental Verification of Controlled Passive Tank. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2013. [Google Scholar]






| Description | Value | Unit |
|---|---|---|
| Displacement | 3850 | ton |
| Water length | 125 | m |
| Beam | 13.8 | m |
| Depth | 7 | m |
| Draft | 4.33 | m |
| Height of CG | 5.6 | m |
| Metacentric height | 1.5 | m |
| Roll period | 9.38 | s |
| Description | Value | Unit |
|---|---|---|
| Height of tank | 4.4 | m |
| Width of tank | 11.23 | m |
| Depth of tank | 5.85 | m |
| Level angle of tank | 0~18 | deg |
| Width of liquid channel | 8.8 | m |
| Width of side tank | 2.44 | m |
| Tank level height | 1.93 | m |
| Distance between CG and center line of liquid channel | 3.76 | m |
| Tank period | 9.38 | s |
| Height of liquid channel | 0.75 | m |
| Air channel number | 6 | - |
| Description | Symbol | Limitation | Unit |
|---|---|---|---|
| Length variation of telescopic rod | ΔL1 | 0~50 | mm |
| Speed of telescopic rod | v1 | 17 | mm/s |
| Length variation of pitch rod | ΔL2 | 0~50 | mm |
| Speed of pitch rod | v2 | 17 | mm/s |
| Roll Angle (°) | Roll Rate (rad/s) | Tank Level Angle (°) | |
|---|---|---|---|
| No tank | −5.15~5.02 | −0.05777~0.05619 | - |
| Passive anti-rolling tank | −3.00~3.85 | −0.03945~0.03889 | −7.07~7.91 |
| Controllable passive anti-rolling tank | −2.14~2.35 | −0.02798~0.02915 | −6.00~5.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Zhao, P.; Li, C.; Song, Z.; Liang, L. Study on the Accessibility Impact of Anti-Rolling Tank on the Offshore Wind O&M Gangway. J. Mar. Sci. Eng. 2023, 11, 848. https://doi.org/10.3390/jmse11040848
Zhang S, Zhao P, Li C, Song Z, Liang L. Study on the Accessibility Impact of Anti-Rolling Tank on the Offshore Wind O&M Gangway. Journal of Marine Science and Engineering. 2023; 11(4):848. https://doi.org/10.3390/jmse11040848
Chicago/Turabian StyleZhang, Songtao, Peng Zhao, Chenyang Li, Ziqi Song, and Lihua Liang. 2023. "Study on the Accessibility Impact of Anti-Rolling Tank on the Offshore Wind O&M Gangway" Journal of Marine Science and Engineering 11, no. 4: 848. https://doi.org/10.3390/jmse11040848
APA StyleZhang, S., Zhao, P., Li, C., Song, Z., & Liang, L. (2023). Study on the Accessibility Impact of Anti-Rolling Tank on the Offshore Wind O&M Gangway. Journal of Marine Science and Engineering, 11(4), 848. https://doi.org/10.3390/jmse11040848






