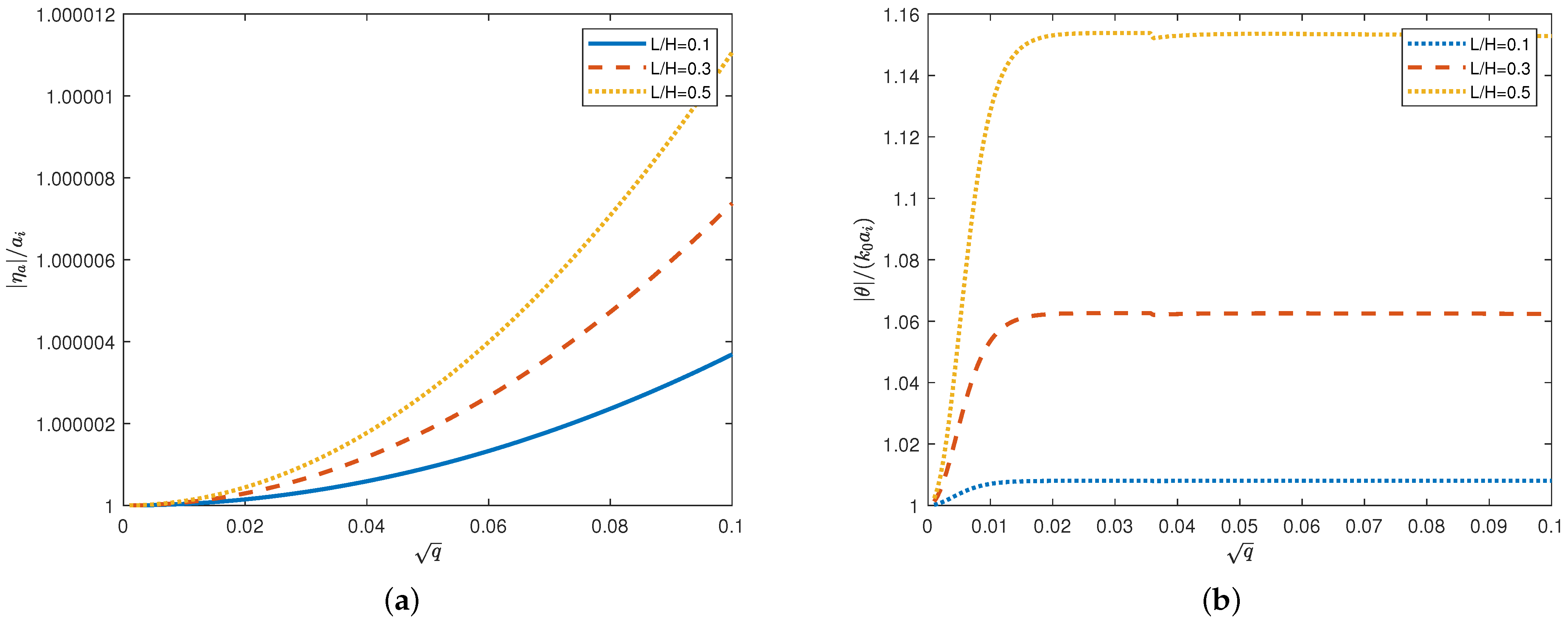1. Introduction
Wave propagating under sea ice cover has been studied intensively for several decades. The importance of this topic has been increasing year by year as the ice reduction accelerates in the polar regions. Thanks to the global temperature rising, sea ice can be found further from the pole, and a chance of shipping through the ice-covered regions increases. New commercial routes through the Arctic can significantly reduce the shipping time and improve its economic efficiency. On the other hand, the amount of natural resources in the polar regions is vast. Gautier et al. [
1] wrote “the United States Geological Survey has assessed the area north of the Arctic Circle and concluded that about 30% of the world’s undiscovered gas and 13% of the world’s undiscovered oil may be found there, mostly offshore under less than 500 meters of water. Undiscovered natural gas is three times more abundant than oil in the Arctic and is largely concentrated in Russia.” The potential of renewable energy, such as solar and wind energies, in the polar regions is too important to be ignored. The economic needs in the polar region have attracted more attention to modeling sea ice.
Modeling sea ice and waves propagating in ice-covered waters is challenging because the properties of the ice change significantly from place to place, see [
2,
3,
4,
5,
6]. They depend on air temperature, water salinity, and how the ice was built up. This makes it difficult to construct a stable and reliable sea ice mechanical model. However, modeling the ice cover as a thin floating elastic plate of constant thickness proved to be a reasonable approach to practical problems with relatively long waves, see [
7]. The ice/water interaction problems become more complicated in the presence of other structures in either water or on ice, or in both of them. Flexural-gravity waves diffracted by vertical cylinders frozen in ice were studied in [
8,
9,
10,
11,
12]. Waves propagating in an ice channel with vertical walls are investigated in [
13,
14,
15,
16,
17]. In all of these studies, the structural motion was not included.
Problems of flexural-gravity wave interaction with a free moving structure are more complicated. Such problems are coupled: deflection of the floating ice plate, flow under the ice, and the motions of the structure should be determined at the same time. A vertical rigid plate built-in a floating ice sheet could be the simplest model of ice/water/structure interaction. This problem is investigated in the present paper using the vertical mode method [
8,
9,
11,
12] for water of finite depth. There are parts of the rigid plate below the ice in water and above the ice. The part of the rigid plate above the ice does not participate in interaction with water, but it changes the mass of the plate and its moment of inertia. The thickness of the plate is assumed to be small, which simplifies the analysis and makes it possible to separate the vertical motion of the plate and the plate rotation. The rigid plate motions are caused by a linear incident wave and are governed by equations of mechanics. A similar problem was considered recently in [
18] but for infinite water depth, where the vertical mode method is not applicable, and for elastic vertical plate.
The approach of the present paper is to divide the original problem in parts, which are easier to solve and validate, and finally combine all of the obtained solutions to arrive at the complete solution of the original problem. The finite depth of the liquid under the floating elastic plate makes it possible to use the so-called vertical modes to represent the velocity potential. The vertical modes accommodate the complex boundary conditions at the elastic plate. Integral transforms also can be used to this aim, see [
10], but they provide the same result as the vertical mode method as it was proved in [
9]. To find the odd part of the velocity potential, the solution of a mixed boundary-value problem is required. This is a challenging problem, which is solved by using the Chebyshev polynomials.
This paper aims to provide a theoretical basis for subsequent research on a floating elastic plate with several built-in vertical plates. The structure of the paper is organized as follows. The formulation of the problem is given in
Section 2. The vertical mode method is applied to solve the problem in
Section 3. Numerical algorithms are described in
Section 4. Numerical results are presented in
Section 5. Conclusions and future work are discussed in
Section 6.
2. Formulation of the Problem
The two-dimensional linear problem of a flexural-gravity wave interacting with a rigid vertical plate built in a floating ice sheet is studied, see
Figure 1. The ice sheet is considered as an infinite thin elastic plate of constant thickness
h. The density of the ice is
, and the ice rigidity is
, where
E and
are the Young’s modulus and Poisson’s ratio of the ice respectively. The liquid under the ice is inviscid, incompressible, and of finite depth
H. The rigid plate built-in the ice sheet is of length
L under the ice and of length
ℓ above the ice, of negligible thickness, and of mass
, and the moment of inertia
with respect to the point is where the rigid plate is in contact with the ice sheet. This point is taken as the origin of the Cartesian coordinate system
, see
Figure 1. The ice/liquid interface corresponds to the line
at equilibrium without any motions of the ice plate and any flow under the plate. The line
corresponds to the bottom of the flow region. Note that
. The liquid flow caused by the ice plate deflection and the rigid plate motions is assumed potential. The flow region
within the linear potential theory is the the strip
with the cut
,
, which corresponds to the submerged part of the rigid plate at equilibrium. The flow region is independent of time within the linear approximation. This is the coupled problem of linear hydroelasticity, where the plate deflection
;
t is the time; the flow under the ice is described by a velocity potential
; and the motions of the rigid plate should be determined at the same time.
The incident flexural-gravity wave,
, is of small amplitude
with a frequency
and wavenumber
, where
and
are related by the dispersion relation [
7],
is the liquid density,
g is the gravitational acceleration, and
,
. The velocity potential of the incident wave is given by
The linear theory of hydroelasticity is applicable if the wave slope,
, is small. The floating ice plate can be treated as a thin elastic plate if the plate thickness
h is much smaller than the incident wave length
, which provides the condition
.
Note that the deflection
is continuous together with its first derivatives at
, but the second and third derivatives,
and
, are, in general, discontinuous at the place of the rigid plate,
. It is convenient to write the thin plate equation separately for the right,
, and the left,
, parts,
where
is the hydrodynamic pressure on the ice/liquid interface, which is given by the linearised Bernoulli equation
The plate deflection in the far field on the left from the rigid plate behaves as
and in the far field on the right from the rigid plate as
where
stands for terms decaying exponentially as
,
and
are the amplitudes and
and
are the phase shifts of the reflected and transmitted flexural-gravity waves correspondingly. The values of
,
,
, and
are to be determined as part of the solution.
The velocity potential
satisfies the Laplace equation in the flow region,
the boundary conditions on the bottom,
the linearized kinematic boundary condition on the ice/liquid interface,
and the conditions on the right,
, and left,
, surfaces of the moving rigid plate,
where
is the inclination angle of the rigid plate;
at equilibrium; when the rigid plate is vertical,
is positive anticlockwise, see
Figure 1. The behavior of the velocity potential as
follows from (
5) and (
6) in a similar way as (
2) follows from the form of the incident deflection wave.
The time-dependent vertical displacement
and inclination angle
of the rigid plate are governed by equations,
where
,
are the bending moment and shear force, respectively; subscript
s stands for solid (ice); subscript
f stands for fluid; and
and
are the mass and the moment of inertia of the rigid plate per unit width, respectively. A rigid plate, which is of length
L below the floating elastic plate and
ℓ above the the floating plate, is of mass
, where
is the density of the rigid plate material and
is the rigid plate thickness. The moment of inertia of such a plate is
.
The bending moment and shear force in the ice plate are proportional to the second and third derivatives of the deflection
with respect to
x,
The hydrodynamic moments acting on the submerged part of the rigid plate are given by
within the linear theory. At the connection point between the floating elastic plate and the rigid plate, we have
No initial conditions are required for the formulated problem (
1)–(
15). We shall determine the time-periodic solution of this problem.
The velocity potential
, the plate deflection
, the vertical displacement of the rigid plate
, and the inclination angle of the rigid plate
are sought in the form
where
and
are complex-valued functions,
and
are complex numbers to be determined, and
ℜ stands for the real part of a complex number. The complex plate deflection
and the velocity potential
are convenient to decompose as
where
and
correspond to the incident wave,
and
are unknown odd with respect to
x functions,
, and
and
are unknown even with respect to
x functions,
. Only the right-hand side of the flow region,
, can be considered from now on. In particular, the matching conditions (
15) read now as
where a prime stands for derivative with respect to
x. The deflections
and
describe outgoing waves in the far field,
where the complex amplitudes
and
are to be determined. Equations (
5), (
6), (
17), and (
20) provide the parameters of the radiated and transmitted waves as
The equations and boundary conditions in the formulated problem (
1)–(
15), which are satisfied in the right part of the flow region,
, are valid for the odd and even components of the solution separately. Using ∗ for either
o or
e, we find
The conditions at
have different forms for odd,
and even components,
The conditions (
26)–(
28) for the even component of the solution imply that there is no flow through
, the slope of the floating plate at this edge is zero, and the edge is connected to the bottom with a spring, see Section 7 in [
19], with the vertical forcing applied to the edge. The conditions (
29)–(
32) for the odd component of the solution imply that the plate edge does not move vertically but can rotate subject to the restoring force and the forcing caused by the incident wave and the hydrodynamic pressure acting on the submerged part of the rigid plate, see [
20]. The far-field conditions (
20) should also be satisfied, where the complex amplitudes
and
are to be determined. These amplitudes and the unknown functions
,
and
,
are proportional to the amplitude of the incident wave
, which can be set unity in the analysis and returned back in the final solution as the factor.
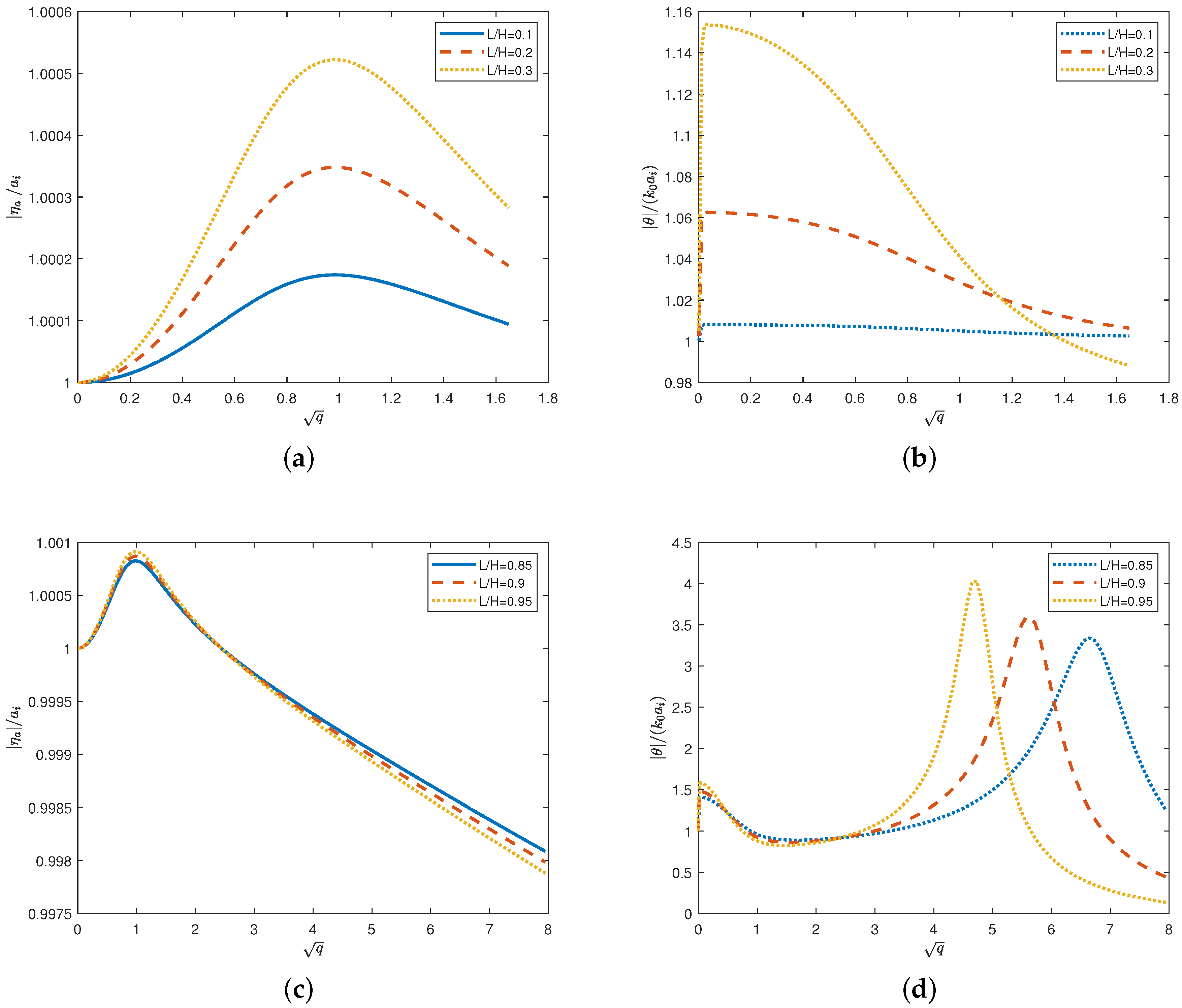
The ratio of amplitude of the reflected wave
to the amplitude of the incident wave
is known as the reflection coefficient
R, and the ratio of amplitude of the transmitted wave
to the amplitude of the incident wave
is known as the transmission coefficient
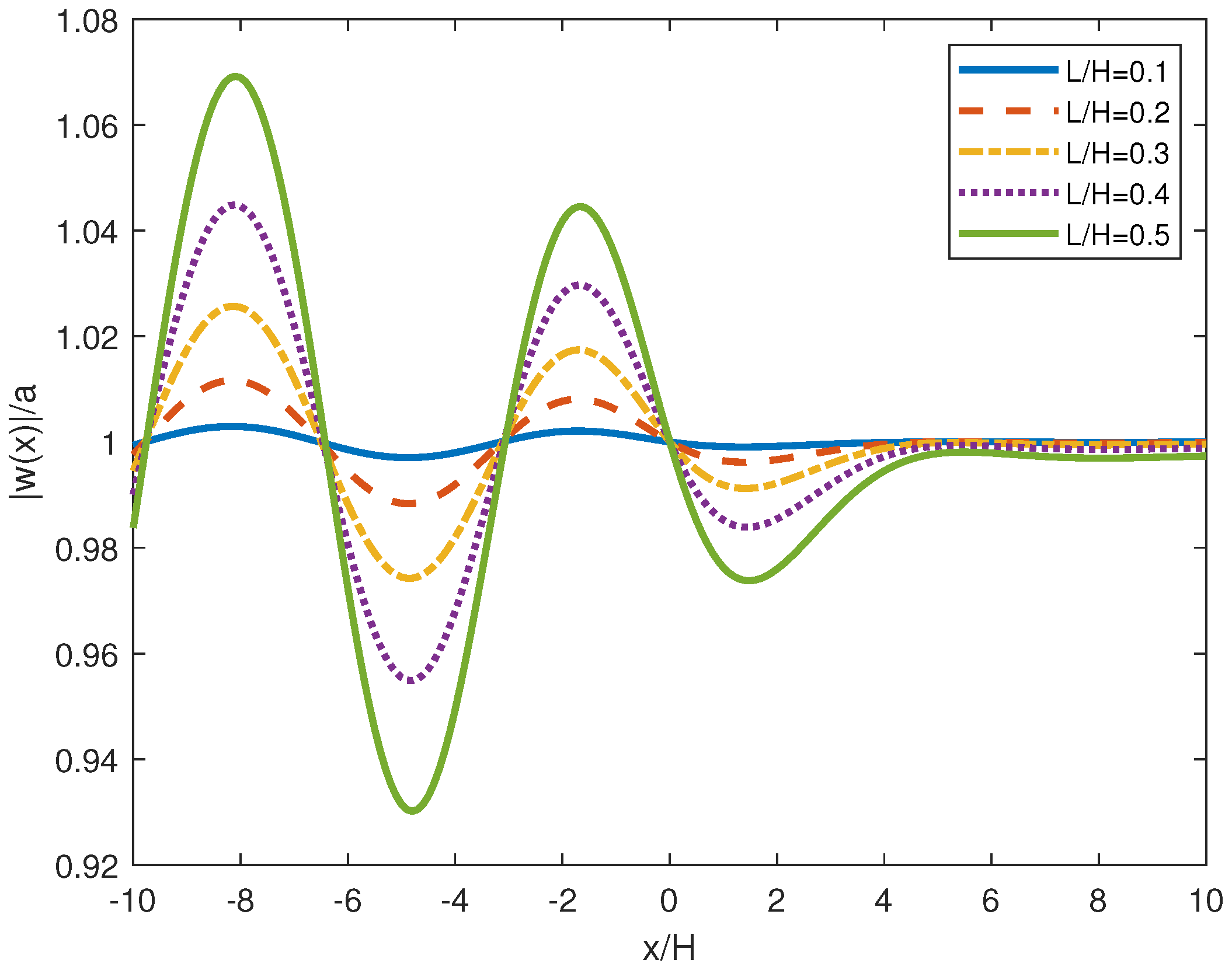
T. We shall investigate these coefficients depending on the wave frequency and parameters of the problem. The distribution of the deflection amplitude
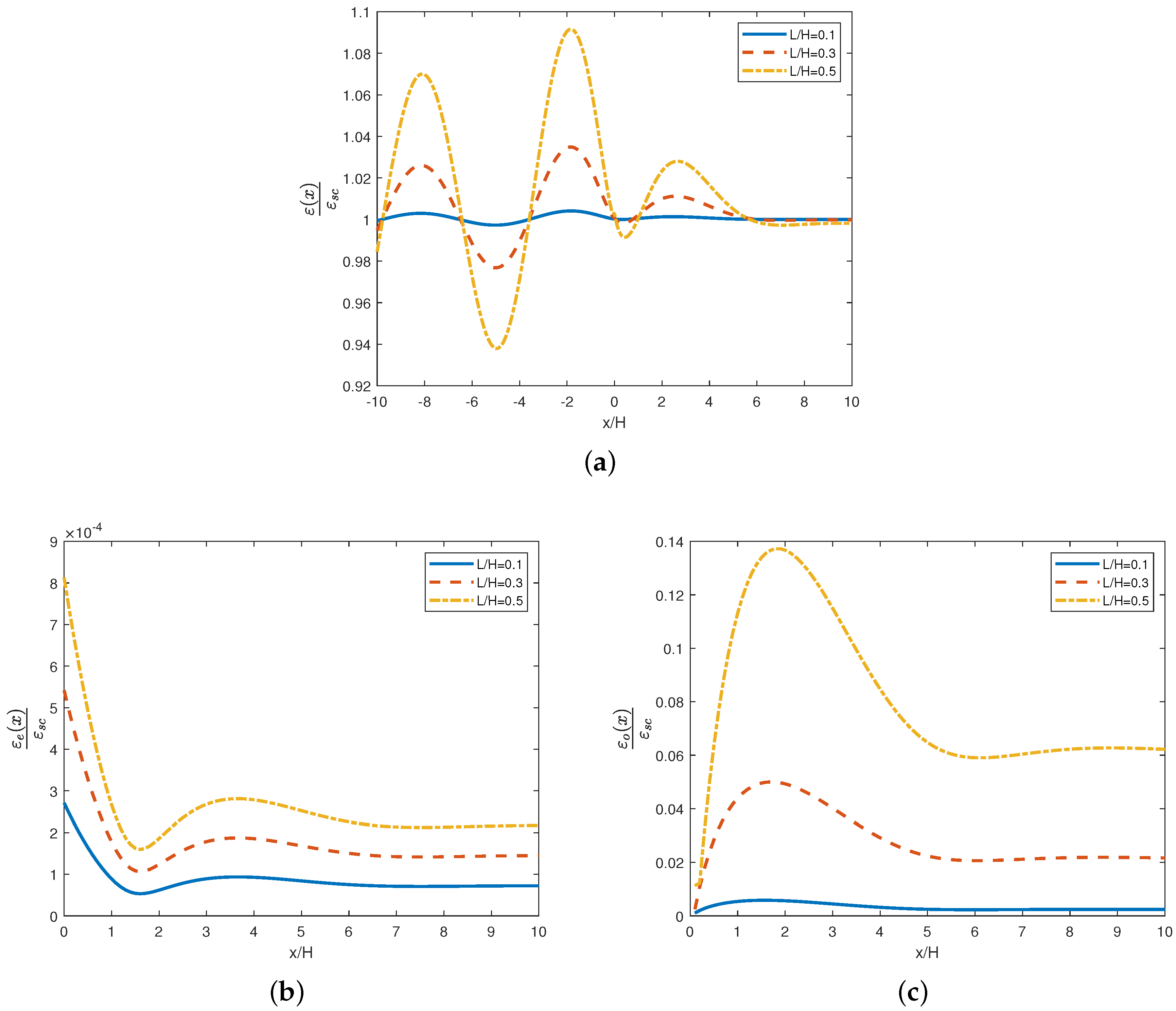
will be studied with focus on the maximum amplitude depending on parameters of the rigid plate. The time-periodic strains in the elastic plate are given by the formula
We are concerned with
depending on the parameters of the problem.
3. Solution of the Problem by the Vertical Mode Method
Note that the odd and even components of the solution are independent of one another and are calculated independently. Both components are obtained by the so-called vertical mode method. The vertical modes of a floating elastic plate were introduced in [
21,
22], applied to two-dimensional problems in [
23,
24], and applied to three-dimensional problems in [
8,
9]. For liquid of depth
H, the vertical modes are given by
where
are the complex roots of the dispersion Equation (
1) with positive imaginary parts. These roots include real positive root
, two complex roots
,
, where
,
, and infinite numbers of pure imaginary roots
,
for
. The modes satisfy the equations
and
. The modes are orthogonal in the following sense,
where the scalar product is defined by
for any two functions
and
defined in the interval
, and
is the dimensionless wavenumber,
, and
. The dispersion relation (
1) written with respect to dimensionless wavenumber
reads
. Equations (
38) and (
39) are similar to Equations (32) and (33) from [
9] but written in the dimensional variables.
The products
satisfy Equations (
22)–(
25) and decay as
except for
. The product
, where
is real and positive, describes a wave propagating towards
. Therefore, a general solution of the boundary-value problem (
20), (
22)–(
25) is given by a superposition,
with undetermined coefficients
, where ∗ stands either for
o (odd component of the solution) or
e (even component of the solution). These coefficients and the complex amplitudes
and
in (
20) are obtained using the conditions (
26)–(
32) at
. Equations (
20) and (
40) provide
and
.
3.1. Even Component of the Plate Deflection
We calculate the following limit for
in two ways, by using (
40) and (
37), where ∗ is changed to
e, and by using the definition (
38) of the scalar product,
In (
42), conditions (
26)–(
28) and equalities
were used. Equating the right-hand sides in (
41) and (
42), we obtain the formula for the coefficients
, where
,
The unknown deflection
at
is obtained by substituting (
43) in (
40), setting
, and resolving the result with respect to
,
Equations (
44), (
43), and (
40) provide the even component of the elastic plate deflection,
The even component of the strain in the plate follows from (
33) as
The complex amplitude of the radiated wave
in (
20) is given by
It is shown in [
9] that
as
. Therefore, the series in (
44), (
45), and (
46) converge quickly. There is no even component of the solution if the mass of the rigid plate
is negligible.
3.2. Odd Component of the Plate Deflection
The odd component is calculated in the same way as the even component in
Section 3.1. The solution is sought in the form (
40), (
34), where ∗ is changed to
o. It is convenient to introduce the unknown derivative
, on the vertical interval
. This derivative is determined using the condition (
31). Note that the new unknown function
is square-root singular at
and
to match the boundary condition at the bottom
. We introduce a new variable
for the interval
, where
, and search the function
as the series
where
are the even Chebyshev polynomials of the first kind and degree
. The limits (
41) and (
42), where
, calculated now for
provide
The integrals in (
50) are denoted as
,
, and
, correspondingly. Multiplying Equation (
35) by
and
y, and integrating the results with respect to
y from
to 0 by parts, we obtain
The series (
48) provides
The coefficients
can be presented using the dimensionless wavenumber
, the parameter
, and the dispersion relation through the modified Bessel functions of complex arguments,
where
are the modified Bessel functions of the first kind and order
.
Equating (
49) and (
50), we find
where
,
, and
are to be determined using the conditions (
29), (
30) and (
31).
The condition (
31) and the series (
40) provide
Multiplying both sides of this equation by
, where
, and integrating with respect to
from 0 to 1, we find
which yields the following system for the coefficients
using (
54) and (
52)
It is seen that
as
. It can be shown that
and
are of order
as
. Therefore, the series for
,
and
converge slowly and should be evaluated with care.
The solution of the system reads
where
,
are solutions of the systems
Substituting (
57) in (
52) and (
54), one finds the coefficients
through two unknown,
and
,
The conditions (
29), (
30), and the series (
40) provide two equations with respect to
and
,
The solution
and
of this system is substituted in (
58), which finalises the calculations of the coefficients
in the odd component of the deflection.
In the important limiting case, where the rigid plate length under the ice plate is equal to the water depth,
, in (
50) we have
,
and the series with
in the definitions of
,
, and
should be removed. Then, the coefficients in the system (
59) and (
60) are readily calculated, which makes the solution of this limiting problem straightforward.
In another limiting case, where the rigid plate is only above the floating plate,
, we use the limits (
49), (
50) but for the potential,
for
. The calculations provide an account for (
29),
Equation (
30), where now the integral is zero, and (
61) give
which together with (
61) explicitly define the coefficients
.
4. Numerical Algorithms
Calculations in this and the following sections are performed for a sea ice plate with ice density
kg/m
, thickness
m, Young’s modulus
N/m
, and Poisson’s ration
, see [
10,
25]. The water density is 1025 kg/m
, the water depth is
m, and the gravitational acceleration is
m/s
. The rigid plate is made of the same ice,
, with the plate length above the floating plate,
m, and the plate length below the floating plate
L varies from 0 m to 10 m. The plate thickness
is 10 cm. Then, the mass of the vertical plate per unit width,
, varies from 91.7 kg/m for
m to 1008.7 kg/m for
m. Correspondingly, the moment of inertia of the vertical plate per unit width,
, varies from 30.6 kgm for
m to 30,597.2 kg/m for
m. The ice rigidity
D is equal approximately to
Nm. The characteristic length of the floating ice plate
is equal to 14.13 m, which is comparable with the water depth. Therefore, the finite depth of the water is important for the selected conditions.
The parameters
and
in the dispersion relation (
1) written with respect to the dimensionless wavenumber
read
are related by the equation
, where
and
. In the selected conditions,
and
. The parameter
is positive for the wave frequencies such that
, where
.
The ice deflection and the velocity of the flow are proportional to the incident wave amplitude within the linear theory of hydroelasticity. We calculate the ice deflection for m, bearing in mind that the deflections for other amplitudes are obtained by using a corresponding factor.
The period of the incident wave is assumed to be between 2 and 30 s, which corresponds to the wave frequency
in the interval
s
s
. This interval provides
, and therefore
. The dispersion relation (
1) provides that this range of the wave frequencies corresponds to the range of the incident wave numbers
and the incident wave length 50.43 m
m. The roots of the dispersion relations are simple because
for the present conditions, see [
8].
Note that the terms of the series (
44) and (
45) decay as
, and the terms of the series (
46) decay as
for
. These series provide the even components of the plate deflection and strains in the plate. The series are evaluated numerically by direct summation. The series for the odd components of the solution decays slowly and care should be taken to evaluate these series with good accuracy.
4.1. Convergence Analysis for Odd Components of the Solution
The accuracy of the numerical solutions for the odd deflection and velocity potential depends on the number of terms
retained in the series (
48) for the auxiliary function
and the number of pure imaginary roots of the dispersion relation
retained in the series (
40) for
and
. Then, the matrix in the algebraic system (
56) is of size
, and the values of each element of this matrix and of the right-hand side of the system are obtained by the summation of
terms.
The series for
, see (
56) converges slowly. The terms in this series are of order of
as
. To find a reasonable value of
, which provides accurate numerical solution, we set
first and increase
starting from 100 with the step
. The convergence of
is demonstrated in
Figure 2, where the maximum value,
, of
for
is shown as a function of
. The maxima are achieved at diagonal elements
.
Figure 2 shows that
provides the numerical values of
with accuracy better than
. To ensure accuracy,
is used in our calculations.
It was shown that the accuracy of the solution depends mainly on but not on . The value of affects the shape of but has little influence on the deflection. is used in the present calculations.
4.2. Roots of the Dispersion Relation
There is a single positive root of the dispersion equation,
, because the left-hand side of this equation is negative at
, and it increases monotonically with the increase in
. The real solution
is calculated by the bisection method, which narrows an interval that contains a root down to
. The pure imaginary roots of the dispersion relation,
, where
, satisfy the equation
where the right-hand side is negative for positive
if
as in our conditions. The visual inspection of the sides of Equation (
63) suggests that
, where
is calculated by iterations,
with the initial guess
. Equation (
64) shows that
as
. This asymptotic formula is used to investigate, and improve if needed, convergence of the series from
Section 3.
As to the complex roots,
and
, where
and
, the values
a and
b are obtained by solving the system of two nonlinear equations,
by the Newton iteration method. Equations (
65) and (
66) yield that
for
. The asymptotic behaviors of
as
were investigated in [
9].