A CFD-Based Data-Driven Reduced Order Modeling Method for Damaged Ship Motion in Waves
Abstract
1. Introduction
2. Methodology
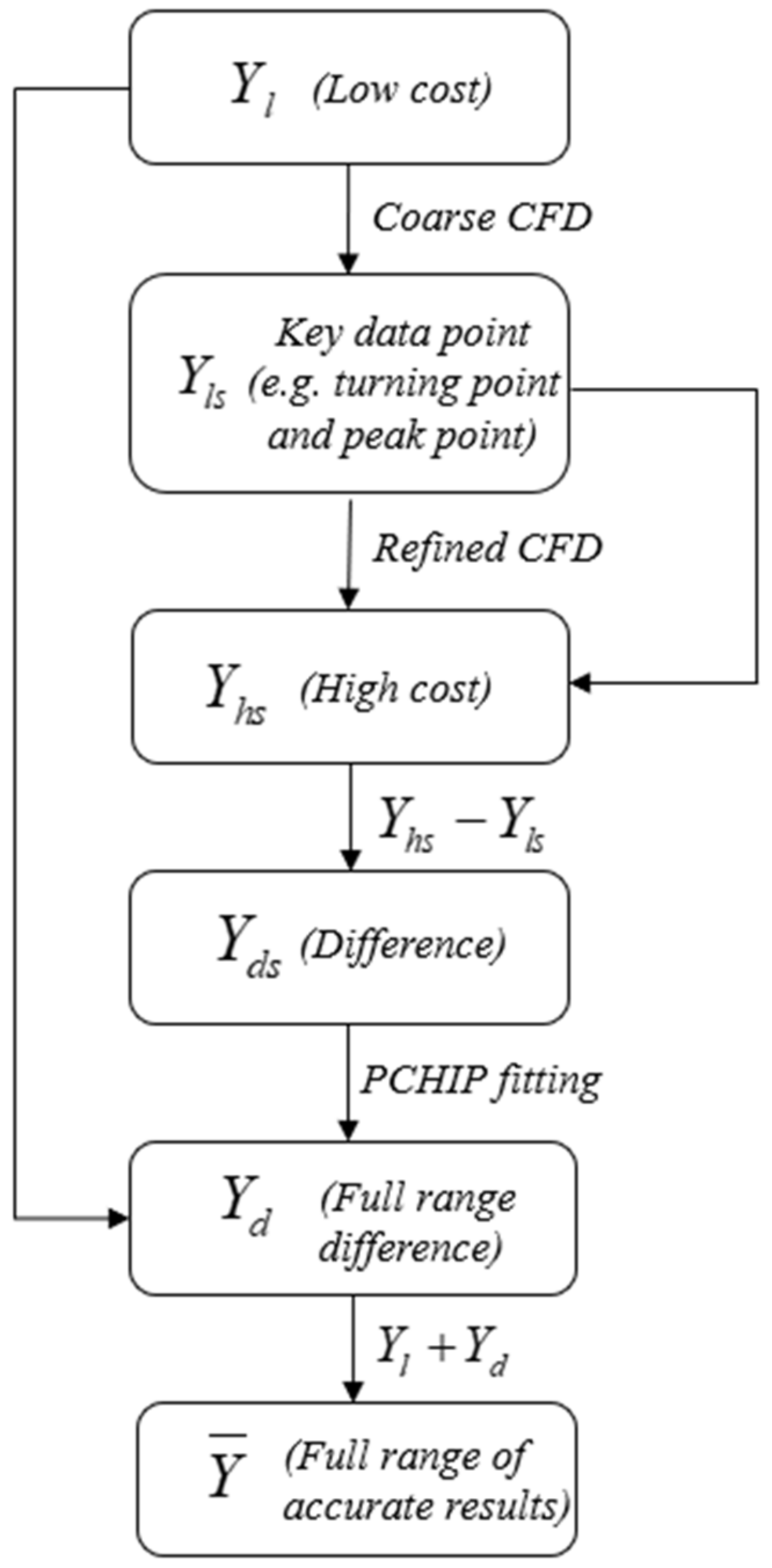
2.1. Data-Driven Reduced Order Modeling
2.2. First-Principle-Based Model-CFD
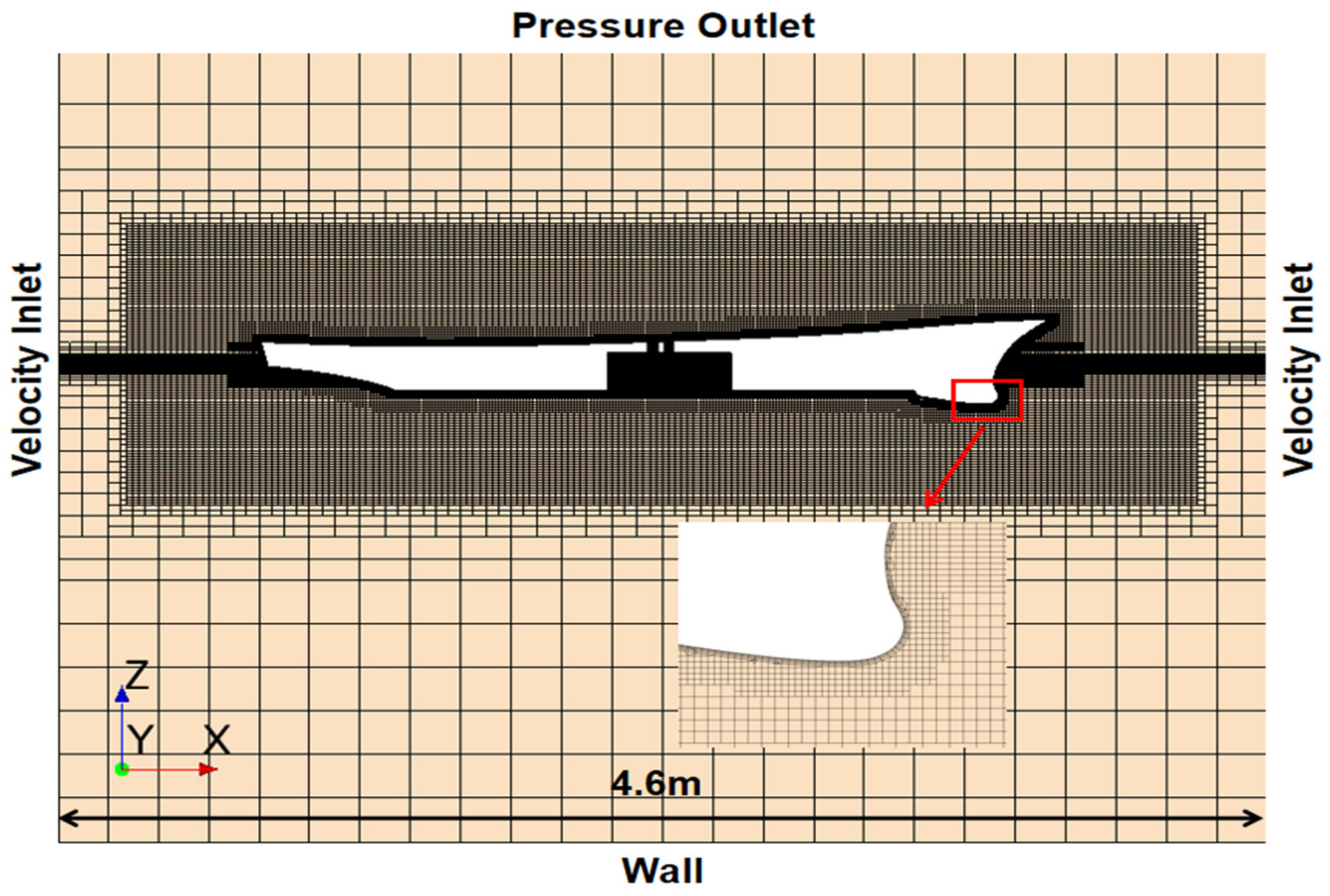
2.2.1. CFD Model and Ship Geometry
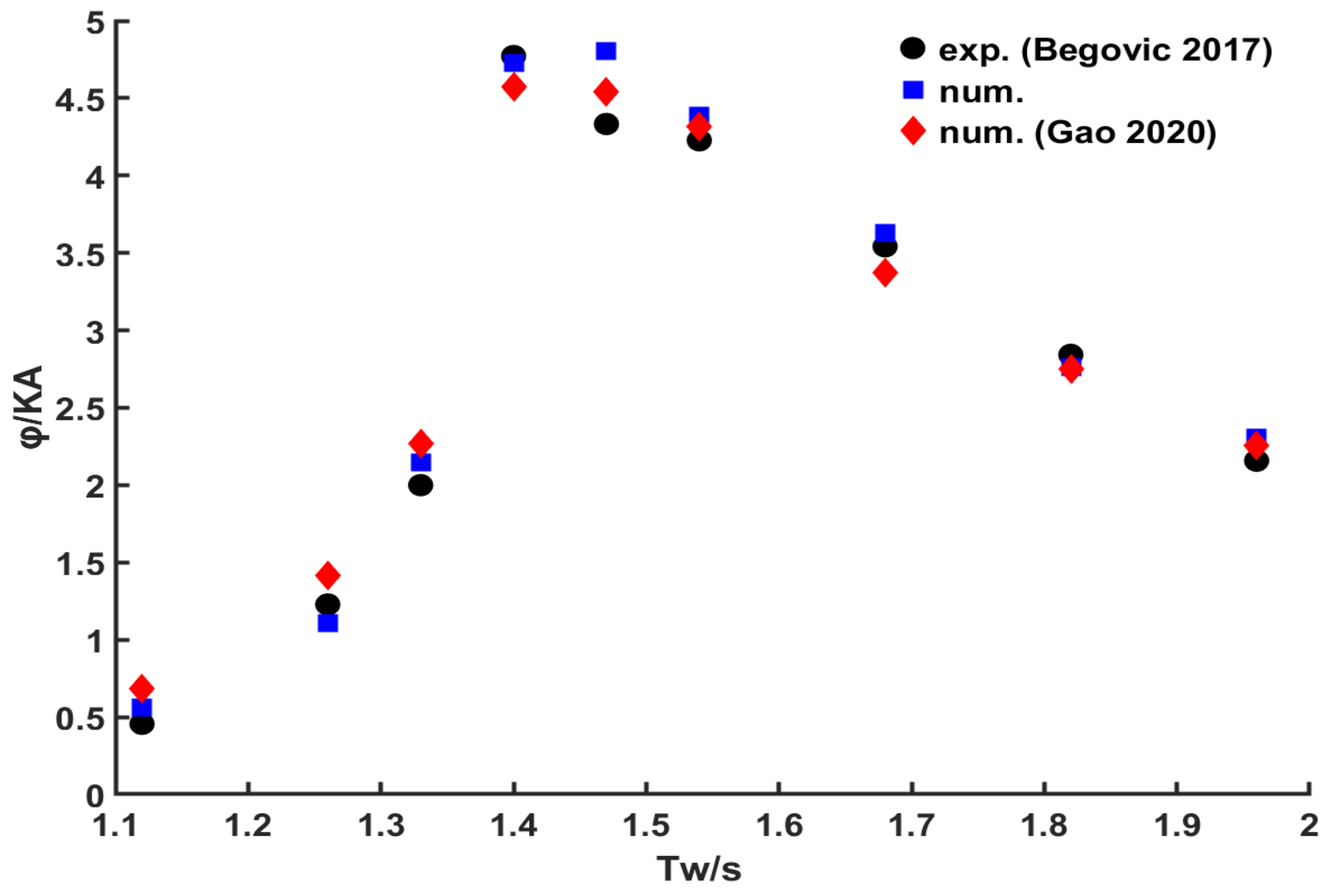
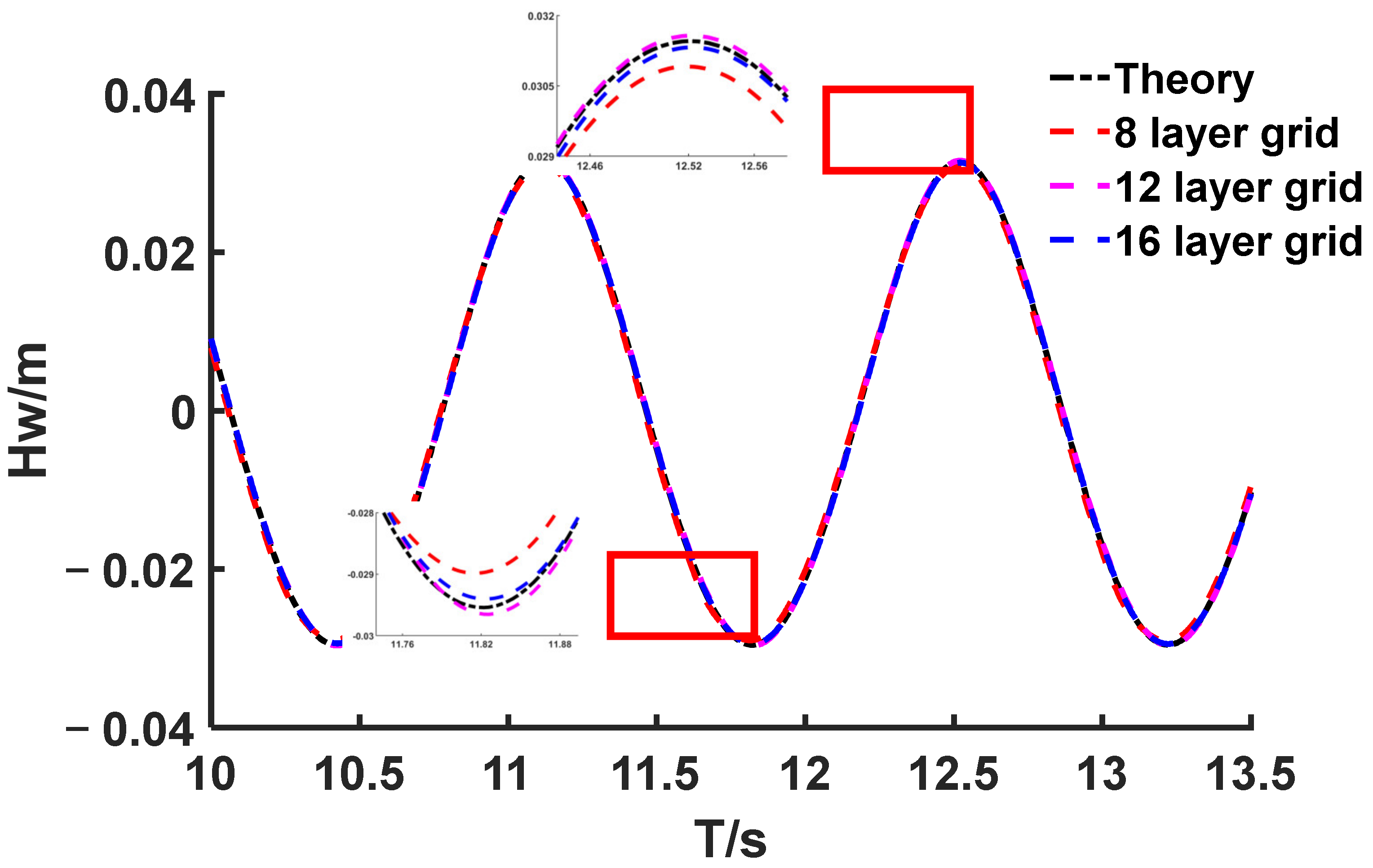
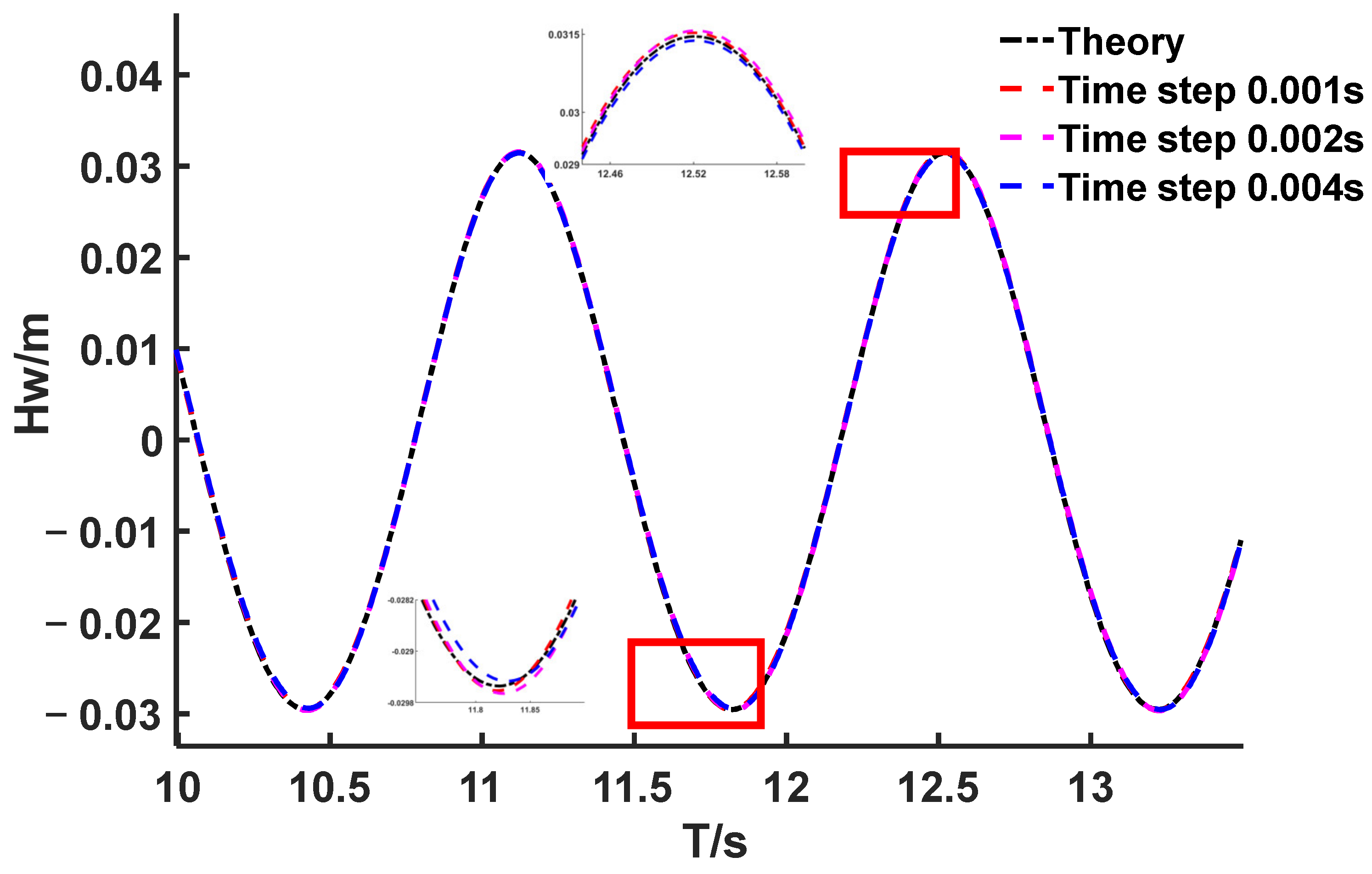
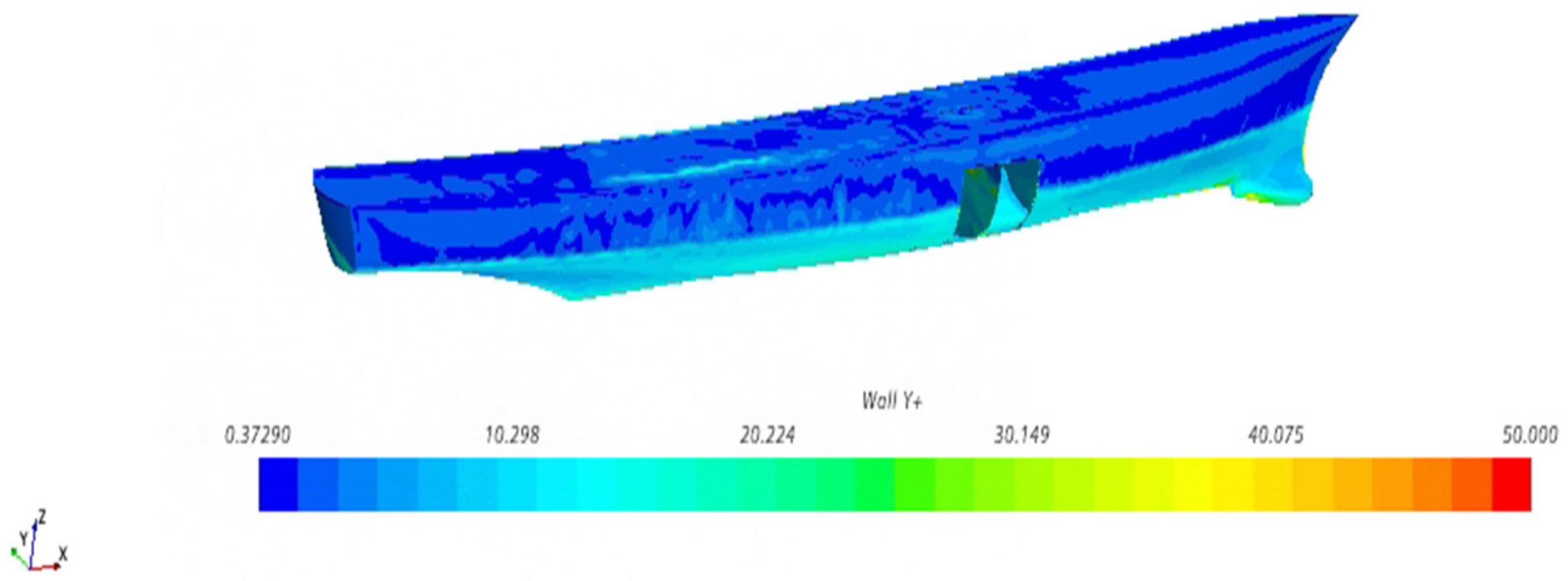
2.2.2. Model Validation
3. Results and Discussion
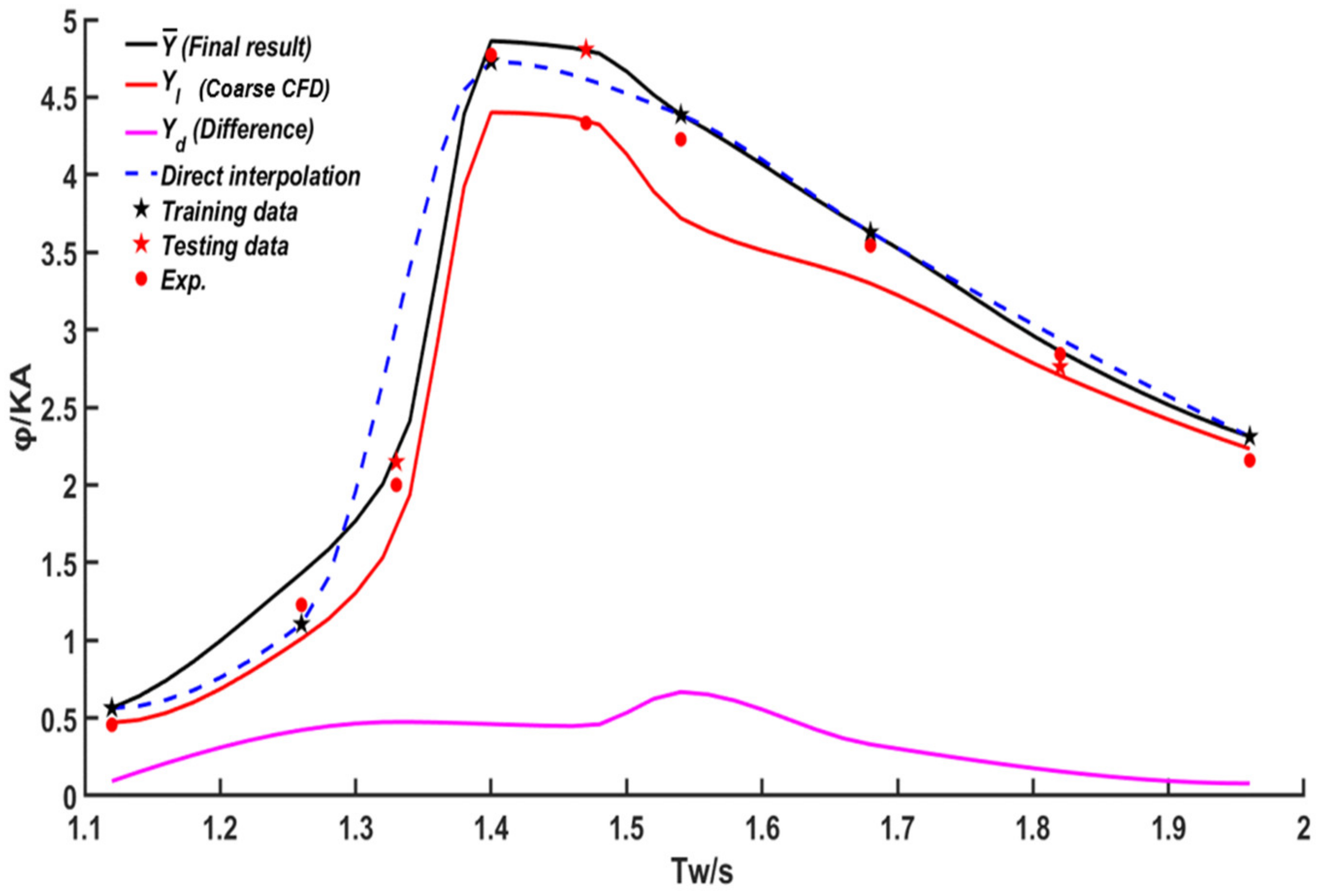
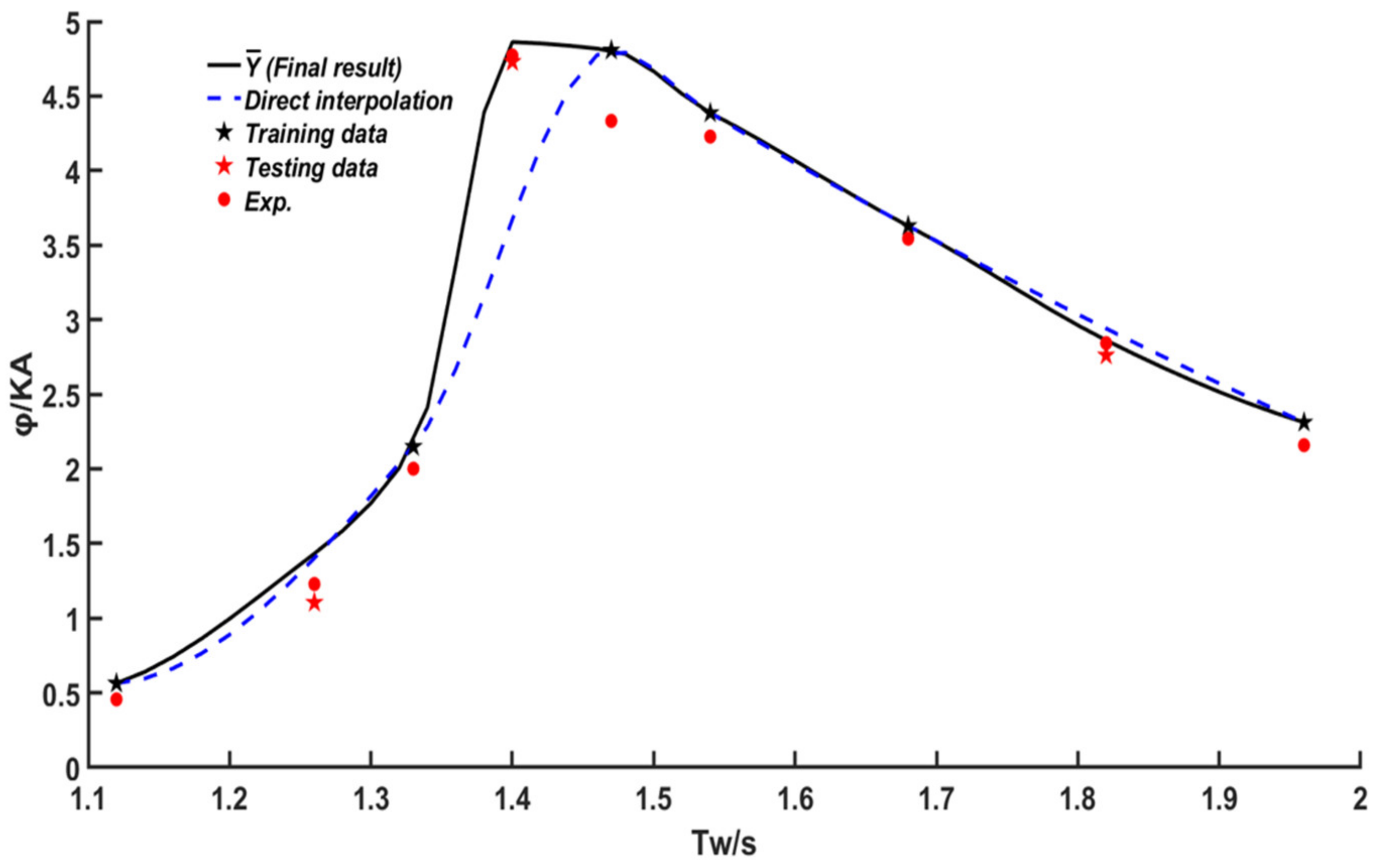
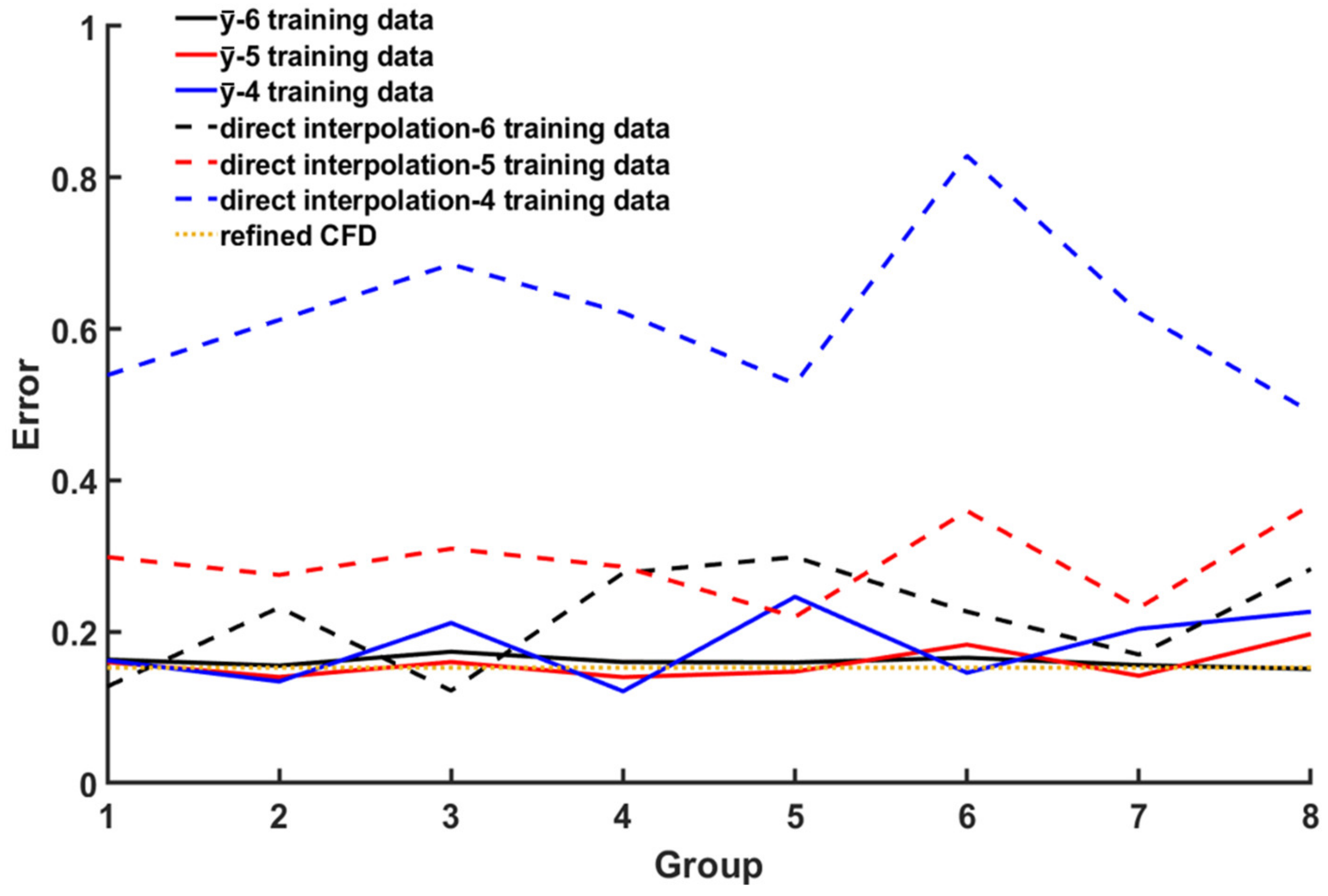
3.1. The Accuracy of the Proposed Model
3.2. Efficiency of the Proposed Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boom, H.; Ferrari, V.; Batenburg, R.; Seo, S.T. SEWOL Ferry Capsizing and Flooding. In Proceedings of the Sustainable and Safe Passenger Ships, Athens, Greece, 4 March 2020. [Google Scholar]
- Ciampalini, A.; Raspini, F.; Bianchini, S.; Tarchi, D.; Vespe, M.; Moretti, S.; Casagli, N. The Costa Concordia last cruise: The first application of high frequency monitoring based on COSMO-SkyMed constellation for wreck removal. ISPRS J. Photogramm. Remote Sens. 2016, 112, 37–49. [Google Scholar] [CrossRef]
- Klingbeil, D.; Klinger, C.; Kinder, J.; Baer, W. Investigations for indications of deliberate blasting on the front bulkhead of the ro-ro ferry MV ESTONIA. Eng. Fail. Anal. 2014, 43, 186–197. [Google Scholar] [CrossRef]
- Gill, G.W.; Wahner, C.M. The Herald of Free Enterprise Casualty and Its Effect on Maritime Safety Philosophy. Mar. Technol. Soc. J. 2012, 46, 72–84. [Google Scholar] [CrossRef]
- Lee, D.; Hong, S.Y.; Lee, G.J. Theoretical and experimental study on dynamic behavior of a damaged ship in waves. Ocean Eng. 2007, 34, 21–31. [Google Scholar] [CrossRef]
- Xu, B.-Z.; Du, J.-L.; Tian, B.-J. Flooding of damaged hold and its affecting factors. J. Dalian Mariti Me Univ. 2004, 30, 52–57. [Google Scholar]
- Zhang, Y.; Hu, T.-N. Time-Domain Simulation of Damaged Ship Based on Fluid Exchange. Ship Eng. (Chin.) 2011, 33, 135–156. [Google Scholar]
- Lee, S.; You, J.-M.; Lee, H.-H.; Lim, T.; Rhee, S.H.; Rhee, K.-P. Preliminary tests of a damaged ship for CFD validation. Int. J. Nav. Archit. Ocean Eng. 2012, 4, 172–181. [Google Scholar] [CrossRef]
- Begovic, E.; Mortola, G.; Incecik, A.; Day, A.H. Experimental assessment of intact and damaged ship motions in head, beam and quartering seas. Ocean Eng. 2013, 72, 209–226. [Google Scholar] [CrossRef]
- Domeh, V.D.K.; Sobey, A.J.; Hudson, D.A. A preliminary experimental investigation into the influence of compartment permeability on damaged ship response in waves. Appl. Ocean Res. 2015, 52, 27–36. [Google Scholar] [CrossRef]
- Acanfora, M.; De Luca, F. An experimental investigation into the influence of the damage openings on ship response. Appl. Ocean Res. 2016, 58, 62–70. [Google Scholar] [CrossRef]
- Acanfora, M.; De Luca, F. An Experimental Investigation on the Dynamic Response of a Damaged Ship with a realistic arrangement of the flooded compartment. Appl. Ocean Res. 2017, 69, 191–204. [Google Scholar] [CrossRef]
- Bašić, J.; Degiuli, N.; Dejhalla, R. Total resistance prediction of an intact and damaged tanker with flooded tanks in calm water. Ocean Eng. 2017, 130, 83–91. [Google Scholar] [CrossRef]
- Chan, H.S.; Atlar, M.; Incecik, A. Global wave loads on intact and damaged Ro-Ro ships in regular oblique waves. Mar. Struct. 2003, 16, 323–344. [Google Scholar] [CrossRef]
- Gao, Z.; Gao, Q.; Vassalos, D. Numerical simulation of flooding of a damaged ship. Ocean Eng. 2011, 38, 1649–1662. [Google Scholar] [CrossRef]
- Gao, Z.; Gao, Q.; Vassalos, D. Numerical study of damaged ship flooding in beam seas. Ocean Eng. 2013, 61, 77–87. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, Y.; Su, Y.; Chen, L. Numerical study of damaged ship’s compartment sinking with air compression effect. Ocean Eng. 2018, 147, 68–76. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, Y.; Su, Y. On damaged ship motion and capsizing in beam waves due to sudden water ingress using the RANS method. Appl. Ocean Res. 2020, 95, 102047. [Google Scholar] [CrossRef]
- Ming, F.R.; Zhang, A.M.; Cheng, H.; Sun, P.N. Numerical simulation of a damaged ship cabin flooding in transversal waves with Smoothed Particle Hydrodynamics method. Ocean Eng. 2018, 165, 336–352. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, J.; Sun, Z.; Moctar, O.e.; Zong, Z. Numerically simulated flooding of a freely-floating two-dimensional damaged ship section using an improved MPS method. Appl. Ocean Res. 2020, 101, 102207. [Google Scholar] [CrossRef]
- Xiao, D.; Yang, P.; Fang, F.; Xiang, J.; Pain, C.C.; Navon, I.M. Non-intrusive reduced order modelling of fluid–structure interactions. Comput. Methods Appl. Mech. Eng. 2016, 303, 35–54. [Google Scholar] [CrossRef]
- Whisenant, M.J.; Ekici, K. Galerkin-Free Technique for the Reduced-Order Modeling of Fluid-Structure Interaction via Machine Learning. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Sufyan, M.; Farooq, H.; Akhtar, I.; Bangash, Z. Pressure mode decomposition analysis of the flow past a cross-flow oscillating circular cylinder. J. Mech. Sci. Technol. 2021, 35, 153–158. [Google Scholar] [CrossRef]
- Wu, P.; Gong, S.; Pan, K.; Qiu, F.; Feng, W.; Pain, C. Reduced order model using convolutional auto-encoder with self-attention. Phys. Fluids 2021, 33, 077107. [Google Scholar] [CrossRef]
- Noman, A.S.; Deeba, F.; Bagchi, A. Health Monitoring of Structures Using Statistical Pattern Recognition Techniques. J. Perform. Constr. Facil. 2013, 27, 575–584. [Google Scholar] [CrossRef]
- Antoniadou, I.; Dervilis, N.; Papatheou, E.; Maguire, A.E.; Worden, K. Aspects of structural health and condition monitoring of offshore wind turbines. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 2015, 373, 14. [Google Scholar] [CrossRef] [PubMed]
- Holmes, G.; Sartor, P.; Reed, S.; Southern, P.; Worden, K.; Cross, E. Prediction of landing gear loads using machine learning techniques. Struct. Health Monit. 2016, 15, 568–582. [Google Scholar] [CrossRef]
- Jian, M.Z.; Zhao, H.D.; Yao, J.J. Application and prospect of Artificial Neural Network. Electron. Des. Eng. 2011, 19, 62–65. [Google Scholar]
- Martić, I.; Degiuli, N.; Majetić, D.; Farkas, A. Artificial Neural Network Model for the Evaluation of Added Resistance of Container Ships in Head Waves. J. Mar. Sci. Eng. 2021, 9, 826. [Google Scholar] [CrossRef]
- Yildiz, B. Prediction of Residual Resistance of a Trimaran Vessel by Using an Artificial Neural Network. Brodogradnja 2022, 73, 127–140. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Golub, G.H.; Reinsch, C. Singular value decomposition and least squares solutions. Numer. Math. 1970, 14, 403. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. SUPPORT-VECTOR NETWORKS. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- MathWorks. MATLAB User’s Manual; MathWorks: Portola Valley, CA, USA, 2020. [Google Scholar]
- Hawkins, D.M. The Problem of Overfitting. J. Chem. Inf. Comput. Sci. 2004, 44, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Wood, S. Fast Stable Direct Fitting and Smoothness Selection for Generalized Additive Models. J. R. Stat. Soc. Ser. B 2008, 70, 495–518. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J.; Smola, A. Learning with Kernels—Support Vector Machines, Regularization, Optimization and Beyond; MIT Press: Cambridge, MA, USA, 2001; Volume 98. [Google Scholar]
- Weymouth, G.D.; Yue, D.K.P. Physics-Based Learning Models for Ship Hydrodynamics. J. Ship Res. 2013, 57, 1–12. [Google Scholar] [CrossRef]
- Pitchforth, D.J.; Rogers, T.J.; Tygesen, U.T.; Cross, E.J. Grey-box models for wave loading prediction. Mech. Syst. Signal Process. 2021, 159, 107741. [Google Scholar] [CrossRef]
- Siemens Digital Industries Software. Simcenter STAR-CCM+ User’s Manual; Siemens Digital Industries Software: Plano, TX, USA, 2020. [Google Scholar]
- Begovic, E.; Day, A.H.; Incecik, A. An experimental study of hull girder loads on an intact and damaged naval ship. Ocean Eng. 2017, 133, 47–65. [Google Scholar] [CrossRef]
- Martic, I.; Degiuli, N.; Farkas, A.; Basic, J. Mesh Sensitivity Analysis for Numerical Simulation of a Damaged Ship Model. In Proceedings of the Twenty-seventh (2017) International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017. [Google Scholar]
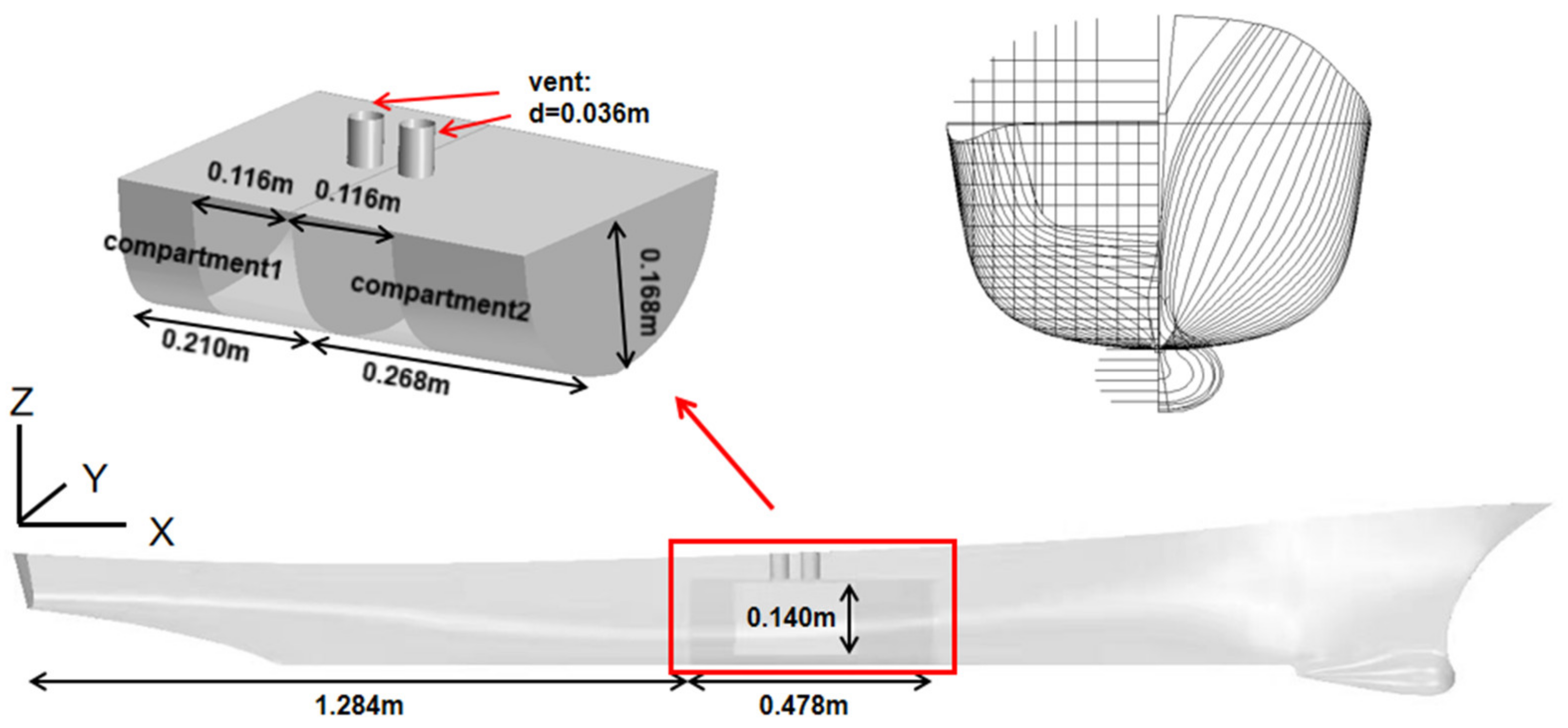
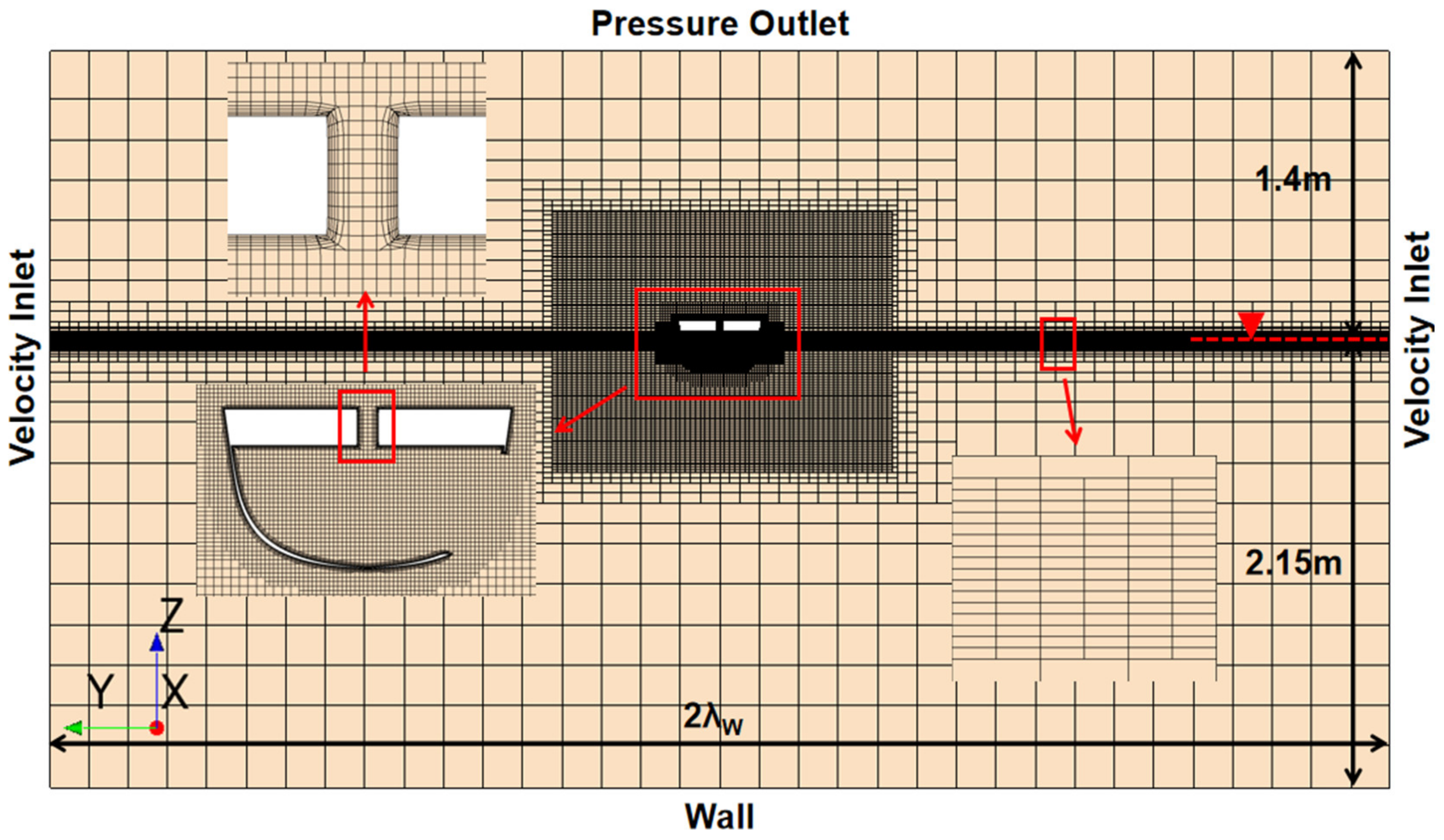


| Parameters | Real Ship Scale | Model Scale |
|---|---|---|
| Scale | 1 | 51 |
| Length (LOA) | 153.3 m | 3.0 m |
| Breadth (BOA) | 20.540 m | 0.403 m |
| Draft (T) | 6.150 m | 0.120 m |
| Displacement (∆) | 8423.3 ton | 63.5 kg |
| Initial stability height (GM) | 1.938 m | 0.038 m |
| Center of gravity (KG) | 7.555 m | 0.148 m |
| Longitudinal position of center of gravity (LCG) | 70.137 m | 1.375 m |
| Roll radius of gyration (Kxx) | 6.932 m | 0.136 m |
| Tw (s) Model Scale | ΛW (M) Model Scale | Hw (m) Model Scale |
|---|---|---|
| 1.12 | 1.958 | 0.039 |
| 1.26 | 2.477 | 0.050 |
| 1.33 | 2.760 | 0.055 |
| 1.40 | 3.058 | 0.061 |
| 1.47 | 3.370 | 0.067 |
| 1.54 | 3.696 | 0.074 |
| 1.68 | 4.386 | 0.088 |
| 1.82 | 5.117 | 0.102 |
| 1.96 | 5.878 | 0.118 |
| Incident Wave Periods (s) | Exp. (Begovic [42]) | Error | |
|---|---|---|---|
| 1.12 | 0.564 | 0.456 | 23.58% |
| 1.26 | 1.104 | 1.228 | 10.08% |
| 1.33 | 2.148 | 2.000 | 7.40% |
| 1.4 | 4.730 | 4.772 | 0.88% |
| 1.47 | 4.807 | 4.333 | 10.94% |
| 1.54 | 4.386 | 4.228 | 3.75% |
| 1.68 | 3.628 | 3.543 | 2.41% |
| 1.82 | 2.761 | 2.842 | 2.85% |
| 1.96 | 2.310 | 2.158 | 7.07% |
| Average error | 7.66% | ||
| Case No. | Incident Wave Periods for Training Data/s | Incident Wave Periods for Testing Data/s |
|---|---|---|
| 1 | 1.12 s, 1.33 s, 1.40 s, 1.54 s, 1.68 s, 1.96 s | 1.26 s, 1.47 s, 1.82 s |
| 2 | 1.12 s, 1.26 s, 1.40 s, 1.54 s, 1.68 s, 1.96 s | 1.33 s, 1.47 s, 1.82 s |
| 3 | 1.12 s, 1.33 s, 1.40 s, 1.54 s, 1.82 s, 1.96 s | 1.26 s, 1.47 s, 1.68 s |
| 4 | 1.12 s, 1.33 s, 1.47 s, 1.54 s, 1.68 s, 1.96 s | 1.26 s, 1.40 s, 1.82 s |
| 5 | 1.12 s, 1.33 s, 1.47 s, 1.68 s, 1.82 s, 1.96 s | 1.26 s, 1.40 s, 1.54 s |
| 6 | 1.12 s, 1.26 s, 1.40 s, 1.54 s, 1.82 s, 1.96 s | 1.33 s, 1.47 s, 1.68 s |
| 7 | 1.12 s, 1.33 s, 1.40 s, 1.47 s, 1.68 s, 1.96 s | 1.26 s, 1.54 s, 1.82 s |
| 8 | 1.12 s, 1.26 s, 1.33 s, 1.47 s, 1.68 s, 1.96 s | 1.40 s, 1.54 s, 1.82 s |
| Case No. | Incident Wave Periods for Training Data/s | Incident Wave Periods for Testing Data/s |
|---|---|---|
| 1 | 1.12 s, 1.33 s, 1.47 s, 1.68 s, 1.96 s | 1.26 s, 1.40 s, 1.54 s, 1.82 s |
| 2 | 1.12 s, 1.26 s, 1.47 s, 1.68 s, 1.96 s | 1.33 s, 1.40 s, 1.54 s, 1.82 s |
| 3 | 1.12 s, 1.33 s, 1.47 s, 1.82 s, 1.96 s | 1.26 s, 1.40 s, 1.54 s, 1.68 s |
| 4 | 1.12 s, 1.26 s, 1.47 s, 1.82 s, 1.96 s | 1.33 s, 1.40 s, 1.54 s, 1.68 s |
| 5 | 1.12 s, 1.26 s, 1.40 s, 1.82 s, 1.96 s | 1.26 s, 1.47 s, 1.54 s, 1.82 s |
| 6 | 1.12 s, 1.33 s, 1.54 s, 1.68 s, 1.96 s | 1.26 s, 1.40 s, 1.47 s, 1.82 s |
| 7 | 1.12 s, 1.26 s, 1.40 s, 1.68 s, 1.96 s | 1.33 s, 1.47 s, 1.54 s, 1.82 s |
| 8 | 1.12 s, 1.33 s, 1.54 s, 1.82 s, 1.96 s | 1.26 s, 1.40 s, 1.47 s, 1.68 s |
| Case No. | Incident Wave Periods for Training Data/s | Incident Wave Periods for Testing Data/s |
|---|---|---|
| 1 | 1.12 s, 1.33 s, 1.47 s, 1.96 s | 1.26 s, 1.40 s, 1.54 s, 1.68 s, 1.82 s |
| 2 | 1.12 s, 1.47 s, 1.68 s, 1.96 s | 1.26 s, 1.33 s, 1.40 s, 1.54 s, 1.82 s |
| 3 | 1.12 s, 1.40 s, 1.54 s, 1.96 s | 1.26 s, 1.33 s, 1.47 s, 1.68 s, 1.82 s |
| 4 | 1.12 s, 1.40 s, 1.68 s, 1.96 s | 1.26 s, 1.33 s, 1.47 s, 1.54 s, 1.82 s |
| 5 | 1.12 s, 1.33 s, 1.54 s, 1.96 s | 1.26 s, 1.40 s, 1.47 s, 1.54 s, 1.82 s |
| 6 | 1.12 s, 1.40 s, 1.47 s, 1.96 s | 1.26 s, 1.33 s, 1.54 s, 1.68 s, 1.82 s |
| 7 | 1.12 s, 1.47 s, 1.54 s, 1.96 s | 1.26 s, 1.33 s, 1.40 s, 1.68 s, 1.82 s |
| 8 | 1.12 s, 1.54 s, 1.82 s, 1.96 s | 1.26 s, 1.33 s, 1.40 s, 1.47 s, 1.68 s |
| Incident Wave Periods/s | Refined CFD Mesh Number/10 k | Rough CFD Mesh Number/10 k |
|---|---|---|
| 1.12 | 483 | 204 |
| 1.26 | 631 | 163 |
| 1.33 | 356 | 161 |
| 1.40 | 375 | 114 |
| 1.47 | 384 | 144 |
| 1.54 | 391 | 149 |
| 1.68 | 462 | 135 |
| 1.82 | 528 | 127 |
| 1.96 | 485 | 112 |
| Case No. | Pure Refined CFD Simulation Time (CPU Hours) | Proposed Model Simulation Time (CPU Hours) | Reduction Rate of Computational Time (%) |
|---|---|---|---|
| 1 | 27,257 | 20,655 | 24 |
| 2 | 19,947 | 27 | |
| 3 | 21,275 | 22 | |
| 4 | 19,770 | 27 | |
| 5 | 19,062 | 30 | |
| 6 | 20,567 | 25 | |
| 7 | 19,770 | 27 | |
| 8 | 18,885 | 31 |
| Case No. | Pure Refined CFD Simulation Time (CPU Hours) | Proposed Model Simulation Time (CPU Hours) | Reduction Rate of Computational Time (%) |
|---|---|---|---|
| 1 | 27,257 | 16,231 | 40 |
| 2 | 15,523 | 43 | |
| 3 | 16,850 | 38 | |
| 4 | 16,142 | 41 | |
| 5 | 17,027 | 38 | |
| 6 | 17,116 | 37 | |
| 7 | 16,408 | 40 | |
| 8 | 17,735 | 35 |
| Case No. | Pure Refined CFD Simulation Time (CPU Hours) | Proposed Model Simulation Time (CPU Hours) | Reduction Rate of Computational Time (%) |
|---|---|---|---|
| 1 | 27,257 | 14,018 | 51 |
| 2 | 12,868 | 47 | |
| 3 | 15,080 | 55 | |
| 4 | 13,753 | 50 | |
| 5 | 14,903 | 555 | |
| 6 | 14,195 | 52 | |
| 7 | 14,195 | 52 | |
| 8 | 14,372 | 53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Sun, L.-y.; Xu, L.-x.; Hu, Y.-l.; Zhang, G.-y.; Zong, Z. A CFD-Based Data-Driven Reduced Order Modeling Method for Damaged Ship Motion in Waves. J. Mar. Sci. Eng. 2023, 11, 686. https://doi.org/10.3390/jmse11040686
Sun Z, Sun L-y, Xu L-x, Hu Y-l, Zhang G-y, Zong Z. A CFD-Based Data-Driven Reduced Order Modeling Method for Damaged Ship Motion in Waves. Journal of Marine Science and Engineering. 2023; 11(4):686. https://doi.org/10.3390/jmse11040686
Chicago/Turabian StyleSun, Zhe, Lu-yu Sun, Li-xin Xu, Yu-long Hu, Gui-yong Zhang, and Zhi Zong. 2023. "A CFD-Based Data-Driven Reduced Order Modeling Method for Damaged Ship Motion in Waves" Journal of Marine Science and Engineering 11, no. 4: 686. https://doi.org/10.3390/jmse11040686
APA StyleSun, Z., Sun, L.-y., Xu, L.-x., Hu, Y.-l., Zhang, G.-y., & Zong, Z. (2023). A CFD-Based Data-Driven Reduced Order Modeling Method for Damaged Ship Motion in Waves. Journal of Marine Science and Engineering, 11(4), 686. https://doi.org/10.3390/jmse11040686