Optimization Study of Marine Energy Harvesting from Vortex-Induced Vibration Using a Response-Surface Method
Abstract
1. Introduction
2. Optimization Methodology
2.1. Concept of Response-Surface Method
2.2. Feasibility Verification of Response-Surface Method
3. Numerical Methods of Modeling Fluid–Structure Interaction
3.1. Computational Fluid Dynamics
3.2. Rigid Body Motions
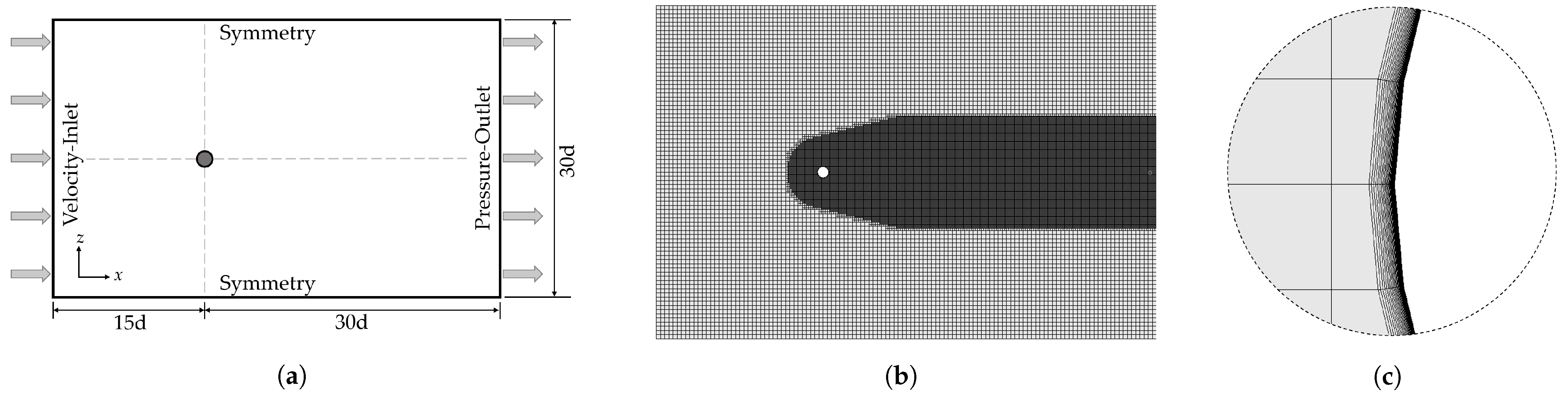
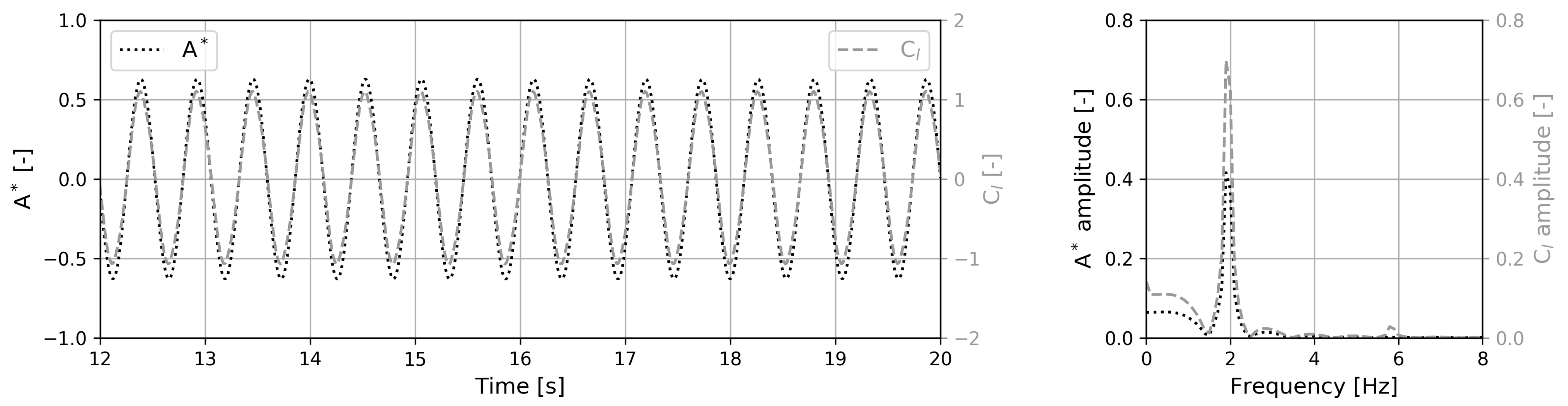
4. Test Case Description and Solution Verification
5. Simulation Design Using a Response-Surface Method
5.1. Simulation Design and Statistical Analysis
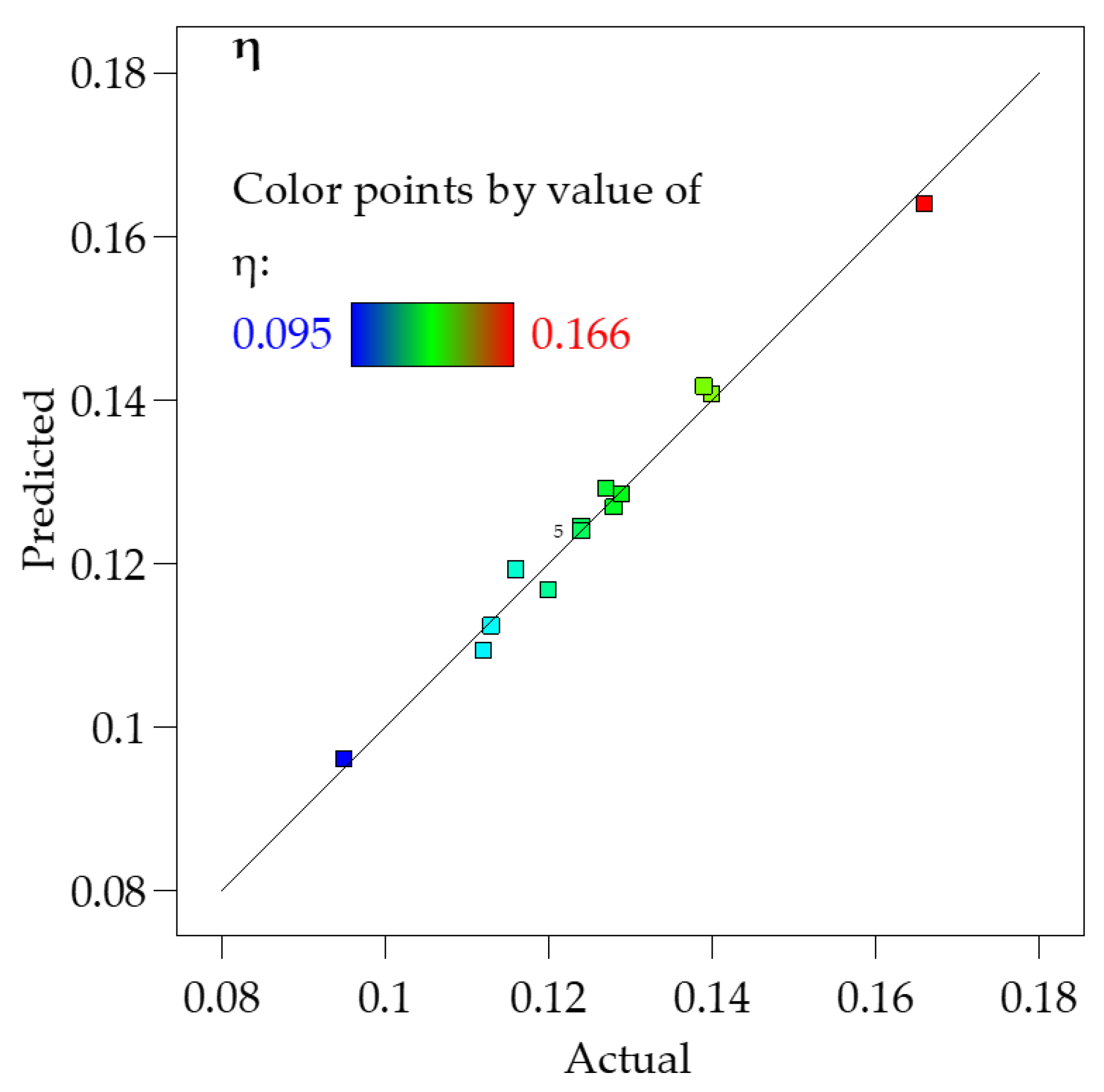
5.2. Verification of Optimum Parameters Using CFD Simulations
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANOVA | Analysis of variance |
| BBD | Box–Behnken design |
| CFD | Computational-fluid dynamics |
| CFL | Courant–Friedrichs–Lewy number |
| DOE | Design-of-experiment |
| DOF | Degree of freedom |
| RANS | Reynolds-averaged Navier–Stokes |
| RSM | Response-surface method |
| RSM-BBD | Box–Behnken design response surface method |
| VIV | Vortex-induced vibration |
| VIVACE | Vortex-induced vibration aquatic clean energy |
| Nomenclature | |
| Time step | |
| Grid size | |
| Numerical error | |
| Error variable | |
| Damping ratio | |
| Energy capture efficiency | |
| Kinematic viscosity | |
| Density | |
| Solution obtained on grid i | |
| Numerical benchmark result | |
| Amplitude ratio | |
| c | Structural damping |
| Drag coefficient | |
| Lift coefficient | |
| d | Diameter |
| Natural frequency | |
| k | Structural stiffness |
| Force vector | |
| Gravity vector | |
| l | Length |
| m | Structural mass |
| Mass ratio | |
| Surface normal vector | |
| p | Pressure |
| P | Ratio of convergence |
| Observed order of accuracy | |
| Theoretical order of convergence | |
| R | Convergence ratio |
| Reynolds number | |
| T | Oscillatory period |
| Uncertainty | |
| v | Free stream velocity |
| Fluid velocity field vector | |
| Reduced velocity | |
| Operating variable | |
| Dimensionless grid height for the first-layer grid |
References
- Khan, M.; Bhuyan, G.; Iqbal, M.; Quaicoe, J. Hydrokinetic energy conversion systems and assessment of horizontal and vertical axis turbines for river and tidal applications: A technology status review. Appl. Energy 2009, 86, 1823–1835. [Google Scholar] [CrossRef]
- Williamson, C.H.; Roshko, A. Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 1988, 2, 355–381. [Google Scholar] [CrossRef]
- Feng, C. The Measurement of Vortex Induced Effects in Flow Past Stationary and Oscillating Circular and D-Section Cylinders. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 1968. [Google Scholar]
- Khalak, A.; Williamson, C. Dynamics of a hydroelastic cylinder with very low mass and damping. J. Fluids Struct. 1996, 10, 455–472. [Google Scholar] [CrossRef]
- Khalak, A.; Williamson, C. Fluid forces and dynamics of a hydroelastic structure with very low mass and damping. J. Fluids Struct. 1997, 11, 973–982. [Google Scholar] [CrossRef]
- Govardhan, R.; Williamson, C. Defining the ‘modified Griffin plot’ in vortex-induced vibration: Revealing the effect of Reynolds number using controlled damping. J. Fluid Mech. 2006, 561, 147–180. [Google Scholar] [CrossRef]
- Williamson, C.; Jauvtis, N. A high-amplitude 2T mode of vortex-induced vibration for a light body in XY motion. Eur. J. Mech.-B/Fluids 2004, 23, 107–114. [Google Scholar] [CrossRef]
- Shi, L.; Yang, G.; Yao, S. Large eddy simulation of flow past a square cylinder with rounded leading corners: A comparison of 2D and 3D approaches. J. Mech. Sci. Technol. 2018, 32, 2671–2680. [Google Scholar] [CrossRef]
- Cravero, C.; Marogna, N.; Marsano, D. A Numerical Study of correlation between recirculation length and shedding frequency in vortex shedding phenomena. WSEAS Trans. Fluid Mech. 2021, 16, 48–62. [Google Scholar] [CrossRef]
- Bearman, P.W. Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 1984, 16, 195–222. [Google Scholar] [CrossRef]
- Sarpkaya, T. A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 2004, 19, 389–447. [Google Scholar] [CrossRef]
- Wu, X.; Ge, F.; Hong, Y. A review of recent studies on vortex-induced vibrations of long slender cylinders. J. Fluids Struct. 2012, 28, 292–308. [Google Scholar] [CrossRef]
- Bernitsas, M.M.; Raghavan, K.; Ben-Simon, Y.; Garcia, E. VIVACE (vortex induced vibration aquatic clean energy): A new concept in generation of clean and renewable energy from fluid flow. In Proceedings of the 25th International Conference on Offshore Mechanics and Arctic Engineering, Hamburg, Germany, 4–9 June 2006; Volume 47470, pp. 619–637. [Google Scholar]
- Chang, C.C.J.; Kumar, R.A.; Bernitsas, M.M. VIV and galloping of single circular cylinder with surface roughness at 3.0 × 104 ≤ Re ≤ 1.2 × 105. Ocean Eng. 2011, 38, 1713–1732. [Google Scholar] [CrossRef]
- Ding, L.; Bernitsas, M.M.; Kim, E.S. 2-D URANS vs. experiments of flow induced motions of two circular cylinders in tandem with passive turbulence control for 30,000< Re< 105,000. Ocean Eng. 2013, 72, 429–440. [Google Scholar]
- Garcia, E.M.; Park, H.; Chang, C.C.; Bernitsas, M.M. Effect of damping on variable added mass and lift of circular cylinders in vortex-induced vibrations. In Proceedings of the 2014 Oceans-St. John’s, St. John’s, NL, Canada, 14–19 September 2014; pp. 1–5. [Google Scholar]
- Narendran, K.; Murali, K.; Sundar, V. Investigations into efficiency of vortex induced vibration hydro-kinetic energy device. Energy 2016, 109, 224–235. [Google Scholar] [CrossRef]
- Ding, L.; Zhang, L.; Wu, C.; Mao, X.; Jiang, D. Flow induced motion and energy harvesting of bluff bodies with different cross sections. Energy Convers. Manag. 2015, 91, 416–426. [Google Scholar] [CrossRef]
- Zhang, B.; Song, B.; Mao, Z.; Tian, W.; Li, B. Numerical investigation on VIV energy harvesting of bluff bodies with different cross sections in tandem arrangement. Energy 2017, 133, 723–736. [Google Scholar] [CrossRef]
- Wu, W.; Wang, J. Numerical simulation of VIV for a circular cylinder with a downstream control rod at low Reynolds number. Eur. J. Mech.-B/Fluids 2018, 68, 153–166. [Google Scholar] [CrossRef]
- Zhang, B.; Mao, Z.; Song, B.; Ding, W.; Tian, W. Numerical investigation on effect of damping-ratio and mass-ratio on energy harnessing of a square cylinder in FIM. Energy 2018, 144, 218–231. [Google Scholar] [CrossRef]
- Raghavan, K.; Bernitsas, M. Experimental investigation of Reynolds number effect on vortex induced vibration of rigid circular cylinder on elastic supports. Ocean Eng. 2011, 38, 719–731. [Google Scholar] [CrossRef]
- Zhang, B.; Mao, Z.; Song, B.; Tian, W.; Ding, W. Numerical investigation on VIV energy harvesting of four cylinders in close staggered formation. Ocean Eng. 2018, 165, 55–68. [Google Scholar] [CrossRef]
- Wang, J.; Li, G.; Zhou, S.; Litak, G. Enhancing wind energy harvesting using passive turbulence control devices. Appl. Sci. 2019, 9, 998. [Google Scholar] [CrossRef]
- Jankovic, A.; Chaudhary, G.; Goia, F. Designing the design of experiments (DOE)–An investigation on the influence of different factorial designs on the characterization of complex systems. Energy Build. 2021, 250, 111298. [Google Scholar] [CrossRef]
- Box, G.E.; Wilson, K.B. On the experimental attainment of optimum conditions. In Breakthroughs in Statistics: Methodology and Distribution; Springer: New York, NY, USA, 1992; pp. 270–310. [Google Scholar]
- Seok, W.; Kim, G.H.; Seo, J.; Rhee, S.H. Application of the design of experiments and computational fluid dynamics to bow design improvement. J. Mar. Sci. Eng. 2019, 7, 226. [Google Scholar] [CrossRef]
- Yi, Q.; Zhang, G.; Amon, B.; Hempel, S.; Janke, D.; Saha, C.K.; Amon, T. Modelling air change rate of naturally ventilated dairy buildings using response surface methodology and numerical simulation. Build. Simul. 2021, 14, 827–839. [Google Scholar] [CrossRef]
- Qian, G.; Xiaobing, Y.; Zhenjiang, W.; Dexin, C.; Jianyuan, H. Optimization of proportioning of mixed aggregate filling slurry based on BBD response surface method. J. Hunan Univ. Nat. Sci. 2019, 46, 47–55. [Google Scholar]
- Zhao, M.; Wu, L.; Song, S.; Tong, M.; Yue, M. Optimization of extraction process of gantaishu granules by Box-Behnken response surface method. Mod. Tradit. Chin. Med. 2022, 42, 56–61. [Google Scholar]
- Tak, B.y.; Tak, B.s.; Kim, Y.j.; Park, Y.j.; Yoon, Y.h.; Min, G.h. Optimization of color and COD removal from livestock wastewater by electrocoagulation process: Application of Box–Behnken design (BBD). J. Ind. Eng. Chem. 2015, 28, 307–315. [Google Scholar] [CrossRef]
- Mohammed, B.B.; Hsini, A.; Abdellaoui, Y.; Abou Oualid, H.; Laabd, M.; El Ouardi, M.; Addi, A.A.; Yamni, K.; Tijani, N. Fe-ZSM-5 zeolite for efficient removal of basic Fuchsin dye from aqueous solutions: Synthesis, characterization and adsorption process optimization using BBD-RSM modeling. J. Environ. Chem. Eng. 2020, 8, 104419. [Google Scholar] [CrossRef]
- Agrawal, M.; Saraf, S.; Pradhan, M.; Patel, R.J.; Singhvi, G.; Alexander, A. Design and optimization of curcumin loaded nano lipid carrier system using Box-Behnken design. Biomed. Pharmacother. 2021, 141, 111919. [Google Scholar] [CrossRef]
- Reghioua, A.; Barkat, D.; Jawad, A.H.; Abdulhameed, A.S.; Al-Kahtani, A.A.; ALOthman, Z.A. Parametric optimization by Box–Behnken design for synthesis of magnetic chitosan-benzil/ZnO/Fe3O4 nanocomposite and textile dye removal. J. Environ. Chem. Eng. 2021, 9, 105166. [Google Scholar] [CrossRef]
- Ferreira, S.C.; Bruns, R.; Ferreira, H.S.; Matos, G.D.; David, J.; Brandão, G.; da Silva, E.P.; Portugal, L.; Dos Reis, P.; Souza, A.; et al. Box-Behnken design: An alternative for the optimization of analytical methods. Anal. Chim. Acta 2007, 597, 179–186. [Google Scholar] [CrossRef]
- Wu, S. Research on VIV Mechanism of Cylinder Oscillator with Damping in Tidal Current Energy Converter. Ph.D. Thesis, Ocean University of China, Qingdao, China, 2015. [Google Scholar]
- Yue, Y. Numerical Simulation of Current-Induced Vibration of a Single Confined Cylinder Generated by Ocean Current Energy. Ph.D. Thesis, Jiangsu University of Science and Technology, Zhenjiang, China, 2019. [Google Scholar]
- Bai, X.; Chen, Y.; Sun, H.; Sun, M. Numerical study on ocean current energy converter by tandem cylinder with different diameter using flow-induced vibration. Ocean Eng. 2022, 257, 111539. [Google Scholar] [CrossRef]
- Palanikumar, K. Introductory Chapter: Response Surface Methodology in Engineering Science. In Response Surface Methodology in Engineering Science; IntechOpen: London, UK, 2021. [Google Scholar]
- Box, G.; Behnken, D. Some new three level second order designs for surface fitting. Stat. Tech. Res. Group Tech. Rep. 1958, 1, 455–475. [Google Scholar]
- Box, G.E.; Behnken, D.W. Some new three level designs for the study of quantitative variables. Technometrics 1960, 2, 455–475. [Google Scholar] [CrossRef]
- Borkowski, J.J. Spherical prediction-variance properties of central composite and Box—Behnken designs. Technometrics 1995, 37, 399–410. [Google Scholar]
- Jiang, C. Mathematical Modelling of Wave-Induced Motions and Loads on Moored Offshore Structures. Ph.D. Thesis, Universität Duisburg-Essen, Duisburg, Germany, 2021. [Google Scholar]
- Jones, W.P.; Launder, B.E. The prediction of laminarization with a two-equation model of turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Ong, M.C.; Utnes, T.; Holmedal, L.E.; Myrhaug, D.; Pettersen, B. Numerical simulation of flow around a smooth circular cylinder at very high Reynolds numbers. Mar. Struct. 2009, 22, 142–153. [Google Scholar] [CrossRef]
- Shao, J.; Zhang, C. Numerical analysis of the flow around a circular cylinder using RANS and LES. Int. J. Comput. Fluid Dyn. 2006, 20, 301–307. [Google Scholar] [CrossRef]
- Xing, T.; Stern, F. Factors of safety for Richardson extrapolation. J. Fluids Eng. 2010, 132, 061403. [Google Scholar] [CrossRef]
- Phillips, T.S.; Roy, C.J. Richardson extrapolation-based discretization uncertainty estimation for computational fluid dynamics. J. Fluids Eng. 2014, 136, 121401. [Google Scholar] [CrossRef]
- Yuan, W.; Sun, H.; Kim, E.S.; Li, H.; Beltsos, N.; Bernitsas, M.M. Hydrokinetic Energy Conversion by Flow-Induced Oscillation of Two Tandem Cylinders of Different Stiffness. J. Offshore Mech. Arct. Eng. 2021, 143, 062001. [Google Scholar] [CrossRef]
- Anwar, M.U.; Khan, N.B.; Arshad, M.; Munir, A.; Bashir, M.N.; Jameel, M.; Rehman, M.F.; Eldin, S.M. Variation in Vortex-Induced Vibration Phenomenon Due to Surface Roughness on Low-and High-Mass-Ratio Circular Cylinders: A Numerical Study. J. Mar. Sci. Eng. 2022, 10, 1465. [Google Scholar] [CrossRef]
- Wang, H.; Yu, H.; Sun, Y.; Sharma, R.N. The influence of reduced velocity on the control of two-degree-of-freedom vortex induced vibrations of a circular cylinder via synthetic jets. Fluid Dyn. Res. 2022, 54, 055506. [Google Scholar] [CrossRef]
- Bernitsas, M.M. Harvesting energy by flow included motions. In Springer Handbook of Ocean Engineering; Springer: New York, NY, USA, 2016; pp. 1163–1244. [Google Scholar]
- Jiang, C.; Chiba, S.; Waki, M.; Fujita, K.; el Moctar, O. Investigation of a Novel Wave Energy Generator Using Dielectric Elastomer. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Virtual, Online, 3–7 August 2020; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 84416, p. V009T09A012. [Google Scholar]
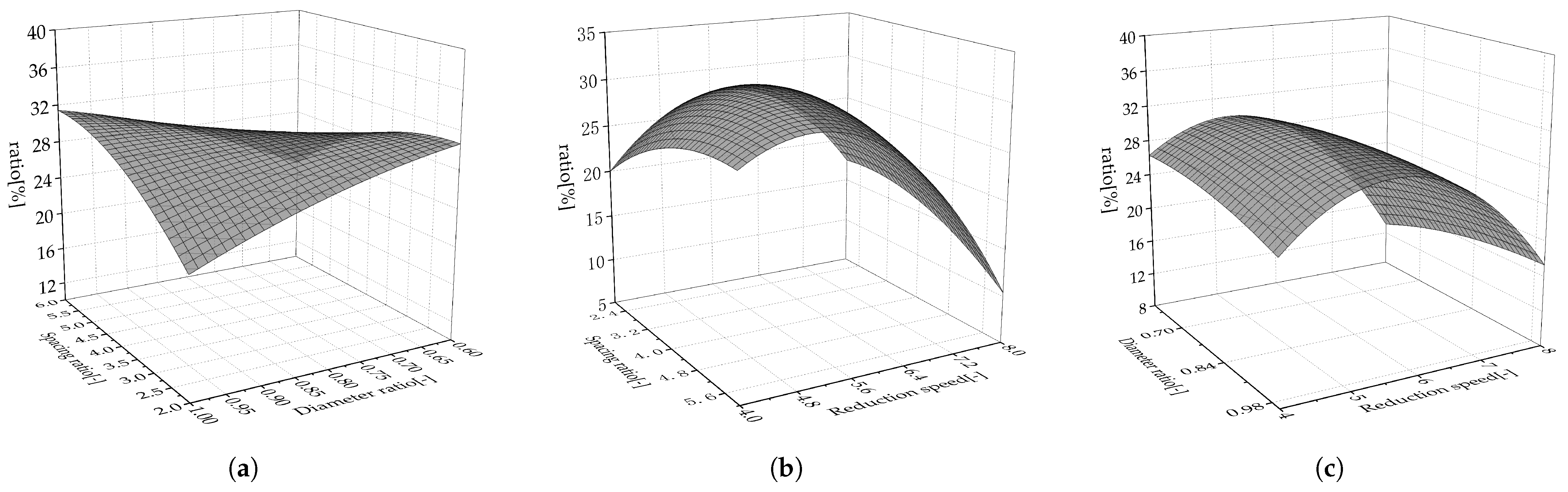


| Run | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | OP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [%] | 29.87 | 18.33 | 35.41 | 21.66 | 29.87 | 27.08 | 14.16 | 29.87 | 25.25 | 16.25 | 22.54 | 9.58 | 28.33 | 29.87 | 16.25 | 29.87 | 26.66 | 36.10 |
| Property | [-] | [-] | [-] | R [-] | [-] | [%] | [%] | [%] | U [%] |
|---|---|---|---|---|---|---|---|---|---|
| 0.5625 | 0.6043 | 0.6075 | 0.077 | 0.6080 | −7.48 | −0.61 | −0.08 | 0.41 | |
| 0.5950 | 0.6075 | 0.6087 | 0.096 | 0.6089 | −2.29 | −0.76 | −0.04 | 0.16 |
| Variables | Symbols | Level −1 | Level 0 | Level 1 |
|---|---|---|---|---|
| Velocity [m/s] | A | 0.55 | 0.65 | 0.75 |
| Stiffness [N/m] | B | 300 | 400 | 500 |
| Mass [kg] | C | 2.60 | 3.00 | 3.40 |
| Run | Factor A Velocity [m/s] | Factor B Stiffness [N/m] | Factor C Mass [kg] | Response Efficiency [-] |
|---|---|---|---|---|
| 1 | 0.55 | 300 | 3.0 | 0.140 |
| 2 | 0.75 | 300 | 3.0 | 0.127 |
| 3 | 0.55 | 500 | 3.0 | 0.166 |
| 4 | 0.75 | 500 | 3.0 | 0.113 |
| 5 | 0.55 | 400 | 2.6 | 0.139 |
| 6 | 0.75 | 400 | 2.6 | 0.095 |
| 7 | 0.55 | 400 | 3.4 | 0.128 |
| 8 | 0.75 | 400 | 3.4 | 0.112 |
| 9 | 0.65 | 300 | 2.6 | 0.120 |
| 10 | 0.65 | 500 | 2.6 | 0.129 |
| 11 | 0.65 | 300 | 3.4 | 0.124 |
| 12 | 0.65 | 500 | 3.4 | 0.116 |
| 13 | 0.65 | 400 | 3.0 | 0.124 |
| Source | Coefficient | Sum of Squares | DOF | Mean Square | f-Value | p-Value |
|---|---|---|---|---|---|---|
| Model | 0.1240 | 0.0034 | 9 | 0.0004 | 55.50 | <0.0001 |
| A | −0.0158 | 0.0020 | 1 | 0.0020 | 290.9 | <0.0001 |
| B | 0.0016 | 0.0000 | 1 | 0.0000 | 3.100 | 0.1218 |
| C | −0.0004 | 1.1 × 10 | 1 | 1.1 × 10 | 0.165 | 0.6968 |
| AB | −0.0100 | 0.0004 | 1 | 0.0004 | 58.64 | 0.0001 |
| AC | 0.0070 | 0.0002 | 1 | 0.0002 | 28.73 | 0.0011 |
| BC | −0.0042 | 0.0001 | 1 | 0.0001 | 10.59 | 0.0140 |
| A | 0.0044 | 0.0001 | 1 | 0.0001 | 11.81 | 0.0109 |
| B | 0.0081 | 0.0003 | 1 | 0.0003 | 40.75 | 0.0004 |
| C | −0.0099 | 0.0004 | 1 | 0.0004 | 60.19 | 0.0001 |
| Residual | - | 0.0000 | 7 | 6.8 × 10 | - | - |
| Adj. R | 0.9684 | - | - | - | - | - |
| Pre. R | 0.7789 | - | - | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, P.; Jia, S.; Li, D.; el Moctar, O.; Jiang, C. Optimization Study of Marine Energy Harvesting from Vortex-Induced Vibration Using a Response-Surface Method. J. Mar. Sci. Eng. 2023, 11, 668. https://doi.org/10.3390/jmse11030668
Xu P, Jia S, Li D, el Moctar O, Jiang C. Optimization Study of Marine Energy Harvesting from Vortex-Induced Vibration Using a Response-Surface Method. Journal of Marine Science and Engineering. 2023; 11(3):668. https://doi.org/10.3390/jmse11030668
Chicago/Turabian StyleXu, Peng, Shanshan Jia, Dongao Li, Ould el Moctar, and Changqing Jiang. 2023. "Optimization Study of Marine Energy Harvesting from Vortex-Induced Vibration Using a Response-Surface Method" Journal of Marine Science and Engineering 11, no. 3: 668. https://doi.org/10.3390/jmse11030668
APA StyleXu, P., Jia, S., Li, D., el Moctar, O., & Jiang, C. (2023). Optimization Study of Marine Energy Harvesting from Vortex-Induced Vibration Using a Response-Surface Method. Journal of Marine Science and Engineering, 11(3), 668. https://doi.org/10.3390/jmse11030668








