Abstract
Along with the rapid development of the economy and the increasing demand for transport quality, renewed attention to multimodal transportation has emerged. However, due to the unpredictable transport environment in the process of multimodal transportation and the uncertainties caused by the change of transport market demand, transport decision-makers face many difficulties in transport planning and routing, which has become an obstacle to the development of multimodal transportation. As an advanced form of multimodal transportation, synchromodal transportation has received extensive attention in recent years. Due to its flexibility and sustainability, synchromodal transportation can effectively deal with the uncertainty in multimodal transportation. Based on the problem of multimodal transportation networks with uncertainties, this paper proposed a mixed time-window-constrained path optimization model with the goal of minimizing the total transportation costs, and proposed corresponding assumptions considering three types of uncertainty. The model could be solved by a genetic algorithm using MATLAB software. Using this model, the best transportation path and the optimal scheme considering synchronization were obtained. The results of the case study showed that synchromodal transportation can adjust the transportation plan in time to respond to uncertainties, thus, effectively reducing transportation costs. This paper favorably supported the introduction of synchromodal transportation, which is of significance to the development of multimodal transportation in the future.
1. Introduction
1.1. Background
In recent years, due to the development of social economy and the improvement of people’s quality of life, the demand for freight transportation has been on the rise, leading to a booming transportation and logistics industry. As a result, multimodal transportation has emerged as an alternative to traditional single-mode transportation. In China, multimodal transportation is becoming increasingly prevalent with the implementation of the “Belt and Road Initiative” and rapid development in roads, waterways, railways, aviation and pipeline infrastructure systems. According to the data of the China Container Industry and Multimodal Transportation Development Report 2020, a total of 690 multimodal transportation lines have been established in China over the past five years, with an average growth rate of container rail–water intermodal transportation volume reaching 27.6%. Additionally, data from the Ministry of Transport indicate that the first three batches of 70 multimodal demonstration projects achieved approximately 4.8 million TEUs of container multimodal transportation in 2020, while national ports completed 6.87 million TEUs of container rail–water intermodal transportation, representing a year-on-year increase of 29.6%. With the increasing use of standardized containers, China’s multimodal transportation structure has become increasingly diversified. The various modes, such as rail–water transportation, road–water transportation, sea–air transportation etc., are all developing rapidly.
However, due to unpredictable environmental factors in multimodal transportation, as well as uncertainties caused by changes in market demand conditions, decision makers face many difficulties when formulating plans and arranging paths for multimodal transportation which is hindering its further development. From the perspective of multimodal transportation operators, it is a complex form of organization which involves combining several modes of transportation. The weather, road conditions and carrier breakdowns are all uncertain factors that can cause delays and disruption to the supply chain, leading to economic losses. From the point of view of cargo owners, timeliness and the economy are both important factors when choosing multimodal transportation, as uncertainties can be detrimental to both. Thus, it is essential for transport decision-makers to effectively manage these uncertainties in order to provide cost-effective transport services for cargo owners in order to ensure successful delivery of goods.
Therefore, it is essential to devise transportation plans in a reasonable and effective manner in order to minimize the impact of uncertainties in multimodal transportation path decision-making.
This study proposes an efficient, flexible and practical multimodal transportation path optimization method through the introduction of synchromodal transportation (ST), which can effectively address the uncertainties inherent in multimodal transportation. It not only responds to the national policy and the future trend of the transportation and logistics industry, but also provides a theoretical reference for further development of multimodal transportation.
1.2. Innovation
Considering the general uncertainty problems in multimodal transportation, this study proposes three assumptions to characterize them and suggests corresponding transport plan change schemes for each assumption to reduce the costs of multimodal transportation.
In this study, ST is introduced as a novel concept in the world to address the uncertainties in multimodal transportation path problems, thus, filling the relative gap in China’s research on ST and providing some reference for scholars studying related issues. Through empirical research, this paper analyzes the flexibility and advantages of ST compared with traditional multimodal transportation, which can generate higher transport benefits and ensure transport elasticity and sustainability, thus, providing a reference for future application of this paradigm in China.
2. Related Works
2.1. Research on the Optimization of Multimodal Transport
Multimodal transportation path optimization is a combinatorial optimization problem, which focuses on the selection of transport paths and modes. Reddy [1] was the first to propose a multimodal transport path optimization model in 1995, assuming that the total cost consists of inter-city transport costs and intra-city transit costs. With the minimum total cost as the optimization goal, it established a 0–1 planning model for the transit of transport vehicles between cities, thus, making an initial contribution to multimodal transport path optimization research. Subsequently, with economic globalization and international trade becoming increasingly prominent, research on multimodal transport path optimization has become an important international research hotspot. Zhao et al. [2] established a multi-objective linear programming model to minimize transportation costs and transfer risks in order to solve the path planning problem of dangerous goods; Mi et al. [3] considered the impact of waiting time caused by time window constraints and fixed schedules, establishing a multimodal transport network path and mode selection model with minimum total cost under mixed-time-window constraints while using the chicken colony optimization (CSO) algorithm to solve it; Kaewfak et al. [4] brought factors influencing the multimodal transport path objective into consideration, utilizing the analytic hierarchy process (AHP) to determine weighting factors for cost, time and inherent risk before combining zero goal programming (ZOGP) to develop a decision support model for selecting optimal paths; Zhao et al. [5] studied dynamic multimodal freight transportation paths’ optimization while proposing a collaborative simulation optimization method for calculating optimal transportation costs. Recently, with the increased requirements of national policies on the environmental benefits of transportation, more research has been conducted to incorporate keywords such as “green” and “low-carbon” into the multimodal transportation path optimization problem. In addition to taking traditional transport time and transport costs into account, carbon emissions are also included in the model optimization goal or constraint conditions. Wang et al. [6] proposed a green multimodal transport organization mode and established a multi-objective multimodal transport performance evaluation framework by utilizing the “witness” software simulation software in combination with sequence relationship analysis and the entropy weight fuzzy analytic hierarchy process to select transport plans with higher energy-conservation and emission-reduction values. Li et al. [7] constructed a multimodal transportation path selection model in a low-carbon environment and solved it through a genetic algorithm and step-by-step method. As such, it has become an important research topic in multimodal transportation path optimization to reduce pollutant emissions generated during the transport process through reasonable transport decisions.
2.2. Research on the Uncertainty Problem in Multimodal Transport
Uncertainties refer to the disordered, probable, fuzzy and approximate attributes in the process of the connection and development of objective things, meaning an inability to predict precise results of relevant events or decisions in advance. Multimodal transportation is a system formed by different combinations of transport modes, which is more vulnerable to uncertainties such as changes and interruptions to transport services caused by bad weather, changes in road conditions, vehicle failure, epidemics and natural disasters. Delbart et al. [8] conducted a comprehensive review of literature related to uncertainties in multimodal transport through Google Scholar and the Hasselt University Library which was divided into three categories: strategic level, tactical level and operational level, based on the number of studies and type of uncertainty divided by the planning level. It was found that across all planning levels, stochastic demand and stochastic transportation time were the most studied types of uncertainties, while research on vehicle failure and cost uncertainties was relatively scarce. Sun et al. [9] considered double uncertainties of railway service capacity and road service travel time using triangular fuzzy numbers for modelling; they established a mixed integer non-linear programming model with fuzzy-chance constraints. Lu et al. [10] established a fuzzy mixed integer linear programming model for intercontinental highway–rail intermodal transportation considering time and train capacity uncertainties; it was solved using triangular fuzzy numbers combined with fuzzy reliability fuzzy measure theory. Zhang et al. [11] established a hybrid robust stochastic optimization (HRSO) model for low-carbon multimodal transport considering double uncertainties of time and demand; they designed a catastrophic adaptive genetic algorithm (CA-GA), based on Monte Carlo sampling to solve it. Fuzzy theory, as well as robust optimization, are the main methods used to solve uncertainty problems in multimodal transportation; algorithms used for solving related problems mainly include meta-heuristics, tabu search, the simulated annealing genetic algorithm and ant colony optimization, but there is a lack comparison between these methods due to differences in variables considered by each study, making it complex to compare solutions without standard reference problem available; most studies use their own data sets as well.
Table 1 summarizes the design factors of multimodal transport optimization studies, with cost being the primary consideration. The majority of studies also take time into account (which is not marked if time is only as a hard constraint in the study). In recent years, studies on the optimization of multimodal transport have increasingly focused on carbon emissions and uncertainty; however, few have incorporated ST.

Table 1.
Studies on multimodal transportation optimization problems.
2.3. Research on Synchromodal Transport
ST is a relatively new concept, which was first introduced and piloted in the Netherlands in 2010; since then, its paradigm has been studied mainly in its country of origin and surrounding European countries (Belgium, Luxembourg, etc.). ST is considered to be the next stage of multimodal transportation involving structured, efficient and synchronous combination of two or more transportation modes [12]. Through ST, carriers or customers can independently choose the best mode at any time according to the operating environment and customer needs to achieve higher flexibility, lower cost and sustainability; thus, it can effectively solve the uncertainty problem in multimodal transportation. In recent years, the topic of multimodal transportation has received new international attention with research focusing on the concept of ST. Van Riessen et al. [13] reviewed three themes of integrated network planning, real-time network planning and creating planning flexibility through a case study of the European Gateway Services (the manager of inland container transport network in Rotterdam), making an overall work for research on ST. Giusti et al. [14] analyzed the critical success factors and six supporting technologies required by synchronous mode logistics and believed that synchromodal mode logistics would improve service quality while meeting customer needs. Sakalys et al. [15] analyzed expert opinions using the multi-criteria decision making (MCDM) method, combined with the average grade conversion weight (ARTIW) method and the analytic hierarchy process (AHP) method, determining five main criteria impacting synchromodality: service quality, efficiency, infrastructure sufficiency, technical properties of terminals and the interaction of technologies.
Recently, the concept and paradigm of ST or synchronization have been widely applied in the field of transportation and supply chain. Larsen et al. [16] proposed a model controller to help suppliers synchronize paths and arrange vehicles in real time according to transportation requirements, aiming to solve the comprehensive problem of container transportation mode combination and transportation paths in multimodal transportation networks. Guo et al. [17] studied the dynamic cargo shipment matching problem of inland ST, proposing a rolling level method to process the real-time information of the new arrival shipment request, and designed a heuristic algorithm to generate the corresponding decision solution. Zhang et al. [18] considered the preferences of decision-makers in ST, designed a multi-objective optimization model based on the fuzzy preferences of decision-makers, described it as the pickup and distribution problem with transshipment (PDPT), and designed an adaptive large neighbourhood search (ALNS) algorithm to solve it. Van Riessen et al. [19] studied the freight fare level combination (CFCM) problem for multiple synchronous container transport networks. Batarliene et al. [20] established a stochastic integer programming model to study simultaneous multimodal container cargo distribution between ports and inland areas. Guo et al. [21] studied the freight matching problem with dynamic and random transportation time in the global ST network. In order to maximize total profit, the Q-learning algorithm was used to simulate and learn the value function of matching goods and transportation services to update the matching decision before the goods arrived at the destination. It is of practical significance to combine the ST with the classical multimodal transportation path optimization problem.
3. Problem Description
Since ST is an advanced form of multimodal transportation, the research on its related issues is usually based on the basic problems of general multimodal transportation. This study considers a multimodal transportation network problem, which can be described as follows: the carrier is responsible for transporting goods from the starting point O to destination D, and adopts a comprehensive transport network that combines multiple transport modes. The network is composed of m nodes (cities), which are connected by arcs. (Take nodes A and B for example.) Different arc types represent m transport modes. The network is described using the multiple edge method, as shown in Figure 1.
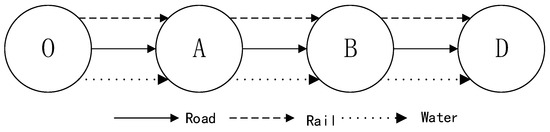
Figure 1.
Diagram of multimodal transport network.
Due to the different transportation paths and modes selected, the resulting transportation costs and transportation time differ. The transshipment of goods between different transportation modes can be realized between two adjacent nodes (cities), generating the transshipment costs and time during the transfer process. In addition, the destination city has a soft time window limit. The goods should arrive within a certain time. If the goods arrive early, the carrier should pay a care and preservation fee, while if late, the carrier should pay the penalty. It is now required to reasonably arrange the combination of transportation modes and paths to achieve the purpose of minimum total cost under different constraints.
4. Synchromodal Transportation Routing Model under Uncertainties
4.1. Model Assumption
(1) The goods can only be transported in one mode and cannot be separated;
(2) The transshipment of goods by transportation mode can only take place at nodes, and up to one transshipment can take place at each node;
(3) There must be only one transportation path and one transportation mode selected for goods between two nodes;
(4) During transportation, the basic condition of the goods will not change or be damaged.
4.2. Mathematical Model
The objective function is shown in Equation (1), indicating that the total cost generated in the total transportation process is the lowest. The first part of the objective function represents the transportation cost of goods between nodes. The second part is the cost of transshipment and transshipment of goods when the mode of transportation changes at the node. The third part represents the penalty cost of the time window for the early or delayed arrival of goods.
This is subject to
Constraint (2) indicates that the transportation time between two nodes is related to the average transportation speed. Constraint (3) means that goods can only be transported by one of the methods when transported at adjacent nodes. Constraint (4) means that the total number of transfers does not exceed 4. Constraint (5) indicates that goods can only be converted to a different transportation mode at most once at a node. Constraint (6) ensures the continuity and accuracy of the conversion between modes of transportation. Constraints (7) and (8) are 0–1 variables.
Due to the flexibility of ST, the best service decision can be specified based on the actual situation to make adjustments to the transport mode to deal with unexpected events. Therefore, this paper considers the following three assumptions (uncertainties):
Assumption 1.
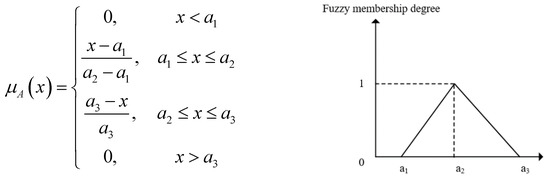
Due to the uncertainty of transportation time caused by train delays, traffic jams, weather changes, channel congestion, etc., when the distance is constant, the average transportation speed vj is considered an uncertain variable, and its determined value is often difficult to obtain accurately, but it is easier to obtain its approximate range. Therefore, it seems feasible to use triangular fuzzy numbers to represent the uncertain variable vj. Therefore, we define vj = (a1, a2, a3), and its membership function μA (x) can be expressed in the form of Figure 2.
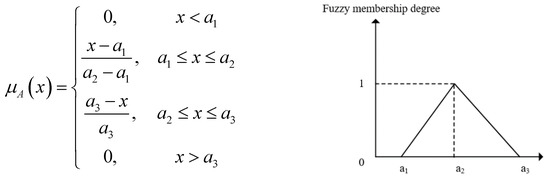
Figure 2.
A triangular fuzzy number.
Assumption 2.
The soft time window (E, L) of goods delivery changes due to unexpected circumstances caused by changes in customer demand, such as the customer’s urgent request for goods to be delivered in advance.
Assumption 3.
The customer requests to change the delivery place of goods, resulting in changes in the destination (city) of the goods delivery.
5. Solution Methodology
5.1. Defuzzification
For Assumption 1, because the model contains uncertain variables, it is necessary to generate a clear and easy-to-solve mathematical model using defuzzification. In this study, the authors used the widely used fuzzy expected value model to defuzzify the fuzzy variable vj. For a given triangular fuzzy number , presence E [] = (a1 + 2·a2 + a3)/4 [22]. Therefore, constraint (2) can be transformed into (9).
5.2. Algorithm Choice
The path optimization problem in this paper belongs to the category of network paths. Network optimization itself is a combinatorial optimization problem and is also an NP-hard problem. There are many special algorithms to solve the network path optimization problem, each of which has its advantages and disadvantages in solving adaptive problems. As a combinatorial optimization problem, it usually has more local extremum points, and the local extremum is not necessarily the global optimal solution to the problem. In addition, for some large-scale problems, the search space of solutions is relatively large and difficult to solve. As a type of random search algorithm, the genetic algorithm (GA) has good performance in dealing with such problems [23]. GA selects all individuals in the population according to the relevant principles, calculates the selection probability based on the fitness function, forms new individuals through a series of individual crossovers and mutations, and finally converges to obtain the optimal solution. The operating process of GA is a typical iteration search process. For the multimodal transport path optimization problem discussed in this paper, the operation steps of GA can be described as follows, and the algorithm flow is shown in Figure 3. More details about the algorithm can be seen in Appendix A.
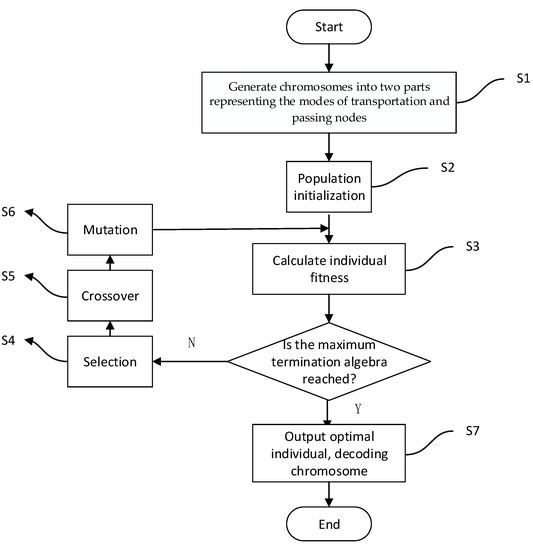
Figure 3.
Genetic algorithm flowchart.
S1: Chromosome coding. The function ‘pop’ was defined to divide a chromosome into two parts. The first part represents the transportation scheme (represented by 1~3), and the second part represents whether to pass each urban node (0 means not to pass, 1 means passing), thus, representing any multimodal transportation scheme from the start to the end;
S2: Initialization. The maximum evolution times was set to nMax = 120, and the initial population number indiNumber = 1000 was generated;
S3: Calculate the individual fitness and set the fitness function ‘indiFit’, which is the objective function of the total transportation cost in this model;
S4: Selection. According to individual fitness, use roulette selection to update the current optimum and historical optimum, which was inherited by the next generation;
S5: Crossover. The single-point crossover was used to randomly find the intersection points of urban nodes and transportation modes, and the new scheme was accepted if it was low in cost and the best in the population;
S6: Mutation. The single-point mutation was used to accept the lower cost scheme.
S7: The maximum termination algebra was set. After reaching the number of iterations, the optimal fitness individual was output, and the lowest total transportation cost scheme after decoding was obtained.
6. Numerical Experiments
In order to verify the feasibility of the model and algorithm, numerical experiments and empirical studies were carried out. All experiments were conducted on a computer equipped with Intel Core i7, 2.6 GHz CPU and 8 GB RAM.
6.1. Case Description
In this paper we designed an ST network. It was assumed that the initial 3TEU container cargo would be transported from Chengdu to Shanghai, China, and a multimodal logistics network with Chengdu as the original point and Shanghai as the destination would be established. This paper selected a hub city with relatively developed transportation and multiple modes of transportation as the node city. The node numbers O, 1, 2, …, D were Chengdu, Xi’an, Chongqing, Guiyang, Zhengzhou, Wuhan, Changsha, Nanchang, Hefei, Nanjing, Hangzhou, Suzhou and Shanghai. There were three modes of transportation between node cities: highway, waterway and railway. The specific network model is shown in Figure 4.
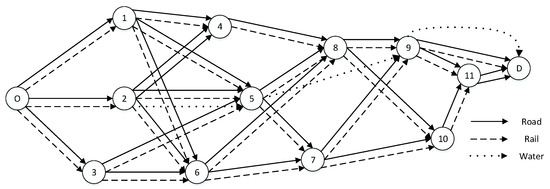
Figure 4.
Schematic diagram of synchromodal transport network.
The transportation distance data of different modes between each node city could be queried through the official website of railway 12306, the ticket network and with the relevant information. (a, b, c) represent the transportation distance of roads, railways and waterways accordingly, and ‘-’ means that there is no direct transportation mode or path between two adjacent nodes. The specific distance data can be seen in Table 2.

Table 2.
Transportation distance of different modes between transportation nodes (unit: km).
According to objective reality, this study assumed that the goods must arrive within the (55,65) time window. If the goods did not arrive during the stipulated time window, a fee of 1000 yuan for each container per hour was charged for storage when arriving early, and a penalty fee of 1200 yuan for each container per hour was charged when arriving late. The speed, cost and carbon emissions of each mode of transport are shown in Table 3. [24] The cost, time and carbon emissions of modes changing and transshipment between different modes of transportation are shown in Table 4 [6].

Table 3.
Basic information for different transportation modes.

Table 4.
Transshipment costs between different transportation modes.
6.2. Results Analysis
First of all, with synchronization not considered, for assumption 1, the model was defuzzified according to the method in Section 5.1 and solved using the genetic algorithm. We set the population size as 200, the maximum number of iterations was 120, the crossover probability was 0.7%, and the mutation probability was 0.005%. The change to the optimal value is shown in Figure 5. The average processing time for each group in the numerical example was approximately 8 s, which was acceptable even extended to larger examples.
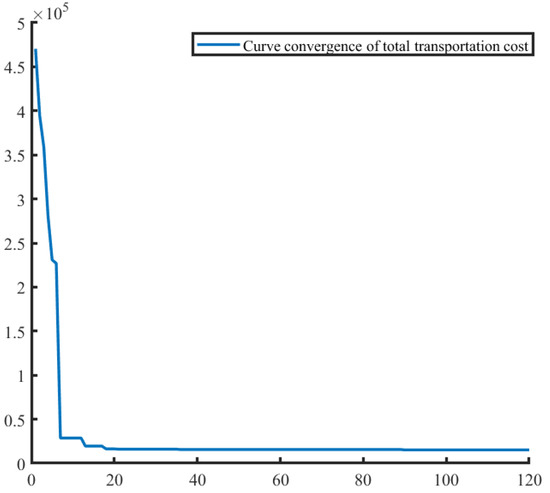
Figure 5.
The variation of the minimum cost value.
As can be seen from Figure 5, the initial model tended to converge around the 20th generation. The optimal transportation scheme generated at this time was O → road → 2 → railway → 5 → waterway → 9 → waterway → D. The total transportation cost was 15,181.5 yuan, the total transportation time was 63.773 h and the total carbon emission was 339.07 kg.
In consideration of the uncertain impact of delay in the actual transportation process, three assumptions were simulated:
Scenario 1.
Road, railway and waterway transportation reach the worst situation due to delay (that is, the average transportation speed is taken as the lower bound of the triangular fuzzy number);
Scenario 2.
The transportation time window is advanced to (50,60);
Scenario 3.
The freight destination is changed from D (Shanghai) to 9 (Nanjing).
At this time, if the transportation scheme cannot be changed promptly, both the corresponding transportation cost and time will be increased, thus, bringing economic losses to the cargo owner and the carrier. However, after considering ST, the transportation scheme can be adjusted immediately. The corresponding optimal transportation path changes and the optimal cost and time changes are shown in Table 5.

Table 5.
Optimal transportation paths considering ST under uncertainties.
As depicted in Table 4, under the ST scheme, uncertainties were taken into account and the transportation mode and path could be adjusted in time to effectively reduce the transportation cost. In the worst case of delays in the road, railway and waterway transportation, the optimal ST scheme reduced the transportation cost by 36.3%, 25.4% and 87.5%, respectively, compared with the original optimal scheme; when the transportation time window was 5 h ahead, the optimal ST scheme could reduce the cost by 45.6%. Similarly, when the transportation destination was changed from Shanghai to Nanjing, the ST scheme reduced the cost by 16.4%. In terms of energy conservation and emissions reductions, although ST may increase the number of transfers, resulting in additional transfer carbon emissions, the total carbon emissions may not be reduced but the emissions during transport will decrease. To sum up, ST is a more flexible and economical transport organization mode, which has advantages over traditional multimodal transportation.
7. Conclusions
Aiming at the uncertainties of multimodal transportation, this paper introduced the ST model and established a path optimization model. Firstly, a traditional multimodal transport network combinatorial optimization problem with a soft-time-window penalty was considered to minimize the total transport cost. Then, corresponding assumptions were put forward for general uncertainties in three multimodal transportation processes, including those of transport time caused by delays and accidents, and changes of transport time window due to alterations in customer demand and transport destination. Triangular fuzzy numbers were employed to represent average transportation speed for reflecting the uncertainty of transportation time. GA was utilized to solve the proposed model. Results from the case study showed that ST has remarkable advantages; it can effectively deal with uncertainty factors in traditional multimodal transport, realize the timely change in transport plans, and bring economic and environmental benefits to multiple stakeholders such as cargo owners and carriers.
However, considering that China has not yet implemented ST, the research in this paper is still at the theoretical level and the following deficiencies exist: (1) This paper mainly considered the uncertainties of time level in the process of multimodal transportation, and ignored the impact of demand uncertainties (i.e., transport volume uncertainties). (2) The transportation scheme change under ST considered in this paper took place at the node and was abstracted as a static path optimization problem, which belongs to integrated network planning; however, the real-time network planning method was also an important topic of ST research [13], so dynamic path optimization problem seems to be a worthy research direction. In addition, (3) the multimodal transport network case used in this study did not have many critical success factors for achieving ST, such as a network, collaboration, trust among stakeholders, relevant ICT/ITS technologies, and physical infrastructure [14], while its practical significance was insufficient. Finally, (4) further studies may be extended to improve the intelligent algorithm to achieve a more reliable solution.
Author Contributions
Conceptualization, X.X.; methodology, X.X. and P.D.; validation, X.X.; formal analysis, X.X.; investigation, X.X.; data curation, X.X.; writing—original draft preparation, X.X.; writing—review and editing, H.W.; visualization, X.X.; supervision, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used to support the findings of this study are included within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Sets: |
| N Multimodal transport network. |
| O, D Origin and destination of the transportation network. |
| A Sets of node cities. |
| M Sets of transportation modes. |
| G Sets of transportation arcs. |
| Parameters: |
| The cargo volume between nodes i and i + 1. |
| If the transportation mode j is used from point i to point i + 1, its value is 1, otherwise it is 0. |
| The transportation distance from point i to point i + 1 using transportation mode j. |
| The fee for unit distance using transportation mode j. |
| If changing the transportation mode from j to k at point i, its value is 1, otherwise it is 0. |
| The transshipment fee if changing the transportation mode from j to k at point i. |
| The quantity of goods. |
| The transportation time from point i to point i + 1 using transportation mode j. |
| T Total transportation time of goods from O to D. |
| The transportation speed using transportation mode j. |
| The unit time storage fees that need to be paid if goods arrives at point D early. |
| The unit time penalties that need to be paid if goods arrives at point D late. |
| (E, L) The soft time window for goods delivery. |
Appendix A
| %% Set GA Control Parameters |
| GA.popsize = 200; % Population size |
| GA.Dim = 11; % total noes - O - D = 13 - 2 |
| GA.Ub = 3; % modes of transportation |
| GA.pc = 0.7; % Crossover probabilities |
| GA.pm = 0.005; % Mutation probabilities |
| GA.pentcof = 100; % Penalty coefficient |
| % GlobalMins = zeros(GA.MaxCycles, 1); |
| % GlobalOptpop = zeros(GA.MaxCycles, 1+2*GA.Dim); %Optimal value update |
| %% |
| nMax = 120; |
| indiNumber = 1000; |
| %% Initialization |
| pop = zeros(GA.popsize,1+2*GA.Dim); |
| n = size(pop,2); %numbers of nodes |
| obJvaL = zeros(GA.popsize, 1); |
| for i = 1: GA.popsize |
| pop(i,:) = popcreat(GA.Ub,GA.Dim); |
| end |
| %% Calculate the population fitness |
| % indiFit = fitness(individual,cityCoor,cityDist); |
| for i = 1: GA.popsize % objective function values |
| [Objfit(i),~,~,totalTime] = Objfun(Modd,GA.Dim,pop(i,:),GA.pentcof); |
| end |
| [value,index] = min(Objfit); |
| tourPbest = pop; |
| tourGbest = pop(index,:); |
| recordPbest = inf*ones(1,GA.popsize); |
| recordGbest = Objfit(index); |
| %% Find the optimal route scheme |
| L_best = zeros(1,nMax); |
| for N = 1:nMax |
| N |
| % Calculate the individual fitness |
| for i = 1: GA.popsize |
| [Objfit(i),~,~,totalTime] = Objfun(Modd,GA.Dim,pop(i,:),GA.pentcof); |
| end |
| % indiFit = fitness(individual,cityCoor,cityDist); |
| % Update the current optimal and historical optimal |
| for i = 1:GA.popsize |
| if Objfit(i) < recordPbest(i) |
| recordPbest(i) = Objfit(i); |
| tourPbest(i,:) = pop(i,:); |
| end |
| if Objfit(i) < recordGbest |
| recordGbest = Objfit(i); |
| tourGbest = pop(i,:); |
| end |
| end |
| [value,index] = min(recordPbest); |
| recordGbest(N) = recordPbest(index); |
| %% Cross operation |
| % crosspop = zeros(size(pop)); |
| % Select operation |
| for i = 1:GA.popsize |
| IX = find(Objfit~ = inf); |
| prob = 1./Objfit(IX)/sum(1./Objfit(IX)); % Select probabilities |
| cuLprob = cumsum(prob); |
| selectionpop = zeros(size(pop)); |
| % roulette selection |
| % for k = 1:GA.popsize |
| % indx = find( rand<cuLprob,1); |
| % j = IX(indx); |
| % selectionpop(k,:) = pop(j,:); |
| % end |
| % pop = selectionpop; |
| xnew1 = pop(i,:); |
| sec = tourPbest; |
| % single-point crossover |
| k = unidrnd(GA.Dim+1); |
| kk = unidrnd(GA.Dim)+GA.Dim+1; |
| temp = xnew1(k); |
| xnew1(k) = sec(k); |
| sec(k) = temp; |
| temp = xnew1(kk); |
| xnew1(kk) = sec(kk); |
| % the new scheme is accepted if it is low in cost |
| [obj,~,~,~] = Objfun(Modd,GA.Dim,xnew1,GA.pentcof); |
| if Objfit(i) > obj |
| pop(i,:) = xnew1; |
| Objfit(i) = obj; |
| end |
| % cross with the best in the population. |
| xnew1 = pop(i,:); |
| sec = tourGbest; |
| % single-point mutation |
| xnew1(k) = unidrnd(GA.Ub); %Ub = 3; |
| xnew1(kk) = unidrnd(2) − 1; %0.1 |
| % the new scheme is accepted if it is low in cost |
| [obj,~,~,~] = Objfun(Modd,GA.Dim,xnew1,GA.pentcof); |
| if Objfit(i) > obj |
| pop(i,:) = xnew1; |
| Objfit(i) = obj; |
| end |
| end |
| %% |
| [value,index] = min(Objfit); |
| L_best(N) = Objfit(index); |
| tourGbest = pop(index,:); |
| end |
References
- Reddy, T.; Khem Chand, B.; Velmurugan, S. Evaluation and augmentation of road-based urban public transport. Indian J. Transp. Manag. 1995, 19, 147–153. [Google Scholar]
- Zhai, C.-X.; Meng, C.; Sui, H.-P.; Li, K.-X. The Optimization Model Construction of Multimodal Transportation Route for Dangerous Goods. In Proceedings of the 3rd Annual International Conference on Management, Economics and Social Development (ICMESD 17), Beijing, China, 29–30 December 2017; pp. 302–306. [Google Scholar]
- Mi, X.; Mei, M.; Zheng, X. Study on Optimal Routes of Multimodal Transport under Time Window Constraints. In Proceedings of the 2019 IEEE 23rd International Conference on Computer Supported Cooperative Work in Design (CSCWD), Porto, Portugal, 6–8 May 2019; pp. 512–516. [Google Scholar]
- Kaewfak, K.; Ammarapala, V.; Huynh, V.-N. Multi-objective optimization of freight route choices in multimodal transportation. Int. J. Comput. Intell. Syst. 2021, 14, 794–807. [Google Scholar] [CrossRef]
- Zhao, Y.; Ioannou, P.A.; Dessouky, M.M. Dynamic multimodal freight routing using a co-simulation optimization approach. IEEE Trans. Intell. Transp. Syst. 2018, 20, 2657–2667. [Google Scholar] [CrossRef]
- Wang, Q.-Z.; Chen, J.-M.; Tseng, M.-L.; Luan, H.-M.; Ali, M.H. Modelling green multimodal transport route performance with witness simulation software. J. Clean. Prod. 2020, 248, 119245. [Google Scholar] [CrossRef]
- Li, H.; Su, L. Multimodal transport path optimization model and algorithm considering carbon emission multitask. J. Supercomput. 2020, 76, 9355–9373. [Google Scholar] [CrossRef]
- Delbart, T.; Molenbruch, Y.; Braekers, K.; Caris, A. Uncertainty in intermodal and synchromodal transport: Review and future research directions. Sustainability 2021, 13, 3980. [Google Scholar] [CrossRef]
- Sun, Y.; Hrušovský, M.; Zhang, C.; Lang, M. A time-dependent fuzzy programming approach for the green multimodal routing problem with rail service capacity uncertainty and road traffic congestion. Complexity 2018, 2018, 8645793. [Google Scholar] [CrossRef]
- Lu, Y.; Lang, M.; Sun, Y.; Li, S. A fuzzy intercontinental road-rail multimodal routing model with time and train capacity uncertainty and fuzzy programming approaches. IEEE Access 2020, 8, 27532–27548. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, F.-Y.; Yuan, X.-M.; Zhang, H.-Y. Low-Carbon Multimodal Transportation Path Optimization under Dual Uncertainty of Demand and Time. Sustainability 2021, 13, 8180. [Google Scholar] [CrossRef]
- SteadieSeifi, M.; Dellaert, N.P.; Nuijten, W.; Van Woensel, T.; Raoufi, R. Multimodal freight transportation planning: A literature review. Eur. J. Oper. Res. 2014, 233, 1–15. [Google Scholar] [CrossRef]
- van Riessen, B.; Negenborn, R.R.; Dekker, R. Synchromodal container transportation: An overview of current topics and research opportunities. In Proceedings of the Computational Logistics: 6th International Conference, ICCL 2015, Delft, The Netherlands, 23–25 September 2015; pp. 386–397. [Google Scholar]
- Giusti, R.; Manerba, D.; Bruno, G.; Tadei, R. Synchromodal logistics: An overview of critical success factors, enabling technologies, and open research issues. Transp. Res. Part E Logist. Transp. Rev. 2019, 129, 92–110. [Google Scholar] [CrossRef]
- Šakalys, R.; Sivilevičius, H.; Miliauskaitė, L.; Šakalys, A. Investigation and evaluation of main indicators impacting synchromodality using ARTIW and AHP methods. Transport 2019, 34, 300–311. [Google Scholar] [CrossRef]
- Larsen, R.B.; Atasoy, B.; Negenborn, R.R. Model predictive control for simultaneous planning of container and vehicle routes. Eur. J. Control 2021, 57, 273–283. [Google Scholar] [CrossRef]
- Guo, W.; Atasoy, B.; van Blokland, W.B.; Negenborn, R.R. A dynamic shipment matching problem in hinterland synchromodal transportation. Decis. Support Syst. 2020, 134, 113289. [Google Scholar] [CrossRef]
- Zhang, Y.; Atasoy, B.; Negenborn, R.R. Preference-based multi-objective optimization for synchromodal transport using Adaptive Large Neighborhood Search. Transp. Res. Rec. 2022, 2676, 71–87. [Google Scholar] [CrossRef]
- Van Riessen, B.; Mulder, J.; Negenborn, R.R.; Dekker, R. Revenue management with two fare classes in synchromodal container transportation. Flex. Serv. Manuf. J. 2021, 33, 623–662. [Google Scholar] [CrossRef]
- Batarlienė, N.; Šakalys, R. Mathematical model for cargo allocation problem in synchromodal transportation. Symmetry 2021, 13, 540. [Google Scholar] [CrossRef]
- Guo, W.; Atasoy, B.; Negenborn, R. Global synchromodal shipment matching problem with dynamic and stochastic travel times: A reinforcement learning approach. Ann. Oper. Res. 2022, 1–32. [Google Scholar] [CrossRef]
- Sun, Y.; Li, X. Fuzzy programming approaches for modeling a customer-centred freight routing problem in the road-rail intermodal hub-and-spoke network with fuzzy soft time windows and multiple sources of time uncertainty. Mathematics 2019, 7, 739. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, X. Optimization of multimodal transport route with mixed time windows. In Proceedings of the CICTP 2018: Intelligence, Connectivity, and Mobility, Beijing, China, 5–8 July 2018; American Society of Civil Engineers: Reston, VA, USA, 2018; pp. 472–481. [Google Scholar]
- Qiwei, L.; Rongzhang, Z. Comparison and analysis of multimodal transport route optimization algorithms considering carbon emissions. Ind. Eng. Manag. 2022, 1–13. (In Chinese) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).