Method for Identifying Materials and Sizes of Particles Based on Neural Network
Abstract
1. Introduction
2. Particle Identification and Particle Signal Characteristics
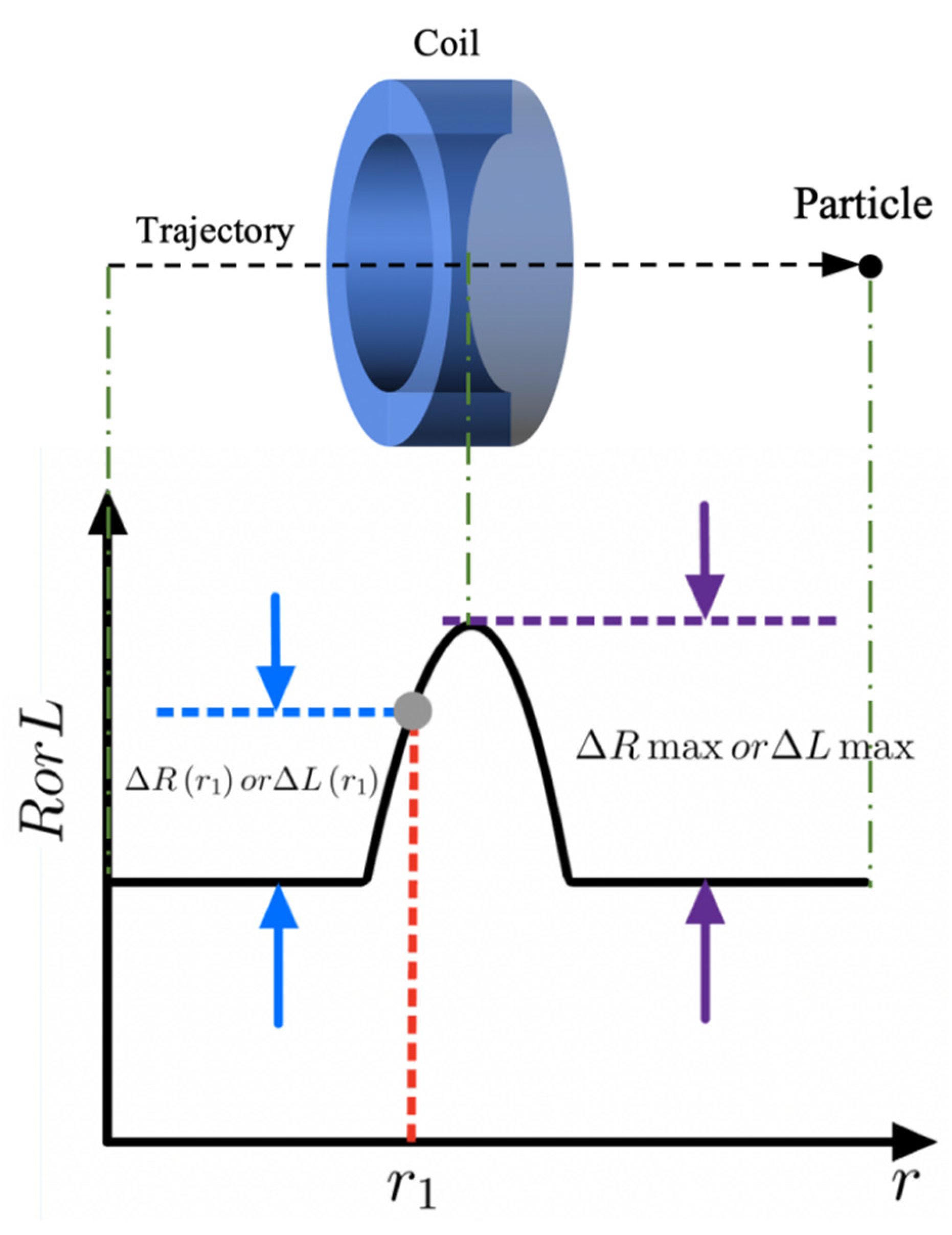
2.1. Particle Signal and Feature Simulation
2.2. Selection of Experimental Particles
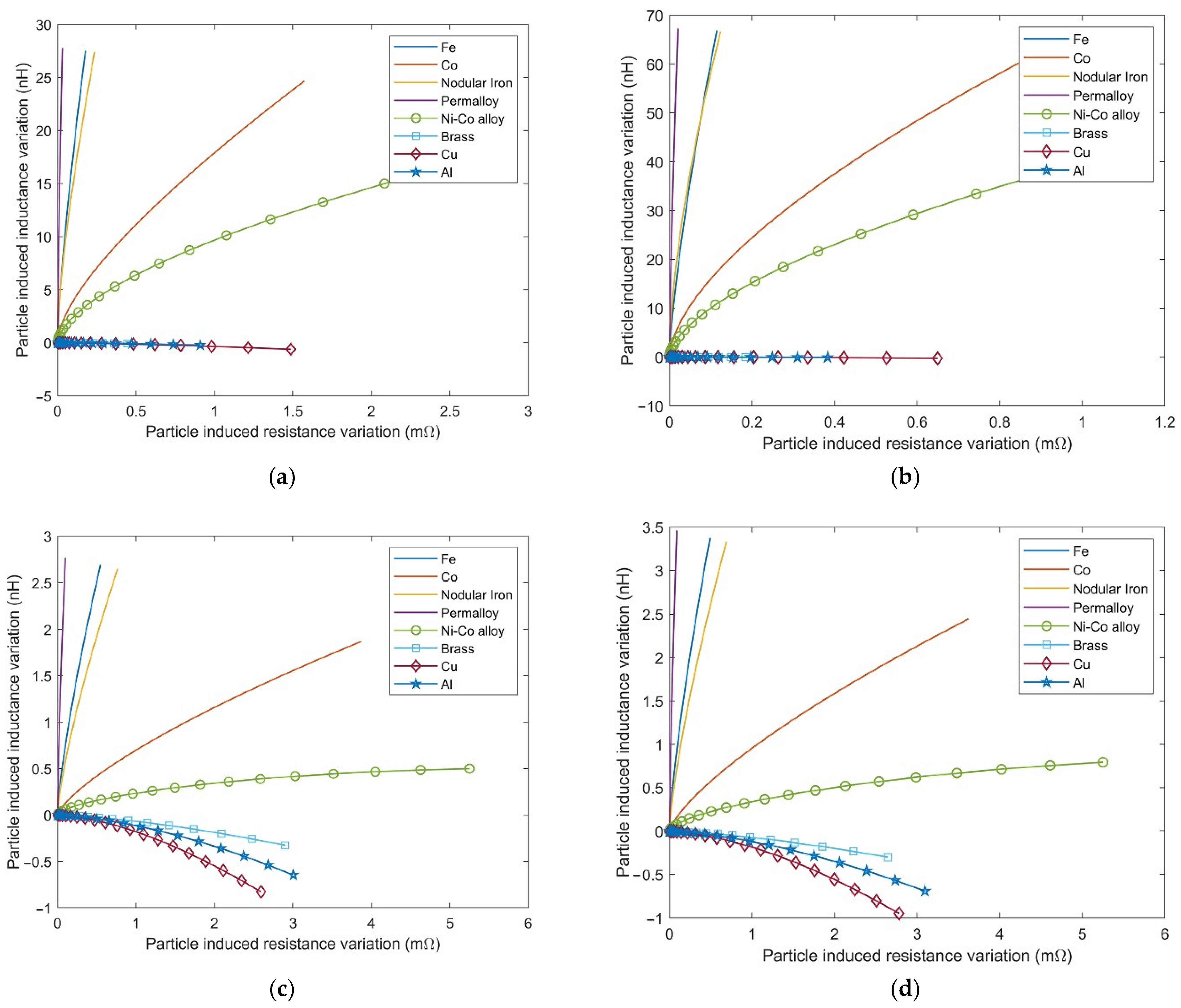
2.3. Characteristics of Particle Signals in a Complex Plane
3. Neural Network Particle Identification Model with Pre-Training
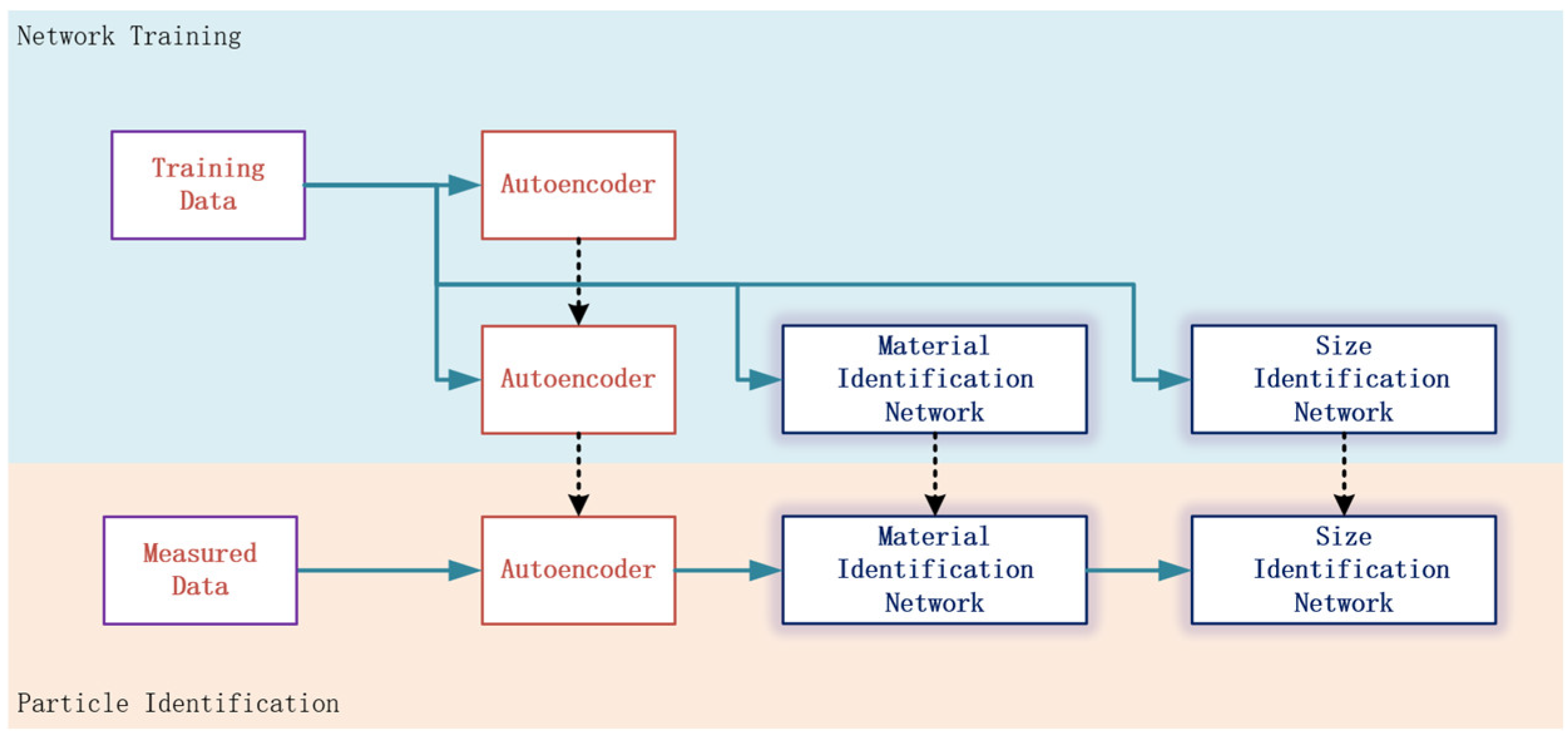
3.1. Neural Network Structure
3.1.1. Autoencoder
3.1.2. Material Identification and Size Identification Network
3.2. Neural Network Model Pre-Training and Autoencoder Training
3.2.1. First-Stage Training
3.2.2. Second-Stage Training
4. Evaluation and Discussion of Pre-Training Identification Performance
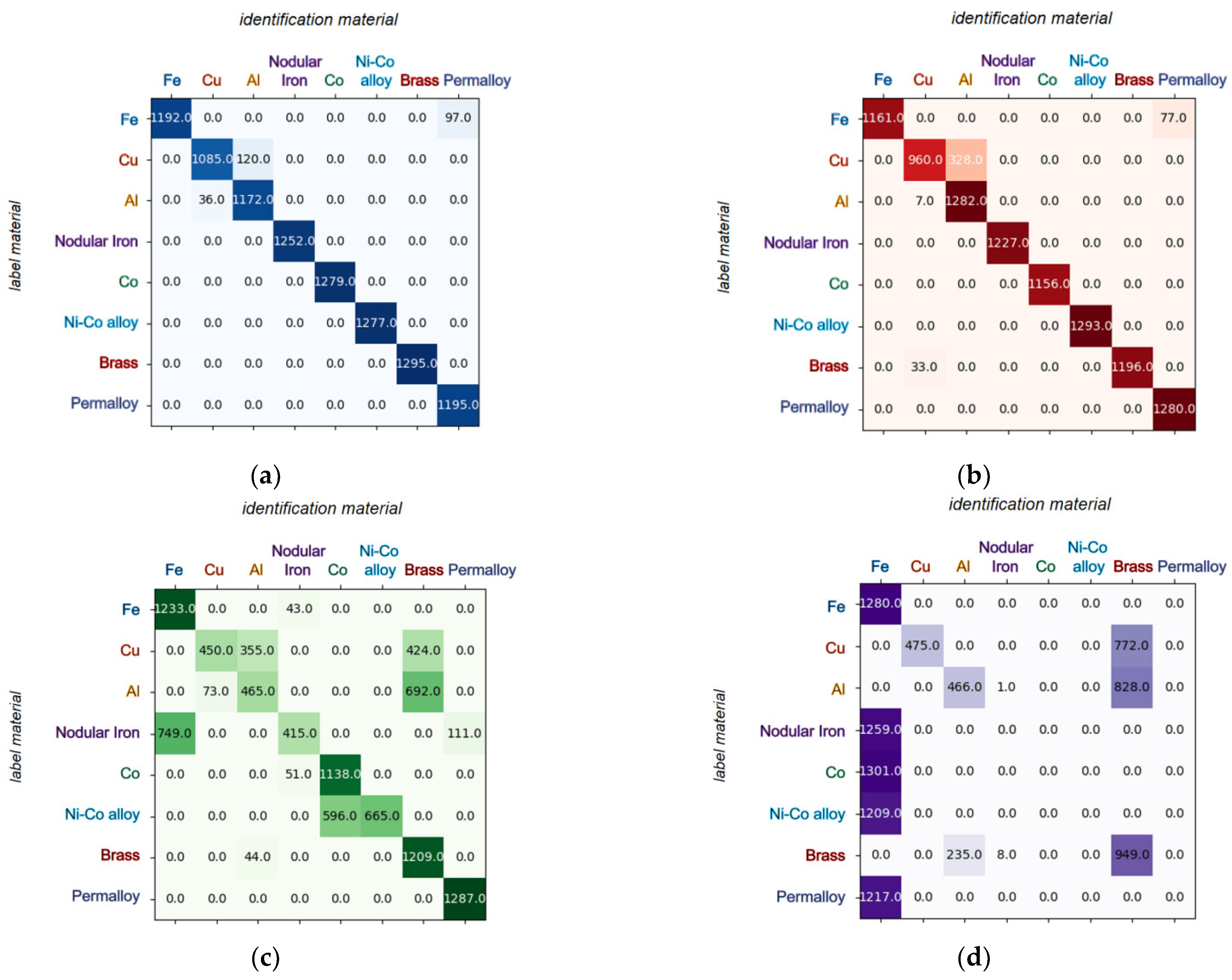
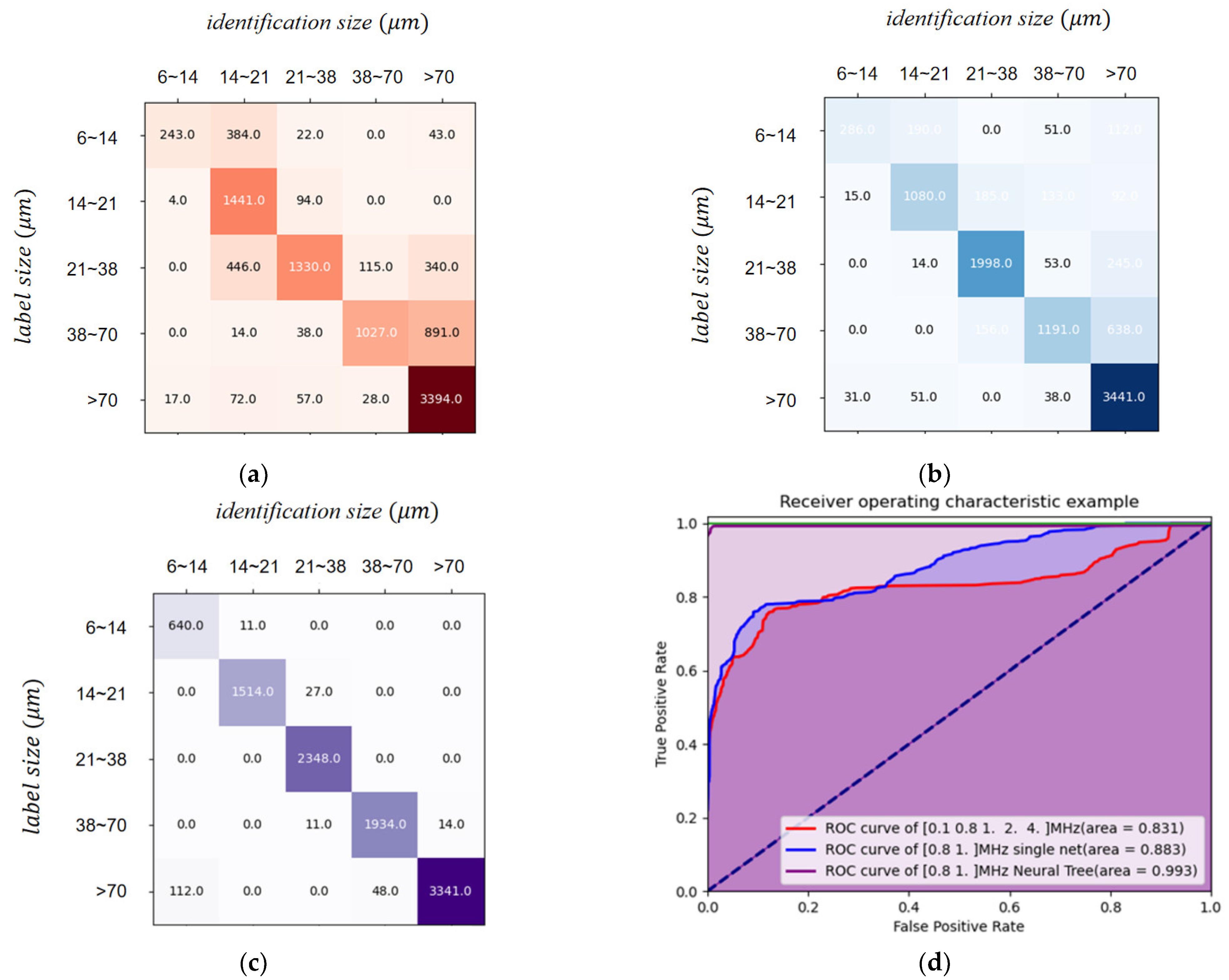
4.1. Confusion Matrix
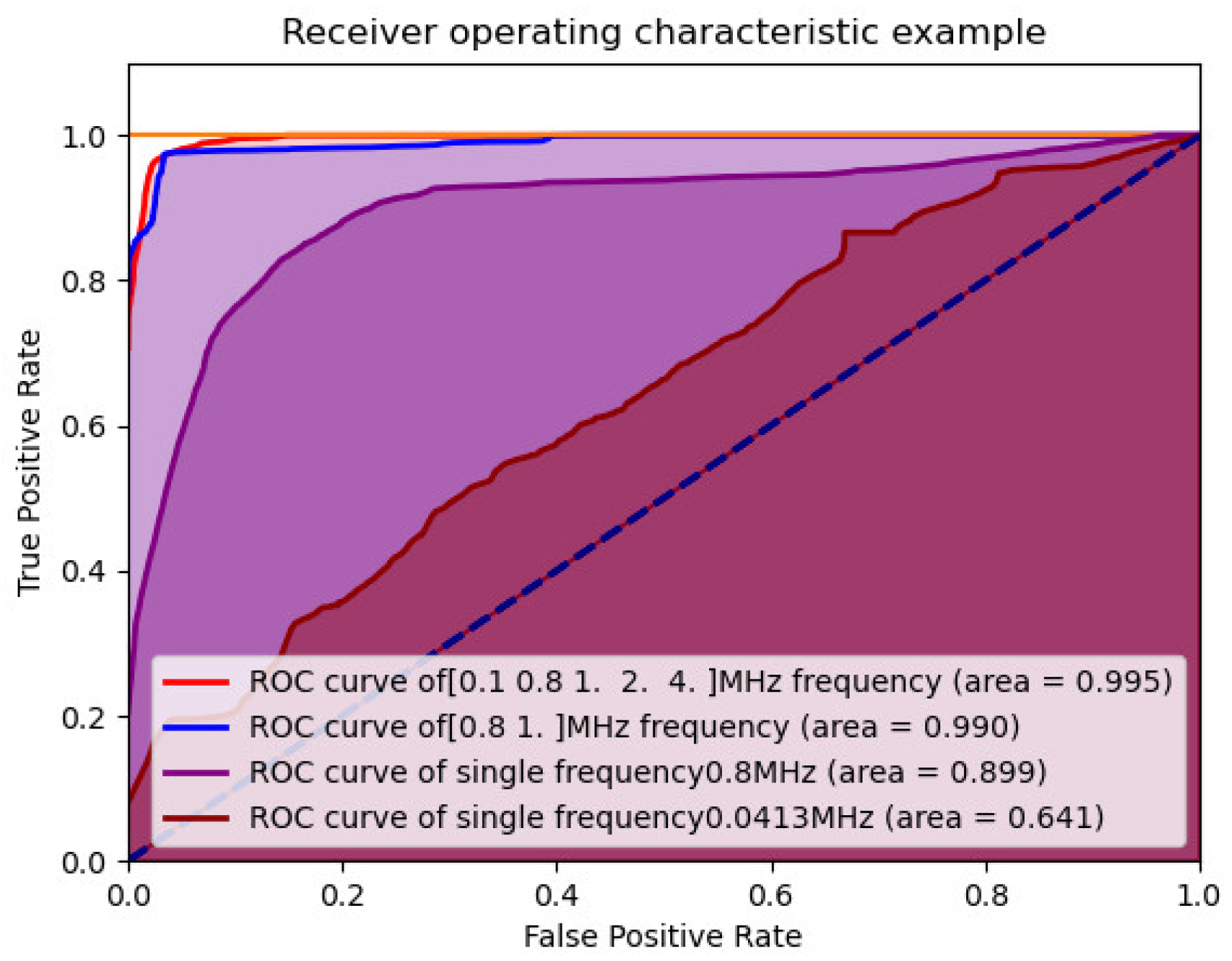
4.2. ROC Curve
4.3. Identification Performance of Particle Material
4.4. Identification Performance of Particle Size
5. Conclusions
- We established a frequency-finding scheme based on particle characteristics, which should be adapted to different engineering scenarios;
- We confirmed that 0.8 MHz and 1 MHz are suitable for two-frequency measurement, which lays a theoretical foundation for the numerical selection of a subsequent multi-frequency measurement sensor.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Teng, H.; Zhang, H.; Liu, E.; Zeng, L.; Chen, H.; Bo, Z. New Method of Measuring Moisture Content in Marine Hydraulic Oil. Ship Eng. 2017, 39, 83–87. [Google Scholar]
- Zhang, H.; Zhang, X.; Guo, L.; Zhang, Y.; Sun, Y. Design of the microfluidic chip of oil detection. Appl. Mech. Mater. 2013, 34, 762–776. [Google Scholar] [CrossRef]
- Zhang, X. Study on Metal Particle Magnetization in Harmonic Field and Mechanism of Microfuidic Oil Detection; Dalian Maritime University: Dalian, China, 2014. [Google Scholar]
- Vasquez, S.; Kinnaert, M.; Pintelon, R. Active fault diagnosis on a hydraulic pitch system based on frequency-domain identification. IEEE Trans. Control Syst. Technol. 2019, 27, 663–678. [Google Scholar] [CrossRef]
- Shi, H.; Zhang, H.; Ma, L.; Rogers, F.; Zhao, X.; Zeng, L. An Impedance Debris Sensor Based on a High-Gradient Magnetic Field for High Sensitivity and High Throughput. IEEE Trans. Ind. Electron. 2021, 68, 5376–5384. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, H.; Tong, H. Review of online detection for wear particles in lubricating oil of aviation engine. Chin. J. Sci. Instrum. 2017, 38, 1561–1569. [Google Scholar]
- Wang, J.; Maw, M.; Yu, X.; Dai, B.; Wang, G.; Jiang, Z. Applications and perspectives on microflfluidic technologies in ships and marine engineering: A review. Microfluid. Nanofluid. 2017, 21, 39. [Google Scholar] [CrossRef]
- Flanagan, I.; Jordan, J.; Whittington, H. Wear-debris detection and analysis techniques for lubricant based condition monitoring. J. Phys. E: Sci. Instrum. 1988, 21, 1011. [Google Scholar] [CrossRef]
- Sun, Y.; Jia, L.; Zeng, Z. Hyper-heuristic capacitance array method for multi-metal wear debris Detection. Sensors 2019, 19, 515. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, P.; Wang, H.; Li, Y.; Lv, C. Ultrasonic echo waveshape features extraction based on QPSO-matching pursuit for online wear debris discrimination. Mech. Syst. Signal Process. 2015, 60–61, 301–315. [Google Scholar] [CrossRef]
- Paras, K.; Harish, H.; Atul, K. Online condition monitoring of misaligned meshing gears using wear debris and oil quality sensors. Ind. Lubr. Tribol. 2018, 70, 645–655. [Google Scholar]
- Iwai, Y.; Honda, T.; Miyajima, T.; Yoshinaga, S.; Higashi, M.; Fuwa, Y. Quantitative estimation of wear amounts by real time measurement of wear debris in lubricating oil. Tribol. Int. 2010, 43, 388–394. [Google Scholar] [CrossRef]
- Du, L.; Zhe, J. A high throughput inductive pulse sensor for online oil debris monitoring. Tribol. Int. 2011, 44, 175–179. [Google Scholar] [CrossRef]
- Zhang, X.; Zeng, L.; Zhang, H.; Huang, S. Magnetization Model and Detection Mechanism of a Microparticle in a Harmonic Magnetic Field. IEEE/ASME Trans. Mechatron. 2019, 24, 1882–1892. [Google Scholar] [CrossRef]
- NIST. SRM Order Request System SRM 2806b—Medium Test Dust (MTD) in Hydraulic Fluid [EB/OL]. Available online: https://www.sigmaaldrich.com/RS/en/product/sial/nist2806b?gclid=CjwKCAiAr4GgBhBFEiwAgwORrd7p80AXn_-qoStcBaSdDcIWYicslCP1qetrIFVv3UnlKMPB1ik9PBoC49IQAvD_BwE&gclsrc=aw.ds (accessed on 16 May 2022).
- Li, Y.; Yu, C.; Xue, B.; Zhang, H.; Zhang, X. A double lock-in amplifier circuit for complex domain signal detection of particles in oil. IEEE Trans. Instrum. Meas. 2021, 71, 3503710. [Google Scholar] [CrossRef]
- Samson, S.; Basri, M.; Fard Masoumi, H.R.; Abdul Malek, E.; Abedi Karjiban, R. An artificial neural network-based analysis of the factors controlling particle size in a virgin coconut oil-based nanoemulsion system containing copper peptide. PLoS ONE 2016, 11, e0157737. [Google Scholar] [CrossRef]
- Kumar, A.; Vishwakarma, A.; Bajaj, V. CRCCN-Net: Automated framework for classification of colorectal tissue using histopathological images. Biomed. Signal Process. Control 2023, 79, 104172. [Google Scholar] [CrossRef]
- Shinde, K.; Kayte, C.N. Fingerprint Recognition Based on Deep Learning Pre-Train with Our Best CNN Model for Person Identification. Electrochem. Soc. Trans. 2022, 107, 2209. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, International Conference on Learning Representations, ICLR, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Liu, J. Optimal Design and Analysis of Intelligent Vehicle Suspension System Based on ADAMS and Artificial Intelligence Algorithms. J. Phys. Conf. Ser. 2021, 2074, 012023. [Google Scholar] [CrossRef]
- Liu, B.; Yuan, P.; Wang, M.; Bi, C.; Liu, C.; Li, X. Optimal Design of High-Voltage Disconnecting Switch Drive System Based on ADAMS and Particle Swarm Optimization Algorithm. Mathematics 2021, 9, 1049. [Google Scholar] [CrossRef]
- Gu, Y.; Zhu, Y. Adams predictor–corrector method for solving uncertain differential equation. Comput. Appl. Math. 2021, 40, 61. [Google Scholar] [CrossRef]
- Mi, A.; Zhang, P. A method of classifier selection based on confusion matrix. J. Henan Polytech. Univ. (Nat. Sci.) 2017, 36, 116–121. [Google Scholar]
- Zhang, K.; Su, H.; Dou, Y. A new multi-classification task accuracy evaluation method based on confusion matrix. Comput. Eng. Sci. 2021, 43, 1910–1919. [Google Scholar]
- Victoria, M.; Antonio, M.; Alfonso, O.; Eduardo, L. Optimization of the area under the ROC curve using neural network supervectors for text-dependent speaker verification. Comput. Speech Lang. 2020, 63, 101078. [Google Scholar]

| Detection Methods | Principles | Advantages | Disadvantages |
|---|---|---|---|
| Inductance Detection Method | Using the magnetization and eddy current effect of oil metal particles under the action of the coil magnetic field to change the field, and then change coil inductance or voltage, according to the change in coil inductance or voltage detection. | Ferromagnetic and non-ferromagnetic particles can be distinguished; Not affected by cleanliness | Particles are indistinguishable when they are aliased |
| Capacitance Detection Method | Metal particles can be measured by using the change in oil capacitance. | Metal and non-metal particles can be distinguished; High sensitivity; Not affected by cleanliness | The measurement accuracy is easily affected by the acid value and water content of oil; Ferromagnetic and non-ferromagnetic particles cannot be distinguished |
| Ultrasonic Detection Method | When the ultrasonic wave acts on the particles in the oil, the particles will scatter or reflect the sound wave, attenuating the ultrasonic wave. Information about the size of the oil particles can be obtained by measuring the attenuation degree and amplitude of the echo. | The size of metal particles can be estimated; Not affected by cleanliness or air bubbles | The particle material cannot be judged |
| Image Detection Method | An image of the pollutant in the fluid is obtained by microscope imaging technology, and the particle size and material property information are rapidly measured using image processing technology. | The morphology and size of particles can be judged; The particle material can be roughly judged | It is difficult to achieve both high precision and real-time performance; Will be affected by cleanliness; The particle material cannot be judged accurately; |
| Optical Method | Information about the metal particles is obtained by measuring the light transmittance of oil. | High sensitivity | The particle material cannot be judged; Will be affected by cleanliness |
| Material | Conductivity, (Siemens/m) | Permeability, (H/m) |
|---|---|---|
| Fe | ||
| Cu | ||
| Al | ||
| Nodular Iron | ||
| Co | ||
| Ni-Co alloy | ||
| Brass | ||
| Permalloy |
| Dataset | Function of Dataset | Frequency | Size of Dataset |
|---|---|---|---|
| Dataset 1 | training | 0.1, 0.8, 1, 2 and 4 MHz | 40,000 |
| Dataset 2 | test | 0.1, 0.8, 1, 2 and 4 MHz | 10,000 |
| Dataset 3 | training | 0.8 and 1 MHz | 40,000 |
| Dataset 4 | test | 0.8 and 1 MHz | 10,000 |
| Dataset 5 | training | 0.8 MHz | 40,000 |
| Dataset 6 | test | 0.8 MHz | 10,000 |
| Dataset 7 | training | 4.13 kHz | 40,000 |
| Dataset 8 | test | 4.13 kHz | 10,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Cao, Y.; Xue, B.; Hua, G.; Zhang, H. Method for Identifying Materials and Sizes of Particles Based on Neural Network. J. Mar. Sci. Eng. 2023, 11, 541. https://doi.org/10.3390/jmse11030541
Zhang X, Cao Y, Xue B, Hua G, Zhang H. Method for Identifying Materials and Sizes of Particles Based on Neural Network. Journal of Marine Science and Engineering. 2023; 11(3):541. https://doi.org/10.3390/jmse11030541
Chicago/Turabian StyleZhang, Xingming, Yewen Cao, Bingsen Xue, Geyang Hua, and Hongpeng Zhang. 2023. "Method for Identifying Materials and Sizes of Particles Based on Neural Network" Journal of Marine Science and Engineering 11, no. 3: 541. https://doi.org/10.3390/jmse11030541
APA StyleZhang, X., Cao, Y., Xue, B., Hua, G., & Zhang, H. (2023). Method for Identifying Materials and Sizes of Particles Based on Neural Network. Journal of Marine Science and Engineering, 11(3), 541. https://doi.org/10.3390/jmse11030541







