Analysis of Interaction between Interior and Exterior Wall Corrosion Defects
Abstract
1. Introduction
2. Establishment of FEM Model
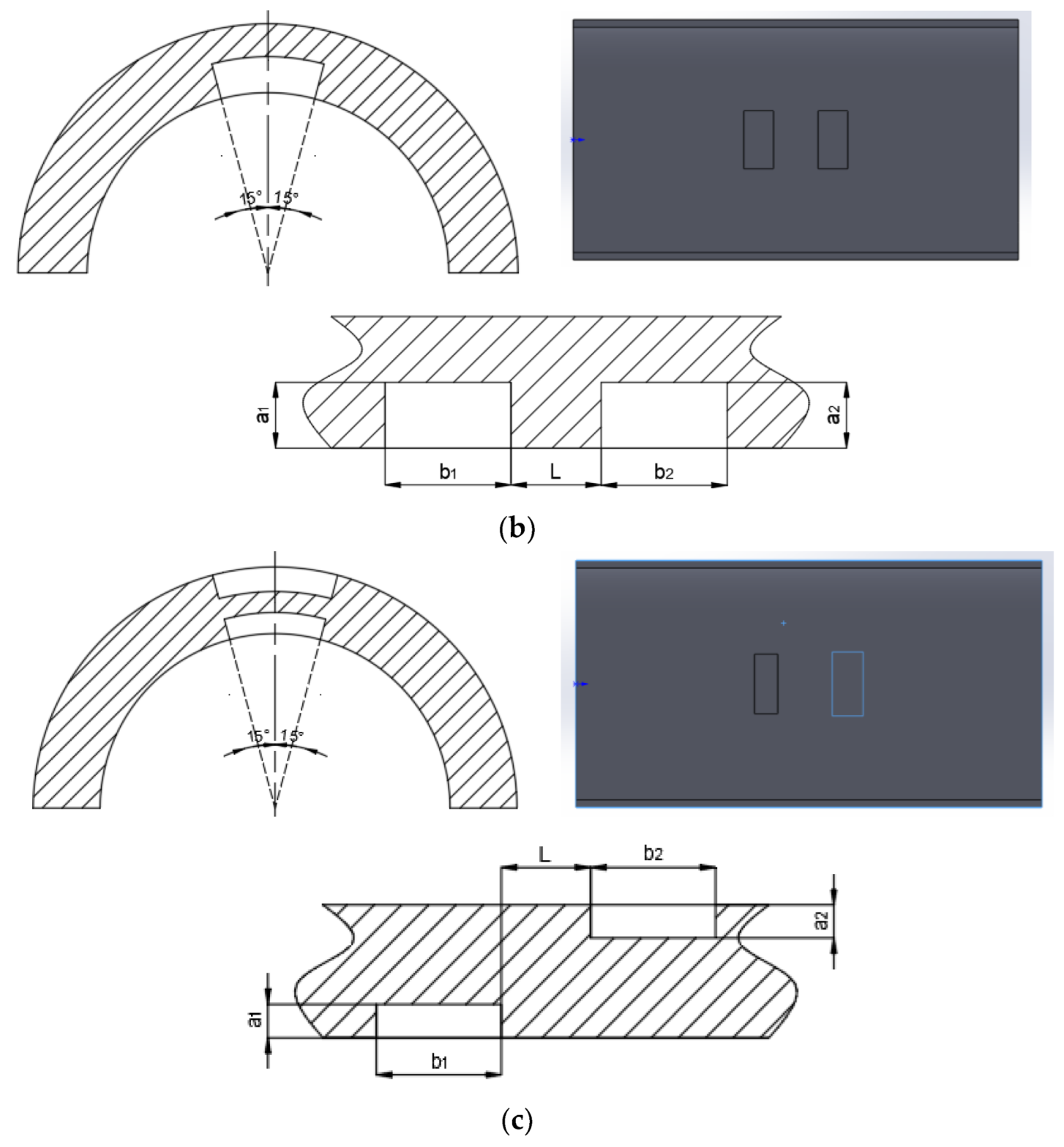
2.1. Establishment and Parameters of the Geometric Model
2.2. FEM Model
2.2.1. Model Constraints
2.2.2. Application of Load
2.2.3. Failure Pressure Solution
2.3. Failure Criterion
2.4. Verification of FEM Results
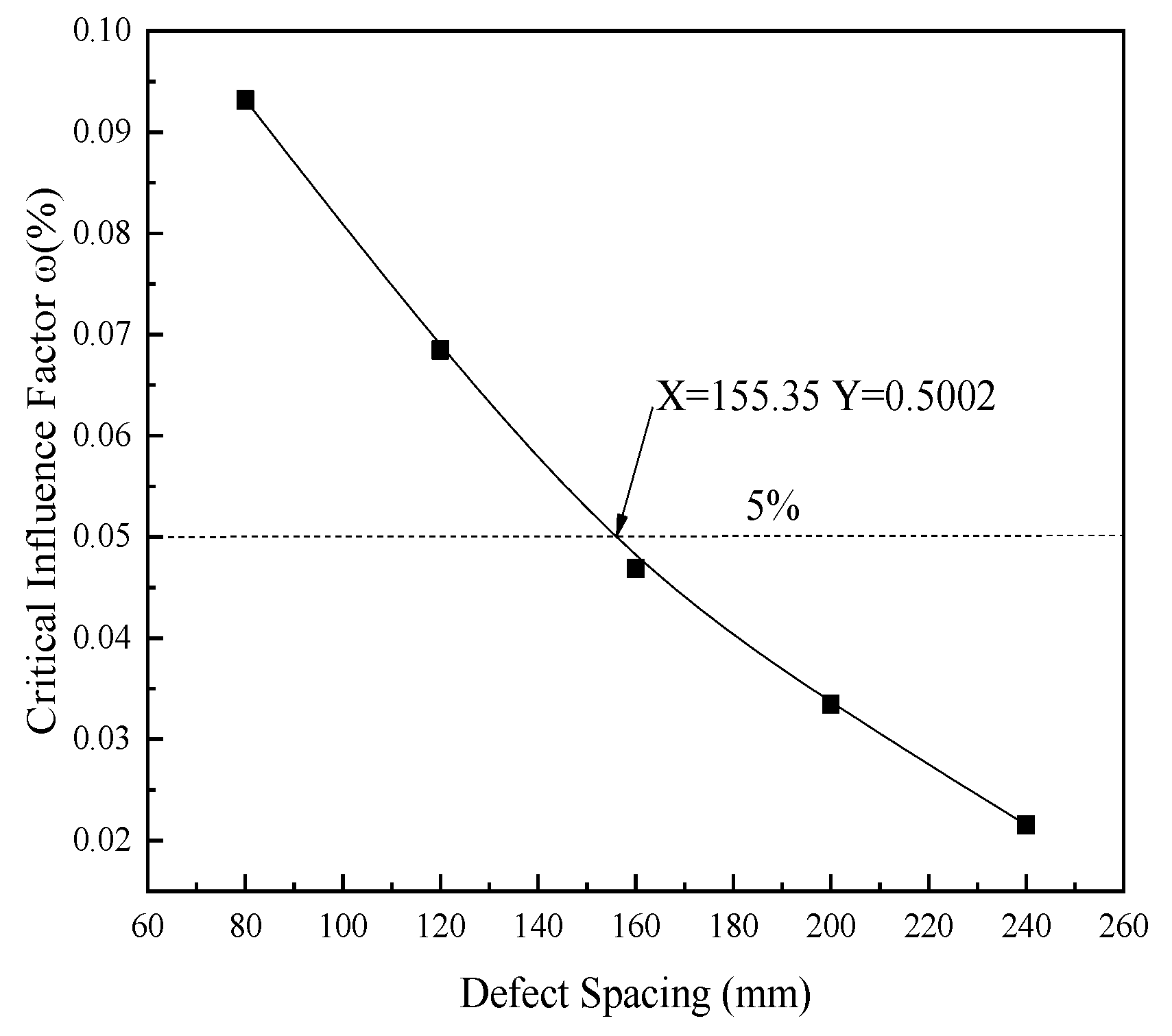
2.5. Critical Distance Calculation Method
2.6. Example of the Critical Distance Calculation
3. Results of the FEM Analysis
3.1. Geometric Model and Stress Nephogram of Different Double Defect Pipe Models
3.2. Impact of Defect Depth on the Critical Distance
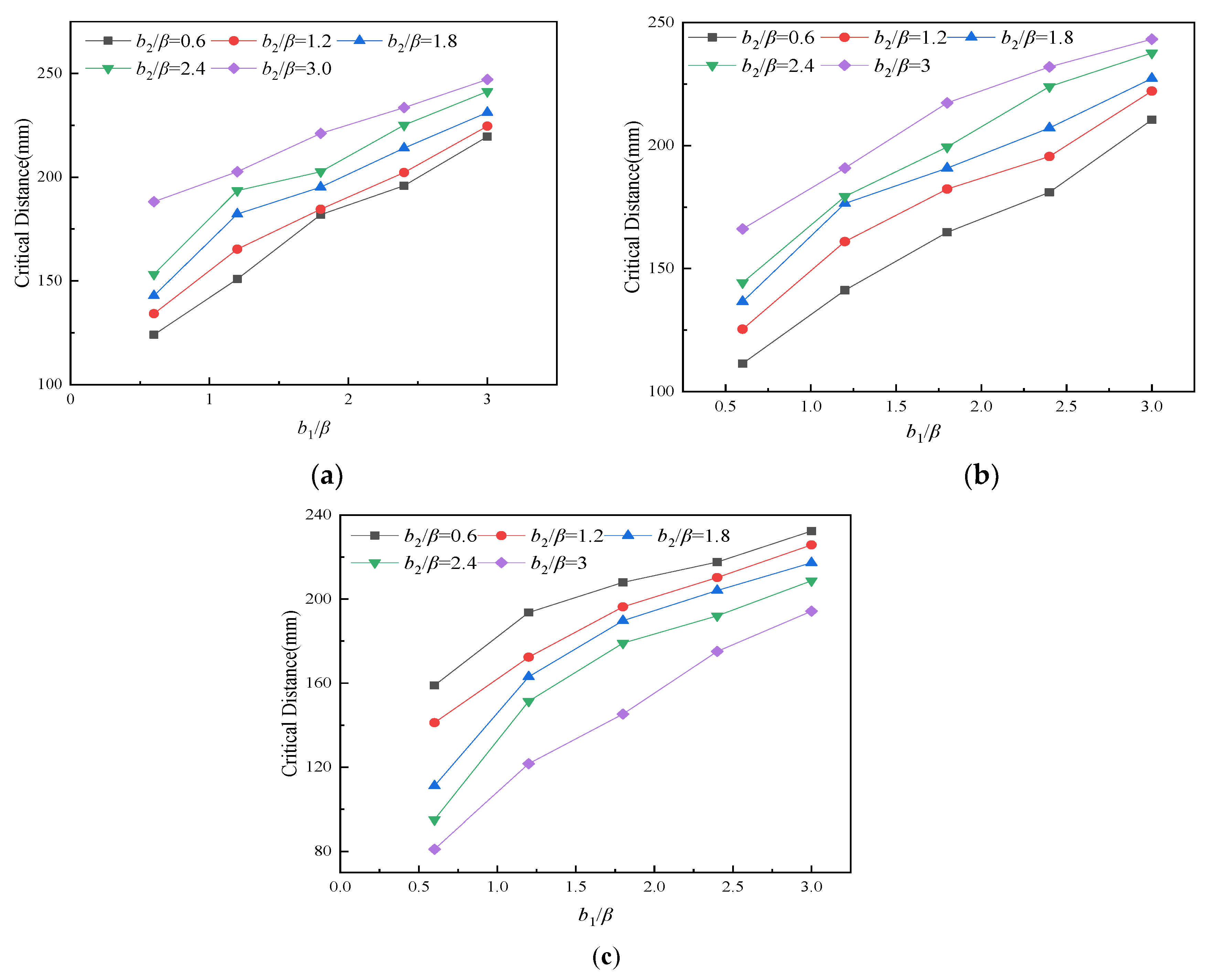
3.3. Impact of Defect Length on the Critical Distance
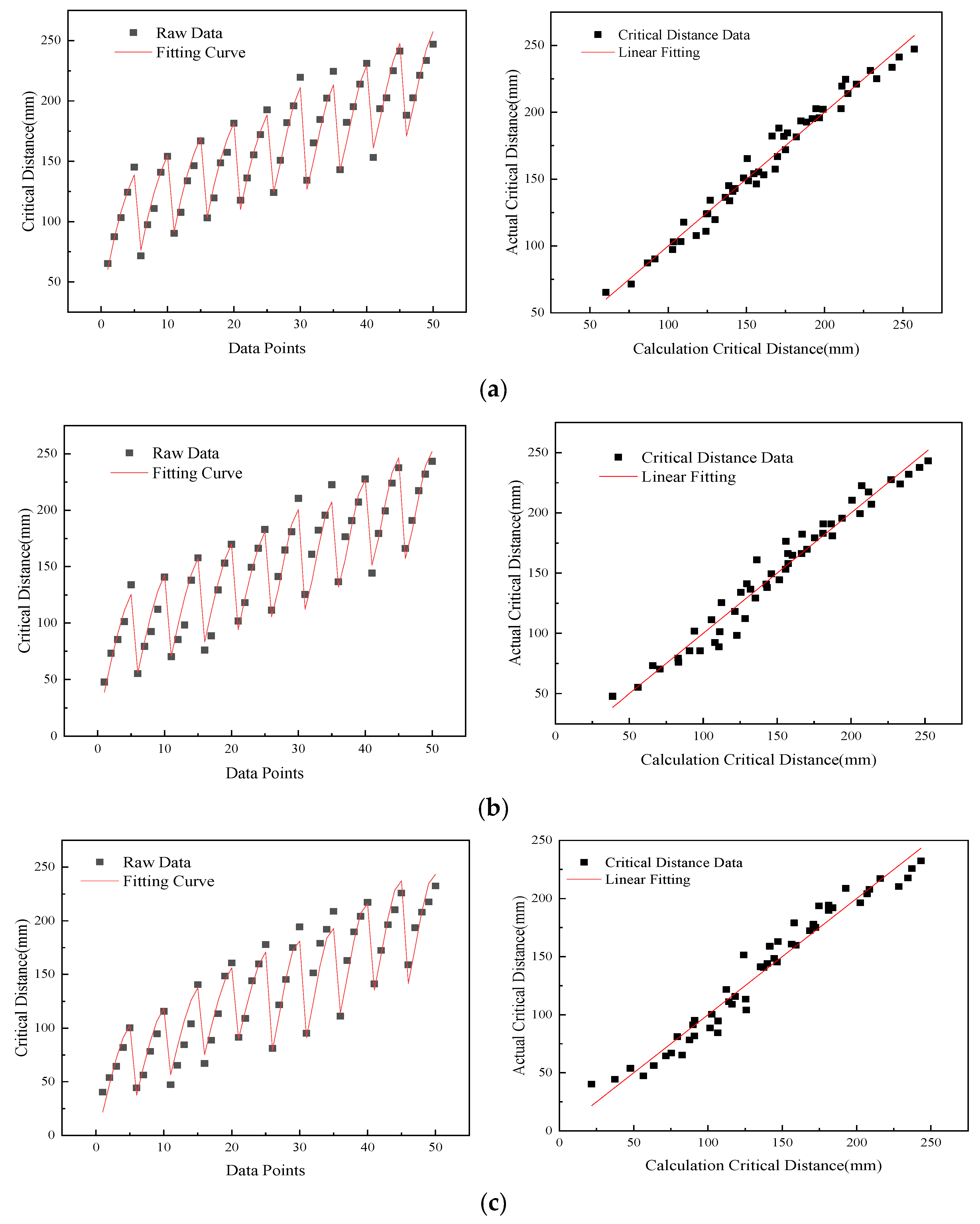
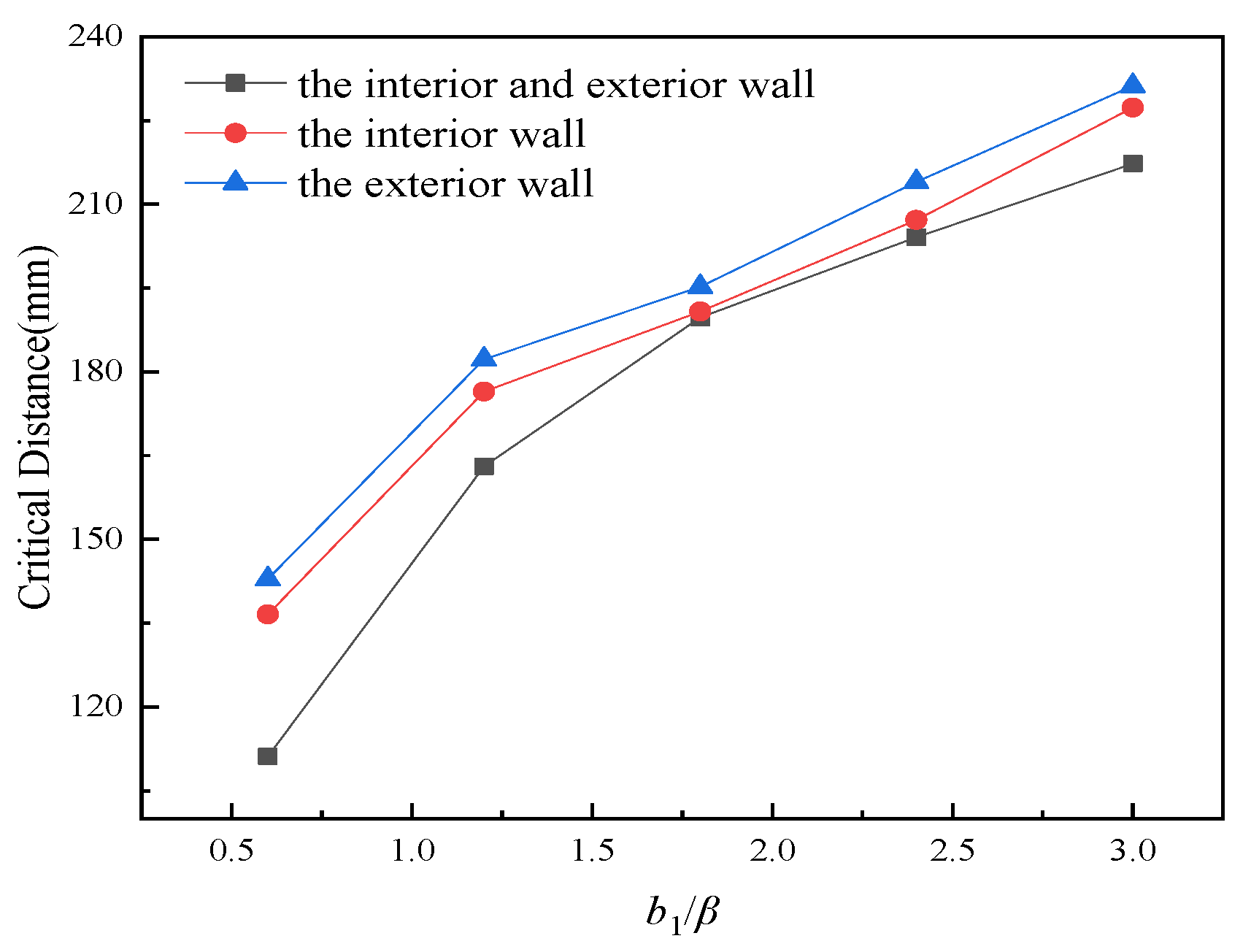
3.4. Critical Distance Fitting Formula of Different Types of Double Defect Pipe Models
3.5. Comparative Analysis of Defect Interaction in Different Types of Double Defect Models
3.5.1. Comparative Analysis of the Critical Distance of Defect Depth
3.5.2. Comparative Analysis of the Critical Distance of Defect Lengths
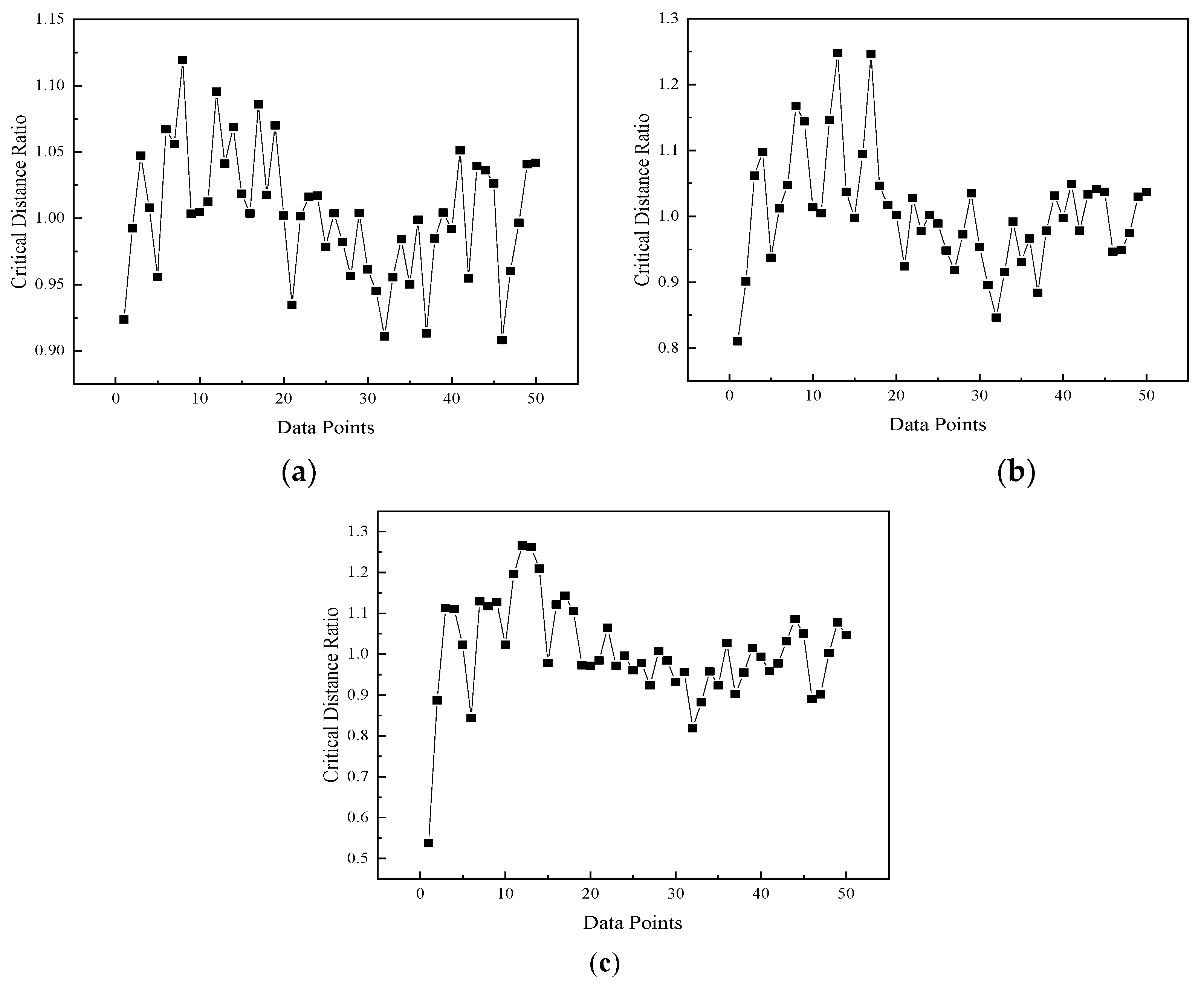
3.6. Applicability Analysis of the Critical Distance Fitting Formula for Different Pipe Models
3.6.1. Conservative Analysis of the Three Models
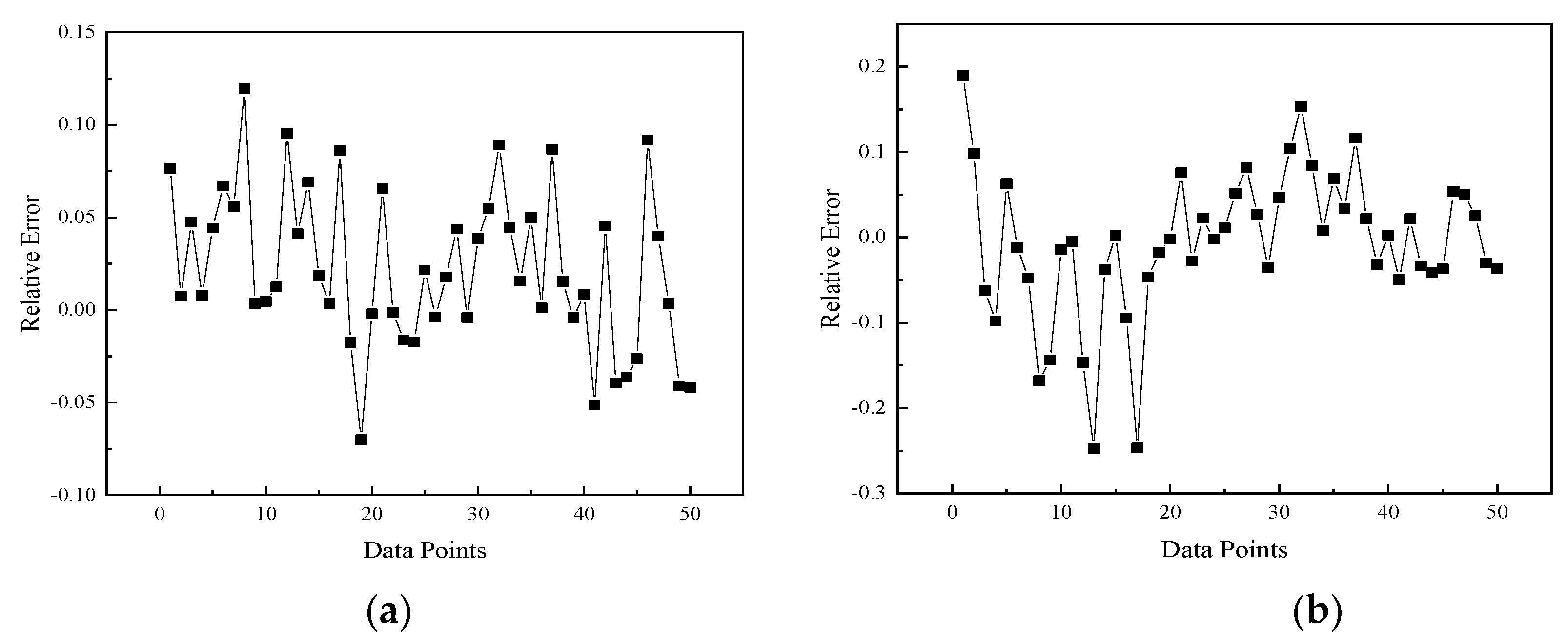
3.6.2. Error Analysis of the Three Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Wharton, J.A.; Shenoi, R.A. Mechano-electrochemical modelling of corroded steel structures. Eng. Struct. 2016, 128, 1–14. [Google Scholar] [CrossRef]
- Srikanth, S.; Sankaranarayanan, T.S.N.; Gopalakrishna, K.; Narasimhan, B.R.V.; Das, T.V.K.; Das, S.K. Corrosion in a buried pressurised water pipeline. Eng. Fail. Anal. 2005, 12, 634–651. [Google Scholar] [CrossRef]
- Cosham, A.; Hopkins, P.; Macdonald, K.A. Best practice for the assessment of defects in pipelines-Corrosion. Eng. Fail. Anal. 2007, 14, 1245–1265. [Google Scholar] [CrossRef]
- Saeedikhani, M.; Blackwood, D.J. Finite element method for thin film corrosion modelling: Where we advanced and where we would like to advance. Corros. Mater. Degrad. 2020, 1, 273–281. [Google Scholar] [CrossRef]
- Moustabchir, H.; Azari, Z.; Hariri, S.; Dmytrakh, I. Experimental and numerical study of stress–strain state of pressurized cylindrical shells with external defects. Eng. Fail. Anal. 2010, 17, 506–514. [Google Scholar] [CrossRef]
- Moustabchir, H.; Arbaoui, J.; Azari, Z.; Hariri, S.; Pruncu, C.I. Experimental/numerical investigation of mechanical behaviour of internally pressurized cylindrical shells with external longitudinal and circumferential semi-elliptical defects. Alex. Eng. J. 2017, 57, 1339–1347. [Google Scholar] [CrossRef]
- Fekete, G.; Varga, L. The effect of the width to length ratios of corrosion defects on the burst pressures of transmission pipelines. Eng. Fail. Anal. 2012, 21, 21–30. [Google Scholar] [CrossRef]
- Duane, S.C.; Roy, J.P. Prediction of the failure pressure for complex corrosion defects. Int. J. Press. Ves. Pip. 2002, 79, 279–287. [Google Scholar]
- Hosseini, A.; Cronin, D.; Plumtree, A. Crack in corrosion defect assessment in transmission pipelines. J. Press. Vessel. Technol. 2013, 135, 8. [Google Scholar] [CrossRef]
- Ma, B.; Shuai, J.; Liu, D.X.; Xu, K. Assessment on failure pressure of high strength pipeline with corrosion defects. Eng. Fail. Anal. 2013, 32, 209–219. [Google Scholar] [CrossRef]
- Sun, M.M.; Li, X.; Liu, J.K. Determination of folias factor for failure pressure of corroded pipeline. J. Press. Vessel. Technol. 2020, 142, 31802. [Google Scholar] [CrossRef]
- Yeom, K.J.; Lee, Y.K.; Oh, K.H.; Kim, W.S. Integrity assessment of a corroded API X70 pipe with a single defect by burst pressure analysis. Eng. Fail. Anal. 2015, 57, 553–561. [Google Scholar] [CrossRef]
- Shuai, Y.; Shuai, J.; Xu, K. Probabilistic analysis of corroded pipelines based on a new failure pressure model. Eng. Fail. Anal. 2017, 81, 216–233. [Google Scholar] [CrossRef]
- Mokhtari, M.; Melchers, R.E. A new approach to assess the remaining strength of corroded steel pipes. Eng. Fail. Anal. 2018, 93, 144–156. [Google Scholar] [CrossRef]
- Majid, Z.A.; Mohsin, R.; Yusof, M.Z. Experimental and computational failure analysis of natural gas pipe. Eng. Fail. Anal. 2012, 19, 32–42. [Google Scholar] [CrossRef]
- Caleyo, F.; González, J.L.; Hallen, J.M. A study on the reliability assessment methodology for pipelines with active corrosion defects. Int. J. Press. Ves. Pip. 2002, 79, 77–86. [Google Scholar] [CrossRef]
- Cerit, M.; Genel, K.; Eksi, S. Numerical investigation on stress concentration of corrosion pit. Eng. Fail. Anal. 2009, 16, 2467–2472. [Google Scholar] [CrossRef]
- Cerit, M. Numerical investigation on torsional stress concentration factor at the semielliptical corrosion pit. Corros. Sci. 2013, 67, 225–232. [Google Scholar] [CrossRef]
- Xu, L.Y.; Cheng, Y.F. Reliability and failure pressure prediction of various grades of pipeline steel in the presence of corrosion defects and pre-strain. Int. J. Press. Ves. Pip. 2012, 89, 75–84. [Google Scholar] [CrossRef]
- Xu, L.Y.; Cheng, Y.F. Development of a finite element model for simulation and prediction of mechanoelectrochemical effect of pipeline corrosion. Corros. Sci. 2013, 73, 150–160. [Google Scholar] [CrossRef]
- Zelmati, D.; Ghelloudj, O.; Amirat, A. Correlation between defect depth and defect length through a reliability index when evaluating of the remaining life of steel pipeline under corrosion and crack defects. Eng. Fail. Anal. 2017, 79, 171–185. [Google Scholar] [CrossRef]
- Chouchaoui, B.A.; Pick, R.J. Behaviour of circumferentially aligned corrosion pits. Int. J. Press. Ves. Pip. 1994, 57, 187–200. [Google Scholar] [CrossRef]
- Chouchaoui, B.A.; Pick, R.J. Behaviour of longitudinally aligned corrosion pits. Int. J. Press. Ves. Pip. 1996, 67, 17–35. [Google Scholar] [CrossRef]
- Benjamin, A.C.; Freire, J.L.F.; Vieira, R.D.; Cunha, D.J.S. Interaction of corrosion defects in pipelines-Part 1: Fundamentals. Int. J. Press. Ves. Pip. 2016, 144, 56–62. [Google Scholar] [CrossRef]
- Benjamin, A.C.; Freire, J.L.F.; Vieira, R.D.; Cunha, D.J.S. Interaction of corrosion defects in pipelines-Part 2: MTI JIP database of corroded pipe tests. Int. J. Press. Ves. Pip. 2016, 145, 41–59. [Google Scholar] [CrossRef]
- Chen, Y.F.; Zhang, H.; Zhang, J.; Liu, X.B.; Li, X.; Zhou, J. Failure assessment of X80 pipeline with interacting corrosion defects. Eng. Fail. Anal. 2015, 47, 67–76. [Google Scholar] [CrossRef]
- Bedairi, B.; Cronin, D.; Hosseini, A.; Plumtree, A. Failure prediction for crack-in-corrosion defects in natural gas transmission pipelines. Int. J. Press. Vessel. Pip. 2012, 6, 90–99. [Google Scholar] [CrossRef]
- Al-Owaisi, S.S.; Becker, A.A.; Sun, W. Analysis of shape and location effects of closely spaced metal loss defects in pressurised pipes. Eng. Fail. Anal. 2016, 68, 172–186. [Google Scholar] [CrossRef]
- Soares, E.; Bruère, V.M.; Afonso, S.M.B.; Willmersdorf, R.B.; Lyra, P.R.M.; Bouchonneau, N. Structural integrity analysis of pipelines with interacting corrosion defects by multiphysics modeling. Eng. Fail. Anal. 2019, 97, 91–102. [Google Scholar] [CrossRef]
- Sun, J.L.; Cheng, Y.F. Assessment by finite element modeling of the interaction of multiple corrosion defects and the effect on failure pressure of corroded pipelines. Eng. Struct. 2018, 165, 278–286. [Google Scholar] [CrossRef]
- Sun, J.L.; Cheng, Y.F. Investigation by numerical modeling of the mechano-electrochemical interaction of circumferentially aligned corrosion defects on pipelines. Thin-Walled. Struct. 2019, 144, 106314. [Google Scholar] [CrossRef]
- Sun, M.M.; Zhao, H.S.; Li, X.; Liu, J.K.; Xu, Z.G. A new evaluation method for burst pressure of pipeline with colonies of circumferentially aligned defects. Ocean. Eng. 2021, 222, 108628. [Google Scholar] [CrossRef]
- Al-Owaisi, S.; Becker, A.A.; Sun, W.; Al-Shabibi, A.; Al-Maharbi, M.; Pervez, T.; Al-Salmi, H. An experimental investigation of the effect of defect shape and orientation on the burst pressure of pressurised pipes. Eng. Fail. Anal. 2018, 93, 200–213. [Google Scholar] [CrossRef]
- Chen, Y.F.; Zhang, H.; Zhang, J.; Li, X.; Zhou, J. Failure analysis of high strength pipeline with single and multiple corrosions. Mater. Design. 2015, 67, 552–557. [Google Scholar] [CrossRef]
- Lo, M.; Karuppanan, S.; Ovinis, M. Failure pressure prediction of a corroded pipeline with longitudinally interacting corrosion defects subjected to combined loadings using FEM and ANN. J. Mar. Sci. Eng. 2021, 9, 281. [Google Scholar] [CrossRef]
- Chen, Y.F.; Li, X.; Zhou, J.; Guan, J. Study on interaction relationship for submarine pipeline with axial corrosion defects. China Ocean. Eng. 2008, 22, 359–370. [Google Scholar]
- Li, X.; Bai, Y.; Su, C.L.; Li, M.S. Effect of interaction between corrosion defects on failure pressure of thin wall steel pipeline. Int. J. Press. Ves. Pip. 2016, 138, 8–18. [Google Scholar] [CrossRef]
- Huang, K.; Yang, L.; Li, A.R. Study on the influencing factors of interference effect of corrosion defects on the inner and outer walls of oil and gas pipelines. Surf. Tech. 2020, 49, 199–204. [Google Scholar]
- Freire, J.L.F.; Vieira, R.D.; Benjamin, A.C. PAR T 1: Experimental techniques in the field of pipeline integrity. Exp. Tech. 2006, 30, 44–50. [Google Scholar] [CrossRef]
- Freire, J.L.F.; Vieira, R.D.; Castro, J.T.P.; Benjamin, A.C. PART 3: Burst tests of pipeline with extensive longitudinal metal loss. Exp. Tech. 2006, 30, 60–65. [Google Scholar] [CrossRef]






| Material | Yield Strength (MPa) | Tensile Strength (MPa) | Modulus of Elasticity (GPa) | Poisson’s Ratio |
|---|---|---|---|---|
| X100 | 690 | 760 | 210 | 0.3 |
| Number | D (mm) | t (mm) | a (mm) | b (mm) | Burst Pressure (MPa) | FEM (MPa) |
|---|---|---|---|---|---|---|
| 1 | 1320 | 22.9 | 11.5 | 1110 | 15.4 | 14.5 |
| 2 | 1320 | 22.9 | 11.5 | 1013 | 15 | 14.2 |
| 3 | 1320 | 22.9 | 11.4 | 609 | 18.1 | 16.5 |
| Defect Spacing (mm) | Pd (MPa) | Ps (MPa) | Critical Influence Factor ω (%) |
|---|---|---|---|
| 80 | 24.03 | 26.27 | 9.32 |
| 120 | 24.59 | 26.27 | 6.85 |
| 160 | 25.09 | 26.27 | 4.69 |
| 200 | 25.42 | 26.27 | 3.35 |
| 240 | 25.71 | 26.27 | 2.15 |
| Model Category | Mean Relative Error | Mean Absolute Error |
|---|---|---|
| exterior wall | −0.0029 | 0.0373 |
| interior wall | −0.0059 | 0.0625 |
| interior and exterior wall | −0.0080 | 0.0864 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Long, M.; Li, X.; Zhang, Z. Analysis of Interaction between Interior and Exterior Wall Corrosion Defects. J. Mar. Sci. Eng. 2023, 11, 502. https://doi.org/10.3390/jmse11030502
Wang Z, Long M, Li X, Zhang Z. Analysis of Interaction between Interior and Exterior Wall Corrosion Defects. Journal of Marine Science and Engineering. 2023; 11(3):502. https://doi.org/10.3390/jmse11030502
Chicago/Turabian StyleWang, Zhanhui, Mengzhao Long, Xiaojun Li, and Zhifang Zhang. 2023. "Analysis of Interaction between Interior and Exterior Wall Corrosion Defects" Journal of Marine Science and Engineering 11, no. 3: 502. https://doi.org/10.3390/jmse11030502
APA StyleWang, Z., Long, M., Li, X., & Zhang, Z. (2023). Analysis of Interaction between Interior and Exterior Wall Corrosion Defects. Journal of Marine Science and Engineering, 11(3), 502. https://doi.org/10.3390/jmse11030502






