Investigation of the Spiral Wave Generation and Propagation on a Numerical Circular Wave Tank Model
Abstract
:1. Introduction
2. Governing Equations
3. Methodology of the Numerical Model
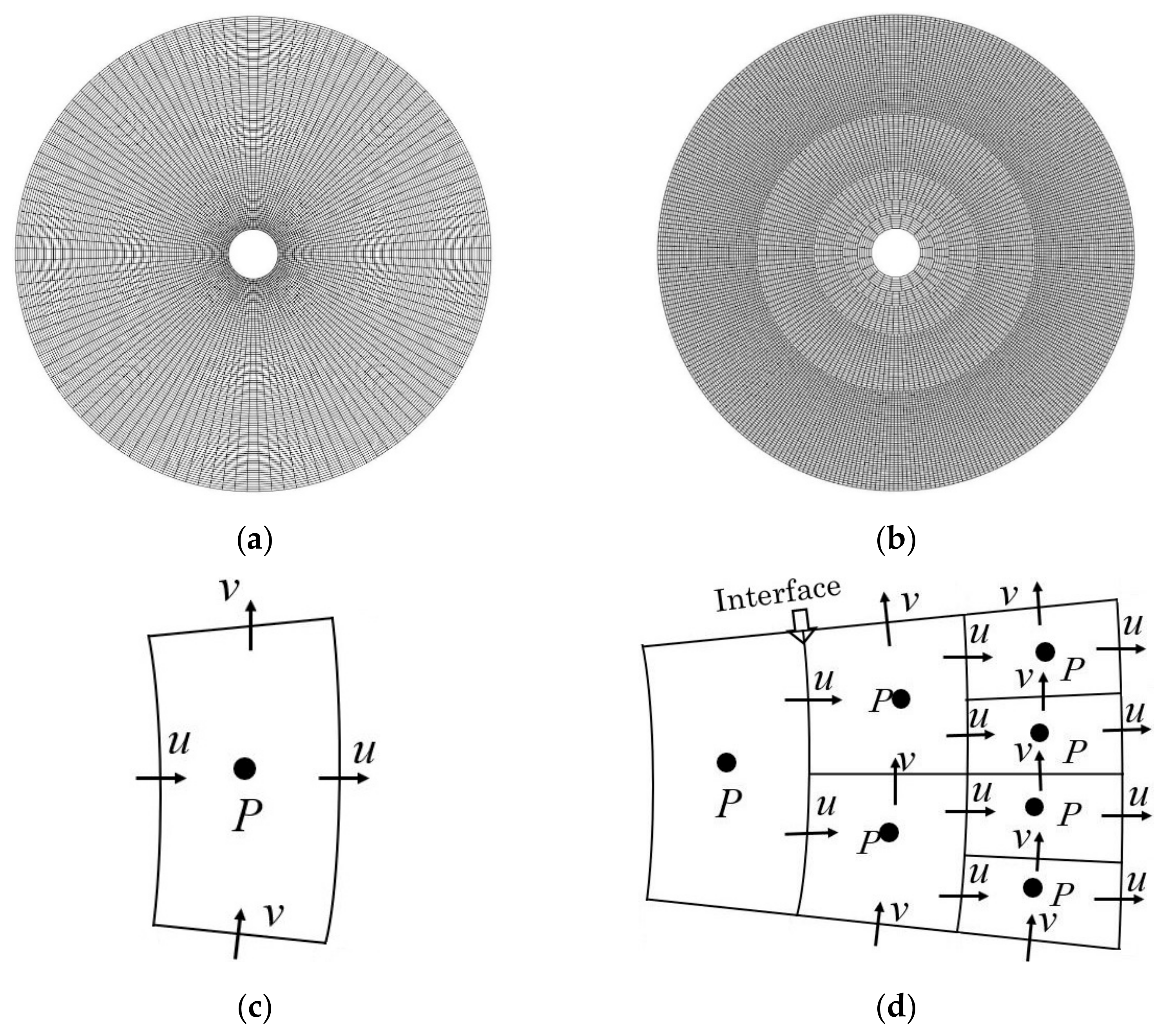
3.1. Grid Generation
3.2. Discretization of the Governing Equations
4. Parameters and Experimental Conditions of the Wave Tank Model
4.1. Numerical Calculations
4.2. Hydraulic Model Experiment
5. Results and Discussion
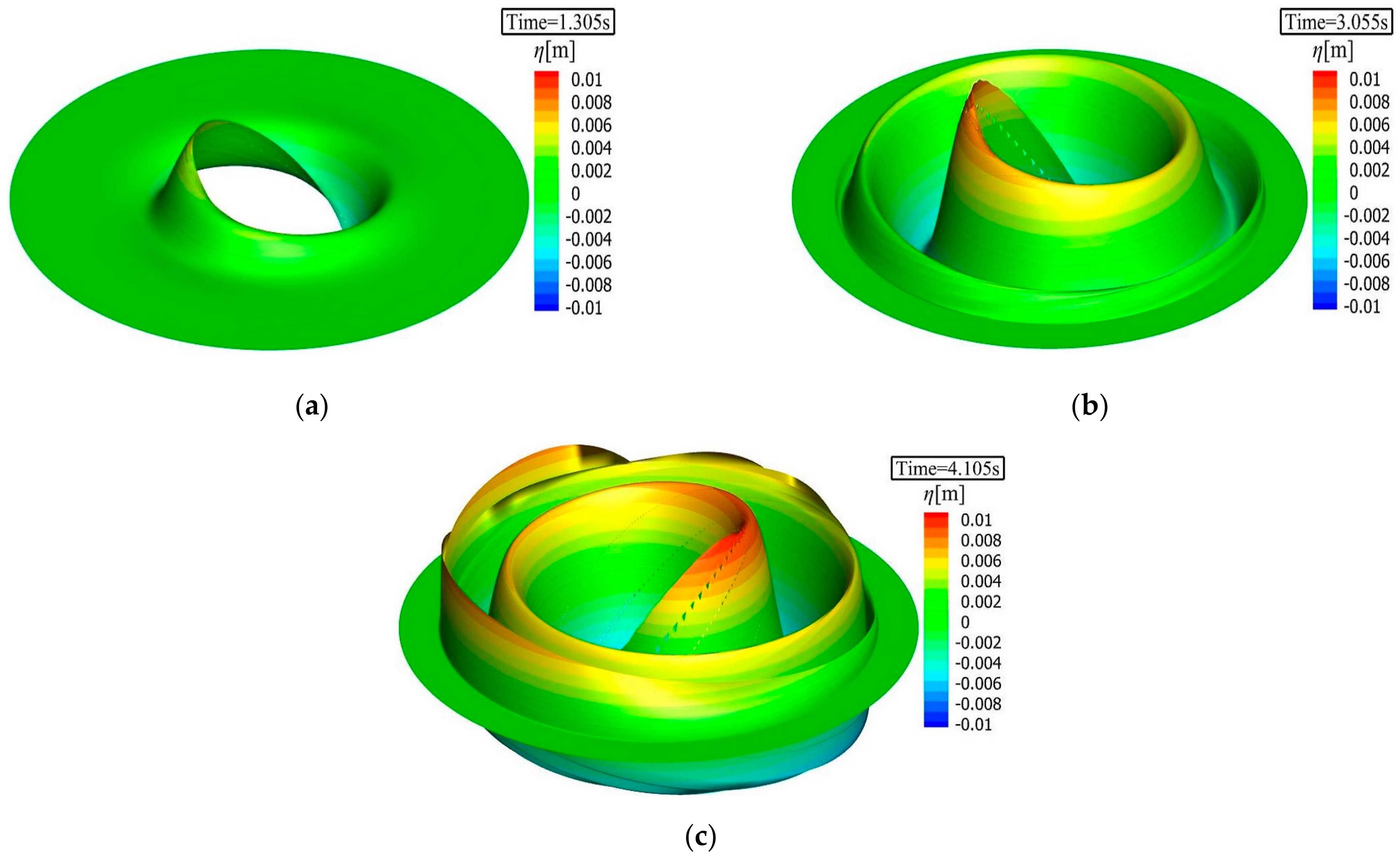
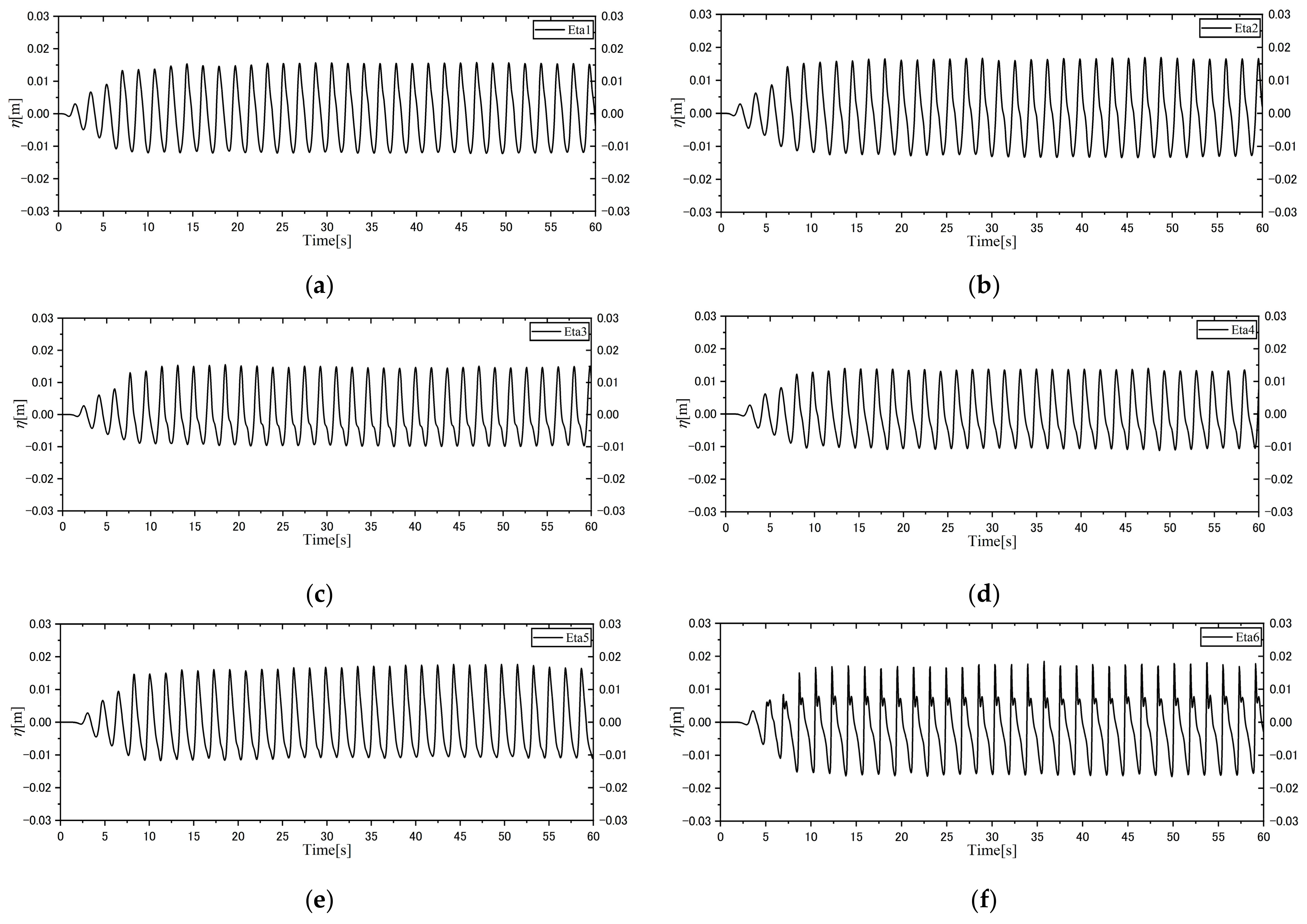
5.1. Spiral Wave Generation
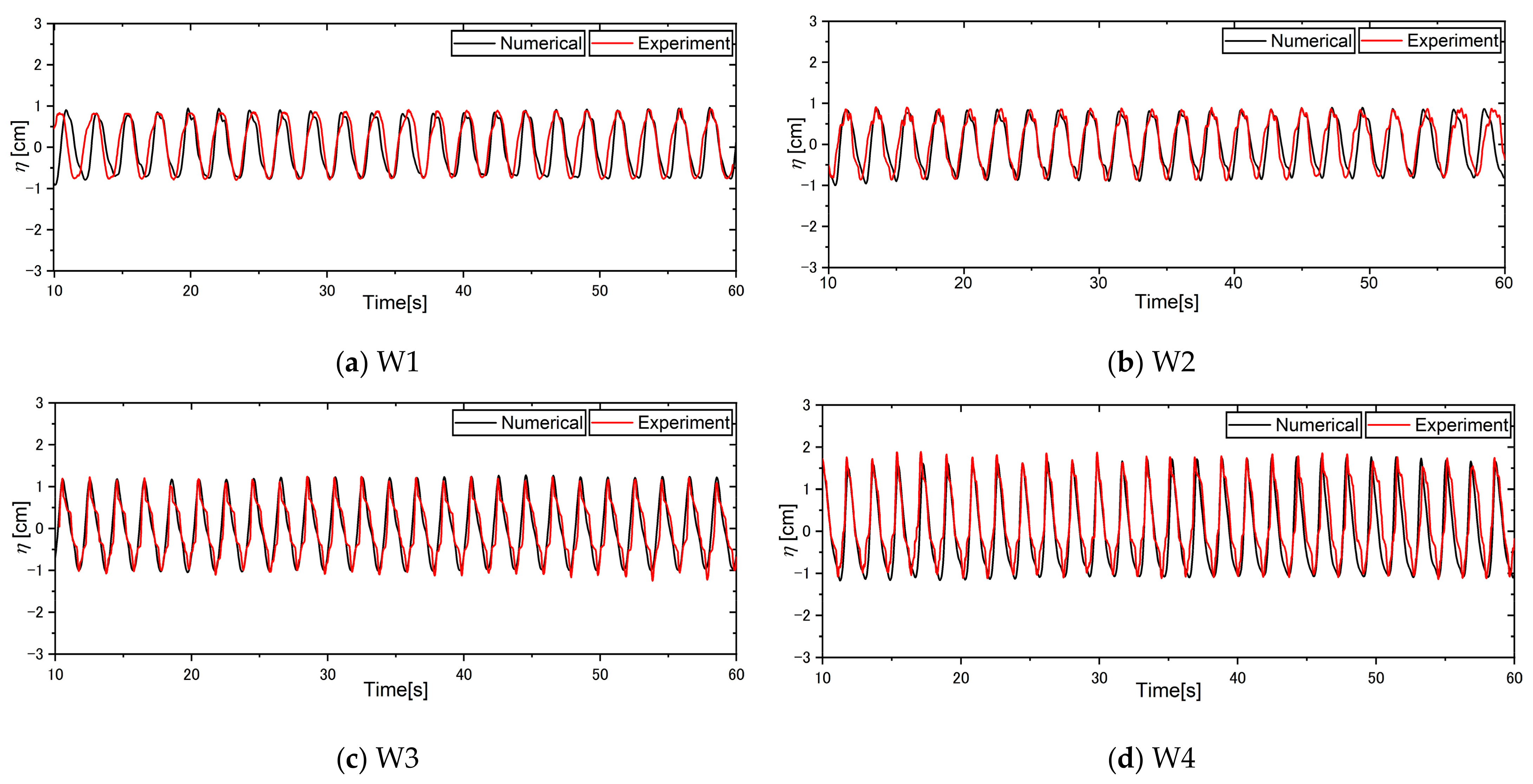
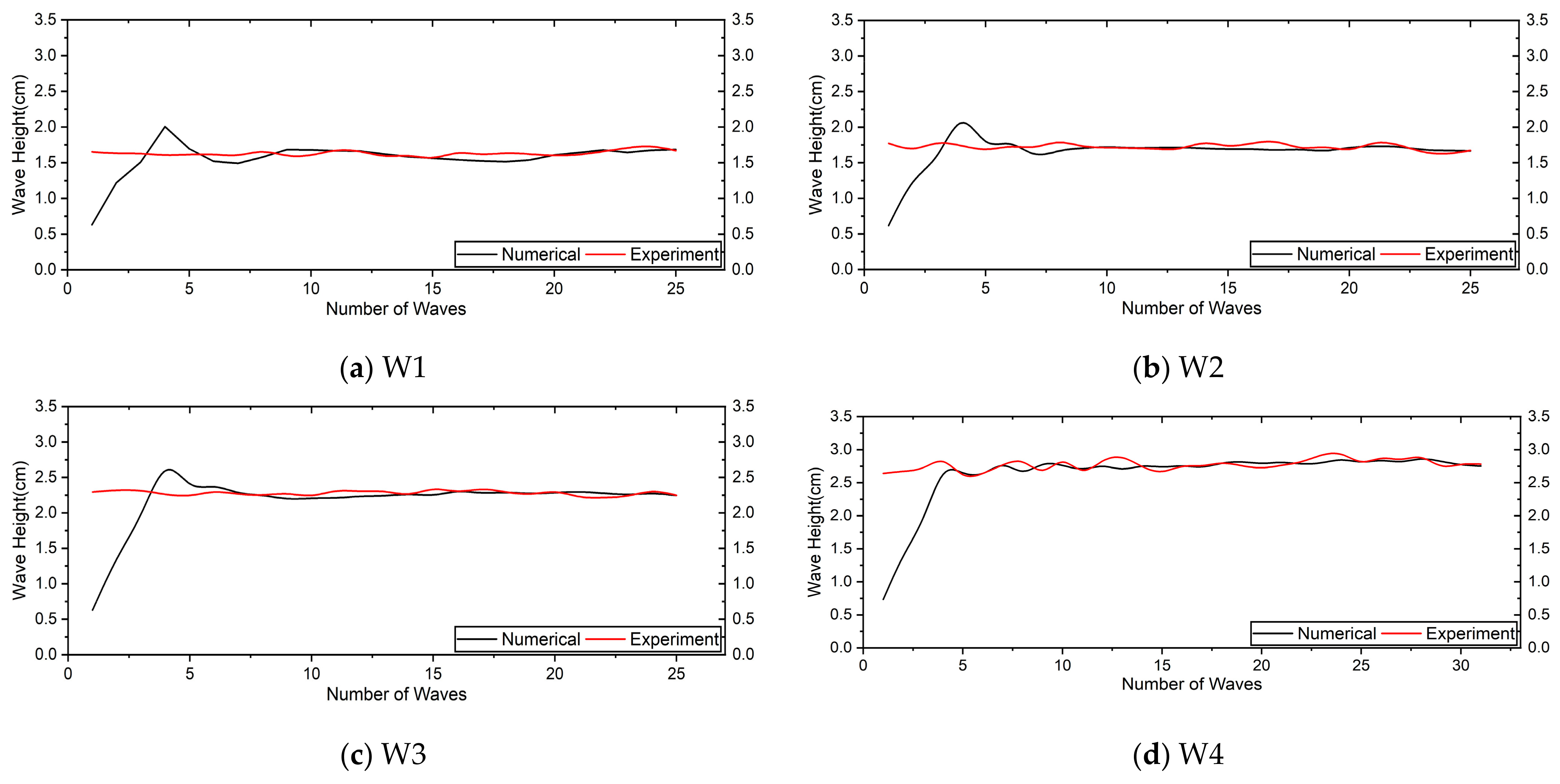
5.2. Model Validation
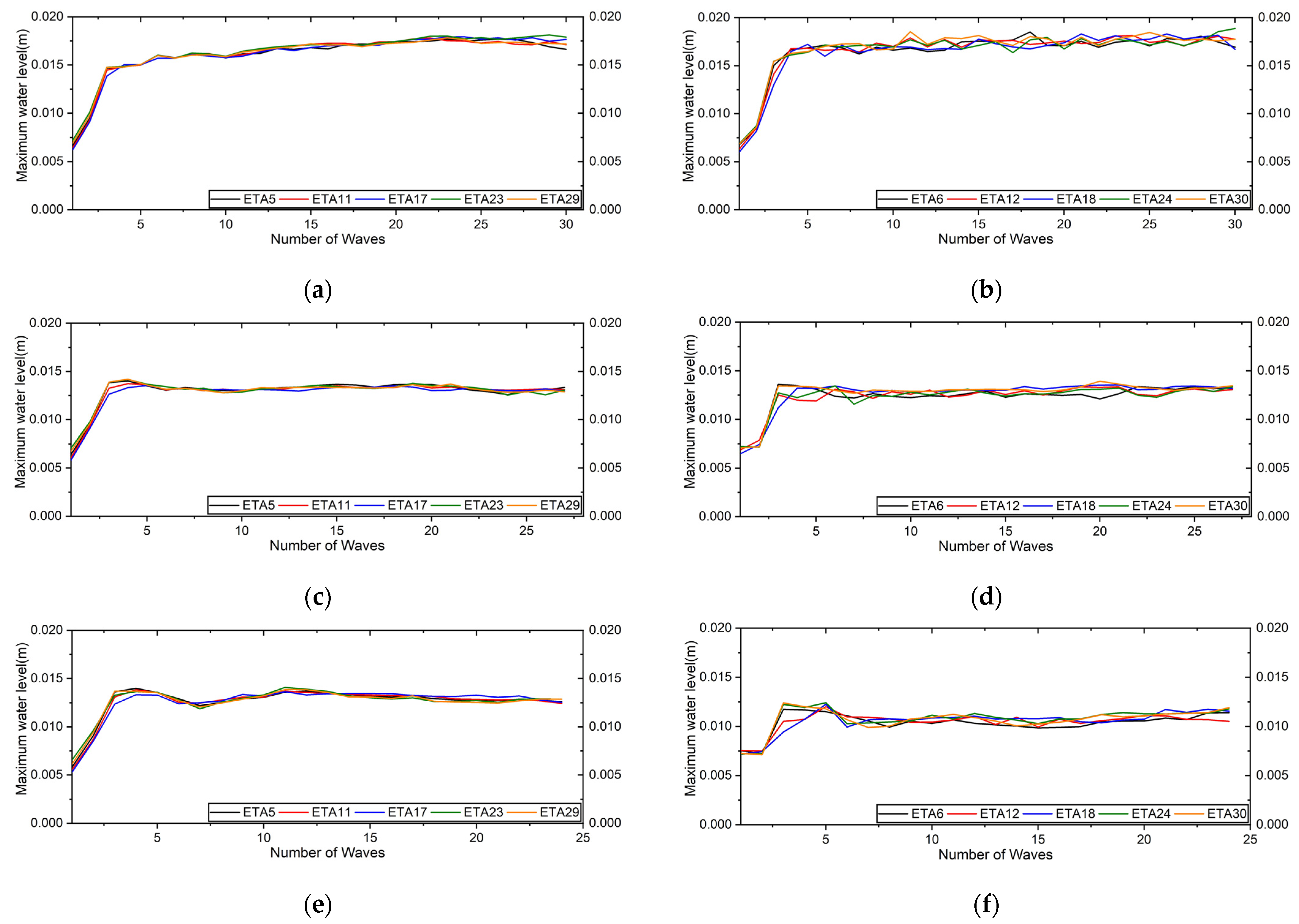
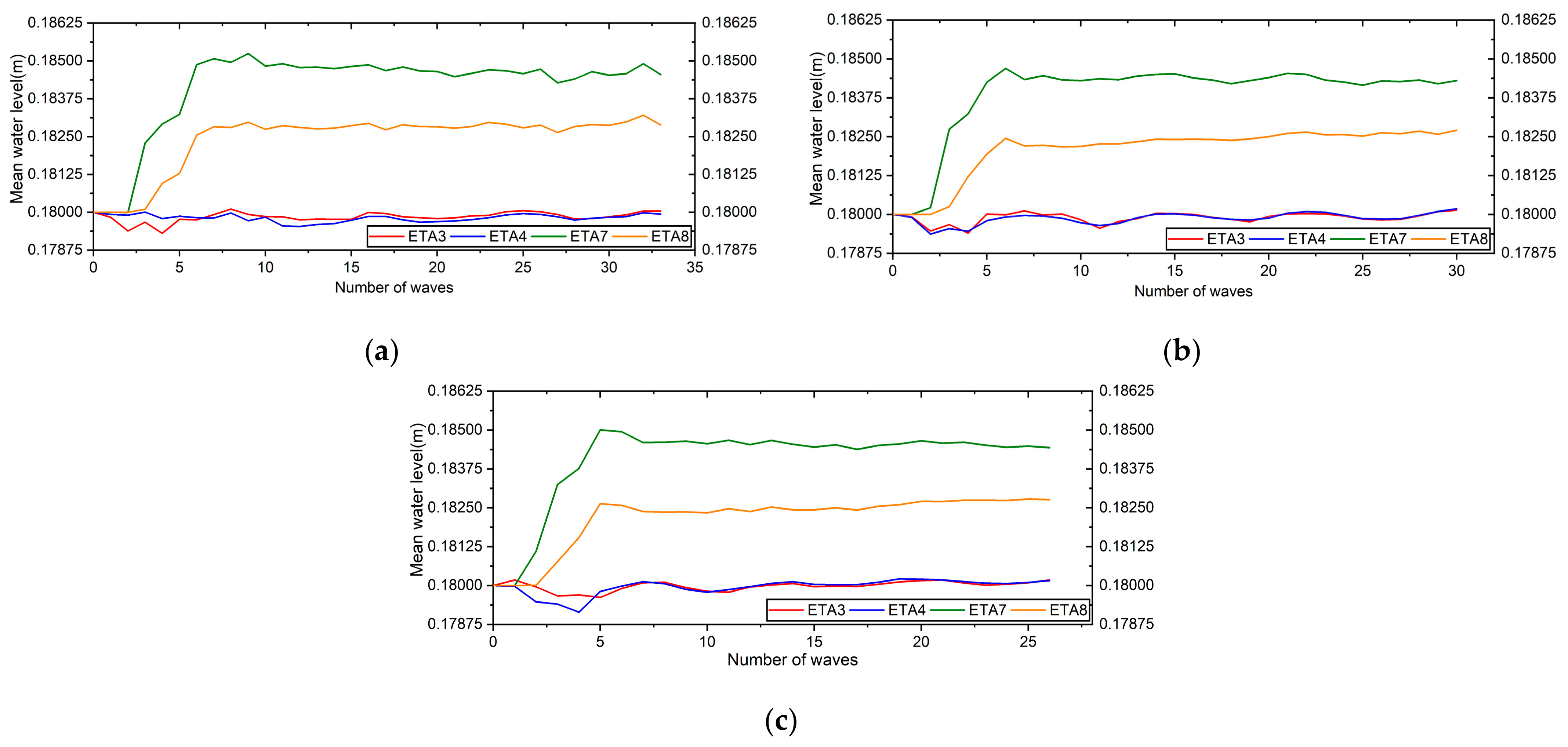
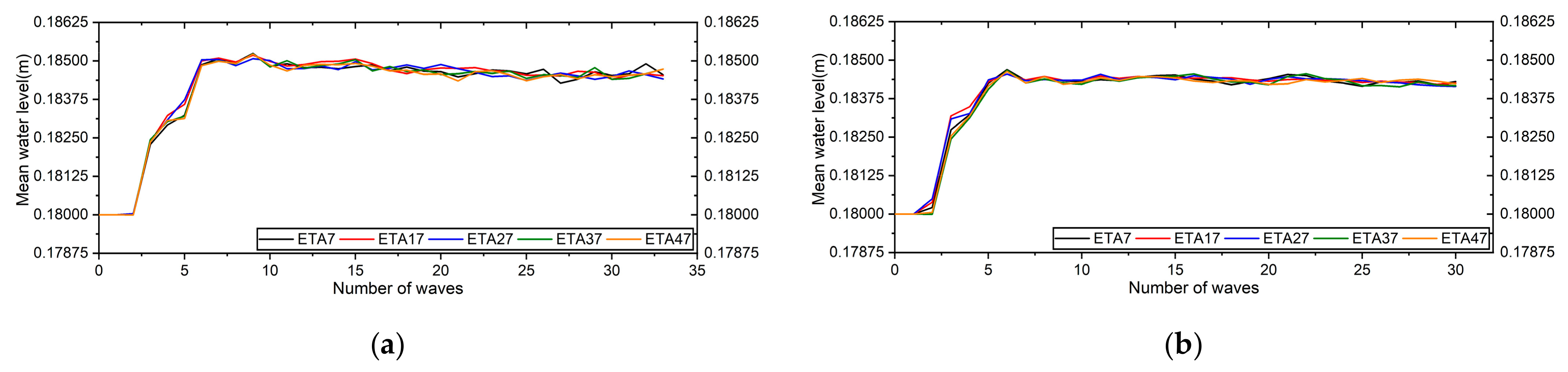
5.3. Wave Characteristics
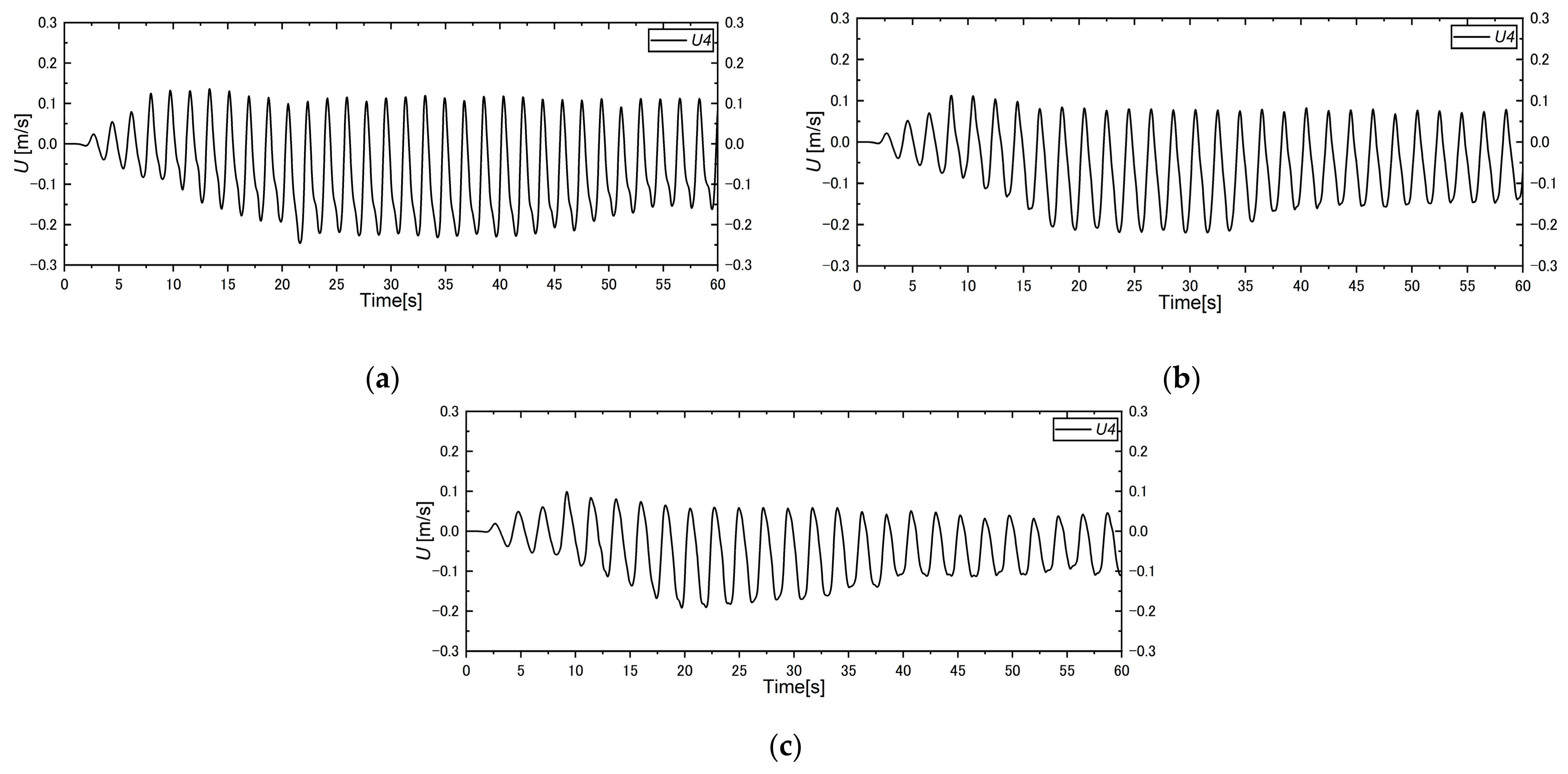
5.4. Comparisons for Different Conditions
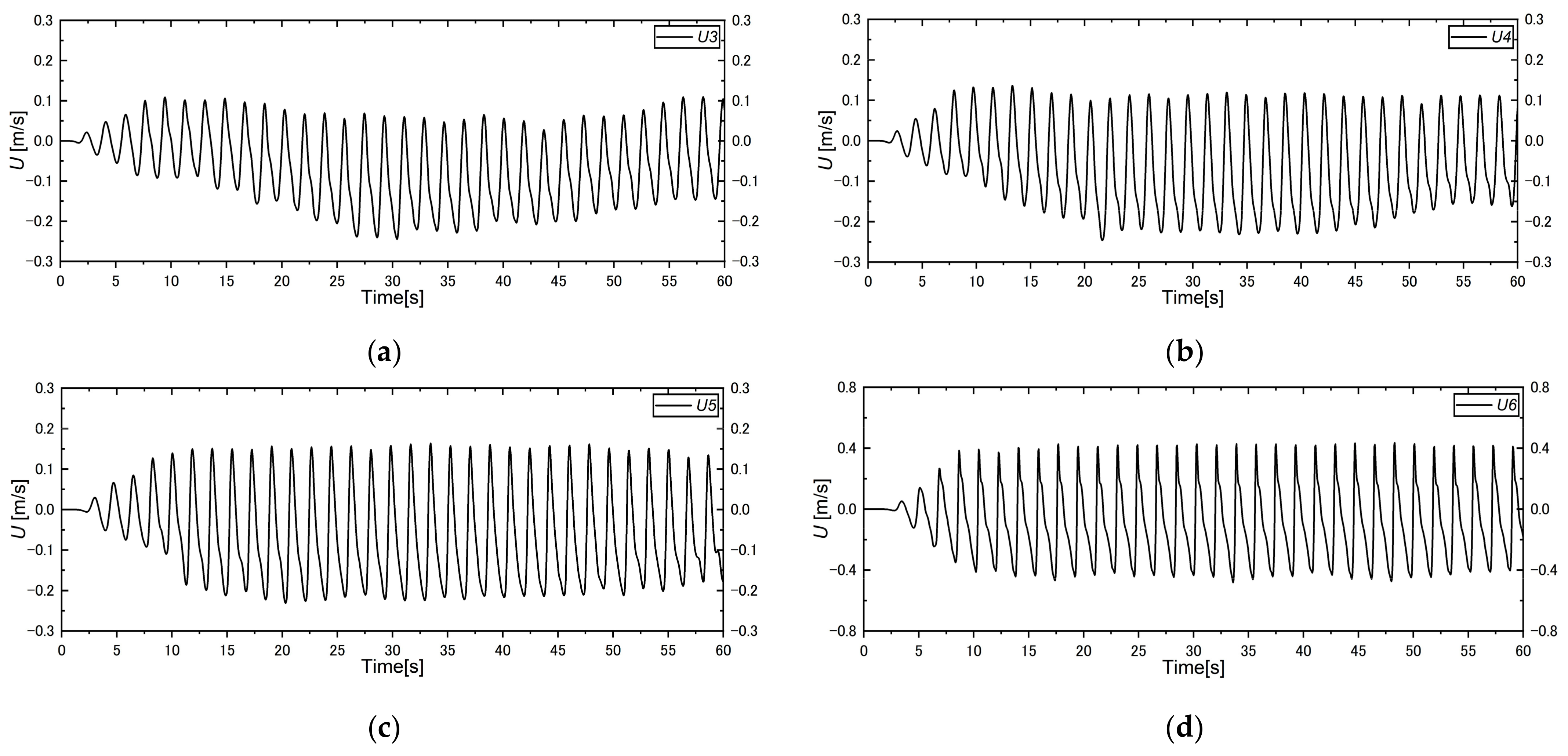
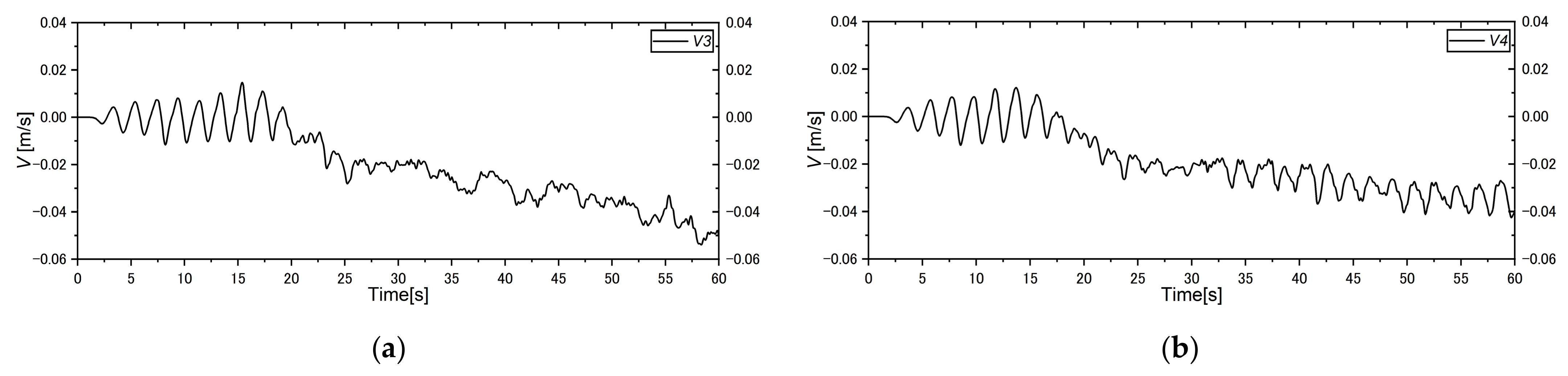
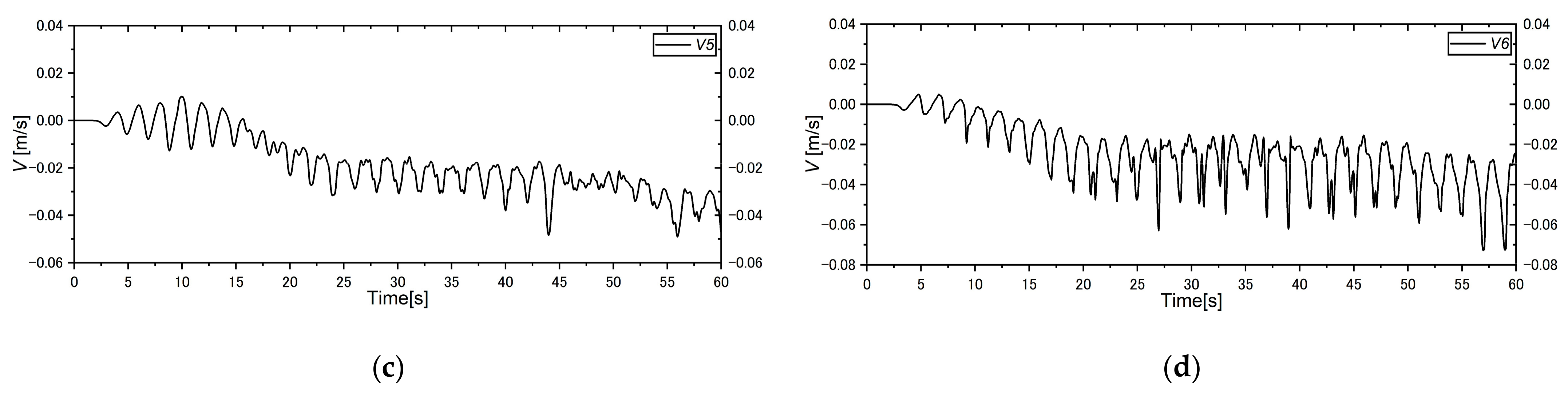
5.5. Cross-Shore and Longshore Velocity Distribution
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sunamura, T.; Horikawa, K. Two Dimensional Beach Transformation Due to Waves. In Proceedings of the 14th International Conference on Coastal Engineering, Copenhagen, Denmark, 24–28 June 1974; American Society of Civil Engineers: Reston, VA, USA, 1974; pp. 920–938. [Google Scholar] [CrossRef]
- Kobayashi, N. Analytical Solution for Dune Erosion by Storms. J. Waterw. Port Coast. Ocean Eng. 1987, 113, 401–418. [Google Scholar] [CrossRef]
- Günaydin, K.; Kabdasli, M.S. Characteristics of coastal erosion geometry under regular and irregular waves. Ocean Eng. 2003, 30, 1579–1593. [Google Scholar] [CrossRef]
- Kobayashi, N.; Lawrence, A.R. Cross-shore sediment transport under breaking solitary waves. J. Geophys. Res. Oceans 2004, 109, C03047. [Google Scholar] [CrossRef]
- Eichentopf, S.; Cáceres, I.; Alsina, J.M. Breaker bar morpho dynamics under erosive and accretive wave conditions in large-scale experiments. Coast. Eng. 2018, 138, 36–48. [Google Scholar] [CrossRef]
- Othman, I.K.; Baldock, T.E.; Callaghan, D.P. Measurement and modelling of the influence of grain size and pressure gradient on swash uprush sediment transport. Coast. Eng. 2014, 83, 1–14. [Google Scholar] [CrossRef]
- Mizuguchi, M.; Horikawa, K. Experimental Study on Longshore Current Velocity Distribution. Bull. Fac. Sci. Eng. 1978, 21, 123–149. [Google Scholar]
- Visser, P.J. Laboratory measurements of uniform longshore currents. Coast. Eng. 1991, 15, 563–593. [Google Scholar] [CrossRef]
- Liangduo, S.; Qinqin, G.; Zhili, Z.; Lulu, H.; Wei, C.; Mingtao, J. Experimental study and numerical simulation of mean longshore current for mild slope. Wave Motion 2020, 99, 102651. [Google Scholar] [CrossRef]
- Multer, R.H. Exact nonlinear model of wave generator. J. Hydraul. Divis. ASCE 1973, 1, 31–47. [Google Scholar] [CrossRef]
- Nakayama, T. Boundary element analysis of nonlinear water wave problems. Int. J. Numer. Methods Eng. 1983, 19, 953–970. [Google Scholar] [CrossRef]
- Lee, J.F.; Leonard, J.W. A time-dependent radiation condition for transient wave-structure interactions. Ocean Eng. 1987, 14, 469–488. [Google Scholar] [CrossRef]
- Lee, J.F.; Kuo, J.R.; Lee, C.P. The Transient Wavemaker Theory. J. Hydraul. Res. 1989, 27, 651–663. [Google Scholar] [CrossRef]
- Williams, A.N.; Crull, W.W. Simulation of directional waves in a numerical basin by a desingularized integral equation approach. Ocean Eng. 2000, 27, 603–624. [Google Scholar] [CrossRef]
- Shih, R.S.; Chou, C.R.; Weng, W.K. Numerical modelling of 3D oblique waves by L-type multiple directional wave generator. In Proceedings of the 19th International Offshore and Polar Engineering Conference, Osaka, Japan, 21–26 July 2009; ISOPE: Mountain View, CA, USA, 2009; Volume 3, pp. 918–925. [Google Scholar]
- Park, J.C.; Kim, M.H.; Miyata, H.; Chun, H.H. Fully nonlinear numerical wave tank (NWT) simulations and wave run-up prediction around 3-D structures. Ocean Eng. 2003, 30, 1969–1996. [Google Scholar] [CrossRef]
- Park, J.C.; Uno, Y.; Sato, T.; Miyata, H.; Chun, H.H. Numerical reproduction of fully nonlinear multi-directional waves by a viscous 3D numerical tank. Ocean Eng. 2004, 31, 1549–1565. [Google Scholar] [CrossRef]
- Li, S.; Shibayama, T. Calculation of wave-induced longshore current in surf zone by using Boussinesq equations. In Proceedings of the 27th International Conference on Coastal Engineering (ICCE), Sydney, Australia, 16–21 July 2000; American Society of Civil Engineers: Reston, VA, USA, 2001; pp. 334–345. [Google Scholar] [CrossRef]
- Larsen, J.; Dancy, H. Open boundaries in short wave simulations a new approach. Coast. Eng. 1983, 7, 285–297. [Google Scholar] [CrossRef]
- Israeli, M.; Orszag, S.A. Approximation of radiation boundary conditions. J. Comp. Phys. 1981, 41, 115–135. [Google Scholar] [CrossRef]
- Lin, P.Z.; Liu, P.L.F. Internal wave-maker for Navier–Stokes equations models. J. Waterw. Port Coast. Ocean Eng. 1999, 125, 207–215. [Google Scholar] [CrossRef]
- Choi, J.; Sung, B.Y. Numerical simulations using momentum source wave-maker applied to RANS equation model. Coast. Eng. 2009, 56, 1043–1060. [Google Scholar] [CrossRef]
- Brorsen, M.; Larsen, J. Source generation of nonlinear gravity waves with the boundary integral equation method. Coast. Eng. 1987, 11, 93–113. [Google Scholar] [CrossRef]
- Ohyama, T.; Nadaoka, K. Development of a numerical wave tank for analysis of nonlinear and irregular wavefield. Fluid Dyn. Res. 1991, 8, 231–251. [Google Scholar] [CrossRef]
- Tanaka, M.; Ohyama, T.; Kiyokawa, T.; Nadaoka, K. Non-reflective multidirectional wave generation by source method. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, 23–28 October 1994; American Society of Civil Engineers: Reston, VA, USA, 1994; pp. 650–664. [Google Scholar] [CrossRef]
- Naito, S. Wave generation and absorption theory and application. In Proceedings of the 16th International Offshore and Polar Engineering Conference, San Francisco, CA, USA, 28 May–2 June 2006; ISOPE: Mountain View, CA, USA, 2006; Volume 2, pp. 81–89. [Google Scholar]
- Ren, X.; Mizutani, N.; Nakamura, T. Development of a numerical circular wave basin based on the two-phase incompressible flow model. Ocean Eng. 2015, 101, 93–100. [Google Scholar] [CrossRef]
- Ren, X.; Gao, Y.; Mizutani, N. Application of the numerical circular wave tank on the simulations of the oblique and multi-directional waves. J. Mar. Sci. Technol. 2015, 20, 711–721. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Harlow, F.; Welch, J.E. Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface. Phys. Fluid 1965, 8, 2182–2189. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulation. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Austin, D.I.; Schlueter, R.S. A numerical model of wave breaking breakwater interactions. In Proceedings of the 18th International Conference on Coastal Engineering, Cape Town, South Africa, 14–19 November 1982; American Society of Civil Engineers: Reston, VA, USA, 1982; Volume 3, pp. 2079–2096. [Google Scholar] [CrossRef]
- Nichols, B.D.; Hirt, C.W.; Hotchkiss, R.S. SOLA-VOF: A Solution Algorithm for Transient Fluid Flow with Multiple Free Boundaries; Report LA-8355; Los Alamos National Lab (LANL): Los Alamos, NM, USA, 1980. [CrossRef]
- Iwata, K.; Kawasaki, K.; Kim, D.S. Breaking limit, breaking and post-breaking wave deformation due to submerged structures. In Proceedings of the 25th International Conference on Coastal Engineering, Orlando, FL, USA, 2–6 September 1996; American Society of Civil Engineers: Reston, VA, USA, 1997; Volume 3, pp. 2338–2351. [Google Scholar] [CrossRef]
- Dalrymple, R.A.; Dean, R.G. The spiral wavemaker for littoral drift studies. In Proceedings of the 13th International Conference on Coastal Engineering, Vancouver, BC, Canada, 10–14 July 1972; American Society of Civil Engineers: Reston, VA, USA, 1972; pp. 689–705. [Google Scholar] [CrossRef]
- Mei, C.C. Shoaling of spiral waves in a circular basin. J. Geophys. Res. 1973, 78, 977–980. [Google Scholar] [CrossRef]
- Trowbridge, J.; Dalrymple, R.A.; Suh, K. A simplified second-order solution for a spiral wave maker. J. Geophys. Res. Oceans 1986, 91, 11783–11789. [Google Scholar] [CrossRef]
- Williams, A.N.; McDougal, W.G. Hydrodynamic analysis of variable draft spiral wavemaker. Ocean Eng. 1989, 16, 401–410. [Google Scholar] [CrossRef]
- Suh, K.; Dalrymple, R.A. Offshore Breakwaters in Laboratory and Field. J. Waterw. Port Coast. Ocean Eng. 1987, 113, 105–121. [Google Scholar] [CrossRef]
- Islam, M.S.; Akita, N.; Nakamura, T.; Cho, Y.-H.; Mizutani, N. Experimental Investigation on the Mechanism of Longshore Sediment Transport Using a Circular Wave Basin. J. Mar. Sci. Eng. 2022, 10, 1189. [Google Scholar] [CrossRef]
- Mizutani, N.; McDougal, W.; Mostafa, A. BEM-FEM combined analysis of nonlinear interaction between wave and submerged breakwater. In Proceedings of the 25th International Conference on Coastal Engineering, Orlando, FL, USA, 2–6 September 1996; American Society of Civil Engineers: Reston, VA, USA, 1996; Volume 1, pp. 2377–2390. [Google Scholar] [CrossRef]
- Nakamura, T.; Mizutani, N. Numerical simulation of wind-induced drift behavior of shipping container floating on water surface using three-dimensional coupled fluid-structure-sediment interaction model. In Proceedings of the 26th Symposium on Computational Fluid Dynamics, Tokyo, Japan, 18–20 December 2012. 10p. [Google Scholar] [CrossRef]
- Kawasaki, K. Numerical simulation of breaking and post-breaking wave deformation process around a submerged breakwater. Coast. Eng. J. 1999, 41, 201–223. [Google Scholar] [CrossRef]
- Kravchenko, A.G.; Moin, P.; Moser, R. Zonal embedded grids for numerical simulations of wall-bounded turbulent flows. J. Comput. Phys. 1996, 127, 421–423. [Google Scholar] [CrossRef]
- Suh, Y.K.; Yeo, C.H. Finite volume method with zonal-embedded grids for cylindrical coordinates. Int. J. Numer. Methods Fluids 2006, 52, 263–295. [Google Scholar] [CrossRef]
- Xue, S.C.; Phan-Thien, N.; Tanner, R.I. Fully three-dimensional, time-dependent numerical simulations of Newtonian and viscoelastic swirling flows in a confined cylinder: Part Ι. Method and steady flows. J. Non-Newton. Fluid Mech. 1999, 87, 337–367. [Google Scholar] [CrossRef]
- He, T.L.; Tao, W.Q.; Qu, Z.G.; Chen, Z.Q. Steady natural convection in a vertical cylindrical envelope with adiabatic lateral wall. Int. J. Heat Mass Transf. 2004, 47, 3131–3144. [Google Scholar] [CrossRef]
- Chorin, A.J. Numerical solution of the Navier-Stokes equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Gaskell, P.H.; Lau, A.K.C. Curvature-compensated convective transport: SMART, a new boundedness-preserving transport algorithm. Int. J. Numer. Methods Fluids 1988, 8, 617–641. [Google Scholar] [CrossRef]
- Popinet, S. Gerris: A tree-based adaptive solver for the incompressible Euler equations in complex geometries. J. Comput. Phys. 2003, 190, 572–600. [Google Scholar] [CrossRef]
- Notay, Y. AGMG Software and Documentation. Available online: http://homepages.ulb.ac.be/~ynotay/AGMG (accessed on 8 June 2021).
- Ubbink, O.; Issa, R. A method for capturing sharp fluid interfaces on arbitrary meshes. J. Comput. Phys. 1999, 153, 26–50. [Google Scholar] [CrossRef]
- Heyns, J.A.; Malan, A.G.; Harms, T.M.; Oxtoby, O.F. Development of a compressive surface capturing formulation for modelling free-surface flow by using the volume of fluid approach. Int. J. Numer. Methods Fluids 2013, 71, 788–804. [Google Scholar] [CrossRef]
- Iwata, K.; Kawasaki, K.; Kanedo, K. Numerical analysis of wave breaking by underwater structures. J. Coast. Eng. JSCE 1995, 42, 781–785. [Google Scholar] [CrossRef]
- Fujiwara, R. A method for modifying a horizontal velocity of irregular waves wave generation by a linear theory. Proc. Civ. Eng. Ocean JSCE 2008, 24, 873–878. [Google Scholar] [CrossRef]




| Zone | M | 5 |
|---|---|---|
| Number of grids in radial direction | 1 | 5 |
| 2–4 | 5, 10, 20 | |
| 5 | 80 | |
| Number of grids in azimuthal direction | 1–5 | 60, 120, 240, 480, 960 |
| Number of grids in vertical direction | 1–5 | 88 |
| Cell size | Δr | 0.03 m | Total calculation Time | 60 s | |
| Δz | 0.75 cm, 1.5 cm | Time step | dt | Max. 0.005 s | |
| Water depth | h | 0.18 m | Measured cross-section | 5 | |
| Wave period | T | 1.80 s, 2.0 s, 2.25 s, 2.50 s | Median particle size of the beach | 0.4 mm | |
| Wave height | H | 1.5 m | Nonlinear drag coefficient | 0.45 | |
| Water density | 1000 kg/m3 | Linear drag coefficient | 25.0 | ||
| Air density | 1.2 kg/m3 | Kinematic viscosity of air | 1.8 × 10−5 Pa.s | ||
| Added mass coefficient | CA | −0.04 | Kinematic viscosity of water | 1.01 × 10−3 Pa.s |
| Case | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Period | 1.82 s | 2.0 s | 2.22 s | 2.50 s |
| Water depth | 18 cm | |||
| Initial Terrain | 1:7 Uniform Slope | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islam, M.S.; Nakamura, T.; Cho, Y.-H.; Mizutani, N. Investigation of the Spiral Wave Generation and Propagation on a Numerical Circular Wave Tank Model. J. Mar. Sci. Eng. 2023, 11, 388. https://doi.org/10.3390/jmse11020388
Islam MS, Nakamura T, Cho Y-H, Mizutani N. Investigation of the Spiral Wave Generation and Propagation on a Numerical Circular Wave Tank Model. Journal of Marine Science and Engineering. 2023; 11(2):388. https://doi.org/10.3390/jmse11020388
Chicago/Turabian StyleIslam, Mohammad Shaiful, Tomoaki Nakamura, Yong-Hwan Cho, and Norimi Mizutani. 2023. "Investigation of the Spiral Wave Generation and Propagation on a Numerical Circular Wave Tank Model" Journal of Marine Science and Engineering 11, no. 2: 388. https://doi.org/10.3390/jmse11020388
APA StyleIslam, M. S., Nakamura, T., Cho, Y.-H., & Mizutani, N. (2023). Investigation of the Spiral Wave Generation and Propagation on a Numerical Circular Wave Tank Model. Journal of Marine Science and Engineering, 11(2), 388. https://doi.org/10.3390/jmse11020388






