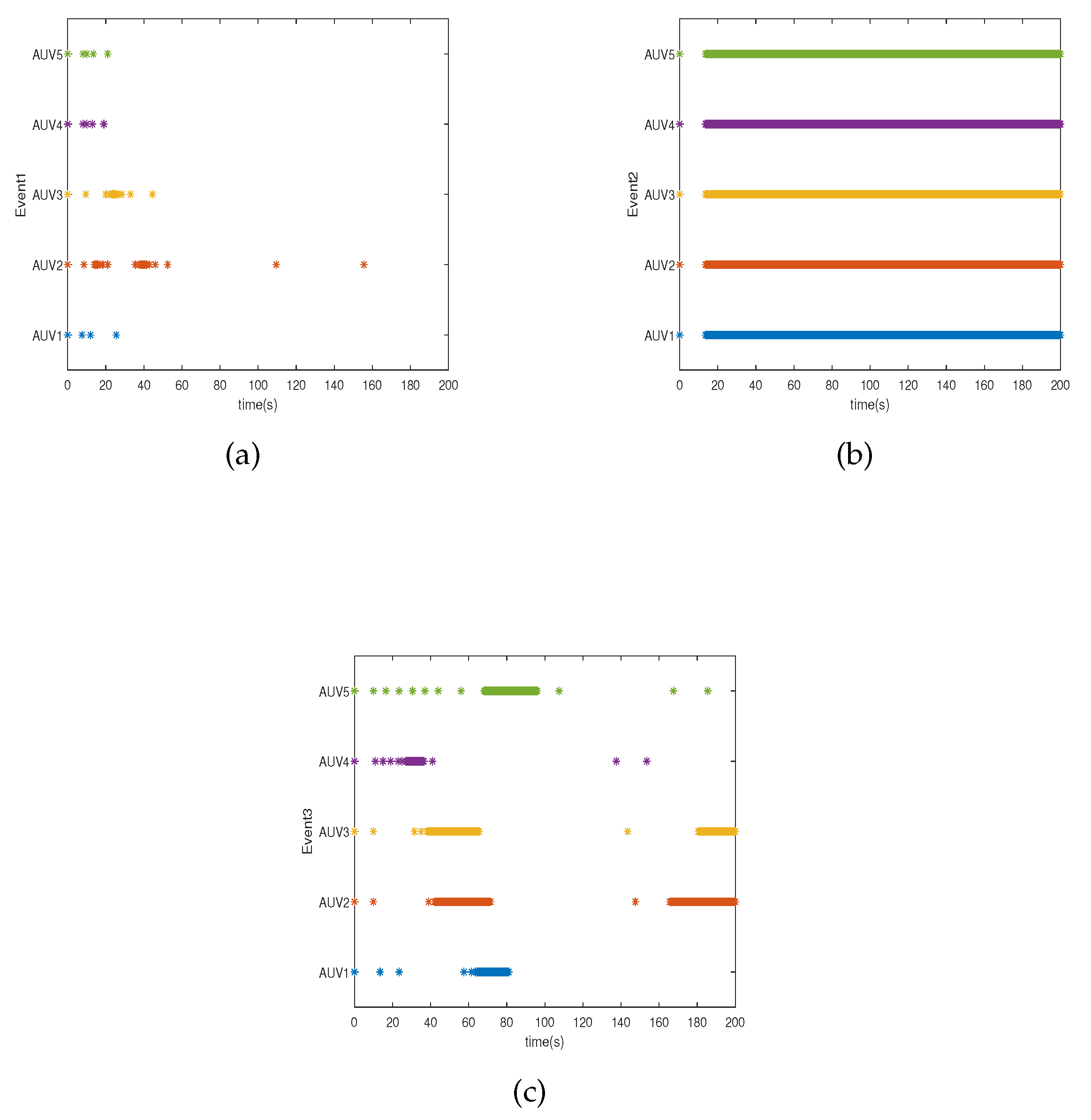1. Introduction
In recent years, increasing attention has been focused on systems for multi-AUVs due to their widespread application. The more complex the task of a system for multi-AUVs, the higher the cooperation requirement. Formation control is a fundamental research topic in systems for multi-AUVs. In addition to the challenges of highly coupled nonlinear hydrodynamics, complex ocean disturbances and limited hardware performance, the formation controller of a system for multi-AUVs must also take the communication topology, communication constraints and information utilization into consideration.
Many scholars have studied the formation control of multi-AUVs. In order to improve the convergence speed of AUV formation control, finite-time and fixed-time stability theories are applied to design the formation controller. Ge Guo [
1] presented a tracking control strategy of AUV formation with model parameter uncertainties and external disturbances. With a disturbance observer and fixed-time sliding control scheme, the follower vehicle can track the leader vehicle with all states globally stabilized within a given settling time. A novel control scheme was presented to accomplish the leader–follower formation control of unmanned surface vehicles (USVs) under model uncertainties, roll motion and environmental disturbances [
2]. A three-dimensional coordination control scheme was proposed by combining the sliding mode control, backstepping technique and leader–follower strategy to deal with coordination control of multiple AUVs [
3].
Multi-agent system consensus refers to the task of a group of agents trying to achieve a common state via local distributed control executed over a communication network, which is an effective method to design a multi-agent system formation controller. Compared with the leader–follower method, consensus control can effectively utilize the information transmitted between neighboring agents, instead of just the leader. Researchers have published many studies on consensus control [
4,
5,
6,
7,
8,
9,
10], such as the fixed-time leader–follower consensus for a high-order time-varying multi-agent system [
4], and on the consensus of multi-agent systems with and without input saturation constraints [
5]. For a multi-AUV system, a leaderless fault-tolerant consensus strategy based on a heterogeneous condensation/communication topology was proposed [
11,
12]. Consensus was applied to a leader–follower recovery system, using the mothership as a leader [
13]. A finite-time velocity-free position consensus tracking control method was investigated for a multi-AUV system taking into consideration the uncertainties of heterogeneous dynamics [
14].
In practical applications, the underwater acoustic communication bandwidth between AUVs is limited due to the performance of communication hardware equipment, which leads to problems with communication constraints. Event-triggered control strategies can use the effective information between neighboring nodes, reducing the requirements for communication conditions and unnecessary energy consumption. An event-triggered fixed-time leader–follower formation controller was designed for a USV [
15]. A sliding mode controller was designed in the presence of model uncertainties, roll motion and environmental disturbances, ensuring a small formation error in finite-time [
2]. Ge Guo [
1] investigated a fixed-time leader–follower formation control method for a group of AUVs with event-triggered acoustic communications and designed a disturbance observer to estimate the compound disturbance, which can be achieved within a finite amount of time independent of the initial estimation error. A finite-time velocity-free rendezvous control method is considered for a multi-AUV system with intermittent and undirected communications [
16].
Underactuated AUVs are widely used in practical applications. The main problem in the design of an underactuated AUV controller is that the number of actuators is fewer than the degrees of freedom, so that the control of the tracking error without an actuator depends on the coupling. Numerous relevant results are obtained for these challenges. The line of sight (LOS) guidance algorithm plays a pivotal role due to its simplicity and intuitiveness, and has been widely applied to path-following for a single AUV or USV. A series of LOS algorithms (proportional LOS, integral LOS and adaptive LOS) were proposed to reduce the external environment disturbances [
17]. Moreover, in the literature on LOS algorithms, an output feedback controller based on linear stability theory and the backstepping technique was proposed to track the desired 3-dimensional trajectory of an underactuated AUV in the Earth reference frame [
18]. For multiple underactuated AUVs, an adaptive formation control of underactuated AUVs was presented [
19], which detailed the additional control inputs and proved the stability of the system by using the Lyapunov stability theory. A 3-dimensional coordinated formation controller was proposed for a system of multiple underactuated AUVs [
20], which combined the singular perturbation theory.
The kinematic characteristics of the underactuated AUV demonstrate that there are few researches currently working on the consensus control of systems for multiple underactuated AUVs. Thrusters and rudders are usually used as the actuators of underactuated AUVs. Most stabilization controller designs for underactuated AUVs are based on the angle errors in a BF spherical coordinate system, such as the heading angle error and pitch angle error. However, the control objective for consensus control is based on the position errors in the Earth reference frame coordinate system. When designing the stabilization controller, it is necessary to transform the position errors in the Earth reference frame coordinate system to the angle errors in the BF spherical coordinate system. The transformation between the different coordinate systems will cause coupling, therefore it is difficult to design the consensus controller for a system of multiple underactuated AUVs.
Motivated by the previous results, this study proposed an average consensus controller for multiple underactuated AUVs based on the BF spherical coordinate system. Firstly, the control objective is proposed on account of the kinetic characteristics of a system of multiple underactuated AUVs. By designing the average consensus control objective, the tracking error kinematic equations of an underactuated AUV are constructed. We decouple the position errors in the Earth reference frame coordinate system into three controllable degrees of freedom in the BF spherical coordinate system, namely the distance, pitch angle and yaw angle errors are stabilized by the thrust, pitching torque and yaw torque controllers, respectively. Then, the backstepping method and fixed-time stability theory are used to design the average consensus controller. The dynamic event-triggered mechanism is adopted in the controller to reduce resource consumption. To the best of our knowledge, this is the first time that the problem of consensus control for a system of multiple underactuated AUVs has been tackled. The principle contributions of this study are as follows:
- 1.
The new consensus control objective for a system of multiple underactuated AUVs based on a BF spherical coordinate system is proposed, which is more adaptive to the kinematic and kinetic characteristics of underactuated AUVs. The tracking error kinematics equation is constructed in a BF spherical coordinate system to reduce the accumulated error that results from the transformation between different coordinate systems.
- 2.
The average consensus strategy is proposed to design a consensus controller for a system of multiple underactuated AUVs. Under the new control objective, the expression between the actuator control variable and the control objective can be constructed, which simplifies the controller design. Moreover, the angle consensus for a system of multiple underactuated AUVs has practical physical significance. Under this control strategy, the states of AUVs can achieve a consensus faster than in the leader–follower strategy.
- 3.
The dynamic event-triggered mechanism is adopted to reduce the unnecessary triggers resulting from the decrease of the system operation-triggered threshold, which reduces the communication requirements and energy consumption in the consensus controller.
2. Mathematical Model and Preliminaries
In this section, graph theory, fixed-time stability theory and useful lemmas are introduced, kinematic and kinetic equations of the AUV model are constructed, the concept of average consensus is proposed and a description of the problem is presented.
2.1. Graph Theory
An undirected graph with N nodes is considered, and is the set of edges. If , they are neighbors and get information from each other. The adjacency matrix satisfies that , , and if , then , otherwise . The degree matrix . The Laplacian matrix .
Lemma 1 ([
21]).
For an undirected graph G, the Laplacian matrix is positive definite. The eigenvalues of the Laplacian matrix L are , and . If satisfies , one can obtain thatwhere . 2.2. Fixed-Time Control Stability Theory
Suppose in the system exists a Lyapunov function
, and the derivative of
satisfies the following inequality:
The system is globally stable in fixed-time. There exists a finite constant
, and the settling time function
T can be estimated by (
3):
2.3. Useful Lemmas
Lemma 2 ([
22]).
Let , the following inequalities hold: Lemma 3 ([
15]).
For and any real numbers , , , the following inequality holds Lemma 4. (Young’s inequality) For , , and , the following inequality holds: 2.4. The AUV Model
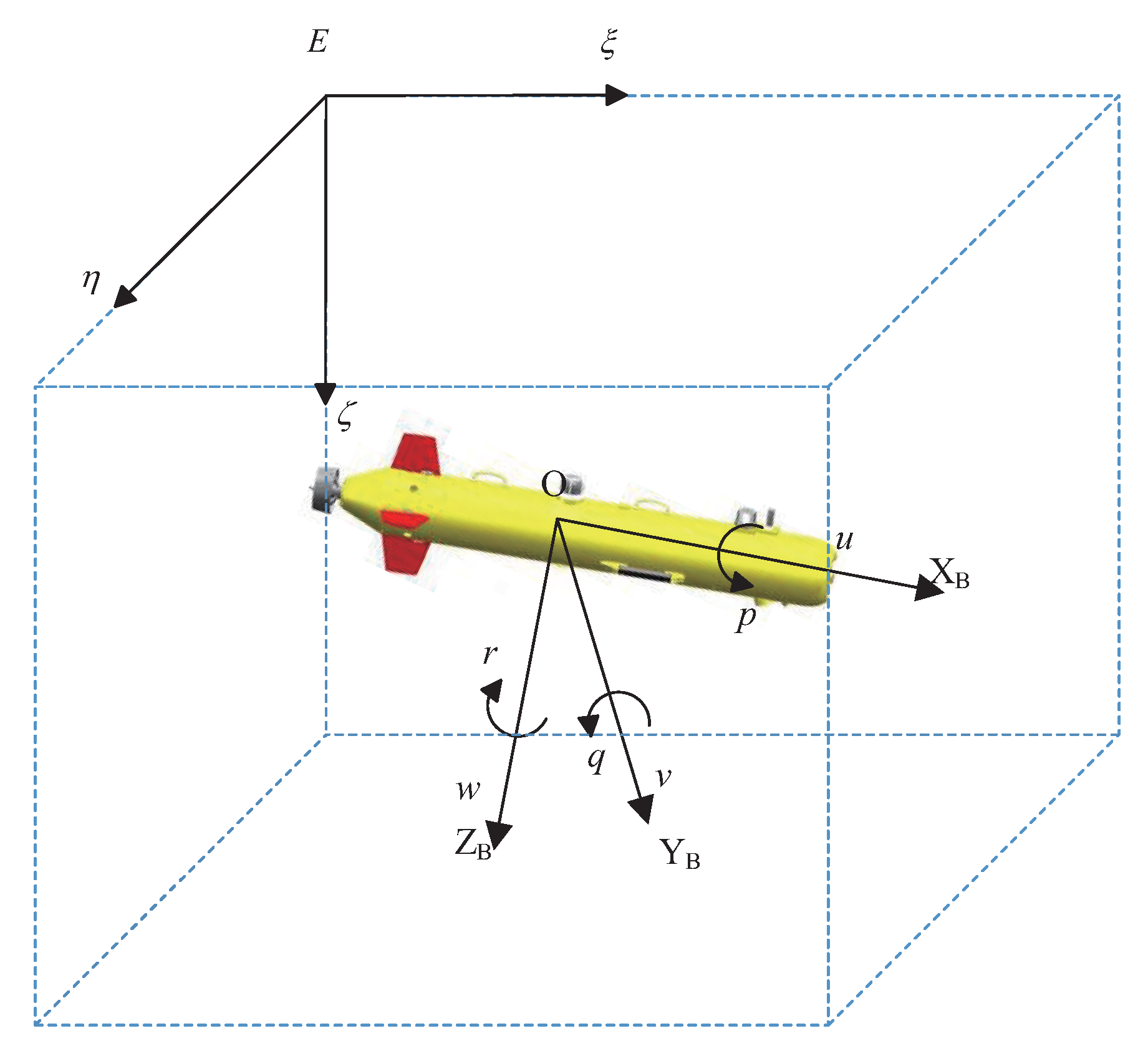
As shown in
Figure 1, it is convenient to use the Earth reference frame and body frame coordinate system to describe the motion of an AUV in 3-D space. Particularly, there are two generalized coordinate vectors
that need to be explained.
denotes the kinematic state of the AUV in the Earth reference frame coordinate system, where
represent the positions, and
represent the attitudes.
denotes the kinetic state of the AUV in the body frame coordinate system, where
are the linear velocities and
are the angular velocities.
The kinematic and kinetic equations of AUVs can be described as follows:
where
denotes the rotation matrix. The inertia matrix and additional inertia matrix are expressed as
and
, respectively.
and
represent the Coriolis centripetal force matrix, and
denotes the damping matrix, where
is the restoring force vector, i.e., the generalized buoyancy and gravitational torque.
Remark 1. In practical applications of underactuated AUVs, the actuator inputs are , where , and are the thrust, pitching torque and yaw torque, respectively. The controllable state variables of the AUV are . The design of the position error stabilization controller is complicated because of the coupling between the controllable variables and the control objective.
2.5. Average Consensus
Consensus controller design is a challenging problem in a system of multiple underactuated AUVs. Based on the kinematic characteristics of the underactuated AUV, this paper proposes the concept of average consensus protocol to simplify the design of the consensus controller for a system of multiple underactuated AUVs.
Definition 1. The system of multiple underactuated AUVs is said to achieve average consensus if for any given bounded initial states (where are the states of the AUV, i) there exists an average consensus protocol, such thatwhere satisfies the following equation: Average consensus protocol is an adaptive expression of consensus protocol for a system of multiple underactuated AUVs. For AUV i, the average consensus protocol generates a virtual reference trajectory by preprocessing the neighboring information. Therefore, the tracking error kinematic equations can be constructed, which simplify the design of the controller. The average consensus protocol and consensus protocol satisfy the following inequality:
Theorem 1. Suppose is a symmetric matrix, . If the eigenvalues of the Laplacian matrix L are , and , the following inequality between the average consensus and consensus protocol holds: Proof of Theorem 1. Define
and
.
satisfies the following Equation (
12):
satisfies the following Equation (
13):
where
E is expressed as follows:
is a symmetric matrix, and
, so the parameter
can be transformed to the following equation:
the eigenvalues of the Laplacian matrix L are
, and
. From (
12) and (
13), one can obtain (
16):
where
is diagonal matrix. Suppose the eigenvalues of the Laplacian matrix of V2 are
, then the following inequality can be obtained:
From Lemma 1 and (
17), the following inequality holds:
This concludes the proof. □
2.6. Problem Description
The consensus control of a system of multiple underactuated AUVs is a challenging research topic. Compared with the full-actuated AUV, the number of actuators in the underactuated AUV is less than the degrees of freedom, so the controllability of an underactuated AUV is affected. The consensus control of a system of multiple underactuated AUVs cannot be directly and completely controlled based on the position error, as that of a full-actuated system of AUVs, so the control objective based on position error convergence is not completely suitable for an underactuated AUV. Based on the dynamic characteristics of the system of underactuated AUVs, the control objective based on the distance and angle errors is designed.
In this paper, a new consensus control objective for a system of multiple underactuated AUVs based on a BF spherical coordinate system is proposed. Different from the traditional consensus control objective, which uses the position error in a Earth reference frame coordinate system, we use the distance
, pitch angle
and yaw angle
in a BF spherical coordinate system to describe the consensus control objective. As shown in
Figure 2, the consensus of a system of multiple underactuated AUVs can be transformed into the average consensus based on Theorem 1. In order to achieve the average consensus of a system of multiple underactuated AUVs, the control objective is designed as follows.
Definition 2. (Control Objective) For each AUV i, the measured states in a BF spherical coordinate system are . The system of multiple underactuated AUVs is said to achieve an average consensus if the tracking error satisfies , where σ is a positive constant. The detailed expression of these errors in shown in (19). Remark 2. Tracking error refers to the difference between the measured signal and the predicted signal. The measured signal used in this paper is p, and the expected signal is indicated as in the control objective, so the difference between the measured signal and the predicted signal is the tracking error .
In this article, we will discuss a kind of system of multiple underactuated AUVs, including
N underactuated AUVs. For each AUV, the kinematic and kinetic characteristics satisfied the equations composed in (
7). Combined with the backstepping method and dynamic event-triggered mechanism, we design a dynamic event-triggered average consensus control law with fixed-time convergence for the system of multiple underactuated AUVs based on a BF spherical coordinate system.
4. Simulation Results
This section presents the simulation results of the fixed-time average consensus for a system of multiple underactuated AUVs using a dynamic event-triggered mechanism. Numerical simulation experiments verified the effectiveness of the new control objective in the BF spherical coordinate system, the control effect of the fixed-time average consensus controller and the effect of the dynamic event-triggered mechanism proposed in this paper. Furthermore, the average consensus strategy and leader–follower strategy are compared on the matter of the formation effect.
The parameter settings of the AUV model are provided in
Table 1. The communication topology shown in
Figure 3 demonstrates that the topology is connected and comprises five AUVs. The communication topology has a spanning tree, and AUV 2, AUV 3 and AUV 4 can obtain the reference trajectory directly.
Simulation results are depicted as follows. The parameter settings for the initial position are presented in
Table 2. Five AUVs started at the initial position and are able to track the reference trajectory and build the desired consensus based on the proposed algorithm. The reference trajectory is expressed as follows:
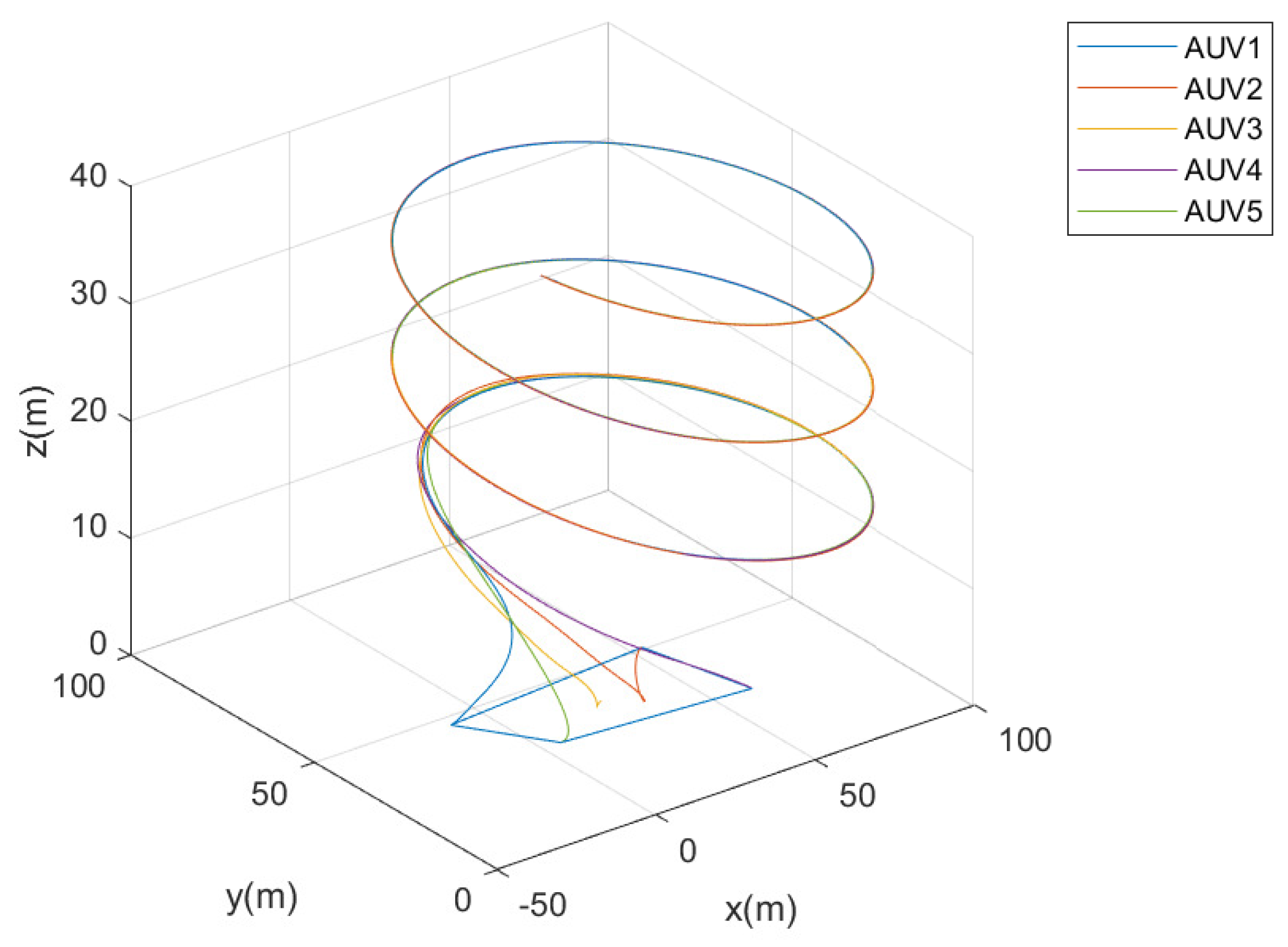
3-dimensional helix tracking consensus results are shown in
Figure 4. Five AUVs beginning at random positions are able to track the reference trajectories and build the desired consensus based on the proposed algorithm. The above figure demonstrates that the yaw angle controller and pitch angle controller can operate efficiently.
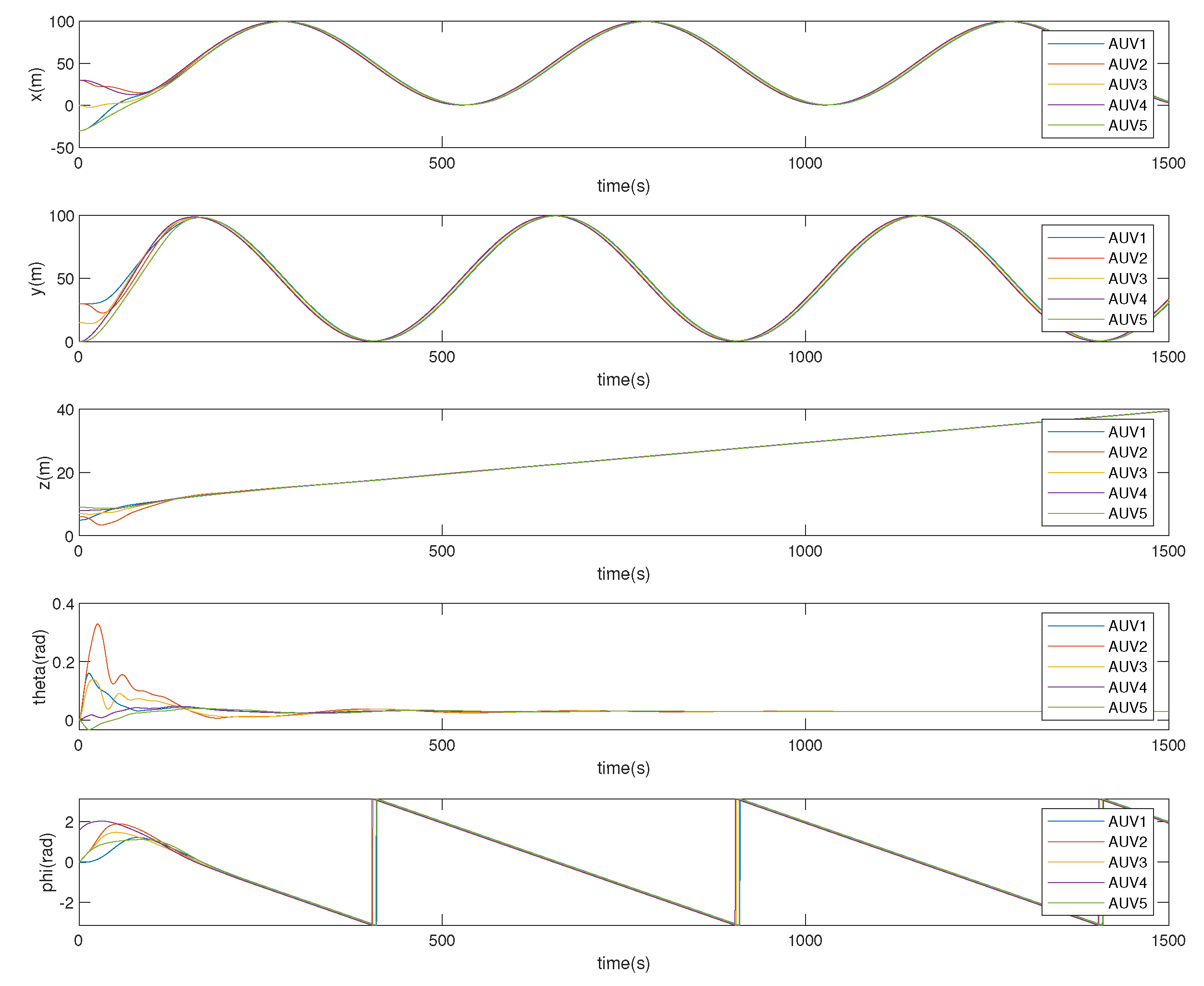
The kinematics state of five AUVs is shown in
Figure 5. The kinematics state and kinetics state converged within 200 s, and five AUVs arrived at the reference trajectory within 200 s. The experimental results demonstrate that the proposed algorithm can achieve good consensus performance, and the fixed-time average consensus strategy proposed in this study can effectively achieve the consensus control of multi-AUV systems.
The slightly different states of the AUVs is caused by the communication connection state between them. All the AUVs could achieve consensus by following the state of the neighboring AUVs by communicating with the reference trajectory. Moreover, because the reference trajectories are helix, the existence of steady-state errors can generate actuator inputs to keep the average consensus.
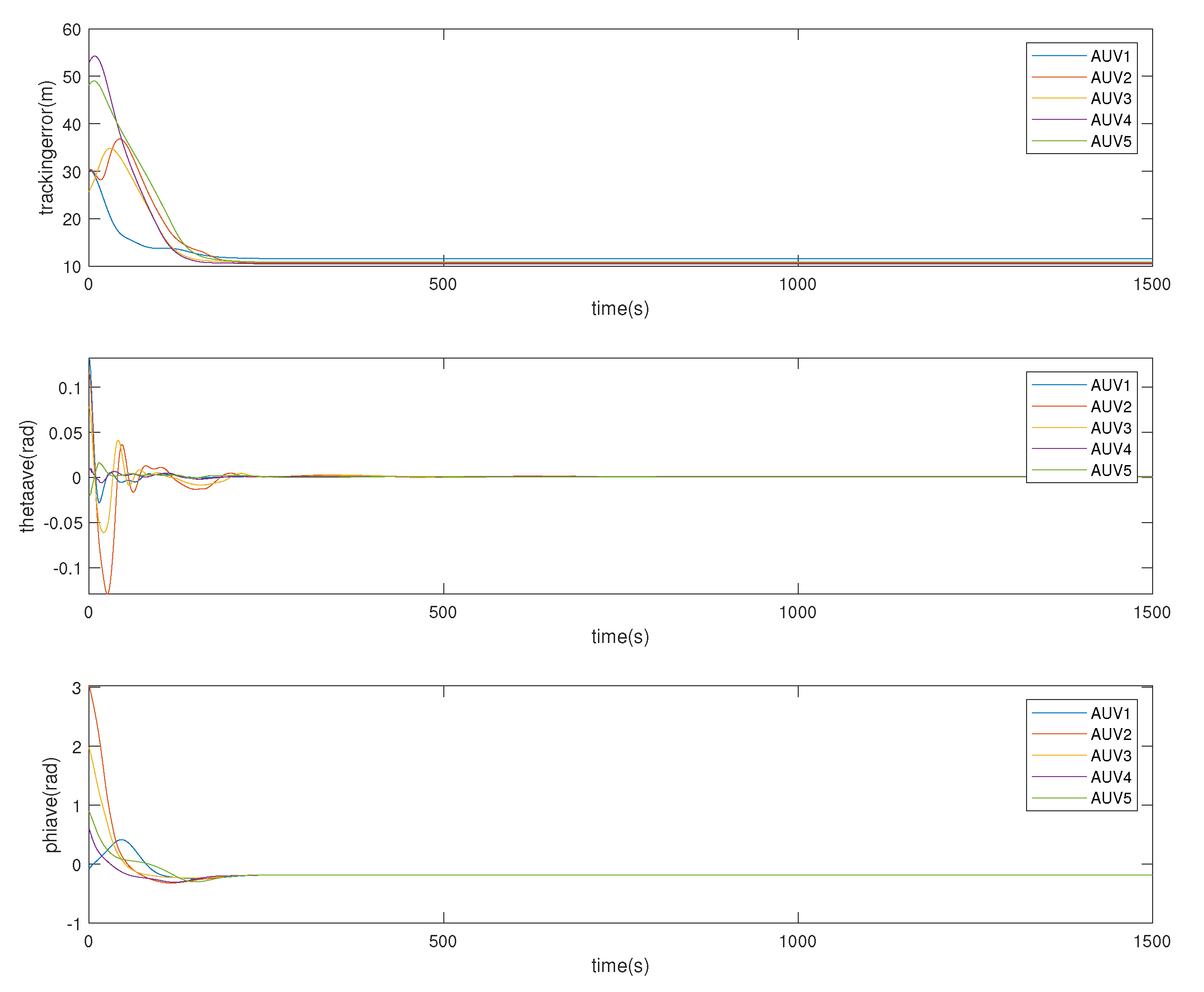
Distance error, pitch angle error and yaw angle error of each AUV under different initial conditions are illustrated in
Figure 6. Each controller has its own convergence time. The pitch angle and yaw angle errors converge to zero within 20 s. The position error converges in 200 s.
The calculation of the tracking error is the sum of the distance between AUV i and the neighboring AUV j. Because the communication topology of an AUV system is not completely connected with the reference trajectory, if AUV i does not obtain the reference trajectory, its response speed will be slightly slower than the AUV that obtains the reference trajectory when the reference trajectory is transformed. Therefore, the delay will cause some tracking error.
The experiment demonstrates that the control objective proposed in this study can satisfy the control requirement for multi-AUV average consensus. The control objective based on distance and angle errors can track the reference trajectory. The yaw angle, pitch angle and thrust actuators can respectively stabilize the control objective, thus the control objective proposed in this study can effectively simplify the controller design process, and the actuators under different degrees of freedom can be controlled separately, which provides a new scheme for the consensus controller design for a system of multiple underactuated AUVs.
In
Table 3, we show the number of triggers under different conditions, and the triggered instants of control signals are shown in
Figure 7. The continuous execution of actuators is avoided, thus the communication and energy consumption requirements are reduced.
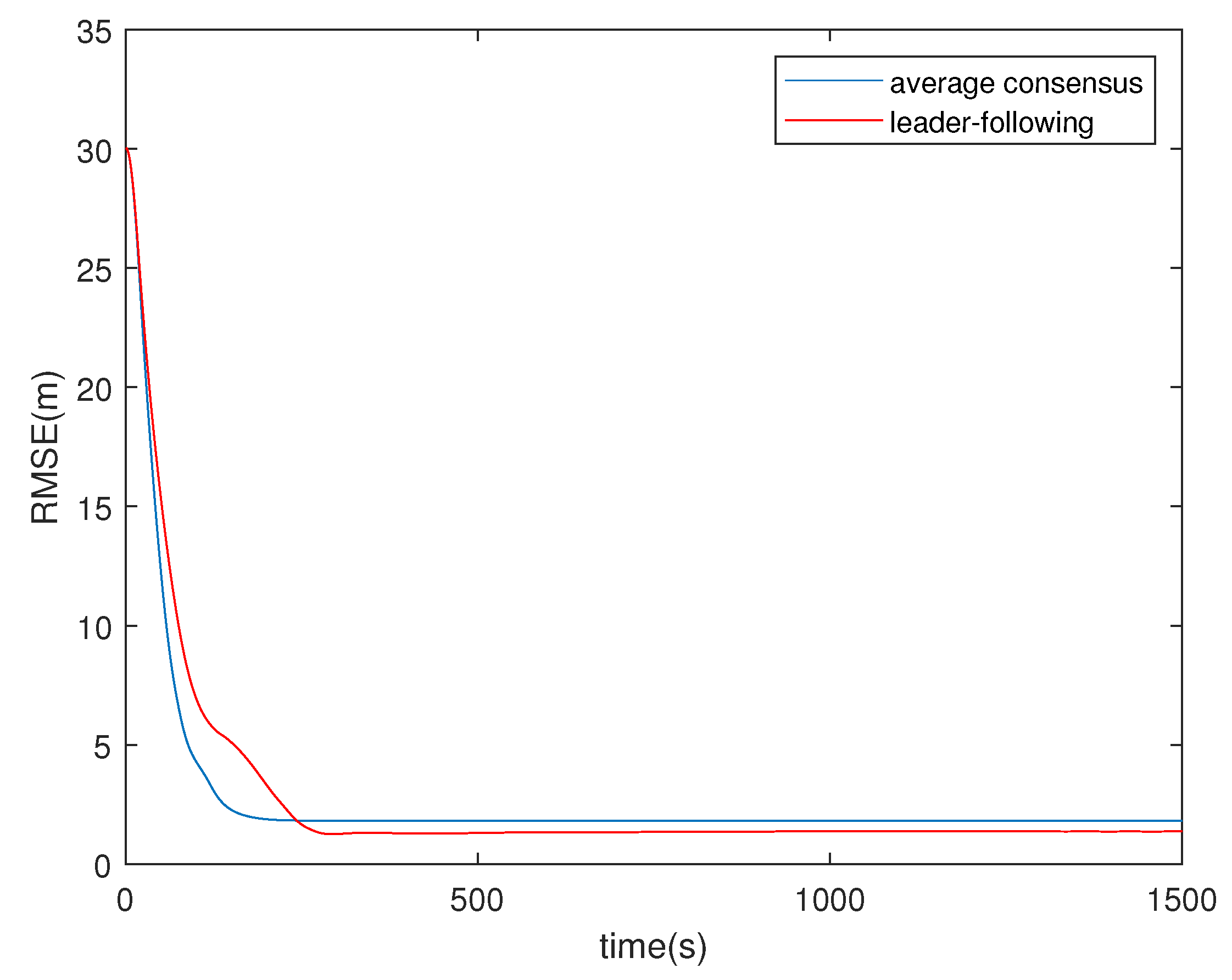
The root-mean-square error (RMSE) of the spatial position of the five AUVs using the average consensus formation strategy and leader–follower strategy are shown in
Figure 8. The average consensus formation strategy is clearly superior to the leader–follower formation strategy in the convergence process. The reason is that compared with the leader–follower method, the average consensus control method proposed in this study has advantages in the speed of state consensus convergence. Because the actuator input obtained by the consensus control law not only depends on the desired reference trajectory, but is also related to the current state of neighboring AUVs, the AUV state between neighboring AUVs can reach consensus faster. The steady-state error of the average consensus method is slightly larger than that of the leader–follower method, due to receiving the information between neighboring AUVs.