Intelligent Model for Dynamic Shear Modulus and Damping Ratio of Undisturbed Marine Clay Based on Back-Propagation Neural Network
Abstract
1. Introduction
2. Experimental Measurements
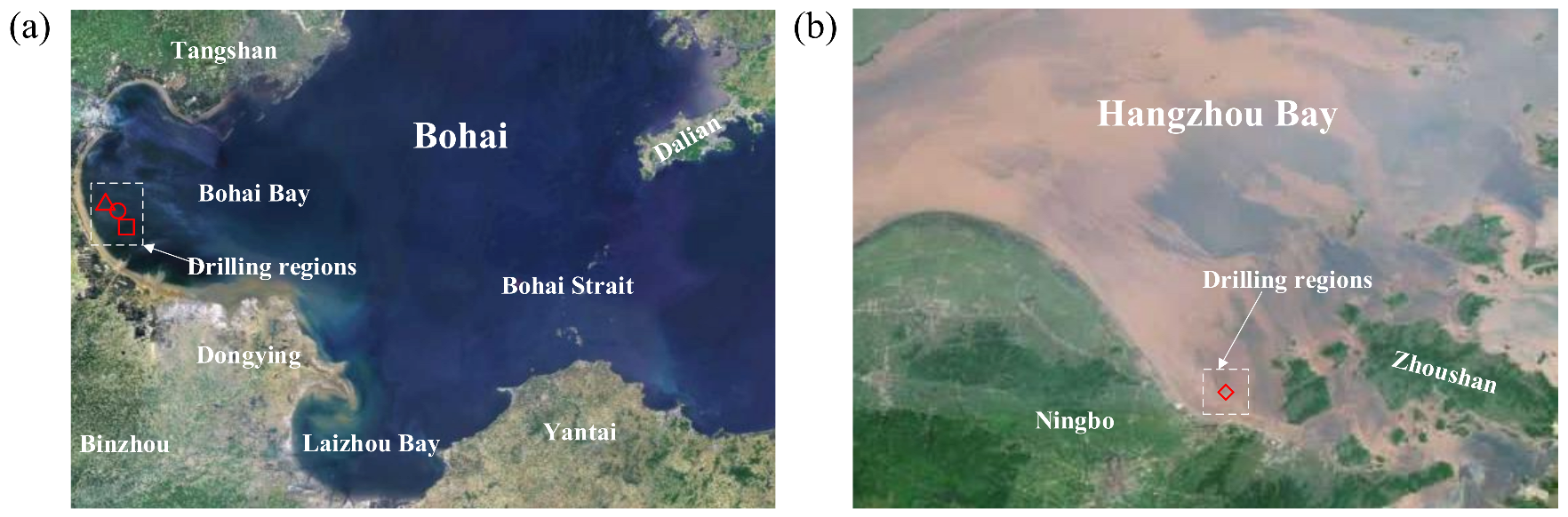
2.1. Materials
2.2. Test Apparatus and Procedure
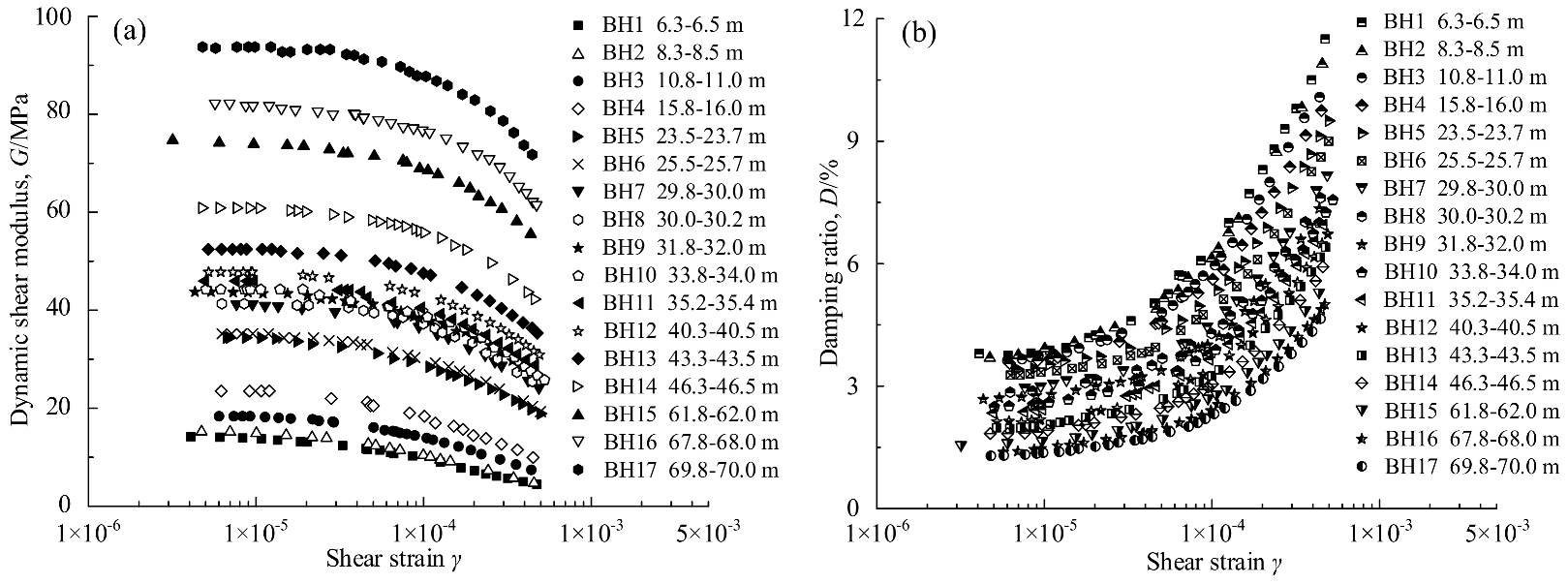
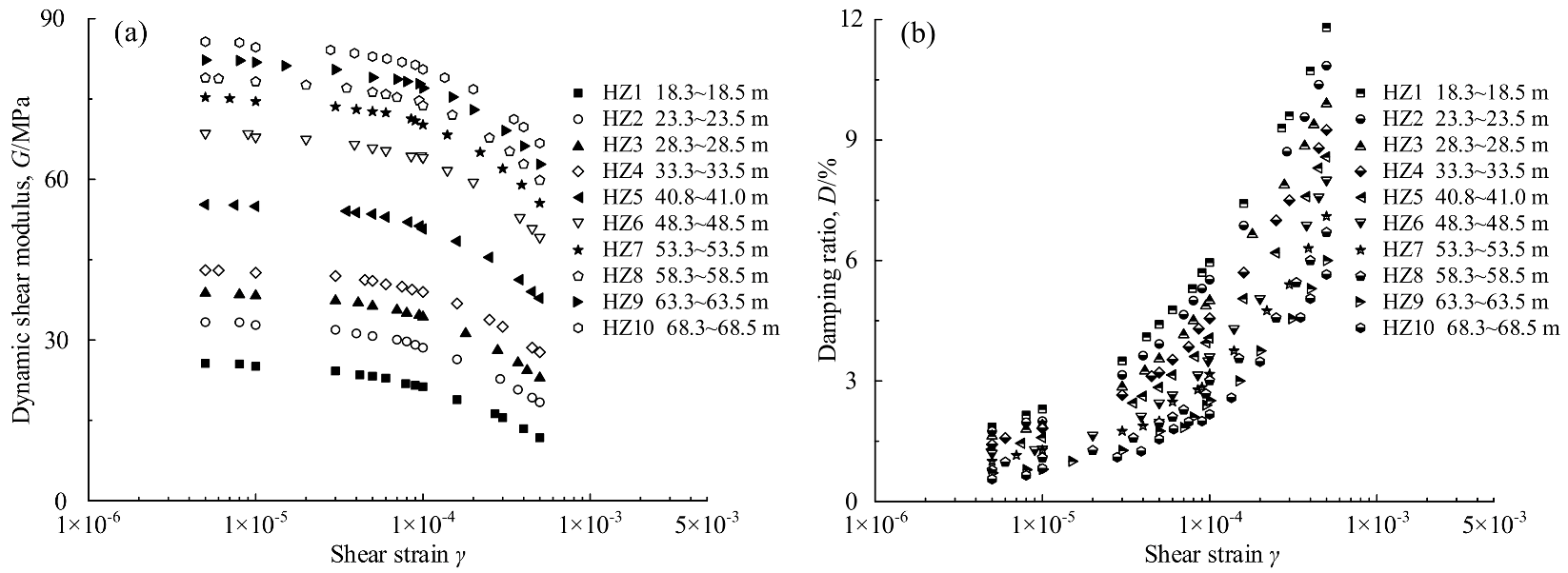
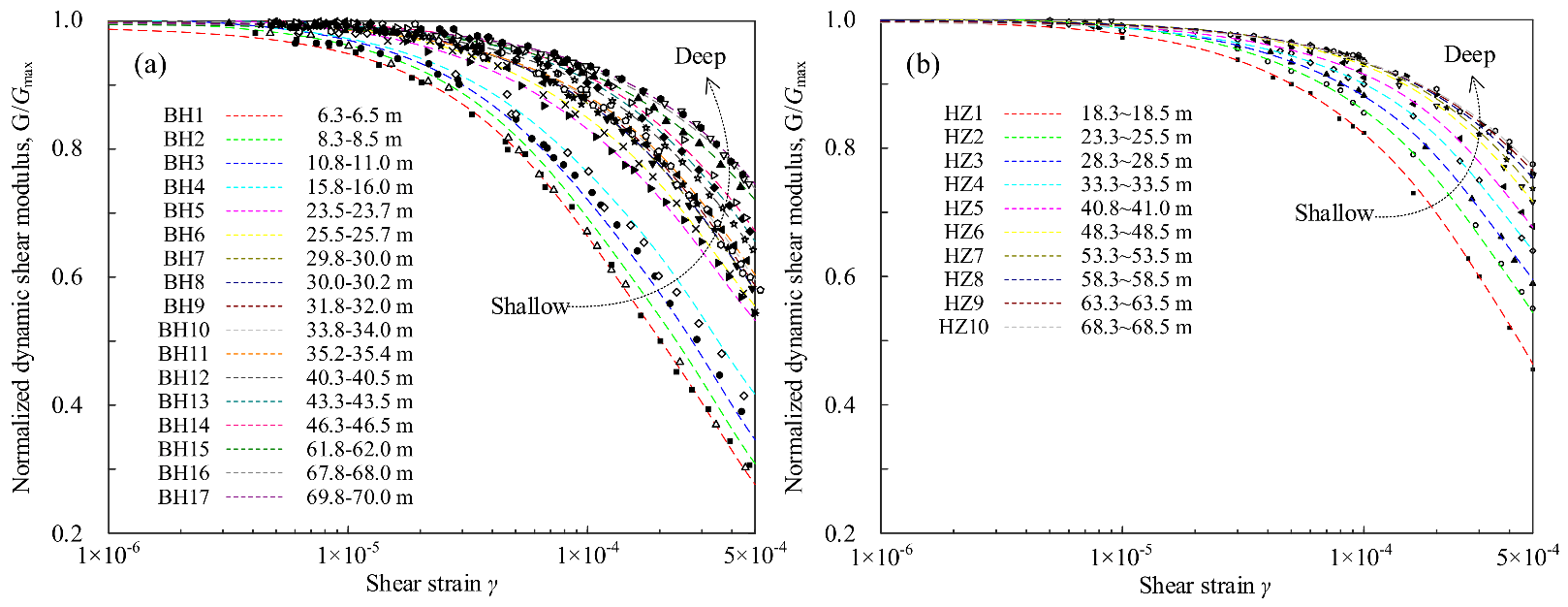
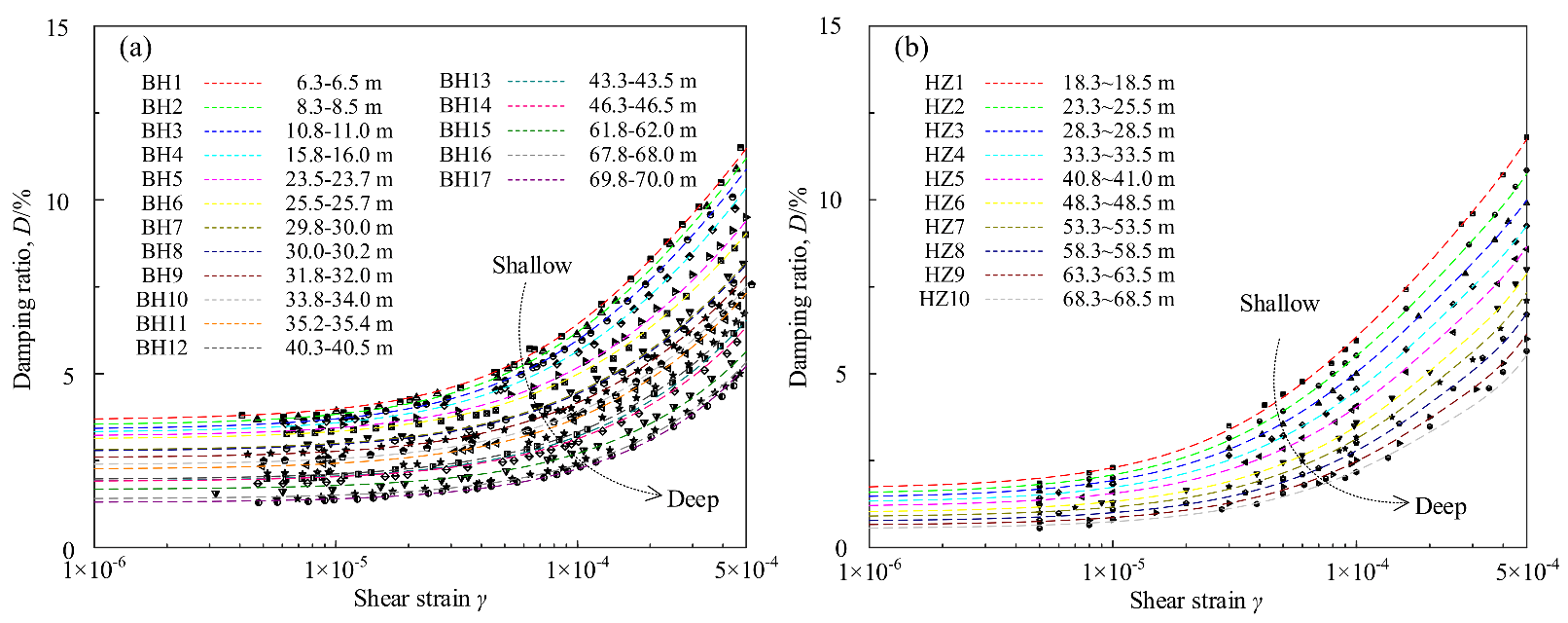
2.3. Experimental Results
3. Intelligent Model
3.1. Model Framework
3.2. Model Settings and Procedures
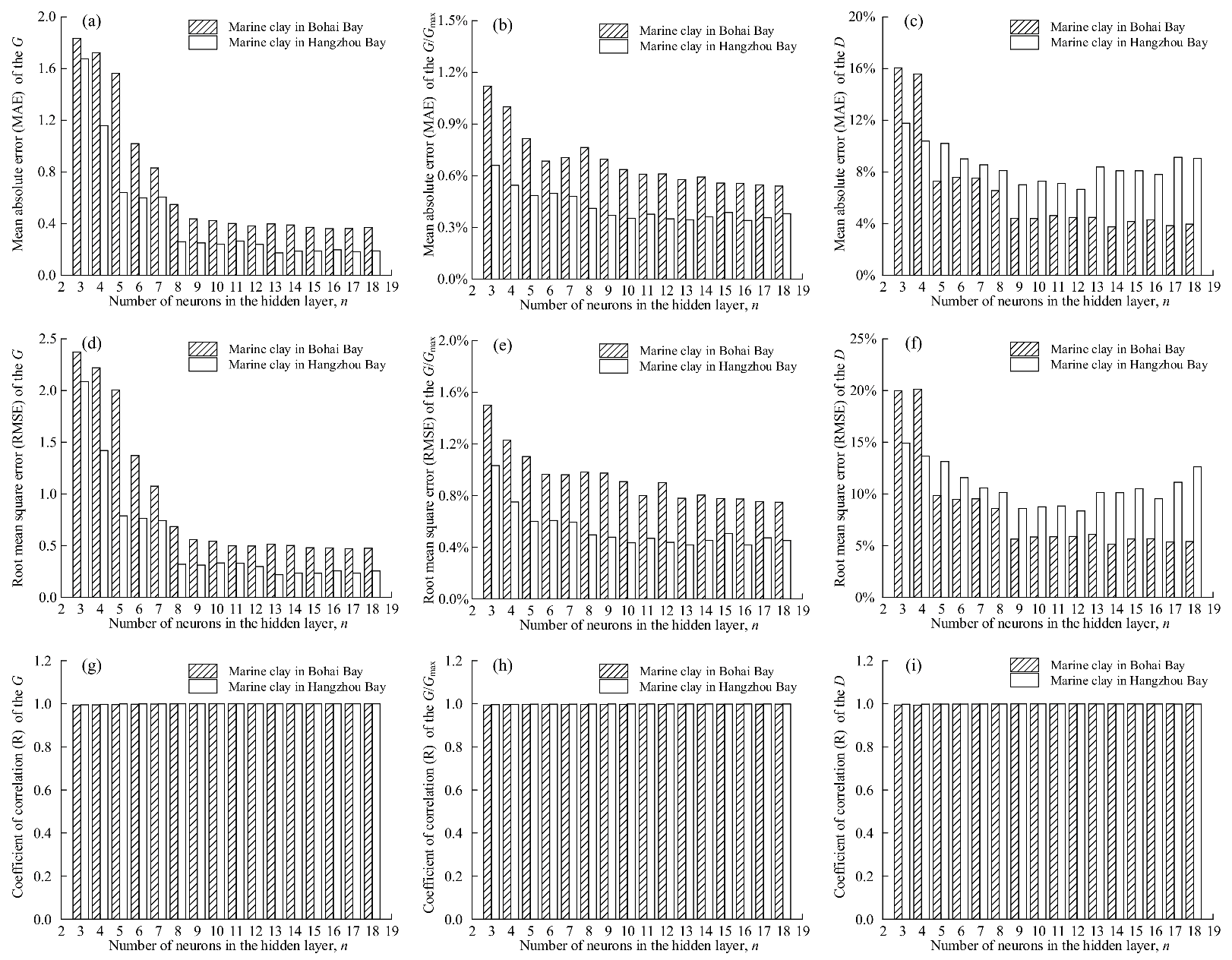
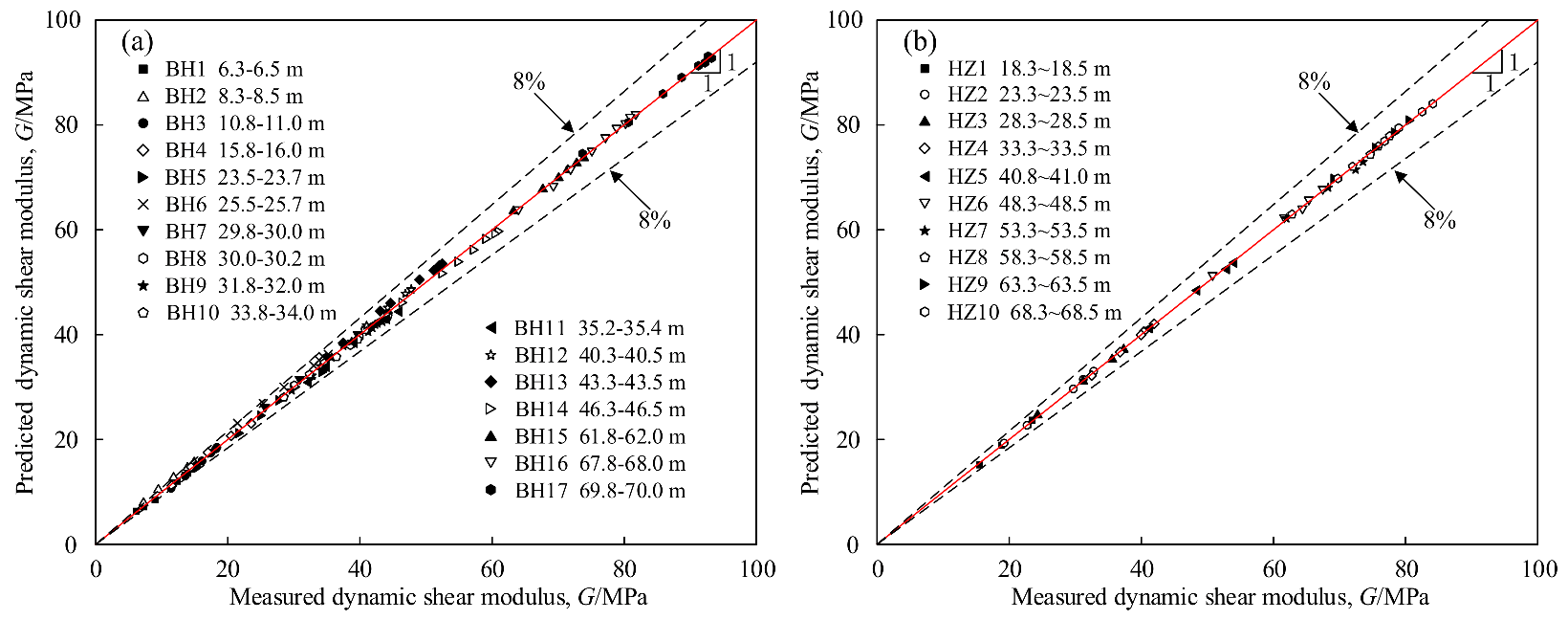
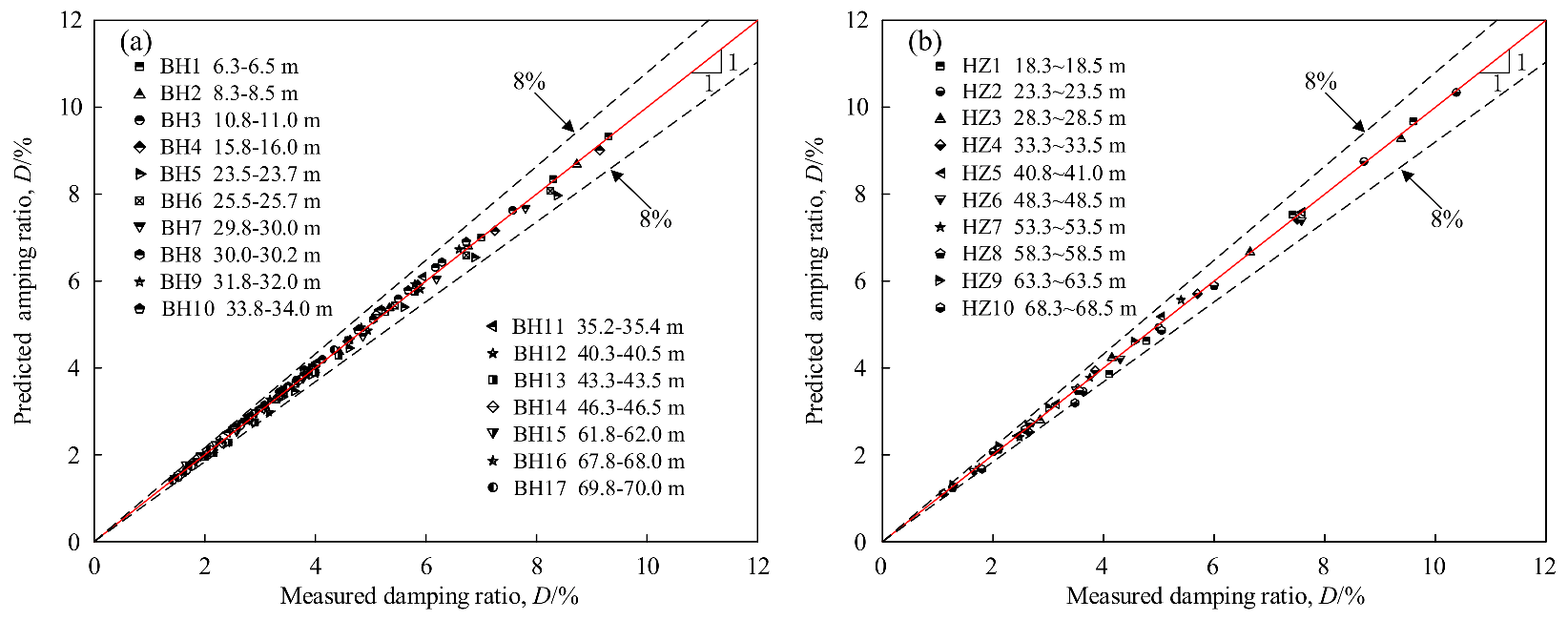
3.3. Model Performance
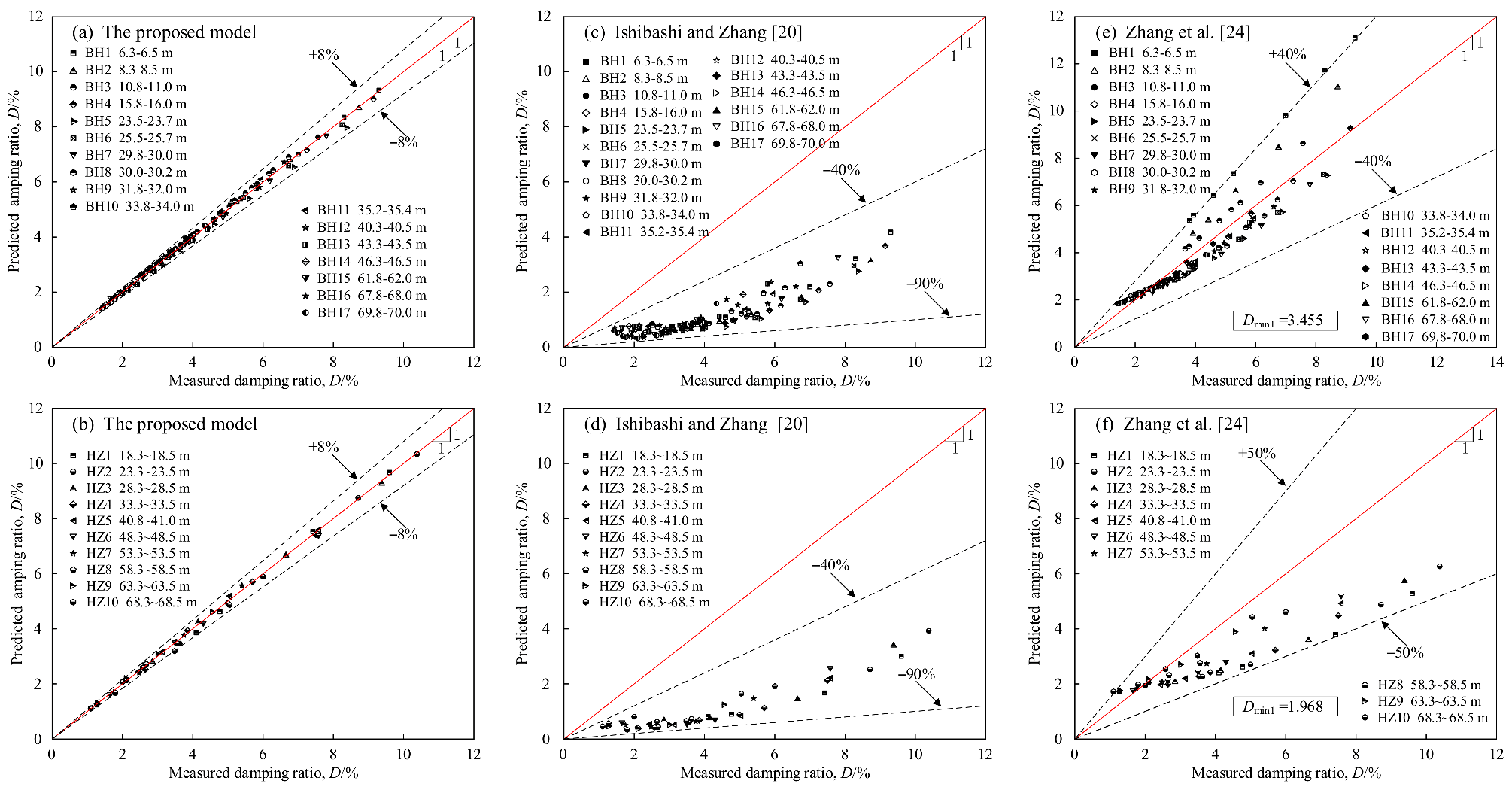
4. Evaluation and Discussion
4.1. Evaluation of Prediction Results
4.2. Comparison with Function Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
References
- Hardin, B.O.; Drnevich, V.P. Shear modulus and damping in soils: Measurement and parameter effects (Terzaghi Leture). J. Soil Mech. Found. Div. 1972, 98, 603–624. [Google Scholar] [CrossRef]
- Vucetic, M.; Dobry, R. Effect of Soil Plasticity on Cyclic Response. J. Geotech. Eng. 1991, 117, 89–107. [Google Scholar] [CrossRef]
- Chen, G.X.; Zhou, Z.L.; Sun, T.; Wu, Q.; Xu, L.Y.; Khoshnevisan, S.; Ling, D.S. Shear modulus and damping ratio of sand–gravel mixtures over a wide strain range. J. Earthq. Eng. 2019, 23, 1407–1440. [Google Scholar] [CrossRef]
- Yang, W.B.; Wu, Q.; Chen, G.X. Dynamic shear modulus prediction method of undisturbed soil in the estuary of the Yangtze River. Rock and Soil Mech. 2019, 40, 3889–3996. [Google Scholar]
- Morsy, A.M.; Salem, M.A.; Elmamlouk, H.H. Evaluation of dynamic properties of calcareous sands in Egypt at small and medium shear strain ranges. Soil Dynam. Earthq. Eng. 2019, 116, 692–708. [Google Scholar] [CrossRef]
- Jafarian, Y.; Javdanian, H. Small-strain dynamic properties of siliceous-carbonate sand under stress anisotropy. Soil Dyn. Earthq. Eng. 2020, 131, 106045. [Google Scholar] [CrossRef]
- Wu, Q.; Ma, W.J.; Liu, Q.F.; Zhao, K.; Chen, G.X. Dynamic Shear Modulus and Damping Ratio of Rubber-Sand Mixtures with a Wide Range of Rubber Content. Mater. Today Commun. 2021, 27, 102341. [Google Scholar] [CrossRef]
- Upreti, K.; Leong, E.C. Effect of mean grain size on shear modulus degradation and damping ratio curves of sands. Géotechnique 2021, 71, 205–215. [Google Scholar] [CrossRef]
- Wu, Q.; Hang, T.Z.; Zhao, K.; Chen, G.X. Reduction of Dynamic Shear Modulus of Saturated Marine Sandy Silt under Complex Stress Conditions. Mar. Georesour. Geotechnol. 2022, 1–11. [Google Scholar] [CrossRef]
- Vrettos, C.; Banzibaganye, G. Effects of specimen size and inertia on resonant column tests applied to sands. Soil Dyn. Earthq. Eng. 2022, 155, 107136. [Google Scholar] [CrossRef]
- Liang, K.; Chen, G.X.; Du, X.L.; Xu, C.S.; Yang, J. A Unified Formula for Small-Strain Shear Modulus of Sandy Soils Based on Extreme Void Ratios. J. Geotech. Geoenviron. Eng. 2023, 149, 04022127. [Google Scholar] [CrossRef]
- Koutsoftas, D.C.; Fisher, J.A. Dynamic properties of two marine clays. J. Geotech. Geoenviron. Eng. 1980, 106, 645–657. [Google Scholar] [CrossRef]
- Vrettos, C.; Savidis, S. Shear modulus and damping for Mediterranean sea clays of medium plasticity. In Earthquakes Geotechnical Engineering; e Pinto, P.S., Balkema, A.A., Eds.; CRC Press: Lisboa, Portugal, 1999; pp. 71–76. [Google Scholar]
- Sun, T.; Chen, G.X.; Zhou, E.Q.; Li, X.J. Experimental study on dynamic shear modulus and damping ratio of silty clay in deep seabed. J. Civ. Eng. 2012, 45, 9–14. [Google Scholar]
- Sun, T.; Chen, G.X.; Zhou, E.Q.; Li, X.J. Experimental study on dynamic shear modulus ratio and damping ratio of shallow marine soils over 100m in Qiongzhou Strait. Chin. J. Geotech. Eng. 2013, 35, 375–382. [Google Scholar]
- Banerjee, S.; Balaji, P. Effect of anisotropy on cyclic properties of Chennai marine clay. Int. J. Geosynth. Ground Eng. 2018, 4, 27. [Google Scholar] [CrossRef]
- Senapati, S.; Banerjee, S.; Thyagaraj, T. Effect of frequency on cyclic response of marine clay saturated with various pore fluids. Int. J. Geotech. Eng. 2021, 15, 1155–1164. [Google Scholar] [CrossRef]
- Li, Y.Y.; Li, P.; Zhu, S. The study on dynamic shear modulus and damping ratio of marine soils based on dynamic triaxial test. Mar. Georesour. Geotec. 2022, 40, 473–486. [Google Scholar] [CrossRef]
- Hardin, B.O.; Drnevich, V.P. Shear modulus and damping in soils: Design equations and curves. J. Soil Mech. Found. Div. 1972, 98, 667–692. [Google Scholar] [CrossRef]
- Ishibashi, I.; Zhang, X. Unified dynamic shear moduli and damping ratios of sand and clay. Soils Found. 1993, 33, 182–191. [Google Scholar] [CrossRef]
- Borden, R.H.; Shao, L.; Gupta, A. Dynamic properties of Piedmont residual soils. J. Geotech. Eng. 1996, 122, 813–821. [Google Scholar] [CrossRef]
- Stokoe, K.H.; Darendeli, M.B.; Andrus, R.D.; Brown, L.T. Dynamic soil properties: Laboratory, field and correlation studies. In Proceedings of the 2nd International Conference on Earthquake Geotechnical Engineering, Lisbon, Portugal, 21-25 June 1999; pp. 811–845. [Google Scholar]
- Darendeli, M. Development of a New Family of Normalized Modulus Reduction and Material Damping Curves. Ph.D. Thesis, University of Texas, Austin, TX, USA, 2001. [Google Scholar]
- Zhang, J.; Andrus, R.D.; Juang, C.H. Normalized shear modulus and material damping ratio relationships. J. Geotech. Geoenviron. Eng. 2001, 131, 453–464. [Google Scholar] [CrossRef]
- ASTM D2487-17; Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM D4015-15; Standard Test Methods for Modulus and Damping of Soils by Fixed-Base Resonant Column Devices. ASTM International: West Conshohocken, PA, USA, 2015.
- Senetakis, K.; Payan, M. Small strain damping ratio of sands and silty sands subjected to flexural and torsional resonant column excitation. Soil Dyn. Earthq. Eng. 2018, 114, 448–459. [Google Scholar] [CrossRef]
- Chen, G.X.; Wu, Q.; Zhao, K.; Shen, Z.F.; Yang, J. A Binary Packing Material–Based Procedure for Evaluating Soil Liquefaction Triggering during Earthquakes. J. Geotech. Geoenviron. Eng. 2020, 146, 04020040. [Google Scholar] [CrossRef]
- Gao, H.M.; Xia, S.S.; Chen, F.Y.; Stuedlein, A.W.; Li, X.; Wang, Z.H.; Shen, Z.F.; Chen, X.M. Dynamic shear modulus and damping of cemented and uncemented lightweight expanded clay aggregate (LECA) at low strains. Soil Dyn. Earthq. Eng. 2021, 142, 106555. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Bayesian interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Qian, N. On the momentum term in gradient descent learning algorithms. Neural Netw. 1999, 12, 145–151. [Google Scholar] [CrossRef]
- Mohammad, A.T.; Mat, S.B.; Sulaiman, M.Y.; Sopian, K.; Al-abidi, A.A. Implementation and Validation of an Artificial Neural Network for Predicting the Performance of a Liquid Desiccant Dehumidifier. Energy Convers. Manag. 2013, 67, 240–250. [Google Scholar] [CrossRef]
- Alzabeebee, S.; Alshkane, Y.M.; Al-Taie, A.J.; Rashed, K.A. Soft Computing of the Recompression Index of Fine-Grained Soils. Soft Comput. 2021, 25, 15297–15312. [Google Scholar] [CrossRef]
- Alzabeebee, S.; Mohammed, D.A.; Alshkane, Y.M. Experimental Study and Soft Computing Modeling of the Unconfined Compressive Strength of Limestone Rocks Considering Dry and Saturation Conditions. Rock Mech. Rock Eng. 2022, 55, 5535–5554. [Google Scholar] [CrossRef]




| Function Forms | Data from | Soil Type |
|---|---|---|
| , where Gmax is the maximum shear modulus; γr is the reference strain; τmax is the maximum shear stress. | Hardin and Drnevich [19] | Cohesive soil and sand |
| , where Dmax is the maximum damping ratio. | ||
| , | Ishibashi and Zh-ang [20] | Sandy soil |
| . | ||
| , where n(PI) is the function related to the plasticity index of soil. | Plastic soil (Silt and Clay) | |
| . | ||
| , where a, b, and c are the curvature coefficient. | Borden et al. [21] | Piedmont residual soil (MH, ML, SM-ML, SM) |
| . | ||
| , where α is the curvature coefficient. | Stokoe et al. [22] Darendeli [23] | Undisturbed soil (CH, CL, CL-ML, MH, ML, SC, SM, SC-SM, SP, SP-SM, SW-SC, SW-SM) |
| , where d is the scaling coefficient, Dmin is the small-strain damping ratio, and DMasing is the modeled masing damping. | Darendeli [23] | |
| , where γr is the reference strain corresponding to the γ value when G/Gmax = 0.5, α is the curvature parameter, γr1 is the reference strain at a mean effective confining stress σm of 100 kPa, Pa is the reference stress at 100 kPa, and k is a stress-correction exponent. | Zhang et al. [24] | Quaternary soil Tertiary and older soil Residual/saprolite soil |
| Torsional shear test, , where Dmin1 is the small-strain damping at σm of 100 kPa. |
| Sample | Soil Depth H/m | Mean Effective Confining Pressure σm/kPa | Specific Gravity Gs | Water Content w/% | Density ρ/g·cm−3 | Plasticity Index PI |
|---|---|---|---|---|---|---|
| BH 1 | 6.3–6.5 | 43 | 2.67 | 40.72 | 1.9 | 15.99 |
| BH 2 | 8.3–8.5 | 56 | 2.69 | 36.45 | 1.9 | 17.15 |
| BH 3 | 10.8–11.0 | 73 | 2.70 | 38.95 | 1.95 | 16.88 |
| BH 4 | 15.8–16.0 | 106 | 2.68 | 37.99 | 1.92 | 16.23 |
| BH 5 | 23.5–23.7 | 157 | 2.67 | 37.87 | 1.97 | 16.98 |
| BH 6 | 25.5–25.7 | 171 | 2.67 | 35.53 | 1.96 | 16.95 |
| BH 7 | 29.8–30.0 | 199 | 2.67 | 38.96 | 1.91 | 15.00 |
| BH 8 | 30.0–30.2 | 201 | 2.71 | 36.17 | 1.97 | 15.06 |
| BH 9 | 31.8–32.0 | 213 | 2.67 | 39.04 | 1.92 | 17.12 |
| BH 10 | 33.8–34.0 | 226 | 2.68 | 36.67 | 1.93 | 12.64 |
| BH 11 | 35.2–35.4 | 235 | 2.69 | 36.82 | 1.93 | 17.23 |
| BH 12 | 40.3–40.5 | 269 | 2.68 | 30.93 | 1.9 | 15.27 |
| BH 13 | 43.3–43.5 | 289 | 2.70 | 38.17 | 1.94 | 15.95 |
| BH 14 | 46.3–46.5 | 309 | 2.68 | 36.08 | 1.93 | 15.34 |
| BH 15 | 61.8–62.0 | 413 | 2.68 | 33.74 | 2.04 | 13.55 |
| BH 16 | 67.8–68.0 | 453 | 2.68 | 31.10 | 1.99 | 15.57 |
| BH 17 | 69.8–70.0 | 466 | 2.67 | 30.84 | 2.01 | 13.14 |
| HZ 1 | 18.3–18.5 | 123 | 2.68 | 15.52 | 1.81 | 15.52 |
| HZ 2 | 23.3–25.5 | 156 | 2.67 | 15.64 | 1.94 | 15.64 |
| HZ 3 | 28.3–28.5 | 190 | 2.70 | 14.37 | 1.97 | 14.37 |
| HZ 4 | 33.3–33.5 | 233 | 2.67 | 15.07 | 2.06 | 15.07 |
| HZ 5 | 40.8–41.0 | 273 | 2.71 | 16.57 | 2.07 | 16.57 |
| HZ 6 | 48.3–48.5 | 323 | 2.70 | 14.76 | 2.07 | 14.76 |
| HZ 7 | 53.3–53.5 | 356 | 2.69 | 13.35 | 2.04 | 13.35 |
| HZ 8 | 58.3–58.5 | 390 | 2.70 | 14.76 | 2.06 | 14.76 |
| HZ 9 | 63.3–63.5 | 423 | 2.70 | 15.97 | 2.06 | 15.97 |
| HZ 10 | 68.3–68.5 | 456 | 2.69 | 14.08 | 2.03 | 14.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Wang, Z.; Qin, Y.; Yang, W. Intelligent Model for Dynamic Shear Modulus and Damping Ratio of Undisturbed Marine Clay Based on Back-Propagation Neural Network. J. Mar. Sci. Eng. 2023, 11, 249. https://doi.org/10.3390/jmse11020249
Wu Q, Wang Z, Qin Y, Yang W. Intelligent Model for Dynamic Shear Modulus and Damping Ratio of Undisturbed Marine Clay Based on Back-Propagation Neural Network. Journal of Marine Science and Engineering. 2023; 11(2):249. https://doi.org/10.3390/jmse11020249
Chicago/Turabian StyleWu, Qi, Zifan Wang, You Qin, and Wenbao Yang. 2023. "Intelligent Model for Dynamic Shear Modulus and Damping Ratio of Undisturbed Marine Clay Based on Back-Propagation Neural Network" Journal of Marine Science and Engineering 11, no. 2: 249. https://doi.org/10.3390/jmse11020249
APA StyleWu, Q., Wang, Z., Qin, Y., & Yang, W. (2023). Intelligent Model for Dynamic Shear Modulus and Damping Ratio of Undisturbed Marine Clay Based on Back-Propagation Neural Network. Journal of Marine Science and Engineering, 11(2), 249. https://doi.org/10.3390/jmse11020249






