An Improved VMD–EEMD–LSTM Time Series Hybrid Prediction Model for Sea Surface Height Derived from Satellite Altimetry Data
Abstract
:1. Introduction
2. Principles and Methods
2.1. Signal Processing Methods
- (1)
- Initially, white noise denoted as is introduced into the original signal .
- (2)
- Subsequently, the EMD method is employed to decompose the initial noisy signal, resulting in n IMFs, represented as , and a residual sequence represented as .
- (3)
- Steps (1) and (2) are iteratively executed for a total of times, in which white noise is added and IMF components are obtained through decomposition in each iteration. Finally, all the components obtained from the IMFs are integrated and averaged to obtain the ultimate result of EEMD signal decomposition.
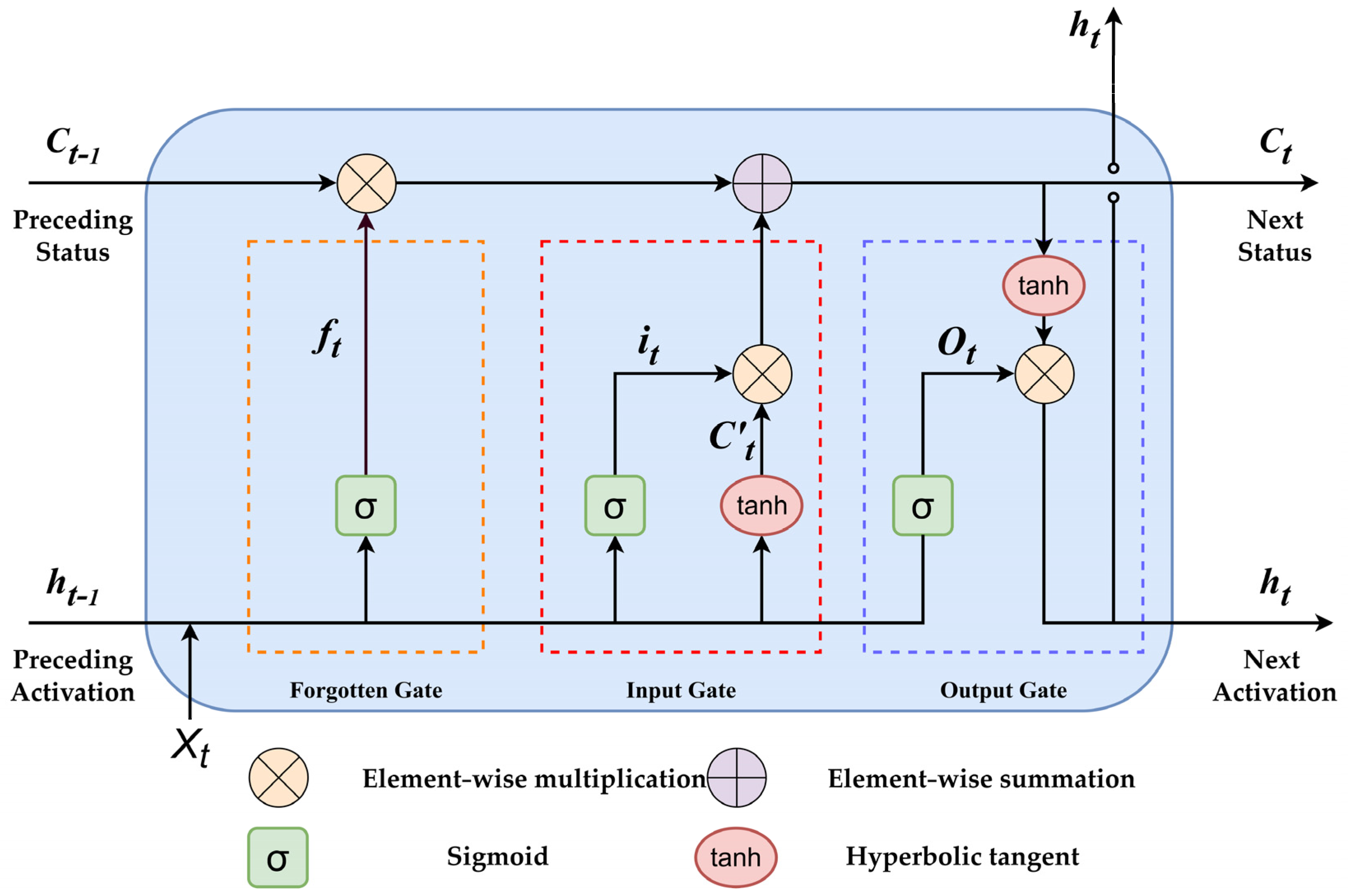
2.2. Long Short-Term Memory
- (1)
- LSTM, through the forget gate (denoted as ), determines whether to discard or retain information related to and is governed by the activation function of the forget gate.
- (2)
- The cell state is updated through the input gate by passing and to the activation function to determine the information update.
- (3)
- The cell state from the previous layer is element-wise multiplied with the forget vector, and then this value is element-wise added to the output of the input gate, resulting in the updated cell state.
- (4)
- Through the output gate , the value of the next hidden state is determined, and this hidden state contains information from previous inputs.
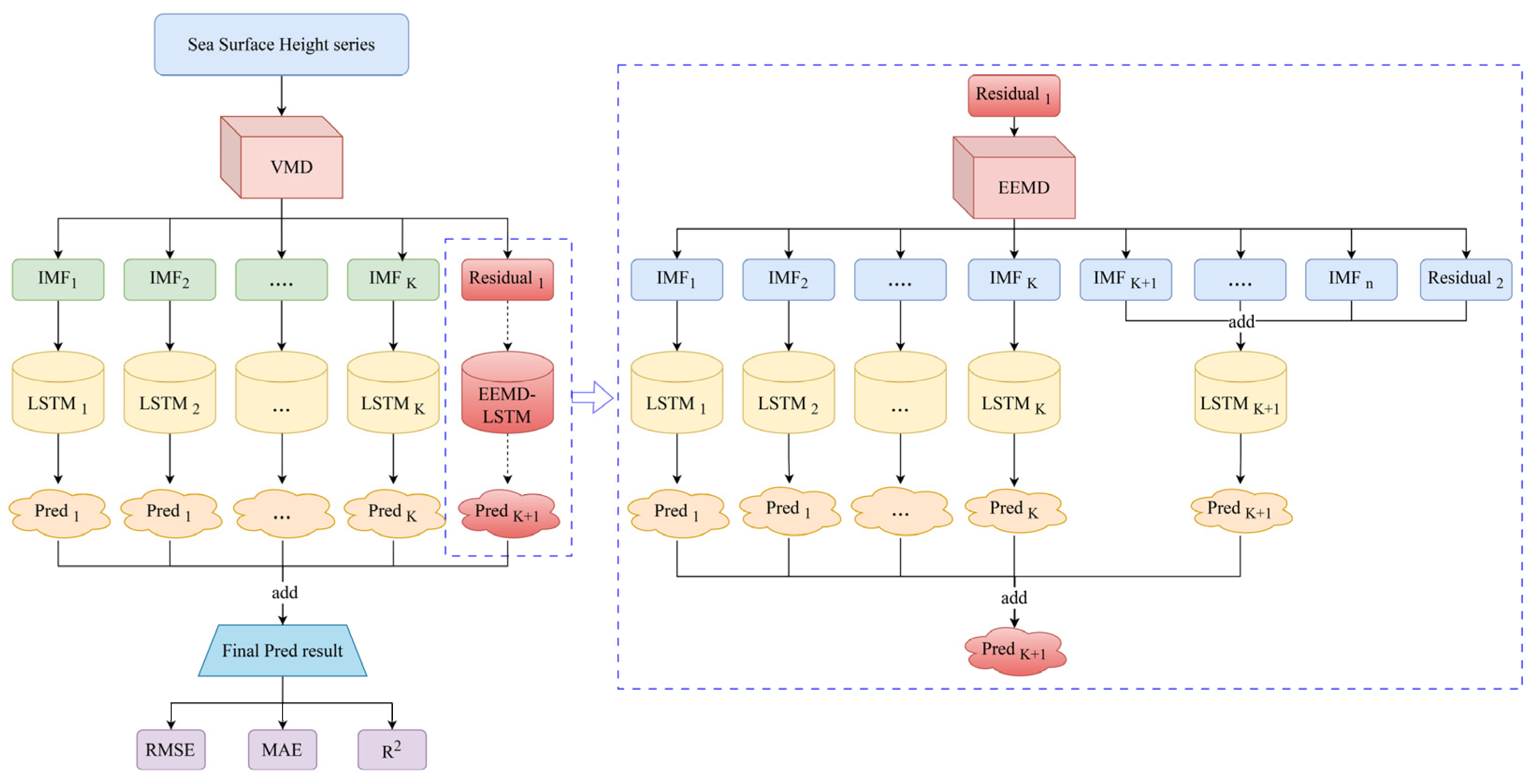
2.3. The VMD–EEMD–LSTM Hybrid Second-Order Decomposition Prediction Model
2.4. Evaluation Index
- (1)
- Root mean square error (RMSE)
- (2)
- Mean absolute error (MAE)
- (3)
- Coefficient of determination (R2)where represents the actual values of sea level, represents the values predicted by each model, is the mean of the actual values of sea level, and n denotes the total number of data points related to sea level. For RMSE and MAE, smaller values indicate higher predictive accuracy, while for R2, values closer to 1 indicate accurate predictions and values closer to 0 suggest that the model has weaker explanatory power.
3. Data and Experiments
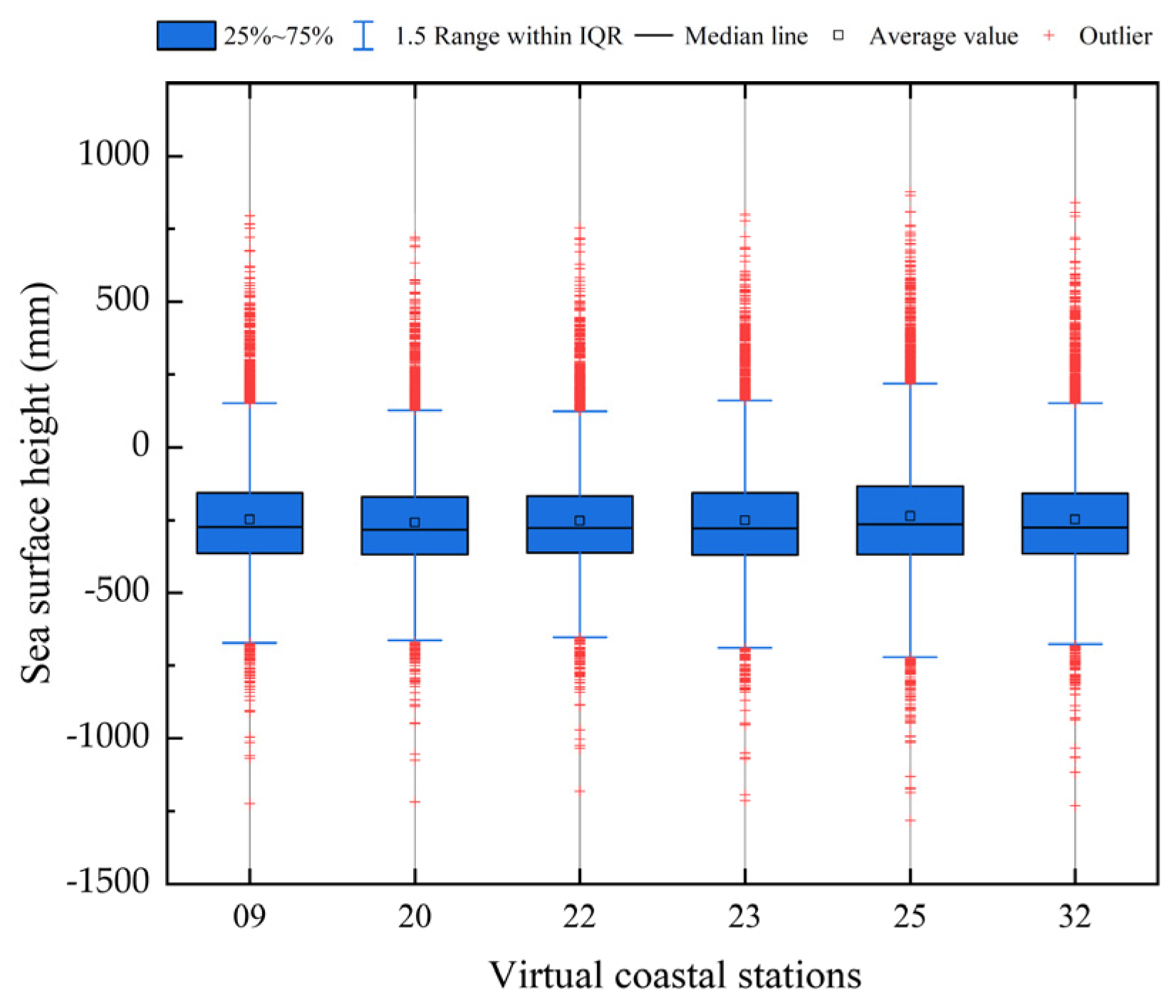
3.1. Data Preprocessing
3.2. Experimental Pretreatment
3.2.1. Parameter Settings of VMD
3.2.2. Parameter Settings of the Model
4. Results and Analysis
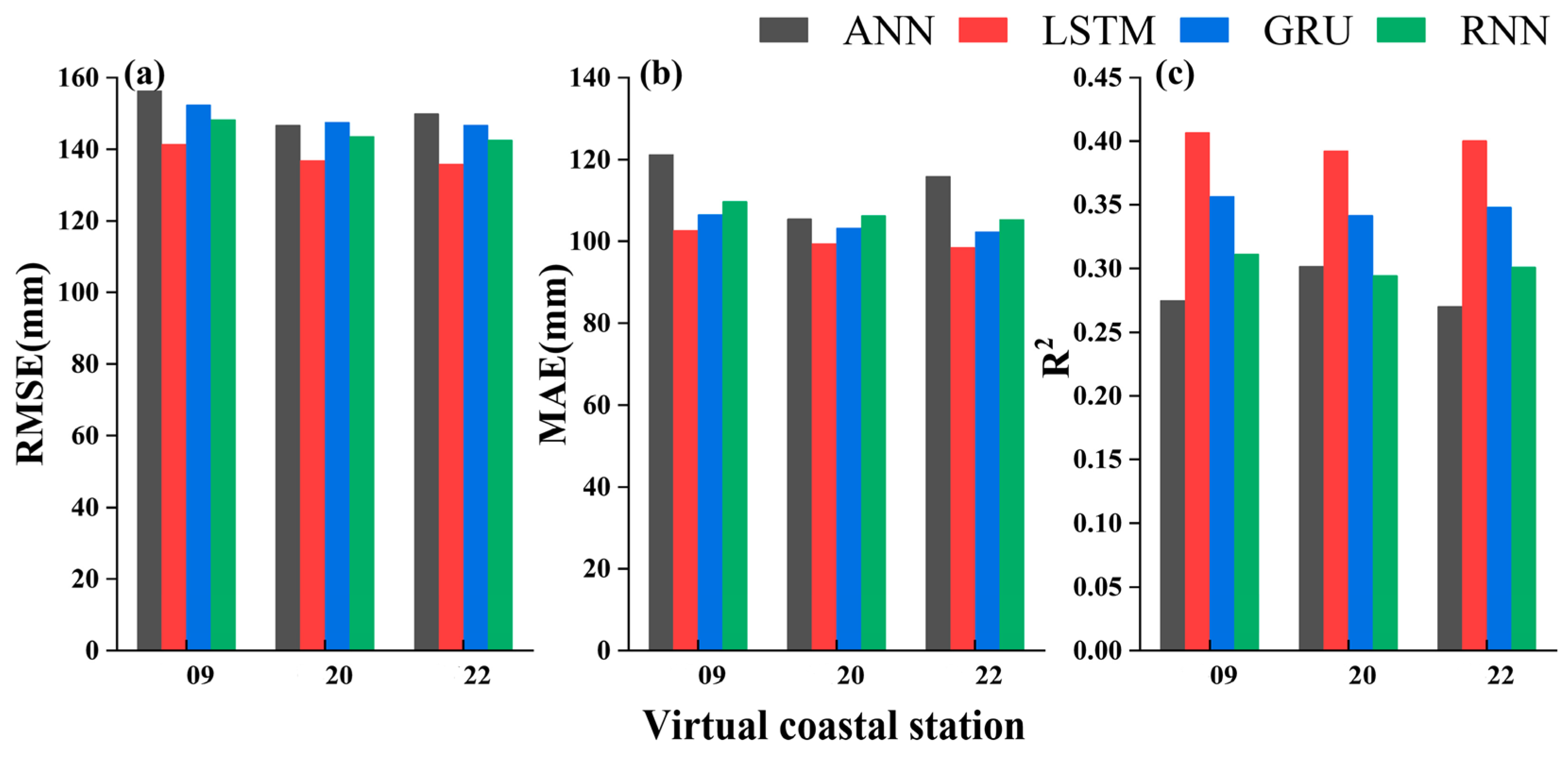
4.1. Analysis of the Predictions of a Single Deep Learning Model
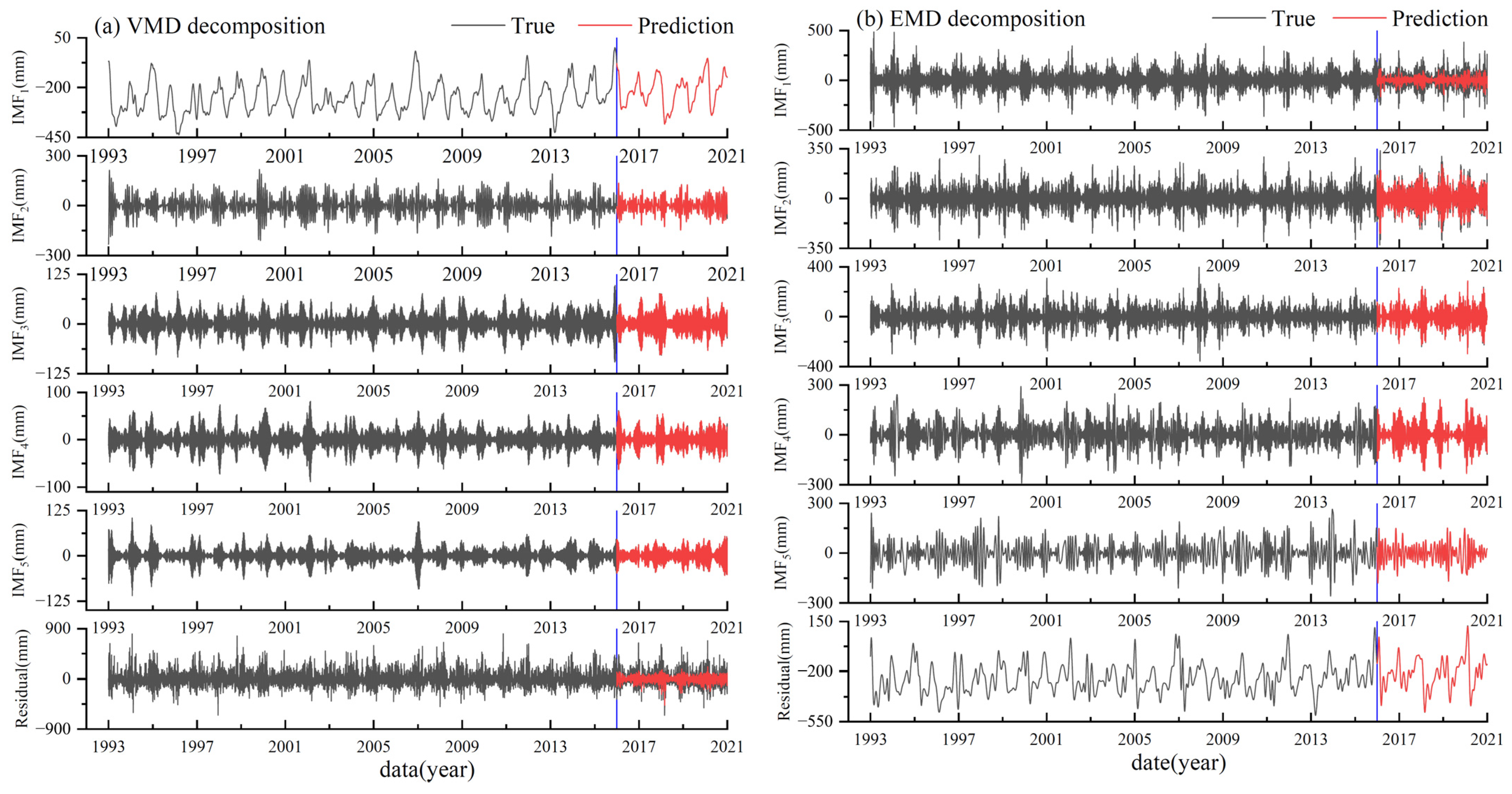
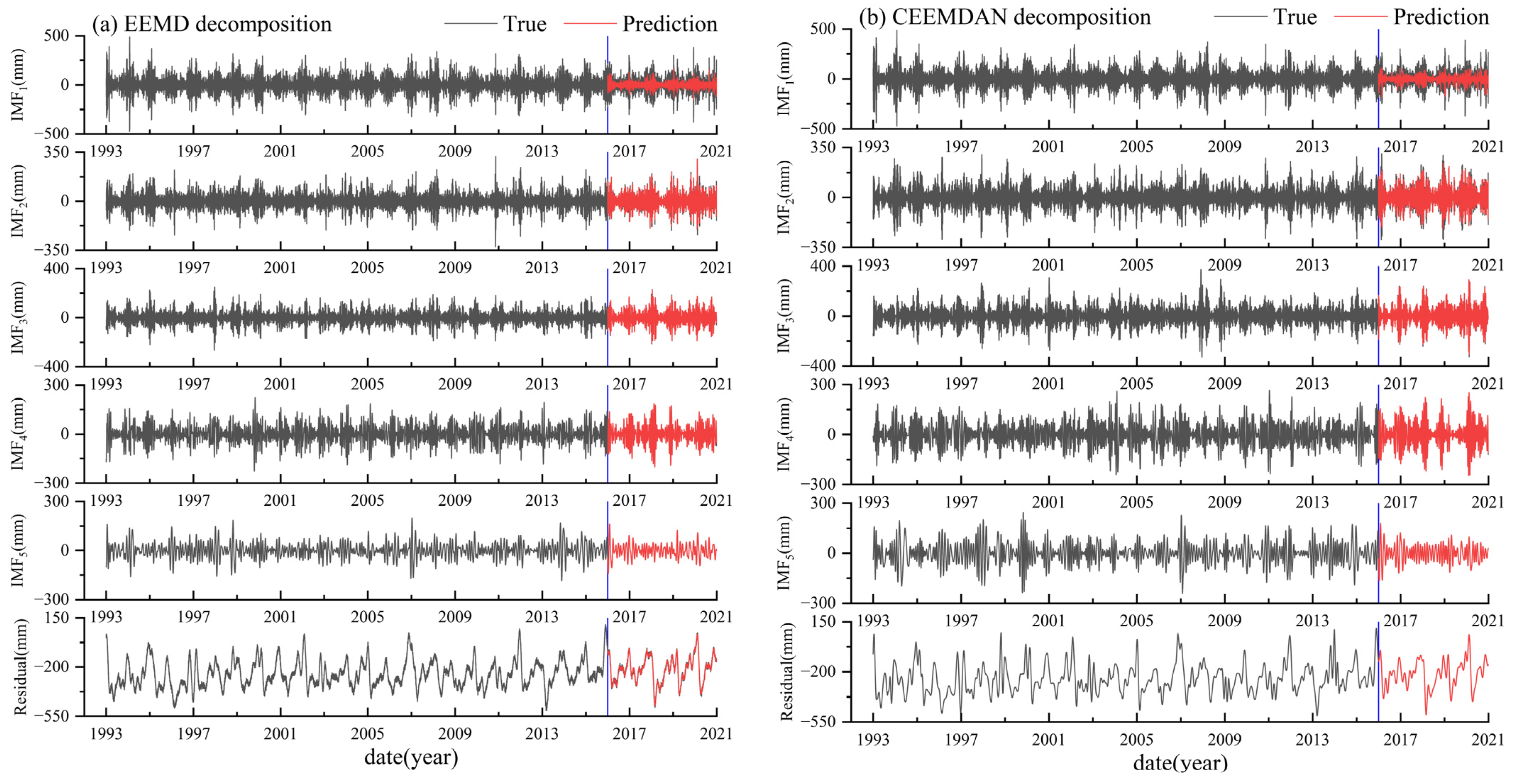
4.2. Analysis of the Hybrid Deep Learning First-Order Decomposition Model
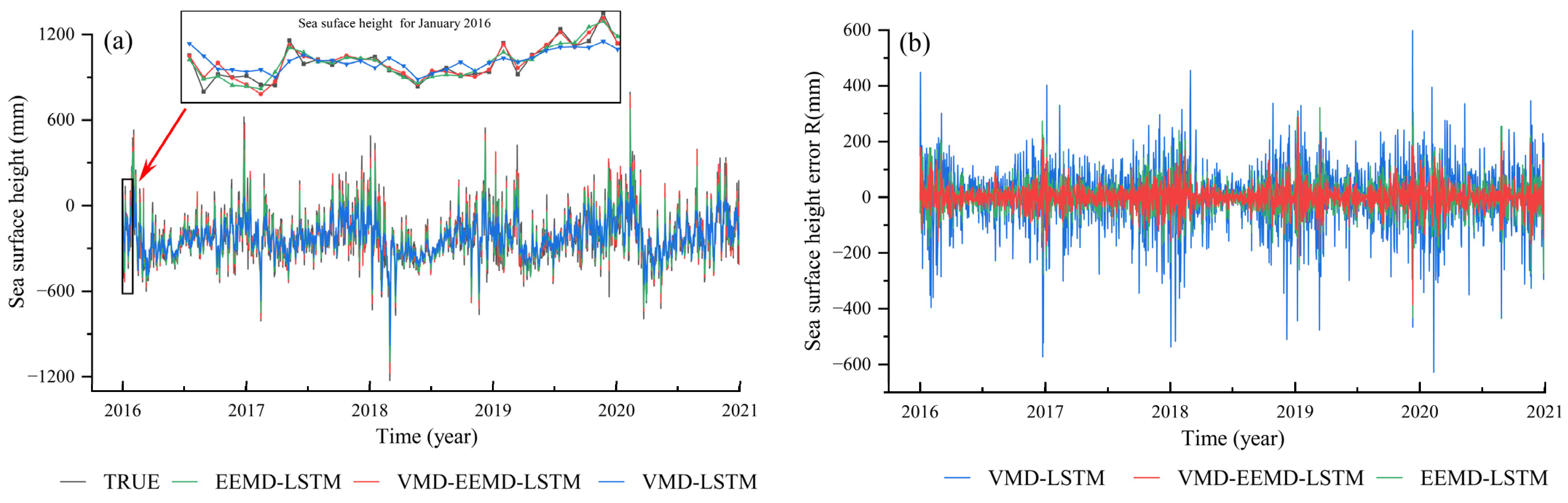
4.3. Analysis of the Predictions of the Mixed VMD–EEMD–LSTM Second-Order Decomposition Model
4.4. Analysis of the Accuracy of the Predictions of the Mixed VMD–EEMD–LSTM Second-Order Decomposition Model
4.4.1. Analysis of the Results of the Evaluation Index
4.4.2. Comparison of the Trend from Satellite Altimetry and Tide Gauge Observations
5. Discussion
6. Conclusions
- (1)
- By comparing the predictions of different individual models, it is evident that the LSTM model exhibits the best predictive performance. However, the average RMSE remains high at 137.9 mm, the average MAE is 100.1 mm, and the average R2 is only 0.4 across different measurement stations. This indicates that single deep learning predictive models often suffer from insufficient feature extraction when dealing with complex time series data, resulting in generally lower predictive accuracy.
- (2)
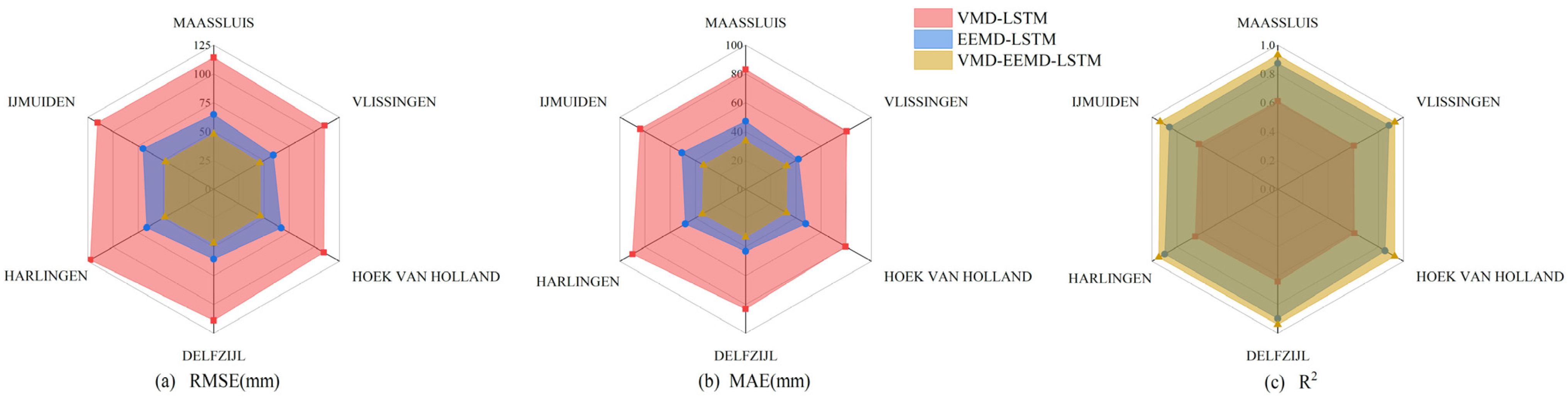
- Comparing the four hybrid prediction models, VMD-LSTM, EMD-LSTM, EEMD-LSTM, and CEEMDAN-LSTM, the VMD-LSTM model has the lowest predictive accuracy across different measurement stations, with an average RMSE of 111.3 mm, an average MAE of 81.0 mm, and an average R2 of 0.6. In contrast, the EEMD-LSTM model demonstrates the highest predictive accuracy, with an average RMSE of 63.8 mm, an average MAE of 45.7 mm, and an average R2 of 0.9. Although the VMD-LSTM model lags behind EMD-LSTM EEMD-LSTM and CEEMDAN-LSTM models in overall predictive accuracy, its individual IMF components exhibit exceptionally high predictive accuracy within the LSTM model. While the IMF components of the EEMD-LSTM model may not match the VMD-LSTM model in predictive accuracy, the overall predictive accuracy of EEMD-LSTM surpasses that of VMD-LSTM.
- (3)
- In conclusion, through a comprehensive analysis of six sets of sea surface height data along the Dutch coast, our experimental results firmly validate the exceptional predictive accuracy of the VMD-EEMD-LSTM hybrid model proposed in this paper (RMSE = 47.2 mm, MAE = 33.3 mm, R2 = 0.9). When compared to the VMD-LSTM model, we observe an average reduction in RMSE by 58.7% and MAE by 60.0% and an improvement in R2 by 49.9%. Similarly, in comparison with the EEMD-LSTM model, we note an average reduction in RMSE by 27.0% and MAE by 28.0% and an improvement in R2 by 6.5%. These results unequivocally demonstrate the significant enhancement in predictive accuracy of sea surface height time series, opening new avenues for future research and affirming the model’s potential for understanding and predicting sea level changes and related environmental phenomena.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cazenave, A.; Llovel, W. Contemporary Sea level rise. Annu. Rev. Mar. Sci. 2010, 2, 145–173. [Google Scholar] [CrossRef] [PubMed]
- Nicholls, R.J.; Cazenave, A. Sea-level rise and its impact on coastal zones. Science 2010, 328, 1517–1520. [Google Scholar] [CrossRef] [PubMed]
- IPCC. Climate Change 2023: Synthesis Report. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2023; pp. 35–115. [Google Scholar]
- Titus, J.G.; Anderson, K.E. Coastal Sensitivity to Sea-Level Rise: A Focus on the Mid-Atlantic Region; Climate Change Science Program: Washinghton, DC, USA, 2009; Volume 4. [Google Scholar]
- Cerqueira, V.; Torgo, L.; Soares, C. Machine learning vs statistical methods for time series forecasting: Size matters. arXiv 2019, arXiv:1909.13316. [Google Scholar]
- Bontempi, G.; Ben Taieb, S.; Le Borgne, Y.A. Machine learning strategies for time series forecasting. In Business Intelligence: Second. European Summer School, eBISS 2012, Brussels, Belgium, 15–21 July 2012; Tutorial Lectures 2; Springer: Berlin/Heidelberg, Germany, 2013; pp. 62–77. [Google Scholar]
- Armstrong, J.S.; Collopy, F. Integration of Statistical Methods and Judgment for Time Series Forecasting: Principles from Empirical Research; John Wiley & Sons: Hoboken, NJ, USA, 1998; pp. 269–293. [Google Scholar]
- Abraham, B.; Ledolter, J. Statistical Methods for Forecasting; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Faruk, D.Ö. A hybrid neural network and ARIMA model for water quality time series prediction. Eng. Appl. Artif. Intel. 2010, 23, 586–594. [Google Scholar] [CrossRef]
- Kalekar, P.S. Time series forecasting using holt-winters exponential smoothing. Kanwal Rekhi Sch. Inf. Technol. 2004, 4329008, 1–13. [Google Scholar]
- Young, P.; Young, P. Alternative Recursive Approaches to Time-Series Analysis. In Recursive Estimation and Time-Series Analysis: An Introduction; Springer: Berlin/Heidelberg, Germany, 1984; pp. 205–230. [Google Scholar]
- Adebiyi, A.A.; Adewumi, A.O.; Ayo, C.K. Comparison of ARIMA and artificial neural networks models for stock price prediction. J. Appl. Math. 2014, 2014, 614342. [Google Scholar] [CrossRef]
- Masini, R.P.; Medeiros, M.C.; Mendes, E.F. Machine learning advances for time series forecasting. J. Econ. Surv. 2023, 37, 76–111. [Google Scholar] [CrossRef]
- Sapankevych, N.I.; Sankar, R. Time series prediction using support vector machines: A survey. IEEE Comput. Intell. Mag. 2009, 4, 24–38. [Google Scholar] [CrossRef]
- Lai, R.K.; Fan, C.Y.; Huang, W.H.; Chang, P.C. Evolving and clustering fuzzy decision tree for financial time series data forecasting. Expert Syst. Appl. 2009, 36, 3761–3773. [Google Scholar] [CrossRef]
- Huang, S.; Wang, D.; Wu, X.; Tang, A. Dsanet: Dual self-attention network for multivariate time series forecasting. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019; pp. 2129–2132. [Google Scholar]
- Tealab, A. Time series forecasting using artificial neural networks methodologies: A systematic review. Future Comput. Inform. J. 2018, 3, 334–340. [Google Scholar] [CrossRef]
- Hajirahimi, Z.; Khashei, M. Hybrid structures in time series modeling and forecasting: A review. Eng. Appl. Artif. Intell. 2019, 86, 83–106. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F.; Gargano, R.; de Marinis, G. Forecasting of extreme storm tide events using NARX neural network-based models. Atmosphere 2021, 12, 512. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F. Neuroforecasting of daily streamflows in the UK for short-and medium-term horizons: A novel insight. J. Hydrol. 2023, 624, 129888. [Google Scholar] [CrossRef]
- Di Nunno, F.; de Marinis, G.; Gargano, R.; Granata, F. Tide prediction in the Venice Lagoon using nonlinear autoregressive exogenous (NARX) neural network. Water 2021, 13, 1173. [Google Scholar] [CrossRef]
- Shikhovtsev, A.Y.; Kovadlo, P.G.; Kiselev, A.V.; Eselevich, M.V.; Lukin, V.P. Application of Neural Networks to Estimation and Prediction of Seeing at the Large Solar Telescope Site. Publ. Astron. Soc. Pac. 2023, 135, 014503. [Google Scholar] [CrossRef]
- Makarynskyy, O.; Makarynska, D.; Kuhn, M.; Featherstone, W.E. Predicting sea level variations with artificial neural networks at Hillarys Boat Harbour, Western Australia. Estuarine. Estuar. Coast. Shelf S. 2004, 61, 351–360. [Google Scholar] [CrossRef]
- Nezhad, S.K.; Barooni, M.; Velioglu Sogut, D.; Weaver, R.J. Ensemble Neural Networks for the Development of Storm Surge Flood Modeling: A Comprehensive Review. J. Mar. Sci. Eng. 2023, 11, 2154. [Google Scholar] [CrossRef]
- Alenezi, N.; Alsulaili, A.; Alkhalidi, M. Prediction of Sea Level in the Arabian Gulf Using Artificial Neural Networks. J. Mar. Sci. Eng. 2023, 11, 2052. [Google Scholar] [CrossRef]
- Balogun, A.L.; Adebisi, N. Sea level prediction using ARIMA, SVR and LSTM neural network: Assessing the impact of ensemble Ocean-Atmospheric processes on models’ accuracy. Geomatics. Geomat. Nat. Haz Risk. 2021, 12, 653–674. [Google Scholar] [CrossRef]
- Lee, T. EMD and LSTM hybrid deep learning model for predicting sunspot number time series with a cyclic pattern. Sol. Phys. 2020, 295, 82. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, Y. Hybrid method for short-term time series forecasting based on EEMD. IEEE Access 2020, 8, 61915–61928. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, F.; Liu, S.; Wu, Y.; Wang, L. A hybrid VMD–BiGRU model for rubber futures time series forecasting. Appl. Soft Comput. 2019, 84, 105739. [Google Scholar] [CrossRef]
- de Siqueira, B.V.P.; de Moraes Paiva, A. Using neural network to improve sea level prediction along the southeastern Brazilian coast. Ocean Model. 2021, 168, 101898. [Google Scholar] [CrossRef]
- Song, C.; Chen, X.; Xia, W.; Ding, X.; Xu, C. Application of a novel signal decomposition prediction model in minute sea level prediction. Ocean Eng. 2022, 260, 111961. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Z.; Wei, H.; Chen, L.; Zhang, H. Hybrid deep learning model for short-term wind speed forecasting based on time series decomposition and gated recurrent unit. Complex Syst. Model. Simul. 2021, 1, 308–321. [Google Scholar] [CrossRef]
- Dabbakuti, J.K.; Peesapati, R.; Kumar, A.K. Design and Development of Artificial Intelligence Enabled IoT Framework for Satellite Based Navigation Services. In IEEE Transactions on Geoscience and Remote Sensing; IEEE: New York, NY, USA, 2023. [Google Scholar]
- Dabbakuti, J.R.K.K.; Jacob, A.; Veeravalli, V.R.; Kallakunta, R.K. Implementation of IoT analytics ionospheric forecasting system based on machine learning and ThingSpeak. IET Radar Sonar Navig. 2020, 14, 341–347. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y.; Li, T.; Xie, X.; Chang, C. Short-term PV power prediction based on optimized VMD and LSTM. IEEE Access 2020, 8, 165849–165862. [Google Scholar] [CrossRef]
- Huang, Y.; Yan, L.; Cheng, Y.; Qi, X.; Li, Z. Coal thickness prediction method based on VMD and LSTM. Electronics 2022, 11, 232. [Google Scholar] [CrossRef]
- Han, L.; Zhang, R.; Wang, X.; Bao, A.; Jing, H. Multi-step wind power forecast based on VMD-LSTM. IET Renew. Power Gen. 2019, 13, 1690–1700. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P.; Goncalves, P. On Empirical Mode Decomposition and Its Algorithms. In Proceedings of the IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing, Antalya, Turkey, 20–23 June 2003; IEEE: New York, NY, USA, 2003; Volume 3, pp. 8–11. [Google Scholar]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Lian, J.; Liu, Z.; Wang, H.; Dong, X. Adaptive variational mode decomposition method for signal processing based on mode characteristic. Mech. Syst. Signal Process. 2018, 107, 53–77. [Google Scholar] [CrossRef]
- Pei, Y.; Wu, Y.; Jia, D. Research on PD signals denoising based on EMD method. Prz. Elektrotechniczny 2012, 88, 137–140. [Google Scholar]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; IEEE: New York, NY, USA, 2011; pp. 4144–4147. [Google Scholar]
- Wu, Z.; Huang, N.E.; Chen, X. The multi-dimensional ensemble empirical mode decomposition method. Adv. Adapt. Data Anal. 2009, 1, 339–372. [Google Scholar] [CrossRef]
- Teja, K.; Tiwari, R.; Mohanty, S. Adaptive denoising of ECG using EMD, EEMD and CEEMDAN signal processing techniques. In Journal of Physics: Conference Series; IOP Publishing: New York, NY, USA, 2020; Volume 1706, p. 012077. [Google Scholar]
- Graves, A.; Graves, A. Long short-term memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar]
- Chen, H.; Lu, T.; He, X.; Sun, X.; Huang, J.; Wang, J.; Yang, S. An improved DFVMD-LSTM hybrid time series model for predicting total solar irradiance. Acta Geodyn. Geomater. 2023, 20, 139–153. [Google Scholar] [CrossRef]
- Sagheer, A.; Kotb, M. Time series forecasting of petroleum production using deep LSTM recurrent networks. Neurocomputing 2019, 323, 203–213. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Li, Z.; Qu, L.; Zhang, J.; Teng, B. A hybrid VMD-LSTM/GRU model to predict non-stationary and irregular waves on the east coast of China. Ocean Eng. 2023, 276, 114136. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, X.; Ren, F.; Shao, Z.; Tian, C. Wind speed prediction using a hybrid model of EEMD and LSTM considering seasonal features. Energy Rep. 2022, 8, 8965–8980. [Google Scholar] [CrossRef]
- Liao, X.; Liu, Z.; Deng, W. Short-term wind speed multistep combined forecasting model based on two-stage decomposition and LSTM. J. Wind Energy 2021, 24, 991–1012. [Google Scholar] [CrossRef]
- Jin, Y.; Guo, H.; Wang, J.; Song, A. A hybrid system based on LSTM for short-term power load forecasting. Energies 2020, 13, 6241. [Google Scholar] [CrossRef]
- Chen, H.; Lu, T.; Huang, J.; He, X.; Yu, K.; Sun, X.; Ma, X.; Huang, Z. An Improved VMD-LSTM Model for Time-Varying GNSS Time Series Prediction with Temporally Correlated Noise. Remote Sens. 2023, 15, 3694. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Chen, X.; Yu, J. Denoising and feature extraction algorithms using NPE combined with VMD and their applications in ship-radiated noise. Symmetry 2017, 9, 256. [Google Scholar] [CrossRef]
- Li, C.; Wu, Y.; Lin, H.; Li, J.; Zhang, F.; Yang, Y. ECG denoising method based on an improved VMD algorithm. IEEE Sens. J. 2022, 22, 22725–22733. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)–Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Ozer, D.J. Correlation and the coefficient of determination. Psychol. Bull. 1985, 97, 307. [Google Scholar] [CrossRef]
- Belonenko, T.V.; Zinchenko, V.A.; Fedorov, A.M.; Budyansky, M.V.; Prants, S.V.; Uleysky, M.Y. Interaction of the Lofoten Vortex with a satellite cyclone. Pure Appl. Geophys. 2021, 178, 287–300. [Google Scholar] [CrossRef]
- Feng, J.; Yuan, Y.; Zhang, T.; Zhang, Z.; Meng, D. Analysis of Ionospheric Anomalies before the Tonga Volcanic Eruption on 15 January 2022. Remote Sens. 2023, 15, 4879. [Google Scholar] [CrossRef]
- Lellouche, J.M.; Greiner, E.; Le Galloudec, O.; Garric, G.; Regnier, C.; Drevillon, M.; Benkiran, M.; Testut, C.E.; Bourdalle-Badie, R.; Gasparin, F.; et al. Recent updates to the Copernicus Marine Service global ocean monitoring and forecasting real-time 1/12∘ high-resolution system. Ocean Sci. 2018, 14, 1093–1126. [Google Scholar] [CrossRef]
- Hoogland, T.; Van den Akker, J.J.H.; Brus, D.J. Modeling the subsidence of peat soils in the Dutch coastal area. Geoderma 2012, 171, 92–97. [Google Scholar] [CrossRef]
- Montillet, J.P.; Melbourne, T.I.; Szeliga, W.M. GPS vertical land motion corrections to sea-level rise estimates in the Pacific Northwest. J. Geophys. Res. Ocean. 2018, 123, 1196–1212. [Google Scholar] [CrossRef]
- Mei, L.; Li, S.; Zhang, C.; Han, M. Adaptive signal enhancement based on improved VMD-SVD for leak location in water-supply pipeline. IEEE Sens. J. 2021, 21, 24601–24612. [Google Scholar] [CrossRef]
- Ding, M.; Shi, Z.; Du, B.; Wang, H.; Han, L. A signal de-noising method for a MEMS gyroscope based on improved VMD-WTD. Meas. Sci. Technol. 2021, 32, 095112. [Google Scholar] [CrossRef]
- Ding, J.; Xiao, D.; Li, X. Gear fault diagnosis based on genetic mutation particle swarm optimization VMD and probabilistic neural network algorithm. IEEE Access 2020, 8, 18456–18474. [Google Scholar] [CrossRef]
- Li, Y.; Wei, H.; Han, Z.; Huang, J.; Wang, W. Deep learning-based safety helmet detection in engineering management based on convolutional neural networks. Adv. Civ. Eng. 2020, 2020, 9703560. [Google Scholar] [CrossRef]
- Wang, S.C.; Wang, S.C. Artificial neural network. In Interdisciplinary Computing in Java Programming; Springer: Berlin/Heidelberg, Germany, 2003; pp. 81–100. [Google Scholar]
- Medsker, L.R.; Jain, L.C. Recurrent neural networks. In Design and Applications; CRC Press: Boca Raton, FL, USA, 2001; Volume 5, p. 2. [Google Scholar]
- Dutta, A.; Kumar, S.; Basu, M. A gated recurrent unit approach to bitcoin price prediction. J. Risk Financ. Manag. 2020, 13, 23. [Google Scholar] [CrossRef]
- He, X.; Montillet, J.P.; Fernandes, R.; Melbourne, T.I.; Jiang, W.; Huang, Z. Sea Level Rise Estimation on the Pacific Coast from Southern California to Vancouver Island. Remote Sens. 2022, 14, 4339. [Google Scholar] [CrossRef]
- Bruni, S.; Fenoglio, L.; Raicich, F.; Zerbini, S. On the consistency of coastal sea-level measurements in the Mediterranean Sea from tide gauges and satellite radar altimetry. J. Geod. 2022, 96, 41. [Google Scholar] [CrossRef]
- Widiputra, H.; Mailangkay, A.; Gautama, E. Multivariate cnn-lstm model for multiple parallel financial time-series prediction. Complexity 2021, 2021, 9903518. [Google Scholar] [CrossRef]
- Ban, W.; Shen, L.; Lu, F.; Liu, X.; Pan, Y. Research on Long-Term Tidal-Height-Prediction-Based Decomposition Algorithms and Machine Learning Models. Remote Sens. 2023, 15, 3045. [Google Scholar] [CrossRef]
- Tang, H.; Bhatti, U.A.; Li, J.; Marjan, S.; Baryalai, M.; Assam, M.; Ghadi, Y.Y.; Mohamed, H.G. A New Hybrid Forecasting Model Based on Dual Series Decomposition with Long-Term Short-Term Memory. Int. J. Intell. Syst. 2023, 2023, 9407104. [Google Scholar] [CrossRef]
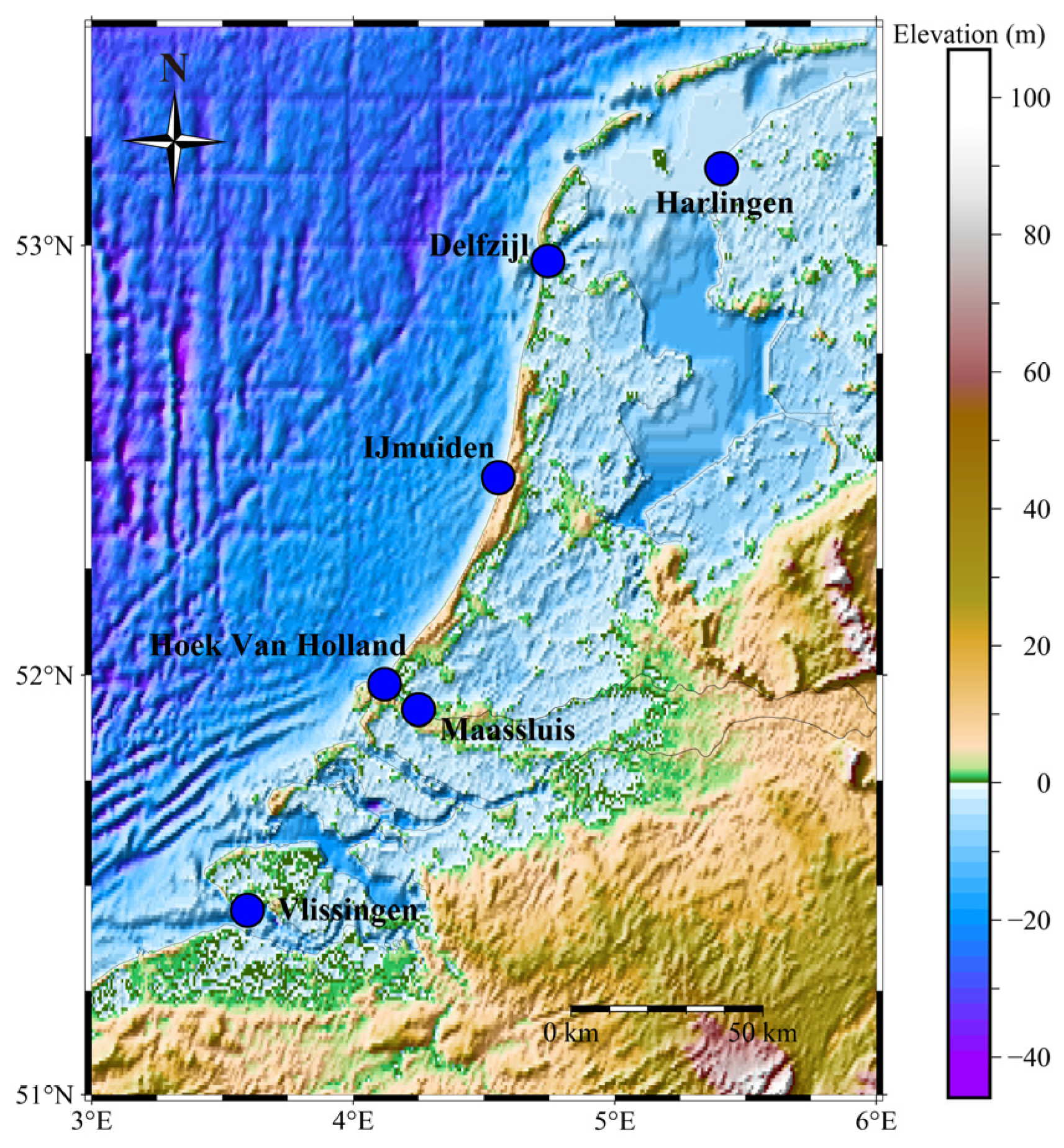
| Virtual Coastal Altimetry Station | ID | Longitude (°) | Latitude (°) | Deletion Rates (%) | Time Span (Years) |
|---|---|---|---|---|---|
| Maassluis | 09 | 4.25 | 51.92 | 0 | 1993.0–2020.9 |
| Vlissingen | 20 | 3.60 | 51.44 | 0 | 1993.0–2020.9 |
| Hoek Van Holland | 22 | 4.12 | 51.98 | 0 | 1993.0–2020.9 |
| Delfzijl | 23 | 4.75 | 52.96 | 0 | 1993.0–2020.9 |
| Harlingen | 25 | 5.41 | 53.18 | 0 | 1993.0–2020.9 |
| IJmuiden | 32 | 4.56 | 52.46 | 0 | 1993.0–2020.9 |
| Model | Series | RMSE (mm) | MAE (mm) | R2 |
|---|---|---|---|---|
| VMD3-LSTM | IMF1 | 0.5 | 0.4 | 1.0 |
| IMF2 | 0.9 | 0.6 | 1.0 | |
| IMF3 | 1.3 | 1.0 | 1.0 | |
| Residual | 125.6 | 91.0 | 0.3 | |
| All | 125.4 | 90.8 | 0.5 | |
| VMD4-LSTM | IMF1 | 0.5 | 0.4 | 1.0 |
| IMF2 | 0.6 | 0.5 | 1.0 | |
| IMF3 | 1.7 | 1.3 | 1.0 | |
| IMF4 | 1.0 | 0.8 | 1.0 | |
| Residual | 118.5 | 86.1 | 0.2 | |
| All | 118.3 | 85.8 | 0.6 | |
| VMD5-LSTM | IMF1 | 0.5 | 0.4 | 1.0 |
| IMF2 | 0.6 | 0.4 | 1.0 | |
| IMF3 | 0.8 | 0.6 | 1.0 | |
| IMF4 | 1.6 | 1.2 | 1.0 | |
| IMF5 | 0.7 | 0.5 | 1.0 | |
| Residual | 114.7 | 83.5 | 0.2 | |
| All | 114.3 | 83.1 | 0.6 | |
| VMD6-LSTM | IMF1 | 0.4 | 0.3 | 1.0 |
| IMF2 | 0.6 | 0.4 | 1.0 | |
| IMF3 | 0.8 | 0.6 | 1.0 | |
| IMF4 | 1.7 | 1.3 | 1.0 | |
| IMF5 | 1.2 | 0.9 | 1.0 | |
| IMF6 | 0.7 | 0.5 | 1.0 | |
| Residual | 115.1 | 85.3 | 0.2 | |
| All | 115.0 | 85.1 | 0.6 | |
| VMD7-LSTM | IMF1 | 0.5 | 0.4 | 1.0 |
| IMF2 | 0.6 | 0.4 | 1.0 | |
| IMF3 | 0.6 | 0.4 | 1.0 | |
| IMF4 | 0.7 | 0.6 | 1.0 | |
| IMF5 | 1.7 | 1.3 | 1.0 | |
| IMF6 | 1.0 | 0.7 | 1.0 | |
| IMF7 | 0.6 | 0.4 | 1.0 | |
| Residual | 111.8 | 83.8 | 0.0 | |
| All | 114.8 | 86.1 | 0.6 |
| Model | ANN | RNN | GRU | LSTM | Instructions |
|---|---|---|---|---|---|
| Training set | 7305 | 7305 | 7305 | 7305 | Training data for model training (1993–2012) |
| Validation set | 1095 | 1095 | 1095 | 1095 | Validation data for tuning the hyperparameters and preventing overfitting (2012–2015) |
| Test set | 1827 | 1827 | 1827 | 1827 | Testing data for evaluating the model’s performance (2015–2020) |
| Epochs | 50 | 50 | 50 | 50 | Number of iterations of the model |
| Learning rate | 0.001 | 0.001 | 0.001 | 0.001 | Hyperparameter controlling the step size of the updates of the model’s parameters |
| Input_size | 1 | 1 | 1 | 1 | Dimensionality of the input layer |
| Output_size | 1 | 1 | 1 | 1 | Dimensionality of the output layer |
| Hidden_size | 256 | 256 | 256 | 256 | Dimensionality of the hidden layer |
| Seq_len | 12 | 12 | 12 | 12 | Length of each sliding data window |
| Batch_size | 16 | 16 | 16 | 16 | Batch size for one-time input in the time series data |
| Model | Series | RMSE (mm) | MAE (mm) | R2 |
|---|---|---|---|---|
| VMD-LSTM | IMF1 | 0.5 | 0.4 | 1.0 |
| IMF2 | 0.6 | 0.4 | 1.0 | |
| IMF3 | 0.8 | 0.6 | 1.0 | |
| IMF4 | 1.6 | 1.2 | 1.0 | |
| IMF5 | 0.7 | 0.5 | 1.0 | |
| Residual | 114.7 | 83.5 | 0.2 | |
| All | 114.3 | 83.1 | 0.6 | |
| EMD-LSTM | IMF1 | 76.6 | 58.4 | 0.2 |
| IMF2 | 34.3 | 23.5 | 0.8 | |
| IMF3 | 7.3 | 4.8 | 1.0 | |
| IMF4 | 1.1 | 0.6 | 1.0 | |
| IMF5 | 0.4 | 0.3 | 1.0 | |
| Residual | 0.8 | 0.5 | 1.0 | |
| All | 82.4 | 61.4 | 0.8 | |
| EEMD-LSTM | IMF1 | 63.0 | 46.0 | 0.3 |
| IMF2 | 17.6 | 11.9 | 0.9 | |
| IMF3 | 2.7 | 1.9 | 1.0 | |
| IMF4 | 0.5 | 0.3 | 1.0 | |
| IMF5 | 0.3 | 0.2 | 1.0 | |
| Residual | 12.2 | 9.7 | 1.0 | |
| All | 65.0 | 47.2 | 0.9 | |
| CEEMDAN-LSTM | IMF1 | 76.9 | 58.1 | 0.2 |
| IMF2 | 33.5 | 23.1 | 0.8 | |
| IMF3 | 6.9 | 4.5 | 1.0 | |
| IMF4 | 1.1 | 0.7 | 1.0 | |
| IMF5 | 0.4 | 0.3 | 1.0 | |
| Residual | 0.4 | 0.3 | 1.0 | |
| All | 82.8 | 61.2 | 0.8 |
| Virtual Coast Altimetry Station | Evaluation Index | Prediction Model | Improvement Ratio (I) | |||
|---|---|---|---|---|---|---|
| VMD-LSTM | EEMD-LSTM | VMD-EEMD-LSTM | I1 (%) | I2 (%) | ||
| Maassluis | RMSE (mm) | 114.3 | 65.0 | 47.8 | 58.2 | 26.5 |
| Vlissingen | 110.3 | 59.4 | 46.0 | 58.3 | 22.5 | |
| Hoek Van Holland | 109.5 | 67.1 | 46.3 | 57.7 | 31.0 | |
| Delfzijl | 113.9 | 60.6 | 46.9 | 58.9 | 22.6 | |
| Harlingen | 122.7 | 66.5 | 48.4 | 60.5 | 27.1 | |
| IJmuiden | 115.4 | 70.3 | 47.8 | 58.6 | 32.0 | |
| Maassluis | MAE (mm) | 83.1 | 47.2 | 33.6 | 59.6 | 28.9 |
| Vlissingen | 80.3 | 42.0 | 32.7 | 59.3 | 22.2 | |
| Hoek Van Holland | 79.5 | 47.9 | 32.6 | 59.1 | 32.0 | |
| Delfzijl | 83.1 | 43.0 | 33.2 | 60.0 | 22.8 | |
| Harlingen | 90.0 | 48.0 | 34.4 | 61.8 | 28.3 | |
| IJmuiden | 83.8 | 50.7 | 33.6 | 60.0 | 33.8 | |
| Maassluis | R2 | 0.6 | 0.9 | 0.9 | −52.5 | −6.6 |
| Vlissingen | 0.6 | 0.9 | 0.9 | −54.0 | −5.2 | |
| Hoek Van Holland | 0.6 | 0.9 | 0.9 | −52.5 | −9.0 | |
| Delfzijl | 0.6 | 0.9 | 0.9 | −46.6 | −4.5 | |
| Harlingen | 0.7 | 0.9 | 1.0 | −44.2 | −5.3 | |
| IJmuiden | 0.6 | 0.9 | 0.9 | −49.3 | −8.6 | |
| Virtual Coastal Altimetry Station | VTG | Co-GNSS | Distance (km) | VLM at Co-GNSS | VTG + VLM | VSSH | |VTG + VLM − VSSH| |
|---|---|---|---|---|---|---|---|
| Maassluis | 2.26 | dlf1 | 11.90 | −0.47 | 1.79 | 2.20 | 0.41 |
| Vlissingen | 2.97 | vlis | 0.40 | −0.80 | 2.17 | 2.10 | 0.07 |
| Hoek Van Holland | 2.43 | hhol | 10.70 | −0.45 | 1.97 | 2.32 | 0.34 |
| Delfzijl | 2.08 | txe2 | 11.30 | −0.33 | 1.75 | 2.42 | 0.67 |
| Harlingen | 3.56 | ters | 24.00 | −1.11 | 2.45 | 2.34 | 0.11 |
| IJmuiden | 1.98 | ijmu | 0.40 | −1.66 | 0.32 | 2.38 | 2.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Lu, T.; Huang, J.; He, X.; Sun, X. An Improved VMD–EEMD–LSTM Time Series Hybrid Prediction Model for Sea Surface Height Derived from Satellite Altimetry Data. J. Mar. Sci. Eng. 2023, 11, 2386. https://doi.org/10.3390/jmse11122386
Chen H, Lu T, Huang J, He X, Sun X. An Improved VMD–EEMD–LSTM Time Series Hybrid Prediction Model for Sea Surface Height Derived from Satellite Altimetry Data. Journal of Marine Science and Engineering. 2023; 11(12):2386. https://doi.org/10.3390/jmse11122386
Chicago/Turabian StyleChen, Hongkang, Tieding Lu, Jiahui Huang, Xiaoxing He, and Xiwen Sun. 2023. "An Improved VMD–EEMD–LSTM Time Series Hybrid Prediction Model for Sea Surface Height Derived from Satellite Altimetry Data" Journal of Marine Science and Engineering 11, no. 12: 2386. https://doi.org/10.3390/jmse11122386
APA StyleChen, H., Lu, T., Huang, J., He, X., & Sun, X. (2023). An Improved VMD–EEMD–LSTM Time Series Hybrid Prediction Model for Sea Surface Height Derived from Satellite Altimetry Data. Journal of Marine Science and Engineering, 11(12), 2386. https://doi.org/10.3390/jmse11122386








