Numerical Study on Wave–Ice Floe Interaction in Regular Waves
Abstract
1. Introduction
2. Numerical Simulation
2.1. General Governing Equations
2.2. Structured Arbitrary Lagrangian–Eulerian (S-ALE) Method
2.3. Penalty Function Method
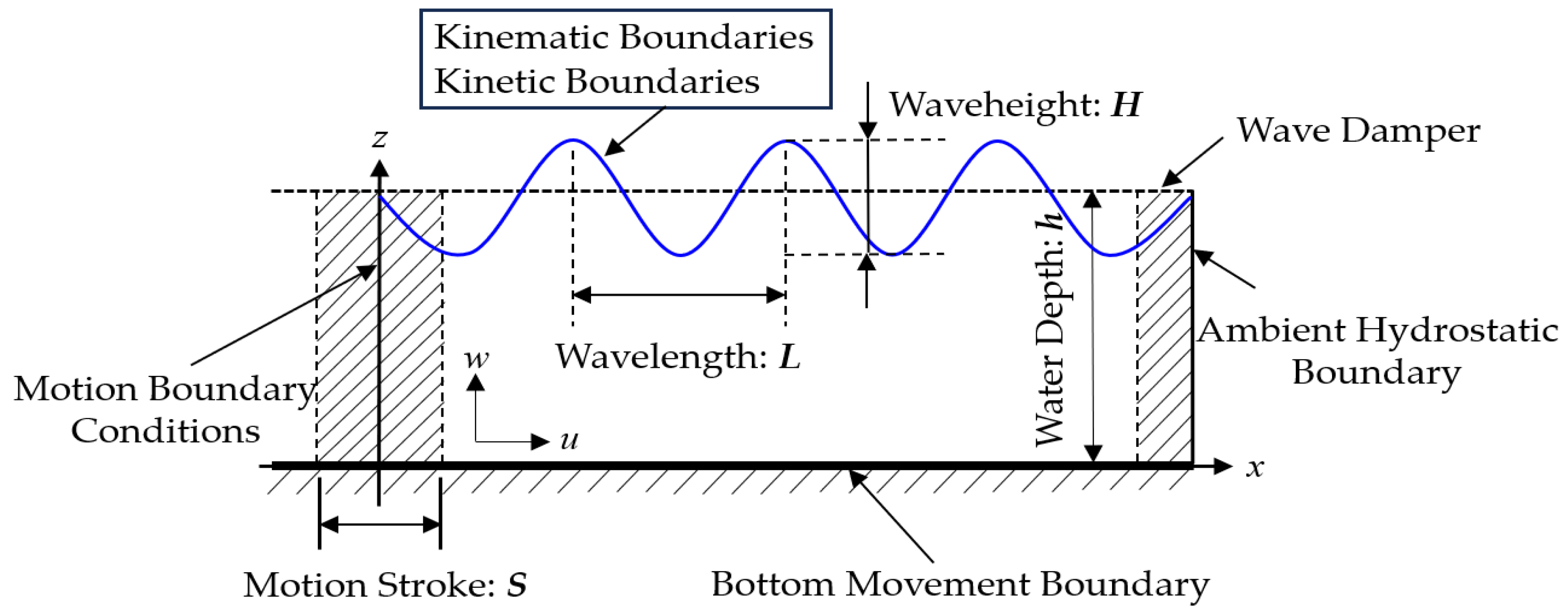
2.4. Numerical Wave Tank
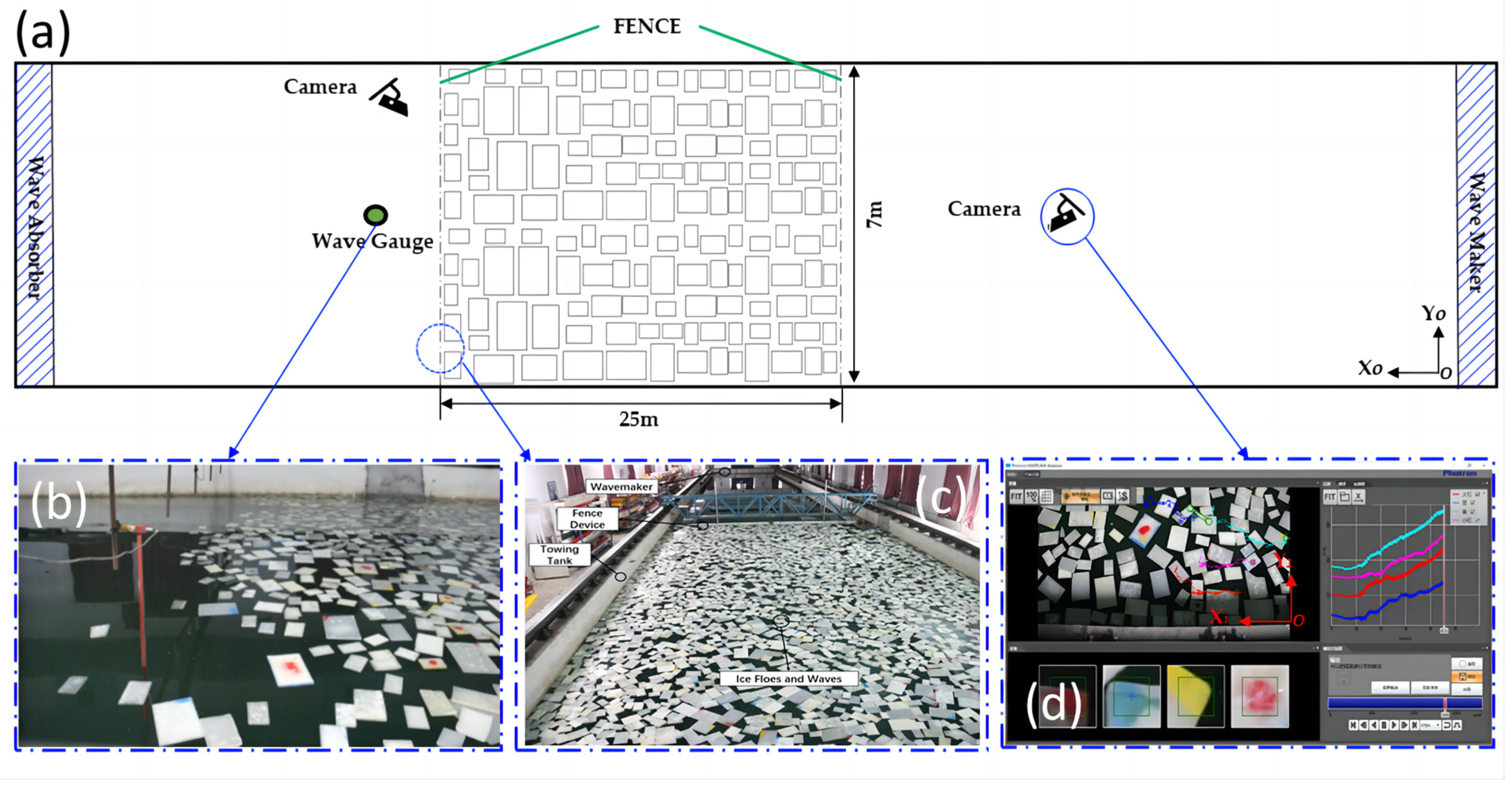
3. Description of Wave–Ice Floe Interaction Model Test
4. Results and Discussion
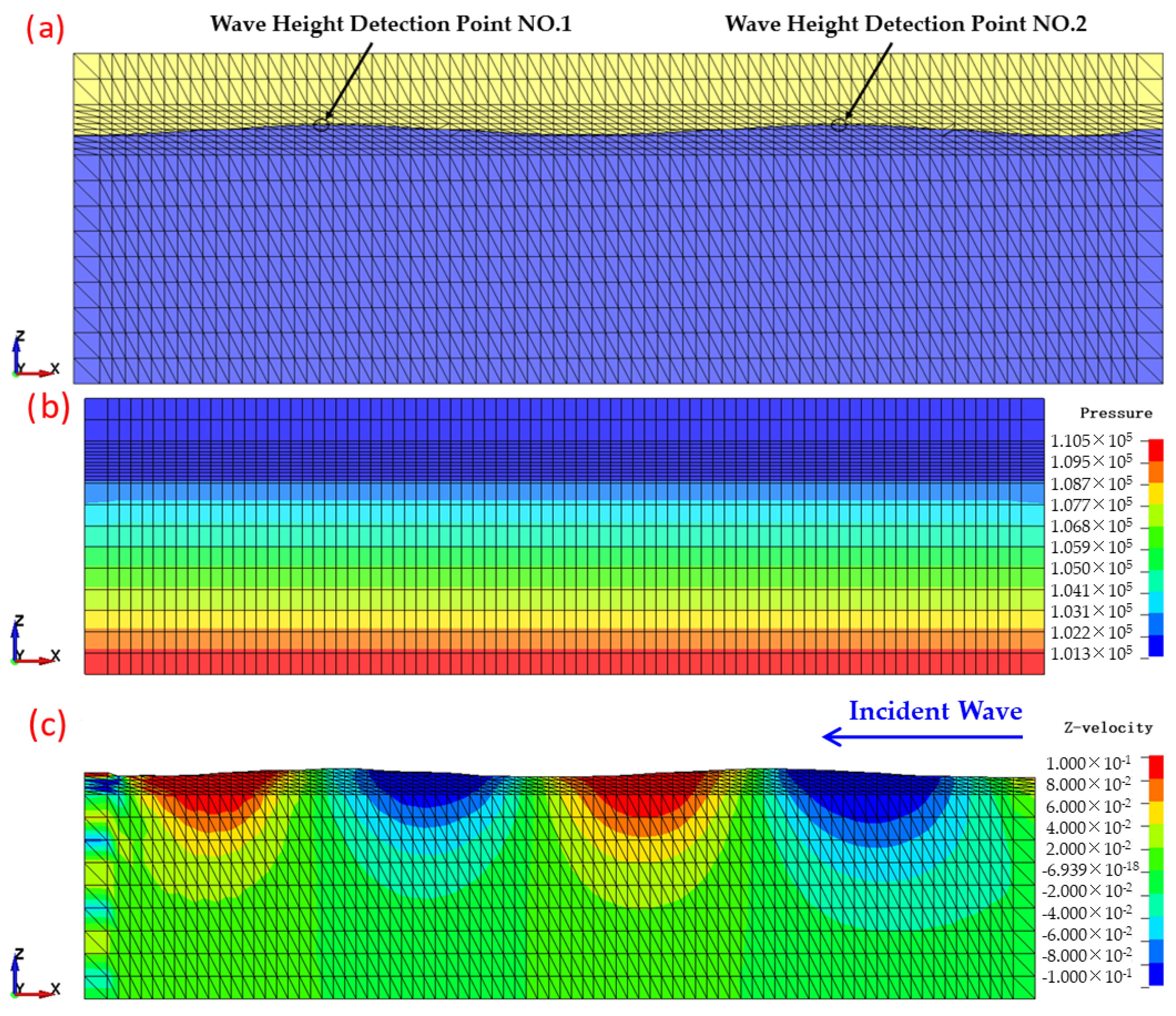
4.1. Wave Accuracy Verification
4.2. Numerical Modeling of Ice Floe–Wave Interaction
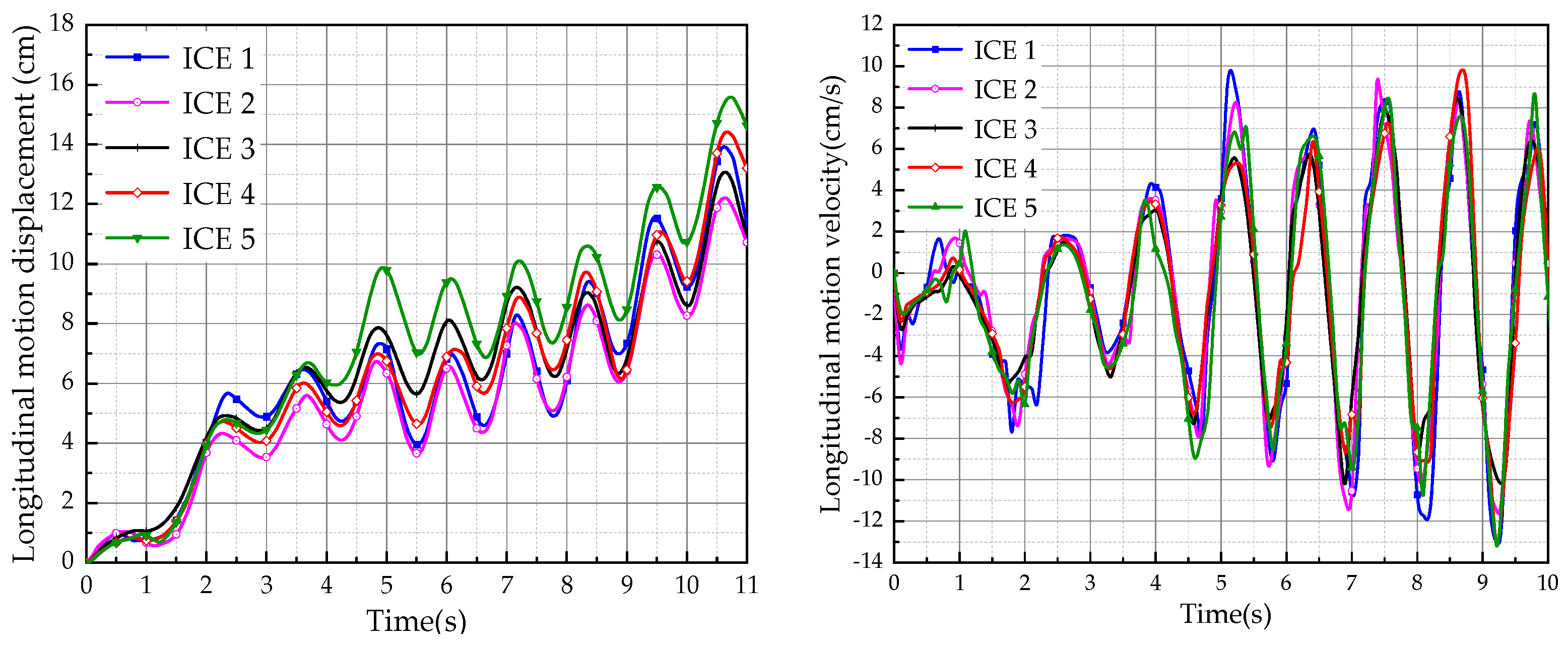
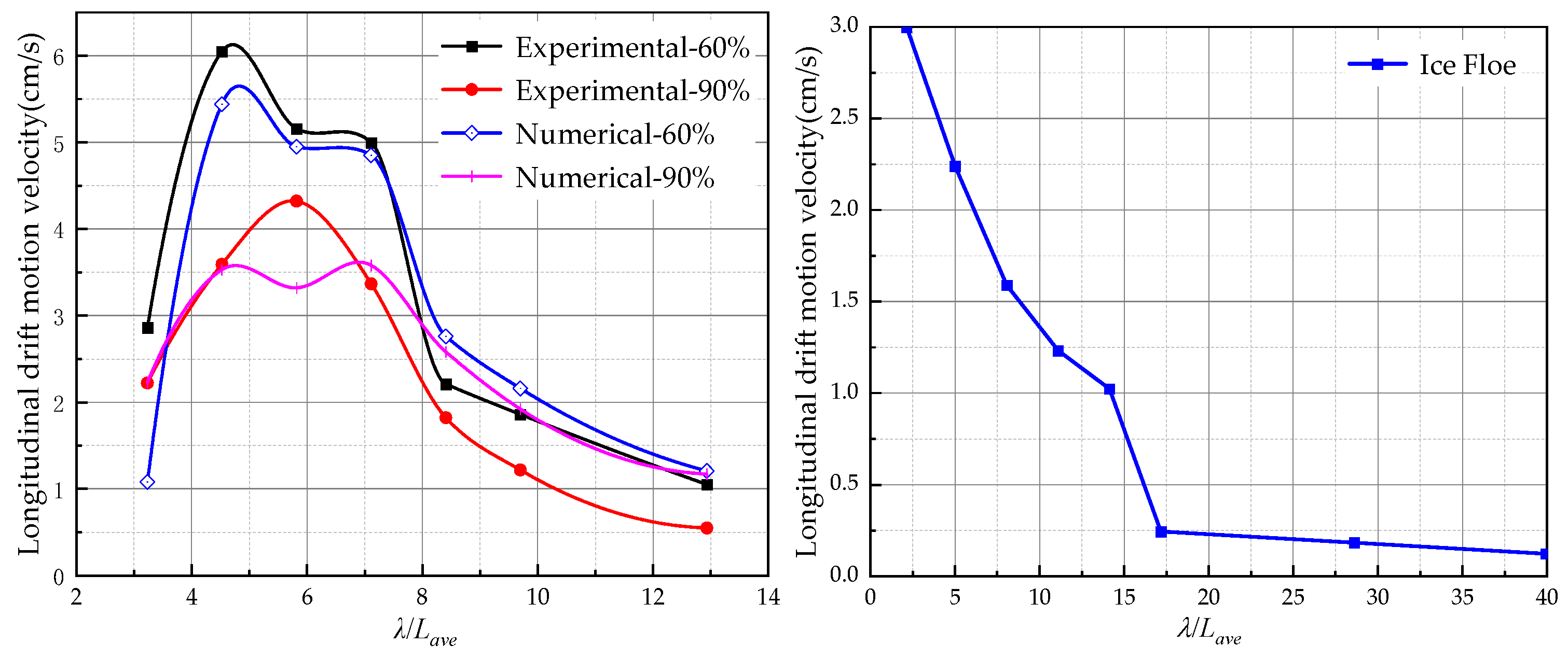
4.3. The Longitudinal Motion Response of Ice Floes under the Influence of Wave Action
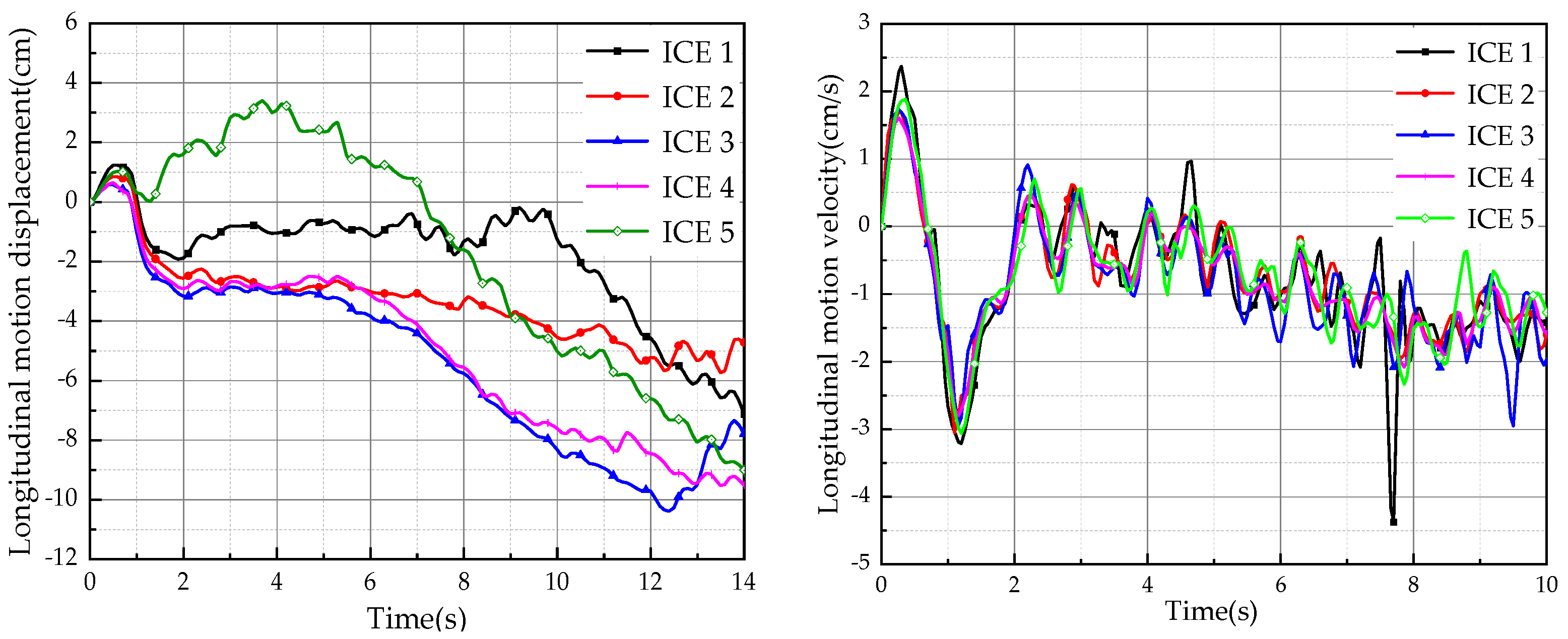
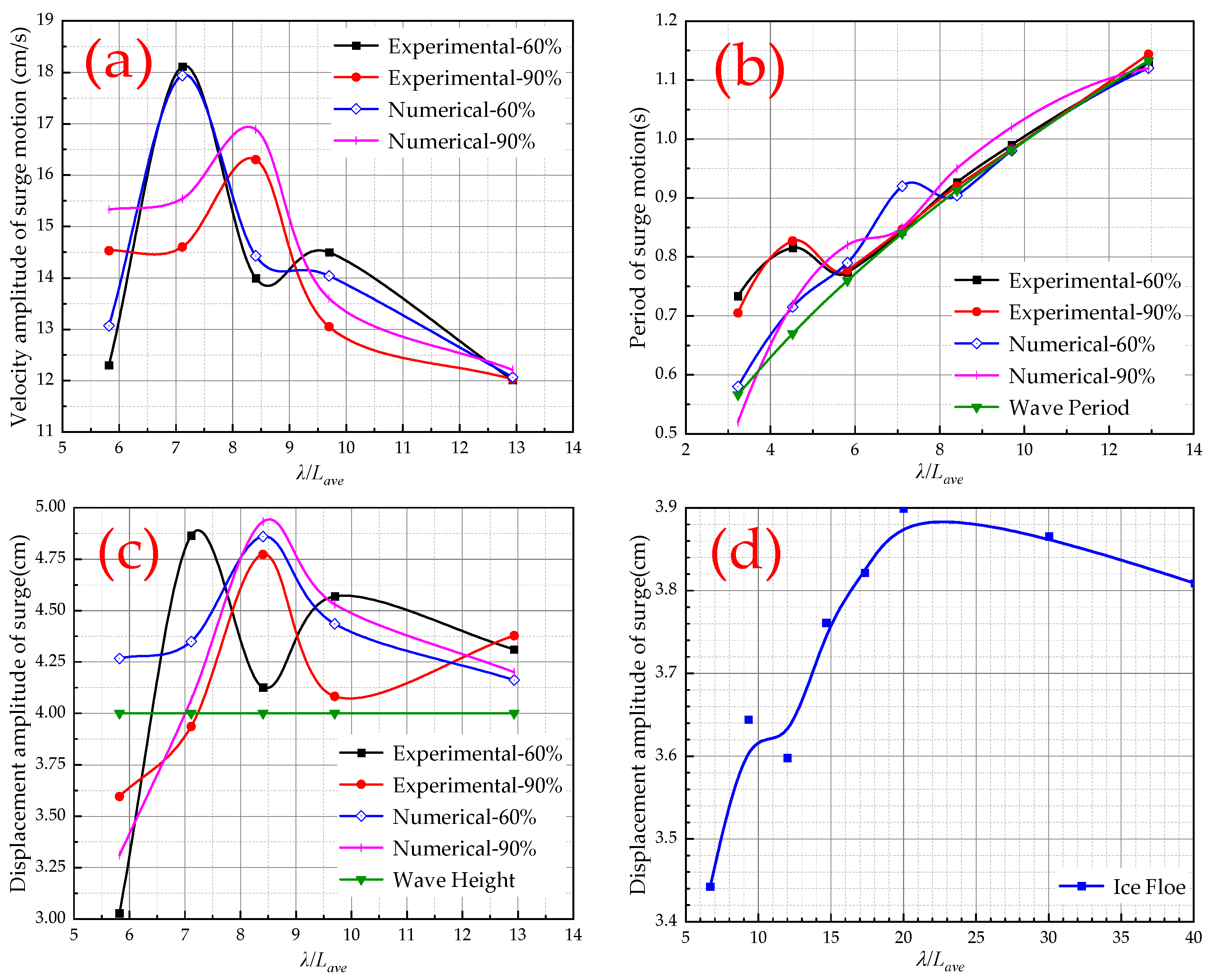
4.4. The Surge Response of Ice Floes under the Influence of Wave Action
5. Conclusions
- (1)
- The longitudinal motion response parameters of ice floes of varying sizes exhibit no consistent and substantial disparities. The longitudinal motion of ice floes in waves manifests in two distinct states, namely irregular and regular, contingent upon the wavelength. Ice floes predominantly engage in irregular motion within the short-wave range, while assuming a regular motion akin to that of isolated ice floes within the long-wave range.
- (2)
- In the context of the irregular motion of ice floes within the short-wave range, it is observed that the mean speed of the longitudinal drift motion of the ice floes exhibits a rapid increase as the wavelength increases. Additionally, the period of the longitudinal surge of the ice floes is slightly greater than that of the wave.
- (3)
- In the long-wave range, the ice floes exhibit regular motion. As the wavelength increases, the mean velocity of the longitudinal drift motion of the ice floes decreases and eventually approaches zero. Conversely, the speed and displacement amplitude of the longitudinal surge motion of the ice floes increase rapidly, surpassing the wave height, and subsequently decrease to approach the wave height as the wavelength increases. Additionally, the response period of the longitudinal surge of the ice floes coincides with the wave period.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Size of Ice Floe (cm × cm) | Amplitude of Surge Speed (cm/s) | Longitudinal Drift Motion Velocity (cm/s) | Amplitude of Surge Velocity (cm/s) | Surge Period (s) |
|---|---|---|---|---|
| 8 × 12 | 12.15 | 0.791 | 12.15 | 1.14 |
| 14 × 21 | 11.87 | 1.153 | 11.87 | 1.13 |
| 16 × 24 | 11.99 | 1.009 | 11.99 | 1.138 |
| 18 × 27 | 12.06 | 1.250 | 12.06 | 1.1 |
| Wavelength (m) | Ice Number | Amplitude of Surge Speed (cm/s) | Mean Value of Longitudinal Drift Motion Velocity (cm/s) | Mean Value of Amplitude of Surge Velocity (cm/s) | Mean Value of Surge Period (s) |
|---|---|---|---|---|---|
| 0.5 | 1 | 4.55 | 1.08 | 4.61 | 0.58 |
| 2 | 7.35 | ||||
| 3 | 4.71 | ||||
| 4 | 2.63 | ||||
| 5 | 3.79 | ||||
| 0.7 | 1 | 10.48 | 5.44 | 10.25 | 0.715 |
| 2 | 8.04 | ||||
| 3 | 10.92 | ||||
| 4 | 10.7 | ||||
| 5 | 11.1 | ||||
| 0.9 | 1 | 15.17 | 4.95 | 13.07 | 0.79 |
| 2 | 9.24 | ||||
| 3 | 13.13 | ||||
| 4 | 13.58 | ||||
| 5 | 14.24 | ||||
| 1.1 | 1 | 17.05 | 4.85 | 17.94 | 0.92 |
| 2 | 16.34 | ||||
| 3 | 18.56 | ||||
| 4 | 17.88 | ||||
| 5 | 19.86 | ||||
| 1.3 | 1 | 12. 9 | 2.76 | 14.43 | 0.904 |
| 2 | 16.41 | ||||
| 3 | 14.83 | ||||
| 4 | 14.21 | ||||
| 5 | 13.82 | ||||
| 1.5 | 1 | 14.58 | 2.16 | 14.04 | 0.98 |
| 2 | 13.05 | ||||
| 3 | 13.86 | ||||
| 4 | 14.49 | ||||
| 5 | 14.22 | ||||
| 2.0 | 1 | 13.12 | 1.207 | 12.07 | 1.12 |
| 2 | 11.96 | ||||
| 3 | 12.02 | ||||
| 4 | 12.44 | ||||
| 5 | 11.91 |
| Wavelength (m) | Ice Number | Amplitude of Surge Speed (cm/s) | Mean Value of Longitudinal Drift Motion Velocity (cm/s) | Mean Value of Amplitude of Surge Velocity (cm/s) | Mean Value of Surge Period (s) |
|---|---|---|---|---|---|
| 0.5 | 1 | 2.48 | 2.23 | 3.12 | 0.52 |
| 2 | 3.13 | ||||
| 3 | 3.99 | ||||
| 4 | 3.46 | ||||
| 5 | 2.52 | ||||
| 0.7 | 1 | 6.38 | 3.53 | 7.69 | 0.72 |
| 2 | 8.9 | ||||
| 3 | 8.76 | ||||
| 4 | 9.3 | ||||
| 5 | 5.09 | ||||
| 0.9 | 1 | 15.13 | 3.32 | 15.33 | 0.82 |
| 2 | 15.28 | ||||
| 3 | 16.23 | ||||
| 4 | 15.1 | ||||
| 5 | 14.9 | ||||
| 1.1 | 1 | 14.91 | 3.58 | 15.54 | 0.85 |
| 2 | 14.43 | ||||
| 3 | 14.07 | ||||
| 4 | 18.46 | ||||
| 5 | 15.84 | ||||
| 1.3 | 1 | 14.82 | 2.58 | 16.89 | 0.95 |
| 2 | 16.76 | ||||
| 3 | 19.2 | ||||
| 4 | 16.25 | ||||
| 5 | 17.46 | ||||
| 1.5 | 1 | 13.66 | 1.92 | 13.6 | 1.02 |
| 2 | 13.4 | ||||
| 3 | 12.61 | ||||
| 4 | 15.58 | ||||
| 5 | 13.19 | ||||
| 2.0 | 1 | 12.06 | 1.17 | 13.21 | 1.12 |
| 2 | 13.19 | ||||
| 3 | 13.03 | ||||
| 4 | 13.42 | ||||
| 5 | 14.36 |
References
- Squire, V.A.; Dugan, J.P.; Wadhams, P.; Rottier, P.J.; Liu, A.K. Of ocean waves and sea ice. Annu. Rev. Fluid Mech. 1995, 27, 115–168. [Google Scholar] [CrossRef]
- Squire, V.A. Of ocean waves and sea-ice revisited. Cold Reg. Sci. Technol. 2007, 49, 110–133. [Google Scholar] [CrossRef]
- Squire, V.A. Ocean wave interactions with sea ice: A reappraisal. Annu. Rev. Fluid Mech. 2020, 52, 37–60. [Google Scholar] [CrossRef]
- Toyota, T.; Kohout, A.; Fraser, A.D. Formation processes of sea ice floe size distribution in the interior pack and its relationship to the marginal ice zone off East Antarctica. Deep Sea Res. Part II Top. Stud. Oceanogr. 2016, 131, 28–40. [Google Scholar] [CrossRef]
- Squire, V.A. A prognosticative synopsis of contemporary marginal ice zone research. Philos. Trans. Royal Soc. A 2022, 380, 20220094. [Google Scholar] [CrossRef]
- Bennetts, L.G.; Bitz, C.M.; Feltham, D.L.; Kohout, A.L.; Meylan, M.H. Theory, modelling and observations of marginal ice zone dynamics: Multidisciplinary perspectives and outlooks. Philos. Trans. Royal Soc. A 2022, 380, 20210265. [Google Scholar] [CrossRef]
- Squire, V.A. Marginal ice zone dynamics. Philos. Trans. Royal Soc. A 2022, 380, 20210266. [Google Scholar] [CrossRef]
- Linton, C.M. Towards a three-dimensional model of wave–ice interaction in the marginal ice zone. J. Fluid Mech. 2010, 662, 1–4. [Google Scholar] [CrossRef]
- Zeng, L.; Xiong, H.; Wu, Q. Review on the interaction between sea ice and waves/currents. J. Theor. Appl. Mech. 2021, 53, 641–654. (In Chinese) [Google Scholar]
- Meylan, M.H.; Squire, V.A. The response of ice floes to ocean waves. J. Geophys. Res. 1994, 99, 891–900. [Google Scholar] [CrossRef]
- Meylan, M.H. Wave response of an ice floe of arbitrary geometry. J. Geophys. Res. Oceans 2002, 107, 3005. [Google Scholar] [CrossRef]
- Wang, C.D.; Meylan, M.H. A higher-order-coupled boundary element and finite element method for the wave forcing of a floating elastic plate. J. Fluids Struct. 2004, 19, 557–572. [Google Scholar] [CrossRef]
- Bennetts, L.G.; Williams, T.D. Wave scattering by ice floes and polynyas of arbitrary shape. J. Fluid Mech. 2010, 662, 5–35. [Google Scholar] [CrossRef]
- Peter, M.A.; Meylan, M.H. Water-wave scattering by vast fields of bodies. SIAM J. Appl. Math. 2010, 70, 1567–1586. [Google Scholar] [CrossRef][Green Version]
- Bennetts, L.G.; Peter, M.A.; Squire, V.A.; Meylan, M.H. A three-dimensional model of wave attenuation in the marginal ice zone. J. Geophys. Res. Oceans 2010, 115. [Google Scholar] [CrossRef]
- Meylan, M.H.; Bennetts, L.G. Three-dimensional time-domain scattering of waves in the marginal ice zone. Philos. Trans. Royal Soc. A 2018, 376, 20170334. [Google Scholar] [CrossRef]
- Guyenne, P.; Părău, E.I. Numerical study of solitary wave attenuation in a fragmented ice sheet. Phys. Rev. Fluid 2017, 2, 034002. [Google Scholar] [CrossRef]
- Xu, B.; Guyenne, P. Nonlinear simulation of wave group attenuation due to scattering in broken floe fields. Ocean Model 2023, 181, 102139. [Google Scholar] [CrossRef]
- Behera, H.; Ng, C.O.; Sahoo, T. Oblique wave scattering by a floating elastic plate over a porous bed in single and two-layer fluid systems. Ocean Eng. 2018, 159, 280–294. [Google Scholar] [CrossRef]
- Hossain, M.; Tsai, C.; Behera, H. Instability mechanism of shear-layered fluid in the presence of a floating elastic plate. Phys. Fluids 2023, 35, 027102. [Google Scholar] [CrossRef]
- Xu, Z.; Tartakovsky, A.M.; Pan, W. Discrete-element model for the interaction between ocean waves and sea ice. Phys. Rev. E 2012, 85, 016703. [Google Scholar] [CrossRef] [PubMed]
- Bai, W.; Zhang, T.; McGovern, D.J. Response of small sea ice floes in regular waves: A comparison of numerical and experimental results. Ocean Eng. 2017, 129, 495–506. [Google Scholar] [CrossRef]
- Huang, L.; Ren, K.; Li, M.; Tuković, Ž.; Cardiff, P.; Thomas, G. Fluid-structure interaction of a large ice sheet in waves. Ocean Eng. 2019, 182, 102–111. [Google Scholar] [CrossRef]
- Wu, T.; Luo, W.; Jiang, D.; Deng, R.; Huang, S. Numerical study on wave-ice interaction in the marginal ice zone. J. Mar. Sci. Eng. 2020, 9, 4. [Google Scholar] [CrossRef]
- Marquart, R.; Bogaers, A.; Skatulla, S.; Alberello, A.; Toffoli, A.; Schwarz, C.; Vichi, M. A computational fluid dynamics model for the small-scale dynamics of wave, ice floe and interstitial grease ice interaction. Fluids 2021, 6, 176. [Google Scholar] [CrossRef]
- Behnen, J.; von Bock und Polach, R.U.F.; Klein, M.; Ehlers, S. Hydrodynamic and mechanic response of a floating flexible ice floe in regular waves with the ICFD method. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Hamburg, Germany, 5–10 June 2022; Volume 85918, p. V006T07A008. [Google Scholar]
- Zhang, N.; Ma, Q.; Zheng, X.; Yan, S. A two-way coupling method for simulating wave-induced breakup of ice floes based on SPH. J. Comput. Phys. 2023, 488, 112185. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, F.; Mikkola, T.; Kujala, P.; Hirdaris, S. A Boundary Element Method for the Prediction of Hydrodynamic Ship–Ice–Wave Interactions in Regular Waves. J. Offshore Mech. Arct. Eng. 2023, 145, 061601. [Google Scholar] [CrossRef]
- Junior, R.A.A.; Mellado-Cusicahua, A.; Shakibaeinia, A.; Cheng, L.Y. A fully Lagrangian DEM-MPS mesh-free model for ice-wave dynamics. Cold Reg. Sci. Technol. 2021, 186, 103266. [Google Scholar]
- Huang, G.; Law, A.W.K.; Huang, Z. Wave-induced drift of small floating objects in regular waves. Ocean Eng. 2011, 38, 712–718. [Google Scholar] [CrossRef]
- McGovern, D.J.; Bai, W. Experimental study on kinematics of sea ice floes in regular waves. Cold Reg. Sci. Technol. 2014, 103, 15–30. [Google Scholar] [CrossRef]
- Bennetts, L.G.; Alberello, A.; Meylan, M.H.; Cavaliere, C.; Babanin, A.V.; Toffoli, A. An idealised experimental model of ocean surface wave transmission by an ice floe. Ocean Model 2015, 96, 85–92. [Google Scholar] [CrossRef]
- Meylan, M.H.; Bennetts, L.G.; Cavaliere, C.; Alberello, A.; Toffoli, A. Experimental and theoretical models of wave-induced flexure of a sea ice floe. Phys. Fluids 2015, 27, 041704. [Google Scholar] [CrossRef]
- Huang, L.; Lu, W.; Yang, J.; Dong, Q. Experimental study on surface waves around a novel model of ice floe. Cold Reg. Sci. Technol. 2022, 193, 103380. [Google Scholar] [CrossRef]
- Toffoli, A.; Pitt, J.P.A.; Alberello, A.; Bennetts, L.G. Modelling attenuation of irregular wave fields by artificial ice floes in the laboratory. Philos. Trans. Royal Soc. A 2022, 380, 20210255. [Google Scholar] [CrossRef] [PubMed]
- Yiew, L.J.; Bennetts, L.G.; Meylan, M.H.; French, B.J.; Thomas, G.A. Hydrodynamic responses of a thin floating disk to regular waves. Ocean Model 2016, 97, 52–64. [Google Scholar] [CrossRef]
- Wang, C.; Song, M.; Guo, C.; Wang, S.; Tian, T.; Luo, W. Experimental study of sea ice motion in waves. J. Cold Reg. Eng. 2020, 34, 04020010. [Google Scholar] [CrossRef]
- Bennetts, L.G.; Williams, T.D. Water wave transmission by an array of floating discs. Proc. Math. Phys. Eng. Sci. 2015, 471, 20140698. [Google Scholar] [CrossRef]
- Park, S.B.; Shin, S.Y.; Shin, D.G.; Park, H.; Jung, K.H.; Suh, S.B.; Lee, J.; Lee, S.J.; Kim, H.S. Experimental study of wave transmission and drift velocity using freely floating synthetic ice floes. Ocean Eng. 2022, 251, 111058. [Google Scholar] [CrossRef]
- Hallquist, J.O. LS-DYNA Keyword User’s Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2007; Volume 970, pp. 299–800. [Google Scholar]
- Chen, H. LS-DYNA structured ALE (S-ALE) solver. In Proceedings of the Fourteenth International LS-DYNA User Conference, Detroit, MI, USA, 12–14 June 2016. [Google Scholar]
- Wang, C.; Wang, J.; Wang, C.; Guo, C.; Zhu, G. Research on vertical movement of cylindrical structure out of water and breaking through ice layer based on S-ALE method. J. Theor. Appl. Mech. 2021, 53, 3110–3123. (In Chinese) [Google Scholar]
- Kim, M.C.; Lee, S.K.; Lee, W.J.; Wang, J.Y. Numerical and experimental investigation of the resistance performance of an icebreaking cargo vessel in pack ice conditions. Int. J. Nav. Archit. Ocean Eng. 2013, 5, 116–131. [Google Scholar] [CrossRef]
- Ye, X.; Fan, W.; Sha, Y.; Hua, X.; Wu, Q.; Ren, W. Fluid-structure interaction analysis of oblique ship-bridge collisions. Eng. Struct. 2023, 274, 115129. [Google Scholar] [CrossRef]
- Airy, G.B. On tides and Waves. In Encyclopedia Metropolitana: Mixed Sciences; Rose, H.J., Ed.; John Joseph Griffin & Co.: London, UK, 1842; Volume 3, p. 1841. [Google Scholar]
- Wang, C.; Wang, J.; Wang, C.; Song, M. Experimental study on longitudinal motion law of ice floes under wave action. J. Huazhong Univ. Sci. Technol. 2022, 50, 143–148. (In Chinese) [Google Scholar]
- Toyota, T.; Haas, C.; Tamura, T. Size distribution and shape properties of relatively small sea-ice floes in the Antarctic marginal ice zone in late winter. Deep Sea Res. Part II Top. Stud. Oceanogr. 2011, 58, 1182–1193. [Google Scholar] [CrossRef]
- Wang, S. Experimental Research on the Resistance Performance of Ice-Going Ships in Marginal Ice Zones; Harbin Engineering: Harbin, China, 2017. (In Chinese) [Google Scholar]

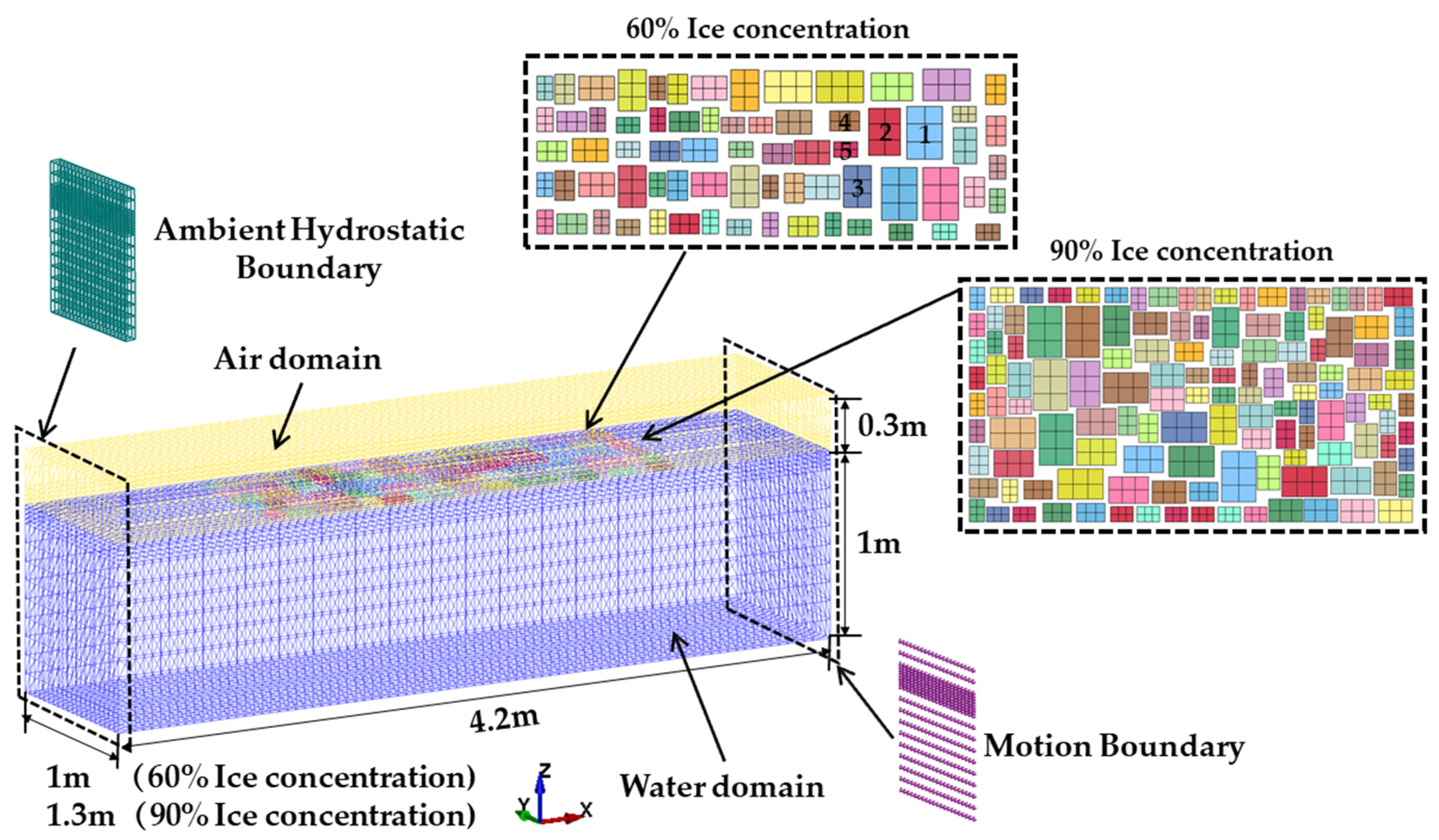
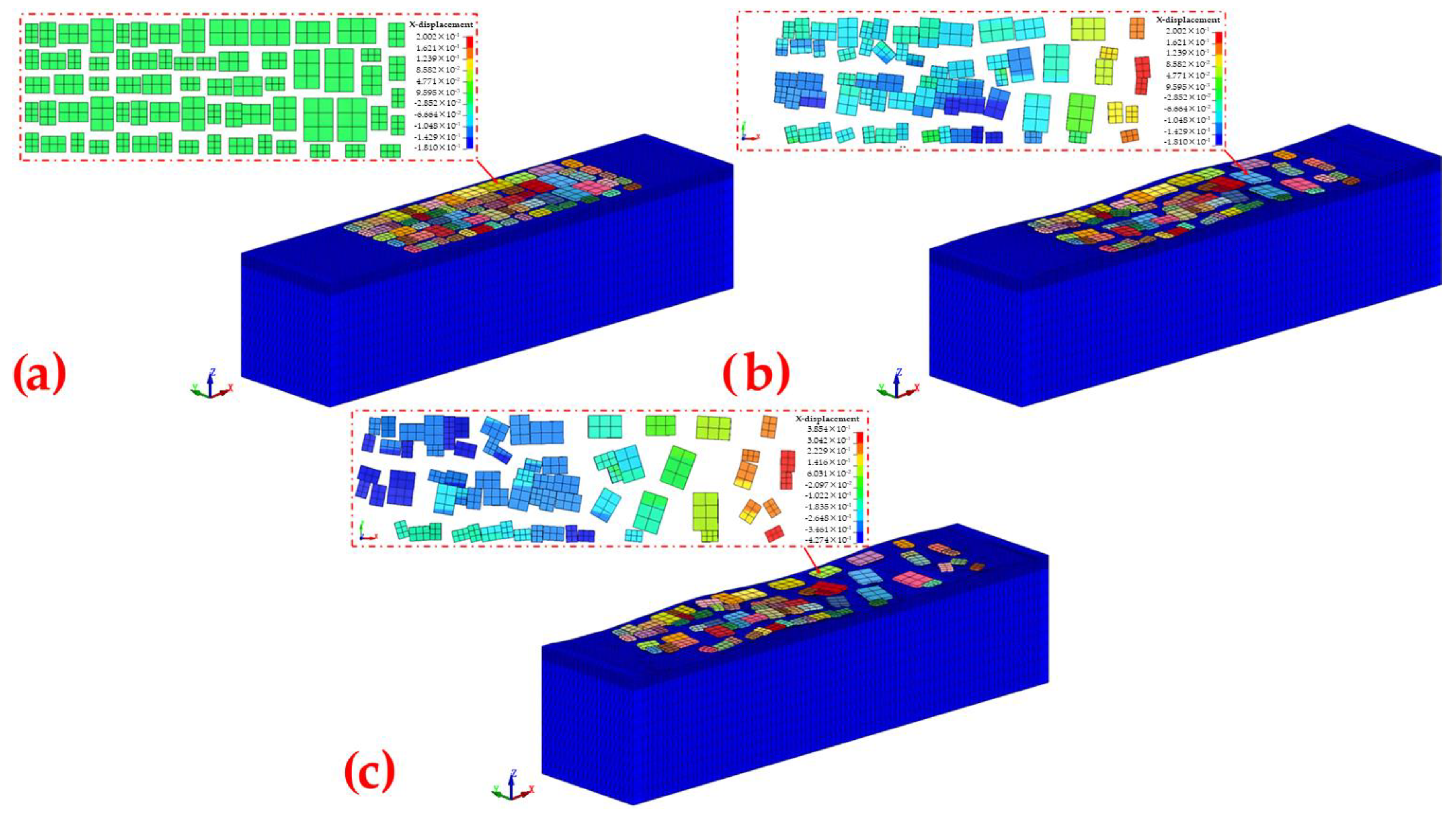
| Size (cm × cm) | Average Calliper Diameter (m) | Thickness (m) | Amount [Pieces] | ||
|---|---|---|---|---|---|
| Model Scale | Full Scale | Model Scale | Full Scale | ||
| 12 × 8 | 0.12 | 5.41 | 0.02 | 0.9 | 4245 |
| 15 × 10 | 0.15 | 6.76 | 2151 | ||
| 18 × 12 | 0.18 | 8.11 | 1225 | ||
| 21 × 14 | 0.21 | 9.46 | 757 | ||
| 24 × 16 | 0.24 | 10.82 | 498 | ||
| 27 × 18 | 0.27 | 12.17 | 343 | ||
| Total | 9219 | ||||
| Name | Air | Water |
|---|---|---|
| Material type | MAT_NULL | MAT_NULL |
| Unit type | SOLID164 | SOLID164 |
| Equation of state | EOS_LINEARPOLYNOMIAL | EOS_LINEARPOLYNOMIAL |
| Density(kg/m3) | 1.1845 | 998.21 |
| Cutoff pressure(Pa) | −10 | −100 |
| Viscosity coefficient(N·s·m−2) | 1.8444 × 10−5 | 8.684 × 10−4 |
| Ice Concentration | Wave Height (m) | Wavelength (m) |
|---|---|---|
| 60%/90% | 0.04 | 0.5 |
| 0.7 | ||
| 0.9 | ||
| 1.1 | ||
| 1.3 | ||
| 1.5 | ||
| 2.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Wang, J.; Wang, C.; Wang, Z.; Zhang, Y. Numerical Study on Wave–Ice Floe Interaction in Regular Waves. J. Mar. Sci. Eng. 2023, 11, 2235. https://doi.org/10.3390/jmse11122235
Wang C, Wang J, Wang C, Wang Z, Zhang Y. Numerical Study on Wave–Ice Floe Interaction in Regular Waves. Journal of Marine Science and Engineering. 2023; 11(12):2235. https://doi.org/10.3390/jmse11122235
Chicago/Turabian StyleWang, Chunhui, Jiaan Wang, Chao Wang, Zeping Wang, and Yuan Zhang. 2023. "Numerical Study on Wave–Ice Floe Interaction in Regular Waves" Journal of Marine Science and Engineering 11, no. 12: 2235. https://doi.org/10.3390/jmse11122235
APA StyleWang, C., Wang, J., Wang, C., Wang, Z., & Zhang, Y. (2023). Numerical Study on Wave–Ice Floe Interaction in Regular Waves. Journal of Marine Science and Engineering, 11(12), 2235. https://doi.org/10.3390/jmse11122235








