Investigation of Energy Loss Mechanism and Vortical Structures Characteristics of Marine Sediment Pump Based on the Response Surface Optimization Method
Abstract
:1. Introduction
2. Analytical Model and Numerical Calculation Method
2.1. Marine Sediment Pump Model
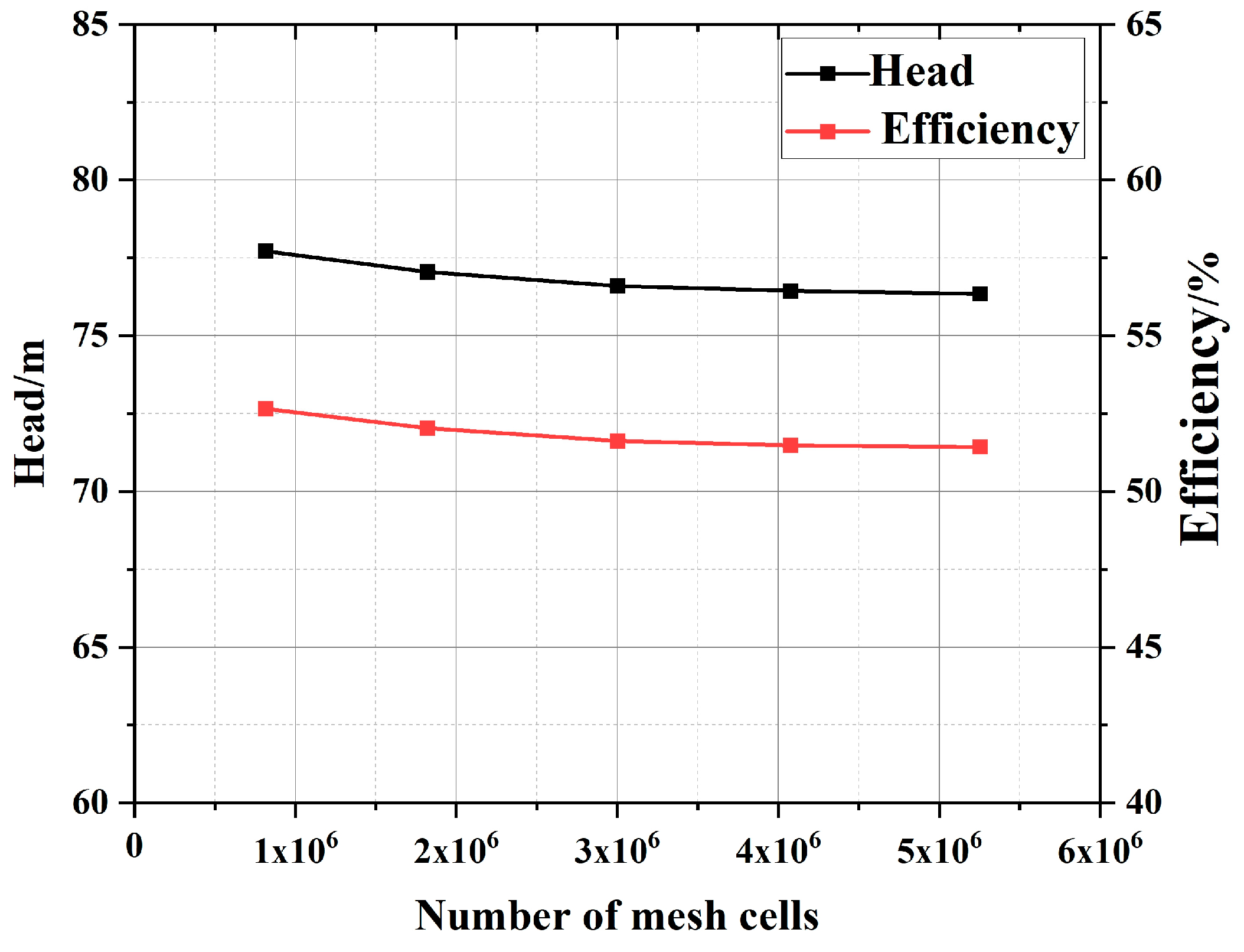
2.2. Mesh Independence Investigation
2.3. Numerical Method and Boundary Conditions
2.4. Experimental and Numerical Calculation Verification
2.4.1. Error Analysis of Test Bench
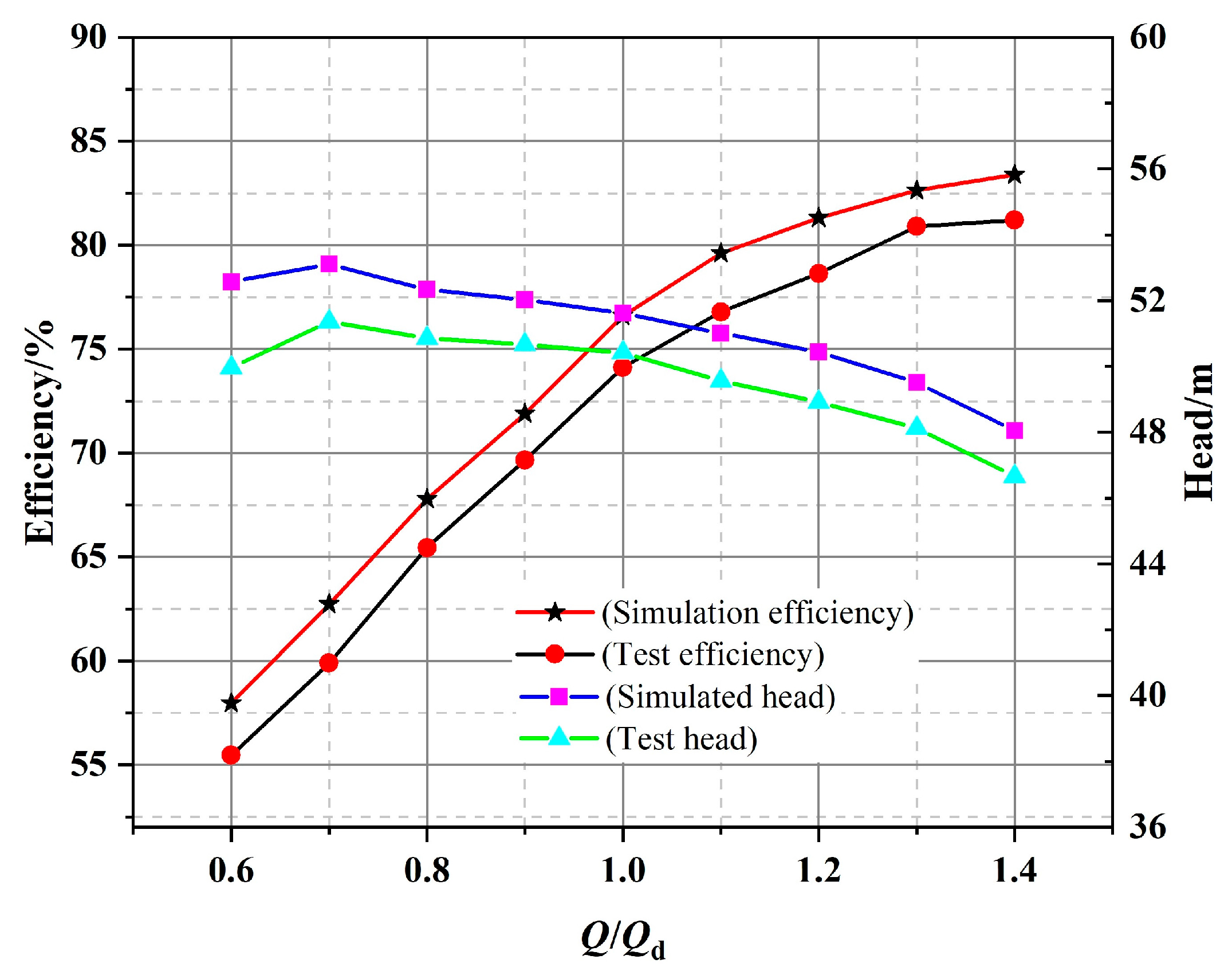
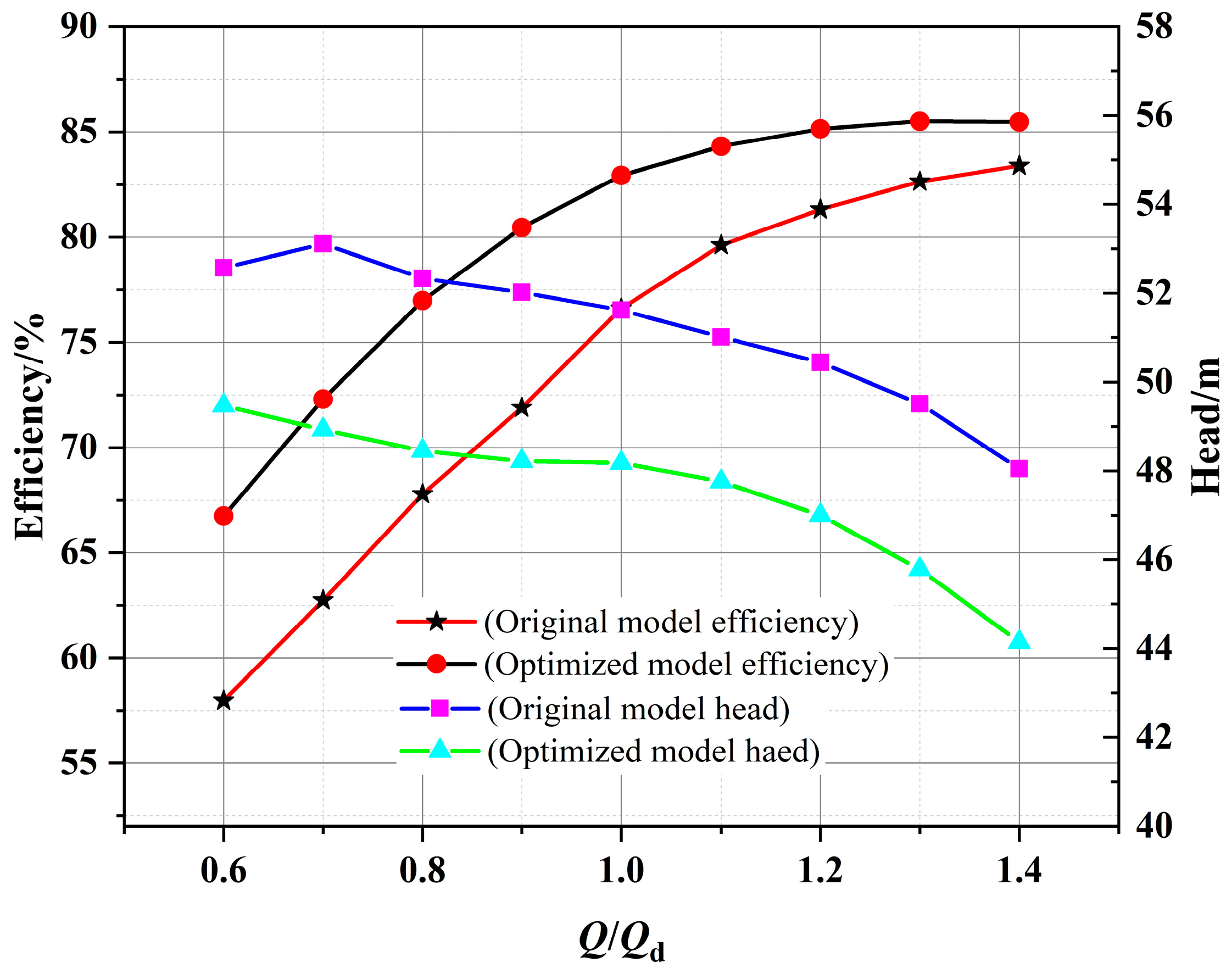
2.4.2. Comparison of Numerical Calculations and Experimental Results
3. Analysis of Response Surface Optimization
3.1. Response Surface Optimization Method
3.2. Analysis of Variance and Response Regression Model Analysis
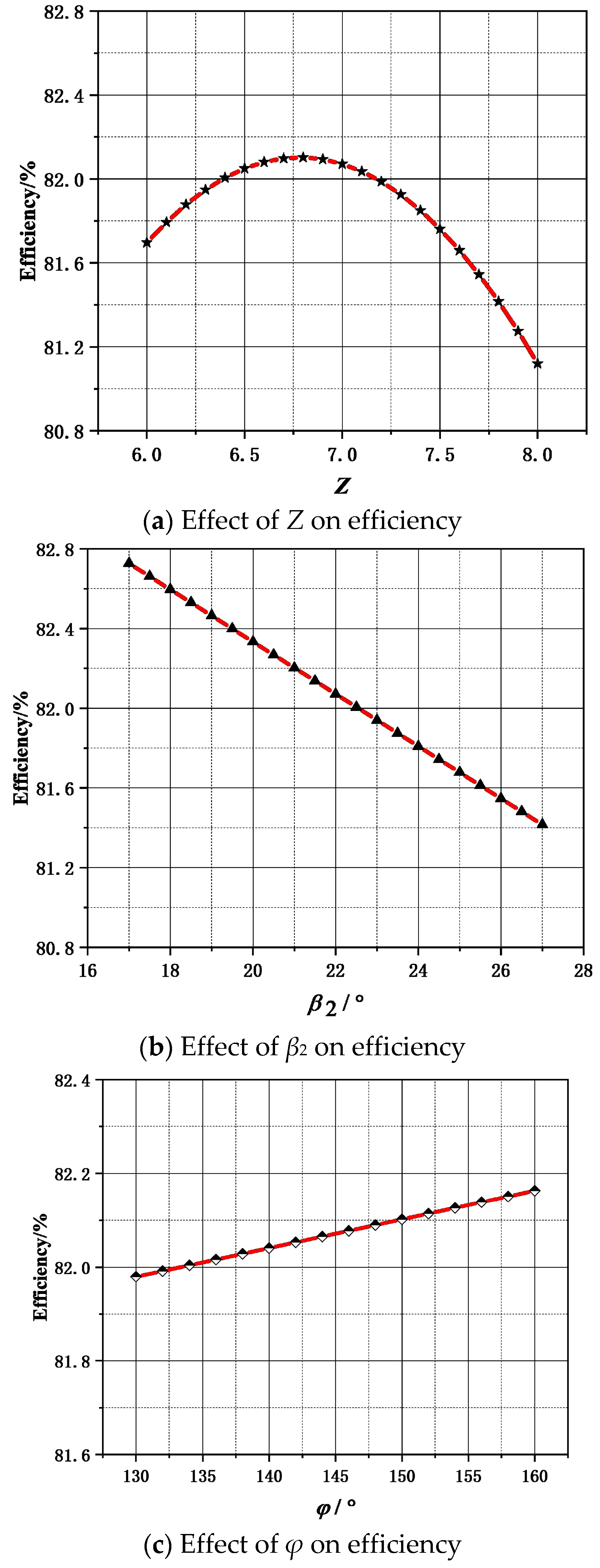
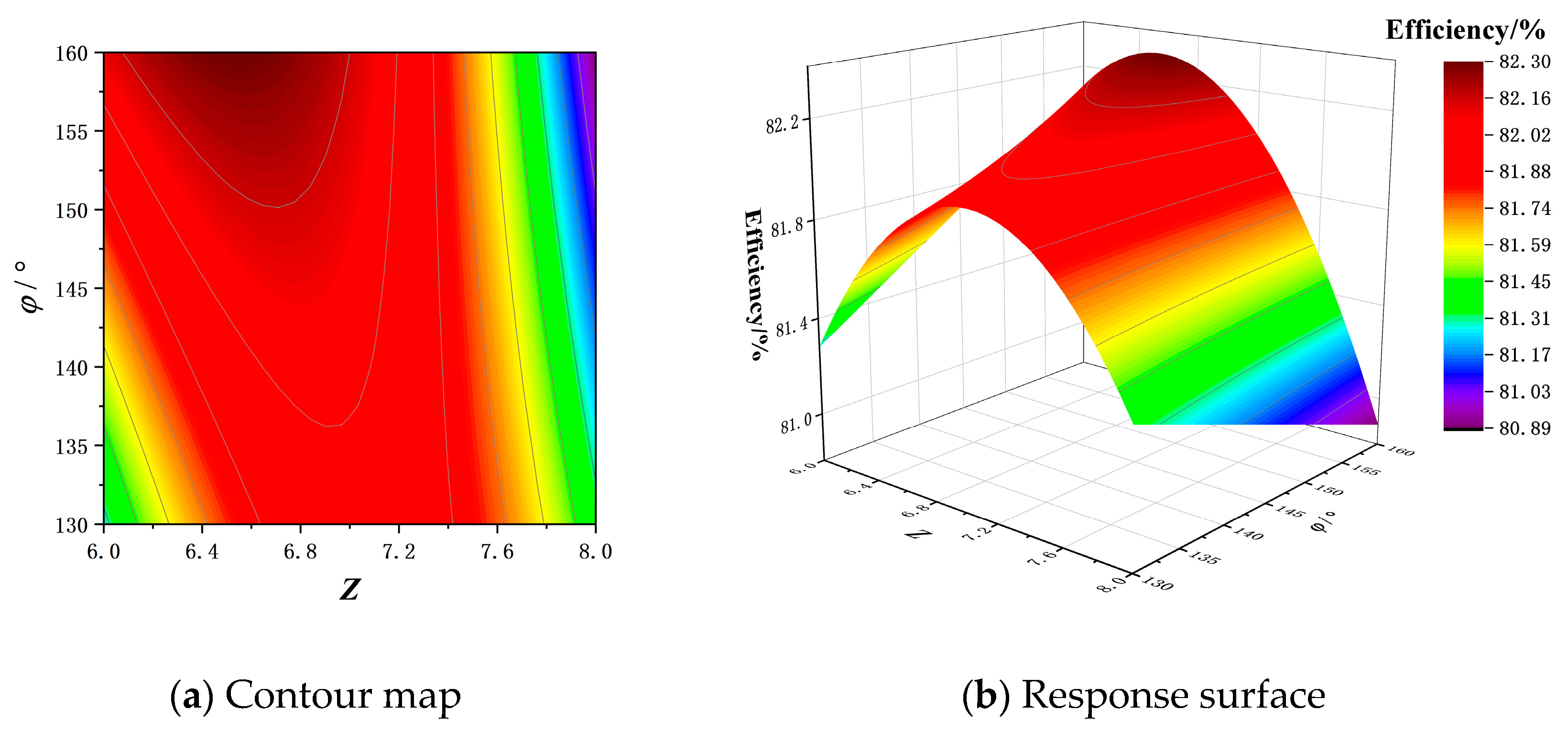
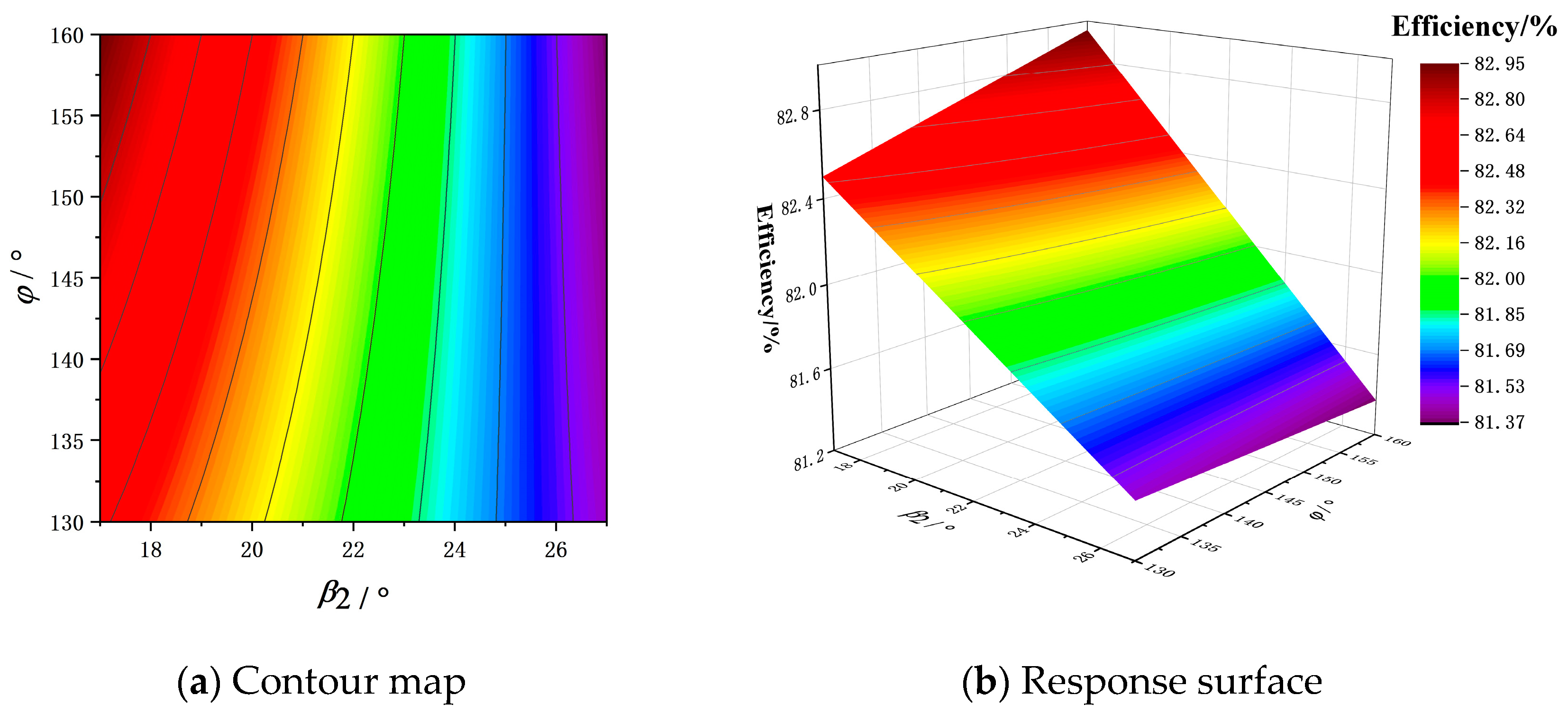
3.3. Analysis of Response Surface Diagram and Contour Diagram
3.4. Analysis of the Prediction Model
4. Analysis of the Internal Flow Field
4.1. Analysis of Flow Field
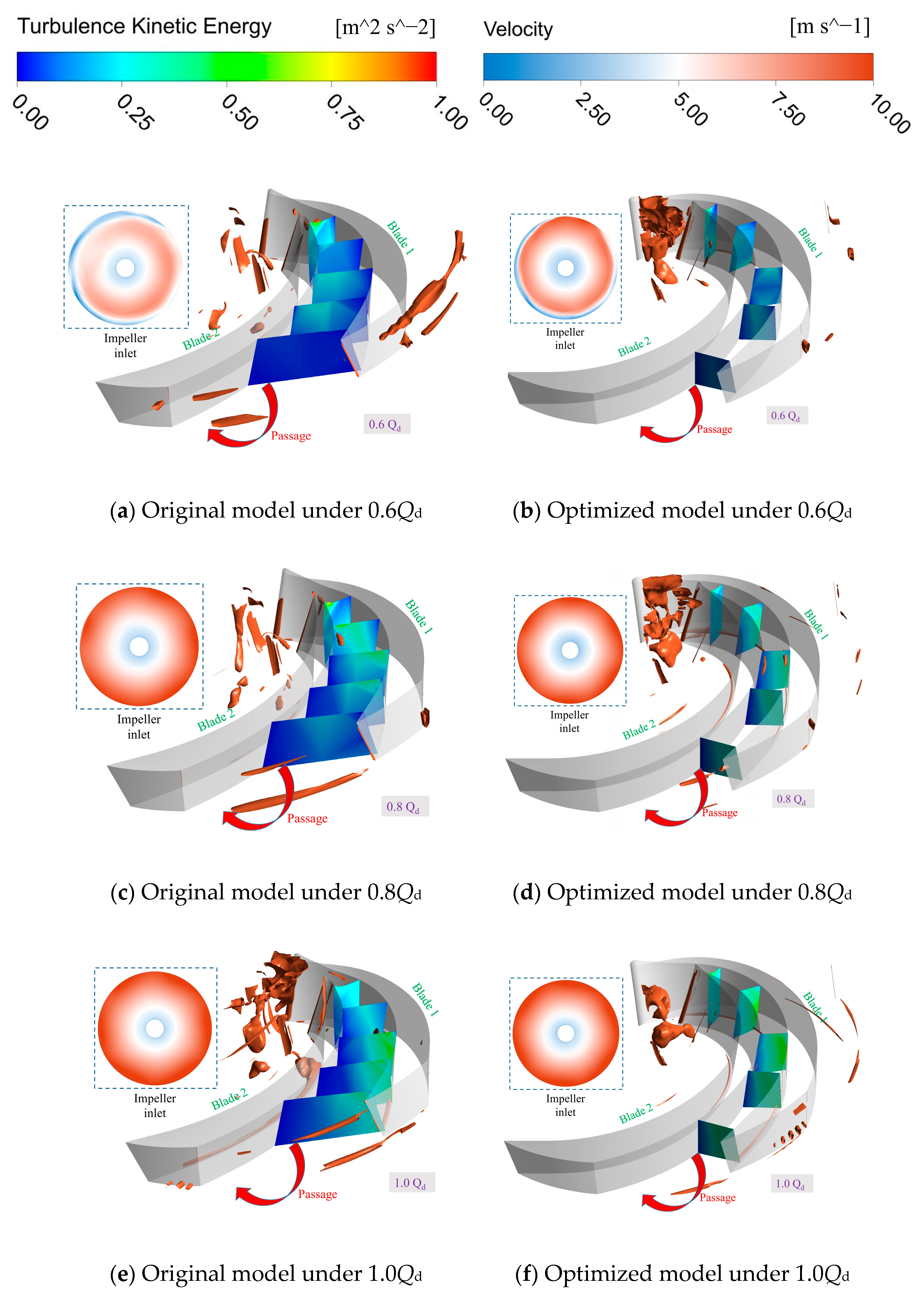
4.1.1. Analysis of Impeller Internal Flow
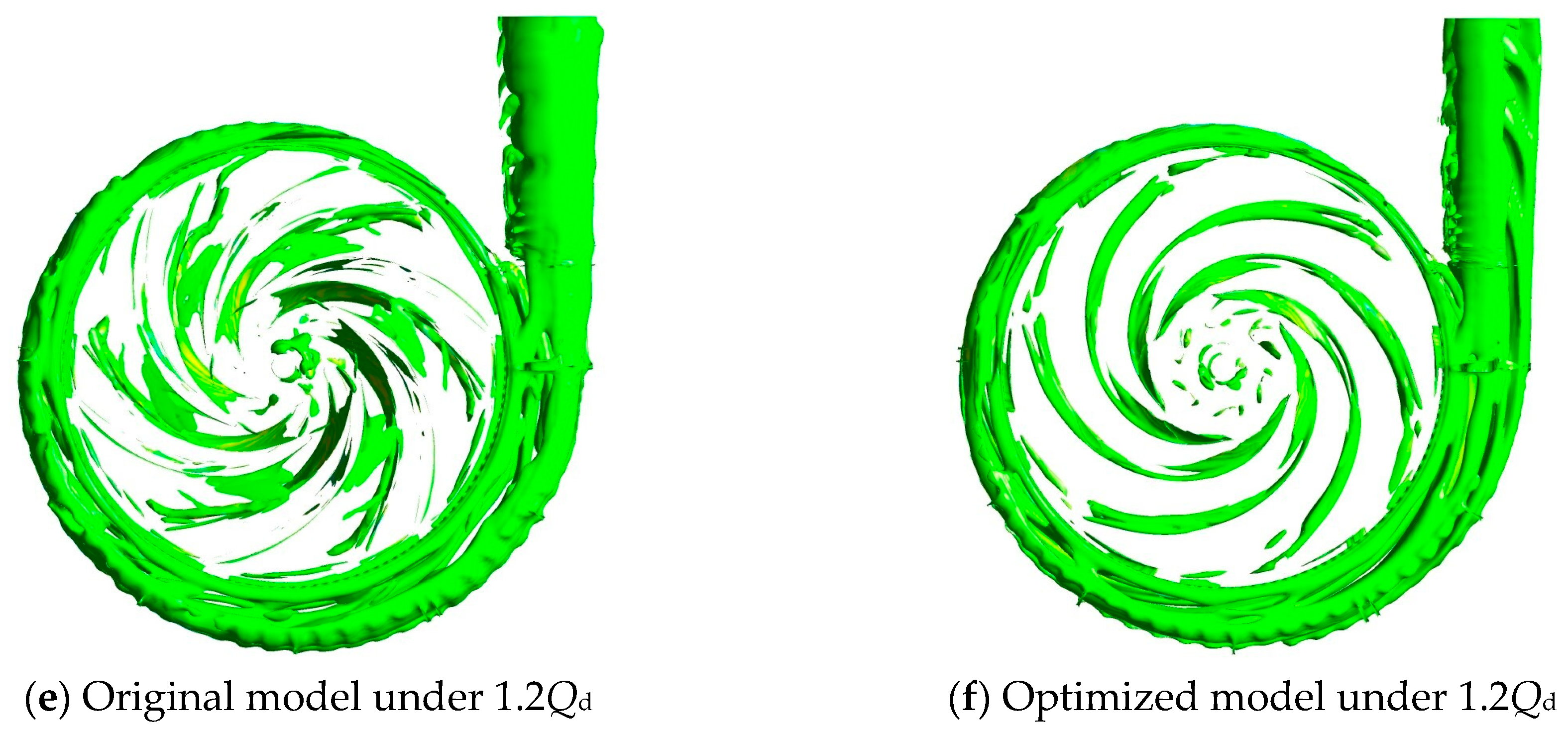
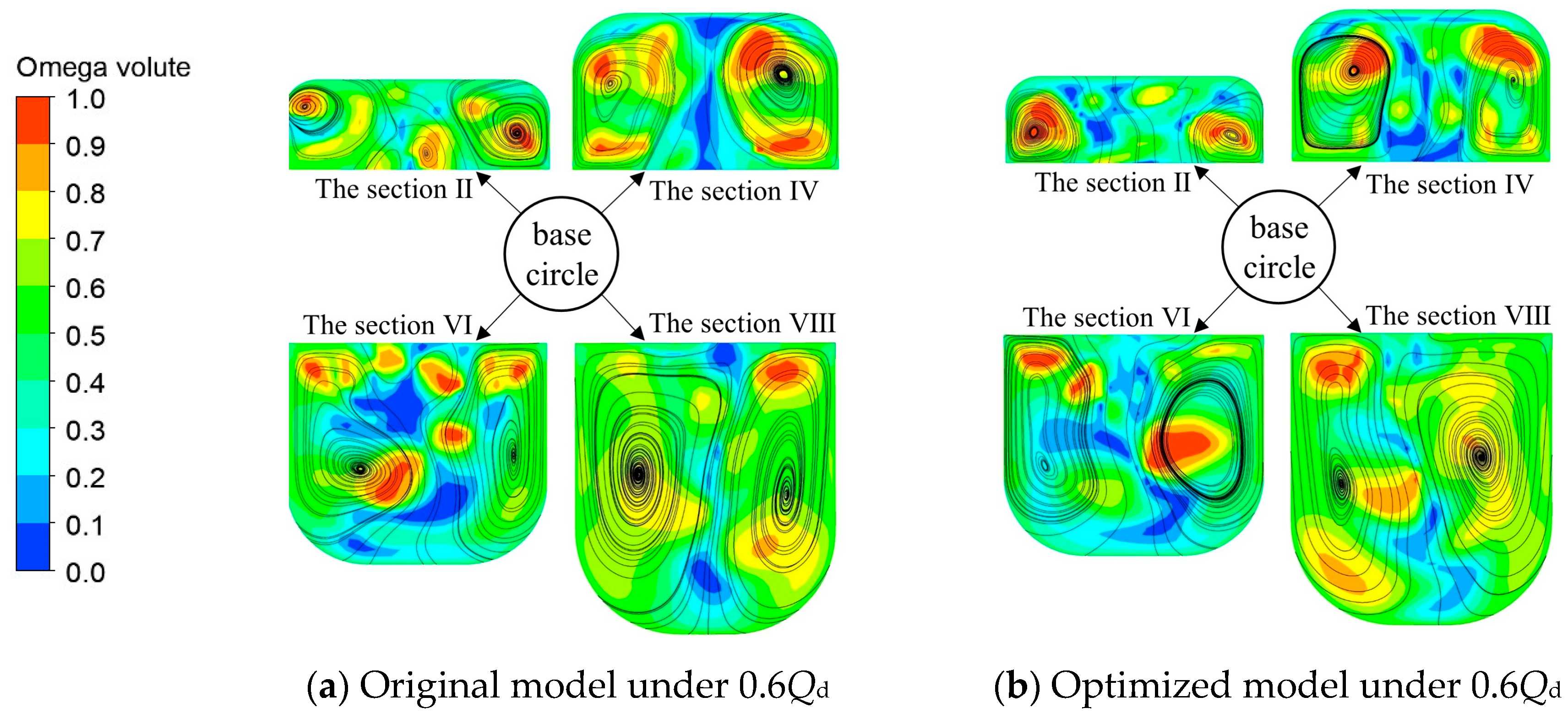
4.1.2. Analysis of Omega Vortex Identification Results
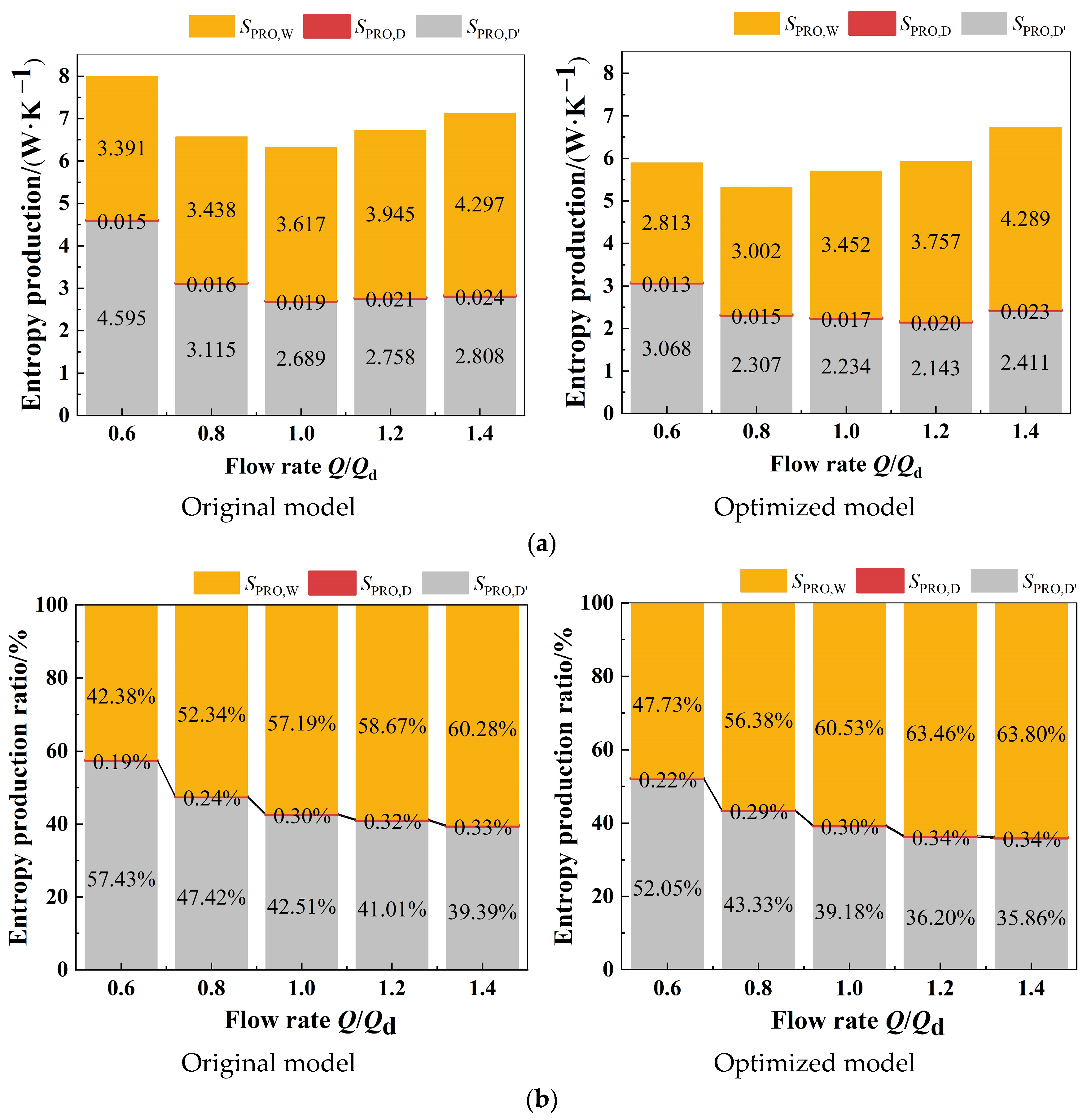
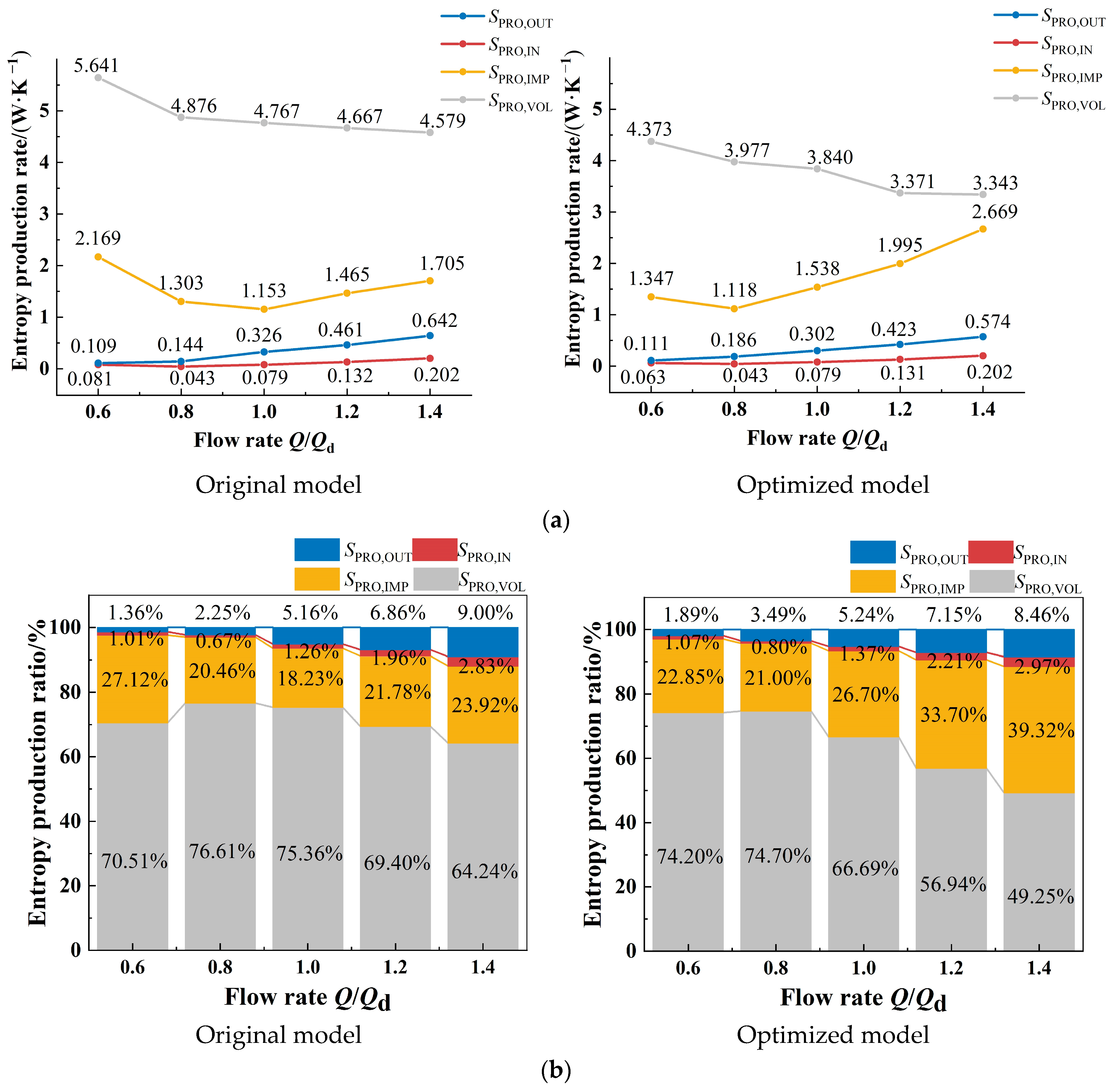
4.2. Analysis of Entropy Production
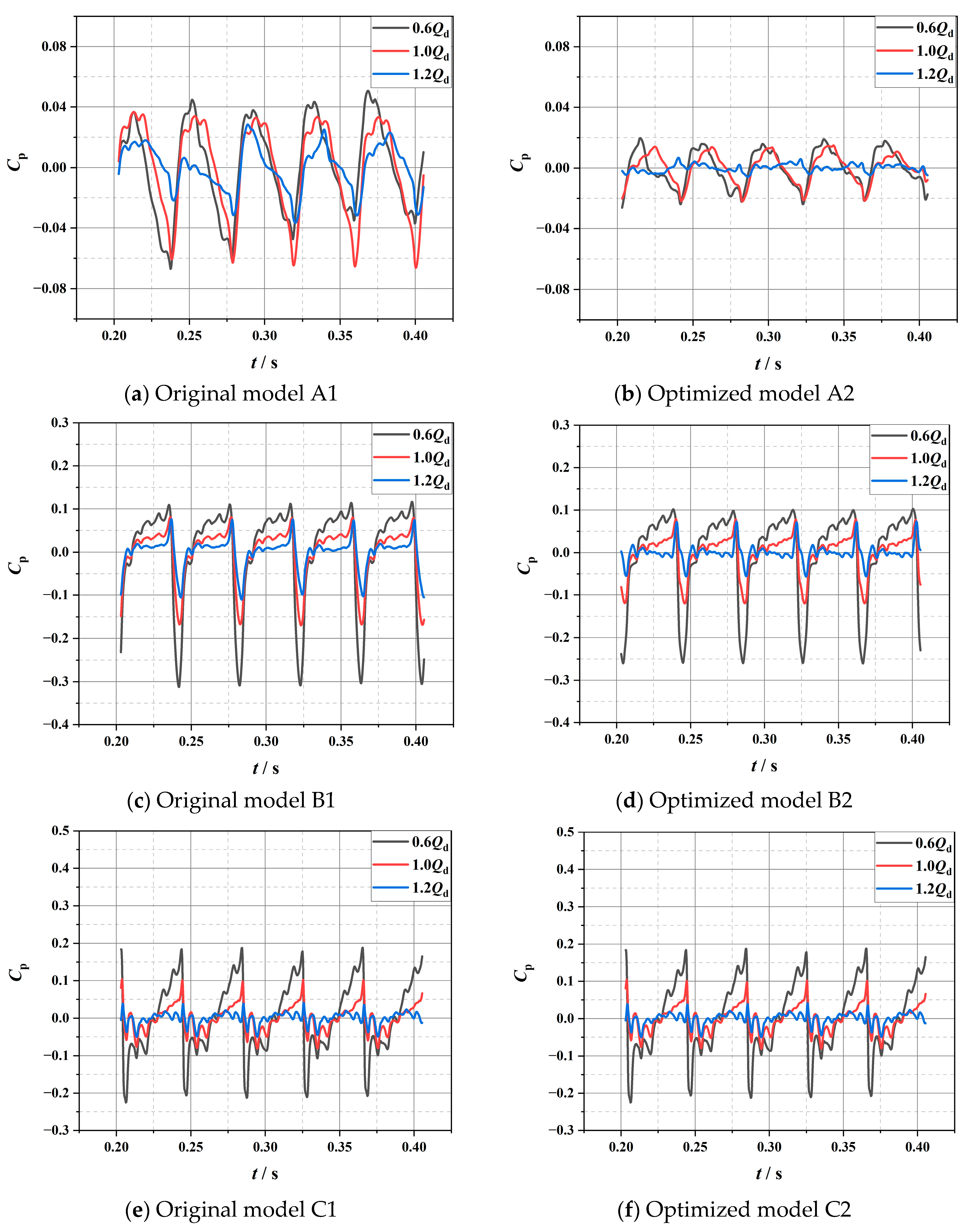
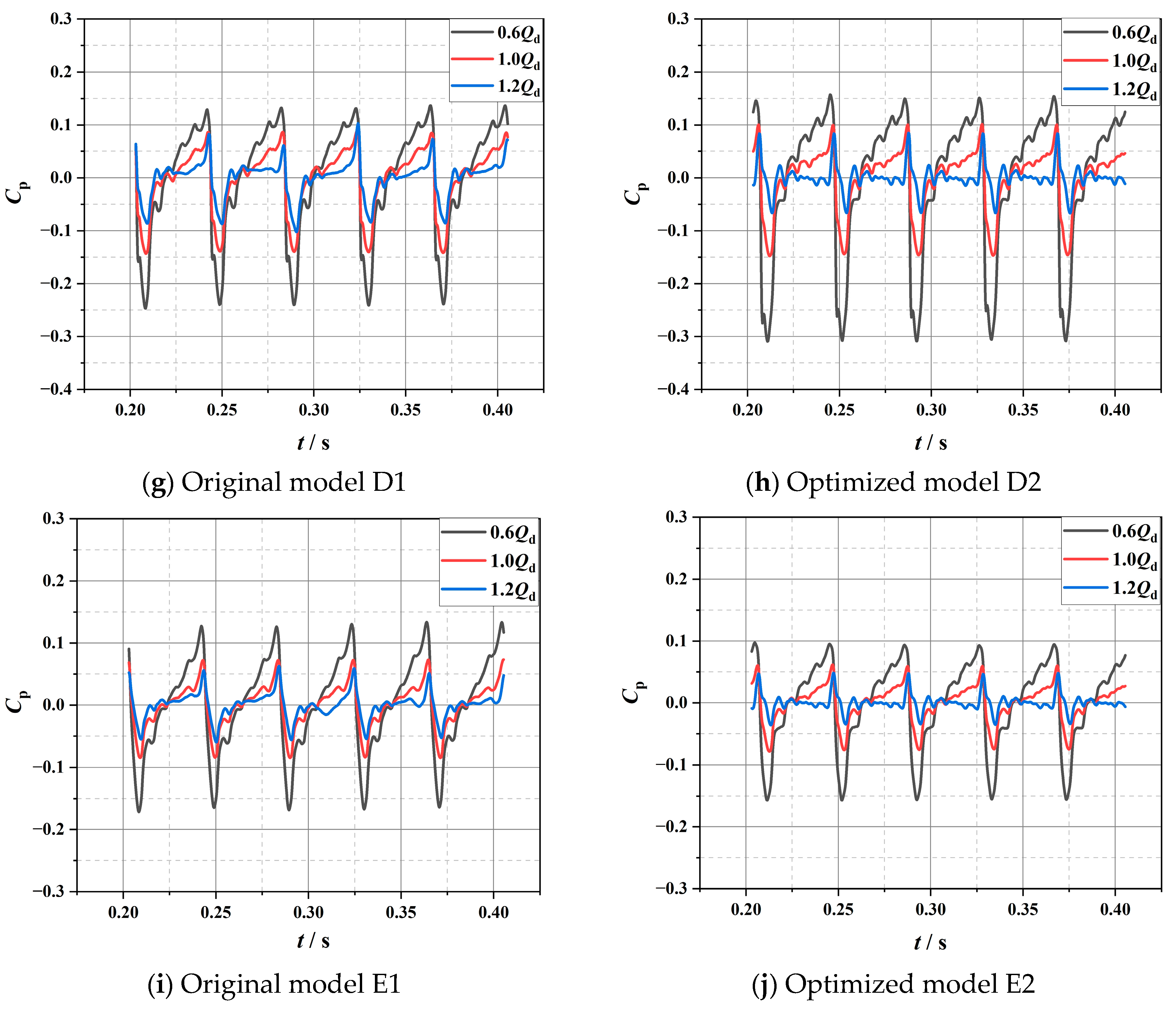
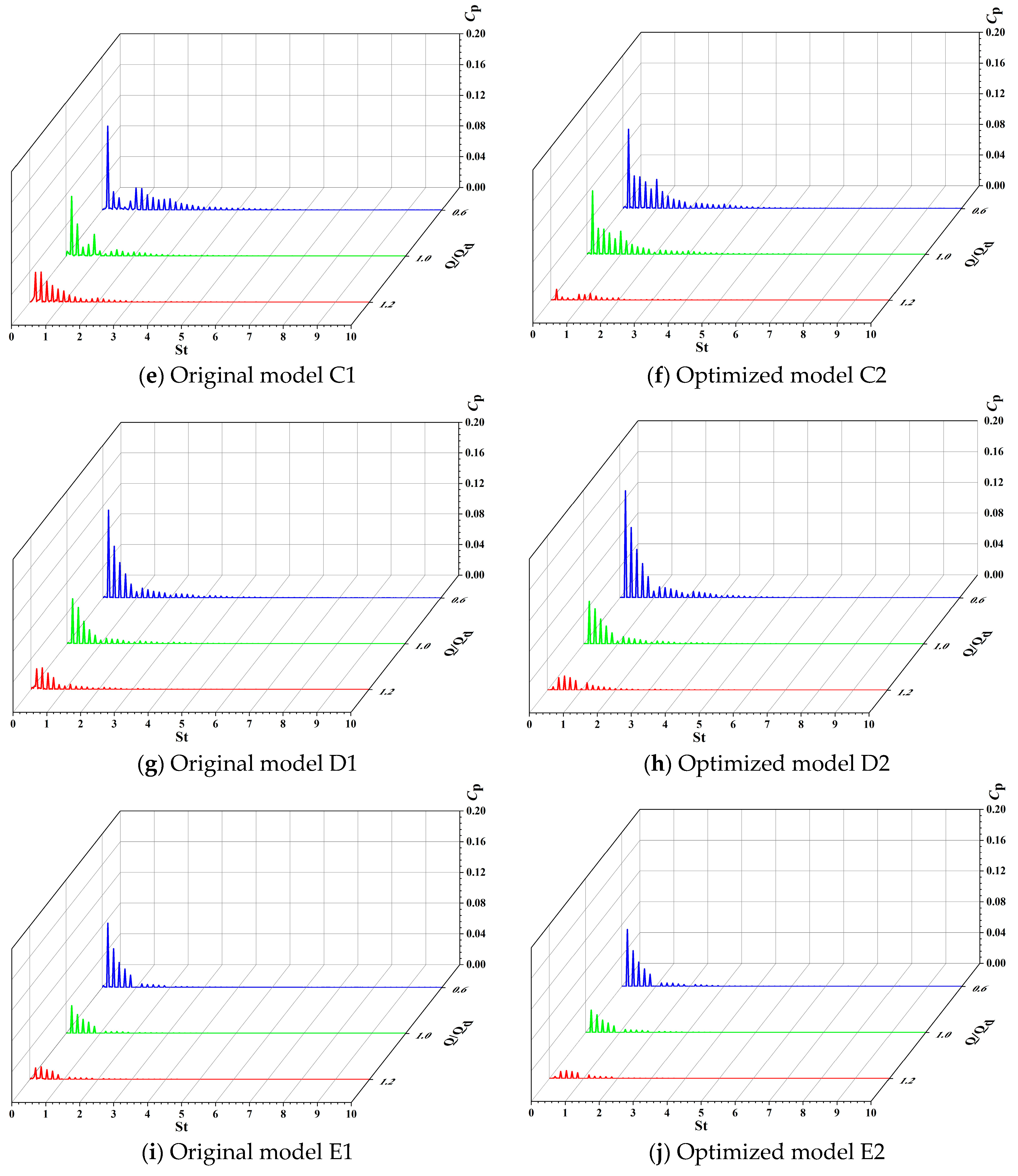
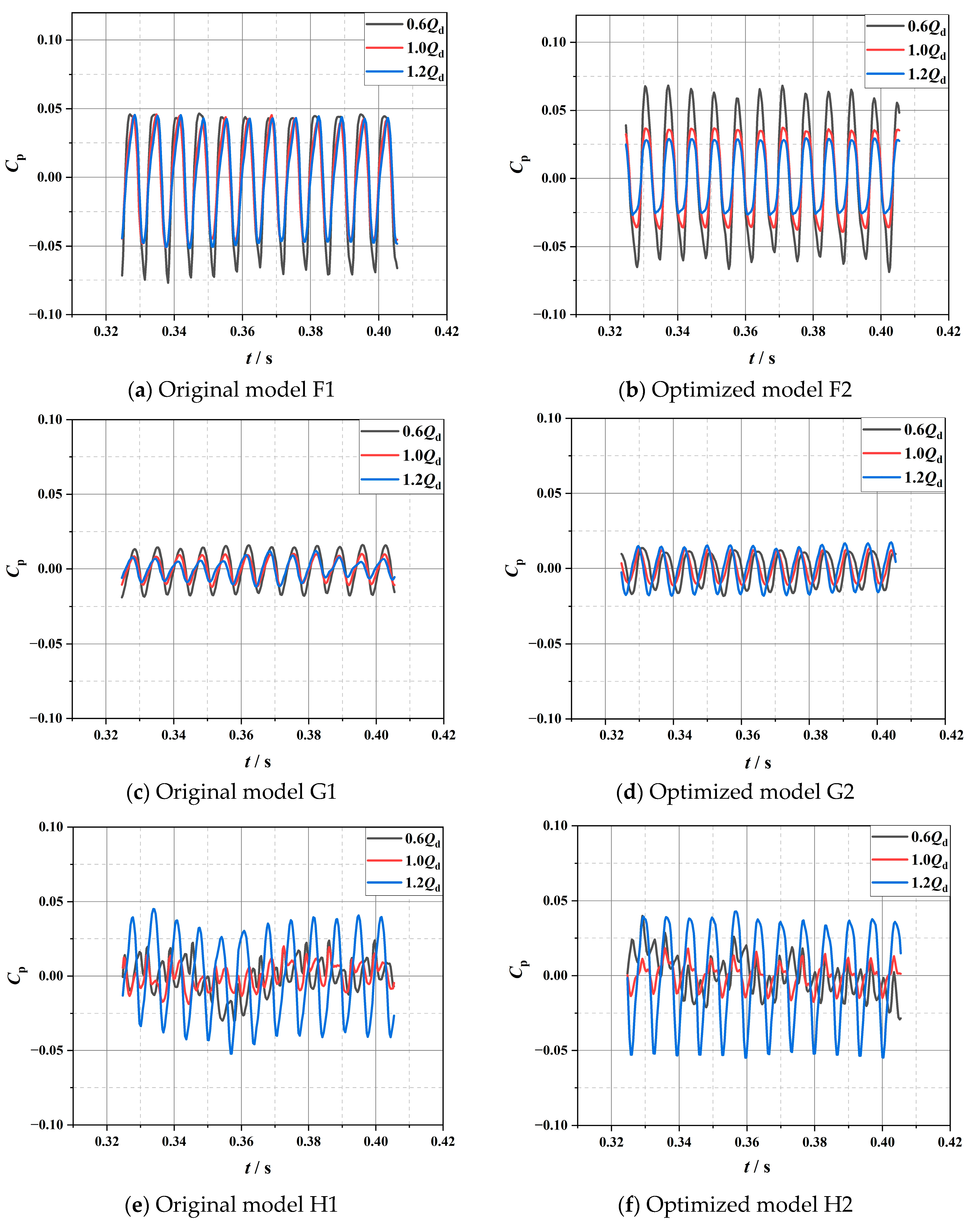
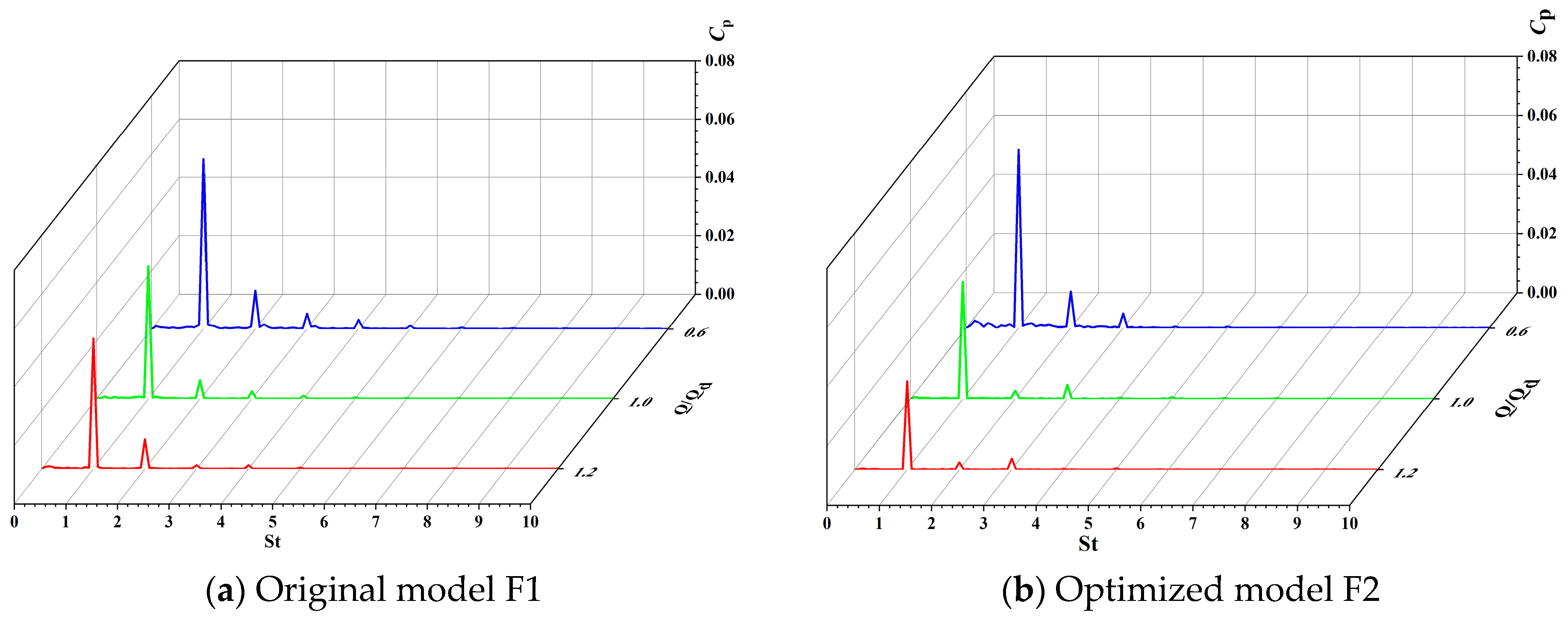
4.3. Analysis of Pressure Fluctuation
4.3.1. Analysis of Impeller Pressure Fluctuation
4.3.2. Analysis of Volute Pressure Fluctuation
5. Conclusions
- (1)
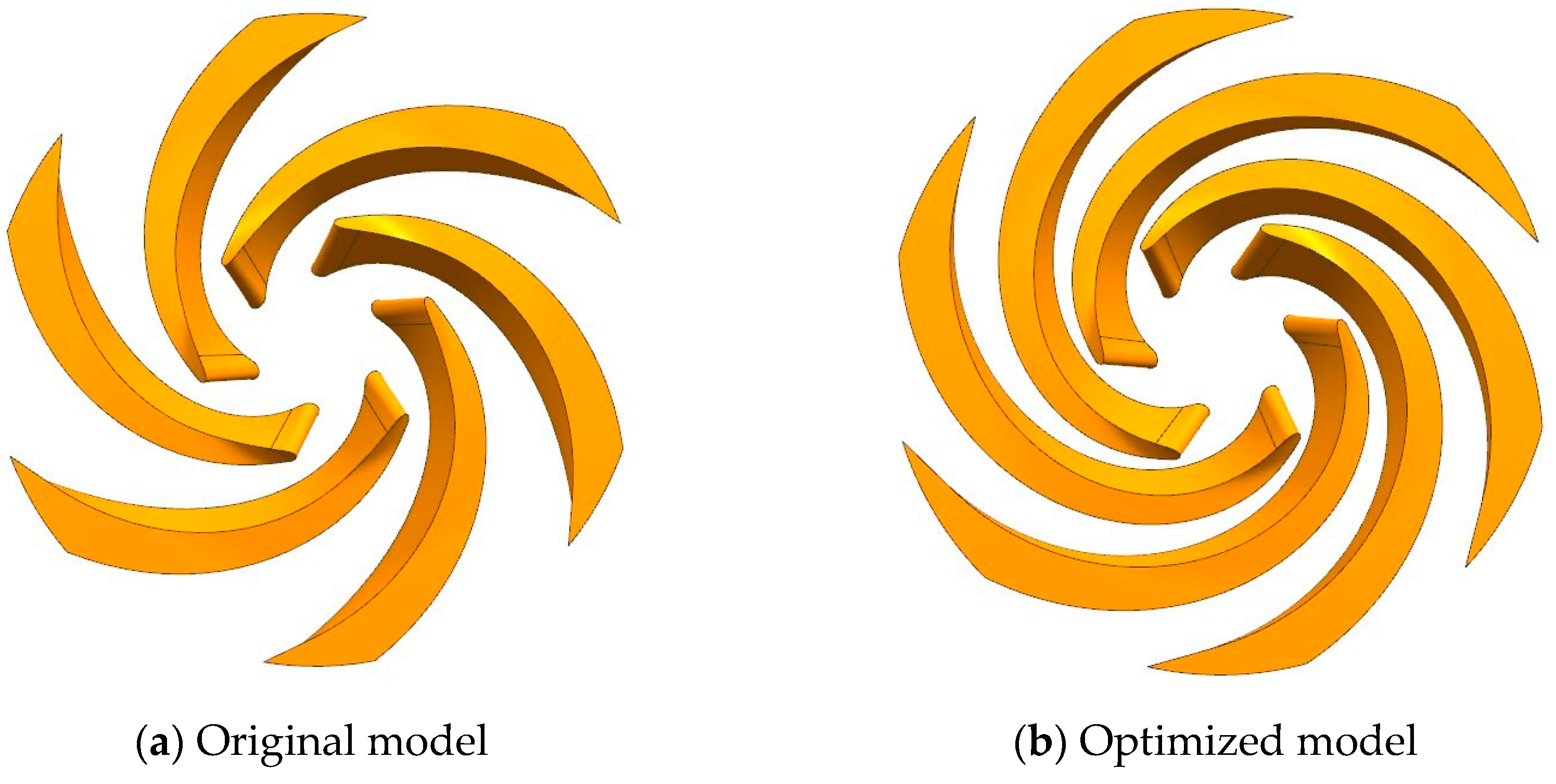
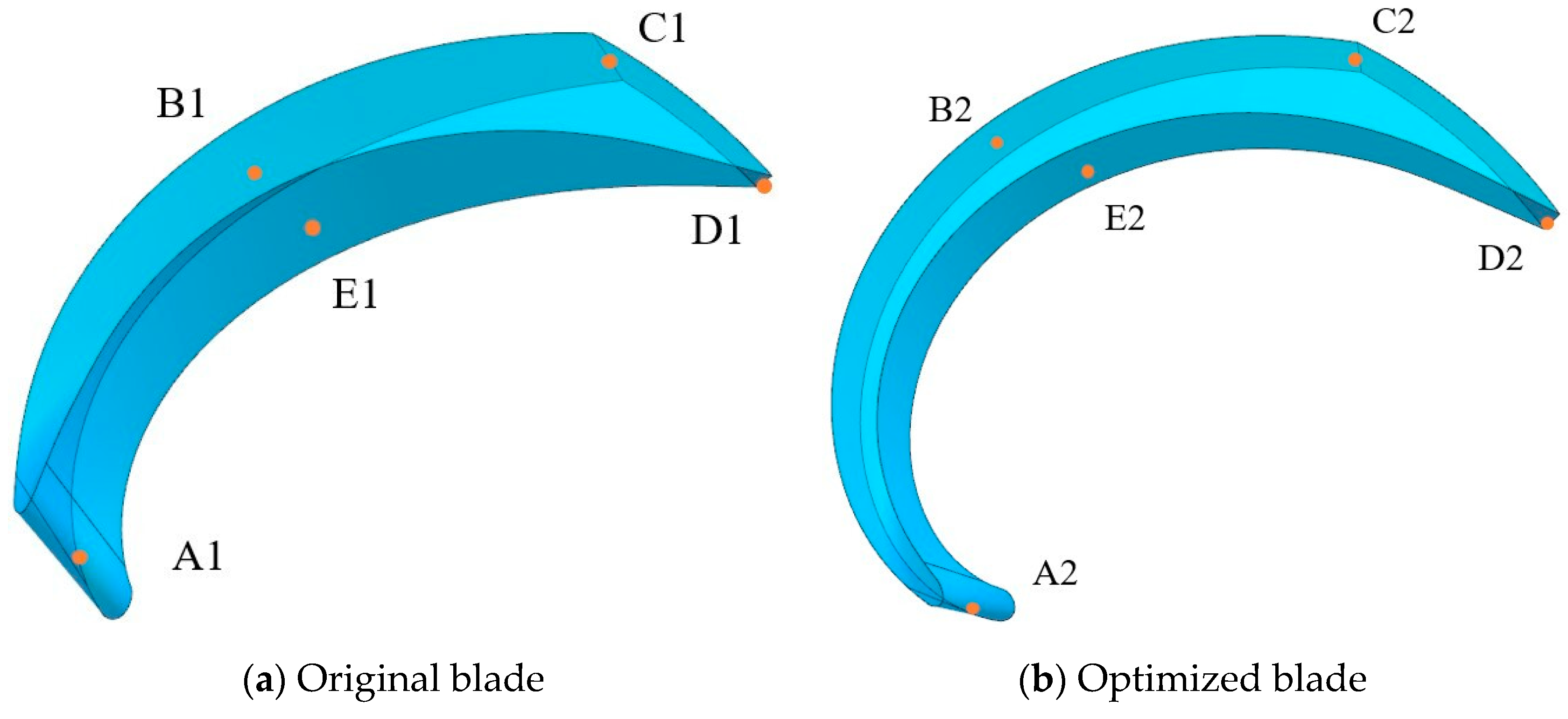
- This study takes efficiency as the optimization goal; uses the four key geometric parameters of the impeller blade number Z, blade inlet angle β1, blade outlet angle β2, and blade wrap angle φ as optimization variables; and uses the central composite bounded design sampling method to generate the marine sediment pump impeller’s optimization plan. The results of the experimental plan are obtained through parametric modeling and numerical calculations, and the result data are analyzed through response surface optimization. Finally, by solving the regression model, the optimal combination of the optimized impeller model is obtained: Z is 6, β1 is 32°, β2 is 17°, and φ is 160°. The optimized model’s efficiency increased by 6.33% under design flow conditions, by more than 2% under overload flow conditions, and by more than 8% under partial load flow conditions. Moreover, the efficient operating area of the marine sediment pump has been significantly expanded. These improvements to the marine sediment pump demonstrate the effectiveness of optimization based on response surface methodology.
- (2)
- By comparing the flow characteristics and vortex distribution of the original and optimized marine sediment pumps under different flow conditions, this study summarizes the following conclusions. First, in the optimized model, the TKE distribution is more uniform under the design and overload flow conditions, while under partial load flow conditions, there are fewer eddies. Secondly, by using the Omega vortex identification method, it is found that the vortex performance of the original and optimized models had similar changing trends under various flow conditions. Under partial load flow conditions, the flow field vortices of the original model are the most turbulent, while the number of vortex structures of the optimized model is greatly reduced. Finally, compared with the original model, the high-Omega-value areas in the volute section of the optimized model are less distributed and more concentrated, and the streamline distribution is more regular, mainly concentrated on both sides of the volute section, which indicates that the fluid flow characteristics at the outlet of the marine sediment pump have been improved.
- (3)
- By studying the changing trends of three types of entropy production in marine sediment pumps, it is found that wall entropy production and direct entropy production show a trend of first increasing and then decreasing when the flow rate increased, while turbulent entropy production continued to decrease. Under different flow conditions, the optimized model reduced wall entropy production and turbulence entropy production compared with the original model, while the direct entropy production was reduced by no more than 1%. Exploring the distribution characteristics of total entropy production under different flow conditions shows that the total entropy produced at the volute is the highest, followed by the impeller, then the outlet, and the total entropy production at the inlet is the lowest. Inside the impeller, under partial load flow conditions, the entropy production of the optimized model is lower than that of the original model. However, the entropy production of the optimized model impeller exceeded that of the original model under overload flow conditions and design conditions. This phenomenon is mainly attributed to the increase in impeller wrap angle and blade curvature in the optimization model, which results in an increase in wall entropy production.
- (4)
- Under different flow conditions, the pressure pulsations of the impeller and volute monitoring points of the original and optimized marine sediment pump are periodic. The main frequency in the impeller frequency domain is the shaft frequency fn, and the secondary frequency is a multiple of the shaft frequency fn. The main frequency of the volute monitoring point is the blade passing frequency (fBPF), and the secondary frequency is the multiple of the blade passing frequency (fBPF). The pressure pulsation on the impeller gradually increases from the blade leading edge to the blade trailing edge, and the pressure pulsation amplitude on the blade pressure surface is greater than the blade suction surface. Compared with the original impeller, the pressure fluctuations at most monitoring points on the optimized impeller are improved, and the flow is more stable. Under partial load flow conditions, the optimized volute pressure pulsation is particularly serious. However, under the design conditions and overload flow conditions, the pressure pulsation is significantly reduced. Overall, the optimized marine sediment pump model performs better in pressure pulsation compared to the original marine sediment pump model, especially under design and overload flow conditions, showing a more obvious improvement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Azizi, R.; Attaran, B.; Hajnayeb, A. Improving accuracy of cavitation severity detection in centrifugal pumps using a hybrid feature selection technique. Meas. J. Int. Meas. Confed. 2017, 108, 9–17. [Google Scholar] [CrossRef]
- Wu, H. Performance optimization design of sewage pump based on orthogonal experiment. Water Pump Technol. 2021, 6, 13–16. [Google Scholar]
- Zhang, N.; Li, Z.; Gao, B. Influence of the blade trailing edge profile on the performance and unsteady pressure pulsations in a low specific speed centrifugal pump. J. Fluids Eng. Trans. Asme 2016, 135, 051106. [Google Scholar]
- Ni, D.; Yang, M.; Gao, B. The internal correlations between unsteady flow and pressure pulsations in a nuclear reactor coolant pump. J. Eng. Thermophys. 2017, 38, 1676–1682. [Google Scholar]
- Yang, F.; Li, Z.; Fu, J. Numerical and experimental analysis of transient flow field and pressure pulsations of an axial-flow pump considering the pump–pipeline interaction. J. Mar. Sci. Eng. 2022, 10, 258. [Google Scholar] [CrossRef]
- Zhai, L.; Lu, C.; Guo, J. Flow characteristics and energy loss of a multistage centrifugal pump with blade-type guide vanes. J. Mar. Sci. Eng. 2022, 10, 180. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, X. Review of design optimization methods for turbomachinery aerodynamics. Prog. Aerosp. Sci. 2017, 93, 1–23. [Google Scholar] [CrossRef]
- Ren, L. Experimental Design and Optimization; Science Press: Beijing, China, 2009. [Google Scholar]
- Bashiri, M.; Derakhshan, S.; Shahrabi, J. Design optimization of a centrifugal pump using particle swarm optimization algorithm. Int. J. Fluid Mach. Syst. 2019, 12, 322–331. [Google Scholar] [CrossRef]
- Wang, W.; Osman, M.; Pei, J. Artificial neural networks approach for a multi-objective cavitation optimization design in a double-suction centrifugal pump. Processes 2019, 7, 23. [Google Scholar] [CrossRef]
- Xu, M.; Zeng, G.; Wu, D. Structural optimization of jet fish pump design based on a multi-objective genetic algorithm. Energies 2022, 15, 16. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, C.; Liu, G. Optimization design of labyrinth seal for piston pump based on response surface method. Fluid Mach. 2021, 49, 44. [Google Scholar]
- Liu, M.; Tan, L.; Xu, Y. Optimization design method of multi-stage multiphase pump based on Oseen vortex. J. Pet. Sci. Eng. 2019, 184, 106532. [Google Scholar] [CrossRef]
- Gan, X.; Pei, J.; Wang, W. Application of a modified MOPSO algorithm and multi-layer artificial neural network in centrifugal pump optimization. Eng. Optim. 2022, 55, 580–598. [Google Scholar] [CrossRef]
- Kim, S.; Yong, K.; Hyung, J. High performance hydraulic design techniques of mixed-flow pump impeller and diffuser. J. Mech. Sci. Technol. 2015, 29, 227–240. [Google Scholar] [CrossRef]
- Kim, J.; Lee, H. Improvement of hydrodynamic performance of a multiphase pump using design of experiment techniques. J. Fluids Eng. 2015, 137, 081301. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, J.; Zhang, Y. Design optimization of centrifugal pump using radial basis function metamodels. Adv. Mech. Eng. 2014, 6, 457542. [Google Scholar] [CrossRef]
- Yuan, S.; Wang, W.; Pei, J. Multi-objective optimization of low-specific-speed centrifugal pump. J. Agric. Eng. 2015, 31, 46–52. [Google Scholar]
- Nourbakhsh, A.; Safikhani, H.; Derakhshan, S. The comparison of multi-objective particle swarm optimization and NSGA II algorithm: Applications in centrifugal pumps. Eng. Optim. 2011, 43, 1095–1113. [Google Scholar] [CrossRef]
- Takayama, Y.; Watanabe, H. Multi-objective design optimization of a mixed-flow pump. Fluids Eng. Div. Summer Meet. 2009, 43727, 371–379. [Google Scholar]
- Aksoy, M.; Babayigit, O.; Kocaaslan, O. Effect of blade wrap angle to centrifugal pump impeller efficiency. In Proceedings of the International Conference: EFM, Kutná Hora, Czech Republic, 19–22 November 2013; pp. 799–806. [Google Scholar]
- Shen, J.; Chen, S.; Xu, J. The influence of y+ and turbulence model on the calculation accuracy of the external characteristics of the pump device. China Rural. Water Conserv. Hydropower 2020, 455, 25–29+34. [Google Scholar]
- Babayigit, O.; Ozgoren, M.; Aksoy, M. Experimental and CFD investigation of a multistage centrifugal pump including leakages and balance holes. Desalin. Water Treat 2017, 67, 28–40. [Google Scholar] [CrossRef]
- Zhang, N.; Yang, M.; Gao, B. Investigation of rotor-stator interaction and flow unsteadiness in a low specific speed centrifugal pump. Stroj. Vestn. J. Mech. Eng. 2016, 62, 21–31. [Google Scholar] [CrossRef]
- Gao, B.; Guo, P.; Zhang, N. Unsteady pressure pulsation measurements and analysis of a low specific speed centrifugal pump. J. Fluids Eng. 2017, 139, 071101. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Y. A review of rotating stall in reversible pump turbine. Mech. Eng. Sci. 2017, 231, 1181–1204. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiu, X.; Chen, F. A selected review of vortex identification methods with applications. J. Hydrodyn. 2018, 30, 767–779. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y.; Yang, Y. New omega vortex identification method. Sci. China Phys. Mech. Astron. 2016, 59, 684711. [Google Scholar] [CrossRef]
- Liu, C.; Gao, Y.; Dong, X. Third generation of vortex identification methods: Omega and Liutex/Rortex based systems. J. Hydrodyn. 2019, 31, 205–223. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, K.; Li, J. Analysis of the vortices in the inner flow of reversible pump turbine with the new omega vortex identification method. J. Hydrodyn. 2018, 30, 463–469. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, Y.; Han, L. Vortex identification and evolution law of mixed flow pump under small flow conditions. Chin. J. Drain. Irrig. Mech. Eng. 2023, 41, 231–238. [Google Scholar]
- Chang, H.; Shi, W.; Li, W. Energy loss analysis of novel self-priming pump based on the entropy production theory. J. Therm. Sci. 2019, 28, 306–318. [Google Scholar] [CrossRef]
- Zhou, L.; Hang, J.; Bai, L. Application of entropy production theory for energy losses and other investigation in pumps and turbines: A review. Appl. Energy 2022, 318, 119211. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]
- Mathieu, J.; Scott, J. An Introduction to Turbulent Flow; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
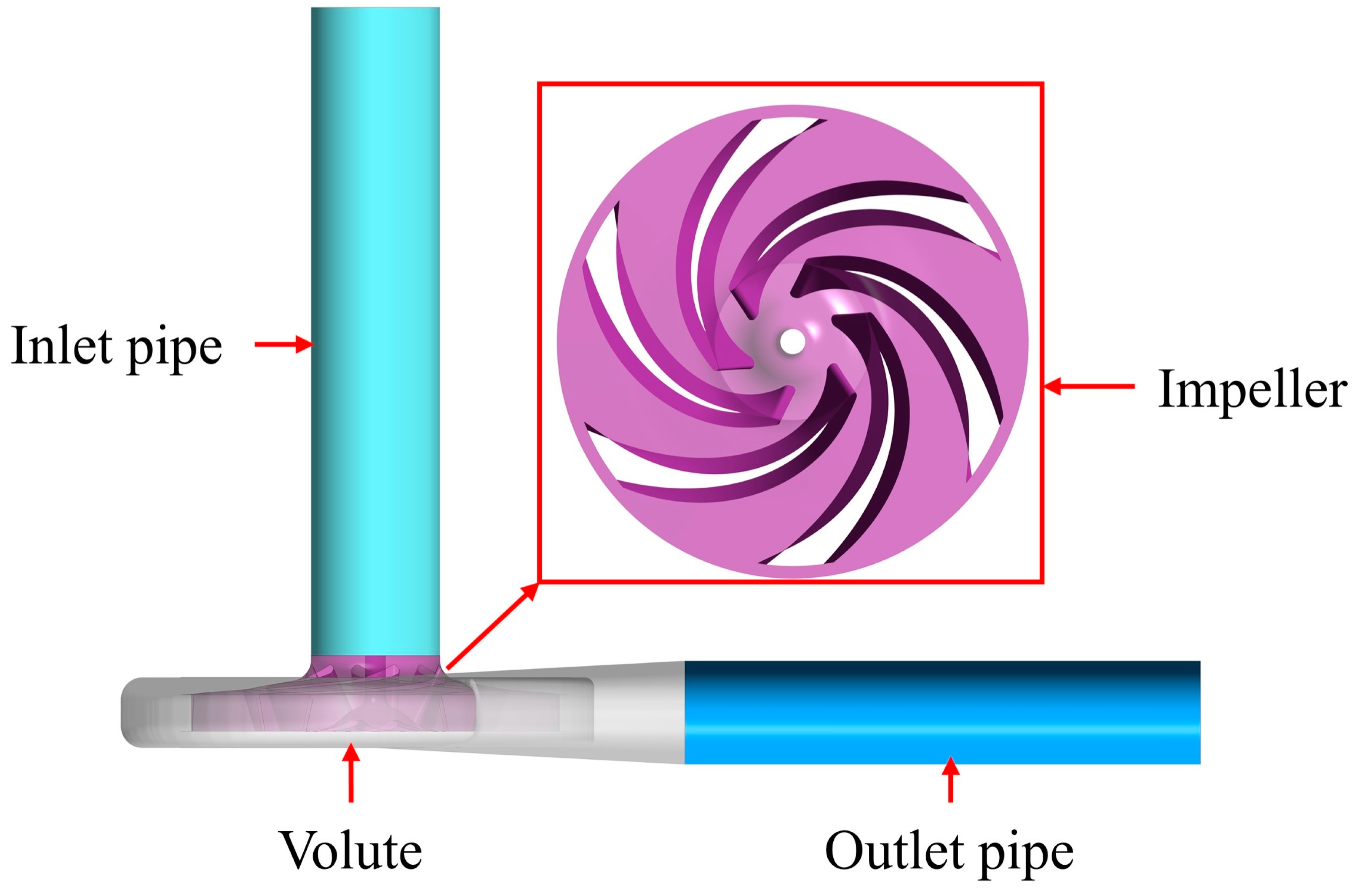
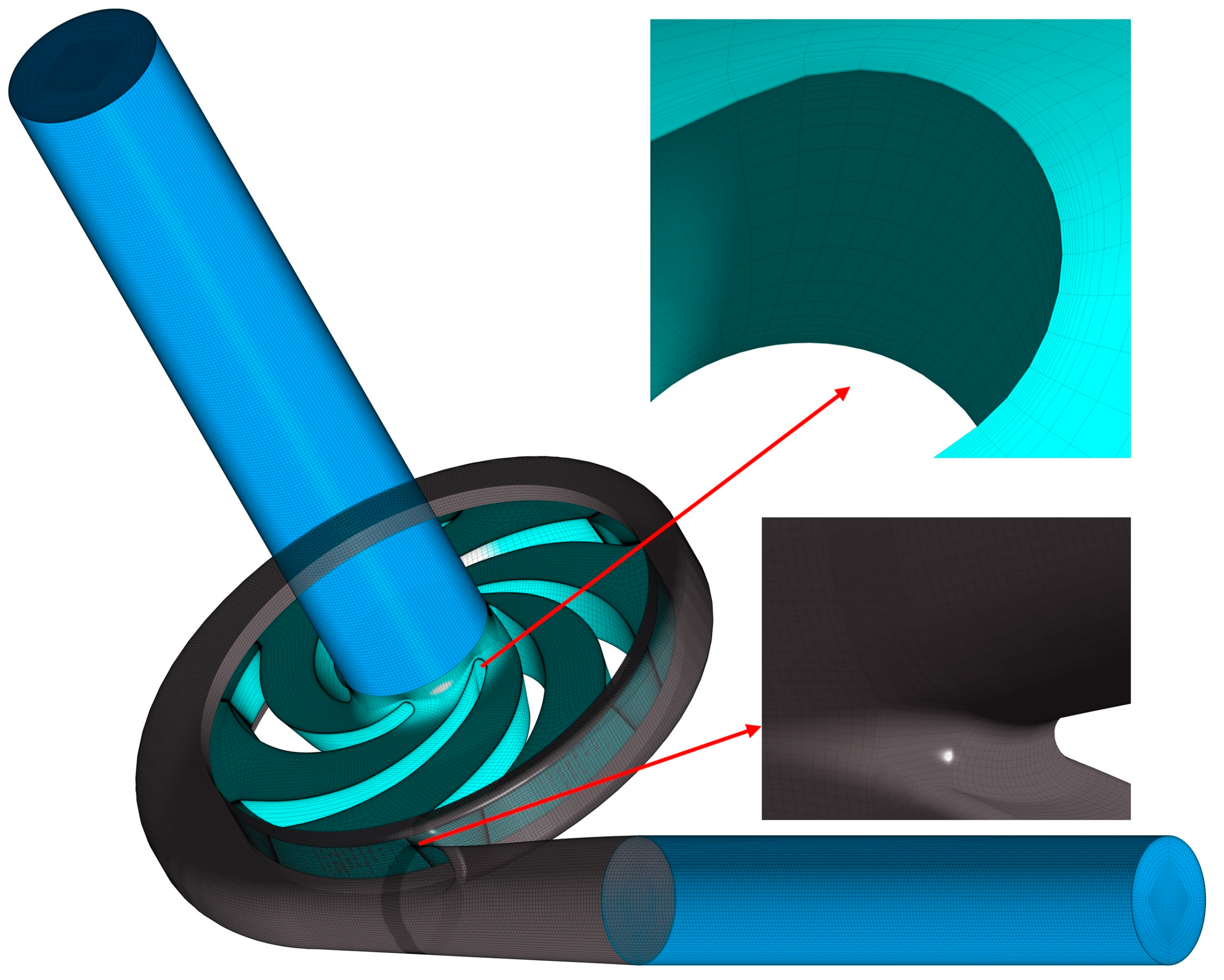









| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Impeller inlet diameter D1/mm | 125 | Blade outlet angle β2/° | 27 |
| Impeller outlet diameter D2/mm | 358 | Blade wrap angle φ/° | 110 |
| Impeller outlet width b2/mm | 36 | Volute base diameter D3/mm | 378 |
| Number of impeller blades Z | 6 | Volute inlet width b3/mm | 68 |
| Blade inlet angle β1/° | 27 | Volute outlet diameter D4/mm | 100 |
| Mesh Cells | Head (m) | Efficiency (%) |
|---|---|---|
| 815,779 | 77.72 | 52.65 |
| 1,819,903 | 77.05 | 52.03 |
| 3,003,478 | 76.60 | 51.62 |
| 4,077,080 | 76.44 | 51.48 |
| 5,253,809 | 76.35 | 51.43 |
| Z (Number) | β1 (°) | β2 (°) | φ (°) |
|---|---|---|---|
| 6 | 27 | 27 | 110 |
| Variable | Z (Number) | β1 (°) | β2 (°) | φ (°) |
|---|---|---|---|---|
| Lower limit | 6 | 22 | 17 | 130 |
| Upper limit | 8 | 32 | 27 | 160 |
| Standard Sequence | Running Program | Factor1: Z x1 | Factor2: β1 x2 | Factor3: β2 x3 | Factor4: φ x4 | Response: Efficiency y |
|---|---|---|---|---|---|---|
| 4 | 1 | 8 | 32 | 17 | 130 | 81.94 |
| 16 | 2 | 8 | 32 | 27 | 160 | 79.59 |
| 19 | 3 | 7 | 22 | 22 | 145 | 82.12 |
| 17 | 4 | 6 | 27 | 22 | 145 | 81.74 |
| 11 | 5 | 6 | 32 | 17 | 160 | 82.93 |
| 10 | 6 | 8 | 22 | 17 | 160 | 81.86 |
| 14 | 7 | 8 | 22 | 27 | 160 | 80.25 |
| 2 | 8 | 8 | 22 | 17 | 130 | 81.65 |
| 24 | 9 | 7 | 27 | 22 | 160 | 82.40 |
| 1 | 10 | 6 | 22 | 17 | 130 | 81.82 |
| 20 | 11 | 7 | 32 | 22 | 145 | 82.11 |
| 23 | 12 | 7 | 27 | 22 | 130 | 81.67 |
| 18 | 13 | 8 | 27 | 22 | 145 | 81.63 |
| 8 | 14 | 8 | 32 | 27 | 130 | 80.68 |
| 25 | 15 | 7 | 27 | 22 | 145 | 82.23 |
| 6 | 16 | 8 | 22 | 27 | 130 | 80.95 |
| 13 | 17 | 6 | 22 | 27 | 160 | 81.47 |
| 7 | 18 | 6 | 32 | 27 | 130 | 80.74 |
| 3 | 19 | 6 | 32 | 17 | 130 | 81.83 |
| 22 | 20 | 7 | 27 | 27 | 145 | 81.19 |
| 9 | 21 | 6 | 22 | 17 | 160 | 82.61 |
| 12 | 22 | 8 | 32 | 17 | 160 | 81.39 |
| 21 | 23 | 7 | 27 | 17 | 145 | 82.70 |
| 5 | 24 | 6 | 22 | 27 | 130 | 80.81 |
| 15 | 25 | 6 | 32 | 27 | 160 | 81.25 |
| Variance Analysis | |||||
|---|---|---|---|---|---|
| Source | Degrees of Freedom | Adj SS | Adj MS | F Value | p Value |
| Model | 14 | 14.2030 | 1.01450 | 19.70 | 0.000 |
| Linear | 4 | 9.4905 | 2.37263 | 46.08 | 0.000 |
| Z | 1 | 1.5371 | 1.53709 | 29.85 | 0.000 |
| β1 | 1 | 0.0648 | 0.06480 | 1.26 | 0.288 |
| β2 | 1 | 7.7356 | 7.73556 | 150.24 | 0.000 |
| φ | 1 | 0.1531 | 0.15309 | 2.97 | 0.115 |
| Square | 4 | 2.4607 | 0.61519 | 11.95 | 0.001 |
| Z × Z | 1 | 0.5374 | 0.53744 | 10.44 | 0.009 |
| β1 × β1 | 1 | 0.0022 | 0.00220 | 0.04 | 0.840 |
| β2 × β2 | 1 | 0.1012 | 0.10124 | 1.97 | 0.191 |
| φ × φ | 1 | 0.0305 | 0.03047 | 0.59 | 0.460 |
| Two-factor interaction | 6 | 2.2517 | 0.37528 | 7.29 | 0.003 |
| Z × β1 | 1 | 0.0827 | 0.08266 | 1.61 | 0.234 |
| Z × β2 | 1 | 0.0127 | 0.01266 | 0.25 | 0.631 |
| Z × φ | 1 | 1.6835 | 1.68351 | 32.70 | 0.000 |
| β1 × β2 | 1 | 0.1173 | 0.11731 | 2.28 | 0.162 |
| β1 × φ | 1 | 0.0613 | 0.06126 | 1.19 | 0.301 |
| β2 × φ | 1 | 0.2943 | 0.29431 | 5.72 | 0.038 |
| Deviation | 10 | 0.5149 | 0.05149 | ||
| Total | 24 | 14.7179 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, G.; Lou, Y.; Yu, D.; Hong, S.; Ji, G.; Ma, L.; Chang, H. Investigation of Energy Loss Mechanism and Vortical Structures Characteristics of Marine Sediment Pump Based on the Response Surface Optimization Method. J. Mar. Sci. Eng. 2023, 11, 2233. https://doi.org/10.3390/jmse11122233
Peng G, Lou Y, Yu D, Hong S, Ji G, Ma L, Chang H. Investigation of Energy Loss Mechanism and Vortical Structures Characteristics of Marine Sediment Pump Based on the Response Surface Optimization Method. Journal of Marine Science and Engineering. 2023; 11(12):2233. https://doi.org/10.3390/jmse11122233
Chicago/Turabian StylePeng, Guangjie, Yuan Lou, Dehui Yu, Shiming Hong, Guangchao Ji, Lie Ma, and Hao Chang. 2023. "Investigation of Energy Loss Mechanism and Vortical Structures Characteristics of Marine Sediment Pump Based on the Response Surface Optimization Method" Journal of Marine Science and Engineering 11, no. 12: 2233. https://doi.org/10.3390/jmse11122233
APA StylePeng, G., Lou, Y., Yu, D., Hong, S., Ji, G., Ma, L., & Chang, H. (2023). Investigation of Energy Loss Mechanism and Vortical Structures Characteristics of Marine Sediment Pump Based on the Response Surface Optimization Method. Journal of Marine Science and Engineering, 11(12), 2233. https://doi.org/10.3390/jmse11122233






