Discrete Element Analysis of Ice-Induced Vibrations of Offshore Wind Turbines in Level Ice
Abstract
:1. Introduction
1.1. Ice-Induced Vibrations in OWTs
1.2. Failure Mode of Sea Ice
1.3. Numerical Methods of Sea Ice
2. Methodology of Sphere-Based DEM for Sea Ice Simulation
2.1. Model Description of Ice–Structure Interaction in DEM
2.2. Governing Equations
2.3. Contact Force Model of Spherical Elements
2.4. Parallel Bonding Model of Spherical Elements
2.5. Bond-Failure Models
- (1)
- Mohr–Coulomb criterion-based bond-failure model
- (2)
- Hybrid fracture energy-based bond-failure model
3. Ice Loads on Cylindric Pile Simulated with Different Bond-Failure Models
4. Ice-Induced Vibration of Offshore Wind Turbine
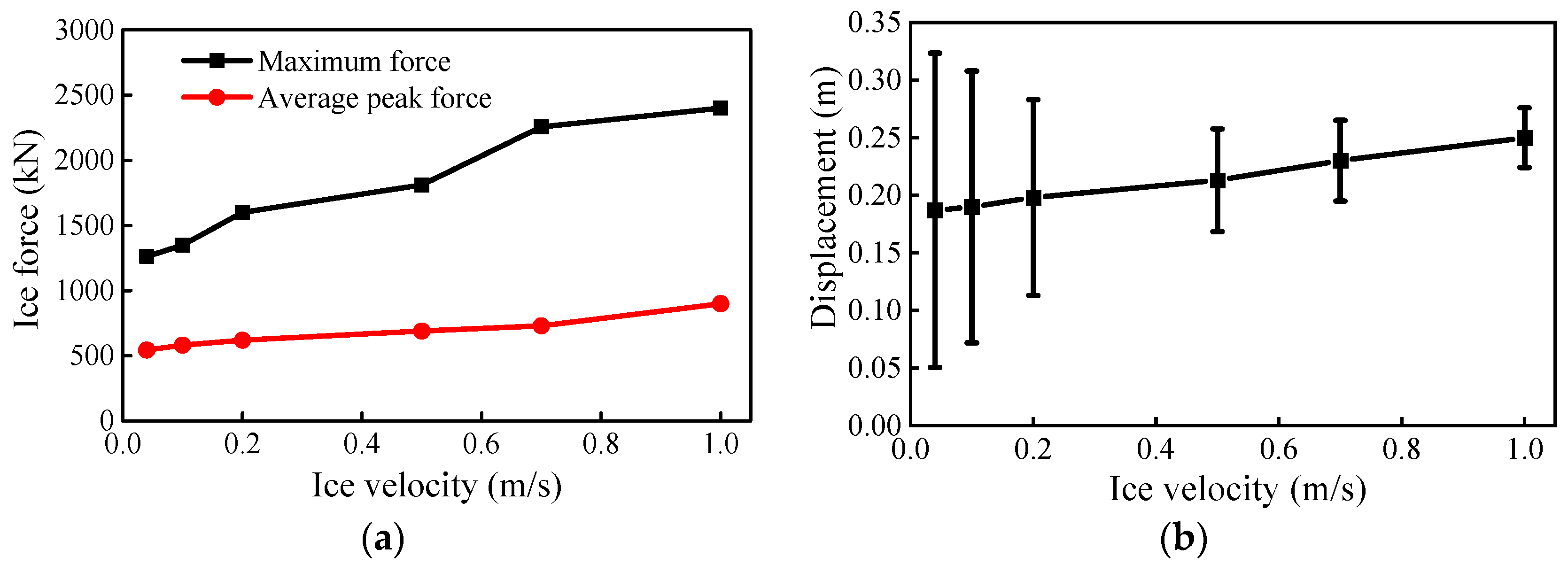
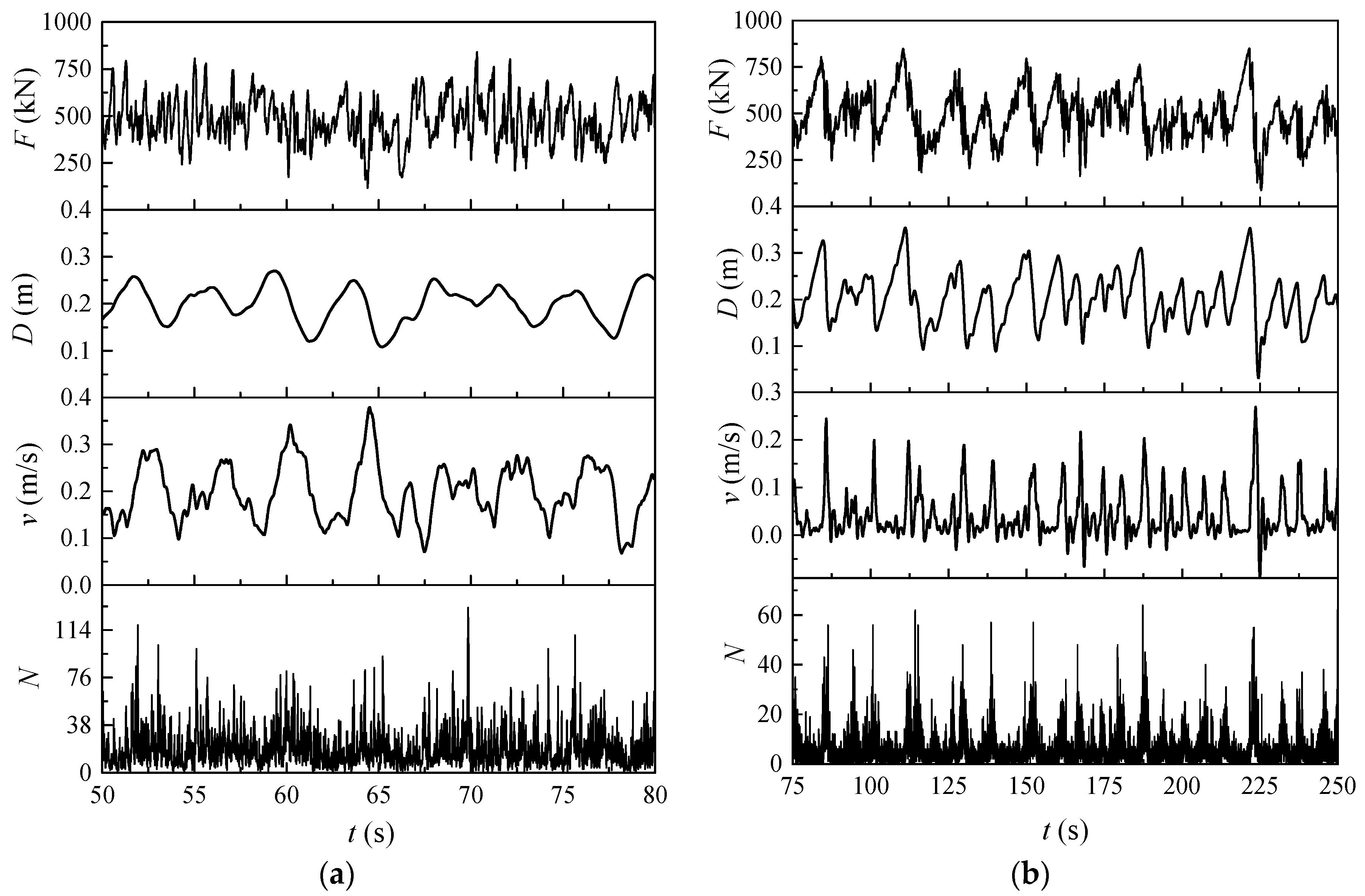
4.1. Influence of Ice Velocity
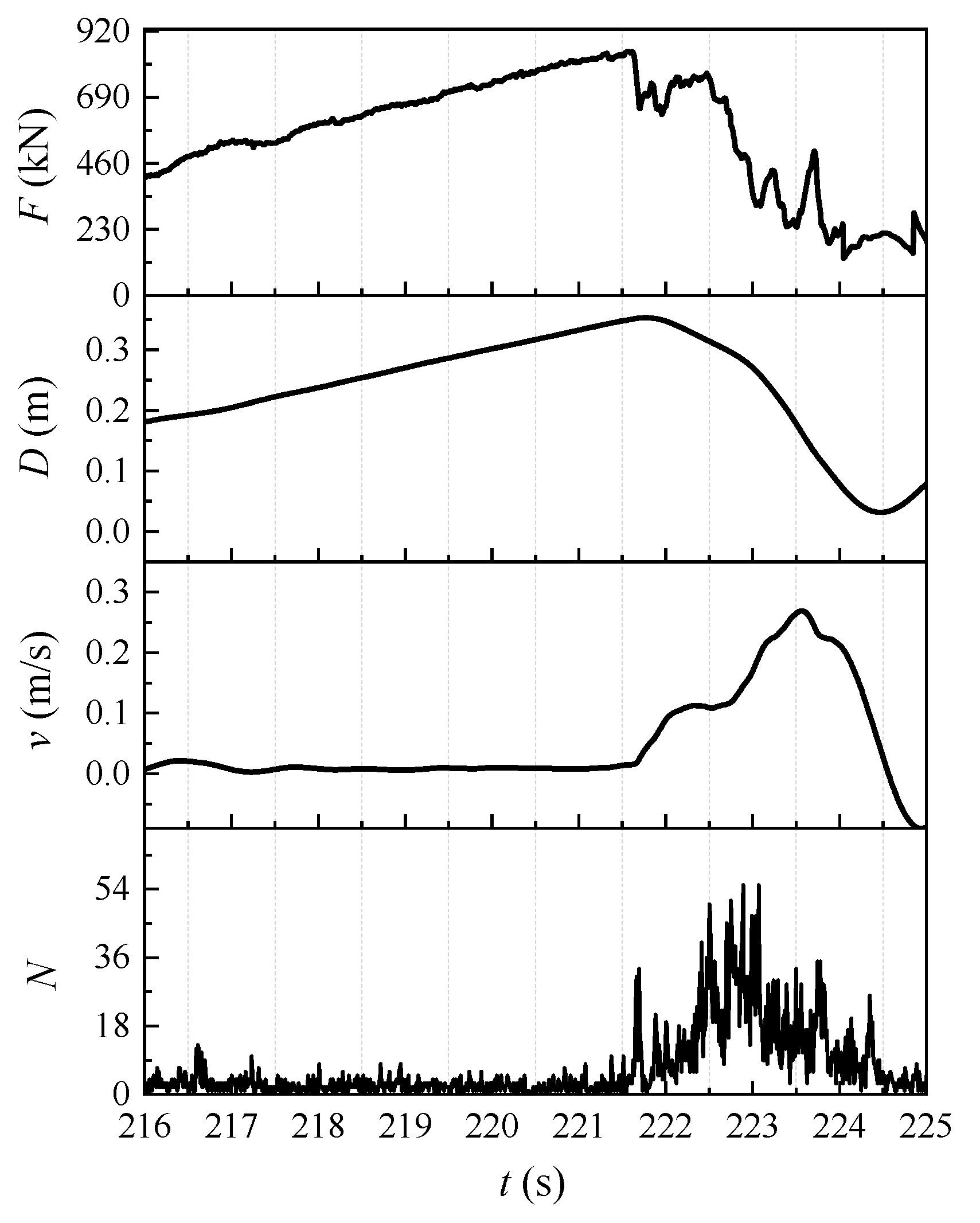
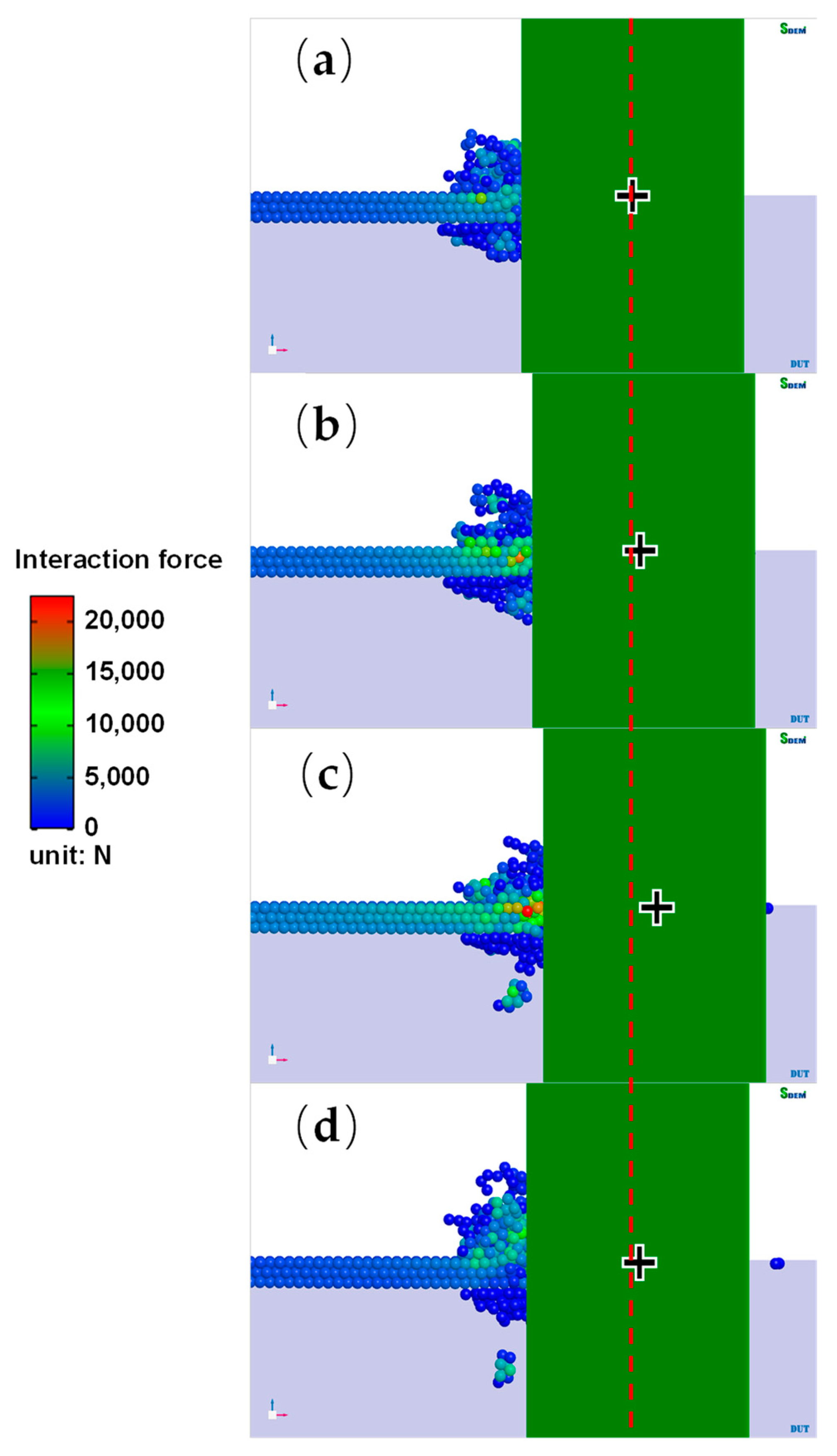
4.2. Discussions
- Ductile crushing failure: When the relative velocity between the sea ice and the structure is relatively small, the sea ice undergoes ductile crushing failure. In this scenario, the interaction between the sea ice and the structure occurs in a manner that leads to ductile failure characteristics. The ice tends to accumulate and crack, and its failure mode is ductile.
- Brittle crushing failure: Conversely, when the relative velocity between the sea ice and the structure is relatively high, the sea ice undergoes brittle crushing failure. This high relative velocity leads to a more brittle failure mode, where the ice fragmentation is rapid, and the front end of the ice sheet loses contact with the structure.
- Ductile-brittle transition: In certain transition regions where the relative velocities are intermediate, a ductile-brittle transition can occur. This implies that the failure mode of the sea ice in these areas may exhibit characteristics of both ductile and brittle compression.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, Y.; Wu, S.; Yu, J.; Xu, Y.; Song, L.; Xu, W. A hybrid multi-criteria decision-making framework for offshore wind turbine selection: A case study in China. Appl. Energy 2022, 328, 120173. [Google Scholar] [CrossRef]
- Wei, S. Offshore Wind Turbine-Ice Interactions. In Encyclopedia of Ocean Engineering; Cui, W., Fu, S., Hu, Z., Eds.; Springer: Singapore, 2020. [Google Scholar]
- Swenson, L.; Gao, L.; Hong, J.; Shen, L. An efficacious model for predicting icing-induced energy loss for wind turbines. Appl. Energy 2022, 305, 117809. [Google Scholar] [CrossRef]
- Barstad, I.; Sorteberg, A.; Mesquita, M.S. Present and future offshore wind power potential in northern Europe based on downscaled global climate runs with adjusted SST and sea ice cover. Renew. Energy 2012, 44, 398–405. [Google Scholar] [CrossRef]
- Wang, X.; Zeng, X.; Yang, X.; Li, J. Feasibility study of offshore wind turbines with hybrid monopile foundation based on centrifuge modeling. Appl. Energy 2018, 209, 127–139. [Google Scholar] [CrossRef]
- Dinh, Q.V.; Doan, Q.V.; Ngo-Duc, T.; Dinh, V.N.; Duc, N.D. Offshore wind resource in the context of global climate change over a tropical area. Appl. Energy 2022, 308, 118369. [Google Scholar] [CrossRef]
- Nord, T.S.; Samardzija, I.; Hendrikse, H.; Bjerkås, M.; Høyland, K.V.; Li, H. Ice-induced vibrations of the Norströmsgrund lighthouse. Cold Reg. Sci. Technol. 2018, 155, 237–251. [Google Scholar] [CrossRef]
- Huang, S.; Huang, M.; Lyu, Y.; Xiu, L. Effect of sea ice on seismic collapse-resistance performance of wind turbine tower based on a simplified calculation model. Eng. Struct. 2021, 227, 111426. [Google Scholar] [CrossRef]
- Wang, X.; Zeng, X.; Yang, X.; Li, J. Seismic response of offshore wind turbine with hybrid monopile foundation based on centrifuge modelling. Appl. Energy 2019, 235, 1335–1350. [Google Scholar] [CrossRef]
- Frederking, R.; Sudom, D. Maximum ice force on the Molikpaq during the April 12, 1986 event. Cold Reg. Sci. Technol. 2006, 46, 147–166. [Google Scholar] [CrossRef]
- Wang, S.; Yue, Q.; Zhang, D. Ice-induced non-structure vibration reduction of jacket platforms with isolation cone system. Ocean Eng. 2013, 70, 118–123. [Google Scholar] [CrossRef]
- Yue, Q.; Qu, Y.; Bi, X.; Kärnä, T. Ice force spectrum on narrow conical structures. Cold Reg. Sci. Technol. 2007, 49, 161–169. [Google Scholar] [CrossRef]
- Nord, T.S.; Øiseth, O.; Lourens, E.M. Ice force identification on the Norströmsgrund lighthouse. Comput. Struct. 2016, 169, 24–39. [Google Scholar] [CrossRef]
- ISO19906; Petroleum and Natural Gas Industries—Arctic Offshore Structures. International Organization for Standardization: Geneva, Switzerland, 2010.
- Sodhi, D.S. A theoretical model for Ice-Structure Interaction. In Proceedings of the OMAE-94 Conference; ASME: New York, NY, USA, 1994; Volume IV, pp. 29–34. [Google Scholar]
- Hendrikse, H.; Metrikine, A. Interpretation and prediction of ice induced vibrations based on contact area variation. Int. J. Solids Struct. 2015, 75–76, 336–348. [Google Scholar] [CrossRef]
- Ji, X.; Oterkus, E. A dynamic ice-structure interaction model for ice-induced vibrations by using van der pol equation. Ocean Eng. 2016, 128, 147–152. [Google Scholar] [CrossRef]
- Abramian, A.K.; Vakulenko, S.A.; Horssen, W.T.V. A mathematical analysis of an extended model describing sea ice-induced frequency lock-in for vertically sided offshore structures. Nonlinear Dyn. 2022, 107, 683–699. [Google Scholar] [CrossRef]
- Snyder, S.A.; Schulson, E.M.; Renshaw, C.E. Effects of prestrain on the ductile-to-brittle transition of ice. Acta Mater. 2016, 108, 110–127. [Google Scholar] [CrossRef]
- Seidela, M.; Hendrikse, H. Analytical assessment of sea ice-induced frequency lock-in for offshore wind turbine monopiles. Mar. Struct. 2018, 60, 87–100. [Google Scholar] [CrossRef]
- Gagnon, R. Spallation-based numerical simulations of ice-induced vibration of structures. Cold Reg. Sci. Technol. 2022, 194, 103465. [Google Scholar] [CrossRef]
- Schulson, E.M. Brittle failure of ice. Eng. Fract. Mech. 2001, 68, 1839–1887. [Google Scholar] [CrossRef]
- Zhang, D.Y.; Wang, G.J.; Yue, Q.J. Evaluation of ice-induced fatigue life for a vertical offshore structure in the Bohai Sea. Cold Reg. Sci. Technol. 2018, 154, 103–110. [Google Scholar] [CrossRef]
- Zhu, B.; Sun, C.; Jahangiri, V. Characterizing and mitigating ice-induced vibration of monopile offshore wind turbines. Ocean Eng. 2021, 219, 108406. [Google Scholar] [CrossRef]
- Dempsey, J.P.; Palmer, A.C.; Sodhi, D.S. High pressure zone formation during compressive ice failure. Eng. Fract. Mech. 2001, 68, 1961–1974. [Google Scholar] [CrossRef]
- Tian, Y.; Huang, Y. The dynamic ice loads on conical structures. Ocean Eng. 2013, 59, 37–46. [Google Scholar] [CrossRef]
- Qu, Y.; Yue, Q.; Bi, X.; Kärnä, T. A random ice force model for narrow conical structures. Cold Reg. Sci. Technol. 2006, 45, 148–157. [Google Scholar]
- Xue, Y.Z.; Liu, R.W.; Li, Z.; Han, D.F. A review for numerical simulation methods of ship–ice interaction. Ocean Eng. 2020, 215, 107853. [Google Scholar] [CrossRef]
- Banerjee, S.; Agarwal, R. Transient reacting flow simulation of spouted fluidized bed for coal-direct chemical looping combustion with different Fe-based oxygen carriers. Appl. Energy 2015, 160, 552–560. [Google Scholar] [CrossRef]
- Gaviño, D.; Cortés, E.; García, J.; Calderón-Vásquez, I.; Cardemil, J.; Estay, D.; Barraza, R. A discrete element approach to model packed bed thermal storage. Appl. Energy 2022, 325, 119821. [Google Scholar] [CrossRef]
- Feng, Y.H.; Dai, Y.J.; Wang, R.Z.; Ge, T.S. Insights into desiccant-based internally-cooled dehumidification using porous sorbents: From a modeling viewpoint. Appl. Energy 2022, 311, 118732. [Google Scholar] [CrossRef]
- Shen, H.H.; Hibler, W.D.; Leppäranta, M. On applying granular flow theory to a deforming broken ice field. Acta Mech. 1986, 63, 143–160. [Google Scholar] [CrossRef]
- Wang, C.; Xu, Z.; Koeppel, B. A discrete element model simulation of structure and bonding at interfaces between cathode and cathode contact paste in solid oxide fuel cells. Renew. Energy 2020, 157, 998–1007. [Google Scholar] [CrossRef]
- Li, Z.; Yu, J.; Yue, Q.; Yu, Y.; Guo, X. Study on meso-mechanical mechanism and energy of moisture content on densification of salix psammophila particles. Renew. Energy 2023, 205, 1071–1081. [Google Scholar] [CrossRef]
- Tuhkuri, J.; Polojärvi, A. A review of discrete element simulation of ice–structure interaction. Phil. Trans. R. Soc. A 2018, 376, 20170335. [Google Scholar] [CrossRef] [PubMed]
- Long, X.; Liu, S.; Ji, S. Discrete element modelling of relationship between ice breaking length and ice load on conical structure. Ocean Eng. 2020, 201, 107152. [Google Scholar] [CrossRef]
- Sun, S.; Shen, H.H. Simulation of pancake ice load on a circular cylinder in a wave and current field. Cold Reg. Sci. Technol. 2012, 78, 21–39. [Google Scholar] [CrossRef]
- Pradana, M.R.; Qian, X.; Ahmed, A. Efficient discrete element simulation of managed ice actions on moored floating platforms. Ocean Eng. 2019, 190, 106483. [Google Scholar] [CrossRef]
- Brædstrup, C.F.; Damsgaard, A.; Egholm, D.L. Ice-sheet modelling accelerated by graphics cards. Comput. Geosci. 2014, 72, 210–220. [Google Scholar] [CrossRef]
- Jou, O.; Celigueta, M.A.; Latorre, S.; Arrufat, F.; Oñate, E. A bonded discrete element method for modeling ship–ice interactions in broken and unbroken sea ice fields. Comput. Part. Mech. 2019, 6, 739–765. [Google Scholar] [CrossRef]
- Di, S.; Xue, Y.; Wang, Q.; Bai, X. Discrete element simulation of ice loads on narrow conical structures. Ocean Eng. 2017, 146, 282–297. [Google Scholar] [CrossRef]
- Guo, L.; Latham, J.P.; Xiang, J. Numerical simulation of breakages of concrete armour units using a three-dimensional fracture model in the context of the combined finite-discrete element method. Comput. Struct. 2015, 146, 117–142. [Google Scholar] [CrossRef]
- Ma, G.; Zhou, W.; Chang, X.L.; Chen, M.X. A hybrid approach for modeling of breakable granular materials using combined finite-discrete element method. Granul. Matter 2016, 18, 7. [Google Scholar] [CrossRef]
- Mcdowell, G.R.; Bolton, M.D.; Robertson, D. The fractal crushing of granular materials. J. Mech. Phys. Solids 1996, 44, 2079–2102. [Google Scholar] [CrossRef]
- Lu, W.; Lubbad, R.; Løset, S. Simulating ice-sloping structure interactions with the cohesive element method. J. Offshore Mech. Arct. Eng. 2014, 136, 031501. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Wang, Y.; Mora, P. Macroscopic elastic properties of regular lattices. J. Mech. Phys. Solids 2008, 56, 3459–3474. [Google Scholar] [CrossRef]
- Pradana, M.R.; Qian, X. Bridging local parameters with global mechanical properties in bonded discrete elements for ice load prediction on conical structures. Cold Reg. Sci. Technol. 2020, 173, 102960. [Google Scholar] [CrossRef]
- Morgan, D.; Sarracino, R.; McKenna, R.; Thijssen, J.W. Simulations of ice rubbling against conical structures using 3D DEM. In Proceedings of the 23rd International Conference on Port and Ocean Engineering under Arctic Conditions (POAC ‘15), Trondheim, Norway, 14–18 June 2015. [Google Scholar]
- Di, S.; Xue, Y.; Bai, X.; Wang, Q. Effects of model size and particle size on the response of sea-ice samples created with a hexagonal-close-packing pattern in discrete- element method simulations. Particuology 2018, 36, 106–113. [Google Scholar] [CrossRef]
- Long, X.; Ji, S.; Wang, Y. Validation of microparameters in discrete element modeling of sea ice failure process. Part. Sci. Technol. 2019, 37, 550–559. [Google Scholar] [CrossRef]
- Zhou, Q.; Xu, W.J.; Liu, G.Y. A contact detection algorithm for triangle boundary in GPU-based DEM and its application in a large-scale landslide. Comput. Geotech. 2021, 138, 104371. [Google Scholar] [CrossRef]
- Williams, J.R.; O’connor, R. A linear complexity intersection algorithm for discrete element simulation of arbitrary geometries. Eng. Comput. 1995, 12, 185–201. [Google Scholar] [CrossRef]
- Huang, P.; Ding, Y.; Miao, Q.; Sang, G.; Jia, M. An improved contact detection algorithm for bonded particles based on multi-level grid and bounding box in DEM simulation. Powder Technol. 2020, 374, 577–596. [Google Scholar] [CrossRef]
- Hopkins, M.; Shen, H. Simulation of pancake-ice dynamics in a wave field. Ann. Glaciol. 2001, 33, 355–360. [Google Scholar] [CrossRef]
- Govender, N.; Wilke, D.N.; Kok, S.; Els, R. Development of a convex polyhedral discrete element simulation framework for NVIDIA Kepler based GPUs. J. Comput. Appl. Math. 2014, 270, 386–400. [Google Scholar] [CrossRef]
- Raji, A.; Favier, J. Discrete element modelling of the compression of an oil-seed bed. In Proceedings of the ASAE International Conference, Toronto, ON, Canada, 18–21 July 1999. [Google Scholar]
- Long, X.; Liu, L.; Liu, S.; Ji, S. Discrete element analysis of high-pressure zones of sea ice on vertical structures. J. Mar. Sci. Eng 2021, 9, 348. [Google Scholar] [CrossRef]
- Benzeggagh, M.L.; Kenane, M. Measurement of Mixed-Mode Delamination Fracture Toughness of Unidirectional Glass/Epoxy Composites with Mixed-Mode Bending Apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]
- Ma, G.; Zhou, W.; Chang, X.L. Modeling the particle breakage of rockfill materials with the cohesive crack model. Comput. Geotech. 2014, 61, 132–143. [Google Scholar] [CrossRef]
- Camanho, P.P.; Davila, C.G.; Moura, M.F.D. Numerical Simulation of Mixed-Mode Progressive Delamination in Composite . Mater. J. Compos. Mater. 2003, 37, 1415–1438. [Google Scholar] [CrossRef]
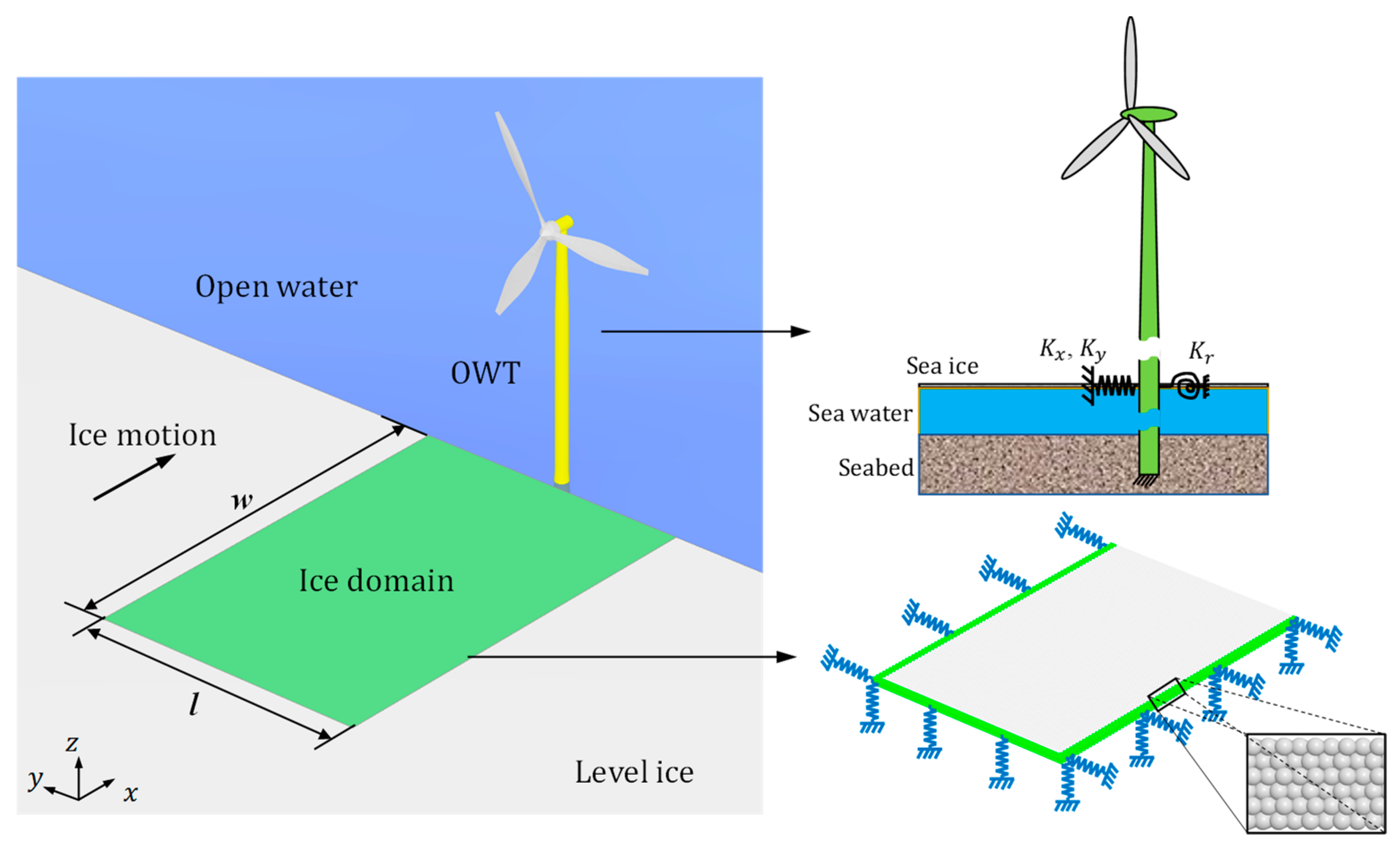

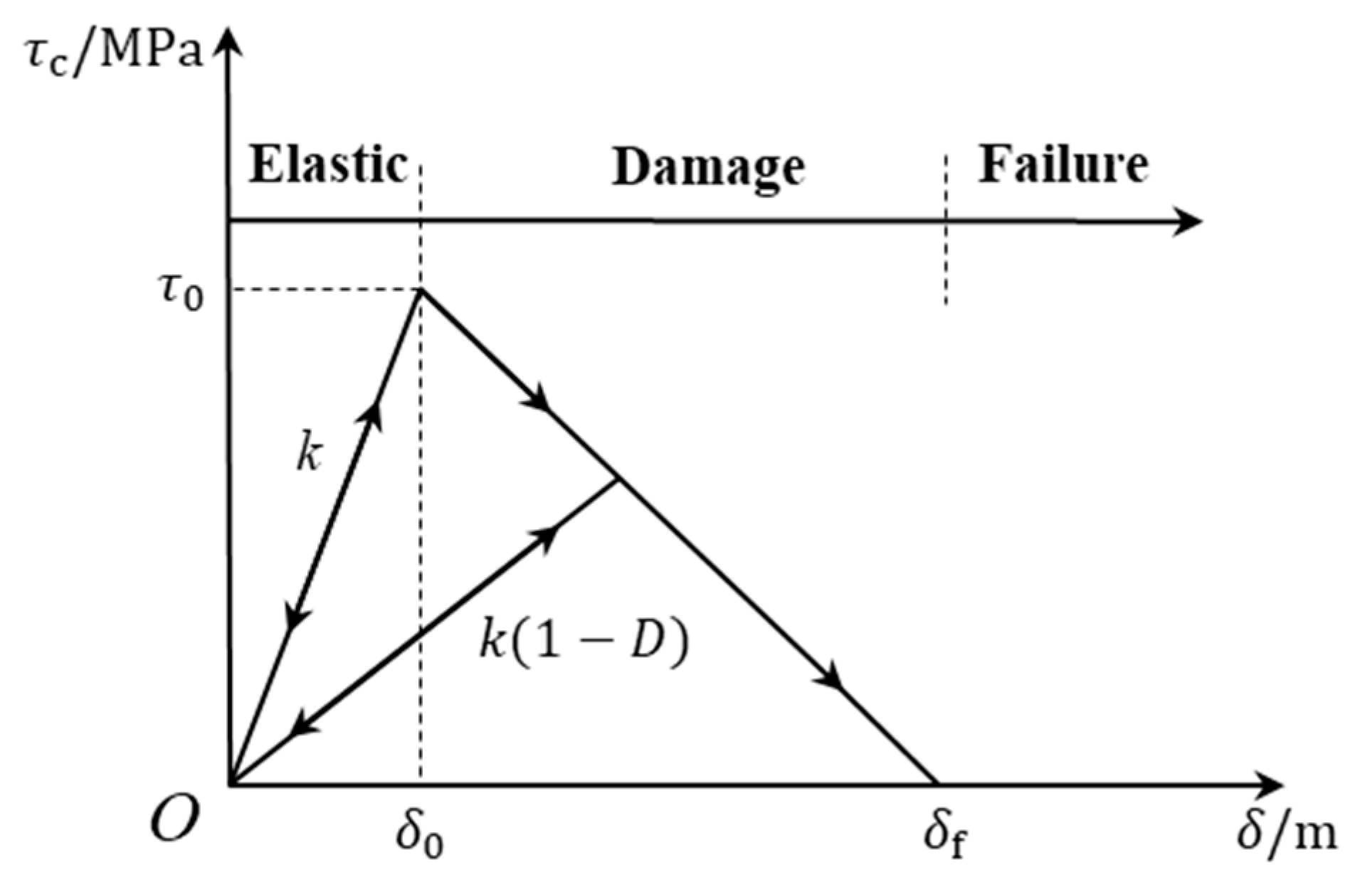

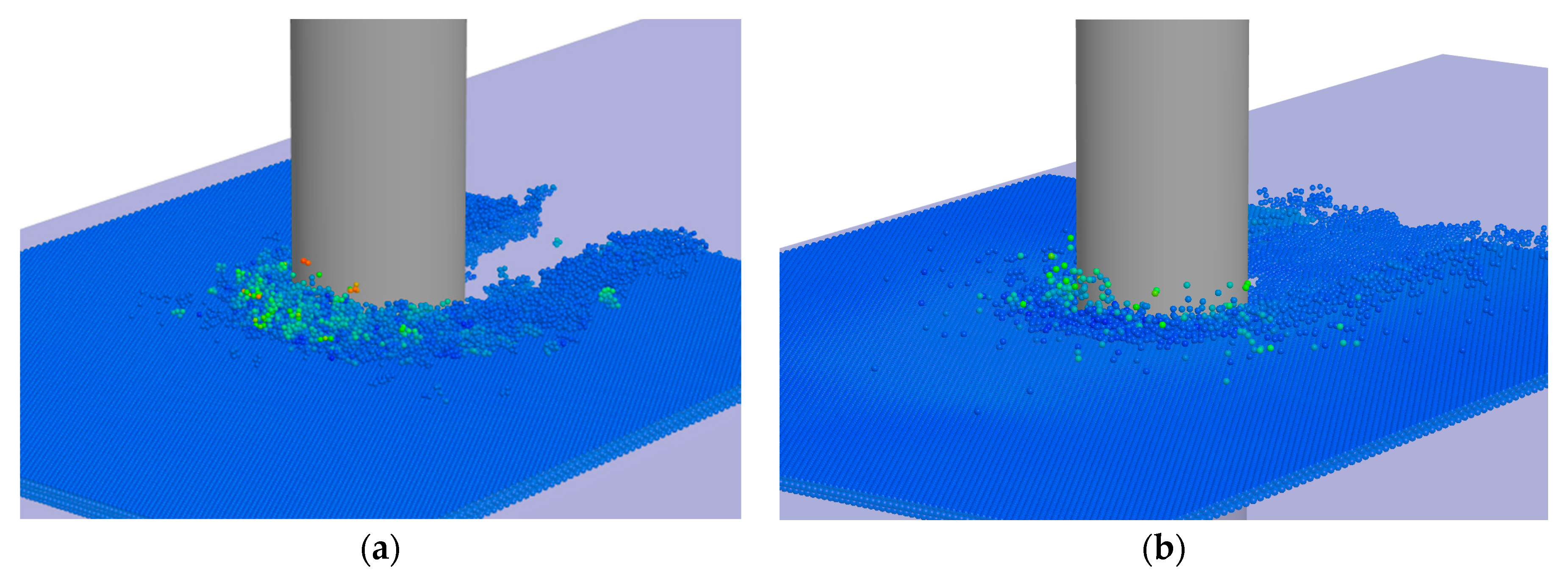
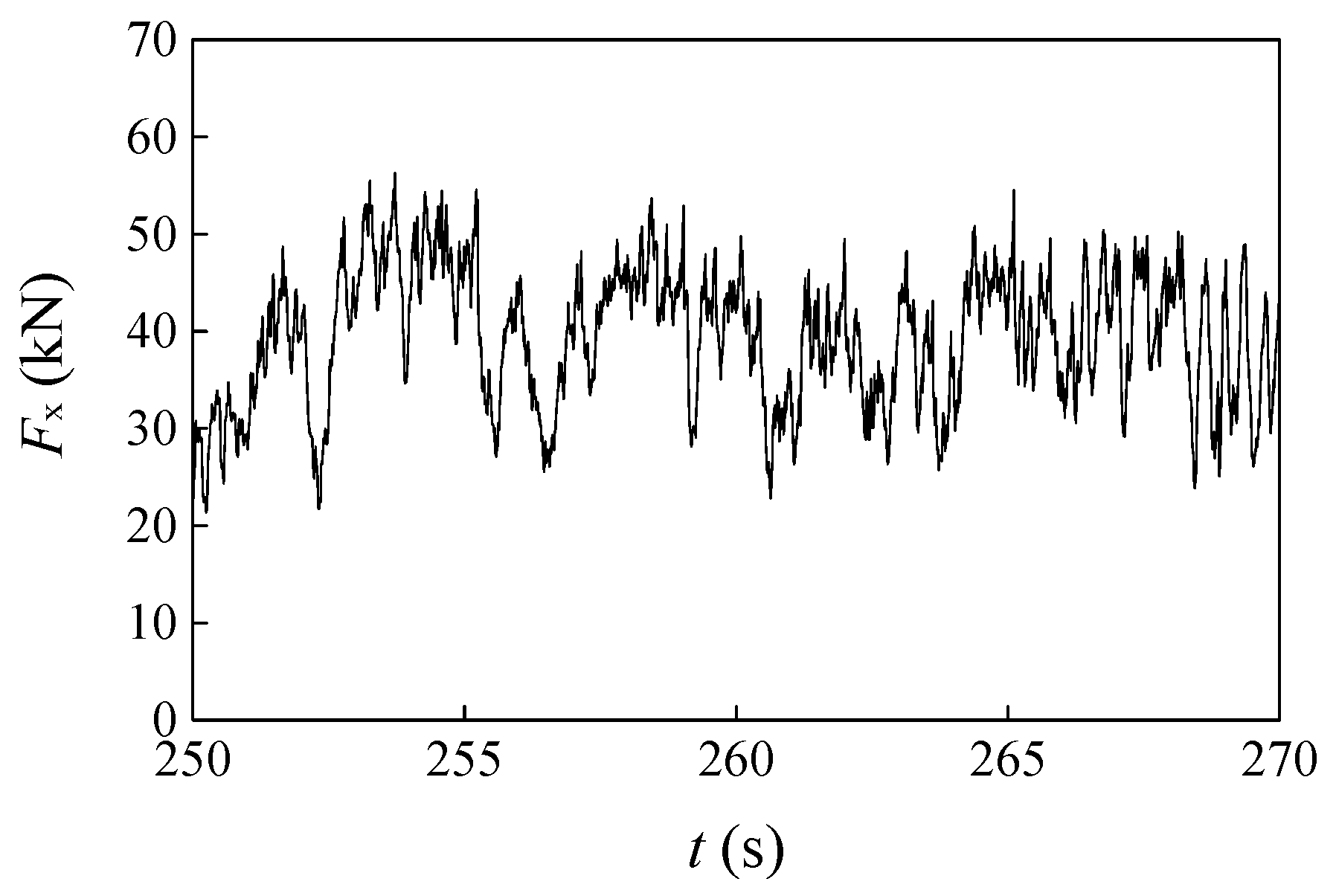
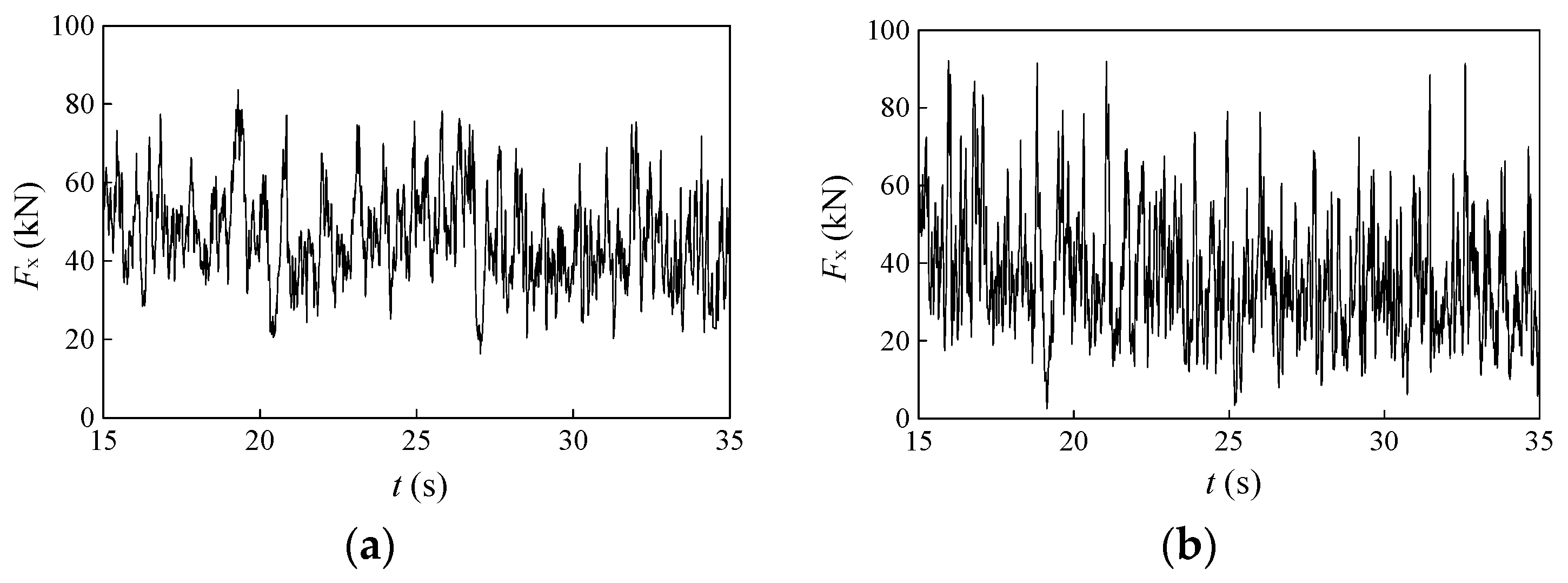
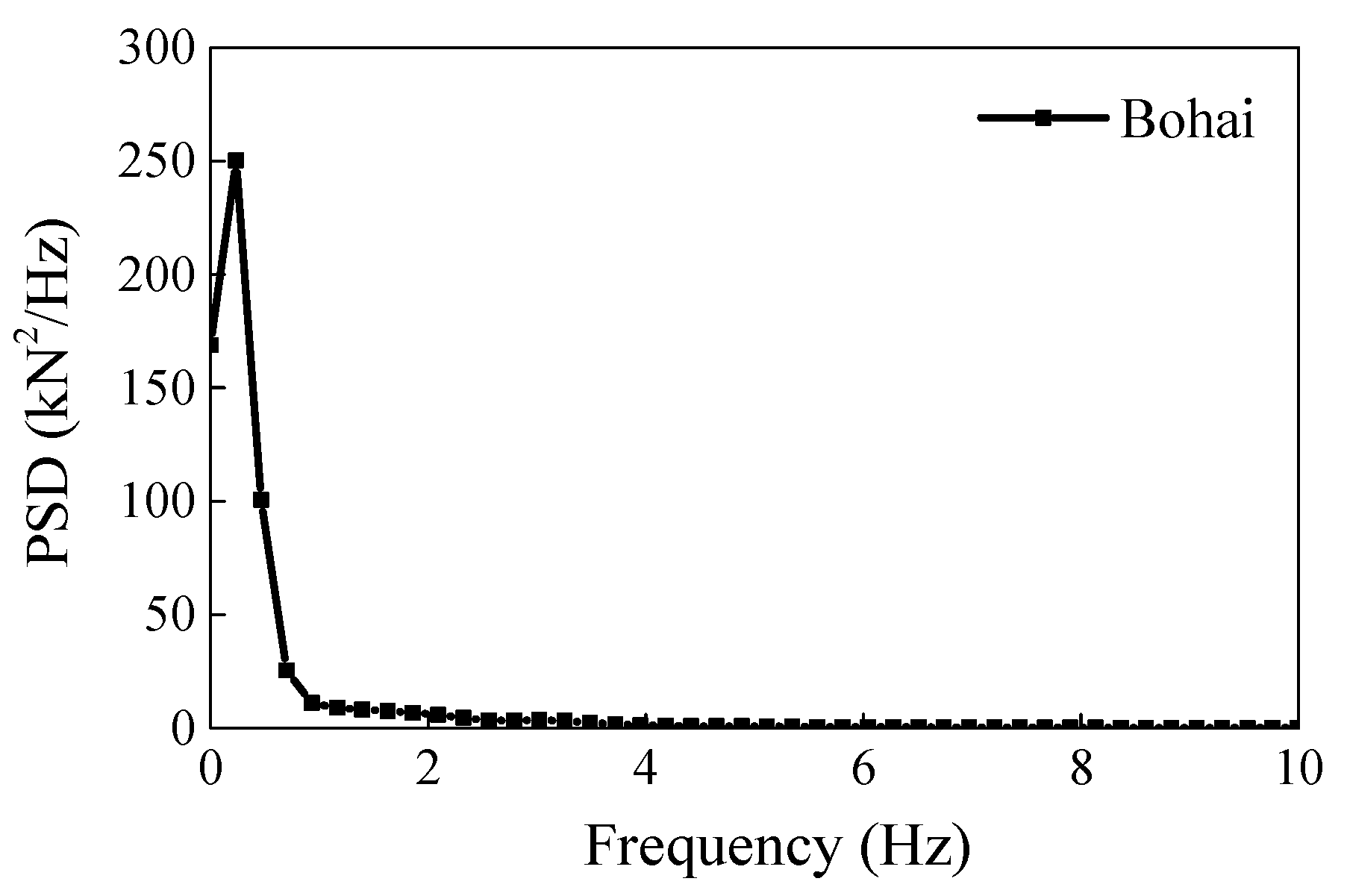


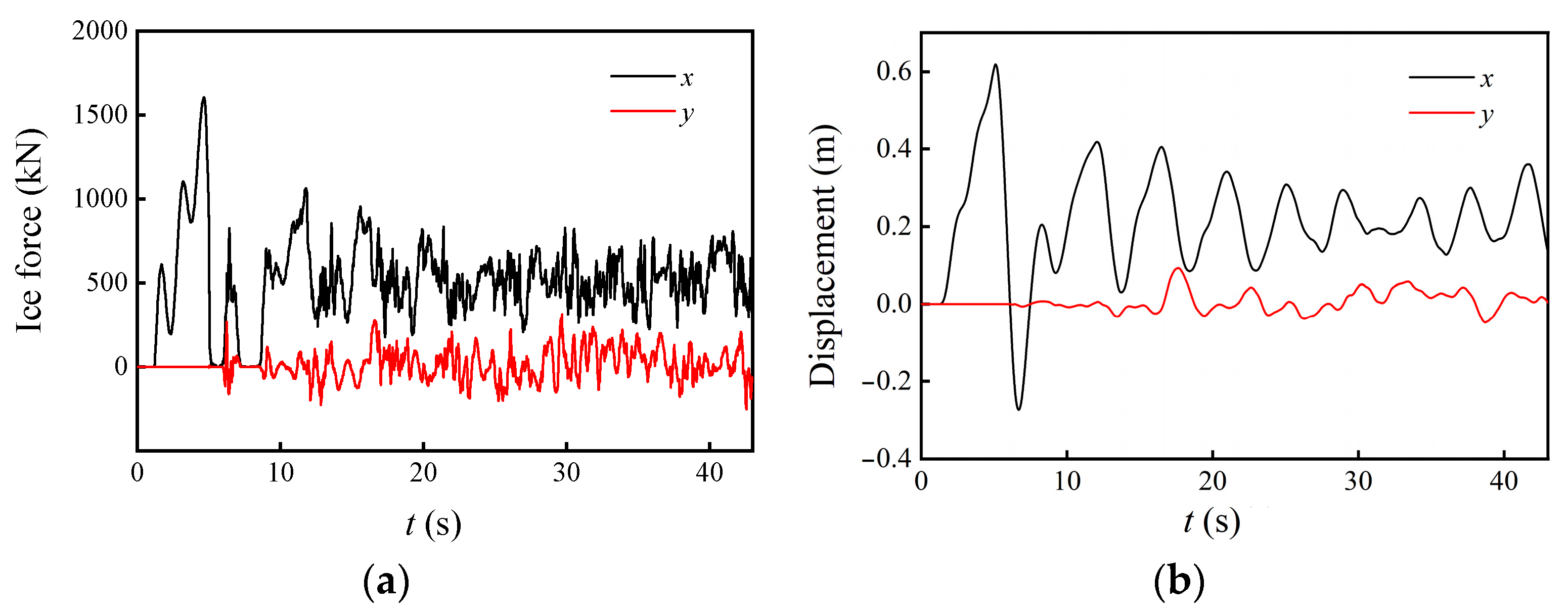
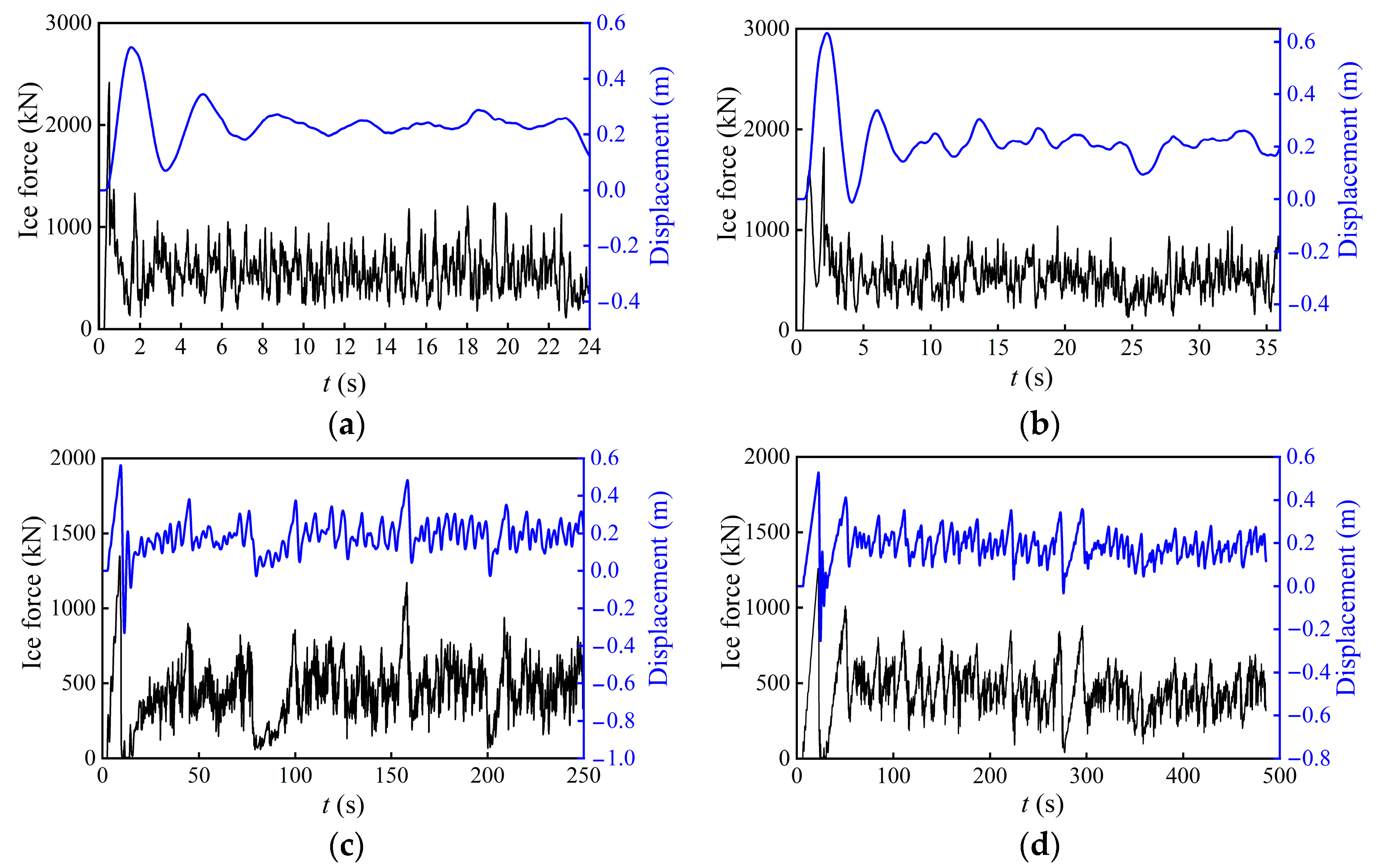
| Definition | Symbol | Value |
|---|---|---|
| Density of sea ice | 920 kg/m3 | |
| Density of seawater | 1035 kg/m3 | |
| Sample size | 20 m 10 m 0.18 m | |
| Element size | 4.48 cm | |
| Normal stiffness | 1.72 × 107 N/m | |
| Shear stiffness | 1.72 × 106 N/m | |
| Internal friction | 0.2 | |
| Normal bonding strength | 0.5 MPa | |
| Shear bonding strength | 0.5 MPa | |
| Sea ice velocity | 0.2 m/s | |
| Drag coefficient | 0.05 | |
| Element number | 608,790 |
| Definitions | Values |
|---|---|
| Structure mass | 7.69 × 105 kg |
| Structure stiffness | 2.42 × 106 N/m |
| Structure damping | 0.15 |
| Natural frequency of structure | 1.77 Hz |
| Structure diameter in waterline | 5.50 m |
| Sea ice thickness | 0.30 m |
| Element size | 0.11 m |
| Bonding strength | 1.01 MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, X.; Liu, L.; Ji, S. Discrete Element Analysis of Ice-Induced Vibrations of Offshore Wind Turbines in Level Ice. J. Mar. Sci. Eng. 2023, 11, 2153. https://doi.org/10.3390/jmse11112153
Long X, Liu L, Ji S. Discrete Element Analysis of Ice-Induced Vibrations of Offshore Wind Turbines in Level Ice. Journal of Marine Science and Engineering. 2023; 11(11):2153. https://doi.org/10.3390/jmse11112153
Chicago/Turabian StyleLong, Xue, Lu Liu, and Shunying Ji. 2023. "Discrete Element Analysis of Ice-Induced Vibrations of Offshore Wind Turbines in Level Ice" Journal of Marine Science and Engineering 11, no. 11: 2153. https://doi.org/10.3390/jmse11112153
APA StyleLong, X., Liu, L., & Ji, S. (2023). Discrete Element Analysis of Ice-Induced Vibrations of Offshore Wind Turbines in Level Ice. Journal of Marine Science and Engineering, 11(11), 2153. https://doi.org/10.3390/jmse11112153







