Hydrodynamic Loads and Overtopping Processes of a Coastal Seawall under the Coupled Impact of Extreme Waves and Wind

Abstract

Driven by strong winds, huge ocean waves can cause devastating destruction to coastal regions during harsh weather events. There is growing evidence showing that extreme waves can occur in both shallow and deep waters. To protect the coast against the destructive power of huge waves, coastal protection facilities, such as seawalls, are often built along the coast. The integrity and stability of these coastal protection facilities are essential to the safety of coastal regions. Since huge waves are often accompanied by strong winds in real ocean environments, to fill the knowledge gap left by previous relevant studies, this study numerically investigates the hydrodynamic loads and overtopping of a coastal seawall model on a sloped beach under the coupled impact of an extreme wave group and wind. The influences of several main factors are considered, such as water depth, wind speed, and significant wave height. The research results reveal that strong wind can greatly increase the average overtopping rate and enhance the hydrodynamic loads exerted by the extreme wave group on the seawall.

1. Introduction

With the action of strong winds, large ocean waves can cause massive destruction to coastal regions during hurricanes. To protect the coast from the damaging power of extreme waves, coastal protection facilities, i.e., seawalls and breakwaters, are often constructed on the coast. These wind-intensified strong waves threaten the integrity and stability of these coastal protection facilities, which are essential to the safety of the coastal region [1,2]. In a real ocean environment, strong winds and ocean waves coexist during hurricanes [3,4]. Therefore, there is important engineering significance and academic value in evaluating the hydrodynamic performance of coastal protection facilities under the coupled impact of extreme waves and wind.

Strong waves are often accompanied by strong winds in real ocean environments. Strong winds can impose noticeable pressure imbalance and surface shear stress forces at the water surface, which can significantly influence wave-shoaling energy [5], as well as the wave-breaking process [6]. Driven by strong winds, ocean surface waves tend to break in advance in a deeper-water region [7]. Meanwhile, wave overtopping of coastal infrastructures and wave runup processes can be greatly affected by strong wind, as reported in the experimental works of Ward et al. [8,9,10]. However, the influence of low-speed wind has been observed to be very limited, and only high-speed wind can greatly increase the runup height of incident waves. In addition, strong winds can significantly affect wave-breaking locations and the breaker type [6]. The average overtopping rate of seawalls can also be greatly enhanced [11]. In addition to experimental work, numerical modeling was conducted to investigate wave–wind interactions. In the simulations, Jeffreys’ sheltering mechanism [12,13] and Miles’ shearing mechanism [14,15] were commonly applied as external forces, imposing pressure and dissipation terms on the water surface. Nevertheless, these classical theories cannot describe the complex dynamics of turbulence effects [16]. By imposing wind shear stress on the ocean surface using an empirical formula, Di Leo et al. [17] evaluated the effect of wind on wave overtopping of vertical walls. In recent years, high-resolution two-phase flow solvers have been applied to analyze the complex phenomena within wave–wind interactions, such as the effects of winds on wave transformation [18], wave overtopping [19], wave breaking [20], wave hydrodynamics of fringing reefs [21], and the joint impact of wind and waves on coastal structures [22].

Flow characteristics around a coastal seawall are impacted by various incident waves, such as tsunami-like waves [23,24], and regular and irregular waves [25,26,27], which have been extensively investigated using theoretical [28], experimental [29], and numerical approaches [30]. Many empirical formulas for analyzing a series of experimental data have been proposed to predict the overtopping rate [31], runup height of water bodies overtopping seawalls [20], and the hydrodynamic loads on the seawall imposed by overtopping water [10]. In recent years, some seawall overtopping manuals have been released, such as EurOtop [32]. However, the above studies ignore the influences of strong winds on the overtopping properties of coastal seawalls. Qu et al. [4] recently studied the influence of wind on the overtopping of seawalls by a solitary wave. It was reported that strong wind can noticeably enhance the average overtopping rate of a seawall. However, a solitary wave is a kind of single-wave model that cannot represent extreme waves in the real world. Furthermore, it is impossible to accurately describe the overtopping properties of seawalls without considering the effects of wind during extreme weather conditions. Although extreme waves occur unpredictably, wave-focusing processes can generate huge waves that can cause massive damage to coastal structures [1]. In addition, increasing observational data show that extreme waves can occur in both deep and shallow waters [33]. Hence, an analysis of the overtopping of seawalls under the joint impact of strong winds and extreme waves, especially when the intactness of the seawall itself is vulnerable to extreme waves, is urgent [34]. Using a high-accuracy, two-phase flow solver, this study numerically investigates the hydrodynamic loads and overtopping of a coastal seawall under the coupled impact of an extreme wave group and wind by discussing the influences of some main factors, such as water depth, wind speed, and significant wave height.

The rest of this paper is organized as follows: Section 2 describes the control equations and the numerical methods of the flow solver and the model validation; the results are discussed in Section 3; and Section 4 summarizes the main research findings.

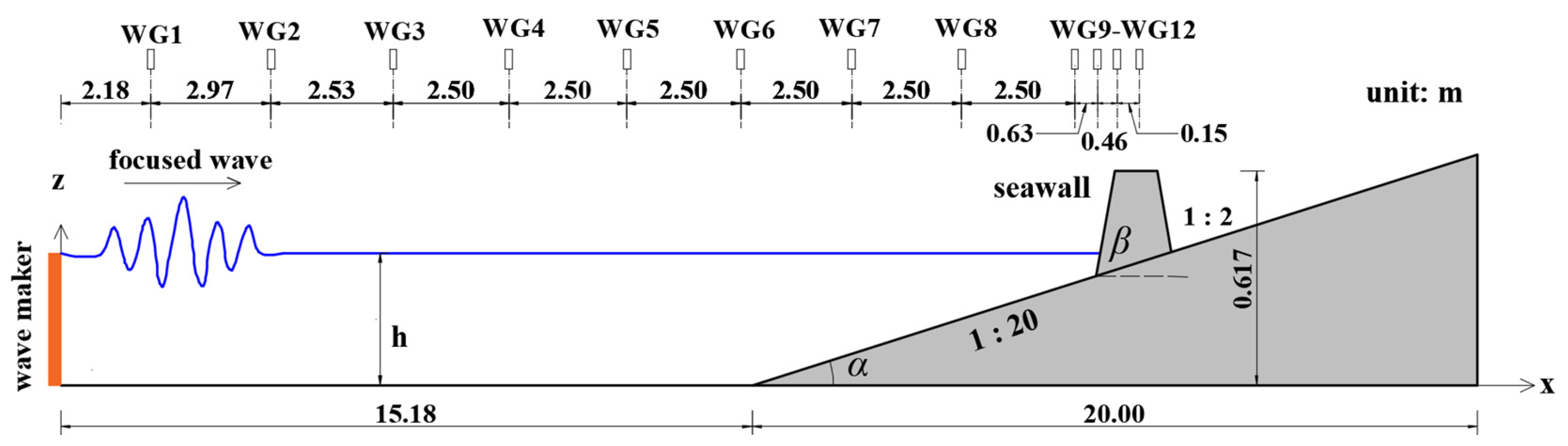
2. Methodology

2.1. Numerical Flow Solver

Complex wave–wind interactions and their coupled impact on coastal seawalls are described using two-phase incompressible flow, whose governing equations can be formulated as

$$\frac{\partial u_i}{\partial x_i}=0$$

(1)

$$\frac{\partial \rho u_i}{\partial t}+{\rho u}_j\frac{\partial u_i}{\partial x_j}=-\frac{\partial p}{\partial x_i}+\frac{\partial }{x_j}\left[{\mu }_{eff}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)\right]+{\rho g}_i$$

(2)

where $t$ is time, $p$ is static pressure, $u_i$ is flow velocity, $\rho$ is the density of the air–water mixture, and ${\mu }_{eff}$ is effective viscosity by adding laminar viscosity (${\mu }_l$) and eddy viscosity (${\mu }_t$). $g_i$ represents the acceleration of gravity in the vertical direction.

In the present study, eddy viscosity (${\mu }_t$) is computed using Wilcox’s $k-\omega$ turbulence model [35]. The governing equations for kinetic energy ($k$) and specific turbulent dissipation ($\omega$) can be formulated as follows

$$\frac{\partial \rho k}{\partial t}+{\rho u}_j\frac{\partial k}{\partial x_j}=\frac{\partial }{\partial x_j}\left[\left({\mu }_l+\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_j}\right]+2{\mu }_t{\left|S_{i,j}\right|}^2-\rho k\omega$$

(3)

$$\frac{\partial \rho \omega }{\partial t}+{\rho u}_j\frac{\partial \omega }{\partial x_j}=\frac{\partial }{\partial x_j}\left[\left({\mu }_l+\frac{{\mu }_t}{{\sigma }_{\omega }}\right)\frac{\partial \omega }{\partial x_j}\right]+2c_{\mu }{c}_{\omega 1}{\rho \left|S_{i,j}\right|}^2-c_{\omega 2}{\rho \omega }^2$$

(4)

where ${\sigma }_{\omega }={\sigma }_k=2$, $c_{\mu }=0.09$, $c_{\omega 1}=\frac{5}{9}$, and $c_{\omega 2}=\frac{5}{6}$. The eddy viscosity can be calculated as ${\mu }_t=\rho \frac{k}{\omega }$. $S$ is calculated as

$$S_{i,j}=\frac{1}{2}\left(\frac{\partial u_j}{\partial x_i}+\frac{\partial u_i}{\partial x_j}\right)$$

(5)

In this study, a high-resolution VOF (volume of fluid) scheme called STACS (Switching Technique for Advection and Capturing of Surfaces) [36] is implemented to compute the air–water interface. Transportation of the VOF ($\gamma$) can be described as

$$\frac{\partial \gamma }{\partial t}+\frac{\partial \gamma u_i}{\partial x_i}=0$$

(6)

where $\gamma$ represents the water volume fraction in a control volume. The value of $\gamma$ is used to determine if the control cell contains air or water as

$$\left\{\begin{array}{cc}\hfill \gamma =0,& air\hfill \\ \hfill 0<\gamma <1,& interface\hfill \\ \hfill \gamma =1,& water\hfill \end{array}\right.$$

(7)

The density and laminar viscosity of the air–water mixture are defined as functions of $\gamma$ as

$$\rho ={\rho }_{air}+\gamma ·\left({\rho }_{water}-{\rho }_{air}\right)$$

(8)

$${\mu }_l={\mu }_{air}+\gamma ·\left({\mu }_{water}-{\mu }_{air}\right)$$

(9)

In the present numerical model, convective terms are discretized with the deferred correction method [37]. The central difference scheme is implemented to discretize the diffusion and pressure gradient terms. The gravity term is treated as a source term. The PISO (Pressure-Implicit Split Operator) method [38] is applied to couple the velocity and pressure. Moreover, the momentum balance interpolation method [39] is applied to transfer the velocity information from the cell centers to the cell control surfaces. For more details regarding the numerical flow solver, readers can refer to Darwish and Moukalled (2006) [36] and Qu et al. (2020) [21].

Linear waves are superposed to generate the focused waves in this study. The first-order water surface elevation (${\zeta }_1$) can be defined as

$${\zeta }_1=\sum _{i=1}^N{a}_{i}cos{\phi }_i$$

(10)

where $a_i$ is the wave amplitude for each wave. ${\phi }_i$ is the wave phase for each wave, which is calculated as

$${\phi }_i=k_{i}x-{\omega }_{i}t-{\epsilon }_i$$

(11)

where $k_i$ and ${\omega }_i$ represent the wave number and wave angular frequency of each wave, respectively. ${\epsilon }_i$ represents the wave phase angle for each wave. ${\epsilon }_i$ should be calculated in such a way that all waves can focus at a specific time ($t_f$) and specific position ($x_f$), as

$${\epsilon }_i=k_i{x}_f-{\omega }_i{t}_f$$

(12)

The wave amplitude ($a_i$) for each wave is determined in terms of wave amplitude ($a_f$) at the focusing position and wave spectrum ($S_i\left(\omega \right)$) as

$$a_i=a_f\frac{S_i\left(\omega \right)∆\omega }{{\sum }_{i=1}^N{S}_i\left(\omega \right)∆\omega }$$

(13)

where $a_f=\frac{1}{2}{H}_s$ and $H_s$ is the significant wave height.

The Pierson–Moskowitz (PM) wave spectrum [40] is used to calculate the wave spectrum ($S_i\left(\omega \right)$) for the irregular waves within the focused waves. $S_i\left(\omega \right)$ is described as a function of wave angular frequency (${\omega }_i$). It determines the distribution of input wave energy as

$$S_i\left(\omega \right)={\left(\frac{{\omega }_p}{{\omega }_i}\right)}^5\mathit{exp}\left(\frac{-5}{4}{\left(\frac{{\omega }_p}{{\omega }_i}\right)}^4\right)$$

(14)

The peak angular frequency (${\omega }_p$) is the input parameter.

The frequency interval ($\Delta \omega$) is calculated as

$$\Delta \omega =\frac{{\omega }_U-{\omega }_L}{N}$$

(15)

where ${\omega }_U$ and ${\omega }_L$ are the upper and lower limits of the wave angular frequency range. $N$ is the total number of waves within the focused waves.

First-order horizontal velocity ($u_1$) and first-order vertical velocity ($w_1$) are calculated as the superpositions of irregular waves within the focused waves as

$$u_1=\sum _{i=1}^N{a}_i{\omega }_i\frac{\mathit{cosh}\left(k_i\left(z+h\right)\right)}{\mathit{sinh}\left(k_{i}d\right)}cos{\phi }_i$$

(16)

$$w_1=\sum _{i=1}^N{a}_i{\omega }_i\frac{\mathit{sinh}\left(k_i\left(z+h\right)\right)}{\mathit{sinh}\left(k_{i}h\right)}sin{\phi }_i$$

(17)

If the wave steepness of the incident irregular wave is relatively large, the effects of the wave–wave interactions can become more apparent [41]. In this case, the wave-to-wave interactions should be considered. Then, second-order wave should be further considered as

$$\zeta ={\zeta }_1+{\zeta }_2$$

(18)

$$u=u_1+u_2$$

(19)

$$w=w_1+w_2$$

(20)

In this study, a second-order wave is determined using the second-order irregular wave theory [42]. The total number of waves within the focused waves is set to $N$ = 60 after careful numerical tests.

In the computation, the horizontal load ($F_H$) and the vertical load ($F_V$) of the seawall are calculated by integrating the pressure and shear stress forces at the surfaces of the seawall. The volume of overtopping water (OTW) is calculated by integrating the volume of the water body behind the seawall. The wave runup height ($R_{up}$) is numerically calculated with a wave gauge at the sloped beach.

2.2. Calibration of the Numerical Flow Solver

This section numerically reproduces the overtopping hydrodynamics of focused waves over a seawall at a beach. The computed water surface elevation, overtopping water volume, and hydrodynamic load at the seawall were compared with the measurements [43]. The experimental work was performed in the COAST Laboratory at the University of Plymouth, UK. The experimental layout is plotted in Figure 1. The width and length of the wave flume were 0.6 m and 35 m, respectively. A beach of 1:20 was located 15.18 m downward from the wave paddle. A seawall model was fixed at a distance of 8.125 m downward from the beach toe. The side slope of the seawall model was 1:2. The seawall top width was 0.3 m. In the experiment, the significant wave height $(H_s$) and water depth ($h$) were 0.171 m and 0.5 m. The peak wave period ($T_p$) was 2.155 s. The vertical distance between the seawall top and the still water surface was 0.117 m. Twelve wave gauges were arranged along the flume to monitor the temporal and spatial variation in water elevation. Moreover, the overtopping water volume was calculated. The model calibration was performed based on a single run of the focused wave group. In the experiment, an overtopping receptacle load cell was used to measure the overtopping volume per unit width. A horizontal load cell was applied to measure the horizontal load per unit width. In the simulation, the wave-focusing position ($x_f$) and time ($t_f$) were set to 20.18 m and 33.0 s. Figure 2 demonstrates the water surface elevations at different locations. As observed in Figure 2, the predicted water elevations are in good agreement with the collected data. The skill number proposed by Willmott [44] was applied to evaluate the degree of agreement between the measurements and numerical predictions. The calculated skill numbers of water elevations were all greater than 0.86, verifying the reliability of the present numerical flow solver. The numerical flow solver can simulate well the temporal and spatial variations in water surface elevations at different locations and the corresponding transforming, breaking, and overtopping processes of focused waves. Figure 3 compares the predicted overtopping water volume with the measurement. It can be seen that the overtopping processes of focused waves are accurately simulated with the numerical flow solver. The predicted overtopping water volume per unit width is 6.69 $\mathrm{L}/\mathrm{m}$, whereas the measured value is 6.37 $\mathrm{L}/\mathrm{m}$. There is less than a 5% difference. Figure 4 depicts the temporal variation in the horizontal load of the seawall. The predicted horizontal load exerted on the whole surface of the seawall agrees well with the experimental data. As demonstrated above, the modeling reliability and accuracy of the numerical flow solver in modeling the hydrodynamic load and overtopping of the coastal seawall under focused wave conditions are well-verified. The capability of the numerical flow solver to simulate the complex wave–wind interactions was carefully verified in our previous works. For reasons of brevity, the relevant simulations are not presented in the present paper, but interested readers may refer to Refs. [3,4].

3. Results and Discussion

In the following sections, the overtopping hydrodynamics of the coastal seawall under the coupled impact of focused waves and wind are carefully analyzed. Influences of the main factors, such as the wind speed, water depth, and significant wave height, are analyzed in detail. A computational schematic is plotted in Figure 5. $H_s$ is the incident significant wave height and h is water depth. $\alpha$ and $\beta$ represent the slope angles of the beach and side slope of the seawall, respectively. The seawall top height is 0.617 m. In the following computations, the peak wave period ($T_p$) is 2.155 s. The beach slope is 1:20, and side slope of the seawall is set to 1:2.

Table 1. Parameter setup and predictions.

Parameter Setup			${\mathit{F}}_{\mathit{H},\mathit{m}\mathit{a}\mathit{x}}(\mathbf{K}\mathbf{N}/\mathbf{m})$	${\mathit{F}}_{\mathit{V},\mathit{m}\mathit{a}\mathit{x}}(\mathbf{K}\mathbf{N}/\mathbf{m})$	${\mathit{R}\mathit{u}\mathit{p}}_{\mathit{m}\mathit{a}\mathit{x}}\left(\mathbf{m}\right)$	${\mathit{O}\mathit{W}\mathit{T}}_{\mathit{m}\mathit{a}\mathit{x}}(\mathbf{L}/\mathbf{m})$
$U_w^{\mathrm{*}}$	0		0.065	0.186	0.026	6.37
	2		0.067	0.186	0.027	6.61
	3		0.067	0.186	0.029	7.25
	4		0.069	0.188	0.032	7.83
	5		0.070	0.192	0.037	8.38
	6		0.075	0.196	0.041	9.67
$\chi$	$U_w^{\mathrm{*}}=0$	0.25	0.057	0.161	0.022	5.99
		0.30	0.061	0.166	0.023	6.20
		0.35	0.065	0.186	0.026	6.37
		0.40	0.072	0.199	0.029	6.61
	$U_w^{\mathrm{*}}=4$	0.25	0.061	0.162	0.025	6.94
		0.30	0.064	0.168	0.028	7.31
		0.35	0.069	0.188	0.032	7.83
		0.40	0.075	0.205	0.036	8.25
$h$	$U_w^{\mathrm{*}}=0$	0.45	0.045	0.093	0.002	0.44
		0.50	0.065	0.186	0.026	6.37
		0.55	0.109	0.229	0.068	17.43
		0.60	0.134	0.403	0.094	25.07
	$U_w^{\mathrm{*}}=4$	0.45	0.045	0.100	0.003	0.95
		0.50	0.069	0.188	0.032	7.83
		0.55	0.122	0.252	0.080	20.10
		0.60	0.153	0.422	0.103	27.21

lists the parameter setups for the computations in this study. The predicted maximum horizontal and vertical loads, maximum runup height of overtopping water after the seawall, and total overtopping volume are also listed.

In the computation, wind velocity with a logarithmic distribution is imposed above the water surface at the inlet, as described in Equation (21).

$$u_w\left(z\right)=\frac{u_{\mathrm{*}}}{\kappa }ln\left(\frac{z}{z_0}\right)$$

(21)

where $u_{\ast }$ represents the friction velocity, and $u_{\ast }=\kappa U_w/ln\left(\delta /z_0\right)$. $U_w$ represents the imposed average wind speed. $\delta$ is the distance between the top of the computational domain and the water surface. The von Karman constant ($\kappa$) is 0.4. $z_0$ is the water surface roughness, and $z_0$ is set to 0.0002 m in the present study for a smooth water surface condition. In addition, the wind speed ($U_w$) is nondimensionalized by the wave celerity of shallow water, such as $U_w^{\ast }=U_w/\sqrt{gh}$.

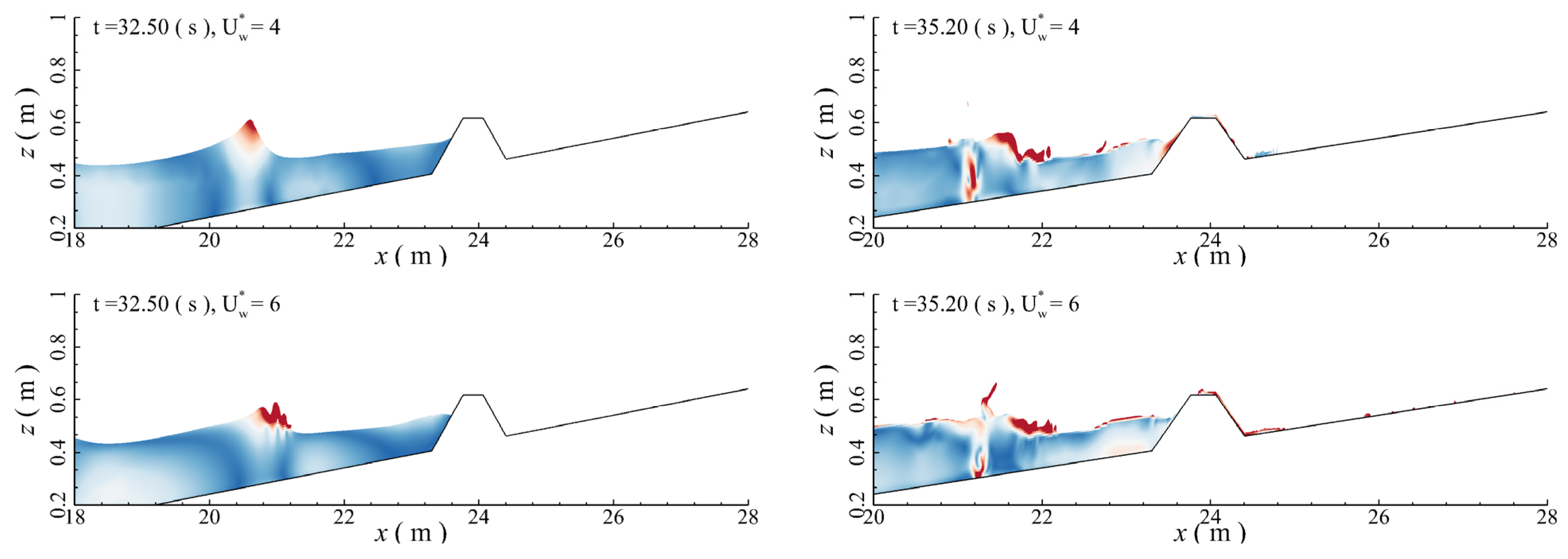
3.1. Complex Flow Phenomena

The overtopping flow close to the coastal seawall under focused wave conditions with the wind is analyzed in this section. The wind speed is $U_w^{\ast }$ = 4, and $U_w^{\ast }=U_w/\sqrt{gh}$. $h$ is 0.5 m, and $H_s$ is 0.171 m. Figure 6 lists the snapshots of velocity contours at different time moments. Because of the existence of wind, water surface oscillations in small amplitude can be observed. As the wave crest gradually approaches the seawall, a high-speed water area is observed at the wave crest. Due to the wind, the water body speed and its region size both increase to some extent. When the wave crest propagates upward from the beach, the wave crest steepens gradually because of the shallowing effects caused by the decrease in water depth and the blocking effects induced by the seawall. The focused waves with the wind can have a steeper wave crest and a larger region of the water body at a high velocity. Due to the blowing effects of wind, wave crests can become increasingly asymmetrical, and wave breaking occurs in advance. Once overtopping occurs, the water body can be divided into two parts. One part continues to run up the beach. The other part is reflected back. Figure 7 shows the water pressure contours of focused waves impacting the seawall. Under strong wind conditions, the incident wave group tends to break in advance. The strengthened breaking surge bore can climb over the top of the seawall, resulting in an increase in the volume of overtopping water. Meanwhile, if a strong wind blows over the water surface, a low-pressure area in blue color is formed at the areas where the slope of the water surface is large and the terrain changes dramatically, such as the wave crest and the top of the seawall (Figure 7b). The low-pressure distribution can finally produce a sucking effect on the transformations of incident waves. Figure 8 depicts a comparison of space distributions of maximum water elevation along the computational domain. Since the wind can exert strong pressure imbalance and surface shear stress forces on the water surface, the maximum water surface elevation of the focused waves under the wind conditions is generally larger than without the wind. Figure 9 depicts the temporal runup processes of overtopping water after the seawall. It shows that the maximum runup height of overtopping water of focused waves with the wind is 25.3% greater than without the wind. Figure 10 shows the temporal variations in the overtopping water volume. It can be seen that the overtopping water volume can increase by 23%, attributed to the onshore wind. The time history of hydrodynamic loads can be noticeably affected by the wind. The wind can increase the wave celerity slightly, resulting in an intensified wave impacting the whole surface of the seawall (Figure 11). In addition, as the wind blows over the seawall, the low-pressure area at the seawall can generate a sucking effect (Figure 7). The onshore wind also affects the breaking forms and breaking positions of different incident waves and eventually leads to certain changes in the hydrodynamic loads at the seawall. The peak value of horizontal load at the seawall under the wind conditions is about 8.11% greater than without the wind. Because of the wind-sucking effects, the peak value of the vertical load is about 7.34% higher than without the wind. As demonstrated above, the strong wind can significantly affect the overtopping hydrodynamics of focused waves at the seawall.

3.2. Effects of Wind Speed

The influences of wind speed on the overtopping of focused waves at the seawall are discussed in this section. $h$ is 0.5 m. $H_s$ is 0.171 m. Five different nondimensional wind speeds were designed, namely, $U_w^{\ast }$ = 0, 2, 3, 4, 5, and 6. Figure 12 depicts the velocity contours at the instances of focused waves overtopping the coastal seawall. When the wind speed gradually increases, wave breaking occurs in advance, and the wave-breaking intensity increases as well. Wave breaking is accompanied by dramatic changes in the water surface. This is mainly attributed to the fact that when the onshore wind speed increases gradually, the intensified wind shear stress at the water surface gradually increases the wave steepness, resulting in the asymmetry of wave shape and leading to wave breaking. Figure 13 shows the variations in the maximum volume of overtopping water per unit seawall width with wind speed. It is observed that if the dimensionless wind speed is smaller than 2 ($U_w^{\ast }\le 2$), the existence of the wind has negligible influence on the variation in the maximum overtopping water volume. If $U_w^{\ast }>2$, the maximum overtopping water volume tends to increase with the dimensionless wind speed. The maximum volume of the overtopping water can increase by 46.37% if $U_w^{\ast }$ varies from 2 to 6. Figure 14 depicts the variations in the peak value of the runup height of the overtopping water body with wind speed. Apparently, if $U_w^{\ast }$ is smaller than 2, the $\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{e}$ wind only has negligible influence on the peak value of the runup height of overtopping water. When $U_w^{\ast }>2$, the peak values of the runup height of overtopping water tend to increase with wind speed at a high rate. The maximum runup height of overtopping water can increase by 55.18% if $U_w^{\ast }$ varies from 2 to 6. Figure 15 shows the variations in the peak values of horizontal and vertical loads at the seawall with $U_w^{\ast }$. The peak value of the horizontal load increases gradually with the wind speed (Figure 15a) since the wind shear stress can enhance the wave impact intensity. However, when $U_w^{\ast }$ is smaller than 3, the increase rate in the peak value of the horizontal load is relatively small. If $U_w^{\ast }$ varies from 3 to 6, the peak value of the horizontal load at the seawall can increase by 11.6%. Figure 15b shows that the peak value of the vertical load can increase gradually with the wind. Because of the sucking influences of the wind over the seawall, the peak value of the vertical load gradually increases. Whereas, when $U_w^{\ast }$ is smaller than 3, the increase rate in the maximum vertical load is also low. If $U_w^{\ast }$ varies from 3 to 6, the peak value of the vertical load at the seawall can increase by 5.61%.

3.3. Effects of the Significant Wave Height

The influences of wind on the overtopping characteristics of the seawall at different significant wave heights are analyzed in the present section. $h$ is kept as 0.5 m. $U_w^{\ast }$ is 4. Four different significant wave height ratios are designed, namely, $\chi =H_s/h$ = 0.25, 0.3, 0.35, and 0.4. Figure 16 shows the variation in the peak value of the overtopping water volume with $\chi$. It is observed that the peak value of the overtopping water volume increases linearly with $\chi$. Overall, focused waves under the wind conditions can generate a higher overtopping water volume. When $\chi$ varies from 0.25 to 0.4, the peak value of the overtopping water volume can increase by 18.94% and 10.37% for focused waves with and without the wind. On average, the peak value of the overtopping water volume of focused waves under the wind conditions is 20.36% larger than without the wind. Figure 17 demonstrates the variation in the peak value of the runup height of the overtopping water body with $\chi$. It can be seen that the peak value of the runup height of overtopping water monotonically increases with $\chi$. When $\chi$ varies from 0.25 to 0.4, the peak value of the runup height of overtopping water of focused waves with and without the wind can increase by 40.2% and 31.11%, respectively. The peak value of the runup height of the overtopping water body of focused waves under onshore wind conditions is larger than without the wind by 21.14% on average. Figure 18 shows the variations in the peak value of the horizontal and vertical loads at the seawall with $\chi$. The peak value of the horizontal load and the peak value of the vertical load both increase monotonically with $\chi$. When $\chi$ varies from 0.25 to 0.4, the peak value of the horizontal load of the focused waves with and without the wind can increase by 23.6% and 26.27%, respectively. At the same time, the peak value of the vertical load of the focused waves with and without the wind can increase by 26.57% and 23.94%, respectively. On average, the peak value of the horizontal load and the peak value of the maximum vertical load of focused waves with the wind are 5.35% and 1.63% greater than without the wind, respectively.

3.4. Effects of Water Depth

Four different water depths were designed, namely, $h$ = 0.45, 0.5, 0.55, and 0.6 m, to analyze the effects of still water depth on the overtopping of the seawall. $H_s$ is kept as 0.171 m. $U_w^{\ast }$ is 4. Figure 19 shows the variations in the peak value of the overtopping water volume with $h$. The maximum overtopping water volume increases gradually with $h$. However, if the water depth is smaller than 0.45 m, negligible overtopping water can be generated, as shown in Figure 19. If $h$ varies from 0.5 to 0.6 m, the peak value of the overtopping water volume of the focused waves with and without the wind can increase by 2.47 times and 2.94 times, respectively. When $h$ is larger than 0.45 m, the peak value of the overtopping water volume of the focused waves with the wind becomes larger than without the wind. On average, the peak value of the overtopping water volume of focused waves with the wind is 15.55% greater than without the wind. Figure 20 depicts the variation in the peak value of the runup height of overtopping water with $h$. It is found that the peak value of the runup height of overtopping water increases monotonically with $h$ because an increase in $h$ can decrease the seawall freeboard height. When $h$ is smaller than 0.45 m, the wind has a negligible impact on the peak value of the runup height of overtopping water, and only slight overtopping water is observed. If $h$ varies from 0.5 m to 0.6 m, the maximum runup height of the overtopping water can increase by 2.22 times and 2.67 times for the focused waves with and without the wind, respectively. When $h$ is larger than 0.45 m, the peak value of the runup height of overtopping water of focused waves with the wind is 17.2% larger on average than without the wind. Figure 21 shows the variation in peak values of horizontal and vertical loads at the seawall with $h$. The peak value of the horizontal load and the peak value of the vertical load both increase monotonically with $h$. However, it can be seen that if $h$ is smaller than 0.5 m, the wind has very negligible effects on the impacting loads of focused waves at the seawall. If $h$ varies from 0.45 m to 0.6 m, the peak value of the horizontal loads at the seawall under focused wave conditions with and without the wind can increase by 2.37 times and 1.97 times, respectively. Meanwhile, the peak value of vertical loads at the seawall for the focused waves with and without the wind can increase by 3.21 times and 3.34 times, respectively. If $h$ is larger than 0.5 m, the peak value of the horizontal load and the peak value of the vertical load at the seawall under focused wave conditions with the wind are 8.66% and 5.92% larger than without the wind, respectively.

4. Conclusions

By applying a high-accuracy two-phase flow solver, this study modeled the complex overtopping of a seawall under focused wave conditions with the wind. Influences of the significant wave height, wind speed, and water depth were investigated in detail. The main research results are summarized as follows:

(1)

The pressure and wind shear stress forces at the water surface can increase the current speed at the water surface and gradually enlarge the wave steepness, which makes wave breaking occur in advance. The wind-strengthened breaking surge bore can increase the total overtopping water volume to some extent. Since the onshore wind can gradually increase the wave celerity, the impact intensity of the breaking surge bores at the seawall can be also enhanced. At the same time, as the wind blows across the surface of the seawall, a low-pressure area can be formed. It can generate a sucking effect on the surface of the seawall, which finally can increase the vertical load of the seawall to some extent.

(2)

If $U_w^{\ast }$ is smaller than 2, the existence of wind has a negligible impact on the peak value of the overtopping water volume. When the wind speed is small ($U_w^{\ast }$ < 2), pressure and wind shear stress imposed at the water surface by the wind are much smaller compared with the hydrostatic force of the water body. However, once $U_w^{\ast }>2$, the peak value of the overtopping water volume tends to increase noticeably with $U_w^{\ast }$. The total overtopping water volume increases by 46.37% if $U_w^{\ast }$ varies from 2 to 6. When $U_w^{\ast }>2$, the peak value of the runup height of overtopping water increases sharply with $U_w^{\ast }$. The maximum value of the runup height increases by 55.18% if $U_w^{\ast }$ $\mathrm{v}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{e}\mathrm{s}$ from 2 to 6. When $U_w^{\ast }<3$, the increase rate in the maximum horizontal load and maximum vertical load is relatively small. If $U_w^{\ast }$ varies from 3 to $6$, the peak values of the horizontal load and vertical load at the seawall can increase by 11.6% and 5.61%, respectively.

(3)

The peak value of the overtopping water volume increases linearly with $\chi$. The maximum overtopping water volume of the focused waves under the wind conditions is 20.36% larger on average than without the wind. The peak value of the runup height of the overtopping water body for the focused waves with the wind is larger than that without the wind by 21.14% on average. The peak values of the horizontal load and the vertical load monotonically increase with $\chi$. The peak values of the horizontal load and the vertical load of the focused waves with the wind are 5.35% and 1.63% greater on average than without the wind at different significant wave height ratios, respectively.

(4)

If $h$ is relatively small, the clearance height between the top of the seawall and the still water level is large. Hence, only negligible overtopping water can be observed. Overall, the total overtopping water volume for the focused waves with the wind is 15.55% greater on average than without the wind. When $h$ is larger than 0.45 m, the peak value of the runup height of overtopping water of the focused waves with the wind is 17.2% greater on average than without the wind. If $h$ is larger than 0.5 m, peak values of the horizontal and vertical loads at the seawall under the focused wave conditions with the wind are 8.66% and 5.92% larger than without the wind, respectively.

(5)

Although this study systematically investigated the overtopping of a seawall under the combined effect of focused waves and wind, there are some limitations. For instance, in a real ocean environment, waves tend to propagate in multiple directions. This study only focuses on unidirectional focused waves. Overtopping of a seawall under multidirectional focused wave conditions will be further studied in the future. In addition, this study only numerically analyzed wind–wave interactions using small-scale modeling. At present, it is still challenging to apply a high-accuracy two-phase flow wave model to study large-scale wind–wave interactions and their joint impact on coastal infrastructures.

It is hoped that the research results of the present study can broaden the understanding of the overtopping processes of seawalls under the coupled impact of onshore wind and extreme waves.