A Spectral Wave Model for Inhomogeneous Water Wave Fields Using the Quasi-Coherent Theory
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Numerical Model
2.1.1. Model Equations
2.1.2. Model Implementation
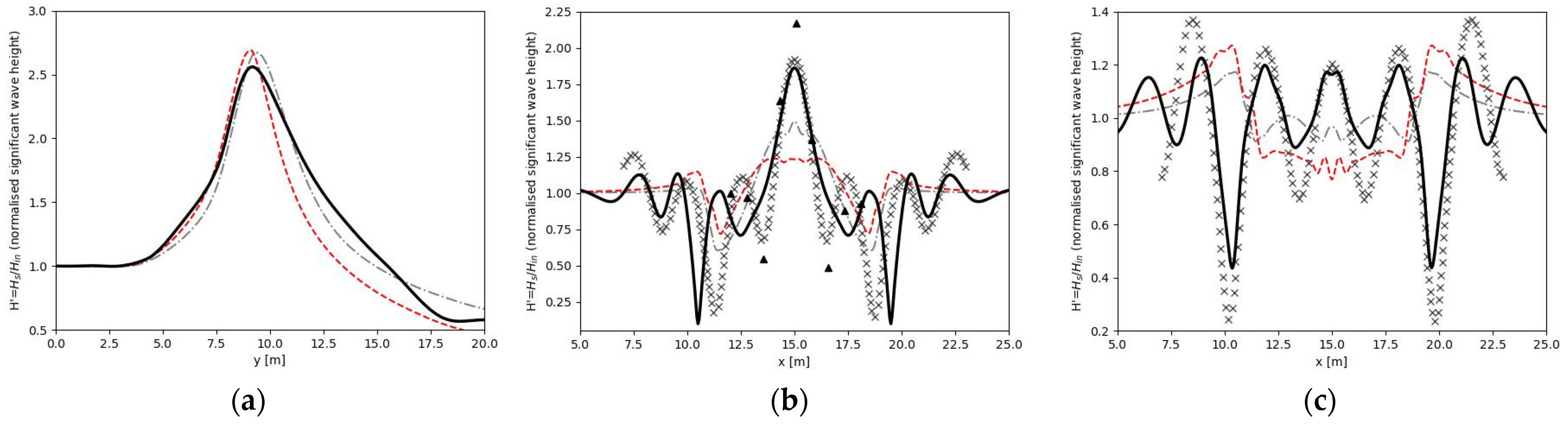
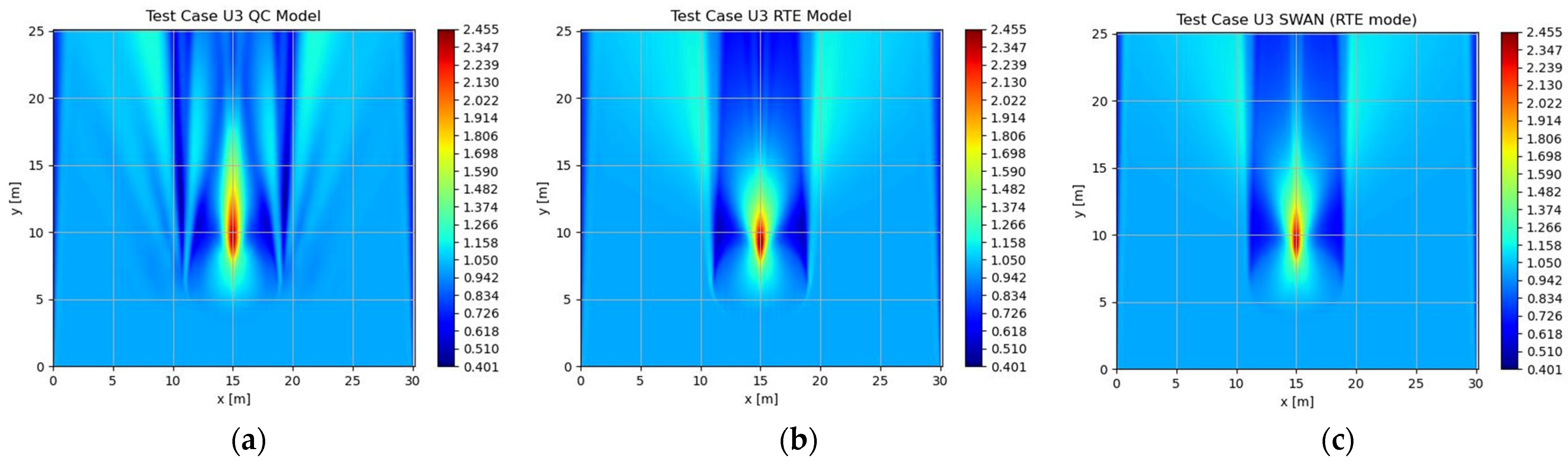
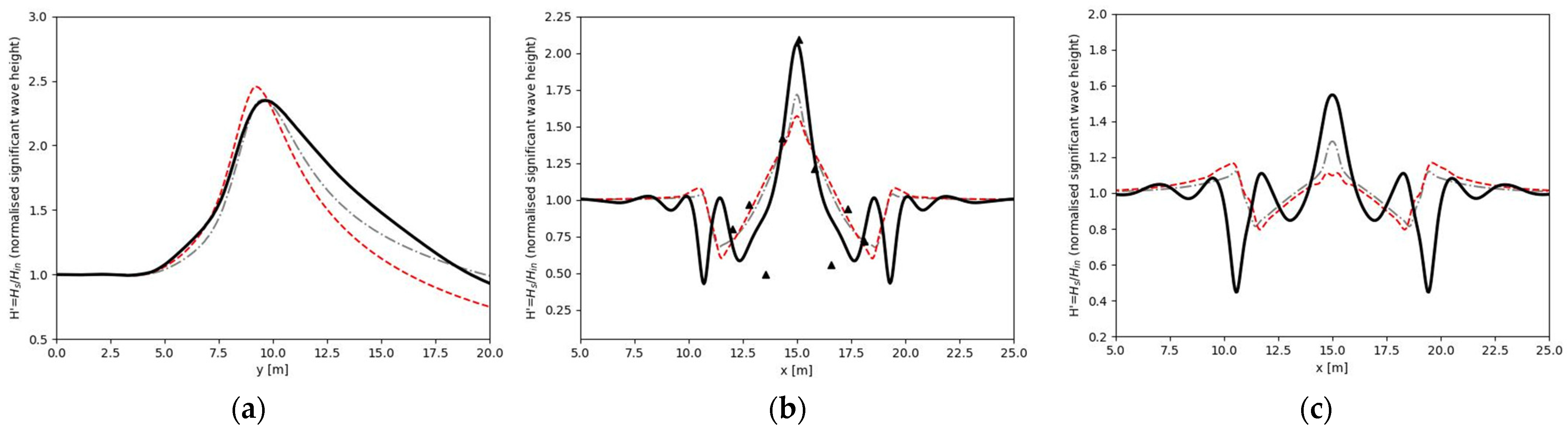
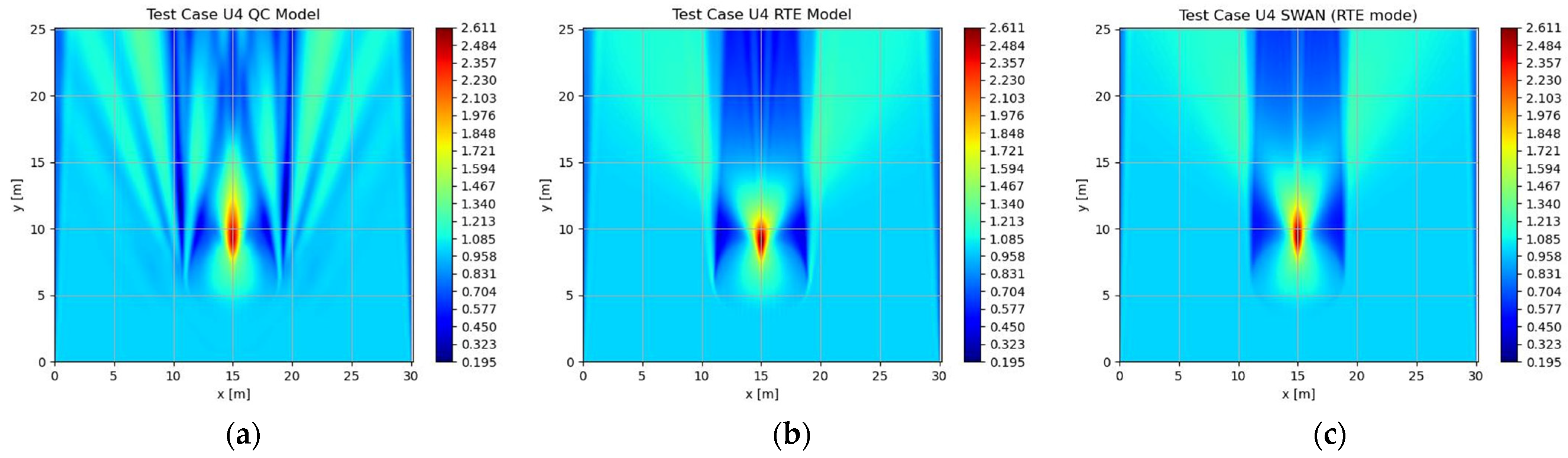
2.2. Test Cases: Waves Propagating over Elliptic Shoal
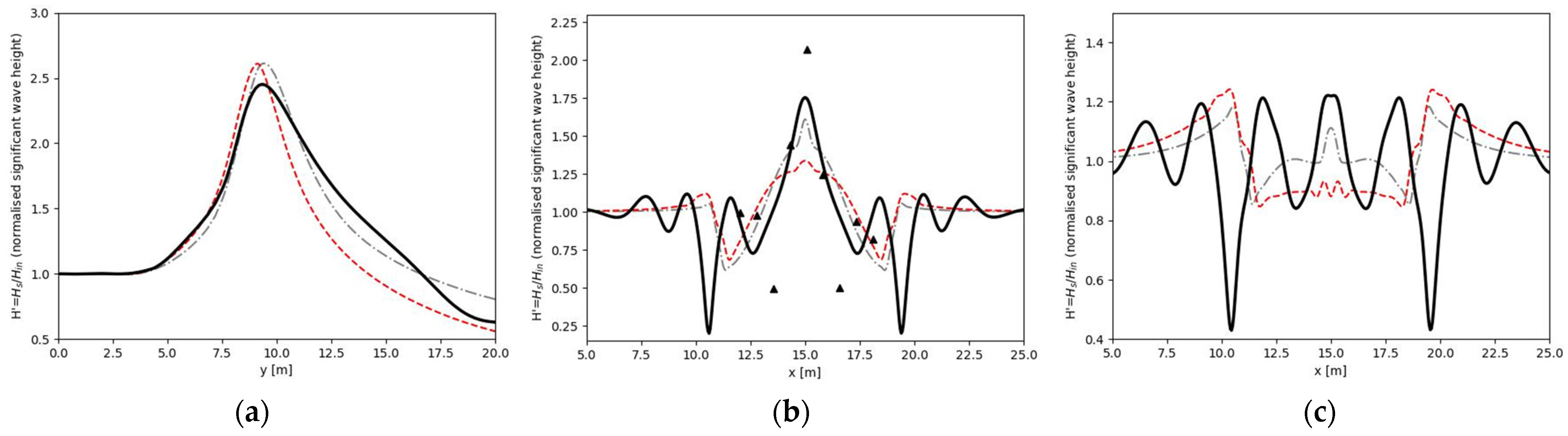
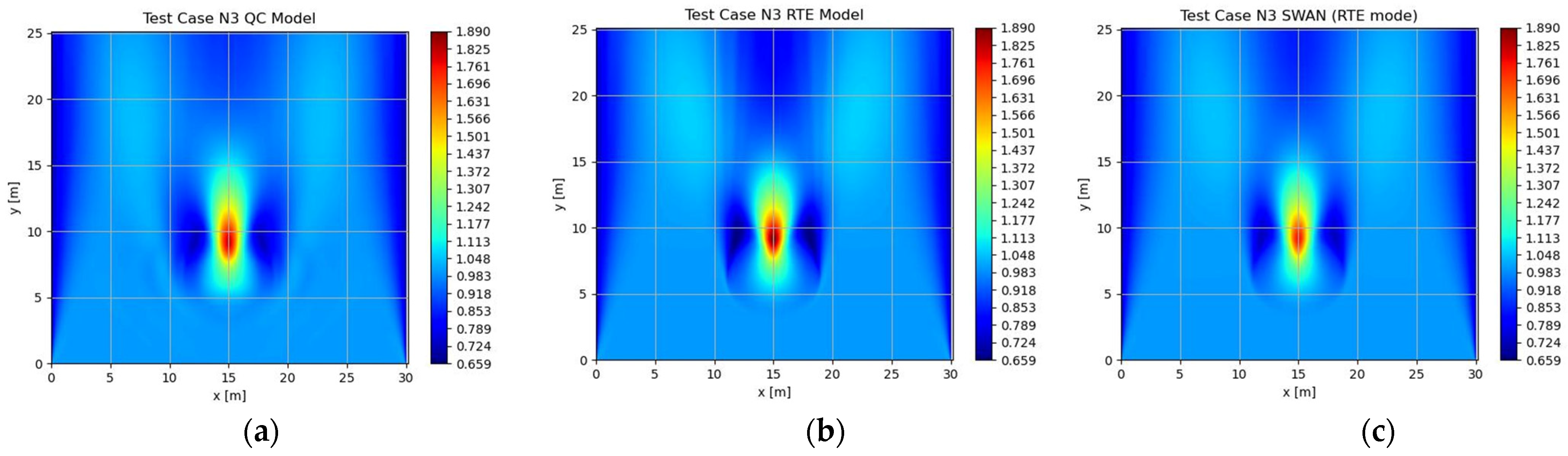
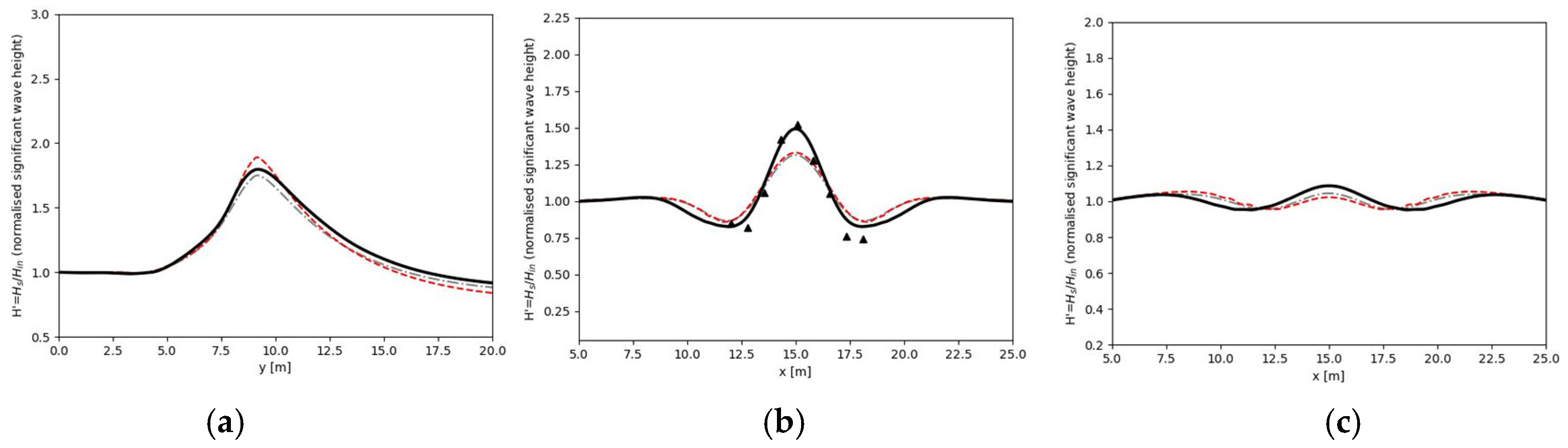
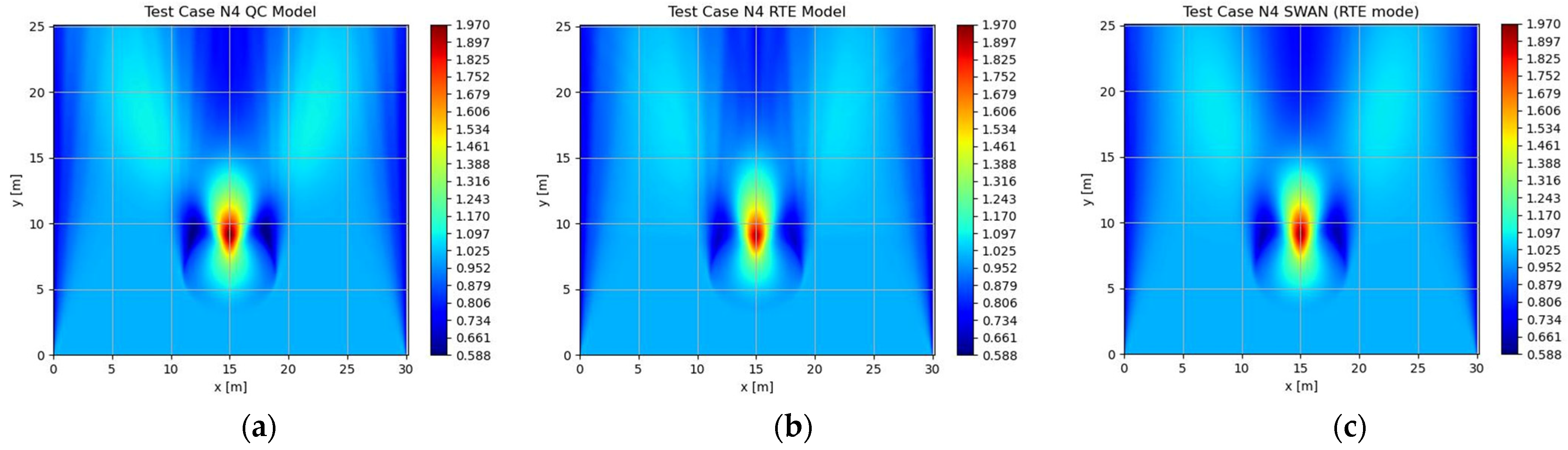
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- The WAMDI Group. The WAM model—A third generation ocean wave prediction model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions 1. Model description and validation. J. Geoph. Res. Oceans 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Tolman, H.L. A third-generation model for wind waves on slowly varying, unsteady, and inhomogeneous depths and currents. J. Phys. Oceanogr. 1991, 21, 782–797. [Google Scholar] [CrossRef]
- Amarouche, K.; Akpınar, A.; Bachari, N.E.I.; Çakmak, R.E.; Houma, F. Evaluation of a high-resolution wave hindcast model SWAN for the West Mediterranean basin. Appl. Ocean. Res. 2019, 84, 225–241. [Google Scholar] [CrossRef]
- Mentaschi, L.; Besio, G.; Cassola, F.; Mazzino, A. Performance evaluation of Wavewatch III in the Mediterranean Sea. Ocean. Model. 2015, 90, 82–94. [Google Scholar] [CrossRef]
- Hoque, M.A.; Perie, W.; Solomon, S.M. Application of SWAN model for storm generated wave simulation in the Canadian Beaufort Sea. J. Ocean. Eng. Sci. 2020, 5, 19–34. [Google Scholar] [CrossRef]
- Makris, C.; Androulidakis, Y.; Karambas, T.; Papadimitriou, A.; Metallinos, A.; Kontos, Y.; Baltikas, V.; Chondros, M.; Krestenitis, Y.; Tsoukala, V.; et al. Integrated modelling of sea-state forecasts for safe navigation and operational management in ports: Application in the Mediterranean Sea. Appl. Math. Model. 2021, 89, 1206–1234. [Google Scholar] [CrossRef]
- Copernicus Marine Environment Monitoring Service, Providing PODUCTS and SERVICES for All Marine Applications. Available online: https://marine.copernicus.eu/ (accessed on 30 July 2023).
- Poseidon System: Monitoring, Forecasting and Information System for the Greek Seas. Available online: https://poseidon.hcmr.gr/ (accessed on 30 July 2023).
- WaveForUs: A Pilot System for the Development and Delivery of Daily Wave and Circulation Forecasts for Public and Emergency Use in the Thermaikos Gulf. Available online: https://wave4us.web.auth.gr/ (accessed on 30 July 2023).
- Rusu, L.; Soares, C.G. Evaluation of a high-resolution wave forecasting system for the approaches to ports. Ocean Eng. 2013, 58, 224–238. [Google Scholar] [CrossRef]
- Anton, I.A.; Rusu, L.; Anton, C. Nearshore wave dynamics at Mangalia Beach simulated by spectral models. J. Mar. Sci. Eng. 2019, 7, 206. [Google Scholar] [CrossRef]
- Cavaleri, L.; Abdalla, S.; Benetazzo, A.; Bertotti, L.; Bidlot, J.-R.; Breivik, Ø.; Carniel, S.; Jensen, R.E.; Portilla-Yandun, J.; Rogers, W.E.; et al. Wave modelling in coastal and inner seas. Prog. Oceanogr. 2018, 167, 164–233. [Google Scholar] [CrossRef]
- Cavaleri, L.; Alves, J.G.; Ardhuin, F.; Babanin, A.V.; Banner, M.L.; Belibassakis, K.; Benoit, M.; Donelan, M.A.; Groeneweg, J.; Herbers, T.H.; et al. Wave Modelling—The State of the Art. Prog. Oceanogr. 2007, 75, 603–674. [Google Scholar] [CrossRef]
- Liu, Q.; Gramstad, O.; Babanin, A. Kinetic equations in a third-generation spectral wave model. J. Fluid Mech. 2021, 910, A50. [Google Scholar] [CrossRef]
- Karambas, T.; Koutitas, C. A breaking wave propagation model based on the Boussinesq equations. Coast. Eng. 1992, 18, 1–19. [Google Scholar] [CrossRef]
- Karambas, T.; Memos, C. Boussinesq model for weakly nonlinear fully dispersive water waves. J. Water. Port. Coast. Ocean Eng. 2009, 135, 187–199. [Google Scholar] [CrossRef]
- Auclair, F.; Bordois, L.; Dossmann, Y.; Duhaut, T.; Paci, A.; Ulses, C.; Nguyen, C. A non-hydrostatic non-Boussinesq algorithm for free-surface ocean modelling. Ocean. Model. 2018, 132, 12–29. [Google Scholar] [CrossRef]
- Lannes, D. Modeling shallow water waves. Nonlinearity 2020, 33, R1–R57. [Google Scholar] [CrossRef]
- Mei, C.C. The applied dynamics of ocean surface waves. Adv. Ser. Ocean. Eng. 1994, 1, 86–89. [Google Scholar] [CrossRef]
- Dingemans, M.W. Water wave propagation over uneven bottoms. Adv. Ser. Ocean. Eng. 1997, 13. [Google Scholar] [CrossRef]
- Porter, D. The mild-slope equations. J. Fluid Mech. 2003, 494, 51–63. [Google Scholar] [CrossRef]
- Melito, L.; Antuono, M.; Brocchini, M. From Boussinesq-type to quasi-3D models: A comparative analysis. J. Hydr. Eng. 2023, 149, 04023025. [Google Scholar] [CrossRef]
- Antuono, M.; Brocchini, M. Beyond Boussinesq-type equations: Semi-integrated models for coastal dynamics. Phys. Fluids 2013, 25, 016603. [Google Scholar] [CrossRef]
- Dimas, A.A.; Fialkowski, L.T. Large-Wave Simulation (LWS) of Free-Surface Flows Developing Weak Spilling Breaking Waves. J. Comp. Phys. 2000, 159, 172–196. [Google Scholar] [CrossRef]
- Leftheriotis, G.A.; Chalmoukis, I.A.; Oyarzun, G.; Dimas, A.A. A Hybrid Parallel Numerical Model for Wave-Induced Free-Surface Flow. Fluids 2021, 6, 350. [Google Scholar] [CrossRef]
- Agnon, Y.; Sheremet, A. Stochastic nonlinear shoaling of directional spectra. J. Fluid Mech. 1997, 345, 79–99. [Google Scholar] [CrossRef]
- Herbers, T.H.C.; Burton, M.C. Nonlinear shoaling of directionally spread waves on a beach. J. Geoph. Res. Oceans 1997, 102, 101–114. [Google Scholar] [CrossRef]
- Herbers, T.H.C.; Orzech, M.; Elgar, S.; Guza, R.T. Shoaling transformation of wave frequency—Directional spectra. J. Geoph. Res. Oceans 2003, 108, 3013. [Google Scholar] [CrossRef]
- Alber, I.E. The effects of randomness on the stability of two—Dimensional surface watertrains. Philos. T. Roy. Soc. 1978, A 363, 525–546. [Google Scholar] [CrossRef]
- Janssen, P.A.E.M. Long-time behaviour of a random inhomogeneous field of weakly nonlinear surface gravity waves. J. Fluid Mech. 1983, 133, 113–132. [Google Scholar] [CrossRef]
- Janssen, T.T. Nonlinear Surface Waves over Topography. Ph.D. Dissertation, Delft University of Technology, Delft, The Netherlands, 2006. [Google Scholar]
- Janssen, T.T.; Herbers, T.H.C.; Battjes, J.A. Evolution of ocean wave statistics in shallow water: Refraction and diffraction over seafloor topography. J. Geoph. Res. Oceans 2008, 113, C03024. [Google Scholar] [CrossRef]
- Stiassnie, M.; Regev, A.; Agnon, Y. Recurrent solutions of Alber’s equation for random water-wave fields. J. Fluid Mech. 2008, 598, 245–266. [Google Scholar] [CrossRef]
- Smit, P.B.; Janssen, T.T. The evolution of inhomogeneous wave statistics through a variable medium. J. Phys. Oceanogr. 2013, 43, 1741–1758. [Google Scholar] [CrossRef]
- Cohen, L. Time-Frequency Analysis; Prentice-Hall Signal Processing: Hoboken, NJ, USA, 1995. [Google Scholar]
- Cohen, L. Phase-Space Differential Equations for Modes. In Pseudo-Differential Operators: Complex Analysis and Partial Differential Equations. Operator Theory: Advances and Applications; Schulze, B.W., Wong, M.W., Eds.; Birkhäuser Basel: Basel, Switzerland, 2009; Volume 205. [Google Scholar] [CrossRef]
- Smit, P.B.; Janssen, T.T.; Herbers, T.H.C. Stochastic modeling of coherent wave fields over variable depth. J. Phys. Oceanogr. 2015, 45, 1139–1154. [Google Scholar] [CrossRef]
- Smit, P.B.; Janssen, T.T.; Herbers, T.H.C. Stochastic modeling of inhomogeneous ocean waves. Ocean. Model. 2016, 96, 26–35. [Google Scholar] [CrossRef]
- Akrish, G.; Smit, P.; Zijlema, M.; Reniers, A. Modelling statistical wave interferences over shear currents. J. Fluid Mech. 2020, 891, A2. [Google Scholar] [CrossRef]
- Akrish, G.; Smit, P.; Zijlema, M.; Reniers, A. A mild-slope formulation based on Weyl rule of association with application to coastal wave modelling. Wave Motion 2023, 122, 103189. [Google Scholar] [CrossRef]
- Vincent, C.L.; Briggs, M.J. Refraction—Diffraction of Irregular Waves over a Mound. J. Wat. Port Coast. Ocean Eng 1989, 115, 269–284. [Google Scholar] [CrossRef]
- Gabor, D. Theory of Communication. Part1: The analysis of information. J. Inst. Electr. Eng. 1946, 93, 429–441. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar] [CrossRef]
- Bastiaans, M.J. Application of the Wigner distribution function in optics. In The Wigner Distribution—Theory and Applications in Signal Processing; Mecklenbräuker, W., Hlawatsch, F., Eds.; Elsevier: Amsterdam, The Netherlands, 1997; pp. 375–426. [Google Scholar]
- Bastiaans, M.J. Transport Equations for the Wigner Distribution Function. Opt. Acta Int. J. Opt. 1979, 26, 1265–1272. [Google Scholar] [CrossRef]
- Swarztrauber, P.N. FFT algorithms for vector computers. Parallel Comput. 1984, 1, 45–63. [Google Scholar] [CrossRef]
- Frigo, M.; Johnson, S. The Design and Implementation of FFTW3. Proc. IEEE 2005, 93, 216–231. [Google Scholar] [CrossRef]
- Van der Vorst, H.A. Bi-CGSTAB: A Fast and Smoothly Converging Variant of Bi-CG for the Solution of Nonsymmetric Linear Systems. SIAM J. Sci. Stat. Comput. 1992, 13, 631–644. [Google Scholar] [CrossRef]
- Bouws, E.; Gunther, H.; Rosenthal, W.; Vincent, C.L. Similarity of the wind wave spectrum in finite depth water1. Spectral form. J. Geoph. Res.-Ocean. 1985, 90, 975–986. [Google Scholar] [CrossRef]

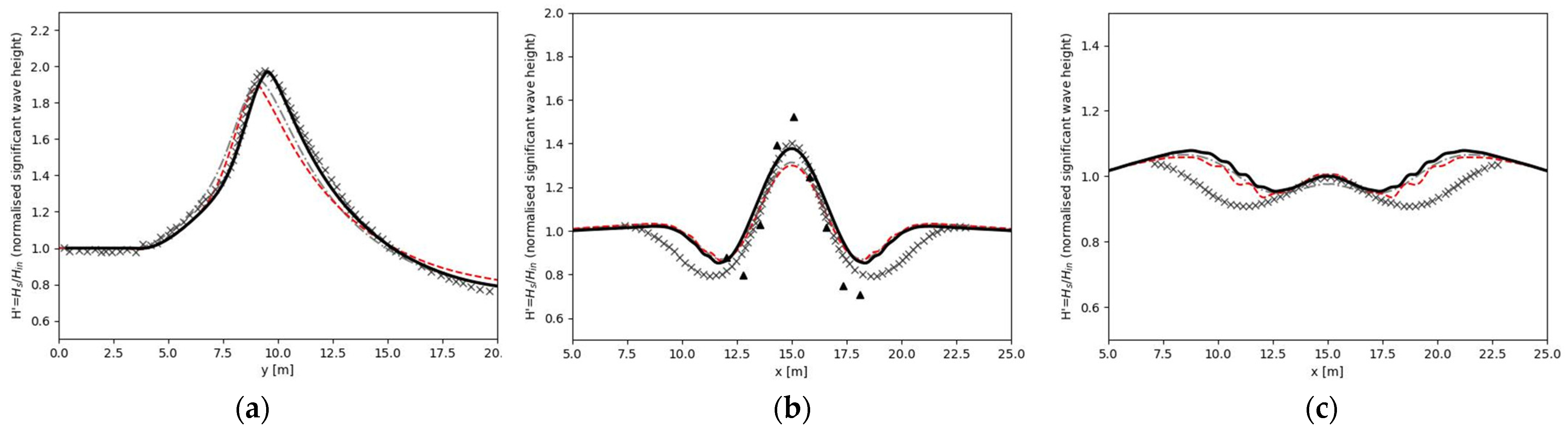
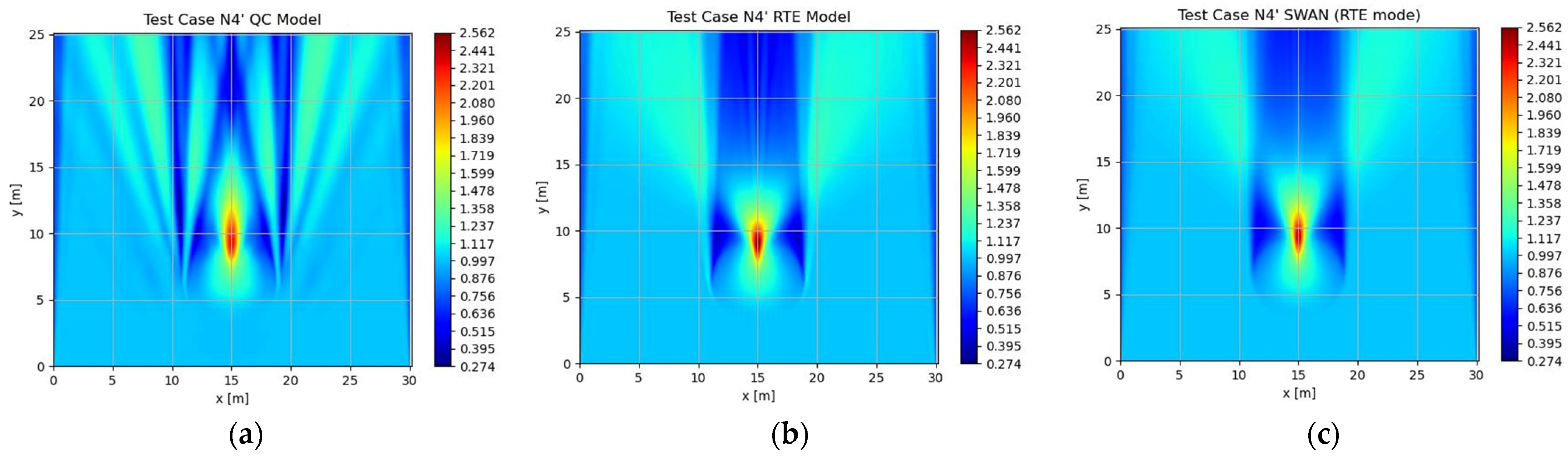
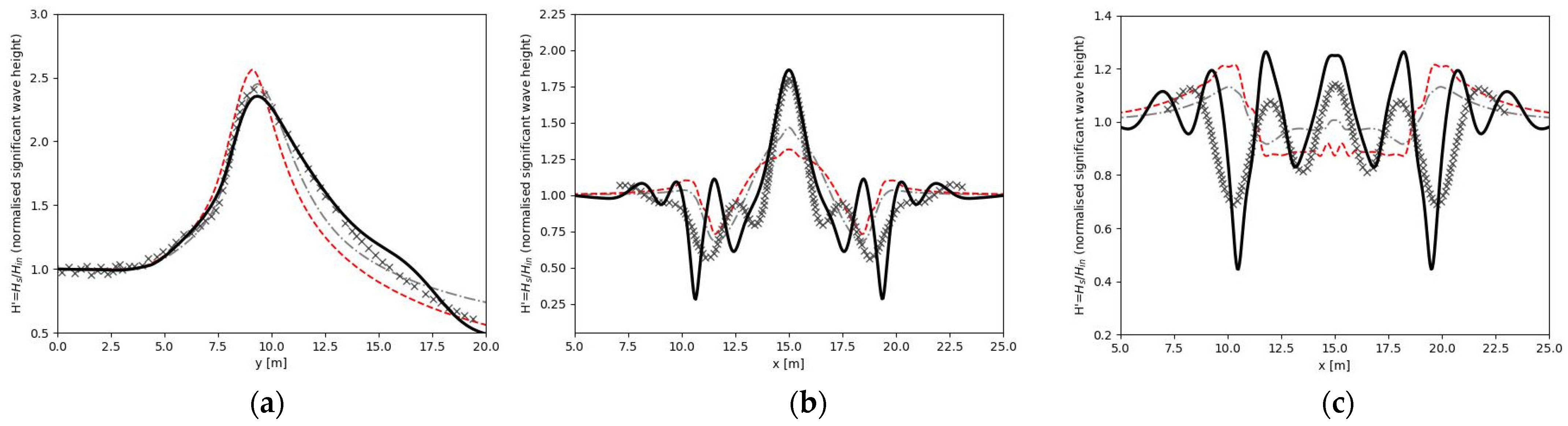
| Test Number | Case ID | Type | Period (Tp) (sec) | Height (Hs) (cm) | A | γ (Peakedness Factor) | σm (Directional Spreading) (deg) |
|---|---|---|---|---|---|---|---|
| 1 | M2 | Monochromatic | 1.30 | 2.54 | --- | --- | --- |
| 2 | U3 | TMA Spectrum | 1.30 | 2.54 | 0.00155 | 2 | 0 |
| 3 | U4 | TMA Spectrum | 1.30 | 2.54 | 0.00047 | 20 | 0 |
| 4 | N3 | TMA Spectrum | 1.30 | 2.54 | 0.00155 | 2 | 30 |
| 5 | N4 | TMA Spectrum | 1.30 | 2.54 | 0.00047 | 20 | 10 |
| 6 | N4‘ | TMA Spectrum | 1.30 | 2.54 | 0.00047 | 20 | 3 |
| Test Number | Case ID | Standard Deviation sd (m/(rad/m)) |
|---|---|---|
| 1 | M2 | 0.0517 |
| 2 | U3 | 1.3019 |
| 3 | U4 | 0.7482 |
| 4 | N3 | 1.3019 |
| 5 | N4 | 0.7482 |
| 6 | N4‘ | 0.7482 |
| Case ID | QC Model of Present Study | Smit and Janssen QC Implementation | RTE Model | SWAN |
|---|---|---|---|---|
| M2 | 0.901 | 0.961 | 0.395 | 0.67 |
| U3 | 0.935 | N/A | 0.789 | 0.848 |
| U4 | 0.851 | N/A | 0.573 | 0.756 |
| N3 | 0.984 | N/A | 0.966 | 0.962 |
| N4 | 0.921 | 0.964 | 0.903 | 0.903 |
| Case ID | Transect 7–9 | Transect 4 | Transect 5 |
|---|---|---|---|
| M2 | N/A | 0.769 | 0.658 |
| N4 | 0.998 | 0.956 | 0.373 |
| N4′ | 0.976 | 0.922 | 0.526 |
| Case ID | Transect 7–9 | Transect 4 | Transect 5 |
|---|---|---|---|
| M2 | 0.972 | 0.904 | 0.85 |
| N4 | 0.997 | 0.998 | 0.994 |
| N4′ | 0.981 | 0.96 | 0.908 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baltikas, V.; Krestenitis, Y.N. A Spectral Wave Model for Inhomogeneous Water Wave Fields Using the Quasi-Coherent Theory. J. Mar. Sci. Eng. 2023, 11, 2066. https://doi.org/10.3390/jmse11112066
Baltikas V, Krestenitis YN. A Spectral Wave Model for Inhomogeneous Water Wave Fields Using the Quasi-Coherent Theory. Journal of Marine Science and Engineering. 2023; 11(11):2066. https://doi.org/10.3390/jmse11112066
Chicago/Turabian StyleBaltikas, Vasilis, and Yannis N. Krestenitis. 2023. "A Spectral Wave Model for Inhomogeneous Water Wave Fields Using the Quasi-Coherent Theory" Journal of Marine Science and Engineering 11, no. 11: 2066. https://doi.org/10.3390/jmse11112066
APA StyleBaltikas, V., & Krestenitis, Y. N. (2023). A Spectral Wave Model for Inhomogeneous Water Wave Fields Using the Quasi-Coherent Theory. Journal of Marine Science and Engineering, 11(11), 2066. https://doi.org/10.3390/jmse11112066







