Implications of Reynolds Averaging for Reactive Tracers in Turbulent Flows
Abstract
:1. Introduction
2. Methods
2.1. Governing Equations
2.1.1. Reynolds Averaging
2.1.2. Reynolds Averaging
2.1.3. Reynolds Averaging as an Analysis Tool
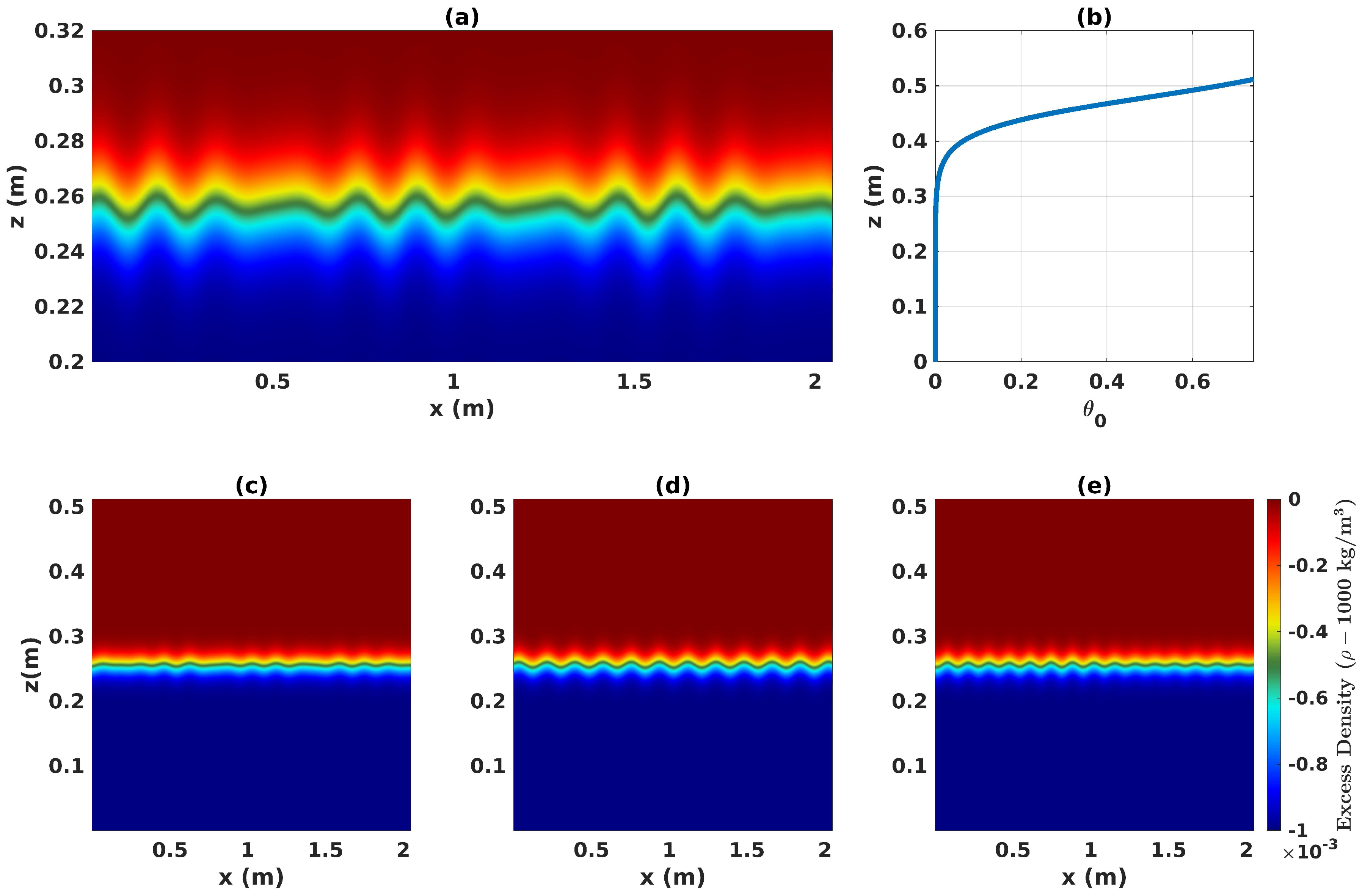
2.2. Numerical Simulation Ensemble Setup
3. Results
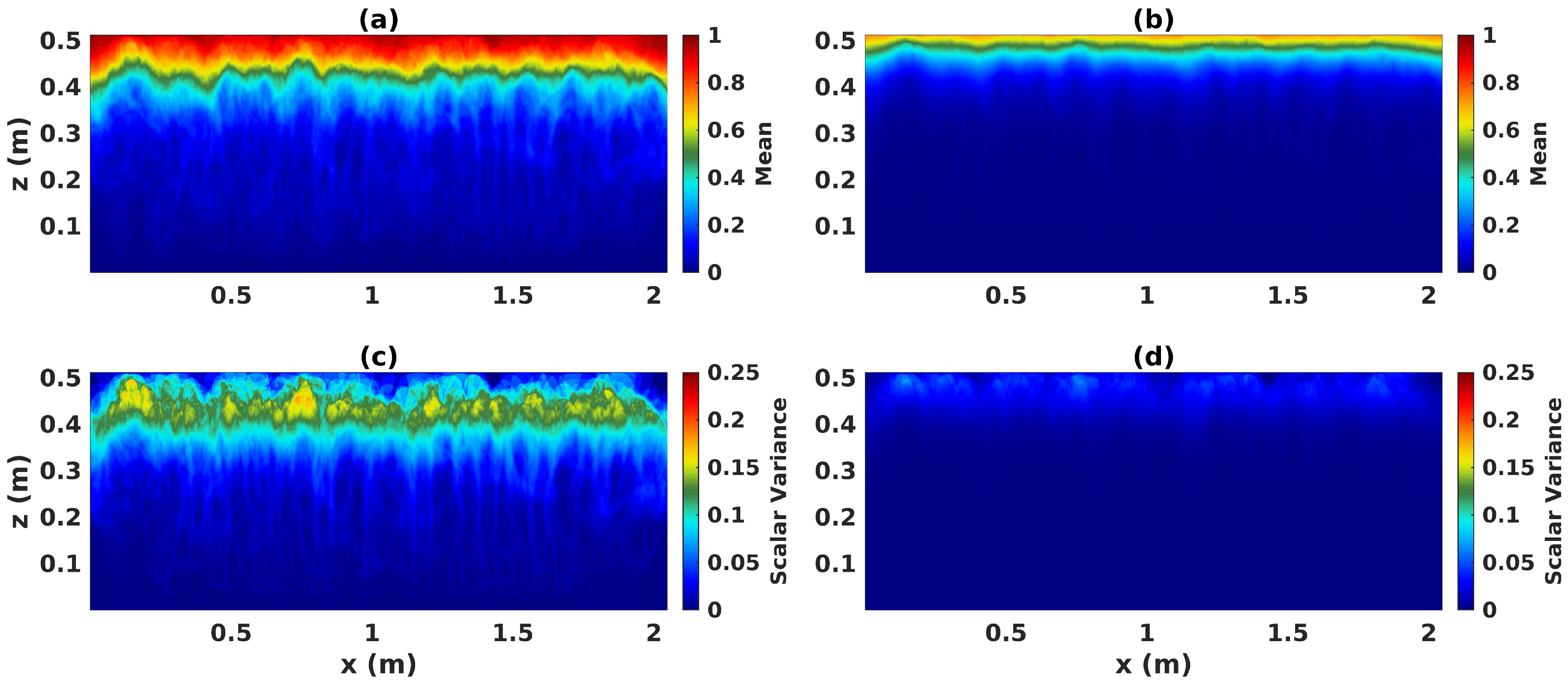
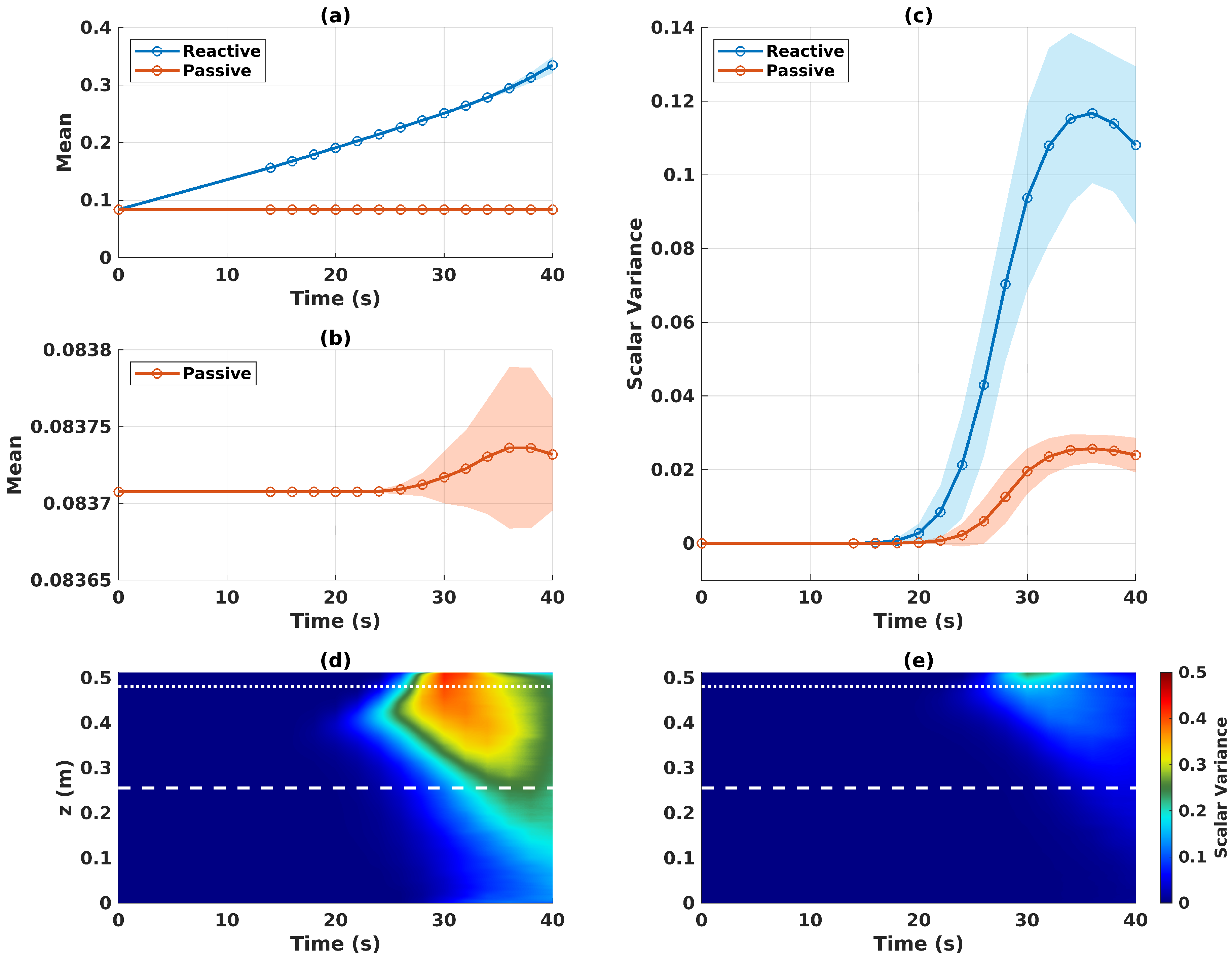
3.1. Tracer Mean and Scalar Variance
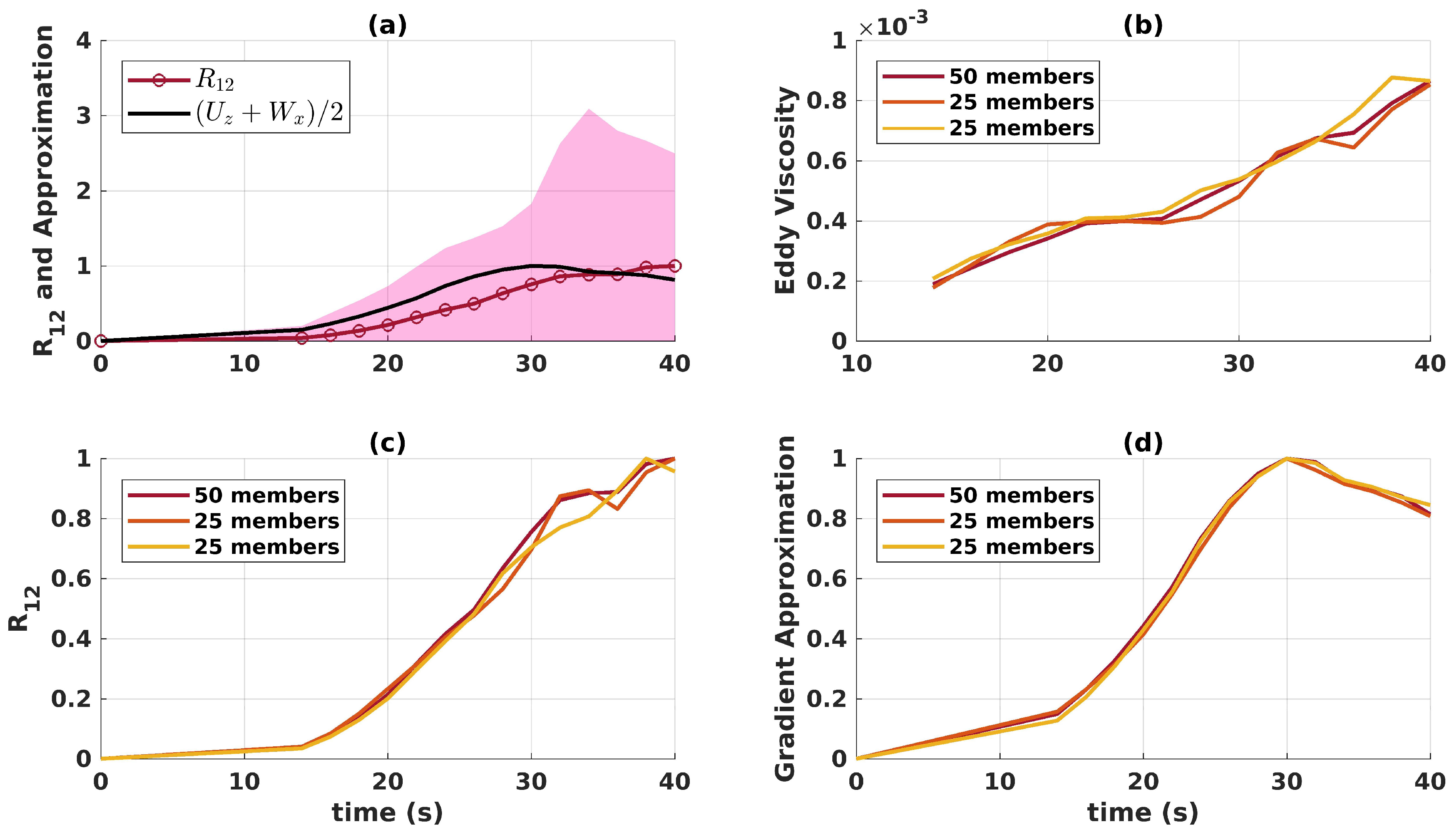
3.2. Reynolds Stresses
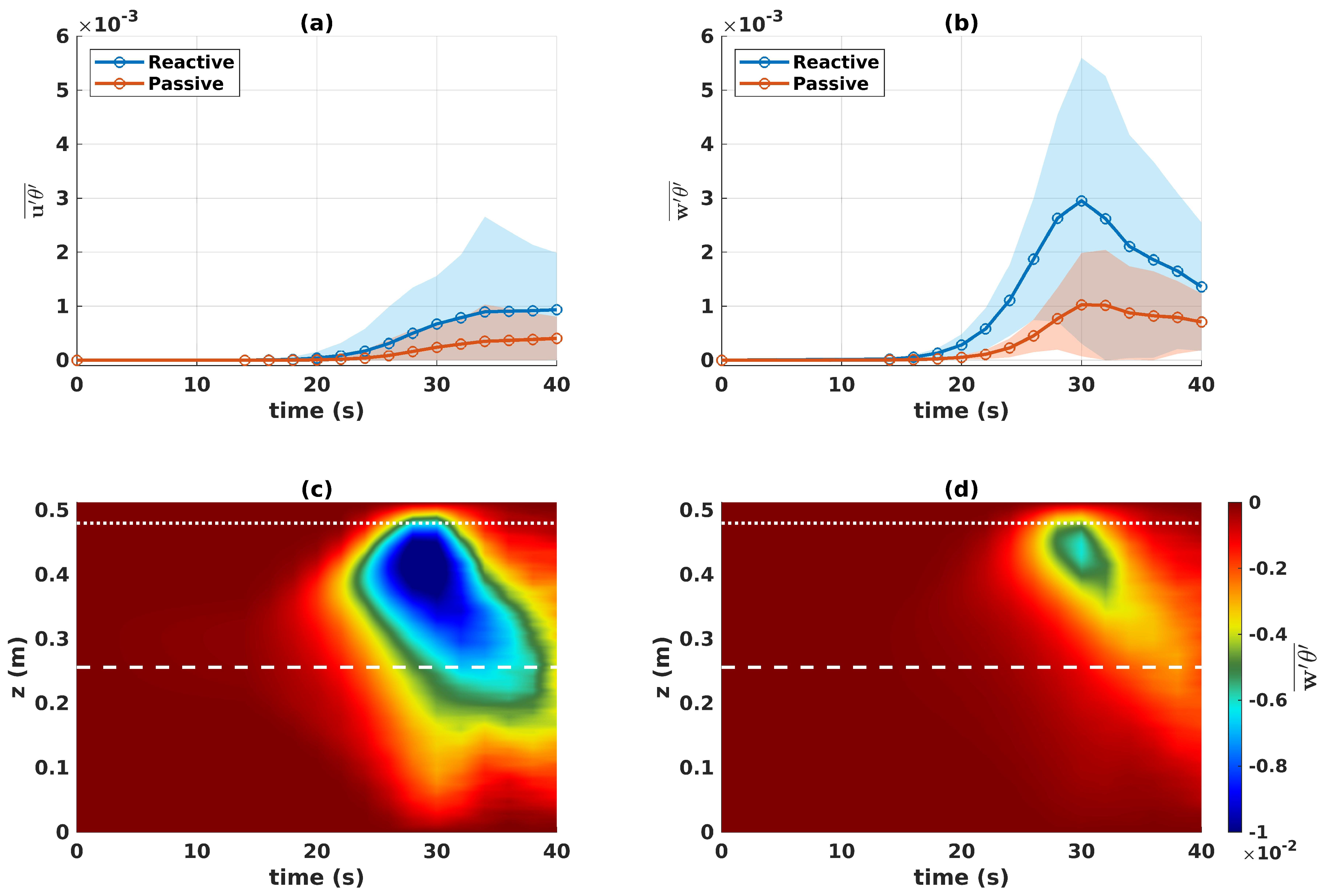
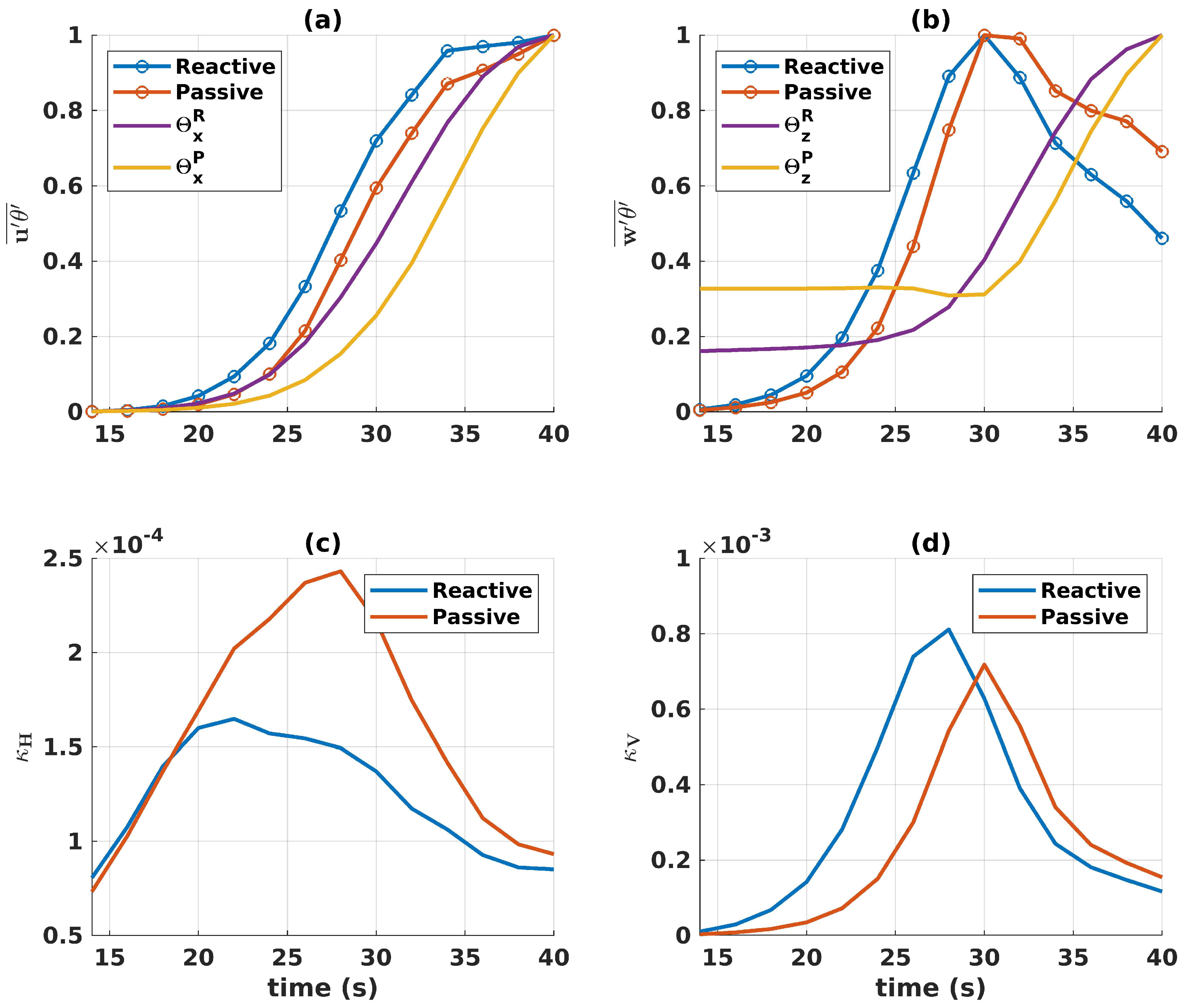
3.3. Eddy Fluxes
4. Conclusions
5. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADR | Advection–reaction–diffusion |
| RANS | Reynolds-averaged Navier–Stokes |
| RT | Rayleigh–Taylor |
References
- Triantafyllou, G.; Yao, F.; Petihakis, G.; Tsiaras, K.; Raitsos, D.; Hoteit, I. Exploring the Red Sea seasonal ecosystem functioning using a three-dimensional biophysical model. J. Geophys. Res. Ocean. 2014, 119, 1791–1811. [Google Scholar] [CrossRef]
- Kamykowski, D. A preliminary biophysical model of the relationship between temperature and plant nutrients in the upper ocean. Deep Sea Res. Part A Oceanogr. Res. Pap. 1987, 34, 1067–1079. [Google Scholar] [CrossRef]
- Resplandy, L.; Lévy, M.; McGillicuddy, D.J., Jr. Effects of eddy-driven subduction on ocean biological carbon pump. Glob. Biogeochem. Cycles 2019, 33, 1071–1084. [Google Scholar] [CrossRef]
- Goldstein, E.D.; Pirtle, J.L.; Duffy-Anderson, J.T.; Stockhausen, W.T.; Zimmermann, M.; Wilson, M.T.; Mordy, C.W. Eddy retention and seafloor terrain facilitate cross-shelf transport and delivery of fish larvae to suitable nursery habitats. Limnol. Oceanogr. 2020, 65, 2800–2818. [Google Scholar] [CrossRef]
- Baustian, M.M.; Meselhe, E.; Jung, H.; Sadid, K.; Duke-Sylvester, S.M.; Visser, J.M.; Allison, M.A.; Moss, L.C.; Ramatchandirane, C.; van Maren, D.S.; et al. Development of an Integrated Biophysical Model to represent morphological and ecological processes in a changing deltaic and coastal ecosystem. Environ. Model. Softw. 2018, 109, 402–419. [Google Scholar] [CrossRef]
- Laurent, A.; Fennel, K.; Kuhn, A. An observation-based evaluation and ranking of historical Earth system model simulations in the northwest North Atlantic Ocean. Biogeosciences 2021, 18, 1803–1822. [Google Scholar] [CrossRef]
- Haidvogel, D.B.; Arango, H.; Budgell, W.P.; Cornuelle, B.D.; Curchitser, E.; Di Lorenzo, E.; Fennel, K.; Geyer, W.R.; Hermann, A.J.; Lanerolle, L.; et al. Ocean forecasting in terrain-following coordinates: Formulation and skill assessment of the Regional Ocean Modeling System. J. Comput. Phys. 2008, 227, 3595–3624. [Google Scholar] [CrossRef]
- Higdon, R.L.; Bennett, A.F. Stability analysis of operator splitting for large-scale ocean modeling. J. Comput. Phys. 1996, 123, 311–329. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- ROMS Wiki Vertical Mixing Parameterizations. Available online: https://www.myroms.org/wiki/Vertical_Mixing_Parameterizations (accessed on 18 August 2023).
- Burchard, H.; Rennau, H. Comparative quantification of physically and numerically induced mixing in ocean models. Ocean Model. 2008, 20, 293–311. [Google Scholar] [CrossRef]
- Brennan, C.E.; Bianucci, L.; Fennel, K. Sensitivity of northwest North Atlantic shelf circulation to surface and boundary forcing: A regional model assessment. Atmosphere-Ocean 2016, 54, 230–247. [Google Scholar] [CrossRef]
- Kumar, R.; Li, J.; Hedstrom, K.; Babanin, A.V.; Holland, D.M.; Heil, P.; Tang, Y. Intercomparison of Arctic sea ice simulation in ROMS-CICE and ROMS-Budgell. Polar Sci. 2021, 29, 100716. [Google Scholar] [CrossRef]
- Sui, Y.; Sheng, J.; Tang, D.; Xing, J. Study of storm-induced changes in circulation and temperature over the northern South China Sea during Typhoon Linfa. Cont. Shelf Res. 2022, 249, 104866. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Dimotakis, P.E. Turbulent mixing. Annu. Rev. Fluid Mech. 2005, 37, 329–356. [Google Scholar] [CrossRef]
- Sreenivasan, K.R. Turbulent mixing: A perspective. Proc. Natl. Acad. Sci. USA 2019, 116, 18175–18183. [Google Scholar] [CrossRef]
- Kundu, P.K.; Cohen, I.M.; Dowling, D.R. Fluid Mechanics; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Alfonsi, G. Reynolds-averaged Navier–Stokes equations for turbulence modeling. Appl. Mech. Rev. 2009, 62, 040802. [Google Scholar] [CrossRef]
- Xiao, H.; Cinnella, P. Quantification of model uncertainty in RANS simulations: A review. Prog. Aerosp. Sci. 2019, 108, 1–31. [Google Scholar] [CrossRef]
- Pozorski, J.; Minier, J.P. Modeling scalar mixing process in turbulent flow. In Proceedings of the First Symposium on Turbulence and Shear Flow Phenomena, Santa Barbara, CA, USA, 12–15 September 1999; Begel House Inc.: Danbury, CT, USA, 1999. [Google Scholar]
- Wyngaard, J.C. Turbulence in the Atmosphere; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Xiao, S.; Yang, D. Effect of oil plumes on upper-ocean radiative transfer—A numerical study. Ocean Model. 2020, 145, 101522. [Google Scholar] [CrossRef]
- Abernathey, R.P.; Marshall, J. Global surface eddy diffusivities derived from satellite altimetry. J. Geophys. Res. Ocean. 2013, 118, 901–916. [Google Scholar] [CrossRef]
- Cole, S.T.; Wortham, C.; Kunze, E.; Owens, W.B. Eddy stirring and horizontal diffusivity from Argo float observations: Geographic and depth variability. Geophys. Res. Lett. 2015, 42, 3989–3997. [Google Scholar] [CrossRef]
- Marshall, J.; Shuckburgh, E.; Jones, H.; Hill, C. Estimates and implications of surface eddy diffusivity in the Southern Ocean derived from tracer transport. J. Phys. Oceanogr. 2006, 36, 1806–1821. [Google Scholar] [CrossRef]
- Sallée, J.; Speer, K.; Morrow, R.; Lumpkin, R. An estimate of Lagrangian eddy statistics and diffusion in the mixed layer of the Southern Ocean. J. Mar. Res. 2008, 66, 441–463. [Google Scholar] [CrossRef]
- Ferrari, R.; Nikurashin, M. Suppression of eddy diffusivity across jets in the Southern Ocean. J. Phys. Oceanogr. 2010, 40, 1501–1519. [Google Scholar] [CrossRef]
- Holloway, G. Estimation of oceanic eddy transports from satellite altimetry. Nature 1986, 323, 243–244. [Google Scholar] [CrossRef]
- Gargett, A.E. Vertical eddy diffusivity in the ocean interior. J. Mar. Res. 1984, 42, 359–393. [Google Scholar] [CrossRef]
- Kamenkovich, I.; Berloff, P.; Haigh, M.; Sun, L.; Lu, Y. Complexity of mesoscale eddy diffusivity in the ocean. Geophys. Res. Lett. 2021, 48, e2020GL091719. [Google Scholar] [CrossRef]
- Smith, K.M.; Hamlington, P.E.; Fox-Kemper, B. Effects of submesoscale turbulence on ocean tracers. J. Geophys. Res. Ocean. 2016, 121, 908–933. [Google Scholar] [CrossRef]
- Radko, T. Double-Diffusive Convection; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Bachman, S.D.; Fox-Kemper, B.; Bryan, F.O. A tracer-based inversion method for diagnosing eddy-induced diffusivity and advection. Ocean Model. 2015, 86, 1–14. [Google Scholar] [CrossRef]
- Pasquero, C. Differential eddy diffusion of biogeochemical tracers. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Prend, C.J.; Flierl, G.R.; Smith, K.M.; Kaminski, A.K. Parameterizing eddy transport of biogeochemical tracers. Geophys. Res. Lett. 2021, 48, e2021GL094405. [Google Scholar] [CrossRef]
- Tergolina, V.B.; Calzavarini, E.; Mompean, G.; Berti, S. Effects of large-scale advection and small-scale turbulent diffusion on vertical phytoplankton dynamics. Phys. Rev. E 2021, 104, 065106. [Google Scholar] [CrossRef] [PubMed]
- Richards, K.J.; Brentnall, S.J. The impact of diffusion and stirring on the dynamics of interacting populations. J. Theor. Biol. 2006, 238, 340–347. [Google Scholar] [CrossRef]
- Lévy, M.; Martin, A.P. The influence of mesoscale and submesoscale heterogeneity on ocean biogeochemical reactions. Glob. Biogeochem. Cycles 2013, 27, 1139–1150. [Google Scholar] [CrossRef]
- Zhang, J.; Tejada-Martínez, A.E.; Zhang, Q. Developments in computational fluid dynamics-based modeling for disinfection technologies over the last two decades: A review. Environ. Model. Softw. 2014, 58, 71–85. [Google Scholar] [CrossRef]
- Zhang, J.; Tejada-Martínez, A.E.; Zhang, Q.; Lei, H. Evaluating hydraulic and disinfection efficiencies of a full-scale ozone contactor using a RANS-based modeling framework. Water Res. 2014, 52, 155–167. [Google Scholar] [CrossRef]
- Angeloudis, A.; Stoesser, T.; Gualtieri, C.; Falconer, R. Effect of three-dimensional mixing conditions on water treatment reaction processes. In Proceedings of the 36th IAHR World Congress, Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- Weerasuriya, A.U.; Zhang, X.; Tse, K.T.; Liu, C.H.; Kwok, K.C. RANS simulation of near-field dispersion of reactive air pollutants. Build. Environ. 2022, 207, 108553. [Google Scholar] [CrossRef]
- Aubagnac-Karkar, D.; Michel, J.B.; Colin, O.; Vervisch-Kljakic, P.E.; Darabiha, N. Sectional soot model coupled to tabulated chemistry for Diesel RANS simulations. Combust. Flame 2015, 162, 3081–3099. [Google Scholar] [CrossRef]
- Beltram Tergolina, V.; Calzavarini, E.; Mompean, G.; Berti, S. Surface light modulation by sea ice and phytoplankton survival in a convective flow model. Eur. Phys. J. Plus 2022, 137, 1387. [Google Scholar] [CrossRef]
- Kelley, D.E. Convection in ice-covered lakes: Effects on algal suspension. J. Plankton Res. 1997, 19, 1859–1880. [Google Scholar] [CrossRef]
- Cabot, W. Comparison of two-and three-dimensional simulations of miscible Rayleigh-Taylor instability. Phys. Fluids 2006, 18. [Google Scholar] [CrossRef]
- Kokkinakis, I.W.; Drikakis, D.; Youngs, D.L. Modeling of Rayleigh-Taylor mixing using single-fluid models. Phys. Rev. E 2019, 99, 013104. [Google Scholar] [CrossRef]
- Abarzhi, S.I. Review of theoretical modelling approaches of Rayleigh–Taylor instabilities and turbulent mixing. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 1809–1828. [Google Scholar] [CrossRef] [PubMed]
- Dalziel, S.; Linden, P.; Youngs, D. Self-similarity and internal structure of turbulence induced by Rayleigh–Taylor instability. J. Fluid Mech. 1999, 399, 1–48. [Google Scholar] [CrossRef]
- Zhou, Q. Temporal evolution and scaling of mixing in two-dimensional Rayleigh-Taylor turbulence. Phys. Fluids 2013, 25. [Google Scholar] [CrossRef]
- Subich, C.J.; Lamb, K.G.; Stastna, M. Simulation of the Navier–Stokes equations in three dimensions with a spectral collocation method. Int. J. Numer. Methods Fluids 2013, 73, 103–129. [Google Scholar] [CrossRef]
- Bracco, A.; Clayton, S.; Pasquero, C. Horizontal advection, diffusion, and plankton spectra at the sea surface. J. Geophys. Res. Ocean. 2009, 114. [Google Scholar] [CrossRef]
- Trefethen, L.N. Spectral methods in MATLAB, volume 10 of Software, Environments, and Tools. Soc. Ind. Appl. Math. 2000, 24, 57. [Google Scholar]
- Harnanan, S.; Soontiens, N.; Stastna, M. Internal wave boundary layer interaction: A novel instability over broad topography. Phys. Fluids 2015, 27. [Google Scholar] [CrossRef]
- Deepwell, D.; Stastna, M.; Carr, M.; Davies, P.A. Interaction of a mode-2 internal solitary wave with narrow isolated topography. Phys. Fluids 2017, 29. [Google Scholar] [CrossRef]
- Hopkins, J.E.; Palmer, M.R.; Poulton, A.J.; Hickman, A.E.; Sharples, J. Control of a phytoplankton bloom by wind-driven vertical mixing and light availability. Limnol. Oceanogr. 2021, 66, 1926–1949. [Google Scholar] [CrossRef]
- Rutherford, K.; Fennel, K.; Atamanchuk, D.; Wallace, D.; Thomas, H. A modelling study of temporal and spatial pCO 2 variability on the biologically active and temperature-dominated Scotian Shelf. Biogeosciences 2021, 18, 6271–6286. [Google Scholar] [CrossRef]



| Simulation Parameter | Value | Dimensionless Number | Value |
|---|---|---|---|
| 2.048 m | |||
| 0.512 m | |||
| 4096 | |||
| 1024 | |||
| g | 9.81 m/s | ||
| 1000 kg/m | |||
| m/s | |||
| m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Legare, S.; Stastna, M. Implications of Reynolds Averaging for Reactive Tracers in Turbulent Flows. J. Mar. Sci. Eng. 2023, 11, 2036. https://doi.org/10.3390/jmse11112036
Legare S, Stastna M. Implications of Reynolds Averaging for Reactive Tracers in Turbulent Flows. Journal of Marine Science and Engineering. 2023; 11(11):2036. https://doi.org/10.3390/jmse11112036
Chicago/Turabian StyleLegare, Sierra, and Marek Stastna. 2023. "Implications of Reynolds Averaging for Reactive Tracers in Turbulent Flows" Journal of Marine Science and Engineering 11, no. 11: 2036. https://doi.org/10.3390/jmse11112036
APA StyleLegare, S., & Stastna, M. (2023). Implications of Reynolds Averaging for Reactive Tracers in Turbulent Flows. Journal of Marine Science and Engineering, 11(11), 2036. https://doi.org/10.3390/jmse11112036






