Research on Safety State Evaluation of Cable-Stayed Bridge Structures across the Sea

Abstract

In response to the lack of relevant research on the health monitoring system and assessment of the structural safety status of a cable-stayed bridge across the sea, the real-time monitoring data was determined by the health monitoring system installed on the bridge structure. Strain and displacement data for the bridge structure were analyzed and processed. Based on operational research principles, a safety condition assessment of the Channel 1 Bridge was conducted using the Analytic Hierarchy Process (AHP). First, the reserve strength method is applied to determine the weight proportion of monitoring indicators such as strain and displacement. Secondly, the weight proportion of each monitoring indicator at different cross-sectional positions is determined. Then, the hierarchical division of the cable-stayed bridge structure is performed from the lowest layer, and the rating level of the Channel 1 Bridge structure is obtained using the variable weight synthesis method. This provides a basis for management decisions in the bridge maintenance department and serves as an example for future safety assessments of medium-span cable-stayed bridges over the sea.

1. Introduction

With the deep implementation of the strategy to build strong transportation in China, transportation construction has entered a new stage of rapid development. It is expected that China could become the first in the world in the number of bridges in the 2030s [1]. With the increasing operation time of bridges, issues related to bridge safety and diseases gradually emerge. Examples of this include cracks in the main bridge girder and the bridge deck, concrete cracks in the piers, and the aging of the stay cables on cable-stayed bridges. In order to ensure the safety and normal operation of bridge structures, bridge safety monitoring systems are widely used in the daily operation of long-span bridges. Currently, the assessment and warning of the safety status of bridge structures is mostly carried out by installing sensors and other monitoring devices on the bridge structures, which enables long-term real-time monitoring of the operating status and the associated physical variables of the bridges [2,3,4,5]. Figueiredo Eloi et al. [6] summarize the concept of structural health monitoring and point out key developments in research and applications of the statistical pattern recognition paradigm observed in bridges in the last three decades, including developments in sensing technology and data analysis, and identify current and future trends to promote more coordinated and interdisciplinary research in the structural health monitoring of bridges. Kvåle AK et al. [7] designed and installed a comprehensive monitoring system on the Bergsøy-Sundstraumen Bridge that monitors acceleration, displacement, and excitation sources such as wind and waves. Combined with long-term extreme response analysis, the study investigated the influence of environmental parameters (i.e., average wind speed, average wind direction, significant wave height, and wave peak period) on the response. In the context of evaluating structural damage in bridge constructions under varying environmental change patterns, Entezami Alireza et al. [8] have introduced a novel dual-hybrid learning approach based on modal frequencies. This technique is able to successfully eliminate different environmental and/or operational variations and correctly detect damage. This method succeeds in mitigating severe environmental effects and accurately detecting damage. Sui Y L et al. [9,10], based on the concept and application of the Internet of Things (IoT) technology, applied IoT technology to bridge health monitoring and safety early warning, improving the level and efficiency of bridge safety operation management. Entezami Alireza et al. [11] proposed a novel unsupervised meta-learning method that entails four steps: initial data analysis, data segmentation, subspace searching by a novel approach called nearest cluster selection, and anomaly detection. Cross-sea cable-stayed bridges, due to the lack of means for inspecting the tall towers, pose great challenges to maintenance work and have become one of the key and difficult issues in bridge management and maintenance. Therefore, it is particularly important to use health monitoring systems to carry out safety assessments of the tower structures of cross-sea cable-stayed bridges.

The AHP [12,13] is a planning technique used to solve complex decision-making problems. It was initially developed by Thomas L. Saaty, a renowned American operations research expert, based on mathematics and psychology, and has since been further developed and refined. The general assessment of bridges itself is a complex decision-making problem in which various elements influence and constrain each other. The AHP is particularly suitable for comprehensive technical condition assessments of bridges [14]. Currently, the AHP is also one of the most commonly used methods in bridge safety assessment. Changqing W. [15] used the AHP to establish a bridge construction safety risk assessment model, proposing safety influencing factors for bridge construction, and providing references for improving the safety of bridge construction. Wei YL et al. [16,17,18,19] have established a prestressed concrete bridge load capacity assessment model based on the AHP. This model effectively captures the performance of in-service prestressed concrete bridges, enhances existing structural models, and optimizes the comprehensive assessment of load-bearing capacity. Jun D et al. [20,21,22,23,24,25] combined the AHP with fuzzy synthesis to assess the safety conditions of existing bridges. The method can exert the brain advantage of evaluation and simplify the computation process. A Lang, Xu Yue et al. [26] have established weight ratios for various indicators within the bridge AHP model and conducted evaluations of bridge safety performance using the Fuzzy Analytic Hierarchy Process (FAHP). This approach overcomes the limitations of the AHP method in assessing construction safety risks for bridges. Tang Z H et al. [27] have used factors influencing the safety and stability of cantilever bridges, together with construction monitoring methods, as a breakthrough point. Using the AHP, they quantified the weights of risk factors associated with the safety and stability of cantilever bridges. This approach validates and, to some extent, reduces subjective influences and makes the assessment more objective and scientific. Consequently, it allows the determination of warning values for key monitoring indicators for the safety and stability of cantilever bridges. Zhang Bingjiang et al. [28,29,30] employed the AHP to model and analyze bridge safety assessments. Based on this, they conducted an in-depth study to improve the weight proportions in the model and introduced the concept of variable weights, which helps to highlight severely damaged components in the bridge structure.

Overall, the AHP is widely used in bridge safety assessment and provides a systematic and effective approach to assessing the complex factors and interactions involved in bridge assessment.

In order to understand the safety conditions during the operational period of a cable-stayed bridge over the sea, studies were carried out to monitor the bridge. Based on the Channel 1 Bridge and its long-term monitoring system, real-time monitoring data on bridge strains and displacements is collected. The monitoring data is analyzed and processed using the AHP to determine the actual safety status of the bridge during its operational process. This creates a basis for bridge maintenance and also gathers experience for the long-term condition monitoring of numerous cable-stayed bridges in our country.

2. Project Overview

The Channel 1 Bridge is an important part of a major sea-crossing bridge in northern China. It serves as a crucial maritime passage connecting the eastern and western districts of the Bay City and is an integral part of the Qinglan Expressway network. The bridge features a steel box girder structure with two towers and two stay cables, with the main span having a continuous, semi-floating configuration with five spans and the individual spans measuring (80 + 90 + 260 + 90 + 80 m).

The Channel 1 Bridge has an H-shaped tower structure with a spacing of 30.5 m between the main beams of the two parallel spans and a spacing of 20.6 m between the two towers. The tower height is 105 m. A total of 96 inclined stay cables are shared by both fields and meet the requirements of the relevant specifications. The steel box girder has a width of 24 m, including wind panels, and a width of 19.9 m without them. The height of the steel box girder section in the middle is 3.5 m. The bridge is designed for seismic performance level VI and load category A for urban areas and highway grade I. Figure 1 shows the overall layout of the Channel 1 Bridge, while Figure 2 shows the front and side views of the bridge.

3. Health Monitoring of Cable-Stayed Bridges over the Sea

The health monitoring of cable-stayed bridges over the sea focuses on the deployment of various types of sensors on-site. These sensors collect data, which is then transmitted to the cloud via a data transmission system. Once the monitoring data is received by the computer, it is stored and subjected to data analysis and processing. This plays a crucial role in providing a solid basis for bridge safety assessment and early warning systems.

3.1. Overview of Bridge Health Monitoring System

The bridge health monitoring system for cable-stayed bridges over the sea consists of several components, including an on-site data acquisition system, a data transmission system, a safety assessment and early warning system, and a data storage system, among others. The relationships between these subsystems within the health monitoring system are shown in Figure 3.

3.2. Bridge Health Monitoring Contents and Sensor Deployment

The main monitoring contents and locations for cable-stayed bridges over the sea include the following:

(1)

Displacement monitoring: Displacement monitoring points are mainly located at the center of the span of each span, where the maximum deflection typically occurs, as well as at the bridge bearings.

(2)

Strain monitoring: Strain monitoring points are typically deployed at the mid-span of each span, at 1/4 and 3/4 positions along the center span, at the bridge bearings, and at characteristic sections of the tower at various heights.

(3)

Monitoring temperature variation: Temperature fluctuations have a significant impact on the stress and deformation of the main beam and the tower structure. Therefore, temperature monitoring is carried out in the middle of each field, at various bearing locations, and different heights of the tower.

(4)

Acceleration monitoring: Acceleration measurement points are usually placed in the middle of each field, at the bearing points, and at the top and bottom of the tower. The mid-span positions mainly monitor vertical acceleration, the bearing locations typically monitor lateral acceleration, and the top and bottom of the tower are generally used to measure multi-directional acceleration.

(5)

Wind load monitoring: Wind loads have a significant impact on tall tower structures, which lead to deformations and vibrations in the towers. In severe cases, this can lead to tower failure and subsequently affect the deformations of the main beam.

(6)

Cable force monitoring: The primary performance of cable-stayed bridges depends on the tension in the cables. By monitoring cable forces, we can understand the magnitude, distribution, and variations of cable stresses. This in turn enables a comprehensive understanding of the structural forces and deformations of the main tower, main beam, and overall structure. The specific locations of the monitoring points are shown in Figure 4.

Based on the experience with manual inspections, the monitoring content and corresponding sensors for the Channel 1 Bridge can be found in

Table 1. Monitoring content and sensors.

Monitoring Project	Monitoring Equipment	Number of Monitoring Points
Environmental wind load	Anemometer	1
Atmospheric environment	Atmospheric thermometer	2
Structural strain	Strain gauge	38
Structural temperature	Temperature sensor	44
Structural deformation	Tilt sensor	2
Earthquake	Seismometer	1
Structural vibration	Accelerometer	13
The tension in a stay	Anchor load cell	12
Tower top and main beam three-dimensional displacement	GPS	3

. Partial sensor configurations are shown in Figure 5, and the sensor deployment is shown in Figure 4. The placement locations and quantities of the sensors are detailed in

Table 2. Sensor placement locations and quantities.

Sensor Types	Position	Sensor Quantity
Vertical Displacement	Edge bearing, midspan	16
	Adjacent bearing, midspan
	Central span end bearings
	Midspan 1/4 point
	Midspan
	Midspan 3/4 point
Acceleration	Edge bearing, midspan	13
	Midspan
	Adjacent bearing, midspan
	Central span end bearings
	Tower top and bottom
Strain	Midspan section	38
	Bearing section
	Midspan 1/4 point section
	Midspan 3/4 point section
	Tower section
Temperature	Bearing section	46
	Midspan section
	Tower section

.

The sampling frequencies, units, and data volumes for each monitoring parameter are provided in

Table 3. Configuration of safety monitoring parameter acquisition.

Sensor Type	Sampling Frequency	Unit	Daily Data Volume
Strain Measurement Point	10 Hz	$\mathsf{\mu }\mathsf{\epsilon }$	866,000
Acceleration Measurement Point	20 Hz	mm/s2	1,628,000
Deflection Measurement Point	10 min/time	mm	166
Temperature Measurement Point	10 min/time	°C	166
Total daily data volume for the entire bridge			Approximately 70 million

.

4. Bridge Structural Safety State Assessment

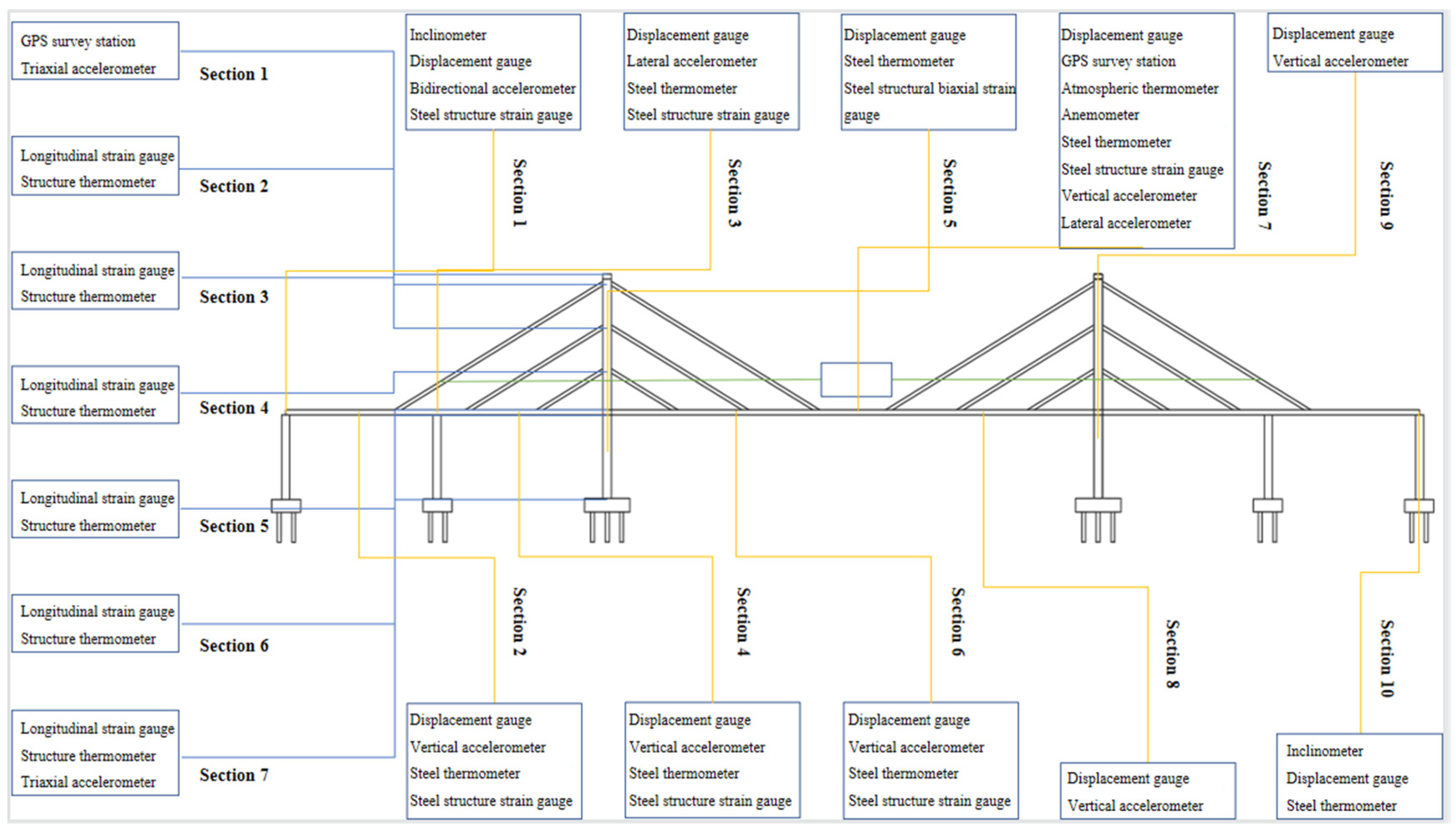
4.1. Establishing Analytic Hierarchy Process Model

As more and more attention has been paid to the structural and operational safety of bridges in recent years, the research and application of methods for evaluating the safety condition of bridges have received great attention, and extensive studies have been carried out. These assessment methods include but are not limited to, traditional comprehensive evaluation, analytical hierarchy process, expert system evaluation, and load test evaluation. In this article, the analytical hierarchy process is used to assess the safety of a cable-stayed bridge across the sea. The fundamental aspect of the analytical hierarchy process is to establish an analytical hierarchy process model that comprehensively reflects the safety status of the bridge, with each evaluation criterion reflecting its importance and independence [31,32]. Taking into account the safety of various evaluation criteria and the operational state of the bridge, the final established AHP model for the safety assessment of the cable-stayed bridge over the sea is shown in Figure 6.

As shown in Figure 6, the AHP model for the safety assessment of the cable-stayed bridge over the sea consists of three levels. The top level represents the overall structural condition of the cable-stayed bridge. The middle level includes the evaluation of static, dynamic, and load-related indicators of the bridge. The lowest level includes strains, cable forces, and displacements of the bridge, as well as acceleration and frequency data, temperature influences, and vehicle loads.

Relying solely on dynamic characteristics when assessing the safety of cable-stayed bridges over the sea can lead to false alarms and false detections. The reasons for these false alarms and missing detections may be due to the harsh environmental conditions in which the cable-stayed bridge is located. The dynamic characteristics of the bridge are subject to the effects of temperature, wind, and other natural factors, which can significantly interfere with on-site monitoring results and cause false alarms. Furthermore, due to the large span and complex structure of cable-stayed bridges over the sea, on-site monitoring systems may be unable to detect changes in dynamic characteristics caused by localized minor damage, resulting in false detections.

In accordance with the hierarchical structure and the subordination relationship, experts are invited to make pairwise comparisons of indicators at the same level, assigning the degree of importance of each level of indicators on a scale from 1 to 9, thus constructing a judgment matrix. The meanings represented by the judgment matrix scale are shown in

Table 4. Judgment matrix scale.

Scale	Meaning
1	Two elements are of equal importance in comparison
3	In comparison, the former is slightly more important than the latter
5	In comparison, the former is significantly more important than the latter
7	In comparison, the former is strongly more important than the latter
9	In comparison, the former is extremely more important than the latter
2, 4, 6, 8	The intermediate value between the two adjacent judgments mentioned above
Reciprocal	Indicating the importance of comparing the interchangeability of the two corresponding factors

.

After calculating the weight vector of indicators and the maximum eigenvalue using the judgment matrix, it’s important to note that the scores in the judgment matrix are derived from the subjective expertise of experts. As a result, inevitable decision errors or one-sided outcomes may occur. Therefore, it is necessary to conduct a consistency check on the judgment matrix to demonstrate the correctness of the assessment results. The specific method for this verification test is as follows:

$$CR=\frac{CI}{RI}$$

(1)

$$CI=\frac{{\lambda }_{\max }-\mathrm{n}}{\mathrm{n}-1}$$

(2)

In this context, n represents the number of elements within the same hierarchical level, ${\lambda }_{\max }$ denotes the maximum eigenvalue of the judgment matrix, and RI stands for the Random Consistency Index (the value of RI is determined based on the value of n, as indicated in

Table 5. Random consistency index values table.

Project	1	2	3	4	5	6	7	8	9	10
RI	0	0	0.58	0.9	1.12	1.24	1.32	1.41	1.45	1.49

). When the CR is less than 0.1, it is considered that the determined values for the importance of elements are reasonable. This signifies that the inconsistency level in constructing the judgment matrix is within an acceptable range, confirming the validity of the judgment matrix. If CR exceeds 0.1, it implies that the judgment matrix is not valid, and adjustments are required for the determined values of the element’s importance.

Experts, based on their own experience, organized discussions and used Santy’s ‘1–9 Scale Method’ to assign relative importance values to primary elements in the safety assessment of the cross-sea cable-stayed bridge (

Table 6. Judgment matrix of primary elements to the target layer.

Cross-Sea Cable-Stayed Bridge Safety State Assessment	Static Performance Indicator Assessment	Dynamic Performance Indicator Assessment	Load Performance Indicator Assessment
Static Performance Indicator Assessment	1	5	5
Dynamic Performance Indicator Assessment	1/5	1	1
Load Performance Indicator Assessment	1/5	1	1

). An assessment matrix is then created using the AHP. The above formula is then applied for a one-time check. If the test is passed, it indicates that the judgment matrix has satisfactory consistency.

After calculation, ${\lambda }_{\max }$ = 3.009, and referring to the table, RI = 0.58. This results in CR = 0.0078 < 0.1. Therefore, the judgment matrix for the first-level elements in the construction of the cable-stayed bridge is deemed consistent through the consistency test. After normalization, the calculated weights for the first-level elements in the safety state assessment of the cross-sea cable-stayed bridge are shown in

Table 7. First-level element weight calculation table.

One-Level Elements	Static Performance Indicator Assessment	Dynamic Performance Indicator Assessment	Load Performance Indicator Assessment
Weightings	0.604	0.198	0.198

.

Based on the calculation results in this section, static indicators with a weight of 60% are considered as the primary basis for analysis. Although using dynamic features for analysis results in false positives and missing positives, dynamic feature analysis is also indispensable, so it is assigned a weight ratio of 20%. The external load reflects the current environment of the bridge and assigns the remaining 20% to the load index. According to the weights of 60%, 20%, and 20%, the overall safety status of the cable-stayed bridge over the sea is comprehensively evaluated.

When the number of elements at the same level is less than 3, RI = 0, and a judgment matrix cannot be constructed. Based on expert experience and previous research [33], in the mean static indicator assessment of cable-stayed bridges over the sea, the strain can reflect the local performance of the bridge, while the displacement can reflect the overall performance. Within this level, the paper assigns a weight of 40% to displacements that can reflect overall performance, a weight of 40% to strains that can reflect local performance, and a weight of 20% to cable forces.

When evaluating the dynamic index of the middle layer, the frequency that can better reflect the dynamic characteristics of the structure is assigned a weight ratio of 80% at this level. Accelerations that are less important relative to frequency receive a weight of 20%.

Since the temperature effect and the vehicle load are equally important when evaluating the load index of the middle layer, in this document a weight ratio of 50% is assigned to the temperature action and the vehicle load.

4.2. Determination of Weights for Bottom-Level Monitoring Indicators

In this paper, the determination of the weights of different indicators and their respective levels ultimately arises from the different importance of the structural information provided by different types of sensors. This results in different sensor types being assigned different weights. Therefore, this paper uses the strength reserve comparison method as a basis [34], in conjunction with the marginal reserve quantity and marginal reserve ratio approaches, to determine the weights of different indicators.

4.2.1. Determination of Weights for Strain Monitoring

In this paper, the weight values of each strain monitoring point are determined using the limit reserve quantity method. First, a comprehensive synthesis of a significant amount of historical data from each strain monitoring point is conducted to determine the maximum strain value at each point. The maximum strain value is processed to obtain the maximum stress, and the maximum stress and the ultimate tensile strength are subtracted, and the difference between the two is the measure of the strain reserve strength at that point. By using the reserve strength measurement of each strain monitoring point, it is possible to determine the weight ratio of each monitoring section as well as the weight ratio of different positions within the same section.

4.2.2. Determination of Weights for Cable Force Measuring Points

This article uses the 10/10~18/2 scaling method to determine the weighting values of each cable force measurement point. In this approach, we integrate the practical considerations of a cable-stayed bridge over the sea, collect expert opinions, and use an extended AHP model with the 10/10~18/2 scaling method to create a hierarchical judgment matrix to calculate the weights of individual cable force measurement points. For example, consider $W(A/B_j)$ as the weight of various indicators $B_j$ with respect to the overall goal $A$. An analysis of the decision matrix is carried out, focusing on the maximum characteristic vector (${\lambda }_{\max }$), the consistency index (CI), and the consistency ratio (CR). If the CR value is less than 0.1, it indicates that the decision matrix has relatively good consistency in the context of bridge construction.

4.2.3. Weight Determination of Displacement Monitoring Points

The determination of the section weights for displacement monitoring points differs from that for strain monitoring points. In this paper, the weight values for displacement monitoring points are determined using the marginal reserve degree method. Typically, the monitoring values of displacement sensors are relatively small. In order to facilitate subsequent analytical calculations, in this article, the numerical results obtained under the combined effects of phase two loading, temperature, prestress, and moving loads are selected as the final calculated values.

According to the specifications, the maximum deflection resulting from the combined effects of internal loads, external loads, and environmental loads on a cable-stayed bridge should not exceed 1/600th of the bridge’s maximum span. Direct analysis of the difference between the specified displacement limits and the calculated displacement values would result in an equal weighting of all displacement monitoring points and thus not take into account the differences in cross-sectional variations between the monitoring points. Thus, a calculation is made by dividing the two, and the quotient is used to create a judgment matrix. This, in conjunction with the limit reserve method, yields the weight percentages for the sections of each displacement monitoring point.

4.2.4. Determination of Weights for Acceleration Measurement Points

The weights for acceleration monitoring points are also determined using the marginal reserve degree method. After calculating and analyzing the monitoring data during the operating period of the bridge, it was found that the acceleration monitoring data stabilizes weekly during normal operation. Therefore, the monitoring values of the acceleration points over a period of 7 days were selected for analysis. The maximum values of each acceleration monitoring point within a week were recorded, and the weighted proportion was calculated using the average of these maximum values over the week.

According to the structural specifications for cable-stayed bridges over the sea, the acceleration limits satisfy Equation (3):

$$\left[A\right]\le \frac{1}{2}\sqrt{f_1}$$

(3)

Whereas, $\left[A\right]$ represents the acceleration limit; $f_1$ represents the first-order frequency of the bridge.

The situation is similar between acceleration monitoring values and displacement monitoring values. Since the values measured on site are significantly below the specified values, a different analysis of both methods would lead to the same weighting of the individual sensor monitoring points and would therefore not reflect the differentiation of different acceleration monitoring points. Therefore, the method of dividing the two values and establishing an importance matrix based on the calculation results is used. Then the weights of each acceleration monitoring point are calculated using the same method.

4.3. Determination of Mathematical Model for Assessment of Bottom-Level Monitoring Indicators

Before carrying out a safety assessment for a cable-stayed bridge over the sea, it is necessary to carry out dimensionless processing of the lowest indicators of the AHP model and evaluate them through assessment. The dimensionless processing method for the lowest level indicators is shown in Equation (4), and the evaluation criteria for the evaluation are shown in Figure 7:

$$f\left(x\right)=\{\begin{array}{l}100,X_0\le X\le X_0{}^{\prime }\\ 100\frac{\left(X-X_{min}\right)}{\left(X_0-X_{min}\right)},X_{min}<X<X_0\\ 100\frac{\left(X_{max}-X\right)}{\left(X_{max}-X_0{}^{\prime }\right)},X_0{}^{\prime }<X<X_{max}\\ 0,X\le X_{min},X\ge X_{max}\end{array}$$

(4)

Whereas, $X$ represents the monitoring data values of the bottom-level indicators:

$X_{min}$ and $X_{max}$ represent the threshold values for the scoring range of the bottom-level indicators;

$X_0^{\prime }$ and $X_0$ represent the optimal range of bottom-level indicators. If the indicator score falls within the range of $X_0^{\prime }$ to $X_0$, it is considered the maximum score.

4.4. Procedure for the Safety Assessment of Cable-Stayed Bridges across the Sea

As part of the research on safety assessment methods for cable-stayed bridges over the sea, the specific steps required in the structural safety assessment of such bridges are as follows:

First, the collected monitoring data from various sensors is organized and analyzed to determine the weight proportions of the individual sensor measurement points. Secondly, the normalization values of various types of indicator parameters are calculated, which are used as the final evaluation values. Then, the displacement indicators are subjected to non-uniformity processing, and the resulting values represent the final displacement indicator evaluation values. Finally, the weighted synthesis method is used to calculate the weights of the intermediate layer in the AHP model, resulting in an overall assessment of the safety of the cable-stayed bridge leads over the sea.

According to the Urban Bridge Condition Index (BCI) regulations, the structural condition of bridge structures is classified into five levels from A to E, which represent the range from excellent condition to dangerous condition [35]. Based on the above rating system, the bridge safety rating classification is determined as shown in

Table 8. Bridge structural condition grading table.

Assessment Score Range	Bridge Structural Condition
(90, 100)	Good (Grade A)	Routine Maintenance Required
(80, 89)	Reminder (Grade B)	Routine Maintenance and Minor Repairs Required
(66, 79)	Warn (Grade C)	After specialized inspection, maintenance, and minor repairs are recommended
(0, 65)	Alarm (Grade D, E)	After inspection, medium or major repair works are advised

.

When assessing the process of a cable-stayed bridge over the sea as part of the AHP, the intermediate layer includes three independent assessment criteria: dynamic analysis, static analysis, and load assessment, each of which gives a corresponding score. By processing the data at the lowest level, scores for the intermediate layer are derived. Then, the overall safety assessment rating of the cable-stayed bridge can be calculated using the weighted synthesis method.

4.5. Safety State Assessment of the Channel 1 Bridge

4.5.1. Determination of Weights for Bottom-Level Monitoring Indicators of Channel 1 Bridge

(1)

Determination of weight for strain monitoring points channel 1 bridge.

This study focuses on the Channel 1 Bridge as a technical background and investigates the collection and processing of strain monitoring data for the Channel 1 Bridge 1 over a 24-h period. The above-mentioned method was used to calculate the force reserves of the strain measuring points at various locations on the cable-stayed bridge over the sea. When determining the weight percentage of the strain monitoring points for the Channel 1 Bridge, the minimum reserve strength amount of each strain monitoring point section was considered as the reserve strength amount. The reserve strength quantities of the strain monitoring sections for the Channel 1 Bridge are shown in

Table 9. Amount of reserve strength for each section.

Location	Section 1	Section 2	Section 3	Section 4	Section 5	Section 6	Section 7
Top left	2.531	2.292	2.562	2.389	2.437	2.394	2.558
Bottom left	2.342	2.593	2.618	1.720	2.338	2.595	2.157
Top right	1.510	2.545	0.962	2.379	2.182	2.617	2.465
bottom right	2.332	2.031	2.396	2.122	1.781	2.142	1.871
Reserve strength measurement	1.510	2.031	0.962	1.720	1.781	2.142	1.871

.

The minimum strength reserves for each section were determined by the difference calculation. A hierarchical analysis judgment matrix was created for the strain monitoring points, and the weights for each strain monitoring section were calculated using the hierarchical analysis judgment matrix. The judgment matrix was constructed as shown in

Table 10. Constructing the judgment matrix.

Location	Section 1	Section 2	Section 3	Section 4	Section 5	Section 6	Section 7
Section 1	1.000	1.347	1.422	0.639	1.242	1.141	1.181
Section 2	0.742	1.000	1.056	0.474	0.922	0.847	0.877
Section 3	0.703	0.947	1.000	0.449	0.873	0.803	0.830
Section 4	1.565	2.108	2.23	1.000	1.943	1.786	1.848
Section 5	0.805	1.085	1.145	0.515	1.000	0.919	0.951
Section 6	0.876	1.180	1.246	0.560	1.088	1.000	1.034
Section 7	0.847	1.141	1.204	0.541	1.052	0.967	1.000

. Normalization was applied to each column of the judgment matrix of the hierarchical analysis. The results are shown in

Table 11. Normalization of the judgement matrix.

Location	Section 1	Section 2	Section 3	Section 4	Section 5	Section 6	Section 7
Section 1	0.153	0.153	0.153	0.153	0.153	0.153	0.153
Section 2	0.113	0.113	0.113	0.113	0.113	0.113	0.113
Section 3	0.108	0.108	0.108	0.108	0.108	0.108	0.108
Section 4	0.239	0.239	0.239	0.239	0.239	0.239	0.239
Section 5	0.123	0.123	0.123	0.123	0.123	0.123	0.123
Section 6	0.134	0.134	0.134	0.134	0.134	0.134	0.134
Section 7	0.130	0.130	0.130	0.130	0.130	0.130	0.130

.

The vertically normalized matrix can be further normalized horizontally to obtain the eigenvalues and eigenvectors of the calculated matrix. The eigenvectors of the matrix represent the weights of each strain monitoring section:

$$\omega =\left[0.1530.1140.1080.2390.1230.1340.130\right]$$

Due to the inherent subjectivity of the AHP, it is necessary to perform a consistency test of the matrix. The formula for the consistency test is presented as Equation (5):

$$CI=\frac{{\lambda }_{\max }-\mathrm{n}}{\mathrm{n}-1}$$

(5)

Here, $\mathrm{n}$ represents the dimension of the judgment matrix; ${\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ denotes the maximum eigenvalue of the importance judgment matrix.

By performing calculations, the consistency test index CI < 0.1 can be determined, and the results show that the judgment matrix is appropriate. Therefore, the weights of the individual stretch sections are shown in

Table 12. Weights of each strain section.

Section	Weight Value Size
Section 1	0.118
Section 2	0.056
Section 3	0.066
Section 4	0.141
Section 5	0.140
Section 6	0.159
Section 7	0.081

. The same method can also be used to calculate the weights of different positions within the same section.

(2)

Weight Determination of Displacement Monitoring Points for Channel 1 Bridge

Similarly, the weights for each displacement monitoring point can be determined at different sections of the Channel 1 Bridge. The results are shown in

Table 13. Weighting values for individual sensor displacement monitoring points.

Monitoring Point	Weight Value Size	Monitoring Point	Weight Value Size
Section 1	0.118	Section 6	0.159
Section 2	0.056	Section 7	0.081
Section 3	0.066	Section 8	0.118
Section 4	0.141	Section 9	0.056
Section 5	0.140	Section 10	0.065

.

(3)

Weight Determination of Acceleration Monitoring Points for Channel 1 Bridge

Similarly, the weights for each acceleration measurement point can be determined, and the corresponding results are shown in

Table 14. Weighting of acceleration points.

Sensor ID	Weight Value Size	Sensor ID	Weight Value Size
SAV1101	0.0266	SAV1106	0.1099
SAH1101	0.0122	SAV1107	0.0170
SAV1102	0.1984	SAH1102	0.1028
SAV1103	0.0168	SAV1108	0.0187
SAV1104	0.0357	SAV1109	0.1283
SAV1105	0.2104	SAV1110	0.1232

.

(4)

Weight Determination of Cable Force Monitoring Points for Channel 1 Bridge

The tension sensors for this cable-stayed bridge over the sea are installed at a total of 12 locations from left to right according to the position of the stay cables, as shown in Figure 5. The navigation bridge consists of two separate double-sided stay cables. Therefore, the tension measurement points are taken from one side, giving a total of 6 measurement points labeled tension 1–6. Finally, the judgment matrix is constructed using the 10/10~18/2 scaling method, and the weight calculation results for each stress measurement point are shown in

Table 15. Matrix for determining the importance of cable force measurement points.

Location	Cable Force 1	Cable Force 2	Cable Force 3	Cable Force 4	Cable Force 5	Cable Force 6
Cable Force 1	1	1	12/8	14/6	14/6	1
Cable Force 2	1	1	14/6	12/8	14/6	1
Cable Force 3	8/12	6/14	1	8/12	1	8/12
Cable Force 4	6/14	8/12	12/8	1	12/8	8/12
Cable Force 5	1	1	14/6	12/8	1	1
Cable Force 6	1	1	12/8	12/8	14/6	1

.

Based on the calculations, the weights for each cable tension measurement point are as follows: 0.2160, 0.2160, 0.0213, 0.0780, 0.0226, and 0.2162. The calculation result $CI=0.000019<0.1$ shows that the weights for each cable tension monitoring point are meaningful in the context of the bridge.

4.5.2. Determining the Evaluation Score for the Channel 1 Bridge

This article takes the actual engineering case of Channel 1 Bridge as a case study and conducts a safety evaluation based on the steps of a safety assessment for cable-stayed bridges over the sea. The evaluation is based on the sensor monitoring data from the Channel 1 Bridge on a specific day. This article uses the Channel 1 Bridge displacement indicator assessment process as an example to illustrate the steps involved in assessing bridge safety. The historical monitoring data of various displacement monitoring points of the Channel 1 Bridge is compiled and summarized to determine the optimal range and extreme values of displacement changes at each monitoring point. The bridge displacement change range for a specific day in the last period for the Channel 1 bridge is selected. The specific data is shown in

Table 16. Statistical data table of the monitored values of the individual displacement sensors.

Sensor ID	Optimal Range	Maximum	Minimum	Measured Maximum	Measured Minimum
Section 1	−0.41–0.25	1.12	−0.70	0.34	−0.32
Section 2	−0.13–0.06	5.09	−4.71	0.38	−0.25
Section 3	−0.03–0.03	0.35	−0.25	0.04	−0.03
Section 4	−0.26–0.08	11.24	−5.28	0.18	−0.16
Section 5	−0.23–0.09	10.16	−5.39	0.16	−0.15
Section 6	−0.17–0	8.04	−4.05	0.15	−0.12
Section 7	−0.07–0.02	0.51	−0.22	0.05	−0.06
Section 8	−0.12–0	1.13	−0.25	0.08	−0.07
Section 9	−0.15–0.06	6.13	−4.76	0.11	−0.25
Section 10	−0.04–0	0.94	−0.26	0.05	−0.03

.

According to the scoring criteria of the safety assessment model for cable-stayed bridges over the sea, the evaluation scores for each displacement monitoring point’s section can be calculated based on the scoring criteria for the lowest-level indicators. The weights and assessment scores for each monitoring point are shown in

Table 17. Assessment scores and weighting values for each displacement monitoring point.

Sensor ID	Weight Value Size	Evaluation Score	Sensor ID	Weight Value Size	Evaluation Score
Section 1	0.118	92.12	Section 6	0.159	98.49
Section 2	0.056	93.47	Section 7	0.081	96.38
Section 3	0.066	99.32	Section 8	0.118	93.71
Section 4	0.141	97.27	Section 9	0.056	97.69
Section 5	0.140	97.30	Section 10	0.065	95.86

.

When calculating according to Table 17, the standardized value for the displacement indicator is 96.26. Since the maximum score for the non-uniform safety coefficient is 0.8, the calculated non-uniform safety coefficient is 0.7326. Therefore, the final score for the shift indicator is set at 96.26 × 0.7326/0.8 = 88.15.

Based on the weights of each level in the AHP model, the final safety assessment score for the Channel 1 Bridge is calculated and presented in

Table 18. Safety assessment score for this waterway bridge.

	Strain	Cable Force	Displacement	Acceleration	Frequency	Thermal Effects	Vehicle Load
Weight	0.24	0.12	0.24	0.04	0.16	0.10	0.10
Score	90.46	92.26	88.15	96.74	100	100	100
Weighted total score	93.81

.

5. Conclusions

Based on the long-term health monitoring data of the Channel 1 Bridge, this study employed the Analytic Hierarchy Process to analyze the strain, displacement, and acceleration results from the bridge’s structural monitoring data and conducted a safety state evaluation. Through the research analysis, the following conclusions were drawn:

• The health monitoring system described in this article enables long-term health monitoring of the cable-stayed bridge over the sea. It is capable of collecting data in real time and transmitting health monitoring data efficiently.
• The Analytic Hierarchy Process method used for the safety assessment of the cable-stayed bridge over the sea allows for efficient and accurate determination of its rating level.
• The calculation results indicate that the overall structural score for the Channel 1 Bridge is 93.81 points, which is within the range of an “A” rating. This suggests that the bridge is in good working condition. Routine maintenance should then be carried out.