Abstract
Due to the complex hydrogeological conditions in coastal regions, the use of internal bracing systems is necessary for supporting coastal foundation pits. This paper introduces a novel prefabricated foundation pit bracing system based on Hollow Concrete-Filled Steel Tube (H-CFST) structures that can be reused, offering significant economic and societal benefits. However, there is a severe lack of research on the application of H-CFST bracing systems. Through model tests and finite element simulations, the load-displacement characteristics and failure modes of prefabricated H-CFST bracing under transverse bending were investigated. The study revealed that when a wall thickness of 1.5 d was chosen, the self-designed hoop effectively mitigated strength and stiffness reduction at the bracing connection point. When the load reached 150 kN, the outer steel tube of the H-CFST components experienced localized yielding, and when the load was increased to 300 kN, the end supports exhibited cracking. Finite element analysis provided a more accurate prediction of bracing failure at 147.18 kN, and it offered valuable insights for optimizing the bracing design. Based on the above research, theoretical methods for calculating the bearing capacity of each bracing component under transverse bending conditions have been proposed and validated against experimental results.
1. Introduction
As a transitional zone between the continental interiors and the open ocean, coastal regions represent the most economically dynamic and project-intensive areas in China [1]. Due to the complex hydrogeological conditions in coastal regions, the use of internal bracing systems for supporting coastal foundation pits is essential [2,3,4]. Taking the example of metro construction in the coastal city of Qingdao in northern China, a large number of coastal metro foundation pits, as shown in Figure 1, have been formed in urban development in recent years to meet the requirements of economic development and transportation [5]. These foundation pits face numerous engineering challenges, such as the fluctuation of groundwater levels [6]. The phenomenon of coastal tides leads to continuous changes in the groundwater levels around the foundation pits, as depicted in Figure 2, significantly impacting the safety of the support structures [7,8,9,10]. Since rivers in coastal areas are usually connected to the sea, tidal-induced changes in the river’s water level can even affect foundation pits that are relatively far from the sea. Consequently, the majority of coastal metro foundation pits in the Qingdao region are supported using internal concrete bracing systems [5,6,11].
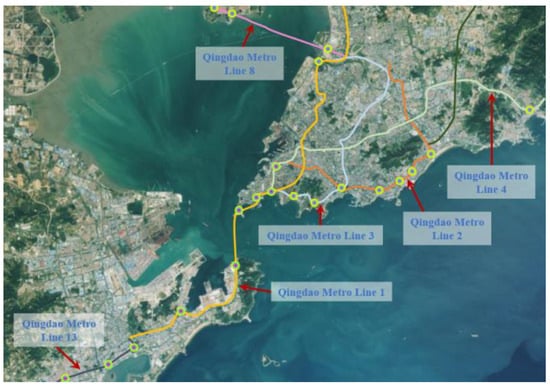
Figure 1.
Coastal foundation pits of Qingdao Metro.
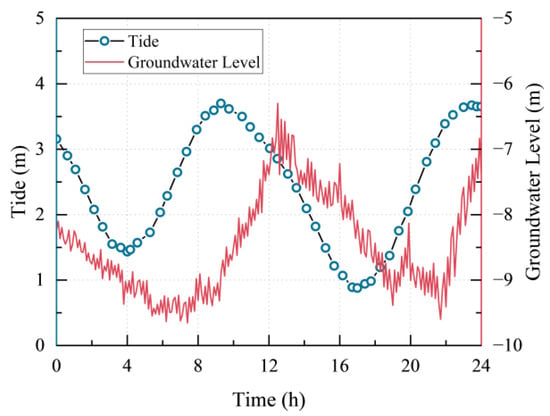
Figure 2.
Groundwater level of a coastal foundation pit on Qingdao Metro Line 8.
However, traditional concrete internal bracing systems have issues related to factors such as weight and reusability [12,13]. Due to the presence of an outer steel section, concrete-filled steel tube (CFST) structures improve the bending and shear strength of core concrete [14,15], with advantages including high stiffness, corrosion resistance, and reusability [16]. The steel tube with hollow concrete infill, abbreviated as H-CFST, developed on this basis can significantly reduce the weight of the member and retain the advantages referred to in [17,18]. When used as interior bracing in the foundation pit in coastal areas, the H-CFST can avoid many problems caused by traditional concrete interior bracing, offering considerable innovation and practical significance. Additionally, eccentric compression fracture and bending fracture are common modes of failure in the bracing of foundation pits. Therefore, studying the mechanical response of the aforementioned new bracing system under transverse bending conditions will establish an important theoretical foundation for its widespread adoption.
Several in-depth studies have been conducted on the load-bearing performance and failure modes of solid/hollow CFST structures, forming a relatively complete theoretical system. The relevant research findings are shown in Table 1.

Table 1.
Previous studies on the subject.
Kuranovas and Kvedaras [18] analyzed the performance of H-CFST compression short-column components at different stress states. The results indicated that in the members with a single-layer steel tube and concrete core, the triaxial stress state occurs only at the contact surface between the concrete core and the steel tube. Zhong and Xu [16] and Han et al. [19] also studied the axial compression behavior of H-CFST columns. They both concluded that the performance of H-CFST columns varied systematically and continuously with changes in confinement ratios and hollow ratios. Yu et al. [22] proposed a unified formula for calculating the compressive capacity of composite circular CFST columns with hollow or solid concrete cores. The formula was further modified by introducing correlation coefficients that were verified through experiments. Ouyang et al. [23] established a new finite element model based on a confining stress field. This model introduced the lateral expansion of concrete and the plastic behavior of steel pipes. Through the simulation of 92 square CFST specimens, it was found that increasing the fillet radius could improve the post-peak performance of square CFST columns. Based on linear elasticity theory. Ekmekyapar et al. [24] conducted experiments on short, middle-length, and long columns having circular CFST components. The results showed that the bearing capacity of the columns was directly affected by the aspect ratio and the relative slenderness ratio, making these important design parameters for the CFST columns. Han et al. [25] conducted a pure torsion analysis on CFST columns using ABAQUS 2022. The model calculations were consistent with the experimental results, demonstrating the necessity of using theoretical models to determine the ultimate torsional strength of the composite components. Mizan et al. [28] argued that existing fiber element models and design specifications do not consider the local buckling of the outer steel tube of concrete-filled double-skin steel tube (CFDST) columns, which might result in an overestimation of the ultimate axial capacity of the column. The concept of effective width was introduced into the calculation model to study the axial compressive straining response in short columns consisting of concrete-filled rectangular steel tubes under various design variables, and an equation was proposed for evaluating the ultimate axial capacity of such columns.
Among these, only a few researchers have studied the mechanical properties of H-CFST components. However, what differentiates the research in this paper is that the aforementioned studies focus on H-CFST columns, which are primarily column-type structures designed to withstand vertical loads. Furthermore, the loading conditions in these studies are varied [16,18,19,20,21]. Most researchers have investigated the mechanical behavior of H-CFST columns under axial compression [16,18,19], while others concentrated on the response of H-CFST columns to impact loads [20,21]. Only Uenaka and Mizukoshi [14], Zhang et al. [26], and Guo et al. [27] conducted research on the mechanical behavior of CFST beam-type structures under load. However, the aforementioned studies focus on solid CFST components rather than H-CFST components. Thus, there is still a lack of reliable theoretical and applied research support for the use of H-CFST components as interior bracing for foundation pits.
This study proposes a prefabricated H-CFST interior bracing system for coastal foundation pits such that the interior bracing system consists of the H-CFST components, hoops, and end supports. The flowchart of the experimental research plan is shown in Figure 3.
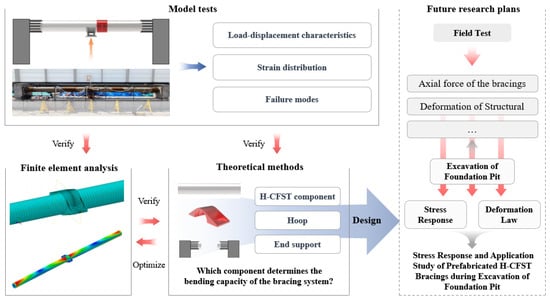
Figure 3.
Flowchart of the experimental research plan.
In order to study the transverse bending performance of prefabricated H-CFST bracing, a transverse bending test model with a scale of 1/2.5 of the original bracing was designed and developed. Through model tests and finite element analysis (FEA), the load-displacement characteristics, strain distribution, and failure modes of the prefabricated H-CFST bracing under transverse bending were investigated. Theoretical methods for calculating the bearing capacity of bracing components under transverse bending conditions have been proposed and validated against experimental results. This study has provided a reference for the field of costal foundation pits support.
2. The Model Test
2.1. Design and Fabrication of the Experimental Model Specimen
This paper reports the development of a test specimen that is on a scale of 1/2.5 of the coastal foundation pit bracing of a Qingdao Metro Line 8 station, taking into account the best site conditions available for the test. The original bracing was designed to have the same strength as the corresponding concrete bracing. It had a length of 20 m and was divided into left and right H-CFST components, with the two H-CFST components connected by the self-designed “hoop”. The H-CFST component was of Q355B steel, the outer diameter was 700 mm, and the wall thickness of the steel tube was 6 mm. The fabrication of the concrete core of grade C80 material with 100 mm wall thickness applied centrifugal technology. The hoop was 35 mm thick and made of Q355B material. The end supports consisted of 30 HRB400 steel bars with a diameter of 20 mm, which overlapped with the steel bars inside the top beam. A schematic diagram of the experimental model is shown in Figure 4.
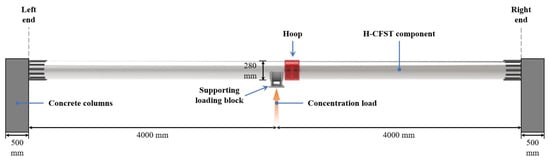
Figure 4.
Schematic diagram of the experimental model.
The experimental model had a length of 9000 mm and a calculated span of 8000 mm. The mid-span section of the experimental model had a diameter of 280 mm, and the wall thickness of the steel tube was 2.4 mm. In order to investigate the performance of bracing under transverse bending, a concentrated force was applied at the intermediate node adjacent to the hoop connection in the middle of the span. The concentrated load was applied using a special supporting loading block so as to avoid local failure in the region of the load introduction and to better simulate the loading in the on-site system.
2.1.1. H-CFST Component Model
The two parts of the prefabricated H-CFST bracing model used for the experiment were similar, and they were connected with a hoop. Their steel material was Q235B, and the internal filling was of grade C30 concrete. The cross-section of the bracing reduced to a scale of 1/2.5 of the original size is shown in Figure 5. The H-CFST component model overlapped with the reinforcement cage of the columns of both ends and was fixed after the poured concrete hardened. One end of 12 HRB400 steel bars with a diameter of 20 mm was welded to the steel pipe of the H-CFST component model, and the other end overlapped with the reinforcement cage inside the column, as shown in Figure 6. Moreover, end plates of 10 mm thickness were set at the nodes at both ends of the bracing to prevent concrete from being injected into the bracing during pouring. The size of the end plate is shown in Figure 7. The schematic diagram of the intermediate node (Hoop) connection is shown in Figure 8.
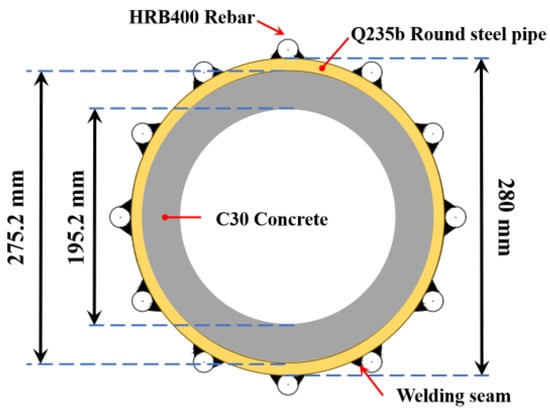
Figure 5.
Schematic diagram of the model cross-section.
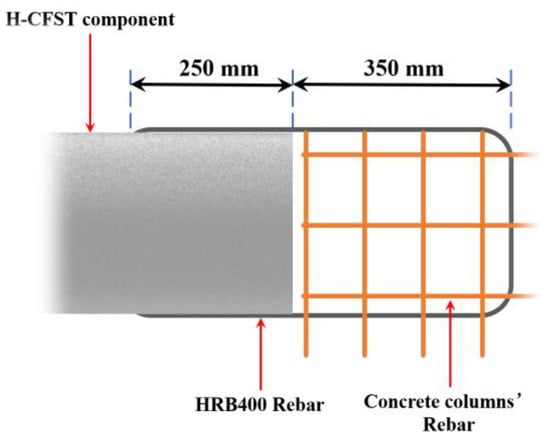
Figure 6.
Schematic diagram of the connection between the concrete column and bracing.

Figure 7.
Schematic diagram of the end plate.
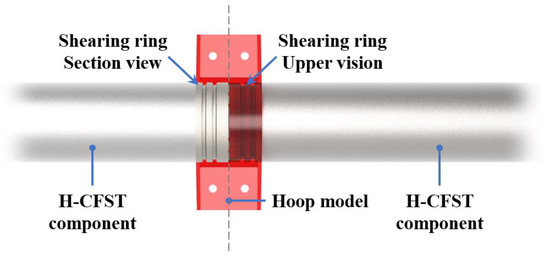
Figure 8.
Schematic diagram of the intermediate node (Hoop) connection.
The H-CFST component model was connected to the hoop by setting a “shear ring” structure at the intermediate node, and the shear ring was welded to the steel pipe of the H-CFST component at the factory with equal intensity. The groove on the shear ring facilitated alignment operation during the bracing connection and improved the stability of the bracing during tension.
2.1.2. Hoop Model
Two H-CFST component models were connected using a hoop of two-halves connected with bolts, and the dimensions are shown in Figure 9.
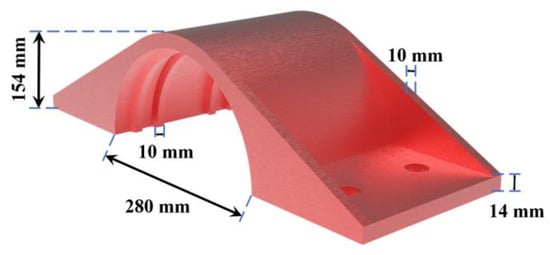
Figure 9.
Schematics of one-half of the hoop model.
The hoop material was Q235B, with a thickness of 14 mm and a slot depth of 10 mm. Both parts of the hoop were provided by rib plates of 10 mm thickness, and the upper and lower parts of the hoop were connected using M30 bolts of grade 12.9.
2.1.3. Counterforce Structure and Supporting Loading Block
The main body of the reaction structure was made of reinforced concrete, including the foundations and columns of both ends. The cross-sectional dimensions of the columns made of C35 concrete were 500 × 500 mm. The foundation was of grade C35 concrete, with a cross-sectional size of 500 × 800 mm. The distance between the top of the foundation and the bottom of the bracing model was 300 mm. The dimensions of the supporting loading block are shown in Figure 10.
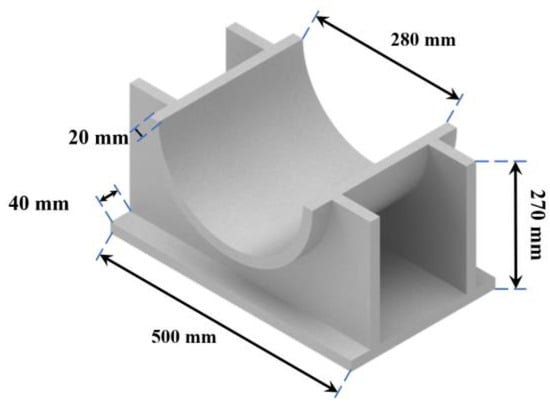
Figure 10.
Main dimensions of the supporting loading block.
The supporting loading block consisted of an arc-shaped steel plate, two rib plates, and a bottom plate. All these components were of Q235B steel of 20 mm thickness.
2.1.4. Fabrication of the Experimental Model
The process of lifting, assembly, and concreting the experimental model on site are presented in Figure 11.
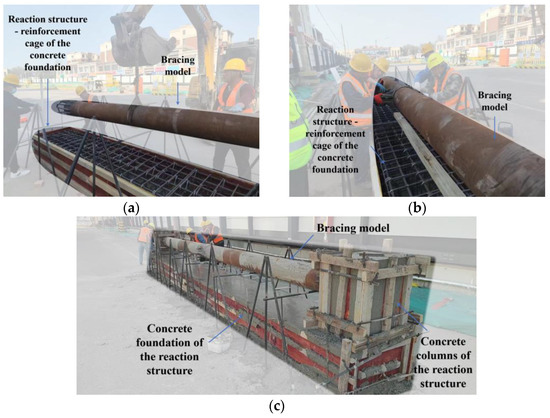
Figure 11.
Fabrication process of the experimental model: (a) Lifting; (b) Mounting; (c) As concreted.
In the fabrication process of the experimental model, the self-designed hoop structure facilitated the seamless connection of two H-CFST components. This was achieved by avoiding the traditional flange joint method, which requires the H-CFST components to be rolled along their longitudinal axes to align the bolt holes [30,31,32]. Due to the substantial volume and weight of internal bracing, this particular step consumed significant manpower and resources during actual construction. Therefore, the self-designed hoop structure offered notable advantages in terms of both cost effectiveness and construction convenience.
2.2. Arrangement of Measuring Points
2.2.1. Arrangement of Strain Measuring Points
The strains in the model structure were measured using the XL2118B strain monitoring instrument (Xieli Technology Development Co., Ltd., Qinhuangdao, China). The employed strain gauges were 120-20AA (Guangce Electronics Co., Ltd., Yiyang, China) with a sensitivity of 20 mV/V. A total of 8 monitoring sections were arranged on the bracing, and their positions are shown in Figure 12. Sections 1 and 8 were set at a distance of 0.5 m from the columns of both ends. Section 5 was set at the centerline of the middle node of the model. Sections 4 and 6 were situated on the H-CFST component at both edges of the intermediate node hoop, with Section 4 on the centerline of the supporting loading block and Section 6 set at a distance of 0.5 m from Section 5. The distance between Sections 3 and 4 was 0.5 m, while Sections 2 and 7 were set on the centerline of the midspan of the corresponding H-CFST component model. The layout of the measurement points is shown in Figure 12. The arrangement of the strain measurement points and measurement conditions are shown in Figure 13.
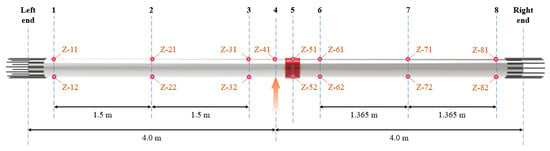
Figure 12.
Layout of the sections to monitor the strains.

Figure 13.
Layout and outlook of some measurement points: (a) General layout, (b) Orientation of a strain gauge, (c) Measuring equipment.
The meaning of each measuring point is as follows: “Z” indicates that the detecting direction of the measuring point is parallel to the bracing axis; the first number represents the section number; when the second number is “1”, it indicates that the measuring point is located on the upper side of the bracing; when the second number is “2”, it indicates that the measuring point is located on the lower side.
2.2.2. Arrangement of Displacement Measuring Points
The displacements of the bracing were measured using the CVok-DU191 digital display dial gauges and their supporting instrument (Xiwaka Precision Measuring Instrument Co., Ltd., Dongguan, China), having a range of 100 mm and accuracy of 0.01 mm. A total of 7 monitoring sections were arranged on the bracing, and the positions of the sections are shown in Figure 14a. The layout of the experimental model and the general arrangement of the displacement measurements are shown in Figure 14b,c.
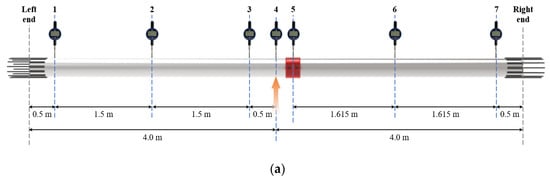

Figure 14.
Monitoring of the displacements in the bracing model: (a) Layout of the sections for displacement monitoring, (b) Setup for measuring the displacements, (c) Data acquisition system of the displacement measurements.
Sections 1 and 7 were set at a distance of 0.5 m from the columns of both ends. Section 5 was set at the centerline of the middle node of the bracing. Section 4 was set at the centerline of the supporting loading block. The distance between Sections 3 and 4 was 0.5 m. Sections 2 and 6 were at the centerline of the corresponding span of the H-CFST component model.
2.3. Loading Method of the Experimental Model
The single-point concentrated load method was used for the experimental model, with the load situated 4.0 m from the central section to the columns of both ends. The supporting loading block was directly below the loading point, and a ZP-30T jack was placed below the supporting loading block.
According to previous studies [18,24,28,33], the loadings of the specimen were applied in a graded manner and arranged as increasing steadily at a rate of approximately 10 kN/min. Each loading procedure consisted of 10 steps such that each loading level was kept for 5 min. Strain and displacement data were automatically collected at one-second intervals. To indirectly assess the condition of the bracing, test loads of 100 kN, 150 kN, 200 kN, and 300 kN were applied consecutively to a test model during loading cycles.
2.4. Model Test Results and Analysis
2.4.1. Load-Displacement Diagrams of the Experimental Model
Figure 15 shows the load-displacement diagrams for the maximum test loads of 100 kN, 150 kN, 200 kN, and 300 kN (taking the mean measured values of displacement measuring point 4 during the loading process of each level).
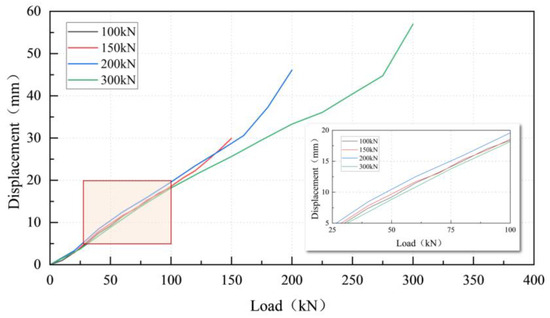
Figure 15.
Load-displacement diagrams for the experimental model, taken as the measured values of point BF-4.
It can be seen that the vertical displacement of the model gradually increased with the increasing test load, and the slopes of each curve were almost equal when the load was less than 150 kN. Compared with the curves of 100 kN and 150 kN, the curves of 200 kN and 300 kN showed a sudden increase in the slope at the later state of loading, and the variation could be divided into two phases, of which the first was is the elastic phase, where the vertical displacement showed a linear correlation with the test load. The second phase was the elastoplastic one, where the steel tube of the H-CFST component began to yield and the vertical displacement of the member accelerated with the increasing test load, resulting in a gradually increasing slope of the curve. This is consistent with the description in reference [33]. It is worth noting that the curves of 200 kN and 300 kN had different starting points at the elastoplastic stage. The starting point of the 200 kN curve was about 150 kN, and that of the 300 kN curve was about 200 kN. The reason for this is that the yield strength of the steel tube in the experimental model experiences strain hardening when loaded up to 200 kN. This is consistent with the description in references [34,35,36].
2.4.2. Variation of Strains with the Load in the Experimental Model
Figure 16 presents the development of strains at each measuring point up to a maximum load of 200 kN, and a good working state was maintained at each measuring point while the strains at the upper and lower measuring points of the experimental model increased with the load.
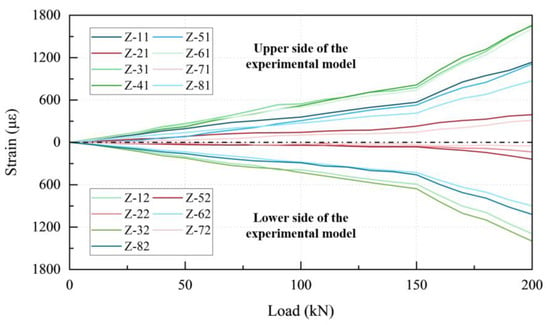
Figure 16.
Development of straining in the experimental model up to a load of 200 kN.
The slope of the curves increased significantly after exceeding 150 kN. This behavior is consistent with the one mentioned earlier. When the load was 150 kN, the maximum strain value at Z-41 was 918.4 με, and the respective stress was 203.4 MPa, i.e., the bracing model was on the verge of yielding. During the loading process, the strain distribution of the upper and lower measurement points was basically symmetrical along the neutral plane of the model, which is consistent with the description in reference [34]. The maximum strain values of each measurement point were distributed within three intervals. Among them, the greatest strains appeared at the loading point, with a maximum value of 1654.3 με at Z-41. The strains at the nodes of both ends of the bracing model were slightly smaller, and the strains in the middlemost section of the two H-CFST components were the smallest, with a minimum value of 49.8 με at Z-72. The straining at the intermediate hoop was not significant compared to the ends of the H-CFST component model, and the strain of 1110.9 με at the measurement point Z-51 was significantly greater than the strain of 238.2 με at the lower measurement point Z-52.
2.4.3. Failure Mode of the Experimental Model
As shown in Figure 15, a vertical displacement of 29.93 mm occurred at the BF-4 measuring point when the test load was 150 kN. At this point, the model exhibited significant bending deformation, and the steel pipe of the model experienced yielding above the loading point and at both ends of the pipe, which is consistent with the results in the references [14,37,38]. Thus, the failure took place at 150 kN. According to the failure criterion based on the deformation in GB 50017-2017 [39], when the cumulative vertical displacement of the mid-span section in the model exceeded 20 mm, which corresponds to 1/400 of the span length, it should be considered failed. Therefore, the bending capacity of the prefabricated H-CFST interior bracing system should be 100 kN.
Due to equipment limitations, the stress state of the concrete inside the steel pipe could only be inferred from the experimental data. According to Figure 15, the elastic phase of the load-displacement diagram at 150 kN was consistent with those at 100 kN, 200 kN, and 300 kN. If the concrete core inside the steel tube is damaged during loading, the overall stiffness of the bracing structure should be reduced. When loading again, the slope of the elastic part of the corresponding load-displacement diagram was expected to increase, but this was not consistent with the test results. Therefore, it can be concluded that the concrete inside the steel pipe was not damaged at this time.
Figure 17 presents the distribution of inelastic deformations in the test model at loadings to different maximum values. The model undergoes inelastic deformation after unloading from 150 kN, with a maximum value of 1.95 mm at BF-4. When unloading from 200 kN, inelastic deformations occurred at all seven measuring points. When loading up to 300 kN, the inelastic deformations developed rapidly, with a maximum value of 32.53 mm at BF-4 and a minimum value of 5.50 mm at BF-1. The displacement values of each measuring point were strictly symmetrical with respect to the loading point.
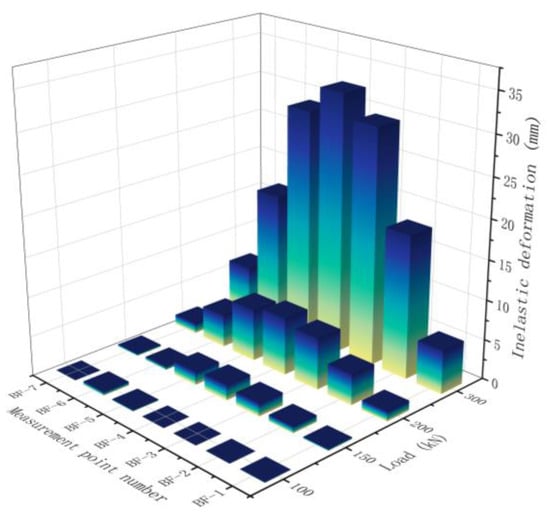
Figure 17.
Values of inelastic deformation in the experimental model after unloading from various maximum loads.
After increasing the maximum load to 300 kN, cracks appeared on columns of both ends for the supporting reactions of the bracing member, as shown in Figure 18. The cracks basically extended 45° outward from the connection between the bracing model and the column.

Figure 18.
Cracking of concrete in the columns of both ends.
Based on the above results, the ultimate transverse bending capacity of the prefabricated H-CFST interior bracing system was determined to be 150 kN. According to the deformation failure criterion specified in GB 50017-2017 [39], the ultimate transverse bending capacity of the system should be taken as 100 kN. Considering the reusability of the prefabricated H-CFST interior bracing system, the design processes should use either the ultimate capacity under the deformation control criterion or apply a reduction factor to the load-carrying capacity under the ultimate limit state. Additionally, the system exhibited two typical failure modes, i.e., local yielding of the steel tube at the loading point and cracking of the two end supports. The failure mode was also mentioned in references [34,40] Therefore, the weak point of the prefabricated H-CFST interior bracing system was not at the connection between the two H-CFST components. The self-designed hoop effectively mitigated or eliminated the strength and stiffness reduction phenomenon at the joints of the entire bracing system.
3. Finite Element Simulations
The basic requirement for the reusability of the prefabricated H-CFST interior bracing system is that the core concrete within the H-CFST components remains undamaged. To further investigate the condition of the core concrete after the bracing reaches the aforementioned failure criteria and to explore whether numerical simulation methods can be used to design and optimize the prefabricated H-CFST interior bracing system, a numerical simulation approach was employed to simulate the loading process of the bracing. The results of these simulations were subsequently validated against the experimental results obtained from the model tests.
3.1. Material Data of the FEA Models
The material data for the FEA models are shown in Table 2.

Table 2.
Material data for the FEA models.
3.2. Element Type, Element Mesh, and Boundary Condition
In order to better validate the experimental results, a finite element model of the same size as the experimental model shown in Figure 19a was established using ABAQUS 2022. The specific meshing details are shown in Figure 19b,c.

Figure 19.
Finite element model and mesh generated for the bracing: (a) Finite element model, (b) Overall mesh, (c) Local mesh.
The two sides of the model were fixedly connected through reference points, and both the concrete core and steel tube were meshed with C3D8R elements with three translational degrees of freedom per node. Computational accuracy and efficiency were fully considered during the meshing process, and the mesh density was increased in areas with complex stress conditions and contact relationships.
3.3. Constitutive Models
3.3.1. Core Concrete
The transverse bending response of concrete was analyzed using the plastic damage model in ABAQUS 2022 [41]. The elastic modulus and Poisson’s ratio of concrete were determined according to the recommendations of ACI Committee 318 [42]:
Han et al. [19] proposed a stress–strain relationship for constrained concrete in compression after simulating CFST components. The equivalent stress–strain model suitable for ABAQUS 2022 finite element analysis was as follows:
where , ; ; ; ; ; ; .
The following stress–strain relationship was used for the concrete in tension [43]:
where , ; ; .
3.3.2. Outer Steel
The quadratic plastic flow model [44] was used to describe the stress–strain relationship for the low-carbon steel of the tube:
where ; ; ; ; ; ; .
3.4. Steel Tube–Concrete Interface
The contact relationship between the steel tube and its core concrete is the key factor in ensuring the authenticity and effectiveness of the simulation results. According to existing studies [25,45], using pressure models in the normal direction of the contact surface and Coulomb friction models in the tangential direction can best reflect synergistic deformations.
According to the Coulomb friction model, the contact surface between the steel tube and concrete can transmit shear stress until it reaches a point (τl) where the shear stress is less than the bond stress. There is a relationship, as follows:
where μ is the frictional factor of the contact surface between the steel tube and concrete and is taken as 0.6; and , in which D and d are the outer diameter and thickness of the steel pipe [45], respectively.
3.5. FEM Results and Analysis
3.5.1. Load-Displacement Diagrams of the Experimental Model
Figure 20 shows the load-displacement diagrams of the test model and the numerical simulation under various test loads.
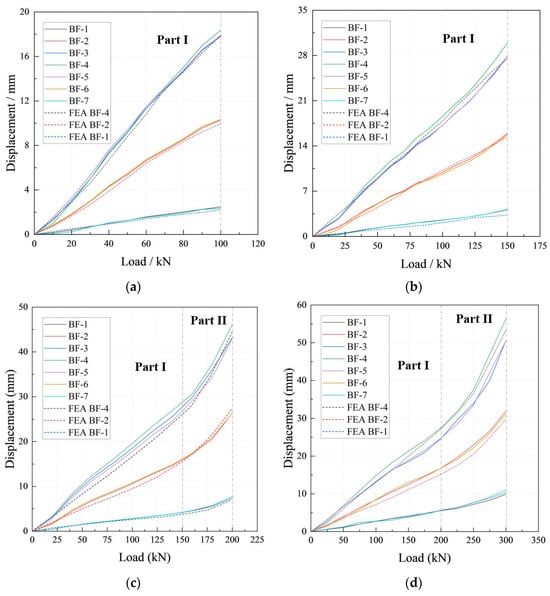
Figure 20.
Load-displacement diagrams for the experimental model and FEM results as loaded up to (a) 100 kN, (b) 150 kN, (c) 200 kN, and (d) 300 kN.
Taking the maximum load of 200 kN as an example, when the load was 200 kN, the vertical displacement of the mid-span section of the model was 46.12 mm, and the FEA result was 44.39 mm. The two results were in good agreement, and the distribution of deflection at each measuring point along the length of the component followed the variation law of the sine half-wave curve [40,46,47]. Due to errors in the production and manufacturing process of the bracing model, as well as certain defects in the material, the measured vertical displacements often tended to be greater than the respective values from the FEM analyses, which is also mentioned in references [40,48].
3.5.2. Variation of Strains with Load in the Experimental Model
The strain distribution along the horizontal direction of the experimental model at 200 kN is shown in Figure 21.
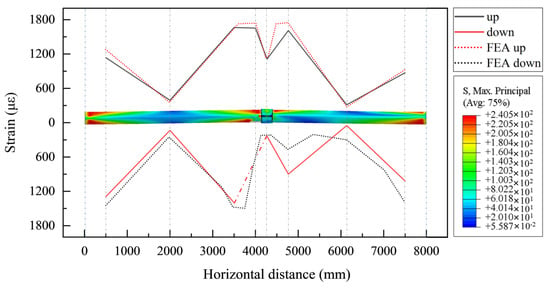
Figure 21.
Distribution of strains along the horizontal distance in the experimental model at a load of 200 kN.
The FEA curve in the figure was obtained by calculating the corresponding numerical simulation results. It was seen that the results of the numerical simulation were in good agreement with the measured values.
3.5.3. Failure Mode of the Experimental Model
The FEA results of the experimental model at a load of 150 kN are shown in Figure 22. In this case, the steel tube of the model yields at the loading position and at both ends, and the maximum stress in the concrete core was 25.10 MPa, which was consistent with the above inference.
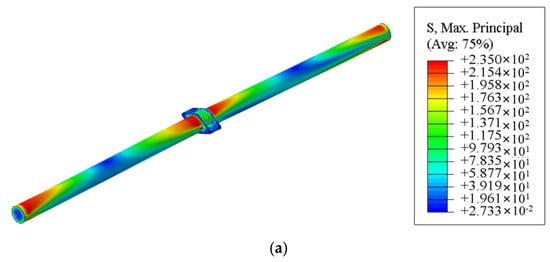
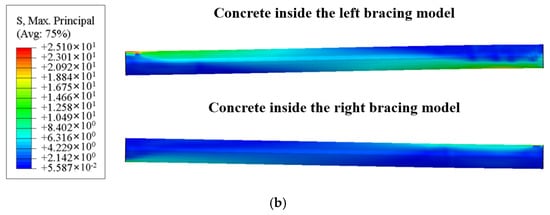
Figure 22.
Stress distribution nephograms: (a) In the steel components of the bracing model, (b) In the concrete inside the steel tube.
The above results indicate that the prefabricated H-CFST interior bracing system designed based on the deformation control criterion did not experience damage to its core concrete unless the two typical failure modes mentioned earlier occurred. Therefore, under the condition that the prefabricated H-CFST interior bracing system was not damaged during usage, the system could be reused multiple times. Additionally, the finite element model established using the methods described earlier could accurately simulate the stress response and failure modes of prefabricated bracing under transverse bending. Hence, it is feasible to consider using numerical simulation methods for the design and optimization of the prefabricated H-CFST interior bracing system.
4. Evaluation of Bearing Capacity
According to the experiments explained above and FEM analyses, the first yielding appeared on the surface of the steel tube, and at increasing maximum loads, cracks would appear in the concrete columns at both ends of the system. It may be further anticipated that if the H-CFST component and the columns of both ends are not damaged, the steel hoop will yield on its tensile zone. On account of the experimental results explained above, the flexural bearing capacity of the H-CFST component, hoop and end supports should be considered and evaluated in the design process. The maximum concentrated load of each component in the middle of the span can be obtained by calculating the maximum bending moments in each component and combining them with the bending moment diagram of the bracing due to transverse loading. The flexural bearing capacity was obtained based on the calculation results above.
The stress state of the experimental model is due to transverse bending, consisting of normal and shear stresses in the cross-section [49]. Because the existence of shear stresses prevents the cross-sections from remaining plane [50], the assumption of planes remaining planes is not applicable here. However, as the shear force is constant over the entire length of the member due to the single point load [51], the displacement due to warping of adjacent cross-sections is uniform and the warping in the section does not change the distribution of normal stresses evaluated based on the assumption of planes remaining planes. Therefore, the next analyses were based on this assumption.
4.1. Bending Capacity of the H-CFST Component
According to the FEM analyses and experimental results, the maximum normal stress in the H-CFST component appeared in the section of maximum bending, and the maximum bending moment M was calculated as:
where is the plastic development coefficient of the H-CFST component; is the composite section modulus of the H-CFST component; is the design value of the combined compressive strength.
was expressed as:
where is the void fraction of the H-CFST component, which is the ratio of void area to total area. The results indicate that the plasticity of concrete increases due to the constraint of the steel tube, i.e., the strain corresponding to the maximum stress increases. The descending branch of the stress–strain curve tended to be uniform [25].
4.2. Bending Capacity of the Hoop
To simplify the calculation, the longitudinal force generated between the H-CFST component and the hoop was assumed to be fully transmitted when subjected to load. According to the FEA and experimental results, the most unfavorable position on the hoop was the cross-section with the maximum bending moment. The simplified model was a statically indeterminate beam where the fixed-end supports were provided by the concrete columns and connecting steel bars, and the reaction forces could be resolved from:
where and are the reaction forces after releasing excess constraints.
From the equations above, the maximum bending moment M could be numerically equated to the concentrated force e in value; it followed that:
4.3. Bending Capacity of the End Supports
In engineering practice, bracing overlapped with the cage of rebars and was connected by the concrete block. Therefore, the bending capacity of the bracing at both end supports equaled the bending capacity of the top beam. The bending capacity of the end supports was expressed as follows:
where is the design value of the axial compressive strength of the concrete; and are the cross-sectional areas of longitudinal ordinary steel bars in the tensile and compressive zones, respectively; is the width of a rectangular section or the web width of an inverted T-shaped section; is the effective height of the cross-section; is the distance from the combined force point of longitudinal ordinary steel bars and prestressed steel bars in the compression zone to the compressed edge of the section.
4.4. Bending Capacity of the Experimental Model
The maximum concentrated load in each component was obtained on account of the experiments, FEM simulations, and theoretical evaluations, as presented in Table 3. The results indicate that the bending capacity of the experimental model was determined by that of the H-CFST component.

Table 3.
Material data for the FEA models.
4.5. Optimization Design of the H-CFST Bracing
Based on the above results, with no damage to other components, the hoop could bear a significantly greater load than the other components. Therefore, the cost-effectiveness of prefabricated H-CFST bracing could be improved further by optimizing the wall thickness of the hoop, which was 14 mm in the experimental model. If d is the wall thickness of the hoop representing the same stiffness and strength as the H-CFST component, then d = 7 mm. Figure 23 presents the results of the FEM analyses for this thickness. It could be seen that the central section of the upper hoop and one side of the steel pipe yielded simultaneously.

Figure 23.
Nephogram of the distribution of stresses in the bracing model when the wall thickness of the hoop is 7 mm.
Figure 24 presents the load-displacement diagrams of the prefabricated H-CFST bracing system with thickness values of 1 d, 1.5 d, 2.0 d, and 2.5 d on the basis of the FEM simulations.
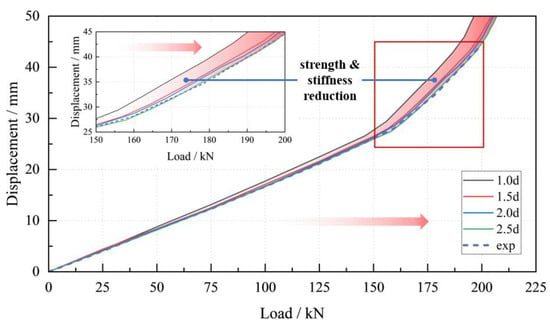
Figure 24.
Load-displacement diagrams for various values of the wall thickness of the hoop.
When the thickness exceeds 1.5 d, the contribution of the increasing wall thickness to the bearing capacity of the bracing will be reduced significantly. Therefore, a wall thickness of 1.5 d is recommended for the hoop in prefabricated H-CFST bracing.
5. Conclusions
This study is focused on the utilization of a prefabricated hollow concrete-filled steel tube (H-CFST) bracing system, which has not yet received extensive research attention in coastal pit engineering. In comparison to traditional concrete bracing systems, this innovative support structure offers increased reusability and cost effectiveness. Through a combination of experimental methods and finite element analysis, an in-depth investigation was conducted into the performance of the prefabricated H-CFST bracing system under transverse bending conditions. This research not only provided essential data for the design of coastal pit supports but also contributed replicable methodologies and results for the broader field of study.
This study introduced theoretical methods for calculating the load-bearing capacity of each component under transverse bending conditions and validated these methods using experimental results. This significantly bolsters the theoretical foundation for the future design and assessment of bracing systems. Importantly, this research demonstrated the feasibility of employing prefabricated H-CFST bracing systems in the challenging context of complex coastal soil and geological conditions. Consequently, it offers novel insights and solutions for the sustainable development of coastal pit engineering.
The following conclusions are based on the results from the experiments, FEM simulations and theoretical analyses of the prefabricated H-CFST bracing:
- The self-designed hoop component significantly mitigated the strength and stiffness reduction phenomenon at the joint of H-CFST components, ensuring that the prefabricated H-CFST bracing system provides safety comparable to traditional concrete bracing in supporting coastal foundation pits;
- Under transverse bending conditions, the prefabricated H-CFST bracing system exhibited two typical failure modes, i.e., local tensile yielding of the steel tube and tensile cracking of end supports;
- Finite element modeling accurately predicted the failure modes of the bracings and provided a reference for the optimized design;
- The theoretical calculation methods using plane section assumption for the bending capacity of bracing components accurately predicted the bending capacity of each component.
As a new form of internal bracing system, the mechanical properties of the prefabricated H-CFST bracing need to be investigated further, as shown in Figure 3. Due to the challenges in replicating the bracing system’s stress conditions during pit excavation in model tests, it is essential to conduct on-site application research on prefabricated H-CFST bracings. The next step will focus on on-site experiments with prefabricated H-CFST bracings and monitoring parameters, such as axial forces and structural deformations. This research aims to investigate the stress response and deformation patterns of prefabricated H-CFST bracings during pit excavation.
Combining the results from on-site experiments with construction practices, standardized procedures will be developed, and reasonable acceptance criteria proposed. This will enhance the application research of prefabricated H-CFST bracings in the field of coastal foundation pit support.
Author Contributions
Data curation, Z.D.; funding acquisition, H.P. and T.L.; investigation, Z.D. and K.W.; methodology, Z.D. and H.P.; project administration, Z.D., H.P., K.W. and T.L.; writing—original draft, Z.D.; writing—review and editing, Z.D., H.P., K.W. and T.L. All authors contributed to the article and approved the submitted version. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China, grant number U2006213 and 42277139.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used to support the findings of this study are included in the article.
Acknowledgments
We appreciate the reviewers for their valuable comments, which were crucial to shaping our manuscript. At the same time, we are also grateful for the financial support provided by the above-mentioned funds.
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Tian, P.; Wang, Z.; Li, J.; Cao, L.; Liu, Y.; Zhang, H.; Ai, S. Spatiotemporal characteristics and driving mechanism of high-intensity development of continental coastal zones in the East China Sea. Geogr. Res. 2023, 42, 156–171. [Google Scholar]
- Lee, H.S.; Choi, Y.-J.; Woo, S.-B. Numerical Models in Coastal Hazards and Coastal Environment. J. Mar. Sci. Eng. 2021, 9, 494. [Google Scholar] [CrossRef]
- Huang, Z.; Mao, C.; Guan, S.; Tang, H.; Chen, G.; Liu, Z. Simulation research on the deformation safety monitoring and evaluation algorithm of coastal soft foundation pit based on big data. Soft Comput. 2023, 27, 1205. [Google Scholar] [CrossRef]
- Armenio, E.; Mossa, M. On the Need for an Integrated Large-Scale Methodology of Coastal Management: A Methodological Proposal. J. Mar. Sci. Eng. 2020, 8, 385. [Google Scholar] [CrossRef]
- Bai, X.-Y.; Chen, X.-Y.; Zhang, M.-Y. “Pile-Steel Support-Anchor” System for Foundation in Rock-Soil Layer. Soil Mech. Found. Eng. 2019, 55, 425–432. [Google Scholar] [CrossRef]
- Zhang, X.-D.; Zhang, S. Simulation of Deep Excavation and Shoring with FEM Based on ADINA. In Proceedings of the International Conference on Civil Engineering and Building Materials (CEBM), Kunming, China, 29–31 July 2011; pp. 3802–3806. [Google Scholar]
- Wang, J.; Yang, T.; Wang, G.; Liu, X.; Xu, N.; Stouthamer, E.; Yin, Y.; Wang, H.; Yan, X.; Huang, X. Control and prevent land subsidence caused by foundation pit dewatering in a coastal lowland megacity: Indicator definition, numerical simulation, and regression analysis. Environ. Earth Sci. 2023, 82, 1–26. [Google Scholar] [CrossRef]
- Liu, N.W.; Peng, C.X.; Li, M.G.; Chen, J.J. Hydro-mechanical behavior of a deep excavation with dewatering and recharge in soft deposits. Eng. Geol. 2022, 307, 106780. [Google Scholar] [CrossRef]
- Cui, J.; Yang, Z.; Azzam, R. Field Measurement and Numerical Study on the Effects of Under-Excavation and Over-Excavation on Ultra-Deep Foundation Pit in Coastal Area. J. Mar. Sci. Eng. 2023, 11, 219. [Google Scholar] [CrossRef]
- Li, J.; Li, M.-G.; Zhang, L.-L.; Chen, H.; Xia, X.-H.; Chen, J.-J. Experimental Study and Estimation of Groundwater Fluctuation and Ground Settlement due to Dewatering in a Coastal Shallow Confined Aquifer. J. Mar. Sci. Eng. 2019, 7, 58. [Google Scholar] [CrossRef]
- Bai, X.; Zhang, M.; Yan, N.; Wang, Y.; Yuan, H. Deformation properties of combined support system of pile-steel support-anchor cable for deep foundation pit in rock-soil combination. J. Cent. South Univ. Sci. Technol. 2018, 49, 454–463. [Google Scholar]
- Cao, P.; Wu, J.; Zhong, D.; Meng, Y.; Cheng, D. Application of Explosive Demolition Technology of Foundation Pit Support Beam based on Axial Hole Layout. Blasting 2017, 34, 96–99, 119. [Google Scholar]
- Hu, J.; Xie, J.; Li, W.; Li, C. Research on the United Supporting Structure of Piled Anchor and Reinforced Concrete Internal Bracing for City Deep Foundation Pit under Complex Surroundings. In Proceedings of the International Conference on Civil Engineering and Building Materials (CEBM), Kunming, China, 29–31 July 2011; p. 1270. [Google Scholar]
- Uenaka, K.; Mizukoshi, M. Lightweight concrete filled steel tubular beam under bending-shear. Structures 2021, 30, 659–666. [Google Scholar] [CrossRef]
- Niyirora, R.; Niyonyungu, F.; Hakuzweyezu, T.; Masengesho, E.; Nyirandayisabye, R.; Munyaneza, J. Behavior of concrete-encased concrete-filled steel tube columns under diverse loading conditions: A review of current trends and future prospects. Cogent Eng. 2023, 10, 2156056. [Google Scholar] [CrossRef]
- Zhong, S.; Xu, G. Behaviors of centrifugal hollow concrete filled steel tube (H-CFST) stub columns under axial compression. J. Harbin Inst. Technol. 2006, 38, 1479–1482,1503. [Google Scholar]
- Wang, H.; Lu, D.; Zhou, Y. Experimental study on seismic behavior of hollow concrete-filled steel tubes(H-CFST) under low cyclic loading. J. Earthq. Eng. Eng. Vib. 2014, 34, 129–136. [Google Scholar]
- Kuranovas, A.; Kvedaras, A.K. Behaviour of hollow concrete filled steel tubular composite elements. J. Civ. Eng. Manag. 2007, 13, 131–141. [Google Scholar] [CrossRef]
- Han, L.; Yao, G.; Zhao, X. Tests and calculations for hollow structural steel (HSS) stub columns filled with self-consolidating concrete (SCC). J. Constr. Steel Res. 2005, 61, 1241–1269. [Google Scholar]
- Ritchie, C.B.; Packer, J.A.; Seica, M.V.; Zhao, X.-L. Behaviour and analysis of concrete-filled rectangular hollow sections subject to blast loading. J. Constr. Steel Res. 2018, 147, 340–359. [Google Scholar] [CrossRef]
- Wang, H.; Zha, X.; Ye, F. Impact resistance of hollow concrete filled-steel tubular members subjected to lateral impact loading. J. Huazhong Univ. Sci. Technol. Nat. Sci. 2010, 38, 107–110. [Google Scholar]
- Yu, M.; Zha, X.; Ye, J.; She, C. A unified formulation for hollow and solid concrete-filled steel tube columns under axial compression. Eng. Struct. 2010, 32, 1046–1053. [Google Scholar]
- Ouyang, Y.; Kwan, A.K.H. Finite element analysis of square concrete-filled steel tube (CFST) columns under axial compressive load. Eng. Struct. 2018, 156, 443–459. [Google Scholar] [CrossRef]
- Ekmekyapar, T.; Al-Eliwi, B.J.M. Experimental behaviour of circular concrete filled steel tube columns and design specifications. Thin Walled Struct. 2016, 105, 220–230. [Google Scholar] [CrossRef]
- Han, L.; Yao, G.; Tao, Z. Performance of concrete-filled thin-walled steel tubes under pure torsion. Thin-Walled Struct. 2007, 45, 24–36. [Google Scholar] [CrossRef]
- Zhang, M.; Guo, X.; Ma, D.; Huang, L.; Wang, W. Design Methods of the Concrete-filled Steel Tube Inner-bracing System for Deep Excavation. J. Beijing Univ. Technol. 2016, 42, 1848–1856. [Google Scholar]
- Guo, X.; Zhang, M.; Ma, D.; Huang, L.; Wang, W.; Wang, C.; Yang, S.; Qiao, J. Case study on braced excavation with P-CFST for top internal support. J. Zhejiang Univ. Eng. Sci. 2019, 53, 51–60. [Google Scholar]
- Mizan, A.; Quan, L.Q.; Ishvarbhai, P.V.; Hadi, M.N.S. Nonlinear analysis of rectangular concrete-filled double steel tubular short columns incorporating local buckling. Eng. Struct. 2018, 175, 13–26. [Google Scholar]
- Wang, Y.-H.; Lu, G.-B.; Zhou, X.-H. Experimental study of the cyclic behavior of concrete-filled double skin steel tube columns subjected to pure torsion. Thin-Walled Struct. 2018, 122, 425–438. [Google Scholar] [CrossRef]
- Yang, H.; Yu, Y.; Kang, L.; Chen, J.; Luo, Y. Study on mechanical behavior of flange-connected CFST column-steel beam joint with external stiffening ring plate. J. Build. Struct. 2022, 43, 157–172. [Google Scholar]
- Chen, X.; Xue, J.; Li, H.; Tu, G.; Lu, X. Performance-based Analysis of Elastoplastic Rotational Behavior of Multi-cell Shaped Concrete-filled Steel Tubular Connection. KSCE J. Civ. Eng. 2023, 27, 4300–4322. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, X.; Zhang, J.; Liu, J.; Cheng, W. Behavior of large-scale connections between circular concrete-filled steel tubular columns and H-section steel beams. Adv. Struct. Eng. 2020, 23, 307–319. [Google Scholar] [CrossRef]
- Yang, M.; Tian, L.J.; Yuan, Y.; Yang, Z.Y. The study on composite trough beam with corrugated steel web wrapped with steel plate: Experiment and bending properties. J. Constr. Steel Res. 2021, 185, 106853. [Google Scholar] [CrossRef]
- Mo, Z.; Qiu, J.; Xu, H.; Xu, L.; Hu, Y. Flexural and longitudinal shear performance of precast lightweight steel-ultra-high performance concrete composite beam. Front. Struct. Civ. Eng. 2023, 17, 704–721. [Google Scholar] [CrossRef]
- Wang, H.; Liu, X.-G.; Yue, Q.-R.; Zheng, M.-Z. Effects of different design factors on the shear performance of assembled steel-concrete composite beam with local laminated joint. Structures 2022, 46, 1881–1895. [Google Scholar] [CrossRef]
- Du, Y.; Gao, D.; Chen, Z.; Deng, X.-F.; Qian, K. Experimental study on the flexural behavior of square high-strength concrete-filled steel tube beams with different CFRP wrapping schemes. Compos. Struct. 2023, 304, 116325. [Google Scholar] [CrossRef]
- Feng, R.; Chen, Y.; Wei, J.; Huang, J.; Huang, J.; He, K. Experimental and numerical investigations on flexural behaviour of CFRP reinforced concrete-filled stainless steel CHS tubes. Eng. Struct. 2018, 156, 305–321. [Google Scholar] [CrossRef]
- Han, L.H. Flexural behaviour of concrete-filled steel tubes. J. Constr. Steel Res. 2004, 60, 313–337. [Google Scholar] [CrossRef]
- GB 50017-2017; Standard for Design of Steel Structures. Ministry of Housing and Urban Rural Development of the People’s Republic of China: Beijing, China, 2017.
- Chen, J.-Y.; Wang, F.-C.; Han, L.-H.; Mu, T.-M. Flexural performance of concrete-encased CFST box members. Structures 2020, 27, 2034–2047. [Google Scholar] [CrossRef]
- Hibbitt, Karlsson, and Sorensen Inc. ABAQUS/Standard User’s Manual; Hibbitt, Karlsson, and Sorensen Inc.: Pawtucket, RI, USA, 2016. [Google Scholar]
- ACI 318-02; Building Code Requirements for Reinforced Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2002.
- Shen, J.; Wang, C.; Jiang, J. Finite Element Analysis of Reinforced Concrete and Limit Analysis of Plates and Shells; Tsinghua University Press: Beijing, China, 1993; Volume 7. [Google Scholar]
- Han, L. Steel Tube Concrete Structure—Theory and Practice; Science Press: Beijing, China, 2004; Volume 3. [Google Scholar]
- Roeder, C.W.; Cameron, B.; Brown, C.B. Composite Action in Concrete Filled Tubes. J. Struct. Eng. 1999, 125, 477–484. [Google Scholar] [CrossRef]
- Hanoon, A.N.; Al Zand, A.W.; Yaseen, Z.M. Designing new hybrid artificial intelligence model for CFST beam flexural performance prediction. Eng. Comput. 2022, 38, 3109–3135. [Google Scholar] [CrossRef]
- Al Zand, A.W.; Badaruzzaman, W.H.W.; Al-Shaikhli, M.S.; Ali, M.M. Flexural performance of square concrete-filled steel tube beams stiffened with V-shaped grooves. J. Constr. Steel Res. 2020, 166, 105930. [Google Scholar] [CrossRef]
- Al Zand, A.W.; Badaruzzaman, W.H.W.; Ali, M.M.; Hasan, Q.A.; Al-Shaikhli, M.S. Flexural performance of cold-formed square CFST beams strengthened with internal stiffeners. Steel Compos. Struct. 2020, 34, 123–139. [Google Scholar] [CrossRef]
- Xu, Z.; Gardner, L.; Sadowski, A.J. Nonlinear stability of elastic elliptical cylindrical shells under uniform bending. Int. J. Mech. Sci. 2017, 128, 593–606. [Google Scholar] [CrossRef]
- Fajuyitan, O.K.; Sadowski, A.J.; Wadee, M.A.; Rotter, J.M. Nonlinear behaviour of short elastic cylindrical shells under global bending. Thin-Walled Struct. 2018, 124, 574–587. [Google Scholar] [CrossRef]
- Wang, J.; Sadowski, A.J. Elastic imperfect tip-loaded cantilever cylinders of varying length. Int. J. Mech. Sci. 2018, 140, 200–210. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).