Random Matrix Theory for Sound Propagation in a Shallow-Water Acoustic Waveguide with Sea Bottom Roughness
Abstract
1. Introduction
2. General Theory
3. Random Sea Bottom Roughness
4. Ornstein–Uhlenbeck Sea Bottom Roughness
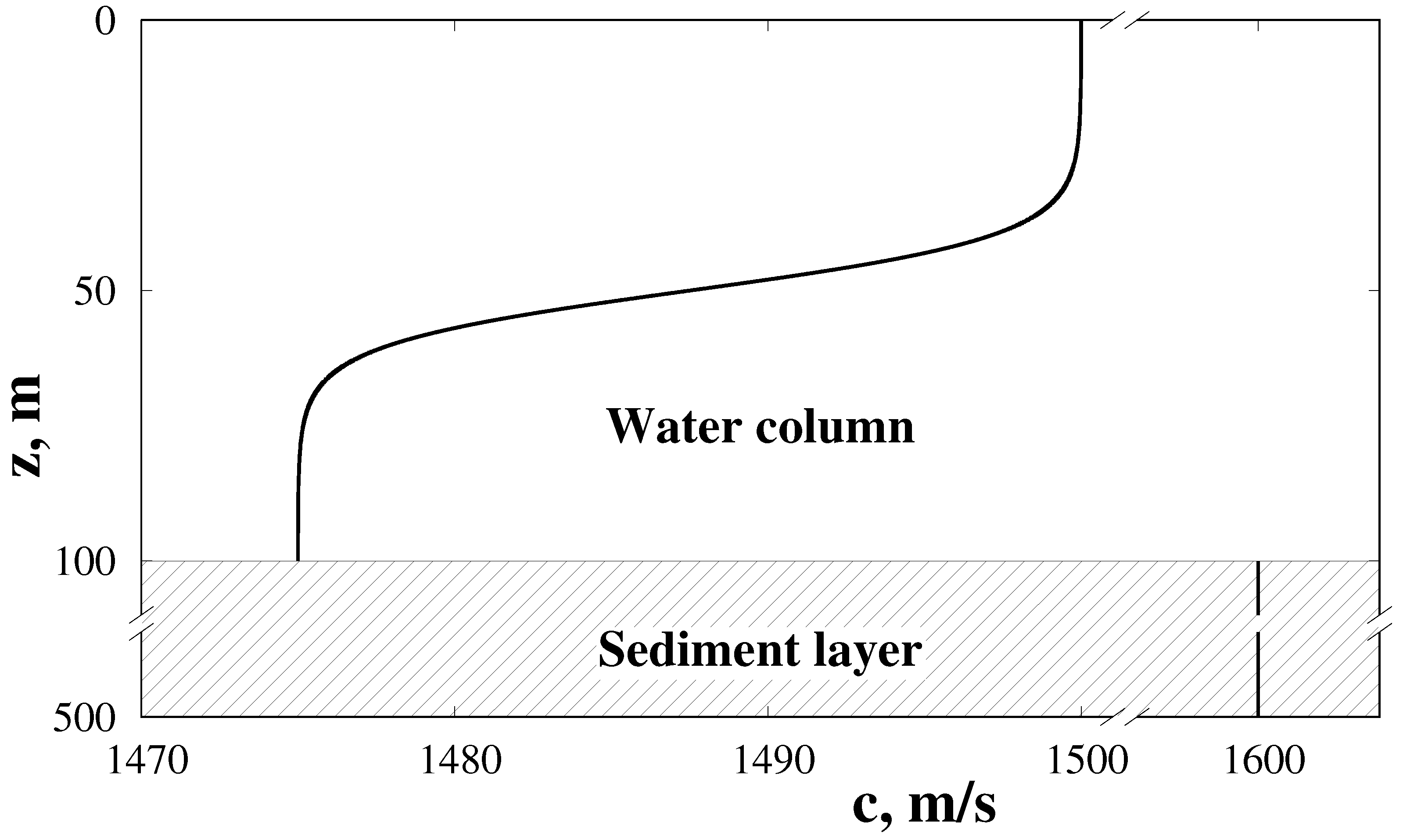
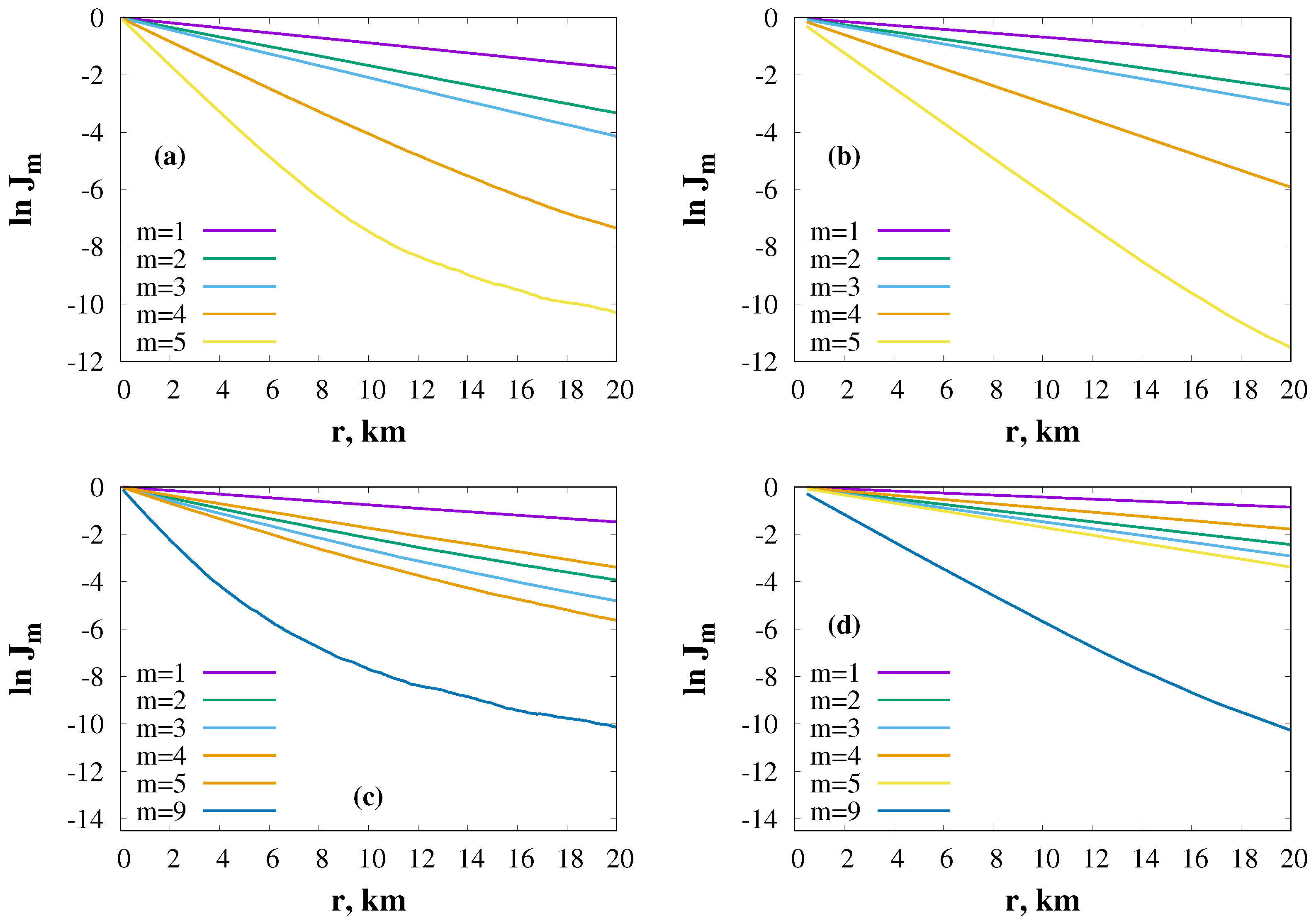
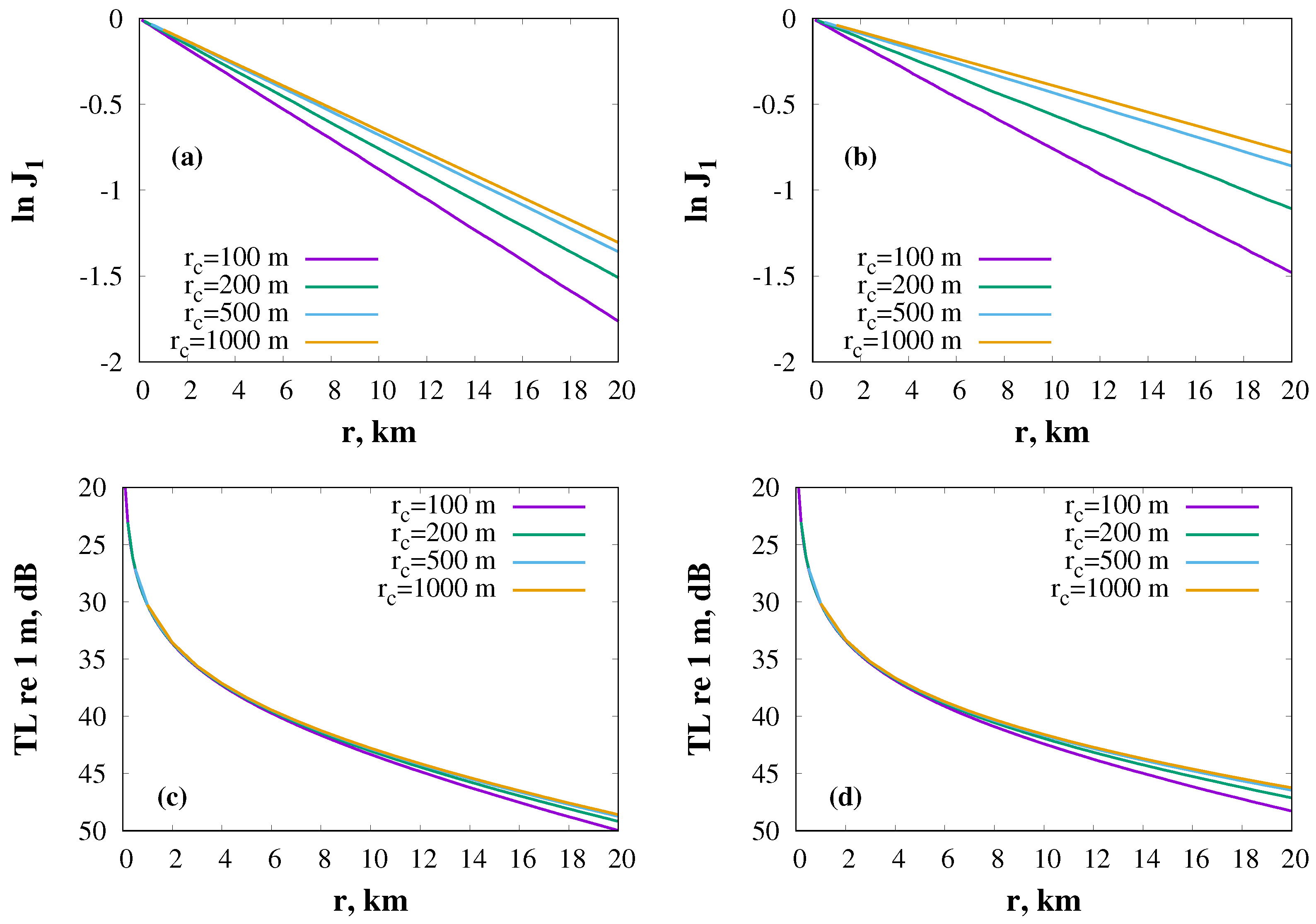
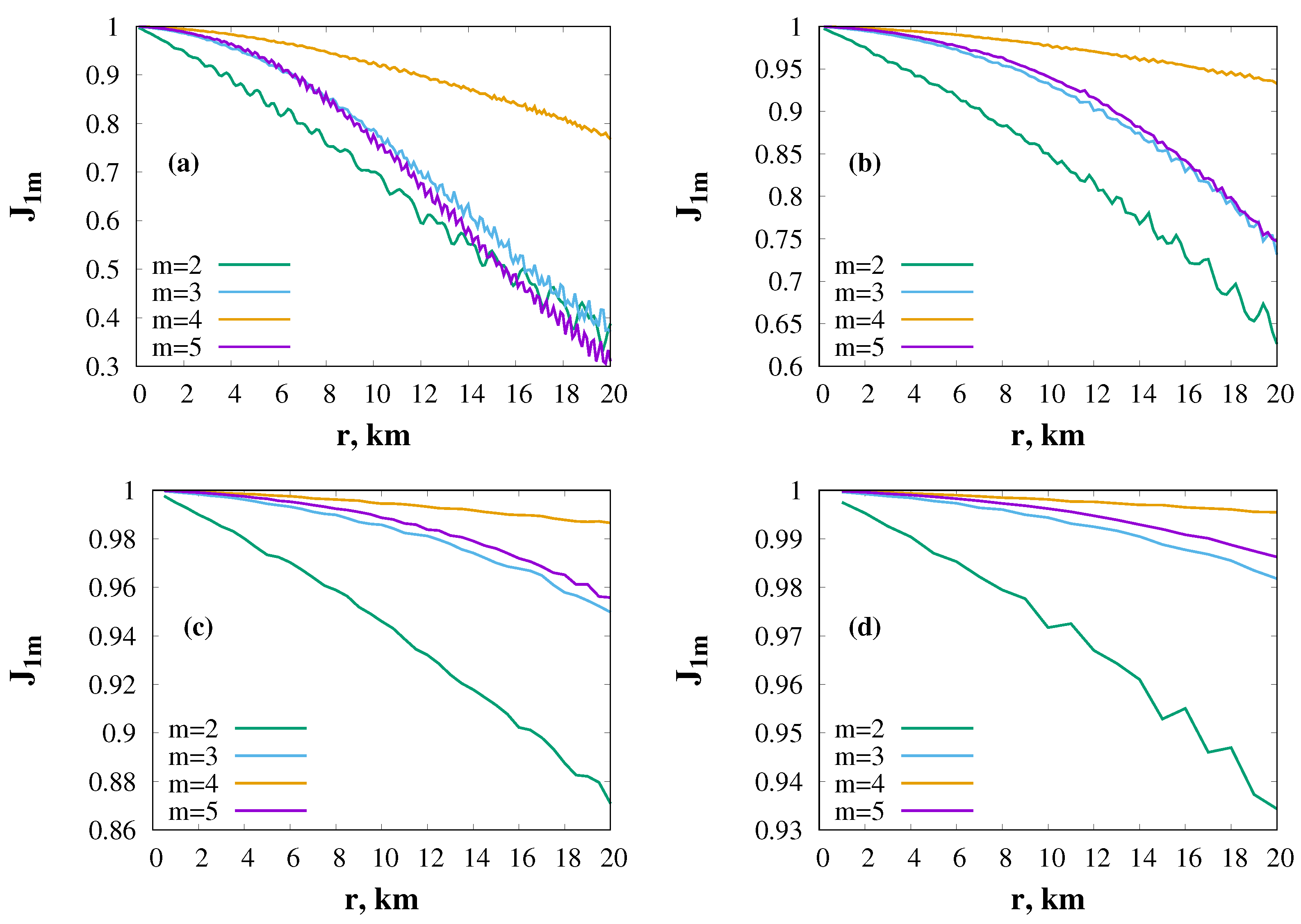
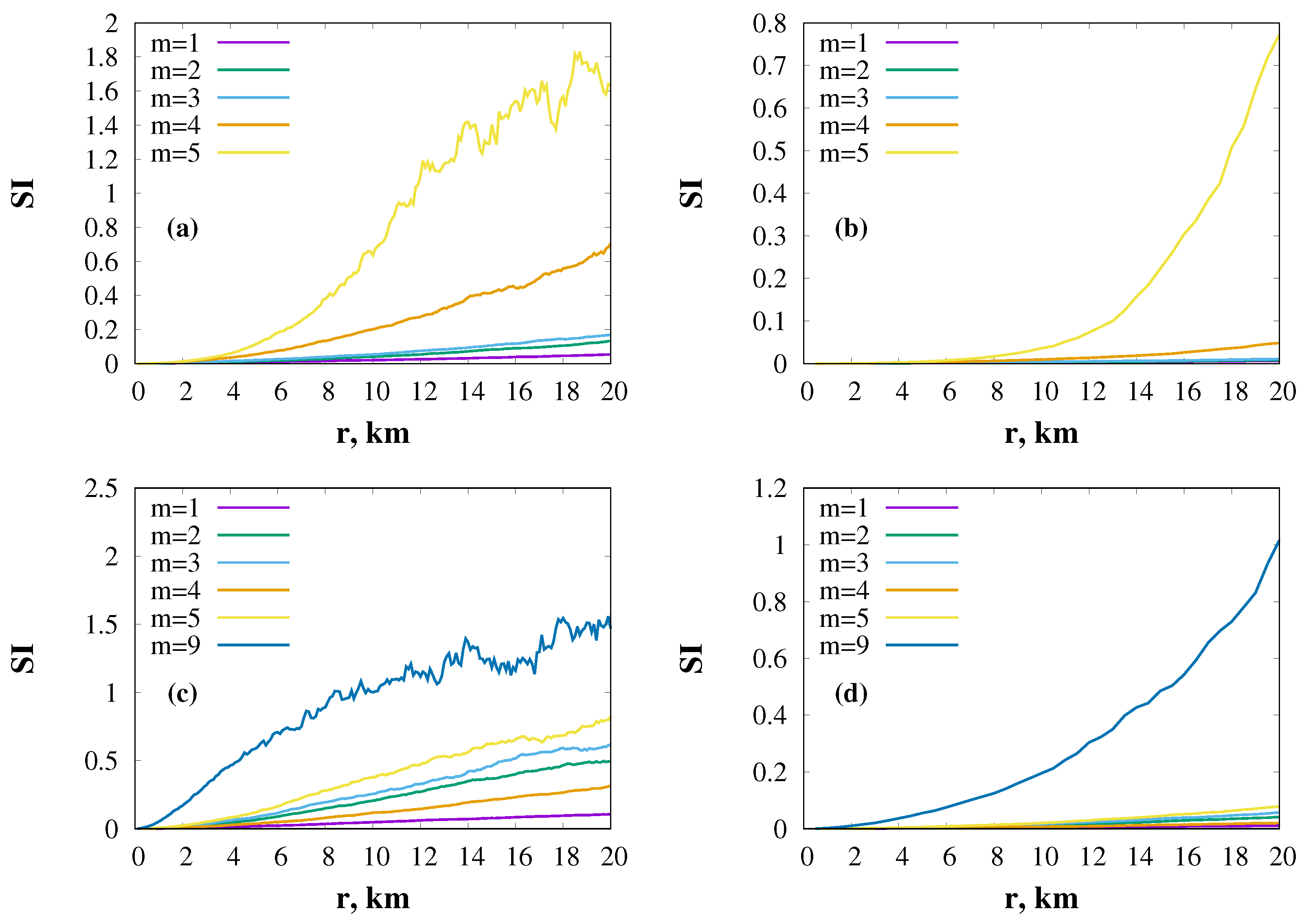
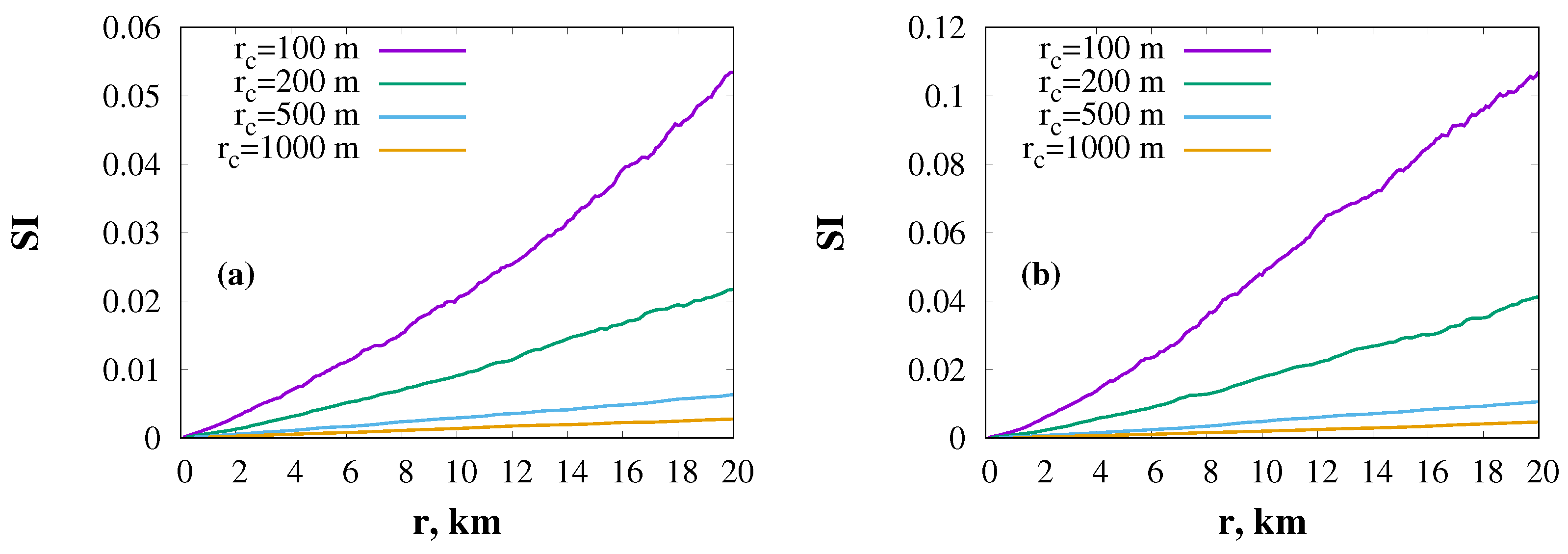
5. Numerical Simulation
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dashen, R.; Flatté, S.M.; Munk, W.H.; Watson, K.M.; Zachariasen, F. Sound Transmission through a Fluctuating Ocean; Cambridge University Press: Cambridge, UK, 2010; p. 320. [Google Scholar]
- Chitre, M.; Shahabudeen, S.; Stojanovic, M. Underwater Acoustic Communications and Networking: Recent Advances and Future Challenges. Mar. Technol. Soc. J. 2008, 42, 103–116. [Google Scholar] [CrossRef]
- Virovlyansky, A.L.; Kazarova, A.Y.; Lyubavin, L.Y. Focusing of sound pulses using the time reversal technique on 100-km paths in a deep sea. Acoust. Phys. 2012, 58, 678–686. [Google Scholar] [CrossRef]
- Morgunov, Y.N.; Golov, A.A.; Burenin, A.V.; Petrov, P.S. Studies of spatiotemporal structure of the acoustic field formed in deep water by a broadband pulsed signal source on the shelf of the Sea of Japan. Acoust. Phys. 2019, 65, 537–544. [Google Scholar] [CrossRef]
- Makarov, D.V.; Komissarov, A.A. Chaos and wavefront reversal for long-range sound propagation. Dokl. Earth Sci. 2022, 507, 1118–1123. [Google Scholar] [CrossRef]
- Tappert, F.D.; Tang, X. Ray chaos and eigenrays. J. Acoust. Soc. Am. 1996, 99, 185–195. [Google Scholar] [CrossRef]
- Worcester, P.F.; Cornuelle, B.D.; Dzieciuch, M.A.; Munk, W.H.; Howe, B.M.; Mercer, J.A.; Spindel, R.C.; Colosi, J.A.; Metzger, K.; Birdsall, T.G.; et al. A test of basin-scale acoustic thermometry using a large-aperture vertical array at 3250-km range in the eastern North Pacific Ocean. J. Acoust. Soc. Am. 1999, 105, 3185–3201. [Google Scholar] [CrossRef]
- Colosi, J.A.; Scheer, E.K.; Flatté, S.M.; Cornuelle, B.D.; Dzieciuch, M.A.; Munk, W.H.; Worcester, P.F.; Howe, B.M.; Mercer, J.A.; Spindel, R.C.; et al. Comparisons of measured and predicted acoustic fluctuations for a 3250-km propagation experiment in the eastern North Pacific Ocean. J. Acoust. Soc. Am. 1999, 105, 3202–3218. [Google Scholar] [CrossRef]
- Beron-Vera, F.J.; Brown, M.G.; Colosi, J.A.; Tomsovic, S.; Virovlyansky, A.L.; Wolfson, M.A.; Zaslavsky, G.M. Ray dynamics in a long-range acoustic propagation experiment. J. Acoust. Soc. Am. 2003, 114, 1226–1242. [Google Scholar] [CrossRef]
- Makarov, D.V.; Kon’kov, L.E.; Petrov, P.S. Influence of oceanic synoptic eddies on duration of modal acoustic pulses. Radiophys. Quantum Electron. 2016, 59, 576–591. [Google Scholar] [CrossRef]
- Katsnelson, B.; Petnikov, V.; Lynch, J. Fundamentals of Shallow Water Acoustics; Springer: New York, NY, USA, 2012; p. 540. [Google Scholar] [CrossRef]
- Dozier, L.B.; Tappert, F.D. Statistics of normal mode amplitudes in a random ocean. I. Theory. J. Acoust. Soc. Am. 1978, 63, 353–365. [Google Scholar] [CrossRef]
- Dozier, L.B.; Tappert, F.D. Statistics of normal mode amplitudes in a random ocean. II. Computations. J. Acoust. Soc. Am. 1978, 64, 533–547. [Google Scholar] [CrossRef]
- Creamer, D.B. Scintillating shallow-water waveguides. J. Acoust. Soc. Am. 1996, 99, 2825–2838. [Google Scholar] [CrossRef]
- Morozov, A.K.; Colosi, J.A. Stochastic differential equation analysis for sound scattering by random internal waves in the ocean. Acoust. Phys. 2007, 53, 335–347. [Google Scholar] [CrossRef]
- Colosi, J.A.; Morozov, A.K. Statistics of normal mode amplitudes in an ocean with random sound-speed perturbations: Cross-mode coherence and mean intensity. J. Acoust. Soc. Am. 2009, 126, 1026–1035. [Google Scholar] [CrossRef]
- Virovlyansky, A.L. Ray-based description of mode coupling by sound speed fluctuations in the ocean. J. Acoust. Soc. Am. 2015, 137, 2137–2147. [Google Scholar] [CrossRef]
- Hegewisch, K.C.; Tomsovic, S. Random matrix theory for underwater sound propagation. Europhys. Lett. 2012, 97, 34002. [Google Scholar] [CrossRef][Green Version]
- Hegewisch, K.C.; Tomsovic, S. Constructing acoustic timefronts using random matrix theory. J. Acoust. Soc. Am. 2013, 134, 3174–3184. [Google Scholar] [CrossRef]
- Xu, C.; Tang, J. A propagation matrix method for the solution of the parabolic equation in ocean acoustics. J. Acoust. Soc. Am. 2019, 146, EL464–EL469. [Google Scholar] [CrossRef]
- Wapenaar, K. Wave-field representations with Green’s functions, propagator matrices, and Marchenko-type focusing functions. J. Acoust. Soc. Am. 2022, 151, 587–608. [Google Scholar] [CrossRef]
- Virovlyansky, A.L.; Zaslavsky, G.M. Manifestation of scarring in a driven system with wave chaos. Chaos Interdiscip. J. Nonlinear Sci. 2005, 15, 023301. [Google Scholar] [CrossRef]
- Smirnov, I.P.; Virovlyansky, A.L.; Edelman, M.; Zaslavsky, G.M. Chaos-induced intensification of wave scattering. Phys. Rev. E 2005, 72, 026206. [Google Scholar] [CrossRef] [PubMed]
- Kon’kov, L.E.; Makarov, D.V.; Sosedko, E.V.; Uleysky, M.Y. Recovery of ordered periodic orbits with increasing wavelength for sound propagation in a range-dependent waveguide. Phys. Rev. E 2007, 76, 056212. [Google Scholar] [CrossRef] [PubMed]
- Virovlyansky, A.L.; Makarov, D.V.; Prants, S.V. Ray and wave chaos in underwater acoustic waveguides. Physics-Uspekhi 2012, 55, 18–46. [Google Scholar] [CrossRef]
- Makarov, D.V.; Kon’kov, L.E.; Uleysky, M.Y.; Petrov, P.S. Wave chaos in a randomly inhomogeneous waveguide: Spectral analysis of the finite-range evolution operator. Phys. Rev. E 2013, 87, 012911. [Google Scholar] [CrossRef]
- Makarov, D. Random Matrix Theory for Low-Frequency Sound Propagation in the Ocean: A Spectral Statistics Test. J. Theor. Comput. Acoust. 2018, 26, 1850002. [Google Scholar] [CrossRef]
- Yang, T.C. Acoustic mode coupling induced by nonlinear internal waves: Evaluation of the mode coupling matrices and applications. J. Acoust. Soc. Am. 2014, 135, 610–625. [Google Scholar] [CrossRef]
- Li, X.; Song, W.; Gao, D.; Gao, W.; Wang, H. Training a U-Net based on a random mode-coupling matrix model to recover acoustic interference striations. J. Acoust. Soc. Am. 2020, 147, EL363–EL369. [Google Scholar] [CrossRef]
- Li, Q.; Sun, C.; Xie, L.; Huang, X. Modulation effects of internal-wave evolution on acoustic modal intensity fluctuations in a shallow-water waveguide. J. Mar. Sci. Eng. 2023, 11, 1686. [Google Scholar] [CrossRef]
- Makarov, D. Random matrix theory for an adiabatically-varying oceanic acoustic waveguide. Wave Motion 2019, 90, 205–217. [Google Scholar] [CrossRef]
- Darmon, M.; Dorval, V.; Baqué, F. Acoustic Scattering Models from Rough Surfaces: A Brief Review and Recent Advances. Appl. Sci. 2020, 10, 8305. [Google Scholar] [CrossRef]
- Ermoshkin, A.V.; Kosteev, D.A.; Ponomarenko, A.A.; Razumov, D.D.; Salin, M.B. Surface Waves Prediction Based on Long-Range Acoustic Backscattering in a Mid-Frequency Range. J. Mar. Sci. Eng. 2022, 10, 722. [Google Scholar] [CrossRef]
- Mello, P.; Yépez, M.; Froufe-Pérez, L.; Sáenz, J. Statistical scattering of waves in disordered waveguides: Universal properties. Phys. A Stat. Mech. Appl. 2006, 372, 203–209. [Google Scholar] [CrossRef][Green Version]
- Froufe-Pérez, L.S.; Yépez, M.; Mello, P.A.; Sáenz, J.J. Statistical scattering of waves in disordered waveguides: From microscopic potentials to limiting macroscopic statistics. Phys. Rev. E 2007, 75, 031113. [Google Scholar] [CrossRef] [PubMed]
- Evans, R.B. A coupled mode solution for acoustic propagation in a waveguide with stepwise depth variations of a penetrable bottom. J. Acoust. Soc. Am. 1983, 74, 188–195. [Google Scholar] [CrossRef]
- Morozov, A.K.; Colosi, J.A. Equations for normal-mode statistics of sound scattering by a rough elastic boundary in an underwater waveguide, including backscattering. J. Acoust. Soc. Am. 2017, 142, EL292–EL298. [Google Scholar] [CrossRef] [PubMed]
- Knobles, D.P.; Sagers, J.D. Forward and backward modal statistics for rough surface scattering in shallow water. J. Comput. Acoust. 2014, 22, 1440004. [Google Scholar] [CrossRef]
- Gulin, O.E.; Yaroshchuk, I.O. On Average Losses of Low-Frequency Sound in a Two-Dimensional Shallow-Water Random Waveguide. J. Mar. Sci. Eng. 2022, 10, 822. [Google Scholar] [CrossRef]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics; Springer: New York, NY, USA, 2011; p. 794. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics Non-Relativistic Theory; Elsevier: Amsterdam, The Netherlands, 2013; Volume 3. [Google Scholar]
- Godin, O.A. A note on differential equations of coupled-mode propagation in fluids. J. Acoust. Soc. Am. 1998, 103, 159–168. [Google Scholar] [CrossRef]
- Trofimov, M.; Kozitskiy, S.; Zakharenko, A.; Petrov, P. Formal Derivations of Mode Coupling Equations in Underwater Acoustics: How the Method of Multiple Scales Results in an Expansion over Eigenfunctions and the Vectorized WKBJ Solution for the Amplitudes. J. Mar. Sci. Eng. 2023, 11, 797. [Google Scholar] [CrossRef]
- Petrov, P.S.; Kazak, M.S.; Petrova, T.N. A generalization of WKBJ method for solving a system describing propagation of coupled modes in underwater acoustics. Phys. Lett. A 2022, 450, 128383. [Google Scholar] [CrossRef]
- Berman, P.R.; Ford, G.W. Spontaneous Decay, Unitarity, and the Weisskopf–Wigner Approximation. In Advances in Atomic, Molecular, and Optical Physics; Arimondo, E., Berman, P., Lin, C., Eds.; Academic Press: Cambridge, MA, USA, 2010; Volume 59, Chapter 5; pp. 175–221. [Google Scholar] [CrossRef]
- de Vega, I.; Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 2017, 89, 015001. [Google Scholar] [CrossRef]
- Fojón, O.; Gadella, M.; Lara, L. The quantum square well with moving boundaries: A numerical analysis. Comput. Math. Appl. 2010, 59, 964–976. [Google Scholar] [CrossRef]
- Rosanov, N.N.; Vysotina, N.V. Soliton in stationary and dynamical traps. JETP Lett. 2014, 100, 508–511. [Google Scholar] [CrossRef]
- Rosanov, N.N.; Vysotina, N.V. Fermi-Ulam problem for solitons. Phys. Rev. A 2015, 91, 013622. [Google Scholar] [CrossRef]
- Thomson, D.J.; Chapman, N.R. A wide-angle split-step algorithm for the parabolic equation. J. Acoust. Soc. Am. 1983, 74, 1848–1854. [Google Scholar] [CrossRef]
- Gardiner, C.W. Handbook of Stochastic Methods; Springer: Berlin, Germany, 1985. [Google Scholar]
- Makarov, D. Application of the discrete variable representation approach to formation of amplitude–phase field distributions on a vertical array in a waveguide. Acoust. Phys. 2021, 67, 397–412. [Google Scholar] [CrossRef]
- Makarov, D.; Petrov, P. Full reconstruction of acoustic wavefields by means of pointwise measurements. Wave Motion 2022, 115, 103084. [Google Scholar] [CrossRef]
- Komissarov, A.A.; Makarov, D.V.; Kholmogorov, A.O.; Shakirov, R.B. Low-Frequency Sound Propagation in an Underwater Waveguide with a Giant Gassy Pockmark. J. Mar. Sci. Eng. 2023, 11, 211. [Google Scholar] [CrossRef]
- Virovlyansky, A.L.; Zaslavsky, G.M. Wave chaos in terms of normal modes. Phys. Rev. E 1999, 59, 1656–1668. [Google Scholar] [CrossRef]
- Colosi, J.A.; Baggeroer, A.B. On the kinematics of broadband multipath scintillation and the approach to saturation. J. Acoust. Soc. Am. 2004, 116, 3515–3522. [Google Scholar] [CrossRef]
- Mo, Q.; Yeh, H.; Manocha, D. Tracing Analytic Ray Curves for Light and Sound Propagation in Non-Linear Media. IEEE Trans. Vis. Comput. Graph. 2016, 22, 2493–2506. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Liu, J. Outdoor Sound Propagation Based on Adaptive FDTD-PE. In Proceedings of the 2020 IEEE Conference on Virtual Reality and 3D User Interfaces (VR), Atlanta, GA, USA, 22–26 March 2020; pp. 859–867. [Google Scholar] [CrossRef]
- Ding, R.; Liu, S. Underwater sound propagation for virtual environments. Vis. Comput. 2021, 37, 2797–2807. [Google Scholar] [CrossRef]
- Trofimov, M.Y.; Kozitskiy, S.; Zakharenko, A. A mode parabolic equation method in the case of the resonant mode interaction. Wave Motion 2015, 58, 42–52. [Google Scholar] [CrossRef]
- Petrov, P.S.; Antoine, X. Pseudodifferential adiabatic mode parabolic equations in curvilinear coordinates and their numerical solution. J. Comput. Phys. 2020, 410, 109392. [Google Scholar] [CrossRef]
- Patsyk, A.; Sivan, U.; Segev, M.; Bandres, M.A. Observation of branched flow of light. Nature 2020, 583, 60–65. [Google Scholar] [CrossRef]
- Kozitskiy, S. Coupled-Mode Parabolic Equations for the Modeling of Sound Propagation in a Shallow-Water Waveguide with Weak Elastic Bottom. J. Mar. Sci. Eng. 2022, 10, 1355. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makarov, D.V.; Petrov, P.S.; Uleysky, M.Y. Random Matrix Theory for Sound Propagation in a Shallow-Water Acoustic Waveguide with Sea Bottom Roughness. J. Mar. Sci. Eng. 2023, 11, 1987. https://doi.org/10.3390/jmse11101987
Makarov DV, Petrov PS, Uleysky MY. Random Matrix Theory for Sound Propagation in a Shallow-Water Acoustic Waveguide with Sea Bottom Roughness. Journal of Marine Science and Engineering. 2023; 11(10):1987. https://doi.org/10.3390/jmse11101987
Chicago/Turabian StyleMakarov, Denis V., Pavel S. Petrov, and Michael Yu. Uleysky. 2023. "Random Matrix Theory for Sound Propagation in a Shallow-Water Acoustic Waveguide with Sea Bottom Roughness" Journal of Marine Science and Engineering 11, no. 10: 1987. https://doi.org/10.3390/jmse11101987
APA StyleMakarov, D. V., Petrov, P. S., & Uleysky, M. Y. (2023). Random Matrix Theory for Sound Propagation in a Shallow-Water Acoustic Waveguide with Sea Bottom Roughness. Journal of Marine Science and Engineering, 11(10), 1987. https://doi.org/10.3390/jmse11101987






