Abstract
A set of Boussinesq-type wave equations with enhanced dispersion characteristics is presented for accurate, efficient, and robust numerical treatment. New arrangement uses three different velocity variables simultaneously in order to keep continuity and momentum equations in simplest conservation forms while improving the dispersion characteristics. This approach allows us to retain all the nonlinear contributions with minimum number of terms. Spatial and time-dependent variations of the seabed are fully accounted for and the effect of external free surface pressure is included. A numerical scheme based on finite differences is developed, and various well-known experimental cases are simulated for testing the performance of the proposed set of equations. Comparisons of simulations with measurements reveal quite satisfactory agreements and, hence, bolster confidence in the wave model.
1. Introduction
Current state-of-the-art wave modeling of nearshore regions prefers Boussinesq-type equations for reliable results with less computational effort. Features such as nonlinear effects, accurate linear shoaling due to water depth changes, and better dispersion characteristics for relatively short wave propagation make Boussinesq models appealing.
Within the last three decades, in line with computational capabilities, considerable progress has been made for improving Boussinesq-type wave equations. Witting [1] was the first to introduce a highly dispersive and highly nonlinear Boussinesq model by using exact continuity and momentum equations in connection with a “new velocity” variable. Madsen, Murray, and Sørensen [2] added definite derivatives of zeroth-order terms to Boussinesq equations to improve the dispersion characteristics. Subsequently, Madsen and Sørensen [3] extended the same approach to spatially varying bottom case. Nwogu [4] derived a set of Boussinesq equations using the “velocity at an arbitrary depth” as the velocity variable instead of the conventionally used depth-averaged or still water level or bottom velocity. The resulting equations have nearly identical dispersion characteristics with those given in [1,2]. The arbitrary depth velocity used in [4] actually corresponds to the new velocity variable of [1] but is physically meaningful. Beji and Nadaoka [5] modified classical equations of Peregrine [6] by partial replacement technique to obtain a Boussinesq set with improved dispersion characteristic while retaining the conventional depth-averaged velocity. Madsen and Schäffer [7] presented Boussinesq equations with high-order dispersion and nonlinearity. Karambas and Memos [8] developed a fully-dispersive Boussinesq model which could be used over slowly varying bathymetry. Higher-order Boussinesq equations with applications to various cases were given in [9]. Klonaris, Memos, and Drønen [10] introduced an integrated Boussinesq model covering various aspects of nearshore dynamics such as rip channels.
In addition to these theoretical advances, different numerical techniques have been explored extensively. Walkley and Berzins [11] employed the finite element approach while Zhan, Li, and Wai [12] used finite differences and Eskilsson and Sherwin [13] applied discontinuous Galerkin methods for the numerical solutions of Boussinesq-type equations. Finite volume schemes for Boussinesq modeling of nearshore wave transformations were developed by Zhou, Zhan, and Li [14]. Nonlinear wave–body interactions were treated within the framework of a unified Boussinesq model [15] in the sense that the computational domain is decomposed into two subdomains comprising a region below the body and another outside of it. A different phenomenon, wave generation by a moving pressure disturbance such as ships, was also simulated using Boussinesq models [16,17]. The relatively difficult subject of inclusion of wave-breaking effect into Boussinesq models was considered in quite a number of studies [18,19,20,21,22,23,24,25]. Kaur, Kumar, and Rajni [26] devised a finite element method to investigate the performance of Boussinesq equations in semi-enclosed basins. Quite recently, in a case study of wave propagation over coral reefs, Watanabe et al. [27] revealed the limitations of Boussinesq-type wave models.
The present work introduces an unconventional approach and employs three different-velocity variables for the purpose of establishing a set of prognostic equations containing lowest-order derivatives and minimum number of terms. Thus, the framework, which is established in line with the pioneering work of Witting [1], diverges substantially from the typical Boussinesq models which are given in terms of a definite velocity variable. Accordingly, the continuity equation is expressed in terms of averaged velocity while the momentum equation is formulated in terms of undisturbed surface velocity. Further, in order to produce a model with better dispersion characteristics, the averaged velocity is not directly related to the surface velocity but is connected via an intermediate velocity variable, which is the velocity at an arbitrary water depth. These kinematic equations relating velocities treat the water depth as both a spatially and temporally varying quantity, keeping all its derivatives without neglecting any term. The resulting set of equations then provides a Boussinesq-type water wave model with improved dispersion characteristics capable of advancing relatively shorter waves over a seabed which may vary in space and time. More importantly, unlike the usual forms of improved Boussinesq-type equations expressed in terms of a single velocity variable, the new arrangement does not contain any third-order derivatives, which hinder accuracy and robustness of the numerical treatment.
For the numerical solution of the proposed equations, a computationally efficient and accurate finite differences formulation is developed. The numerical scheme uses a staggered grid system with two time-level variables. The entire set of equations is solved by treating the x- and y-components in decoupled manner; hence, the scheme is iterated until a preset accuracy condition is satisfied. Five different simulations are carried out to demonstrate various aspects of the wave model, such as linear shoaling over spatially changing depths, tsunami-like wave generation due to an impulsive bed movement, nonlinear wave transformations, and combined refraction-diffraction over varying bathymetry. Except for the shoaling simulation, which is tested against conservation of energy flux concept, all the simulations are compared with the corresponding experimental measurements, which are the most frequently used ones in the relevant literature. Overall, the results of simulations agree well with the measurements, demonstrating the reliability of the proposed set of equations.
2. Governing Equations
2.1. Continuity Equation
The depth-integrated continuity equation as expressed for a free surface flow bounded below by a spatially and temporally varying bed is given by [28]
where is the free surface displacement, is the water depth, ∇ is the two-dimensional gradient operator, , and is the vertically-averaged horizontal velocity vector with x- and y-components only, and defined as with being the horizontal velocity vector. Equation (1), as expressed above in terms of the mean horizontal velocity, is exact.
2.2. Momentum Equation
An alternative form of momentum equation for irrotational nonlinear free surface flows, which is exact, is given in [29]:
where and are, respectively, the time derivatives of the horizontal velocity vector and vertical velocity component , while and stand for the indicated variables evaluated at the free surface , and, finally, is the externally applied surface pressure while is the water density. Once the vertical dependency of the velocity field is specified, the momentum equation of any depth-integrated wave model, as in [28,29,30], may be obtained from (2). To proceed further, the z-dependence of the velocity field must be specified. Following the Boussinesq approach, the velocity variables are expanded in power series in z:
where the terms and for represent the horizontal velocity vector and the vertical velocity component at the undisturbed still water level . Although used conventionally without questioning, the use of velocities at may be perplexing from the physical point of view when wave troughs are considered. This, however, does not pose a real problem as the introduction of these velocities is an entirely mathematical process and actual physical existence of these velocities is immaterial.
In order for horizontal and vertical velocity expressions given in (3) to be admissible, they must satisfy the kinematic conditions as represented by the continuity equation, irrotationality condition, and bottom condition for a movable seabed :
in which stands for the material derivative operator and subscript t for partial differentiation with respect to time. After making use of all the conditions stated in (4), the following expressions are obtained for the horizontal velocity vector and the vertical velocity component w:
where the terms up to the second order are kept in , while w contains only first-order terms so that irrotationality condition, , is fulfilled. Note that the bottom movement velocity is directly transmitted to w. Intermediate steps of obtaining (5) and (6) can be found in [28].
At this stage, Equations (5) and (6) can be directly substituted into (2) to obtain a momentum equation in terms of surface variables , , and , since the terms proportional to z and in and w cancel each other out as a result of already imposed irrotationality condition . The substitution yields
where the surface velocities and can be evaluated by letting in Equations (5) and (6), respectively. Except for temporal derivatives of h and surface pressure, Equation (7) is identical to the one proposed in [29]; yet, it is not fully nonlinear simply because the velocity components, (5) and (6), are necessarily truncated at a limited order. For a detailed explanation concerning the order of nonlinearity, the reader is directed to Witting [1].
Experience shows that keeping all the nonlinear terms in (7) seriously hampers the robustness of any numerical scheme; therefore, in accordance with the classical Boussinesq approximations (see p. 53, [31]), the nonlinear terms proportional to the vertical velocity w and terms involving products of derivatives are completely neglected:
Equations (1) and (8) can be used to establish a Boussinesq model, provided that and are related to each other. Integrating Equation (5) from to , dividing by the total depth , and finally inverting the resulting equation to express in terms of as described in (p. 508) [32] give
which may be simplified to the usual form by omitting the nonlinear terms
Equations (1), (7), and (9) as a highly-nonlinear model or (1), (8), and (10) as a weakly-nonlinear model make up a complete system that can be solved quite efficiently and accurately by applying an appropriate numerical approach such as a finite difference formulation. Momentum equation, (7) or (8), is first used to advance to a new time level. Using this newly computed velocity on the left side of (9) or (10) gives new time level . Finite difference representation of (9) or (10), when treated separately for the x- and y- directions, results in a tridiagonal matrix which can be solved very efficiently. Finally, solving Equation (1) by employing the newly computed for the surface displacement completes the cycle for a time step.
Instead of a single velocity variable, simultaneous use of two different velocities, and , is the unusual aspect of the scheme just described. While the continuity equation is expressed in terms of the mean velocity, the momentum equation is expressed in terms of the still water level velocity. These two different velocities are then related through a kinematic expression, Equation (9) or (10). The main advantage of this arrangement is clearly in the conservation forms of Equations (1) and (7) or (8). More importantly, continuity equation is exact with minimum number of terms when expressed in terms of the mean velocity. Likewise, momentum equation, whether it be (7) or (8), contains minimum number of terms when expressed in terms of the still water level velocity. Therefore, by keeping the number of terms as few as possible and the order of derivatives as low as possible, the numerical discretization errors are minimized. It must be emphasized that preliminary use of irrotationality condition in the derivation of Equation (2) contributes remarkably to the reduction of number of terms in the momentum equation, especially when all the nonlinear terms are retained. Despite all these numerical advantages, both these models, just like the standard Boussinesq model of Peregrine [6], remain weakly dispersive. The next step then makes an improvement in this respect by introducing an intermediate velocity to the system.
2.3. Intermediate Velocity Variable
Our aim now is to extend the dispersion properties of the wave model to relatively deep waters; therefore, instead of following the scheme just described above, an intermediate velocity variable is introduced. Accordingly, the velocity at an arbitrary water depth is used as an intermediate in connecting the velocity at the still water level and the depth-averaged velocity. Specification of the arbitrary depth-level is performed in such a manner as to obtain a better dispersion relation for the resulting wave equations. The concept of “velocity at an arbitrary depth” was first introduced by Nwogu [4]; this concept is, in essence, the same as the “new velocity” variable of Witting [1] but is quite meaningful from the physical point of view.
Equation (5) expresses the horizontal velocity vector for any given depth z in terms of the still velocity vector . Setting z to an arbitrary depth , yet to be specified, and denoting the corresponding velocity variable by results in
By successive approximations, (11) can be inverted to express as a function of :
which relates the still water level velocity to the velocity at an arbitrary depth . Now, using the above expression for in Equation (5) gives, for the horizontal velocity vector ,
Integrating (13) from to and then dividing by the total depth yields
which, when is neglected, reduces to the classical Boussinesq approach:
Introduction of an intermediate velocity variable changes the dispersion properties of the resulting equations. This point is demonstrated next.
2.4. Linear Dispersion Relationship of Wave Model
In order to obtain the linear dispersion relationship of the wave model corresponding to the formulation with an intermediate velocity variable, as expressed in terms of in (15) and given by (12) are substituted into the linearized forms of (1) and (8), respectively.
where the depth is assumed constant, while surface pressure is dismissed and the notation is adopted as introduced by Nwogu [4]. Note that when expressed in terms of a single velocity variable , the continuity equation contains a new term with third spatial derivatives and likewise momentum equation has a term with second spatial derivatives plus time derivative. The presence of these terms inevitably introduces considerable numerical inaccuracies into any finite difference scheme. Moreover, unlike Equation (1), the above continuity equation is not exact to all orders and, as such, gives rise to further errors in computations.
Using and in (16) and (17) results in
in which is the wave amplitude, and are the amplitudes of horizontal velocity components, , is the cyclic wave frequency, and are, respectively, x- and y-components of the wave number vector , and is the angle wave propagation direction makes with the x-axis. In order to have a nontrivial solution for the matrix system of (18), the discriminant must vanish. Equating the discriminant to zero yields the dispersion relationship corresponding to (16) and (17):
where . On the other hand, linear theory or the second-order Stokes theory dispersion relationship is given by . Expressing as a Maclaurin series, dividing both sides by , and establishing the Padé approximant [33] gives
which is correct up to and including . Comparing (19) and (20) reveals that must be if they are to be identical. There are different ways of determining such as minimizing the error within a preset range; the approach adopted here is in accord with the asymptotic expansions underlying behind Boussinesq theory and is therefore preferred. Finally, setting reduces (19) to the “standard” Boussinesq dispersion relationship as well as making in (15) so that the entire system becomes the classic Boussinesq model of Peregrine [6]. Figure 1 depicts three different dispersion relations; namely, the exact one according to linear theory , the classic Boussinesq model as described by Equation (19) for , and, finally, the improved Boussinesq model corresponding to . Obviously, the improved model is a better approximation to the exact expression over a much wider range in relative depth . It is also noted that all the improved Boussinesq models (Witting [1]; Madsen, Murray, and Sørensen [2]; Nwogu [4]; Beji and Nadaoka [5]) yield identical dispersion relations to the present one when their parameters are specified in accordance with the Padé approximant given in Equation (20).
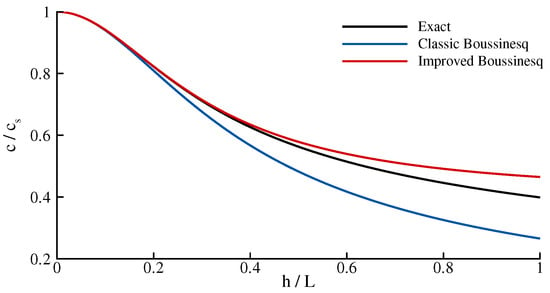
Figure 1.
Exact (black line), classic Boussinesq (blue line) , and improved Boussinesq (red line) phase velocities as normalized by shallow water phase velocity for relative depths .
3. Numerical Formulation
In any numerical scheme, the conservation of mass is the primary factor for computational accuracy; therefore, use of a continuity equation in exact conservation form with minimum number of terms, as formulated in terms of the mean horizontal velocity in equation (1), is amply justified. On the other hand, neglect of high-order nonlinear contributions involving multiplication of derivatives in a momentum equation may be justified by arguing that their beneficial effects are quite likely to be counterbalanced and even exceeded by unavoidable numerical inaccuracies. Furthermore, since the sufficiency of weakly nonlinear models for practical applications has been confirmed by the work of Bonnefoy et al. [34], as re-iterated in Stiassnie [35], it is deemed quite adequate, at least for the present purposes, to use Equation (8) instead of (7).
The numerical scheme begins by first obtaining new time level value of for the entire domain from the momentum Equation (8):
The next step uses newly computed value on the left side of (12) for determining corresponding via an implicit discretization:
Then, the depth-averaged new time level velocity is computed from (15) with the aid of newly obtained :
At this point, it is worthwhile to indicate that the dispersion characteristics of the model may be carried to higher levels by simply including higher-order terms in (22) and (23) without making any other change in the scheme as remarked in [1]. Finally, is used in the continuity equation,
to advance the surface displacement to the new time level over the entire domain. Here, this scheme is carried out by employing a finite difference discretization of the equations as described next; however, other numerical techniques such as finite elements or a combination of different approaches may, of course, be used.
3.1. Finite Difference Discretization of Equations
Finite difference discretization of equations is accomplished in a staggered-time and staggered-grid system. Four time levels, t, , , and , are used. Horizontal velocity components are computed at t and time levels while surface displacements , water depths h, and surface pressure values (if used) are evaluated at and time levels. Likewise, velocities are placed at different grid points from surface elevations, as shown in Figure 2. Water depths and surface pressure values are placed at the same grid points with surface elevations, although not indicated in the figure. This grid system is slightly different from the Arakawa-C grid (see p. 194, [36]) in the sense that surface elevations are located at the grid intersections instead of the middle of cells. Such placing enables the introduction of wave field by specifying surface elevations along the boundaries, which is essentially more convenient than introducing the velocities. An alternative discretization based on the Arakawa-C grid was also developed and tested. Results showed only slight differences; hence, due to the advantage of direct feeding of the surface elevation along the incoming boundary, the present scheme was adopted. Nevertheless, depending on the preferences, the Arakawa-C grid system may confidently be used as an equally accurate and robust alternative.
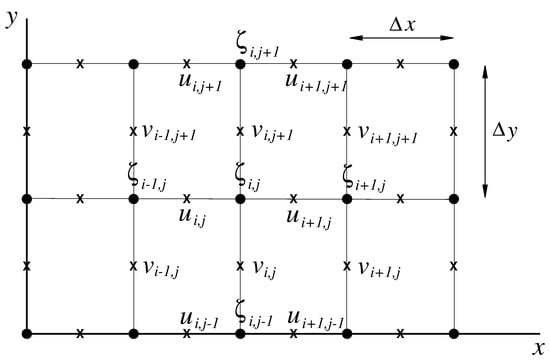
Figure 2.
Staggered arrangement of surface displacements and velocities on the grid used for finite difference approximation.
According to the numerical scheme outlining the x-component of the horizontal velocity vector at the still water level for the new time level , , is computed from the discretized x-momentum equation:
where subscripts i and j are multipliers of spatial increments and in the x- and y-directions, respectively. Superscript k denotes the time level multiplying , the time step. In Equation (25), only the first term appearing in time derivative is considered as unknown; all the other new time velocities are treated as known. Thus, (25) is used to solve values explicitly along all the x-directions for the entire domain. Note that both the surface elevation and pressure are evaluated at mid-time steps according to the staggered time arrangement. Hence, the scheme decouples the x- and y-directions completely and uses an iterative approach in time. Computational trials revealed that three time iterations guarantee four decimal places of accuracy between the third and fourth iteration for all the simulations presented in this work.
A discretized form of y-momentum equation for computing values can fairly easily be obtained from (25) by interchanging the velocity variables, indices, and spacial increments with their counterparts. For instance, would be , while would be , and, more specifically, would be in the y-sweep discretization. In order to avoid repetition, the y-direction discretization is omitted. The next stage is to compute values by the use of Equation (22):
where
The parentheses in stand for the same contents as the preceding one but for water depths at the time level . The term can be written down from by interchanging the indices as explained after Equation (25). The parameter is defined as or . For , , indicating that the velocity used is nearly at mid-depth: .
’s on the left of (26) are already computed from (25) and ’s are treated as known so that for a single x-direction, , the unknown values on the right of (26) constitute a tridiagonal matrix system which can be solved very efficiently by a double-sweep Thomas algorithm at each time step. An important feature of (26) together with (27) is the inclusion of all the spatial and temporal derivatives of water depth; accordingly, possible time-dependent movements of the seabed due to sea-quakes are accounted for, and the so-called mild slope approximation is not adopted.
For the y-sweep, the corresponding discretization can be established from (26) in exactly the same way as described above for the y-momentum equation. Being an implicit discretization, this stage of computations renders the entire numerical scheme implicit, hence making it possible to use relatively larger time and spatial steps compared to explicit schemes. The next step is the computation of from (23), as follows.
in which the terms involving water depths are evaluated exactly as formulated in (27). The terms on the right side of (28) are all known or treated as known; therefore, ’s are obtained easily after evaluating the terms on the right.
The preceding steps are repeated for the y-direction equations; thus, provisional values of and are obtained for the entire domain. At the final stage, the continuity equation is used to solve for the new time level surface displacements:
Entire computations, x-sweep, y-sweep, and continuity are iterated for accurate results. As indicated previously, based on simulation trials, three iterations are observed to be sufficient for reaching four decimal places of agreement between the third and fourth iterations for all variables.
3.2. Treatment of Boundaries
Three different boundary conditions are used in the simulations presented here: incoming boundary condition, where incident wave field is introduced, outgoing boundary condition, where wave field radiates out without being reflected back, and wall boundary condition on both sides of the domain along the x-axis, which is taken as the main propagation wave direction. Simulation of waves generated by a sudden bottom movement is an exception, where radiation condition is used at the incoming boundary too, and waves are generated by an upthrust of the bed in a definite limited region within the domain.
At the incoming boundary, wave field is introduced by specifying the surface elevation at the new time level just before solving the continuity equation. For sinusoidal waves,
where is the incident wave amplitude, the cyclic wave frequency corresponding to the period T, the time step, the running index in the y-direction, and the running index denoting time level. Running index k should not be confused with the wave number k used in (19) and (20). If the incident waves are not sinusoidal they can be introduced by specifying the appropriate function.
At the outgoing boundary, one-dimensional linear wave equation admitting the solution for waves moving in the positive -direction is used. Here, is the wave celerity component in the x-direction. The discretized form of the equation is
where n denotes the last node number in the x-direction and , with m being the last node number in the y-direction. Note that time and space derivatives are both centered at and .
In case the radiation condition is not used at a free boundary, the discretization is performed by one-sided finite differences approximation. For instance, if the waves are to freely cross a left-side boundary, the discretization of is performed as follows:
Finally, wall condition requires that the velocities normal to the wall be zero; namely, , , , or , depending on the boundary where wall condition is applied. For the surface elevation, the wall condition is satisfied by considering a mirrored image of the free surface such that or . Accordingly, on the outgoing boundary with , is implemented as
which results in hence is thus determined and can be used to evaluate the derivatives wherever appropriate. Elaboration of other possible boundary conditions in detail is beyond the main scope of this work and therefore not attempted.
4. Simulations
Five different simulations are carried out by the use of the numerical scheme proposed for the wave propagation model developed here. The first simulation serves three different purposes: to check the ability of the wave model to simulate wave amplitude variations over varying bathymetry, and to test the performance and resolution dependence of the numerical scheme.
4.1. Wave Propagation over Varying Depths
In practical applications of nearshore wave models, the ability to accurately compute linear wave shoaling is of primary importance, as exploited in detail in [37,38]. This simulation accordingly considers a sinusoidally varying depth in the x-direction, which is taken as the main wave propagation direction. The x-dependent water depth is then defined as
where is the water depth at the beginning of domain , is the mid-domain water depth, and is the entire domain length in the x-direction. The bottom topography is depicted in Figure 3.
Figure 3.
Sinusoidal variation of bottom (black) according to Equation (34) and still water level (blue). Vertical axis normalized by water depth at and horizontal axis by total domain length .
Incident waves are sinusoidal with period and a very small amplitude to ensure linearity. Although the case is unidirectional, simulations were carried out for two dimensions with domain width and run for 100 periods so that the efficiency of numerical radiation boundary could be tested as well.
Figure 4 shows two cases for different dispersion parameters, both using resolution, as described below. Envelopes are drawn by computing wave amplitude a from the constancy of energy flux , where is the group velocity according to linear theory. The graph at the top is the improved dispersion case , while the bottom is the standard Boussinesq model . Since incident wave field is relatively short, , performance of the classic model is inferior.
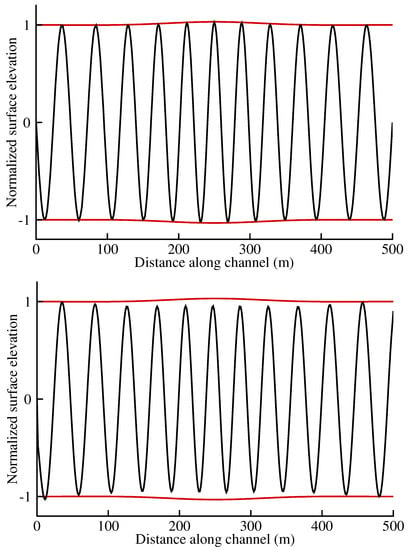
Figure 4.
Normalized surface elevation (black) and conservation of energy flux envelope (red) for improved (top) and classic model (bottom).
More simulations were carried out for five different resolutions with by setting and so that the Courant number was unity for every case, although it was not required for numerical stability. Here, L is the mean wavelength computed by taking the average of incoming and mid-channel values, T is the wave period, and is the phase celerity. Each simulation was carried out for 100 wave periods. In this way, the sensitivity of the numerical scheme to the adopted resolution could be tested by comparing the observed maximum difference with the corresponding exact value obtained from the constancy of energy flux concept. Figure 5 depicts the maximum relative error percentages for each N as computed from , while the curve is a power fit to these points. Error percentages decrease in an asymptotic manner and indicate a robust convergence of numerical results to true values.
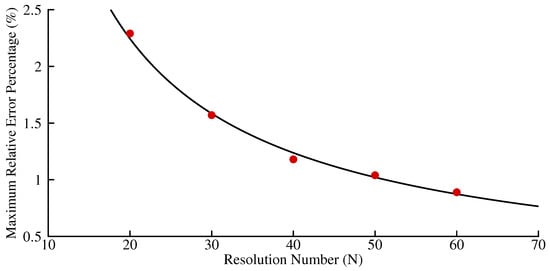
Figure 5.
Maximum relative error percentages (red circles) for different resolutions N and power fit (black line) to these values.
4.2. Waves Generated by Bottom Movement
Hammack [39] studied tsunami generation and propagation by theoretical and experimental means. In particular, the experiments conducted in a wave tank fitted with a bottom wave generator are quite valuable for testing the performance of wave models. Here, measured wave profiles generated by an impulsive upthrust of a bed unit located at the upstream end of the tank are compared with numerical simulations performed by specifying the temporal change of water depth in accordance with the experiments.
where is the still water depth, the height of bed upthrust, a the exponential time decay coefficient, the total length of moving bed segment, and H the Heaviside step function. Accordingly, at time , the bed segment impulsively begins its upward motion with a nonzero velocity, , and reaches its maximum height with exponentially decaying velocity. To quantify the relative rapidness of bed motions, Hammack [39] defined a time-size ratio , with being the characteristic time indicating the duration of bed motion. Accordingly, denotes impulsive bed motions, transitional bed motions, and creeping bed motions. With these definitions, the experimental case considered here has the following generation parameters: , , , , and , so that the bed segment rises to the height in seconds and continues its rise exponentially at the same rate to . Figure 6 shows the rise of bed segment for three different instants, . denotes the instantaneous height of the bed segment while stands for the total length of the wave tank in the x-direction. Moving bed segment is drawn in the middle of the tank for clear visualization, although in the experiments it is placed at the upstream.
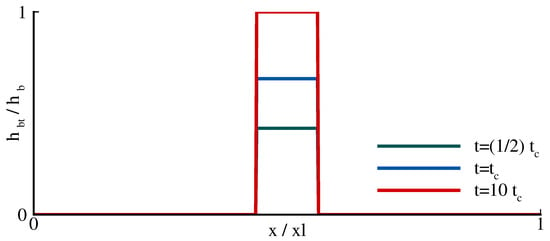
Figure 6.
Time-dependent movement of the bed shown for three different instants: (green), (blue), and (red). Vertical axis normalized by maximum bed upthrust and horizontal axis by total wave tank length .
Numerical simulation was carried out with a temporal resolution and spatial resolution in the x-direction; thus, the Courant number was unity for shallow water phase celerity . Since this simulation is numerically 1-D (physically 2-D), both the tank width and were arbitrarily selected as . Figure 7 compares the computed wave forms with experimental measurements at four different locations (a) at the outer edge of the moving bed segment , (b) at 20 water depths downstream , (c) at 180 water depths downstream , and (d) at 400 water depths downstream . For the first two stations, the wave model performs quite well both in terms of wave profile and the phase. Farther downstream, the third station still shows a good profile agreement despite a phase mismatch, which was rectified by taking the station location as instead of . The last station exhibits both profile and phase discrepancies; again, the phase discrepancy was removed by setting instead of for the station location. Phase shifts of the last two locations were introduced to allow clear comparisons of wave forms. The most likely reason for these phase mismatches is bottom friction, as the depth is very shallow. Exactly the same problem was observed in the numerical simulations of Hammack [39], who attributed these mismatches possibly to “the presence of viscous energy losses and boundary stresses in the experiments”.
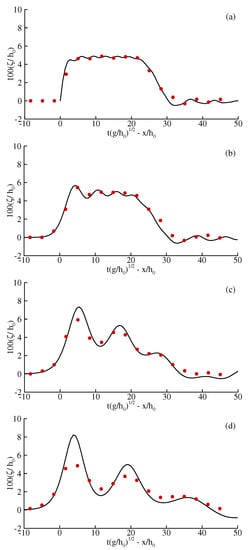
Figure 7.
Downstream surface profiles of Hammack’s measurements (red circles) and numerical simulation (black line) for an impulsive bed upthrust. (a) At the edge of bed unit , (b) 20 water depths downstream , (c) 180 water depths downstream , and (d) 400 water depths downstream .
4.3. Nonlinear Wave Propagation over a Submerged Bar
Nonlinear wave propagation over a submerged trapezoidal bar for regular and irregular waves was investigated both experimentally and numerically [40,41]; the measurements were used for testing relevant numerical schemes. Due to shoaling and harmonic generation over the up-slope and horizontal crest of bar and subsequent de-shoaling with harmonic decomposition, these experiments pose challenging cases to test the linear and nonlinear shoaling as well as dispersion characteristics of wave models. Among several sets of measurements, sinusoidal waves with period and incident wave height are considered here; all the details concerning experimental setup, a sketch of bottom topography, and measurement locations can be found in [41]. Water depth variations along the wave flume are defined by
where all the quantities are in meters. Computations were carried out by setting , which corresponded to approximately sampling rate of records, and so that the Courant number at the incoming boundary was , which proved to be a very good choice for satisfactory results. Figure 8 shows time domain surface profiles as measured and computed for the last 5 periods of a total 20-period run at six different gauge locations. Time series recorded by Gauge 1 was directly used to feed the incident wave profile into the numerical model and is not shown. For all six gauges, the simulated profiles agree very closely with the measured ones.
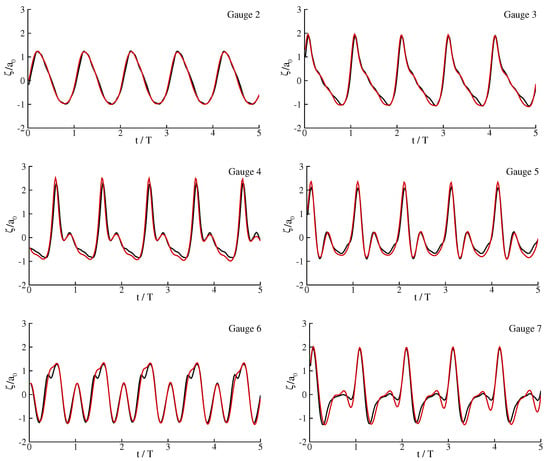
Figure 8.
Measurements (black) of nonlinear wave evolution over a submerged bar and corresponding numerical simulations (red) for six different wave gauge locations.
4.4. Nonlinear Wave Convergence over a Topographical Lens
Whalin [42] conducted experiments of nonlinear wave convergence in a wave basin of length and width over a topographical lens built by evenly spaced semicircular steps. As waves propagate over the topography, they converge along the midline of the tank and their amplitudes increase. Waves then become nonlinear and give rise to higher harmonics which evolve with distance. Experiments provide measurements of primary wave and harmonic amplitudes along the midline of the tank for several locations. All the details can be found in [42]. Equations describing the bathymetry are given by
where all the quantities are in meters. Experiments simulated here are regular waves with periods and corresponding incident wave amplitudes , and in water depth of at the incoming boundary. All the simulations were carried out with a spanwise discretization , where is the tank width. Time and x-direction resolutions were set to and , with being the mean wavelength in the domain so that the mean Courant number was unity. It is emphasized, however, that making the Courant number unity is not a stability requirement; it is merely performed to minimize possible phase errors. Simulations were carried out for 40 wave periods for waves, 20 periods for , and 12 periods for so that a fully developed wave field could be established for each case.
Figure 9 shows the bathymetry and perspective view of simulated waves for the case. Figure 10 compares measurements and computed values for the primary wave and its harmonics for waves from top to bottom. Harmonic amplitudes were computed by Fourier transforming time series of simulated surface elevations for the last three periods for each case. While overall agreement of computations with measurements are quite good for the case, discrepancies observed for the second and third harmonics of the case are pronounced. The case renders a barely acceptable agreement. These relatively poor performances observed for the latter cases cannot be attributed to a definite reason; however, the step-like construction of the experimental bottom topography might have played a role, especially when the wide scatter in measurements is considered. It should also be pointed out that such disagreements are not specific to the present wave model; similar drawbacks are observed for other studies reported in the literature.
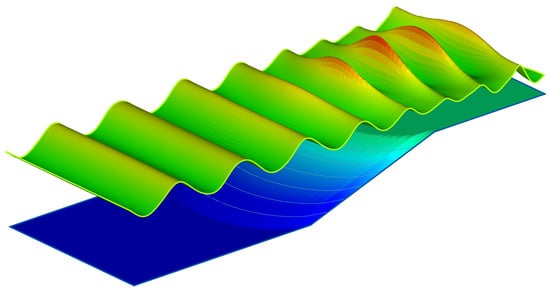
Figure 9.
Bathymetry and simulated view of the fully developed numerical wave tank for the case of Whalin [42]. Axes are omitted due to different vertical scales for bathymetry and wave field.
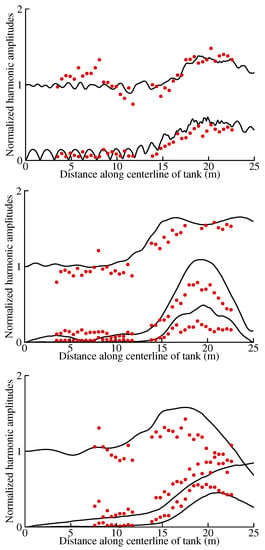
Figure 10.
Variations of normalized harmonic amplitudes along the centerline for incident waves of (top), (middle), and (bottom). Measurements (scatter) and computations (solid line).
4.5. Combined Refraction–Diffraction over an Elliptic Shoal
Combined effects of refraction and diffraction on a moderately nonlinear wave field were investigated via experimental measurements and wave model predictions by Berkhoff, Buoy, and Radder [43]. Experiments were carried out at a basin of length and width for obliquely shoaling bottom topography and obliquely oriented elliptic shoal, which made a 20° angle with incident wavefronts. Waves at the seaward boundary had an amplitude to water depth ratio of with water depth and period . Mathematically, the bottom topography is defined as
where all the quantities are in meters. Details concerning the experiments can be found in [43].
Simulation was performed with , , and for 35 wave periods. Here, is approximately the mean wavelength within the domain and is the basin width. Three different resolutions attempted for , , and revealed that the results differed insubstantially. Wave heights were computed from the maxima and minima determined during the last three periods of simulation at the locations corresponding to the measurement stations.
Figure 11 shows the bottom topography of the basin and a perspective view of the wave field at the end of 35 periods of simulation. Converged and diverged wave patterns and cnoidal wave forms in shallower regions near the end of basin are striking aspects of the wave field. Experimental measurements were performed for eight sections; three of these were lengthwise along the x-direction, while the remaining five were crosswise in the y-direction. Figure 12 shows the longitudinal, 1–3, and transverse 4–8 sections. Although some discrepancies exist, the overall performance of the wave model is quite acceptable for this challenging test case with complex bathymetry.
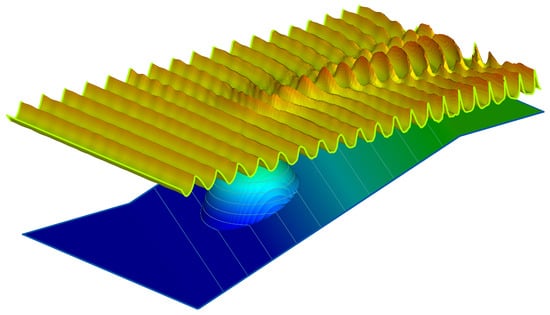
Figure 11.
Basin bathymetry and simulated view of fully developed wave field for experiment in Berkhoff, Buoy, and Radder [43]. Axes are omitted due to different vertical scales for bathymetry and wave field.
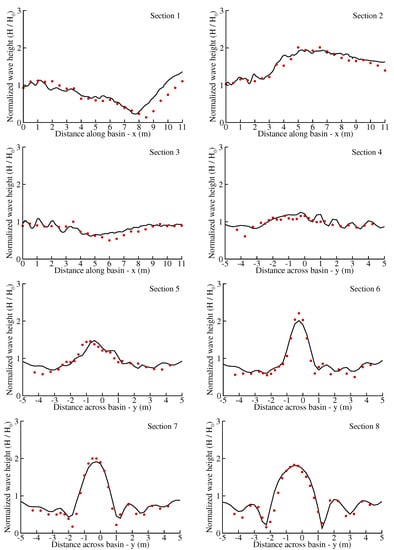
Figure 12.
Lengthwise (sections 1–2) and crosswise (sections 4–8) wave height variations for experiments in Berkhoff, Buoy, and Radder [43]. Experimental measurements (scatter) and numerical simulations (solid line).
5. Concluding Remarks
A completely new arrangement of Boussinesq-type wave equations is presented to achieve numerically more accurate and robust computations. Simultaneous employment of three different velocity variables allows the use of continuity and momentum equations in the simplest forms as well as providing improved dispersion characteristics to the wave model. Furthermore, separate treatment of kinematic equations connecting the different velocity variables makes it possible to retain all the terms involving water depth variations in time and space, thus endowing the wave model with capabilities to accurately generate and propagate waves due to sea-quakes as well. A useful theoretical extension would be to recast these equations into a curvilinear coordinate system, as in [44], for practical applications in irregular domains.
From the numerical point of view, the continuity and momentum equations of the proposed set, each composed of the least number of terms possible, contain only the first-order derivatives in time and space, thus minimizing the discretization errors in addition to resulting in explicit formulations. Only the intermediate velocity variable, the velocity at an arbitrary depth, is computed via an implicit formulation. However, this part of the computations alone is sufficient to make the entire scheme implicit, thus enabling the use of relatively larger spatial and time steps. With an overall decoupled system of computations, the computational efficiency of the entire scheme is maximized without incurring any penalties on the accuracy of results. This point is tested in different simulations capturing various aspects of wave transformations which reveal the reliability of the proposed wave model and numerical scheme. Nevertheless, it is always possible to produce different numerical schemes with higher accuracy at the cost of some more computational effort. Possible future works in this direction may result in even more satisfactory numerical solutions of the proposed equations.
Funding
This research received no external funding.
Data Availability Statement
All the data obtained from computations are available upon request.
Conflicts of Interest
The author declares no conflict of interest.
References
- Witting, J.M. A unified model for the evolution of nonlinear water waves. J. Comput. Phys. 1984, 56, 203–236. [Google Scholar] [CrossRef]
- Madsen, P.A.; Murray, R.; Sørensen, O.R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Coast. Eng. 1991, 15, 371–388. [Google Scholar] [CrossRef]
- Madsen, P.A.; Sørensen, O.R. A new form of the Boussinesq equations with improved linear dispersion characteristics: Part 2. A slowly-varying bathymetry. Coast. Eng. 1992, 18, 183–204. [Google Scholar] [CrossRef]
- Nwogu, O. Alternative form of Boussinesq equations for nearshore propagation. J. Waterw. Port Coast. Ocean Eng. 1993, 9, 618–638. [Google Scholar] [CrossRef]
- Beji, S.; Nadaoka, K. A formal derivation and numerical modelling of the improved Boussinesq equations for varying depth. Ocean Eng. 1996, 23, 691–704. [Google Scholar]
- Peregrine, D.H. Long waves on a beach. J. Fluid Mech. 1967, 27, 815–827. [Google Scholar] [CrossRef]
- Madsen, P.A.; Schäffer, H.A. Higher-order Boussinesq-type equations for surface gravity waves: Derivation and analysis. Phil. Trans. R. Soc. Lond. A 1998, 356, 3123–3184. [Google Scholar] [CrossRef]
- Karambas, T.V.; Memos, C.D. Boussinesq model for weakly nonlinear fully dispersive water waves. J. Waterw. Coast. Ocean Eng. 2009, 135, 187–199. [Google Scholar] [CrossRef]
- Memos, C.D.; Klonaris, G.T.; Chondros, M.K. On higher-order Boussinesq-type wave models. J. Waterw. Coast. Ocean Eng. 2016, 142, 04015011. [Google Scholar] [CrossRef]
- Klonaris, G.T.; Memos, C.D.; Drønen, N.K. High-order Boussinesq-type model for integrated nearshore dynamics. J. Waterw. Coast. Ocean Eng. 2016, 142, 04016010. [Google Scholar] [CrossRef]
- Walkley, M.; Berzins, M. A finite element method for the two-dimensional extended Boussinesq equations. Int. J. Numer. Methods Fluids 2002, 39, 865–885. [Google Scholar] [CrossRef]
- Zhan, J.M.; Li, Y.S.; Wai, O.W.H. An accurate finite difference scheme for Boussinesq equations. Int. J. Comput. Fluid Dyn. 2004, 18, 421–430. [Google Scholar] [CrossRef]
- Eskilsson, C.; Sherwin, S.J. Spectral/hp discontinuous Galerkin methods for modelling 2D Boussinesq equations. J. Comput. Phys. 2006, 212, 566–589. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhan, J.; Li, Y. High-order finite volume WENO schemes for Boussinesq modelling of nearshore wave processes. J. Hydraul. Res. 2016, 54, 646–662. [Google Scholar] [CrossRef]
- Bossi, U.; Engsig-Karup, A.P.; Eskilsson, C.; Ricchiuto, M. A spectral/hp element depth-integrated model for nonlinear wave-body interaction. Comput. Methods Appl. Mech. Eng. 2019, 348, 222–249. [Google Scholar] [CrossRef]
- Bayraktar, D.; Beji, S. Numerical simulation of waves generated by a moving pressure field. Ocean Eng. 2013, 59, 231–239. [Google Scholar] [CrossRef]
- David, C.G.; Roeber, V.; Goseberg, N.; Schlurmann, T. Generation and propagation of ship-borne waves -Solutions from a Boussinesq-type model. Coast. Eng. 2017, 127, 170–187. [Google Scholar] [CrossRef]
- Basco, D.R. A qualitative description of wave breaking. J. Waterw. Port Coast. Ocean Eng. 1985, 111, 171–187. [Google Scholar] [CrossRef]
- Kennedy, A.B.; Chen, Q.; Kirby, J.T.; Dalrymple, R.A. Boussinesq modeling of wave transformation, breaking and run-up. I: 1D. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 39–47. [Google Scholar] [CrossRef]
- Chen, Q.; Kirby, J.T.; Dalrymple, R.A.; Kennedy, A.B.; Chawla, A. Boussinesq modeling of wave transformation, breaking and run-up. II: 2D. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 48–56. [Google Scholar] [CrossRef]
- D’Alessandro, F.; Tomasicchio, G.R. The BCI criterion for the initiation of breaking process in Boussinesq type equations wave models. Coast. Eng. 2008, 55, 1174–1184. [Google Scholar] [CrossRef]
- Roeber, V.; Cheung, K.F.; Kobayashi, M.H. Shock-capturing Boussinesq-type model for nearshore wave processes. Coast. Eng. 2010, 57, 407–423. [Google Scholar] [CrossRef]
- Tissier, M.; Bonneton, P.; Marche, F.; Chazel, F.; Lannes, D. A new approach to handle wave breaking in fully non-linear Boussinesq models. Coast. Eng. 2012, 67, 54–66. [Google Scholar]
- Roeber, V.; Cheung, K.F. Boussinesq-type model for energetic breaking waves in fringing reef environments. Coast. Eng. 2012, 70, 1–20. [Google Scholar] [CrossRef]
- Fang, K.Z.; Liu, Z.B.; Zou, Z.L. Fully nonlinear modeling wave transformation over fringing reefs using shock-capturing Boussinesq model. J. Coast. Res. 2016, 32, 164–171. [Google Scholar] [CrossRef]
- Kaur, S.; Kumar, P.; Rajni. Non-linear periodic long waves based on Boussinesq equation for shallow water waves: A coupled FEM modeling. Ocean Eng. 2022, 245, 110469. [Google Scholar] [CrossRef]
- Watanabe, M.; Kan, H.; Toguchi, K.; Nakashima, Y.; Roeber, V.; Arikawa, T. Effect of the structural complexity of a coral reef on wave propagation: A case study from Komaka Island, Japan. Ocean Eng. 2023, 287, 115632. [Google Scholar]
- Beji, S. Improved Boussinesq-type equations for spatially and temporally varying bottom. Coast. Eng. J. 2018, 60, 318–326. [Google Scholar] [CrossRef]
- Beji, S. Note on conservation equations for nonlinear surface waves. Ocean Eng. 1998, 25, 607–613. [Google Scholar]
- Nadaoka, K.; Beji, S.; Nakagawa, Y. A fully dispersive and weakly nonlinear model for water waves. Proc. R. Soc. Lond. A 1997, 453, 303–319. [Google Scholar] [CrossRef]
- Abbott, M.B. Computational Hydraulics: Elements of the Theory of Free Surface Flows; Pitman: London, UK, 1979. [Google Scholar]
- Mei, C.C. The Applied Dynamics of Ocean Surface Waves; World Scientific: Singapore, 1989. [Google Scholar]
- Baker, G.S., Jr.; Graves-Morris, P. Padé Approximants; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
- Bonnefoy, F.; Haudin, F.; Michel, G.; Semin, B.; Humbert, T.; Aumaître, S.; Berhanu, M.; Falcon, E. Observation of resonant interactions among surface gravity waves. J. Fluid Mech. 2016, 805, R3. [Google Scholar] [CrossRef]
- Stiassnie, M. On the strength of the weakly nonlinear theory for surface gravity waves. J. Fluid Mech. 2017, 810, 1–4. [Google Scholar] [CrossRef]
- Kantha, L.H.; Clayson, C.A. Numerical Models of Oceans and Oceanic Processes; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Simarro, G. Energy balance, wave shoaling and group celerity in Boussinesq-type wave propagation models. Ocean Model. 2013, 72, 74–79. [Google Scholar] [CrossRef]
- Simarro, G.; Orfila, A.; Galan, A. Linear shoaling in Boussinesq-type wave propagation models. Coast. Eng. 2013, 80, 100–106. [Google Scholar] [CrossRef]
- Hammack, J.L. A note on tsunamis: Their generation and propagation in an ocean of uniform depth. J. Fluid Mech. 1973, 60, 769–799. [Google Scholar] [CrossRef]
- Beji, S.; Battjes, J.A. Experimental investigation of nonlinear wave propagation over a bar. Coast. Eng. 1993, 19, 151–162. [Google Scholar] [CrossRef]
- Beji, S.; Battjes, J.A. Numerical simulation of nonlinear wave propagation over a bar. Coast. Eng. 1994, 23, 1–16. [Google Scholar] [CrossRef]
- Whalin, R.W. The Limit of Applicability of Linear Wave Refraction Theory in a Convergence Zone; Research Report H-71-3; U.S. Army Corps of Engineers, The Waterways Experiment Station: Vicksburg, MS, USA, 1971. [Google Scholar]
- Berkhoff, J.C.W.; Booy, N.; Radder, A.C. Verification of numerical wave propagation models for simple harmonic linear water waves. Coast. Eng. 1982, 6, 255–279. [Google Scholar] [CrossRef]
- Beji, S.; Nadaoka, K. Fully dispersive nonlinear water wave model in curvilinear coordinates. J. Comput. Phys. 2004, 198, 645–658. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).