Step Approximation on Water Wave Breaking and Dissipation over Variable Bottoms across the Surf Zone
Abstract
1. Introduction
2. Materials and Methods
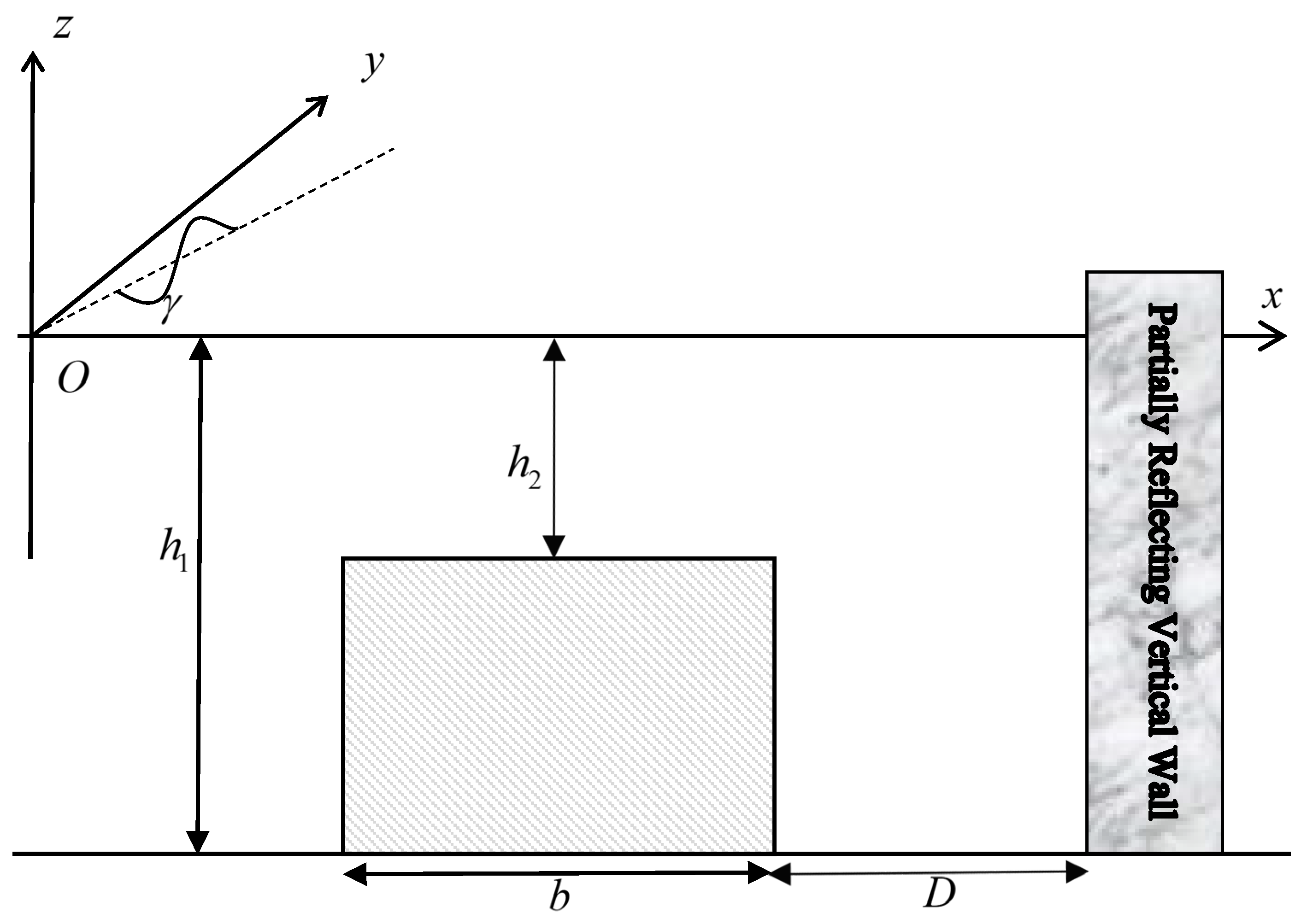
2.1. Problem Definition
2.2. Eigenfunction Matching Method
2.3. Wave Breaking and Dissipation
2.4. Wave Force
3. Results
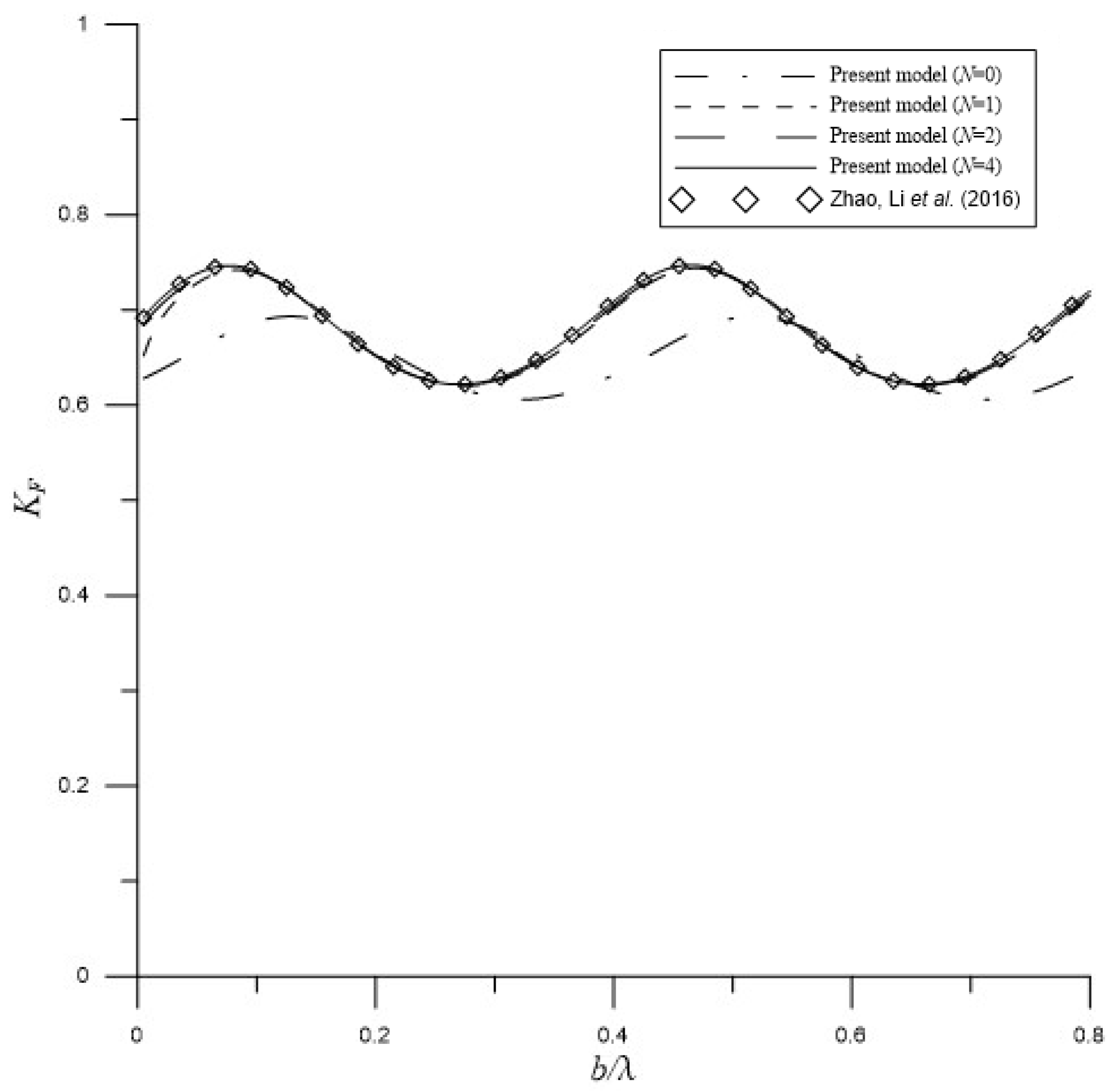
3.1. Rectangular Breakwater Close to a Partially Reflecting Vertical Wall
3.2. Constructive and Destructive Bragg Scattering by Periodic Half-Cosine Shaped Breakwaters
3.3. Oblique Incidence
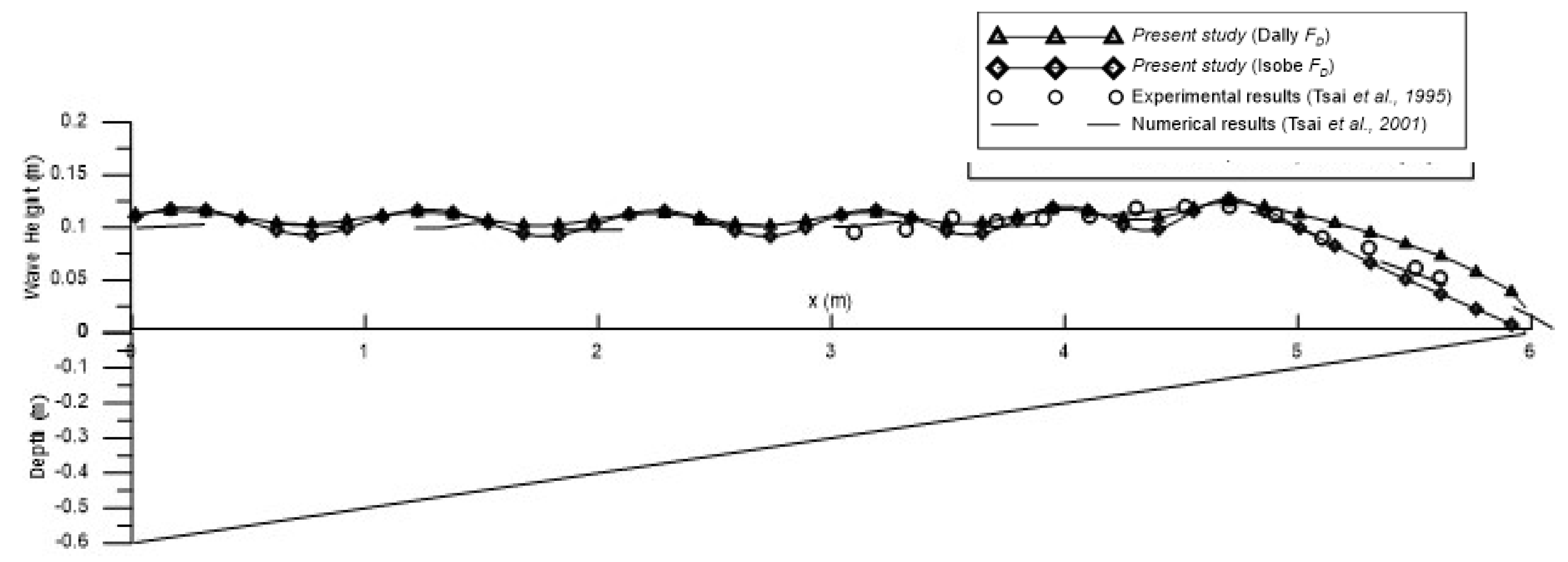
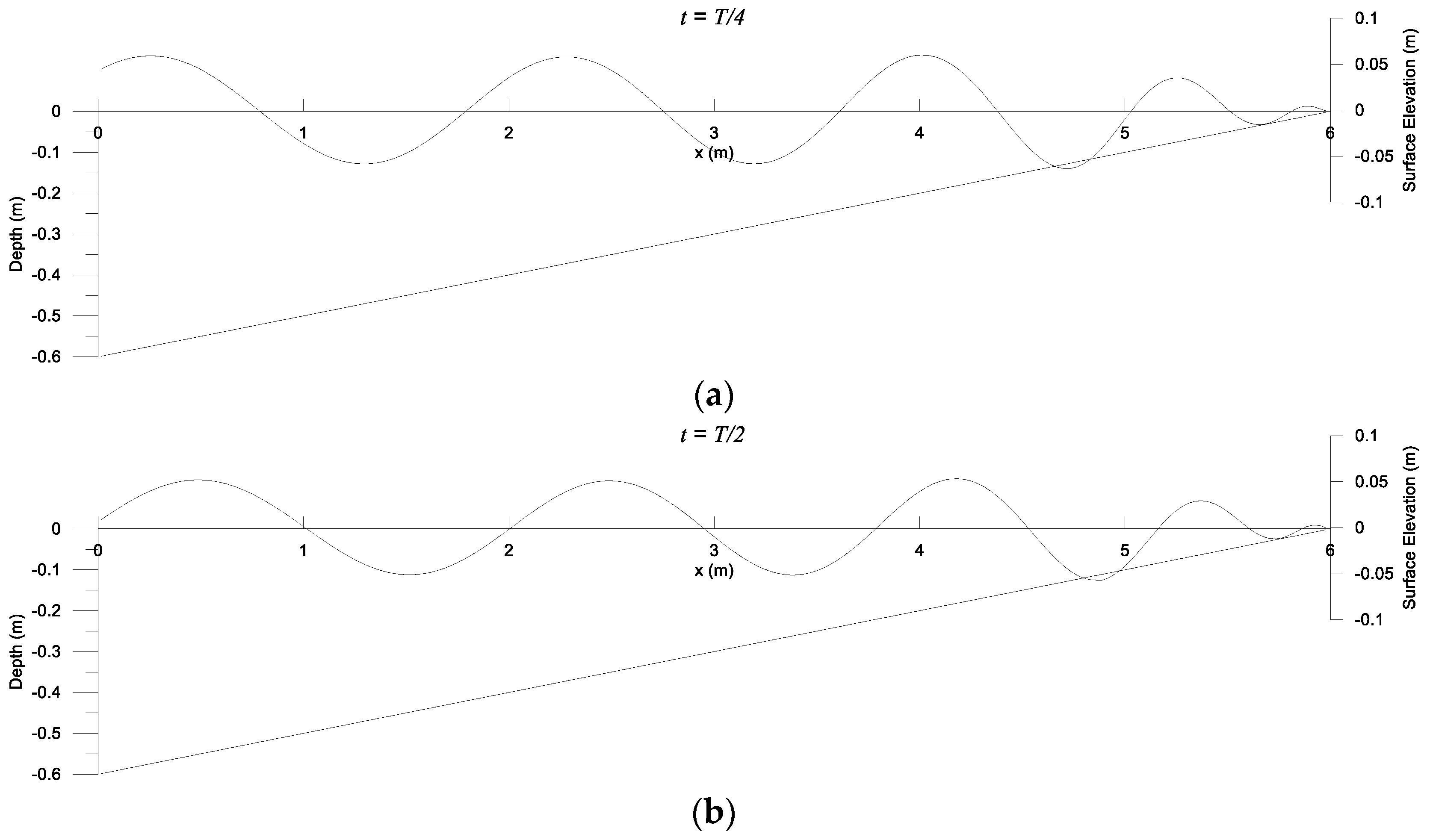
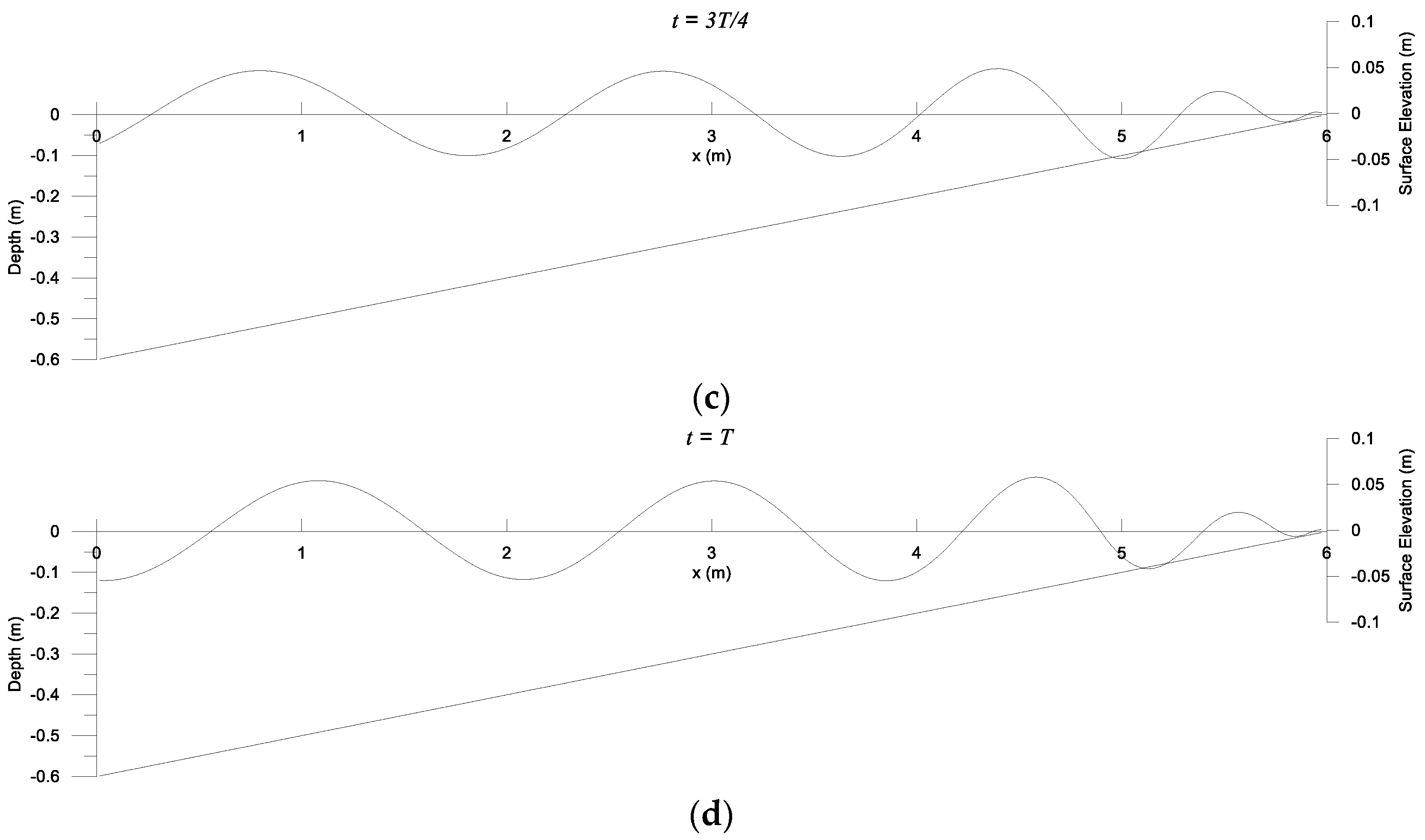
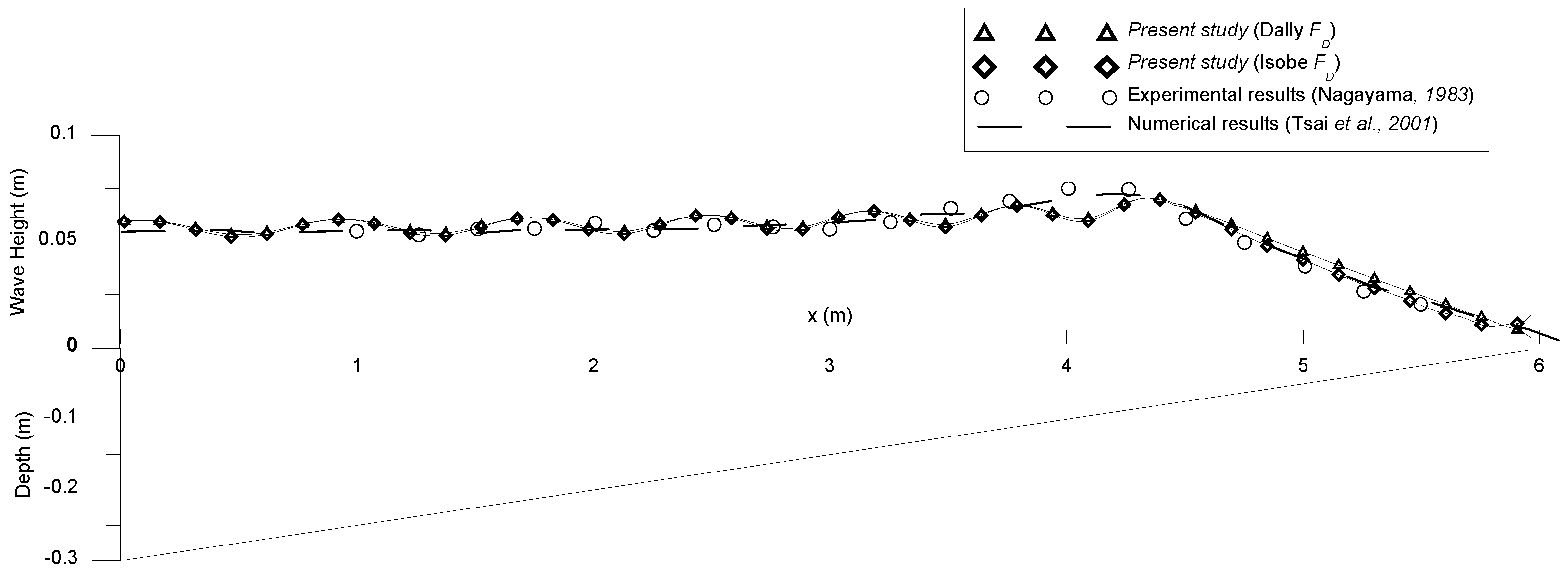
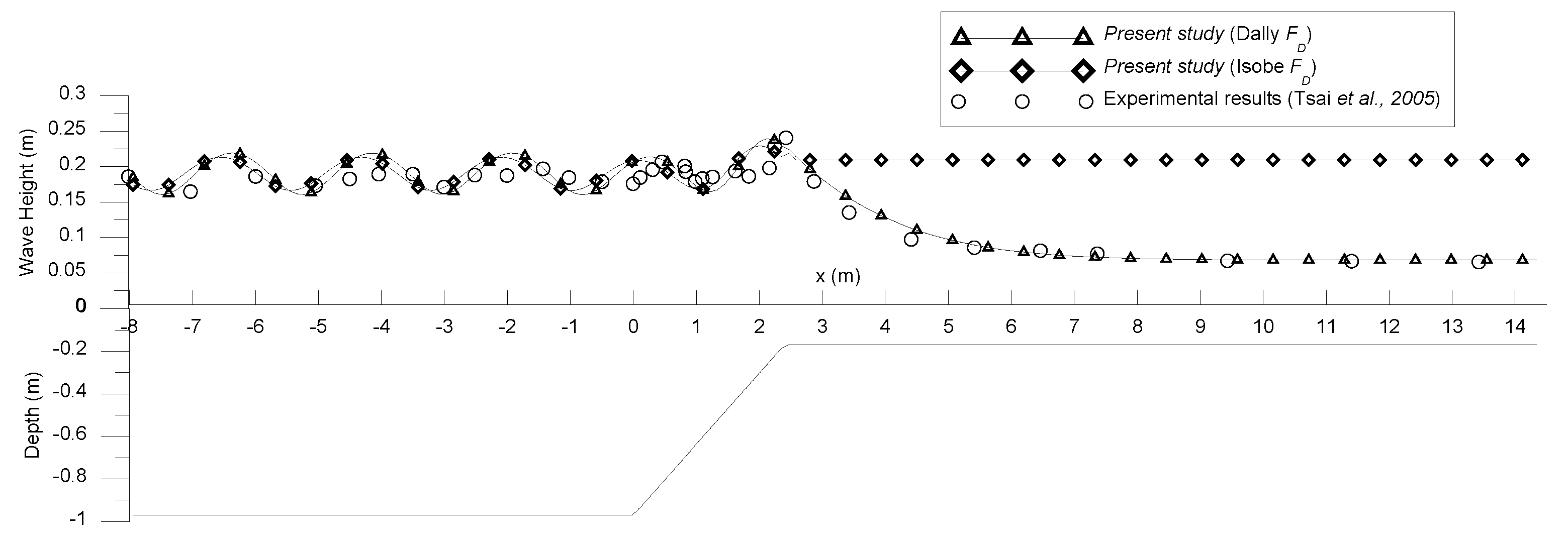
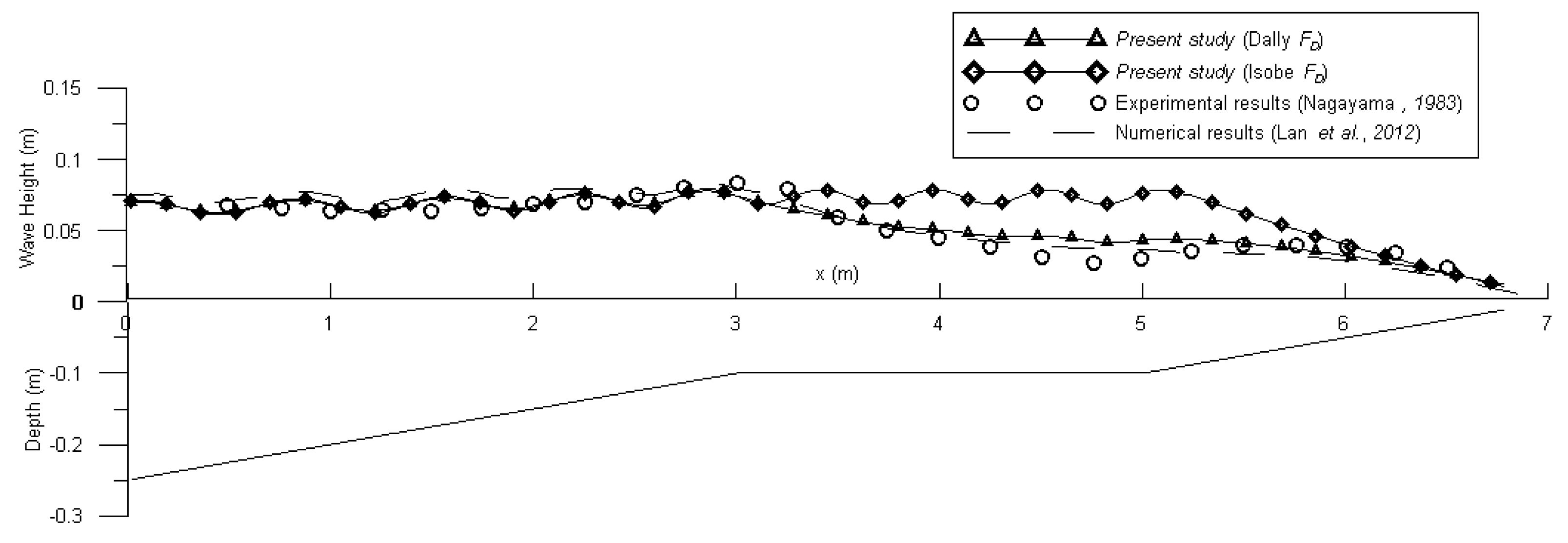
3.4. Water Wave Breaking and Dissipation by Mild Slopes
4. Discussion
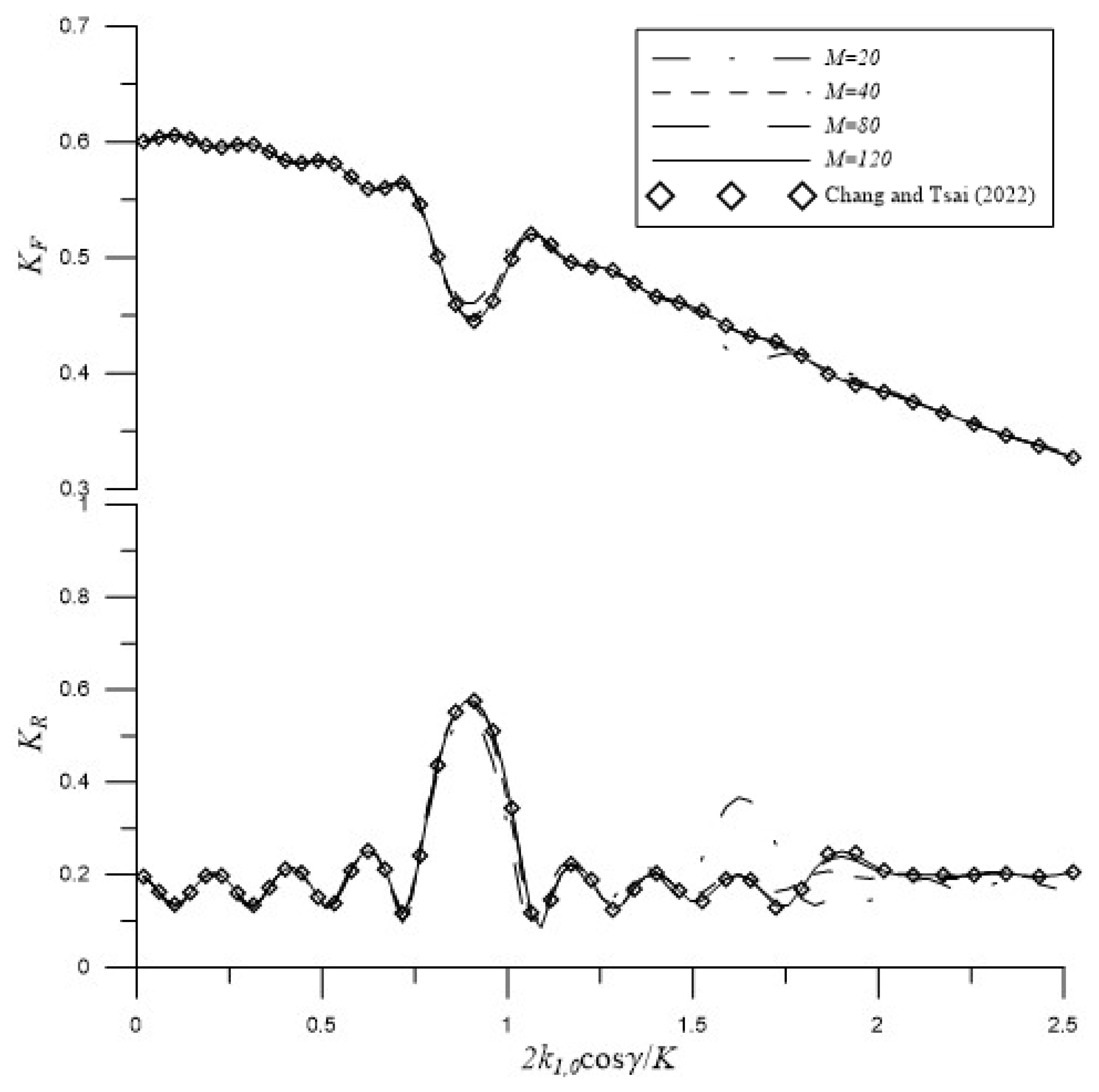
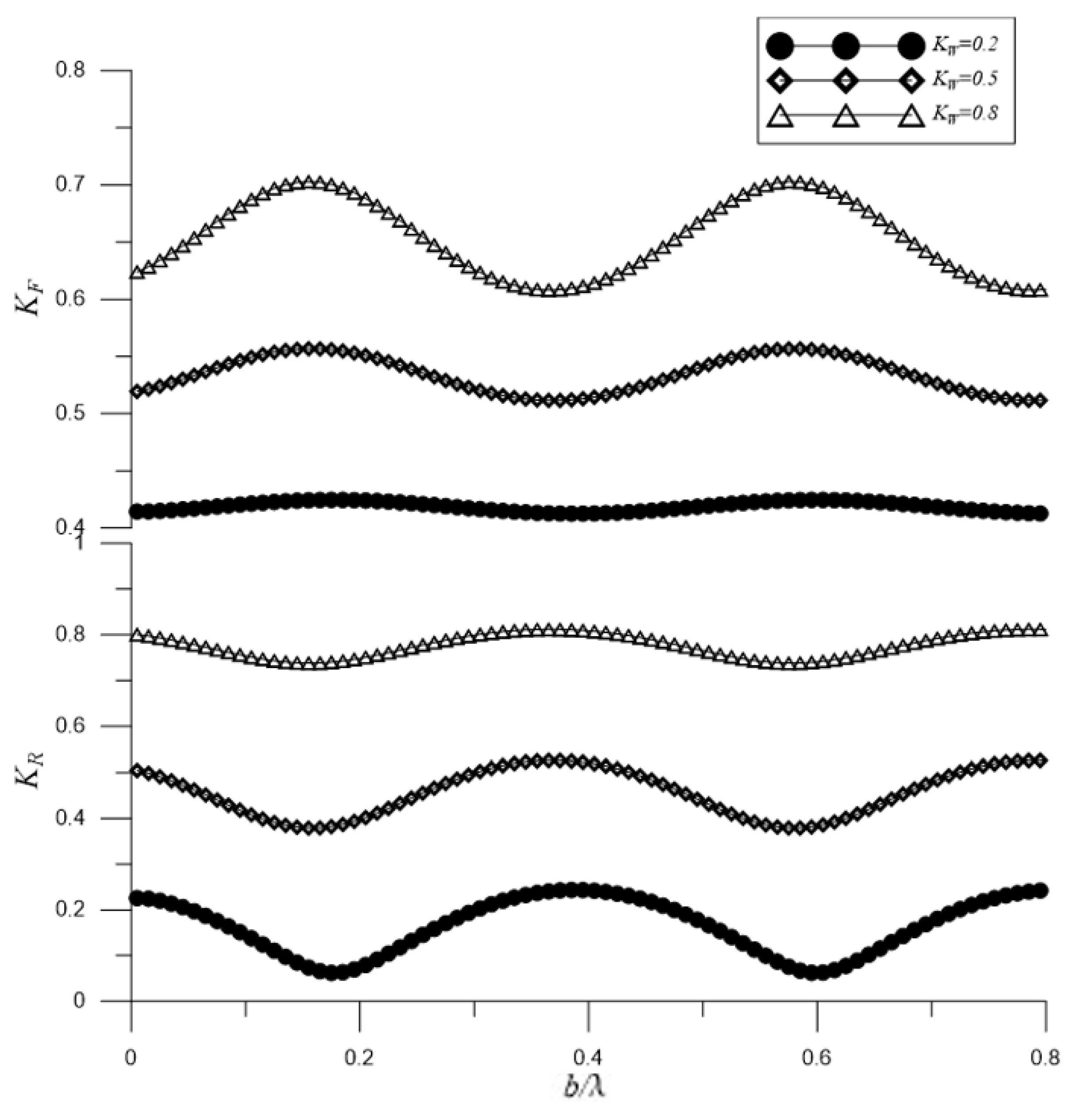
4.1. Parametric Analysis on Wave Scattring by Rectangular Breakwater in Front of Partially Reflecting Vertical Wall
4.2. Wave Breaking and Dissipation by Steep Slopes
4.3. Wave Breaking and Dissipation by Composite Slopes
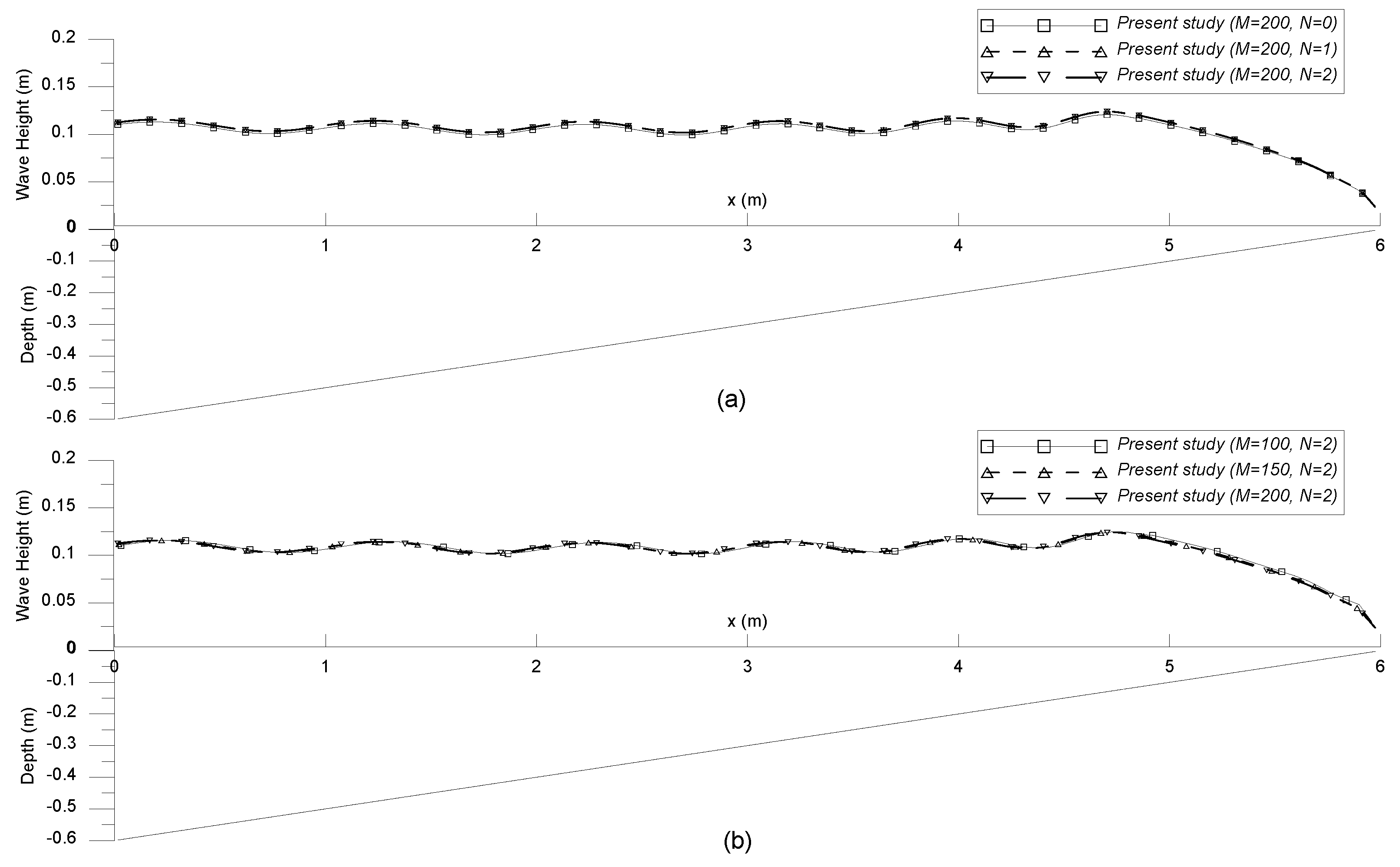
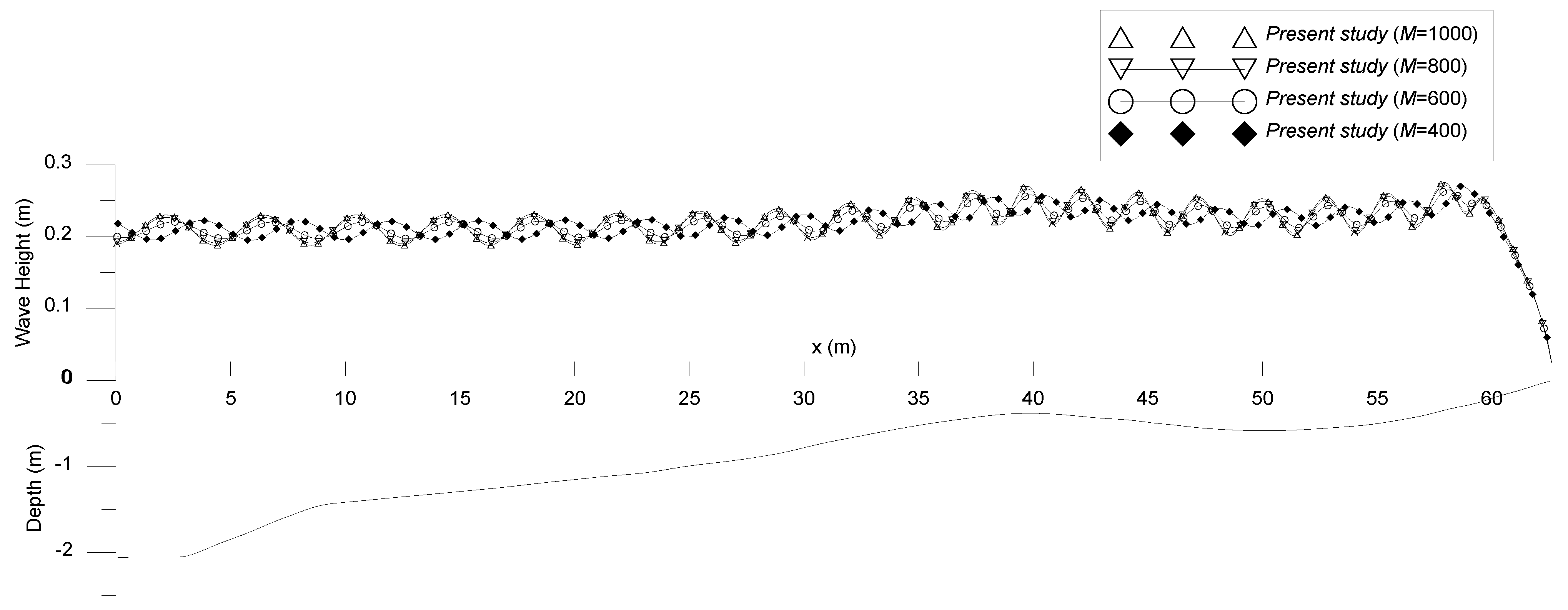
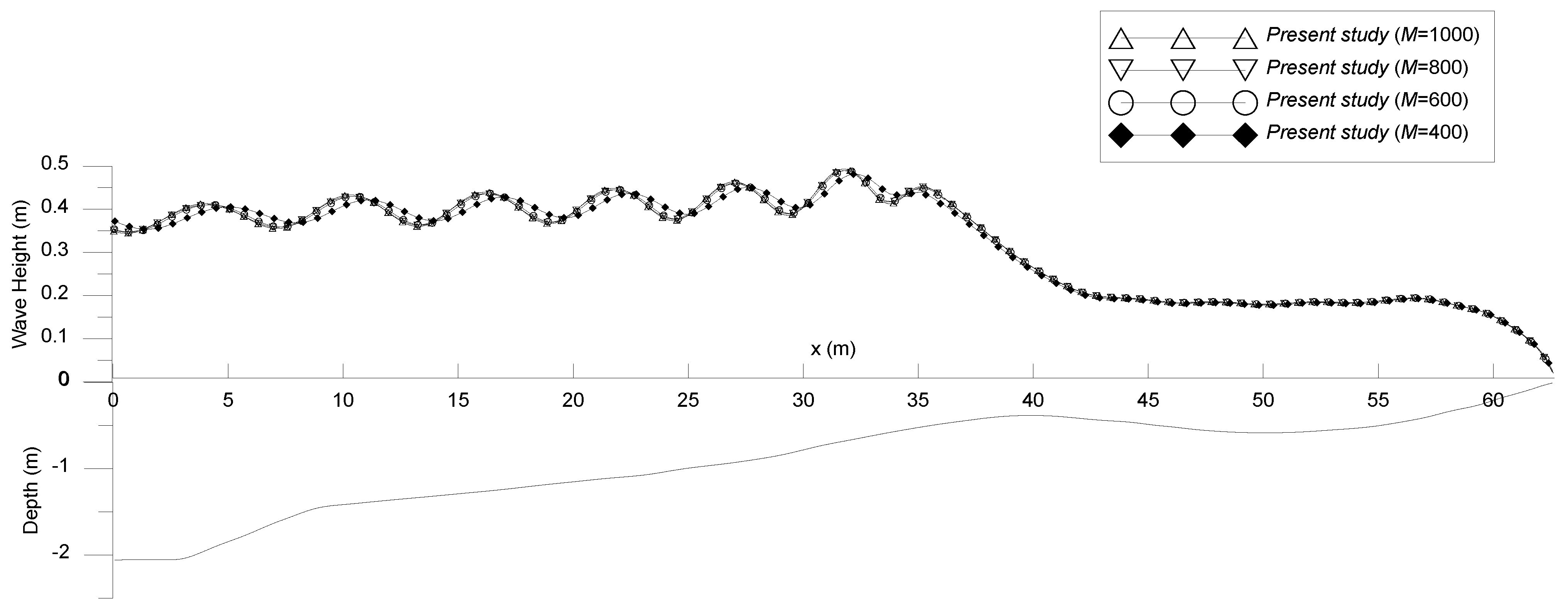
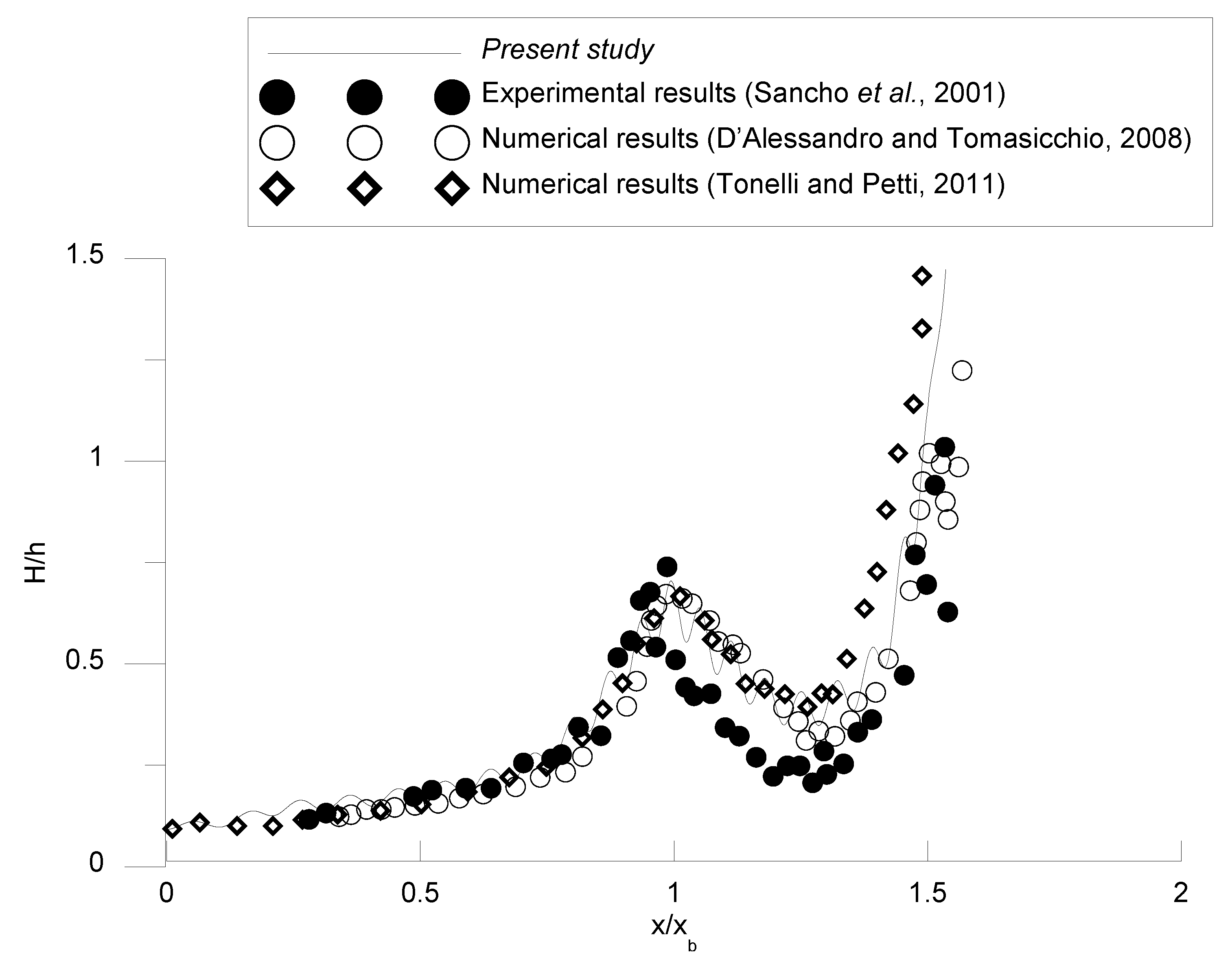
4.4. Wave Breaking and Dissipation by a Barred Beach
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goda, Y. Random Seas and Design of Maritime Structures; World Scientific Publishing: Singapore, 2010. [Google Scholar]
- Isaacson, M.; Qu, S. Waves in a harbour with partially reflecting boundaries. Coast. Eng. 1990, 14, 193–214. [Google Scholar] [CrossRef]
- Elchahal, G.; Younes, R.; Lafon, P. The effects of reflection coefficient of the harbour sidewall on the performance of floating breakwaters. Ocean Eng. 2008, 35, 1102–1112. [Google Scholar] [CrossRef]
- Behera, H.; Khan, M.B. Numerical modeling for wave attenuation in double trapezoidal porous structures. Ocean Eng. 2019, 184, 91–106. [Google Scholar] [CrossRef]
- Pakozdi, C.; Kendon, T.E.; Stansberg, C.-T. Breaking Wave Impact on a Platform Column: An Introductory CFD Study. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; pp. 645–654. [Google Scholar]
- Xiang, T.; Istrati, D.; Yim, S.C.; Buckle, I.G.; Lomonaco, P. Tsunami loads on a representative coastal bridge deck: Experimental study and validation of design equations. J. Waterw. Port Coast. Ocean. Eng. 2020, 146, 04020022. [Google Scholar] [CrossRef]
- Berkhoff, J.C.W. Computation of combined refraction-diffraction. In Proceedings of the 13th International Conference on Coastal Engineering, Vancouver, BC, Canada, 10–14 July 1972; pp. 471–490. [Google Scholar]
- Takano, K. Effets d’un obstacle parallelepipedique sur la propagation de la houle. La Houille Blanche 1960, 15, 247–267. [Google Scholar] [CrossRef]
- Massel, S.R. Extended refraction-diffraction equation for surface waves. Coast Eng. 1993, 19, 97–126. [Google Scholar] [CrossRef]
- Belibassakis, K.; Touboul, J.; Laffitte, E.; Rey, V. A mild-slope system for bragg scattering of water waves by sinusoidal bathymetry in the presence of vertically sheared currents. J. Mar. Sci. Eng. 2019, 7, 9. [Google Scholar] [CrossRef]
- Belibassakis, K.; Touboul, J. A nonlinear coupled-mode model for waves propagating in vertically sheared currents in variable bathymetry—Collinear waves and currents. Fluids 2019, 4, 61. [Google Scholar] [CrossRef]
- O’Hare, T.J.; Davies, A.G. A comparison of two models for surface-wave propagation over rapidly varying topography. Appl. Ocean Res. 1993, 15, 1–11. [Google Scholar] [CrossRef]
- Devillard, P.; Dunlop, F.; Souillard, B. Localization of gravity waves on a channel with a random bottom. J. Fluid Mech. 1988, 186, 521–538. [Google Scholar] [CrossRef]
- Tsai, C.C.; Lin, Y.-T.; Hsu, T.-W. On the weak viscous effect of the reflection and transmission over an arbitrary topography. Phys. Fluids 2013, 25, 043103–043121. [Google Scholar] [CrossRef]
- Tsai, C.-C.; Tai, W.; Hsu, T.-W.; Hsiao, S.-C. Step approximation of water wave scattering caused by tension-leg structures over uneven bottoms. Ocean Eng. 2018, 166, 208–225. [Google Scholar] [CrossRef]
- Tseng, I.-F.; You, C.-S.; Tsai, C.-C. Bragg reflections of oblique water waves by periodic surface-piercing and submerged breakwaters. J. Mar. Sci. Eng. 2020, 8, 522. [Google Scholar] [CrossRef]
- Tran, C.-T.; Chang, J.-Y.; Tsai, C.-C. Step approximation for water wave scattering by multiple thin barriers over undulated bottoms. J. Mar. Sci. Eng. 2021, 9, 629. [Google Scholar] [CrossRef]
- Tsai, C.-C.; Chou, W.-R. Comparison between consistent coupled-mode system and eigenfunction matching method for solving water wave scattering. J. Mar. Sci. Technol.-Taiw. 2015, 23, 870–881. [Google Scholar] [CrossRef]
- McCowan, J. XXXIX. On the highest wave of permanent type. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1894, 38, 351–358. [Google Scholar] [CrossRef]
- Goda, Y. A Synthesis of Breaker Indices. Proc. Jpn. Soc. Civ. Eng. 1970, 1970, 39–49. [Google Scholar] [CrossRef] [PubMed]
- Weggel, R.J. Maximum Breaker Height. J. Waterw. Harb. Coast. Eng. Div. 1972, 98, 529–548. [Google Scholar] [CrossRef]
- Svendsen, I. Analysis of surf zone turbulence. J. Geophys. Res. 1987, 92, 5115–5124. [Google Scholar] [CrossRef]
- Goda, Y. Reanalysis of Regular and random breaking wave statistics. Coast. Eng. J. 2010, 52, 71–106. [Google Scholar] [CrossRef]
- Robertson, B.; Hall, K.; Zytner, R.; Nistor, I. Breaking Waves: Review of Characteristic Relationships. Coast. Eng. J. 2013, 55, 1350002. [Google Scholar] [CrossRef]
- Dally, W.R.; Dean, R.G.; Dalrymple, R.A. Wave height variation across beaches of arbitrary profile. J. Geophys. Res. 1985, 90, 11917–11927. [Google Scholar] [CrossRef]
- Battjes, J.A.; Janssen, J.P.F.M. Energy loss and set-up due to breaking of random waves. Coast. Eng. Proc. 1978, 1, 32. [Google Scholar] [CrossRef]
- Isobe, M. A parabolic equation model for transformation of irregular waves due to refraction, diffraction and breaking. Coast. Eng. Jpn. 1987, 30, 33–47. [Google Scholar] [CrossRef]
- Tsai, C.-P.; Chen, H.-B.; Hsu, J.R.C. Calculations of wave transformation across the surf zone. Ocean Eng. 2001, 28, 941–955. [Google Scholar] [CrossRef]
- Tsai, C.-P.; Chen, H.-B.; Hwung, H.-H.; Huang, M.-J. Examination of empirical formulas for wave shoaling and breaking on steep slopes. Ocean Eng. 2005, 32, 469–483. [Google Scholar] [CrossRef]
- Lan, Y.-J.; Kuo, Y.-S.; Hsu, T.-W.; Lin, T.-Y. Numerical simulation of wave transformation across the surf zone over a steep bottom. Ocean Eng. 2012, 41, 33–38. [Google Scholar] [CrossRef]
- Hsu, T.-W.; Chang, J.-Y.; Lan, Y.-J.; Lai, J.-W.; Ou, S.-H. A parabolic equation for wave propagation over porous structures. Coast Eng. 2008, 55, 1148–1158. [Google Scholar] [CrossRef]
- Tsai, C.-C.; Chang, Y.-H.; Hsu, T.-W. Step approximation on oblique water wave scattering and breaking by variable porous breakwaters over uneven bottoms. Ocean Eng. 2022, 253, 111325. [Google Scholar] [CrossRef]
- Mei, C.C.; Stiassnie, M.A.; Yue, D.K.-P. Theory and Applications of Ocean Surface Waves: Part 1: Linear Aspects; World Scientific: Singapore, 2005. [Google Scholar]
- Silva, R.; Salles, P.; Palacio, A. Linear waves propagating over a rapidly varying finite porous bed. Coast Eng. 2002, 44, 239–260. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Y.; Li, H. Wave interaction with a partially reflecting vertical wall protected by a submerged porous bar. J. Ocean. Univ. China 2016, 15, 619–626. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, H.-j.; Liu, Y. Oblique wave scattering by a submerged porous breakwater with a partially reflecting sidewall. J. Mar. Sci. Technol. 2017, 25, 3. [Google Scholar]
- Meade, R.; Winn, J.N.; Joannopoulos, J. Photonic Crystals: Molding the Flow of Light; Pinceton Univiversity Press: Princeton, NJ, USA, 2008; p. 305. [Google Scholar]
- Li, X.S. An overview of SuperLU: Algorithms, implementation, and user interface. ACM Trans. Math. Softw. 2005, 31, 302–325. [Google Scholar] [CrossRef]
- Chang, J.-Y.; Tsai, C.-C. Wave forces on a partially reflecting wall by oblique Bragg scattering with porous breakwaters over uneven bottoms. J. Mar. Sci. Eng. 2022, 10, 409. [Google Scholar] [CrossRef]
- Kirby, J.T.; Anton, J.P. Bragg Reflection of Waves by Artificial Bars. In Coastal Engineering 1990; ASCE: Reston, VA, USA, 1991; pp. 757–768. [Google Scholar]
- Tsai, C.-C.; Lin, Y.-T.; Chang, J.-Y.; Hsu, T.-W. A coupled-mode study on weakly viscous Bragg scattering of surface gravity waves. Ocean Eng. 2016, 122, 136–144. [Google Scholar] [CrossRef]
- Mei, C.C. Resonant reflection of surface water waves by periodic sandbars. J. Fluid Mech. 1985, 152, 315–335. [Google Scholar] [CrossRef]
- Dalrymple, R.A.; Kirby, J.T. Water waves over ripples. J. Waterw. Port Coast. Ocean. Eng. 1986, 112, 309–319. [Google Scholar] [CrossRef]
- Tsai, C.-P.; Chen, H.-B.; Hsu, H.T. Estimation of wave height deformation in surf zone. J. Harb. Technol. 1995, 10, 93–111. [Google Scholar]
- Nagayama, S. Study on the Change of Wave Height and Energy in the Surf Zone. Bachelor’s Thesis, Yokohama National University, Yokohama, Japan, 1983. [Google Scholar]
- Sancho, F.; Mendes, P.; Carmo, J.; Neves, M.; Tomasicchio, G.; Archetti, R.; Damiani, L.; Mossa, M.; Rinaldi, A.; Gironella, X. Wave Hydrodynamics over a Barred Beach. In Ocean Wave Measurement and Analysis 2001; ASCE: Reston, VA, USA, 2002; pp. 1170–1179. [Google Scholar]
- Tonelli, M.; Petti, M. Simulation of wave breaking over complex bathymetries by a Boussinesq model. J. Hydraul. Res. 2011, 49, 473–486. [Google Scholar] [CrossRef]
- D’Alessandro, F.; Tomasicchio, G.R. The BCI criterion for the initiation of breaking process in Boussinesq-type equations wave models. Coast Eng. 2008, 55, 1174–1184. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, J.-Y.; Tsai, C.-C. Step Approximation on Water Wave Breaking and Dissipation over Variable Bottoms across the Surf Zone. J. Mar. Sci. Eng. 2023, 11, 62. https://doi.org/10.3390/jmse11010062
Chang J-Y, Tsai C-C. Step Approximation on Water Wave Breaking and Dissipation over Variable Bottoms across the Surf Zone. Journal of Marine Science and Engineering. 2023; 11(1):62. https://doi.org/10.3390/jmse11010062
Chicago/Turabian StyleChang, Jen-Yi, and Chia-Cheng Tsai. 2023. "Step Approximation on Water Wave Breaking and Dissipation over Variable Bottoms across the Surf Zone" Journal of Marine Science and Engineering 11, no. 1: 62. https://doi.org/10.3390/jmse11010062
APA StyleChang, J.-Y., & Tsai, C.-C. (2023). Step Approximation on Water Wave Breaking and Dissipation over Variable Bottoms across the Surf Zone. Journal of Marine Science and Engineering, 11(1), 62. https://doi.org/10.3390/jmse11010062







