Numerical Simulation on the Local Scour Processing and Influencing Factors of Submarine Pipeline
Abstract
1. Introduction
2. Numerical Methods
2.1. Continuity Equations
2.2. The Turbulence Model
2.3. Sediment Transport Model
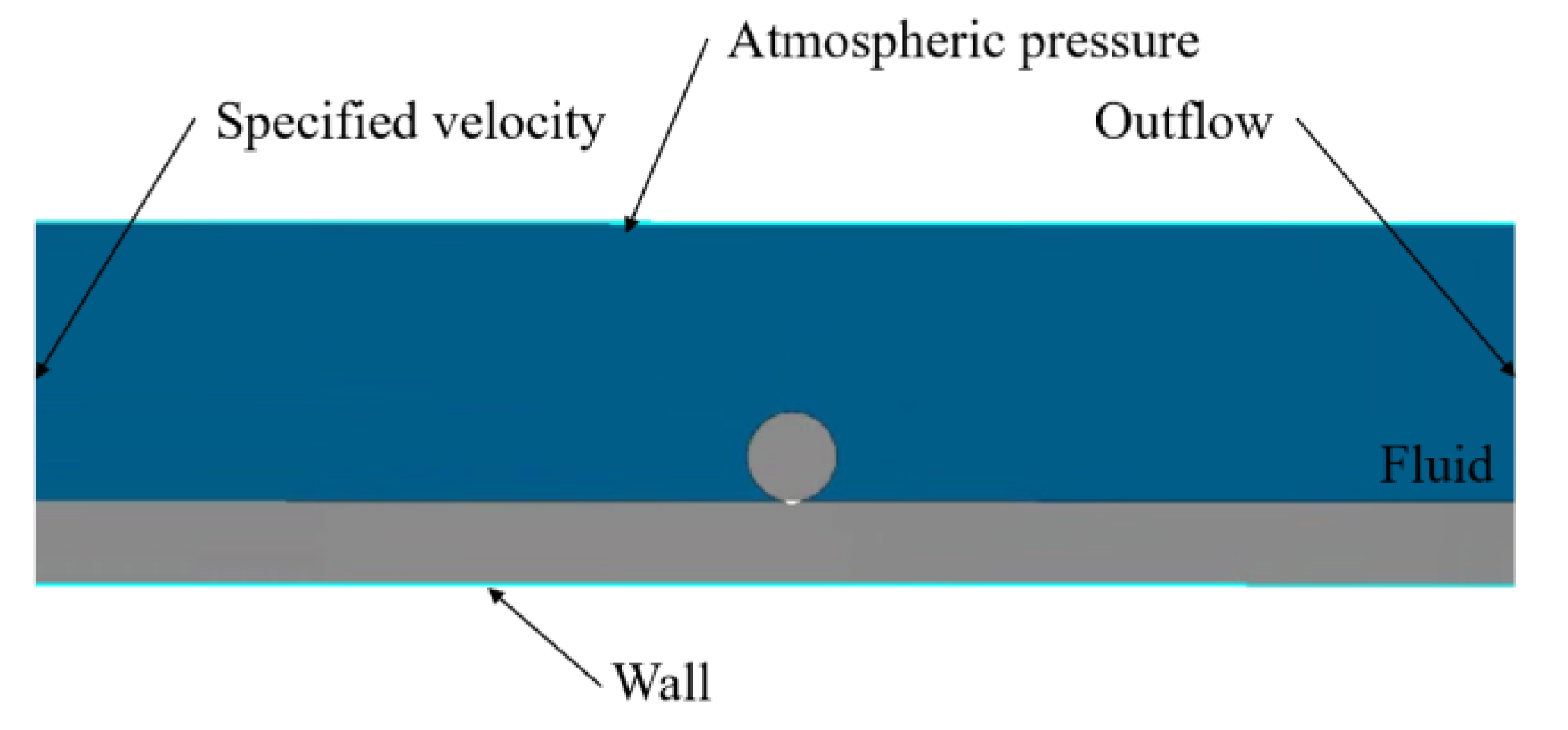
2.4. Boundary Conditions
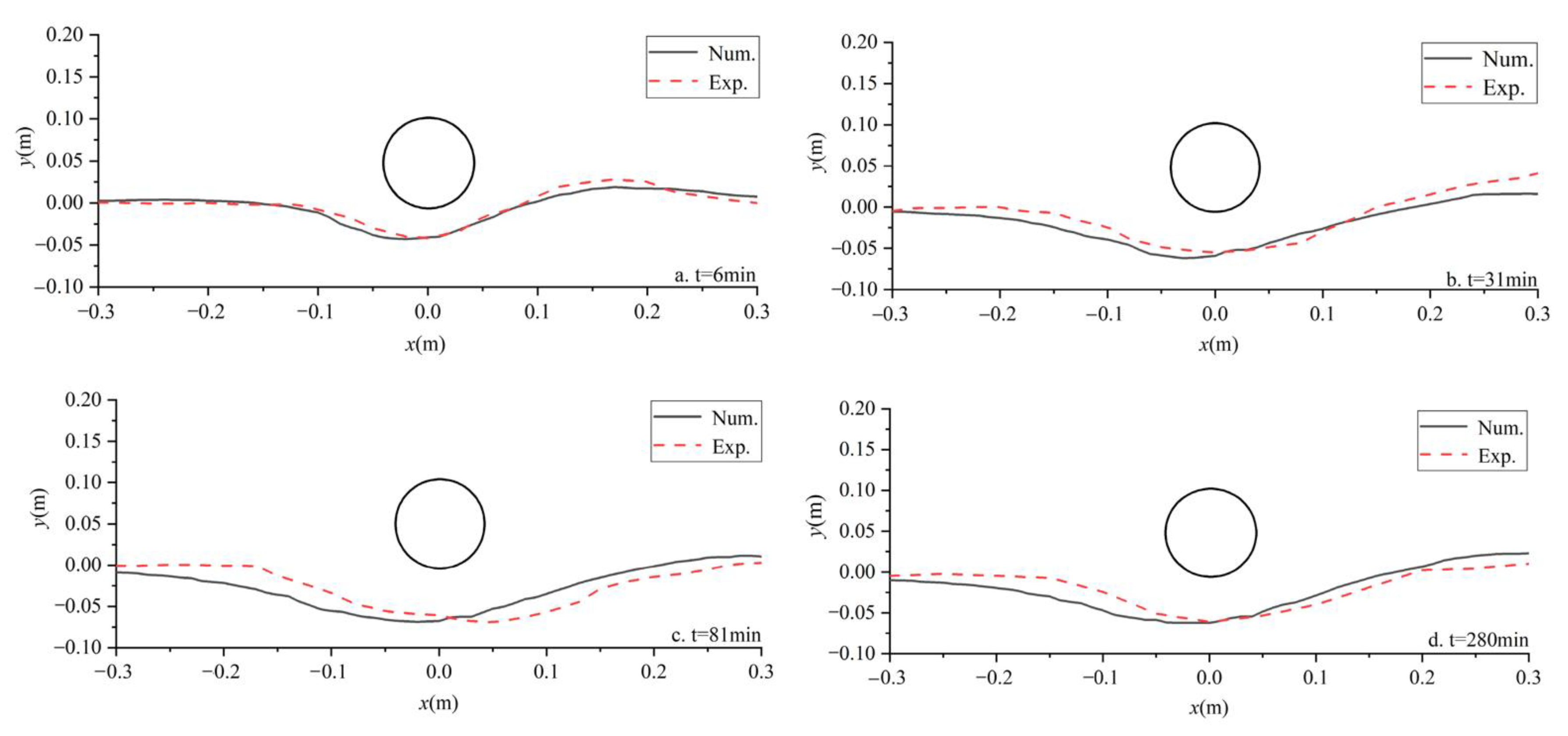
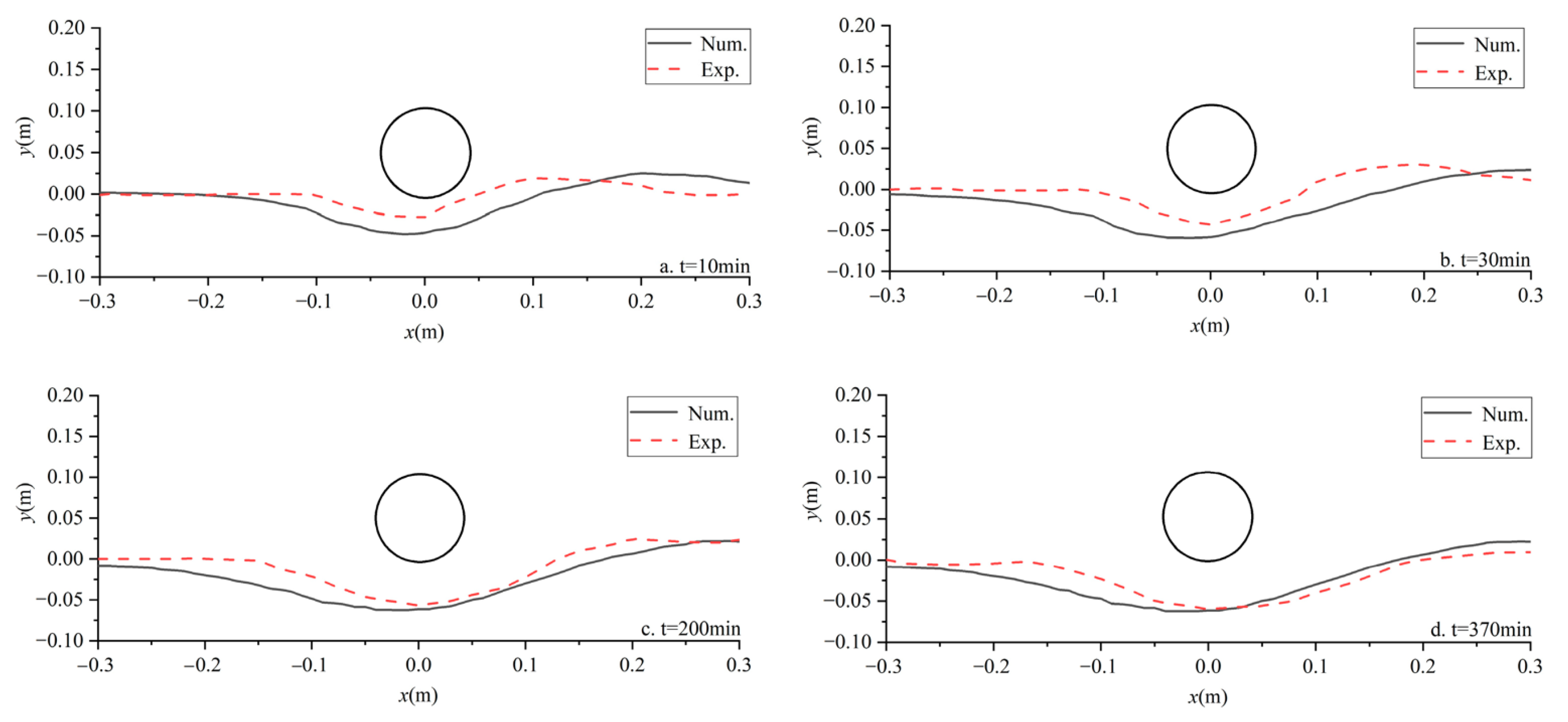
3. Validation Models
4. Numerical Results and Discussion
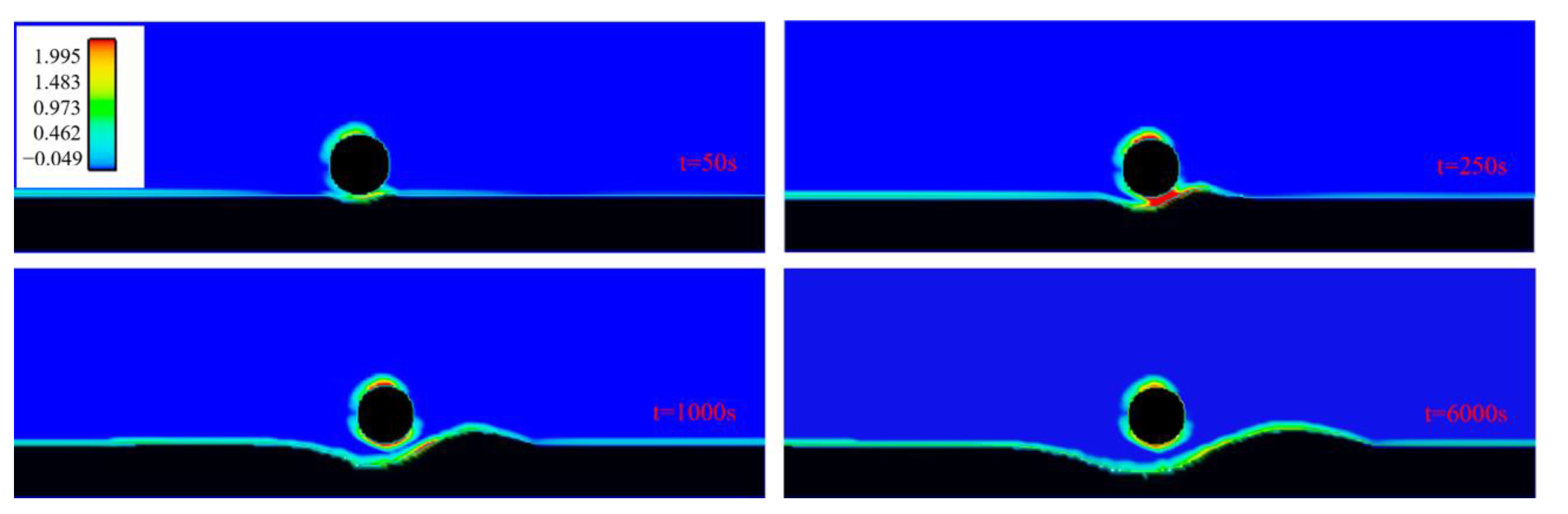
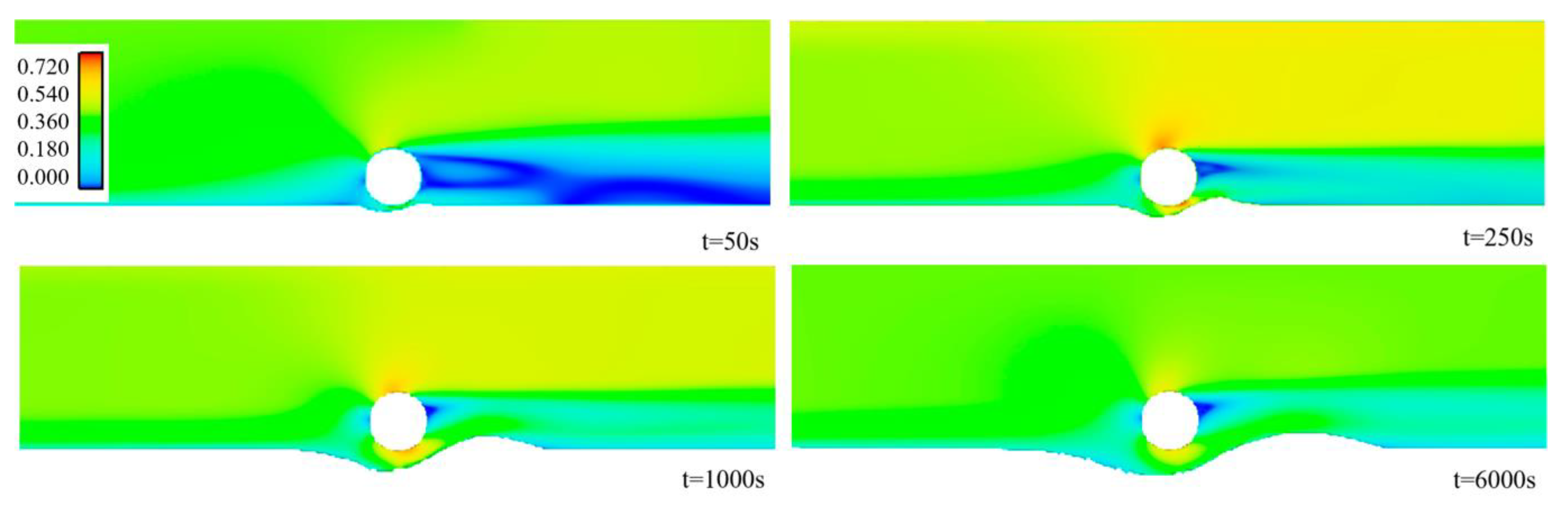
4.1. Process of Scour
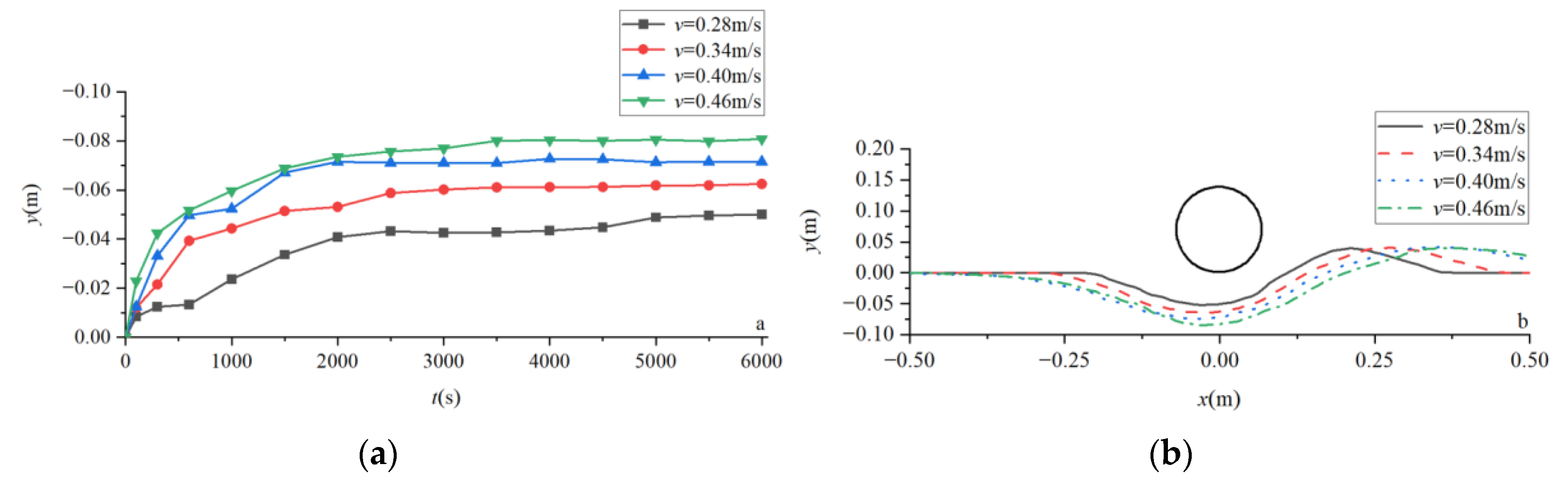
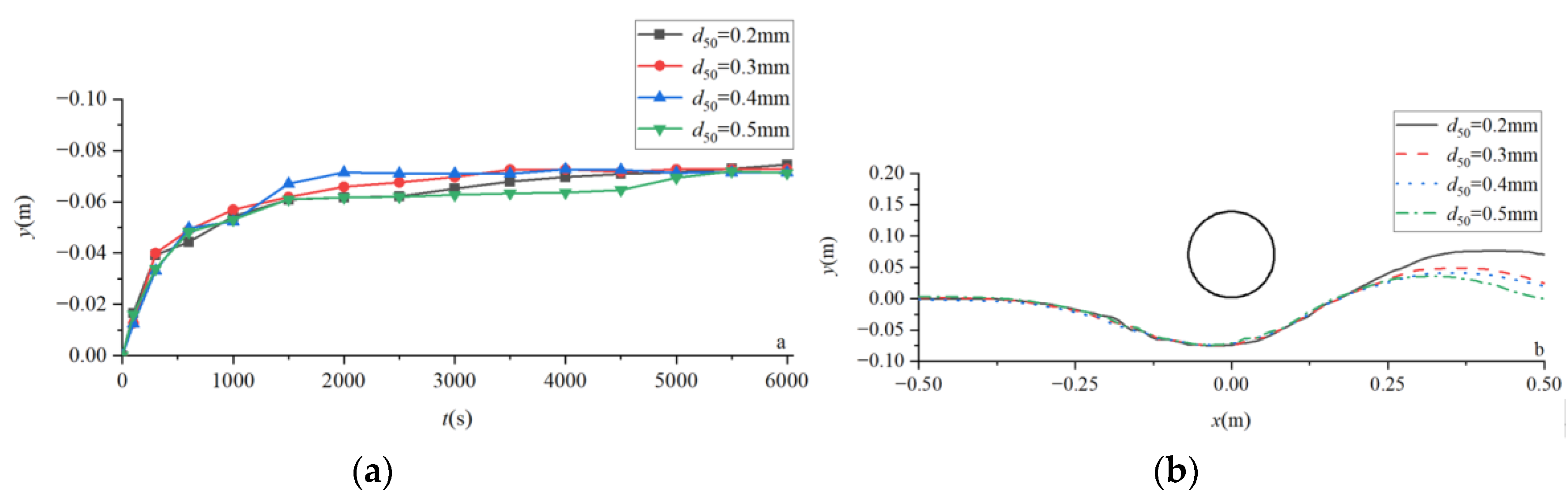
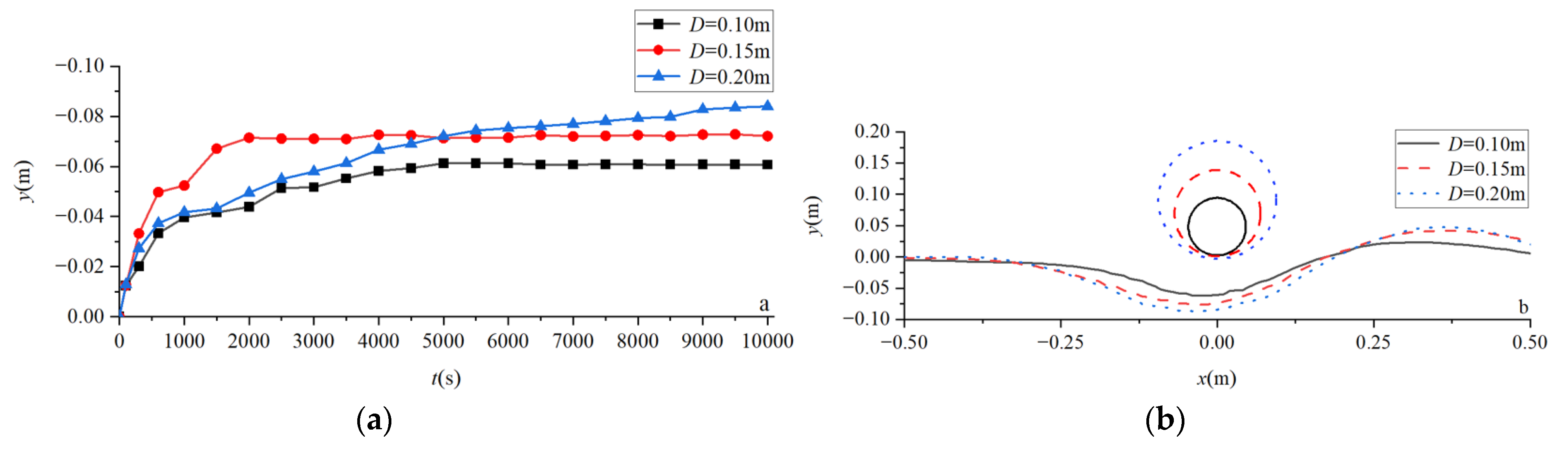
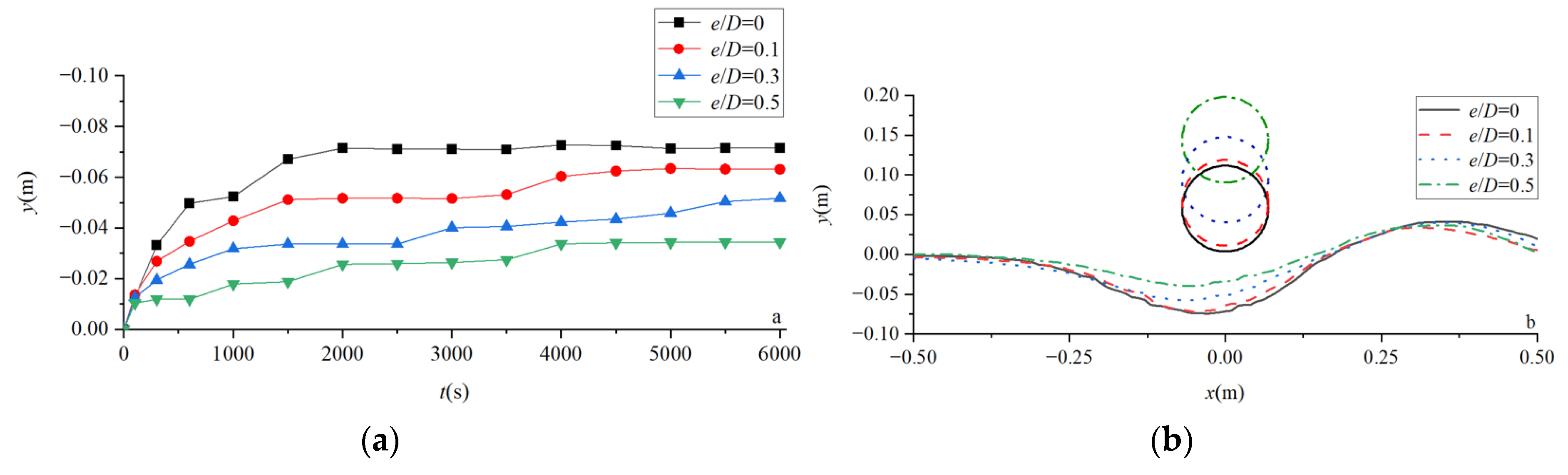
4.2. Scour Depth and Terrain under the Influence of Multiple Factors
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kjeldsen, S.P.; Gjorsvik, O.; Bringaker, K.G.; Jacobsen, J. Local scour near offshore pipelines. In Proceedings of the Second International Conference on Port and Ocean Engineering Under Arctic Conditions (POAC), Reykjavik, Iceland, 27–30 August 1973. Paper Available Only as Part of the Complete. [Google Scholar]
- Ibrahim, A.; Nalluri, C. Scour prediction around marine pipelines. In Proceedings of the 5th International offshore mechanics and arctic engineering Symposium, Tokyo, Japan, 13–18 April 1986; pp. 679–684. [Google Scholar]
- Mao, Y. The Interaction between a Pipeline and an Erodible Bed; Series Paper; Technical University of Denmark: Lyngby, Denmark, 1987. [Google Scholar]
- Chiew, Y.M. Mechanics of local scour around submarine pipelines. J. Hydraul. Eng. 1990, 116, 515–529. [Google Scholar] [CrossRef]
- Li, F.; Cheng, L. Numerical model for local scour under offshore pipelines. J. Hydraul. Eng. 1999, 125, 400–406. [Google Scholar] [CrossRef]
- Brørs, B. Numerical modeling of flow and scour at pipelines. J. Hydraul. Eng. 1999, 125, 511–523. [Google Scholar] [CrossRef]
- Moncada-M, A.T.; Aguirre-Pe, J. Scour below pipeline in river crossings. J. Hydraul. Eng. 1999, 125, 953–958. [Google Scholar] [CrossRef]
- Liang, D.; Cheng, L.; Li, F. Numerical modeling of flow and scour below a pipeline in currents: Part II. Scour simulation. Coast. Eng. 2005, 52, 43–62. [Google Scholar] [CrossRef]
- Dey, S.; Singh, N.P. Clear-water scour below underwater pipelines under steady flow. J. Hydraul. Eng. 2008, 134, 588–600. [Google Scholar] [CrossRef]
- Cheng, L.; Zhao, M. Numerical model for three-dimensional scour below a pipeline in steady currents. In Proceedings of the 5th International Conference on Scour and Erosion (ICSE-5), San Francisco, CA, USA, 7–10 November 2010; pp. 482–490. [Google Scholar]
- Etemad-Shahidi, A.; Yasa, R.; Kazeminezhad, M.H. Prediction of wave-induced scour depth under submarine pipelines using machine learning approach. Appl. Ocean. Res. 2011, 33, 54–59. [Google Scholar] [CrossRef]
- Azamathulla, H.; Zakaria, N.A. Prediction of scour below submerged pipeline crossing a river using ANN. Water Sci. Technol. 2011, 63, 2225–2230. [Google Scholar] [CrossRef] [PubMed]
- Najafzadeh, M.; Barani, G.A.; Azamathulla, H.M. Prediction of pipeline scour depth in clear-water and live-bed conditions using group method of data handling. Neural Comput. Appl. 2014, 24, 629–635. [Google Scholar] [CrossRef]
- Zhao, M.; Vaidya, S.; Zhang, Q.; Cheng, L. Local scour around two pipelines in tandem in steady current. Coast. Eng. 2015, 98, 1–15. [Google Scholar] [CrossRef]
- Zhang, Q.; Draper, S.; Cheng, L.; Zhao, M.; An, H. Experimental study of local scour beneath two tandem pipelines in steady current. Coast. Eng. J. 2017, 59, 1750002. [Google Scholar] [CrossRef]
- Zhao, E.; Shi, B.; Qu, K.; Dong, W.; Zhang, J. Experimental and numerical investigation of local scour around submarine piggyback pipeline under steady current. J. Ocean. Univ. China 2018, 17, 244–256. [Google Scholar] [CrossRef]
- Ajdehak, E.; Zhao, M.; Cheng, L.; Draper, S. Numerical investigation of local scour beneath a sagging subsea pipeline in steady currents. Coast. Eng. 2018, 136, 106–118. [Google Scholar] [CrossRef]
- Zang, Z.; Tang, G.; Chen, Y.; Cheng, L.; Zhang, J. Predictions of the equilibrium depth and time scale of local scour below a partially buried pipeline under oblique currents and waves. Coast. Eng. 2019, 150, 94–107. [Google Scholar] [CrossRef]
- Parsaie, A.; Haghiabi, A.H.; Moradinejad, A. Prediction of scour depth below river pipeline using support vector machine. KSCE J. Civ. Eng. 2019, 23, 2503–2513. [Google Scholar] [CrossRef]
- Hu, D.; Tang, W.; Sun, L.; Li, F.; Ji, X.; Duan, Z. Numerical simulation of local scour around two pipelines in tandem using CFD–DEM method. Appl. Ocean. Res. 2019, 93, 101968. [Google Scholar] [CrossRef]
- Hu, K.; Bai, X.; Zhang, Z. Prediction model of pipeline scour depth based on BP neural network optimized by genetic algorithm. In Proceedings of the 30th International Ocean and Polar Engineering Conference, Virtual, 11–16 September 2020; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2020. [Google Scholar]
- Li, Y.; Ong, M.C.; Fuhrman, D.R.; Larsen, B.E. Numerical investigation of wave-plus-current induced scour beneath two submarine pipelines in tandem. Coast. Eng. 2020, 156, 103619. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B. Flow-3D User’s Manual; Flow Science Inc.: Santa Fe, NM, USA, 1988; p. 107. [Google Scholar]
- Soulsby, R.L. Dynamics of marine sands: A manual for practical applications. Oceanogr. Lit. Rev. 1997, 9, 947. [Google Scholar]
- Mastbergen, D.R.; van Den Berg, J.H. Breaching in fine sands and the generation of sustained turbidity currents in submarine canyons. Sedimentology 2003, 50, 625–637. [Google Scholar] [CrossRef]
- Meyer-Peter, E.; Müller, R. Formulas for bed-load transport. In IAHSR 2nd Meeting, Stockholm, Appendix 2; IAHR: Madrid, Spain, 1948. [Google Scholar]


| Total number of grids | 41,000 | 52,000 | 67,600 |
| Scour depth | 0.0642 m | 0.0621 m | 0.0618 m |
| Time | 75,200 s | 88,490 s | 124,270 s |
| Parameters | v | D | d50 | e/D | ρ | ρs |
|---|---|---|---|---|---|---|
| Value | 0.4 m/s | 0.15 m | 0.4 mm | 0 | 1000 kg/m3 | 2650 kg/m3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, K.; Bai, X.; Vaz, M.A. Numerical Simulation on the Local Scour Processing and Influencing Factors of Submarine Pipeline. J. Mar. Sci. Eng. 2023, 11, 234. https://doi.org/10.3390/jmse11010234
Hu K, Bai X, Vaz MA. Numerical Simulation on the Local Scour Processing and Influencing Factors of Submarine Pipeline. Journal of Marine Science and Engineering. 2023; 11(1):234. https://doi.org/10.3390/jmse11010234
Chicago/Turabian StyleHu, Ke, Xinglan Bai, and Murilo A. Vaz. 2023. "Numerical Simulation on the Local Scour Processing and Influencing Factors of Submarine Pipeline" Journal of Marine Science and Engineering 11, no. 1: 234. https://doi.org/10.3390/jmse11010234
APA StyleHu, K., Bai, X., & Vaz, M. A. (2023). Numerical Simulation on the Local Scour Processing and Influencing Factors of Submarine Pipeline. Journal of Marine Science and Engineering, 11(1), 234. https://doi.org/10.3390/jmse11010234







