Abstract
Hull form optimization becomes prone to the curse of dimensionality as the number of design variables increases. The traditional sensitivity analysis method requires massive computational fluid dynamics (CFD) computations and analyzing the effects of all variables on the output; thus, it is extremely time-consuming. Considering this, the development of a rapid and effective dimensionality reduction method is particularly important. The Karhunen–Loève (K–L) transform method projects data from a high-dimensional space onto a low-dimensional space in the direction of the eigenvectors corresponding to large-variance eigenvalues. It extracts the principal components that represent the hull offset information to represent the hull geometric characteristics by analyzing the relationship between the variables in the sample offset matrix. The geometric information matrices of new hull forms can be rapidly reconstructed from the principal components. Compared with direct optimization methods, fewer variables are used to control the deformation of the hull form from the perspective of geometric deformation, avoid a large number of CFD calculations, and improve the efficiency of optimization. This study examined the relevant K–L matrix solution methods and the corresponding hull form reconstruction methods and proposed eigenvalue-based hull form reconstruction equations. The K–L transform method was combined with a previously developed multidisciplinary platform for a comprehensive optimization of ship hydrodynamic performance for hull form optimization, and its effectiveness was verified by using it to optimize DTMB 5415. The results showed that the K–L transform–based dimensionality reduction method significantly reduces the time consumption of optimization while maintaining an acceptable optimization performance.
1. Introduction
With the rapid development of computer technology, computational fluid dynamics (CFD) has been significantly advancing. Ship designers have introduced optimization technology into ship design and have combined it with CFD technology to develop a CFD-based method for automatic hull form optimization. The CFD method substantially reduces the time and economic costs compared with a ship model test. However, for complex optimization problems or scenarios with many design variables, it can have a very high computation cost and even lead to the curse of dimensionality. Therefore, effectively reducing the number of design variables and the dimensionality of the design space is a major problem in hull form design optimization.
Currently, the above problem is solved mainly using the sensitivity analysis (SA) method. The SA method can qualitatively or quantitatively assess the effects of the input variables on the output objective function. Cheng et al. [1] proposed an uncertainty and sensitivity analysis framework for ship motion data, in which the sensitivity and uncertainty of the samples or weights generated by an artificial-neural-network-based surrogate model are analyzed. Hu et al. [2] adjusted an airfoil curve using control points and a free-form deformation technique and reduced the dimensionality of control variables by SA. Guan et al. [3] used an SA procedure to estimate the effects of the values assigned to the key calculation parameters of a fully parametric hull form optimization algorithm on the calculation process and results. Hamed [4] numerically optimized a trimaran hull form using an optimization platform, with the total resistance and the propeller intake flow defined as the study objectives. Moreover, information about highly significant regions of a hull was obtained by surface SA based on an adjoint solver. Jung [5] introduced examples of SA of the effects on the added resistance and speed loss in waves caused by the variations in ship dimensions. SA has been proven to be a feasible method for dimensionality reduction, and variance-based SA has been widely used to determine variables that are unimportant for this purpose. Therefore, Liu et al. [6] implemented variance-based SA in a hull form optimization model and identified a variable that did not affect dimensionality reduction. Guan et al. [7] developed an automatic calculation framework for the resistance of a small-waterplane-area twin hull at different speeds, for which a fully parametric model was established to realize automatic geometric transformation. They also performed an SA of all parameters to the resistance and a correlation analysis between the design variables and the resistance, including the calculation and examination of the correlation coefficients. Jeon et al. [8] identified important hull form parameters and estimated their optimal values that satisfied the required intercept time of mission competence and the turning rate of a specific underwater vehicle based on SA. Coppedè et al. [9] proposed a computational framework for the hydrodynamic shape optimization of complex hull forms and applied it to improve the calm-water performance of the KRISO Container Ship. They also performed a preliminary SA of the mesh size to reduce the computational burden of the CFD solver. Fu et al. [10] proposed a multiobjective optimization method for autonomous underwater gliders based on the fast elitist nondominated sorting genetic algorithm (NSGA-II) and performed an SA of the variables. In hull form optimization, models of the input variables and performance indicators are established to compare the effects of the variables on the ship performance. This enables identification of the important variables and elimination of the variables with the minimum effects on the performance, to realize dimensionality reduction.
SA requires calculation of the effects of all variables on the output and, thus, has a high computational cost. Different from SA, the Karhunen–Loève (K–L) transform reduces data dimensionality by projecting data in the direction of the eigenvectors corresponding to large eigenvalues based on an analysis of the data matrix. K–L transform–based dimensionality reduction needs to consider only the relationships between the variables in the sample data matrix and does not require calculating the effects of the variables on the objective function.
Considering that K–L and directional seismic wave methods can extract target signals and suppress random noise, Yue et al. [11] used these methods to solve the problem of difficulty in the separation of weak effective signals. Fan et al. [12] developed a spatiotemporal model based on the K–L decomposition, a multilayer perceptron, and a long short-term memory network for estimating temperature distributions by a three-step procedure. Ahuja et al. [13] suggested that a large-sized discrete Fourier transform of a colored random process approximates the behavior of the K–L transform in terms of achieving approximate decorrelation between frequency-domain terms. Trudu et al. [14] proposed a new method for computing the K–L transform for application to complex voltage data for the detection and noise reduction of astronomical signals. Siripatana et al. [15] applied a generalized K–L expansion that incorporated the construction of a reference basis of spatial modes and a coordinate transformation to the prior field. Reed and Roberts [16] applied the K–L transform to a 44-group version of the 2-D C5G7 benchmark problem. Allaix and Carbone [17] proposed a method for the discretization of random fields by combining a K–L series expansion and the finite element method. Azevedo et al. [18] studied the numerical approximation of a homogeneous Fredholm integral equation of the second kind associated with the K–L expansion of Gaussian random fields. Liu et al. [19] proposed to encode the third spectral information with an adaptive K–L transform and mathematically proved that interspectral correlations are preserved in two-dimensional randomly encoded spatial information. Ai [20] obtained the K–L expansion and distribution identity for a demeaned stationary Ornstein–Uhlenbeck process and applied them to the small-deviation asymptotic behavior of the L2 norm and Laplace transform of the process. Chowdhary and Najm [21] introduced a Bayesian K–L expansion procedure that allows developing a probabilistic model based on the principal components and accounts for the inaccuracies due to a limited sample size. Feng et al. [22] suggested that a K–L representation of a target random medium can be efficiently estimated by projecting reconstructed samples onto the K–L basis. Diez et al. [23,24,25] elaborated the mathematical principle behind the K–L transform and applied it to the optimization of the David Taylor Model Basin (DTMB) 5415 hull form for the first time. Using control points as the design variables based on a free-form deformation technique, they reduced the initial number of design variables from 29 to 4 using the K–L transform. Concurrently, 95% variability of the original design space was retained. In addition, the convergence speed was improved while achieving optimization results approximate to those without dimensionality reduction.
In hull form optimization, the dimensionality of the hull form geometric information matrix can be reduced using the K–L transform to extract several principal components to represent the geometric characteristics of the full shape. This allows for rapid reconstruction of the geometric information matrix of a new hull form and the control of hull form variability using a few variables from the perspective of geometric transformation. Consequently, complex CFD computations are avoided, and the time cost is reduced.
The remainder of this paper is structured as follows: Section 1 presents the mathematical principle, derivation, and geometric implications of the K–L transform and the detailed steps and procedure of using it to reduce dimensionality. Section 2 describes the methods for solving the eigenvalues and eigenvectors of the covariance matrices. Section 3 discusses the methods for obtaining the eigenvalues of a matrix. Section 4 proposes a K–L transform–based method for hull form reconstruction, which serves as the basis for applying the K–L transform to the geometric transformation of a hull form. Section 5 presents the multidisciplinary platform developed for a comprehensive optimization of ship hydrodynamic performance and its application to the optimization of the DTMB 5415 hull form. Section 6 summarizes this study and provides an outlook for future research.
2. K–L Transform Method
2.1. Basic Principle of K–L Transform
Harold [26,27,28] proposed the K–L transform, by which discrete signals are transformed into a series of uncorrelated coefficients. The K–L transform describes a sample using fewer features, thereby reducing the dimensionality of the feature space. Its most salient advantage is decorrelation, and it is the best transform in terms of the mean square error (MSE). Its mathematical definition is as follows.
For a discrete case, a uniform sampling is performed on x(t) in interval a ≤ t ≤ b; thus, x can be expressed using the following vector form:
x is expanded using a system of orthonormal vectors as follows:
x is estimated with a finite series d as follows:
Thus, the MSE is
because ,
Setting yields
When the orthogonality condition is satisfied, the following equations can be obtained using the Lagrange multiplier method:
Thus, it can be concluded that when x is expanded in the eigenvector direction of matrix Ψ, the MSE of truncation reaches the minimum value. When x is approximated with d number of uj, the MSE of truncation is
where λj represents the eigenvalues of matrix Ψ.
Thus, the MSE of truncation when x is expanded using the eigenvectors corresponding to the largest d number of eigenvalues of the matrix is smaller than that from the expansion of x using d coordinates in any other orthogonal coordinate system. The percentage ratio of the sum of the d largest eigenvalues to the sum of all eigenvalues, β, is referred to as the feature contribution rate, to which a threshold is assigned during dimensionality reduction. The orthogonal coordinate system consisting of the d eigenvectors used in the expansion is referred to as the d-dimensional K–L transform coordinate system in the D-dimensional space where x is located. The coefficient for the expansion of x in the K–L coordinate system is referred to as the K–L transform of x.
2.2. K–L Transform–Based Data Dimensionality Reduction Process
The K–L transform represents an orthogonal transform , where vectors are mapped onto vectors and the components of vector Y are uncorrelated, that is,
where is the mean of the original data and C is the covariance matrix of the demeaned data.
The covariance matrix is subjected to eigendecomposition, and the resulting eigenvalues are arranged in a descending order as follows:
where λi represents the eigenvalues and Zi represents the eigenvectors corresponding to λi.
The dimensionality after dimensionality reduction depends on the threshold assigned to β, with a larger threshold leading to a larger retained variance and a smaller MSE. If the predefined threshold is satisfied and the dimensionality of the original matrix can be reduced to K, the threshold of β is defined as
For a transformation matrix A consisting of the eigenvectors corresponding to the largest K eigenvalues, the mapping relationship from X to Y is
Figure 1 shows a flowchart of the dimensionality reduction process using the K–L transform. The detailed steps are as follows:
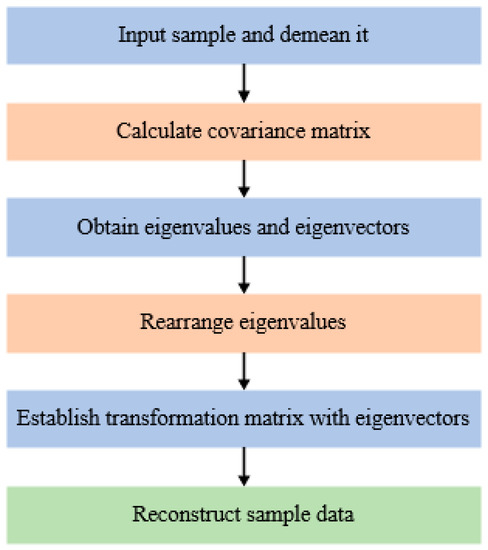
Figure 1.
Flowchart of dimensionality reduction using the K–L transform.
- (1)
- An M × N sample dataset (where M and N are the numbers of samples and feature dimensions, respectively) is demeaned.
- (2)
- The covariance matrix of the demeaned sample data matrix is calculated.
- (3)
- The eigenvalues and eigenvectors of the resulting N × N covariance matrix are calculated.
- (4)
- The eigenvalues are arranged in a descending order, and their corresponding eigenvectors are arranged in a corresponding order.
- (5)
- A threshold is assigned to β. If the ratio of the sum of the K (K < N) largest eigenvalues to the sum of all eigenvalues (feature contribution rate) is larger than the threshold, the dimensionality of the original data can be reduced to K. An N × K transformation matrix is established using the eigenvectors corresponding to the largest K eigenvalues.
- (6)
- An M × K matrix is obtained by multiplying the normalized M × N sample data matrix with the N × K transformation matrix, thereby reducing the dimensionality of the sample data matrix from N to K.
As shown in Figure 1, the core of dimensionality reduction using the K–L transform is obtaining the eigenvalues of the covariance matrix. In the following, we discuss and present the investigation on the methods for solving the eigenvalues and eigenvectors of the covariance matrix and reducing the solution time.
3. Methods for Eigenvalue of Matrix
The core step of the K–L transform method is solving the eigenvalues and eigenvectors of the covariance matrix of the sample data matrix. The methods for obtaining the eigenvalues of matrices mainly include the Jacobi iteration and rapid principal component analysis (PCA) methods, as described below.
3.1. Jacobi Iteration Method
Low-order linear equations, such as AX = B, are typically solved using the pivot elimination method. However, engineering problems frequently involve computer-aided solutions of large sparse matrix equations, which need to be obtained using an iterative method. Its major principle is as follows:
Consider the following equations:
where coefficient matrix A is nonsingular and . These equations can be transformed to obtain the following iteration equations:
where x(0) represents the initial vectors and x(k) represents the vectors at the k-th iteration.
The matrix form is as follows: First, the coefficient matrix, A, of the equations is decomposed into three components, that is, A = L + D + U:
where D, L, and U are the diagonal, lower triangular, and upper triangular matrices, respectively.
Thus, the following matrix formulation can be derived:
which can be rearranged as
which can be simplified as
Thus, the Jacobi iteration equations can be expressed in the following matrix form:
From the above process, the Jacobi iteration method involves a simple calculation process, requiring only the multiplication of matrices in each iteration. However, it has remarkable disadvantages, including a low convergence speed and a large computer memory requirement.
3.2. Rapid PCA Method
PCA requires the calculation and eigendecomposition of the covariance matrix of the input sample data to obtain its eigenvalues and eigenvectors. For a sample data matrix X of size n × d (where n and d are the numbers of samples and feature dimensions, respectively), its covariance matrix S is a d × d square matrix. Extremely complex calculations are required when d is large. The rapid PCA algorithm solves the transposed matrix of the covariance matrix, instead of directly solving the covariance matrix. The dimensionality of the covariance matrix of the transposed matrix depends on the number of samples. When the number of feature dimensions is much larger than the number of samples, the transposed matrix can be very easily solved using the rapid PCA algorithm.
The derivation of the rapid PCA algorithm is as follows: For an n × d matrix of a sample dataset Z with the number of samples, n, much smaller than the number of feature dimensions, d, the covariance matrix is
The transposed matrix of the covariance matrix is
S and R have the same nonzero eigenvalues:
Multiplying both sides of the above equation with ZT yields
Thus, the eigenvectors of S are ZTv.
From the above equations, the eigenvalues and eigenvectors of the original covariance matrix can be obtained by solving those of its transposed matrix.
From the principles of the two methods described above, the Jacobi iteration method is typically suitable for obtaining computer-aided eigenvalues of matrices. It can deal with moderate computational complexity; however, it requires a long solution time in cases of massive computations. The rapid PCA algorithm is suitable when the number of feature dimensions is much larger than the number of samples. By solving the feature matrix of the transposed matrix, it transforms a high-dimensional matrix to be solved into a low-dimensional matrix, thereby improving the computational efficiency.
We previously developed a multidisciplinary platform for a comprehensive optimization of ship hydrodynamic performance (SHIPMDO-WUT) using a radial basis function (RBF)– based interpolation method [29,30,31,32,33] for hull form modification. In this method, the number of discrete points on a hull surface usually reaches thousands, resulting in tens of thousands of dimensions of covariance matrix, making the direct eigendecomposition of the covariance matrix considerably difficult. Because the number of feature dimensions is much larger than the number of samples, the covariance matrix was solved using the rapid PCA method, thereby substantially reducing the dimensionality by eigendecomposition and improving the solution efficiency.
4. K–L Transform–Based Hull Form Reconstruction Method
The core of the K–L transform–based hull form reconstruction method is solving the problem that the design variables in the projected dimensionality-reduced matrix are not points on the hull surface and do not have physical relevance. This problem makes obtaining a new hull form directly by RBF modification impossible. This study developed a transformation-matrix-based method for offset matrix reconstruction that can ensure surface smoothness of the new reconstructed hull form. In the following, the hull form reconstruction process is described, including the presentation of the derivation of its equations and the application of the process to actual cases.
4.1. Hull Form Reconstruction Process
In the K–L transform–based dimensionality reduction, a sample offset matrix of hull forms obtained by varying the original hull form is subjected to dimensionality reduction to obtain projection and eigenvector matrices. Each column of the projection matrix following the dimensionality reduction represents a new design variable, which is a combination of the initial variables and does not correspond to a discrete point on the hull surface. Because the new design variables do not have physical relevance, a new hull form cannot be obtained by surface modification, thus necessitating another method to generate it. The process of generating a new hull form using the new design variables is referred to as hull form reconstruction. Figure 2 shows a flowchart of the hull form reconstruction process. The steps are detailed as follows:
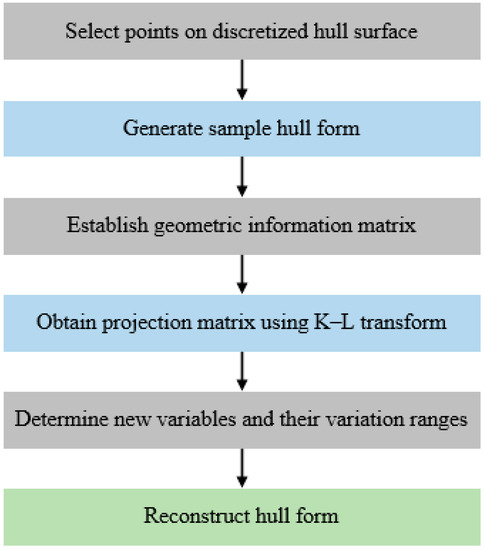
Figure 2.
Flowchart of hull form reconstruction.
- (1)
- Using SHIPMDO-WUT, a hull surface is discretized [29,30,31,32,33], and a certain number of variable points are selected as the design variables.
- (2)
- A certain number of samples are collected using the uniform experimental design method to generate a sample offset matrix and the corresponding hull forms using the RBF-based shape modification method.
- (3)
- For each sample hull form generated, M offset points are selected, and their x-, y-, and z-coordinates are arranged in a geometric information matrix.
- (4)
- The covariance matrix of the demeaned geometric information matrix is calculated using the K–L transform method to obtain its eigenvalues and eigenvectors. The eigenvectors are arranged according to the eigenvalues, and a threshold of β is assigned to generate a transformation matrix. The sample offset matrix is normalized and multiplied with the transformation matrix to produce a projection matrix.
- (5)
- The new design variables in the dimensionality-reduced projection matrix and their respective variation ranges are defined.
- (6)
- Hull form reconstruction is performed using the hull form reconstruction equations to obtain the hull offset matrix and generate the corresponding hull form.
In the hull form reconstruction method, the core problem is the reconstruction of the new offset matrix from the dimensionality-reduced projection matrix. In the following, this core problem is discussed.
N sample hull forms are sampled. For each hull form, M offset points are selected, and their x-, y-, and z-coordinates are arranged as a geometric information matrix, which can be expressed as
The geometric information matrices of the N sample hull forms are used as the basis function. Subsequently, the offset matrix of each hull form is decomposed into a linear combination of several sample hull forms as follows:
The mean of each column is subtracted from the elements in the corresponding column. The geometric characteristics of each demeaned sample hull form can be expressed as
The demeaned geometric information matrices of all sample hull forms can be expressed as
The covariance matrix of the geometric information matrices can be obtained as
The covariance matrix is subjected to eigendecomposition to obtain the eigenvalues and the corresponding eigenvectors as follows:
where λj represents the eigenvalues and uj represents the eigenvectors.
The threshold of β, which determines the dimensionality after dimensionality reduction, is calculated as
The eigenvalues are arranged in a descending order. The eigenvectors corresponding to the first Mp eigenvalues constitute the transformation matrix,
Each geometric information matrix is reconstructed to obtain the offsets of the corresponding reconstructed hull form as follows:
where represents the new design variables, represents the retained eigenvectors, and is the mean geometric information matrix, that is, a matrix consisting of the means of the geometric information of all sample hull forms.
In summary, in the K–L transform/dimensionality reduction–based hull form reconstruction, the offset matrix of a hull form can be obtained using Equation (35). This is possible when the mean geometric information matrix, values of the new design variables, and retained eigenvector matrix (i.e., transformation matrix) are known, thereby generating a new hull form.
4.2. Examples of Hull Form Reconstruction
As shown in Figure 3, the Series 60 hull form was optimized using SHIPMDO-WUT. First, the Series 60 hull surface was discretized. The model consisted of two surfaces, and each surface was discretized in the U and V directions into a 40 × 30 point cloud. As shown in Figure 4, 10 variable points are selected and defined to be variables in the Y-direction. Table 1 lists their respective variation ranges. Using a uniform experimental design, 50 samples were collected, and the surface was varied using the RBF method; consequently, a sample offset matrix of 50 sample hull forms was obtained, with each hull surface represented as a 40 × 30 point cloud. The offset matrix was subjected to dimensionality reduction using the K–L transform procedure, with the threshold of β set as 95%. Accordingly, a total of 180,000 eigenvalues were obtained, which were arranged in a descending order. Except for the first 50 eigenvalues, all eigenvalues were approximately zero. Based on Table 2, the sum of the first 5 eigenvalues is 10.17 and that of the first 50 eigenvalues is 10.61. The first 10 eigenvalues are significant in magnitude, based on Table 3. Figure 5 shows the distribution of the 10 largest eigenvalues. The percentage ratio of the sum of the first 5 eigenvalues to the sum of all eigenvalues is 95.9%, which is higher than the preset threshold (95%), as shown in Figure 6. Thus, the eigenvectors corresponding to the first 5 eigenvalues were selected to constitute the transformation matrix.

Figure 3.
Schematic of a 3D model of Series 60.

Figure 4.
Distributions of variable and fixed points on the Series 60 hull surface (blue: fixed points; red: variable points).

Table 1.
S60 variation ranges of variables.

Table 2.
Five largest eigenvalues.

Table 3.
Ten largest eigenvalues of S60.
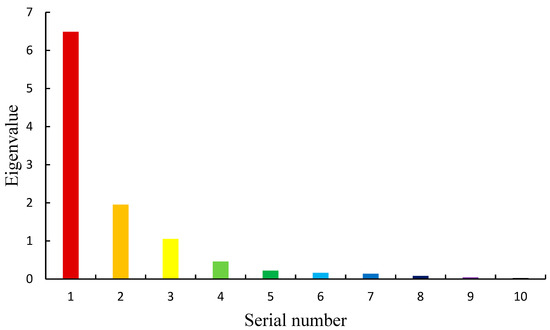
Figure 5.
Distributions of the 10 largest eigenvalues.
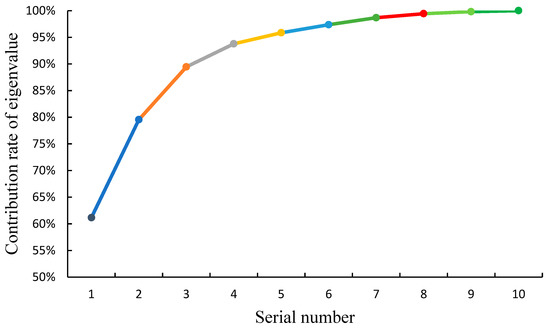
Figure 6.
Contribution rates of the 10 largest eigenvalues.
The hull surface was reconstructed by feeding a random set of new variables into Equation (36). Figure 7, Figure 8 and Figure 9 show the line plans of the reconstructed hull forms.
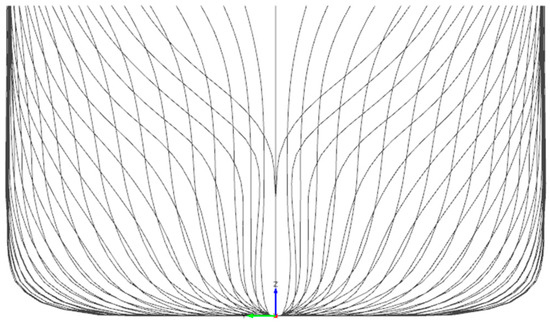
Figure 7.
Line plan of reconstructed hull form KLE-5.
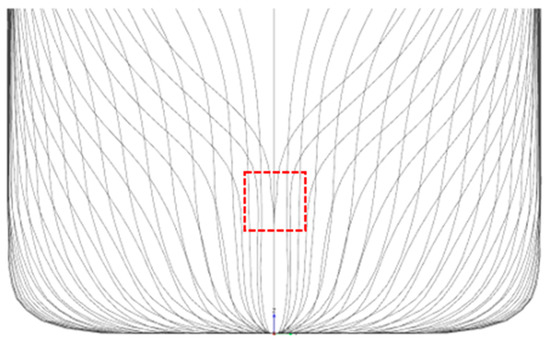
Figure 8.
Line plan of reconstructed hull form KLE-4.
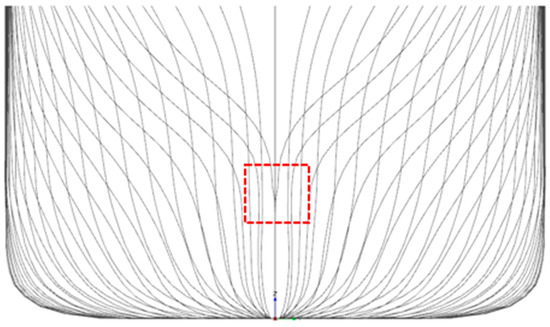
Figure 9.
Line plan of reconstructed hull form KLE-3.
First, the threshold of β for dimensionality reduction was set as 95% by default. The eigenvectors corresponding to the 5 largest eigenvalues were used to constitute the transformation matrix. The reconstructed hull form (KLE-5) had smooth molded lines, indicating that the 5 principal components were adequate to retain most of the geometric information in the original space and, thus, could replace the initial 10 design variables.
When the threshold of β was set as 90%, the eigenvectors corresponding to the 4 largest eigenvalues were used to constitute the transformation matrix. The percentage ratio of the sum of the 4 largest eigenvalues to the sum of all eigenvalues was 94.1%. Figure 8 shows the line plan of the reconstructed hull surface (KLE-4).
When the threshold of β was changed to 85%, the number of eigenvectors retained in the transformation matrix decreased to 3, because the percentage ratio of the sum of the 3 largest eigenvalues to the sum of all eigenvalues was 89.8%. Figure 9 shows the line plan of the hull form reconstructed after dimensionality reduction (KLE-3).
The body plans of KLE-4 and KLE-3 exhibited unsmooth molded lines compared with that of KLE-5. Based on the principle of the K–L transform, a smaller threshold of β leads to a smaller number of retained eigenvalues, a smaller number of corresponding eigenvectors, and a lower dimensionality of the transformation matrix. Consequently, a lower dimensionality of the design space is achieved after dimensionality reduction. In addition, exclusion of eigenvectors corresponding to large eigenvalues leads to an increased MSE and loss of information and, thus, an unsmooth surface of the reconstructed hull form. Thus, an excessively small threshold of β for dimensionality reduction using the K–L transform will lead to retention of an inadequate number of principal components, loss of information, and finally, an unsmooth surface of the reconstructed hull form. For hull form optimization, a 95% threshold of β for dimensionality reduction is safe to ensure that the major geometric information in the design space is retained after dimensionality reduction.
5. Optimization of Wave-Making Resistance Coefficient for DTMB 5415
5.1. Optimized Object
Figure 10 shows a three-dimensional (3D) model of DTMB 5415. Table 4 lists the major parameters of the model. Lwl is the waterline length, Bwl is the maximum waterplane width, Lcb is the longitudinal center of buoyancy (LCB), and T is the draft. Cb is the block coefficient, Cm is the fullest cross-section area, ∇ is the volume of displacement, and Swet is the wetted surface area.

Figure 10.
Schematic of a 3D model of DTMB 5415.

Table 4.
Major parameters of DTMB 5415.
5.2. Description of Optimization Problem
- (1)
- Objective of optimization
The objective of optimization was to minimize the wave-making resistance (WMR) coefficient Cw at Froude number Fr = 0.22.
- (2)
- Setting of optimization variables
The DTMB 5415 hull surface was discretized into a 40 × 30 point cloud. Some points on the bow, centerline of the stern, and deck side line were fixed. Figure 11 shows the locations of the fixed points (blue dots) on the hull surface. Ten points on the bow are selected as variable points Y1–Y10. The red dots in Figure 11 represent the positions of the variable points on the hull surface. The variable points are defined as variable in the Y-direction; that is, their Y-coordinates are the design variables to be optimized. Table 5 summarizes the variation ranges of the variable points.

Figure 11.
Distributions of variable and fixed points (blue: fixed points; red: variable points).

Table 5.
DTMB variation ranges of variables.
- (3)
- Constraint conditions.
Hydrostatic constraint: Constraint on the volume of displacement: .
Constraint on the LCB: .
Geometric constraints: Some points on the stern, deck side line, and centerline were fixed to ensure the ship length, width, and molded depth did not vary.
5.3. CFD Simulation
This study used the commercial software SHIPFLOW as CFD solver. Solve the wave-making resistance coefficient based on potential flow theory. Create a surface mesh using the XMESH module in SHIPFLOW. Then the wave-making resistance coefficient is obtained by surface mesh with fine precision. The mesh distribution is shown in Figure 12.

Figure 12.
SHIPFLOW meshes of DTMB 5415.
The wave resistance coefficient Cw and the friction coefficient Cf are calculated by the formulas of SHIPFLOW and the International Towing Tank Conference (ITTC). The results are then compared with the experimental data. The specific calculation formula is as follows:
Re is the Reynolds number.
The resistance coefficients calculated by SHIPFLOW and ITTC formulas are in good agreement with the experimental data. Therefore, SHIPFLOW meets the requirements of simulation optimization. The data comparison is shown in Figure 13. The relevant SHIPFLOW calculation results are verified in [34,35].
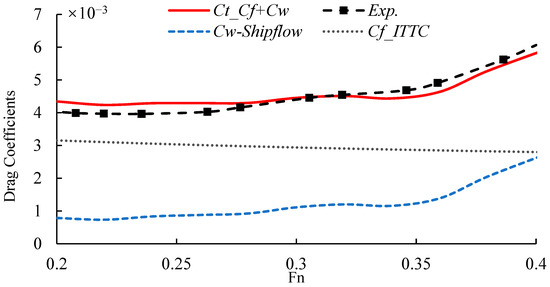
Figure 13.
Data comparison chart of DTMB 5415.
5.4. Optimization Process
The whole optimization process is based on SHIPMDO-WUT, a comprehensive optimization platform for ship hydrodynamic performance developed by our team. The optimization process is shown in Figure 14.
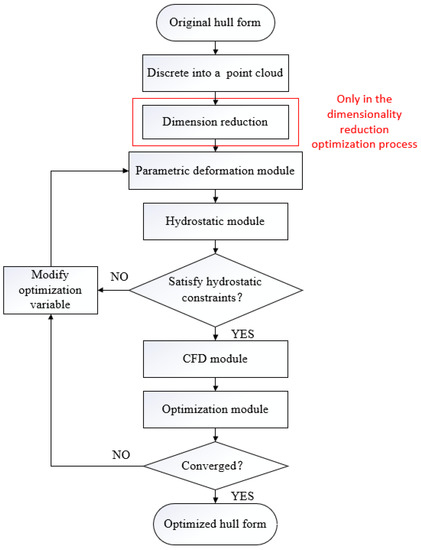
Figure 14.
Optimization process based on the SHIPMDO-WUT platform.
- (1)
- Direct optimization process
First, the original ship is discretized into 40 × 30 spatial point clouds, and the invariant points and variable points are selected according to the ship optimization experience. Then, based on the hull surface deformation method of radial basis function interpolation, the parametric deformation is realized, and the deformed hull is subjected to hydrostatic calculation to select the hull that meets the hydrostatic constraints. Finally, the hull that meets the hydrostatic constraints is imported into the SHIPFLOW software to calculate the wave-making resistance, and the iterative optimization is carried out based on the multiobjective particle swarm optimization (MOPSO) of the optimization algorithm module. If the convergence condition is satisfied, the optimized ship type is obtained, and if the convergence condition is not satisfied, the optimization variables need to be modified.
- (2)
- Dimensionality reduction optimization process
The overall optimization process is consistent with the above. The difference is that the optimization variable in the direct optimization process is the variable point Y-direction coordinate value. However, the optimization variables in the dimension reduction optimization process are based on the optimization variables in the direct optimization process, which are obtained by the K–L transformation method.
5.5. Optimization Results
Direct optimization and optimization using the K–L transform–based dimensionality reduction reconstruction method were performed to compare their optimization performances and efficiencies. The results are discussed below.
- (1)
- Results of direct optimization
Using the hydrodynamic performance optimization platform, the Y-coordinates of the 10 variable points were defined as the design variables, and the hull surface was modified by varying the coordinates using the RBF method. The WMR was calculated using SHIPFLOW. A particle swarm optimization algorithm was used, with both the number of particles and iterations set as 50. The hull surface was directly optimized.
The resulting optimal hull form had a WMR coefficient of Cw = 4.90 × 10−4 and a WMR of 3.328 N, whereas the original shape hull had a WMR coefficient of Cw = 6.83 × 10−4 and a WMR of 4.647 N. Thus, direct optimization decreased the WMR coefficient and WMR by 28.25% and 28.38%, respectively. The optimized hull form had a larger volume of displacement and smaller LCB and wetted surface area than the original hull form. Figure 15 shows the optimization convergence curve. The objective function is observed to converge after approximately 3000 iterations. Table 6 and Table 7 summarize the optimization results and the variations in the hydrostatic parameters, respectively. Figure 16 and Figure 17 compare the line plans of the optimized and original hull forms. The shape of the bulbous bow of the optimized hull form is not markedly different from that of the original hull form. The optimized hull form is concave near the bow part of the design waterline, making the design waterline appear slenderer and changing the geometric shape under the design waterline from V- to U-shaped compared with the original hull form.
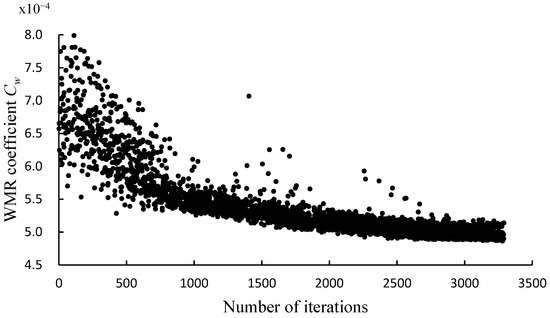
Figure 15.
Optimization convergence curve of direct optimization.

Table 6.
Optimization results of direct optimization.

Table 7.
Comparison of hydrostatic parameters of direct optimization.
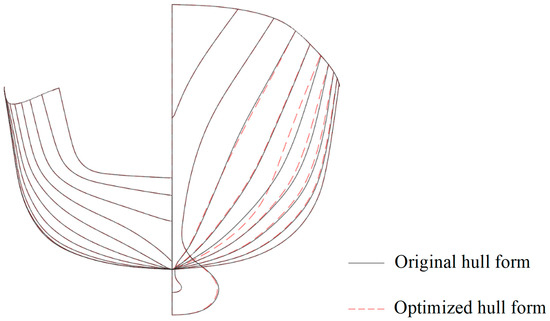
Figure 16.
Comparison of body plan views of direct optimized and original hull forms.

Figure 17.
Comparison of profile views of direct optimized and original hull forms.
- (2)
- Results of dimensionality reduction optimization
The uniform experimental design method was used to sample the 10 design variables (Y1–Y10) described above to obtain 200 samples. The hull form was varied using the RBF method to generate 200 sample hull forms, which were screened to retain only those shapes that satisfied the predefined constraints of the volume of displacement and LCB. The offset information of the sample hull forms that satisfied the constraints was used to generate the offset matrix. A total of 113 sample hull forms satisfied the constraint conditions. The 3D model of DTMB 5415 was divided into three surfaces. Each surface was discretized into a 40 × 30 point cloud, generating a total of 3600 points. Each point was divided into three dimensions of x, y, and z. Thus, the offset matrix for a sample hull form had a size of 113 × 10,800.
The dimensionality was reduced using the K−L transform procedure, with the threshold of β set as 95%. A total of 406,800 eigenvalues were obtained and arranged in a descending order. Except for the first 113 eigenvalues, all eigenvalues were approximately zero. The sum of the first 6 eigenvalues was 2.95 (Table 8), and the sum of the first 113 eigenvalues was 3.065. The first 10 eigenvalues were significant in magnitude (Table 9). The ratio of the sum of the first 6 eigenvalues to the sum of the total eigenvalues was 96.24%, which was larger than the preset threshold of β (95%); this can be seen from Figure 18. Figure 19 shows the distribution of the first 6 eigenvalues. Thus, the eigenvectors corresponding to the first 6 eigenvalues after dimensionality reduction constituted the transformation matrix, which was projected to obtain new design variables P1–P6.

Table 8.
Six largest eigenvalues.

Table 9.
Ten largest eigenvalues.
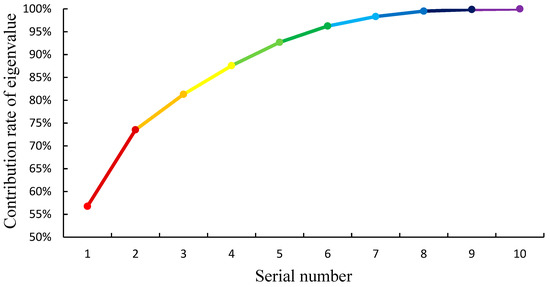
Figure 18.
Contribution rates of eigenvalues.
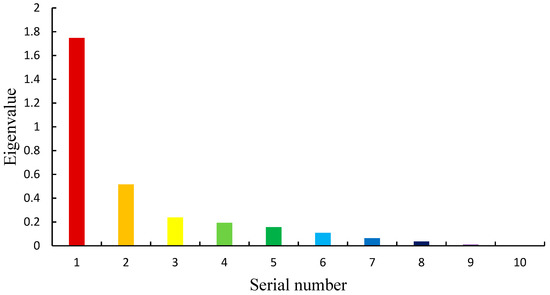
Figure 19.
Distribution of eigenvalues.
The offsets of the reconstructed hull forms were obtained using Equation (35). The original hull form was optimized using the new design variables, P1–P6. The WMR coefficient was calculated using SHIPFLOW. A particle swarm optimization algorithm was used, with both the number of particles and iterations set as 50.
The optimized hull form had a WMR coefficient of Cw = 4.98 × 10−4 and a WMR of 3.394 N, representing decrease of 27.07% and 26.96% compared with those of the original hull form, respectively. The optimized hull form had a larger volume of displacement, larger wetted surface area, and slightly smaller LCB than the original hull form. Figure 20 shows the convergence curve for the WMR optimization. The objective function is observed to converge after approximately 1000 iterations. Table 10 shows the optimization results, and Table 11 compares the hydrostatic parameters of the original and optimized hull forms. Figure 21 and Figure 22 compare the original and optimized hull forms. The bulbous bow shape of the optimized hull form does not vary markedly from that of the original hull form. The optimized hull form is concave near the design waterline at the bow, making the design waterline appear slenderer and changing the geometric shape under the design waterline from V- to U-shaped compared with the original hull form.
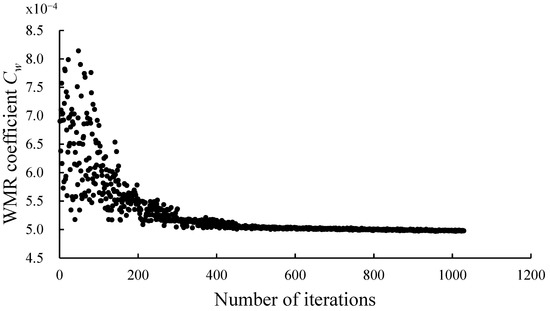
Figure 20.
Optimization convergence curve of dimensionality reduction optimization.

Table 10.
Optimization results of dimensionality reduction optimization.

Table 11.
Comparison of hydrostatic parameters of dimensionality reduction optimization.
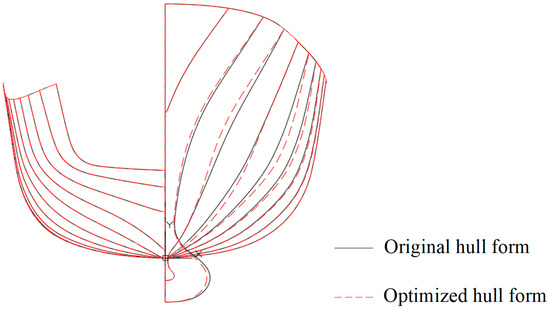
Figure 21.
Comparison of body plan views of dimensionality reduction optimized and original hull forms.

Figure 22.
Comparison of profile views of dimensionality reduction optimized and original hull forms.
- (3)
- Comparison of direct and dimensionality reduction optimization results.
Figure 23 and Figure 24 compare the line plans of the hull forms obtained using the two different optimization methods. The bulbous bow shape obtained from the dimensionality reduction optimization is slightly slenderer than that obtained from the direct optimization. The hull form is concave in the design waterline near the bow, making the design waterline appear slender. Moreover, it is convex in that near the midship, making the design waterline appear fuller and changing the geometric shape under the design waterline from V- to U-shaped. Figure 25, Figure 26 and Figure 27 compare the wave disturbances of the hull forms obtained using the two optimization methods and the original hull form. The original hull form has markedly more scattered waves than the hull forms obtained by both the direct and dimensionality reduction optimizations. However, the hull form obtained by the dimensionality reduction optimization has fewer scattered waves than that by the direct optimization, as indicated by the red ellipses. Figure 28 compares the transverse cross sections of the longitudinal waves at y/lpp = 0.12. Owing to the optimized bow shape, the hull forms obtained by the direct and dimensionality reduction optimizations have low-magnitude wave disturbances around the hull, which are favorable, and markedly low waves at the bow and midship, which decrease the WMR. Table 12 and Table 13 compare the results and time consumptions and the hydrostatic parameters of the hull forms obtained by the two optimizations, respectively. The hull forms obtained by the two optimizations have larger volumes of displacement and LCBs closer to the stern than the original hull form. The optimal hull forms obtained by the two optimizations and the original hull form do not have significantly different wetted surface areas. The hull form obtained by the dimensionality reduction optimization has a larger wetted surface area, a larger volume of displacement, and an LCB closer to the stern than that obtained by the direct optimization. Compared with the WMR coefficient of the original hull form (Cw = 6.833 × 10−4), those of the hull forms obtained by the direct and dimensionality reduction optimizations decrease by 28.25% and 27.07%, respectively. Compared with the WMR of the original hull form, those of the hull forms obtained by the direct and dimensionality reduction optimizations decrease by 28.38% and 26.96%, respectively. Thus, the results of the direct and dimensionality reduction optimizations do not differ significantly.
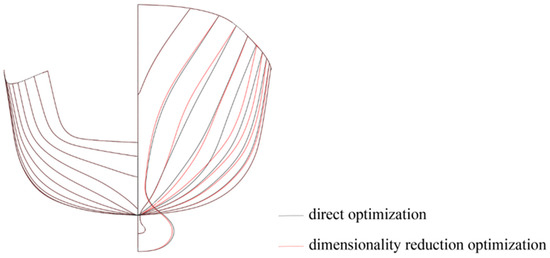
Figure 23.
Comparison of body plan views of hull forms obtained by direct and dimensionality reduction optimizations.

Figure 24.
Comparison of profile views of hull forms obtained by direct and dimensionality reduction optimizations.
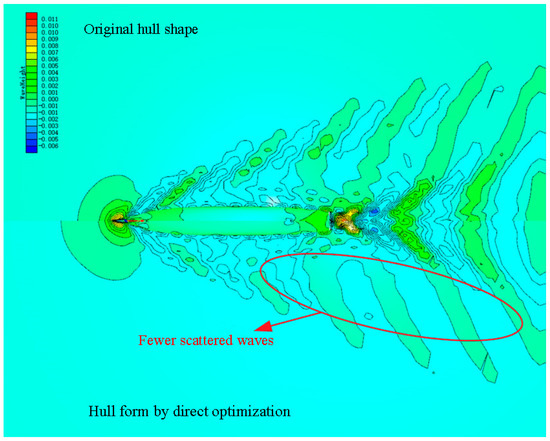
Figure 25.
Comparison of wave disturbances of original hull form and hull form obtained by direct optimization.
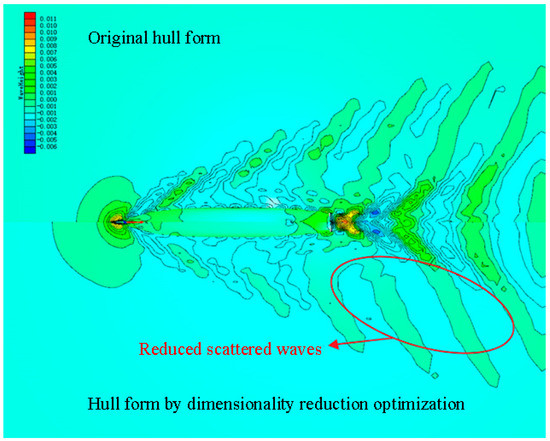
Figure 26.
Comparison of wave disturbances of original hull form and hull form obtained by dimensionality reduction optimization.
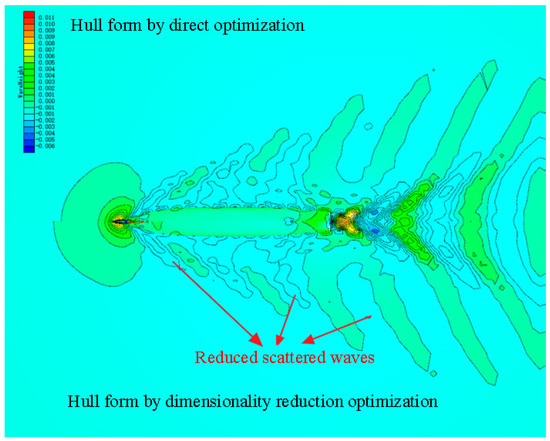
Figure 27.
Comparison of wave disturbances of hull forms obtained by direct and dimensionality reduction optimizations.
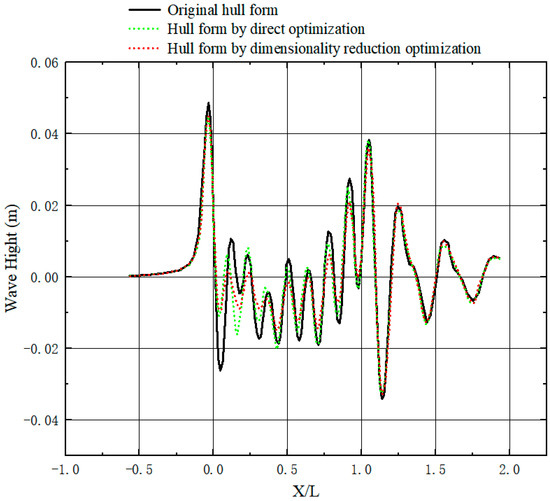
Figure 28.
Comparison of transverse cross sections of longitudinal waves at y/lpp = 0.12.

Table 12.
Comparison of optimization results.

Table 13.
Comparison of hydrostatic parameters of three hull forms.
Both optimizations were performed using a computer equipped with a 6-core 12-thread i7-8700 CPU, 16 G memory, and 64-bit operating system. The direct optimization converged after approximately 3000 iterations, consuming 15 h. The dimensionality reduction optimization reduced the number of design variables from 10 to 6 and converged after 1000 iterations, consuming 5 h, representing a 75% time saving. This suggests that the K–L transform–based hull form reconstruction method effectively reduces the number of design variables, considerably reduces the time consumption of optimization, and improves the efficiency of optimization while yielding results that differ insignificantly from those by the direct optimization.
6. Conclusions
This study derived the equations for a K–L transform–based hull form reconstruction method and optimized the DTMB 5415 hull form by dimensionality reduction and direct optimizations. The following can be concluded from the results. The dimensionality reduction reduced the number of design variables, markedly reduced the number of iterations at optimization convergence, and significantly reduced the computation time compared with the direct optimization. The results yielded by the dimensionality reduction and direct optimizations differed insignificantly. This suggests that the K–L transform–based dimensionality reduction method reduces the time consumption and improves the optimization efficiency while retaining the variability of the design space. This proves the feasibility of the developed hull form optimization method combining the dimensionality reduction method and SHIPMDO-WUT.
During the study, several aspects could not be investigated thoroughly due to time constraints, and these are summarized as follows:
- (1)
- The K–L transform is a linear dimensionality reduction method and assumes the presence of a linear relationship between data. Thus, its dimensionality reduction performance could be limited on nonlinear data. This study did not investigate the application of nonlinear dimensionality reduction methods, which will be tested in the future.
- (2)
- To reduce the computation time, the sample data used in the dimensionality reduction optimization performed in this study only included the geometric information of the hull and excluded its physical information. The consideration of physical information requires a detailed computation of the ship performance in the early stage, and the physical information of a new hull form can be directly obtained by dimensionality reduction reconstruction. This is a major direction for future research.
Author Contributions
Conceptualization: C.W., H.C. and Z.L.; methodology: C.W., H.C. and Z.L.; software: B.F., C.Z. and X.C.; validation: C.W. and H.C.; formal analysis: C.W., H.C. and Z.L.; data curation: C.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant numbers 51979211, 52271327, 52271330), Key Research and Development Plan of Hubei Province (2021BID008), and 111 Project (BP0820028).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in this article (tables and figures).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| m | the waterline length | |
| m | the longitudinal center of buoyancy | |
| m | the maximum waterplane width | |
| m | ||
| / | the block coefficient | |
| / | the fullest cross-section area | |
| m3 | the volume of displacement | |
| m2 | the wetted surface area | |
| Fr | / | Froude number |
| Rw | N | the wave-making resistance |
| Cw | / | the wave-making resistance coefficient |
References
- Cheng, X.; Li, G.; Skulstad, R. Data-driven uncertainty and sensitivity analysis for ship motion modeling in offshore operations. Ocean Eng. 2019, 179, 261–272. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, G.; Li, D. Shape optimization of airfoil in ground effect based on free-form deformation utilizing sensitivity analysis and surrogate model of artificial neural network. Ocean Eng. 2022, 257, 514–527. [Google Scholar] [CrossRef]
- Guan, G.; Yang, Q.; Gu, W. A new method for parametric design and optimization of ship inner shell based on the improved particle swarm optimization algorithm. Ocean Eng. 2018, 169, 551–566. [Google Scholar] [CrossRef]
- Hamed, A. Multi-objective optimization method of trimaran hull form for resistance reduction and propeller intake flow improvement. Ocean Eng. 2022, 244, 352–366. [Google Scholar] [CrossRef]
- Jung, Y.-W.; Kim, Y. Hull form optimization in the conceptual design stage considering operational efficiency in waves. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2019, 233, 745–759. [Google Scholar] [CrossRef]
- Liu, Q.; Feng, B.; Liu, Z.; Zhang, H. The improvement of a variance-based sensitivity analysis method and its application to a ship hull optimization model. J. Mar. Sci. Technol. 2017, 22, 694–709. [Google Scholar] [CrossRef]
- Guan, G.; Zhuang, Z.; Yang, Q. Design parameter sensitivity analysis for SWATH with minimum resistance at design and service speeds. Ocean Eng. 2021, 240, 961–972. [Google Scholar] [CrossRef]
- Jeon, M.; Yoon, H.K.; Hwang, J. Analysis of the dynamic characteristics for the change of design parameters of an underwater vehicle using sensitivity analysis. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 508–519. [Google Scholar] [CrossRef]
- Coppedè, A.; Gaggero, S.; Vernengo, G. Hydrodynamic shape optimization by high fidelity CFD solver and Gaussian process based response surface method. Appl. Ocean Res. 2019, 90, 841–851. [Google Scholar] [CrossRef]
- Fu, X.; Lei, L.; Yang, G. Multi-objective shape optimization of autonomous underwater glider based on fast elitist non-dominated sorting genetic algorithm. Ocean Eng. 2018, 157, 339–349. [Google Scholar] [CrossRef]
- Yue, Y.; Han, C.; Cui, Y. TSP wavefield separation and noise suppression based on the LC-KL-DSW method. J. Appl. Geophys. 2022, 197, 552–560. [Google Scholar] [CrossRef]
- Fan, Y.; Xu, K.; Wu, H. Spatiotemporal Modeling for Nonlinear Distributed Thermal Processes Based on KL Decomposition, MLP and LSTM Network. IEEE Access 2020, 8, 11–21. [Google Scholar] [CrossRef]
- Ahuja, R.; Lall, B.; Prasad, S. On impropriety for a large-sized discrete fourier transform of a real-valued stationary process. Signal Process. 2022, 193, 397–402. [Google Scholar] [CrossRef]
- Trudu, M.; Pilia, M.; Hellbourg, G.; Pari, P.; Antonietti, N.; Maccone, C.; Melis, A.; Perrodin, D.; Trois, A. Performance analysis of the Karhunen–Loève Transform for artificial and astrophysical transmissions: Denoizing and detection. Mon. Not. R. Astron. Soc. 2020, 494, 69–83. [Google Scholar] [CrossRef]
- Siripatana, A.; Le Maitre, O.; Knio, O. Bayesian inference of spatially varying Manning’s n coefficients in an idealized coastal ocean model using a generalized Karhunen-Loève expansion and polynomial chaos. Ocean Dyn. 2020, 70, 1103–1127. [Google Scholar] [CrossRef]
- Reed, R.L.; Roberts, J.A. Application of the Karhunen-Loève Transform to the C5G7 benchmark in the response matrix method. Ann. Nucl. Energy 2017, 103, 350–355. [Google Scholar] [CrossRef]
- Allaix, D.L.; Carbone, V.I. An efficient coupling of FORM and Karhunen–Loève series expansion. Eng. Comput. 2016, 32, 1–13. [Google Scholar] [CrossRef]
- Azevedo, J.S.; Wisniewski, F.; Oliveira, S.P. A Galerkin method with two-dimensional Haar basis functions for the computation of the Karhunen–Loève expansion. Comput. Appl. Math. 2018, 37, 1825–1846. [Google Scholar] [CrossRef]
- Liu, L.; Yan, J.; Zheng, X.; Peng, H.; Guo, D.; Qu, X. Karhunen-Loève transform for compressive sampling hyperspectral images. Opt. Eng. 2015, 54, 014106. [Google Scholar] [CrossRef]
- Ai, X. A note on Karhunen–Loève expansions for the demeaned stationary Ornstein–Uhlenbeck process. Stat. Probab. Lett. 2016, 117, 113–117. [Google Scholar] [CrossRef]
- Chowdhary, K.; Najm, H.N. Bayesian estimation of Karhunen–Loève expansions; A random subspace approach. J. Comput. Phys. 2016, 319, 280–293. [Google Scholar] [CrossRef]
- Feng, J.W.; Cen, S.; Li, C.F.; Owen, D.R.J. Statistical reconstruction and Karhunen-Loève expansion for multiphase random media. Int. J. Numer. Methods Eng. 2016, 105, 3–32. [Google Scholar] [CrossRef]
- Diez, M.; Campana, E.F.; Andstern, F. Design-space dimensionality reduction in shape optimization by Karhunen–Loève expansion. Comput. Methods Appl. Mech. Eng. 2015, 283, 1525–1544. [Google Scholar] [CrossRef]
- Diez, M.; Serani, A.; Campana, E.F. Design-Space Dimensionality Reduction for Single- and Multi-Disciplinary Shape Optimization. In Proceedings of the 17th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Diez, M.; Serani, A.; Stern, F. Combined Geometry and Physics Based Method for Design-space Dimensionality Reduction in Hydrodynamic Shape Optimization. In Proceedings of the 31st Symposium on Naval Hydrodynamics, Monterey, CA, USA, 11–16 September 2016. [Google Scholar]
- Hotelling, H. Note on Edgeworth’s Taxation Phenomenon and Professor Garver’s Additional Condition on Demand Functions. Econometrica 1933, 1, 408–409. [Google Scholar] [CrossRef]
- Hotelling, H.; Hotelling, F. A new analysis of duration of pregnancy data. Am. J. Obstet. Gynecol. 1932, 23, 643–657. [Google Scholar] [CrossRef]
- Hotelling, H. Demand Functions with Limited Budgets. Econometrica 1935, 3, 66–78. [Google Scholar] [CrossRef]
- Feng, B.; Zhan, C.; Liu, Z. Application of Basis Functions for Hull Form Surface Modification. J. Mar. Sci. Eng. 2021, 9, 1005. [Google Scholar] [CrossRef]
- Chang, H.; Zhan, C.; Liu, Z.; Cheng, X.; Feng, B. Dynamic sampling method for ship resistance performance optimisation based on approximated model. Ships Offshore Struct. 2021, 16, 386–396. [Google Scholar] [CrossRef]
- Cheng, X.; Feng, B.; Liu, Z. Hull surface modification for ship resistance performance optimization based on Delaunay triangulation. Ocean Eng. 2018, 153, 333–344. [Google Scholar] [CrossRef]
- Cheng, X.; Feng, B.; Chang, H. Multi-objective optimisation of ship resistance performance based on CFD. J. Mar. Sci. Technol. 2019, 24, 152–165. [Google Scholar] [CrossRef]
- Ouyang, X.; Chang, H.; Feng, B. Information Matrix-Based Adaptive Sampling in Hull Form Optimisation. J. Mar. Sci. Eng. 2021, 9, 973. [Google Scholar] [CrossRef]
- Qiang, Z.; Bai-Wei, F.; Zu-Yuan, L.; Hai-Chao, C.; Xiao, W. Optimization method for hierarchical space reduction method and its application in hull form optimization. Ocean Eng. 2022, 262, 112–129. [Google Scholar] [CrossRef]
- Qiang, Z.; Hai-Chao, C.; Bai-Wei, F.; Zu-Yuan, L.; Cheng-Sheng, Z. Research on knowledge-extraction technology in optimisation of ship-resistance performance. Ocean Eng. 2019, 179, 325–336. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).