Optimization Design of Pressure Hull for Long-Range Underwater Glider Based on Energy Consumption Constraints
Abstract
1. Introduction
2. Optimization Problem of Pressure Hull for Underwater Gliders
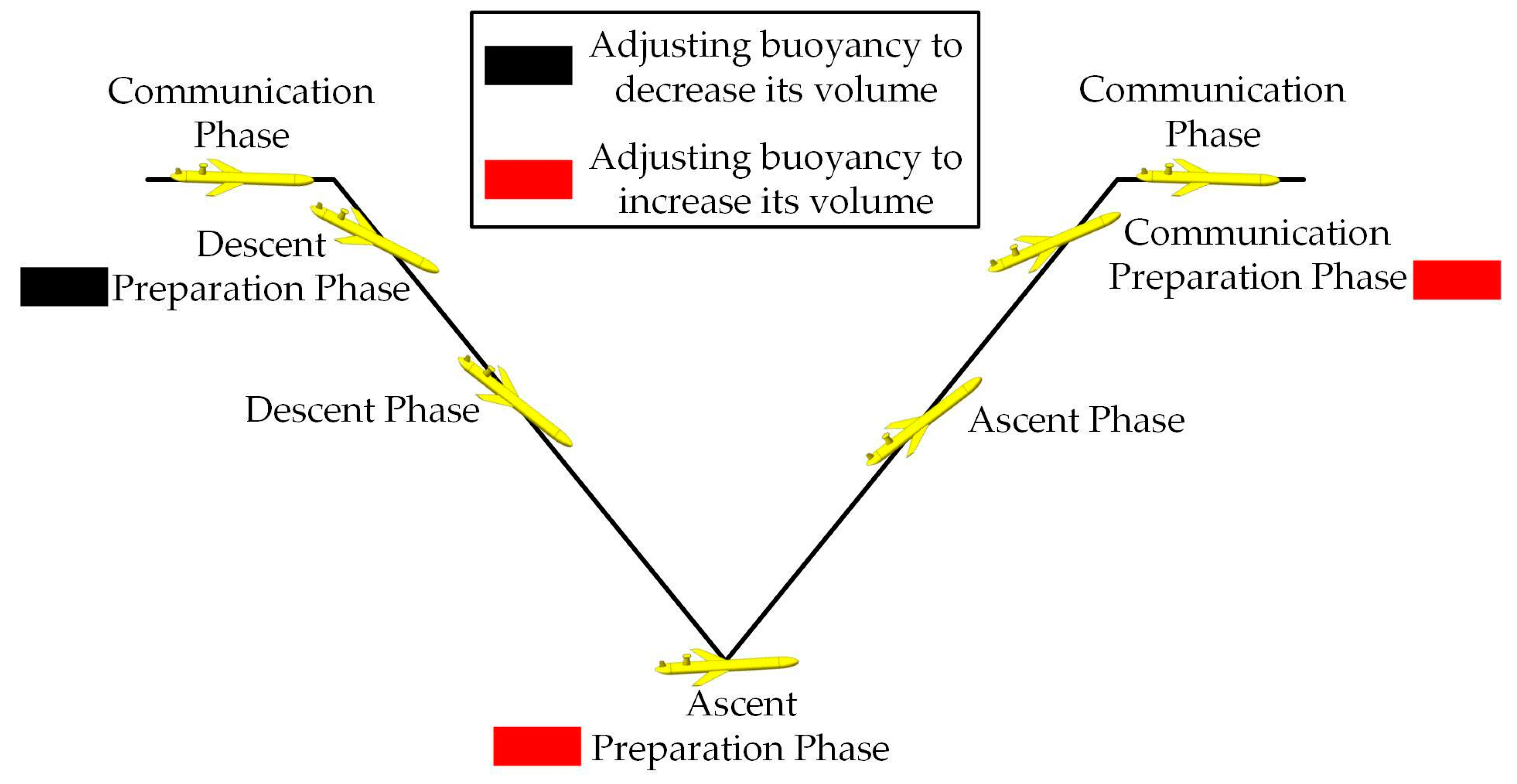
2.1. Underwater Gliders Buoyancy Variation
2.2. Conventional Optimization Problems of the Pressure Hull
2.3. Optimization Objective of the Pressure Hull
3. Deformation and Mass Calculation Models
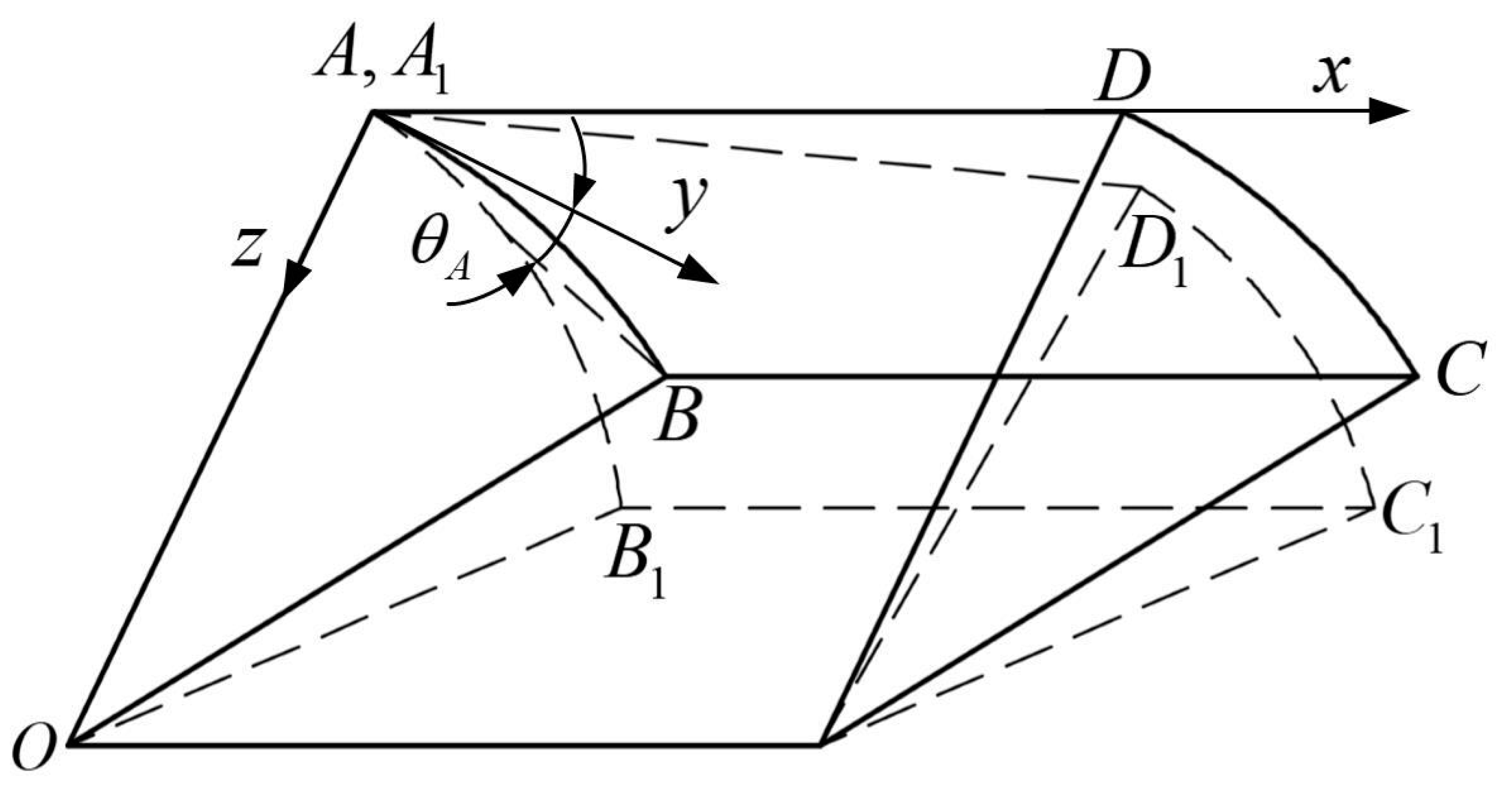
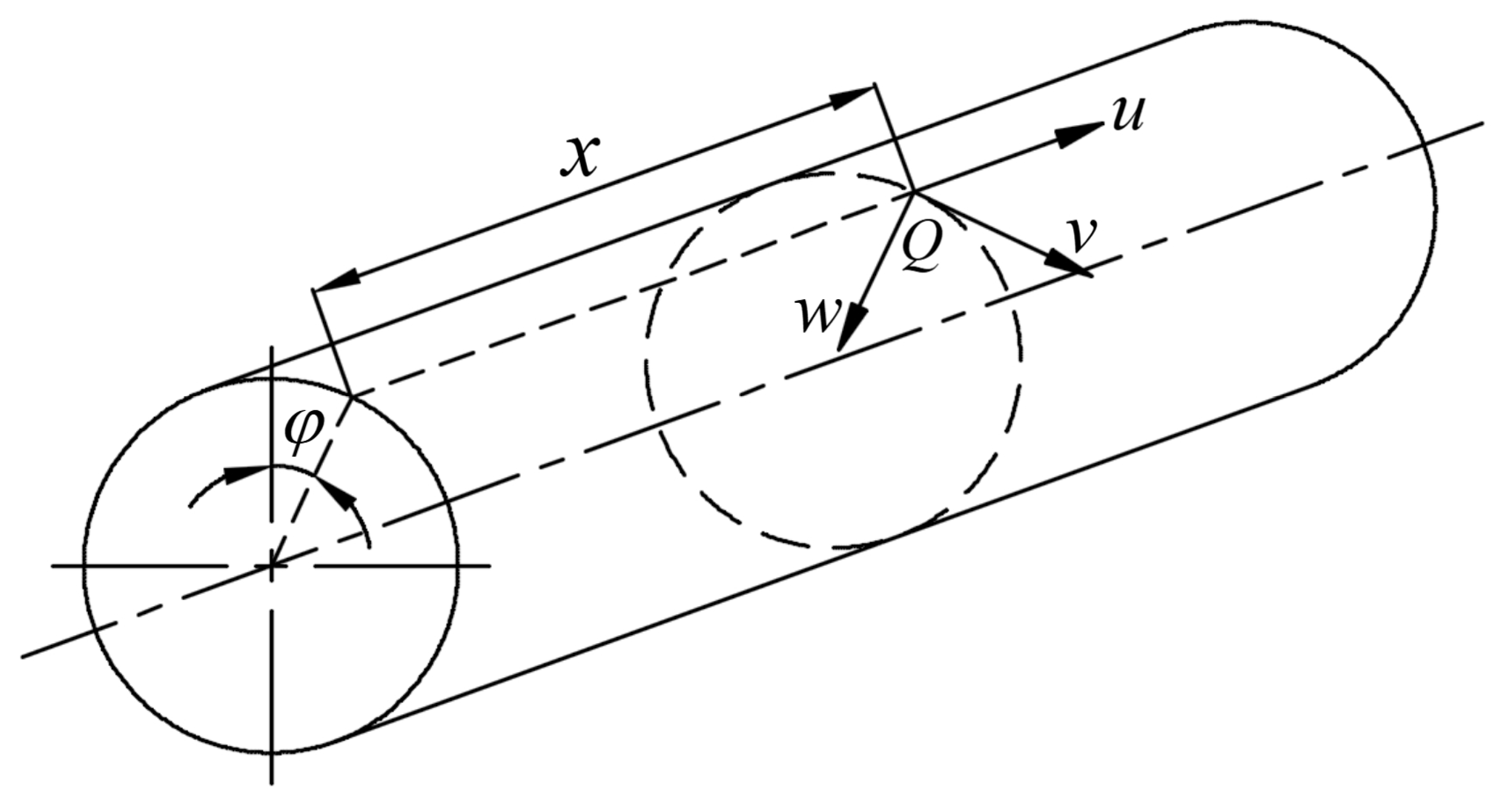
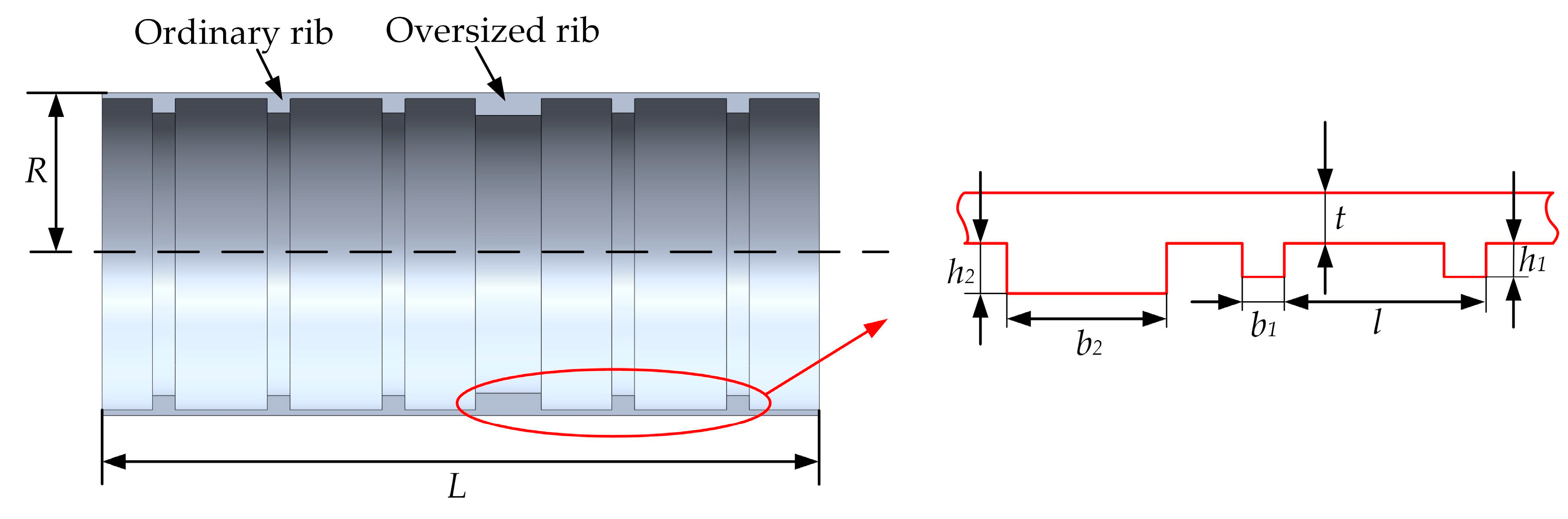
3.1. Geometric Structure and Parameter Definition
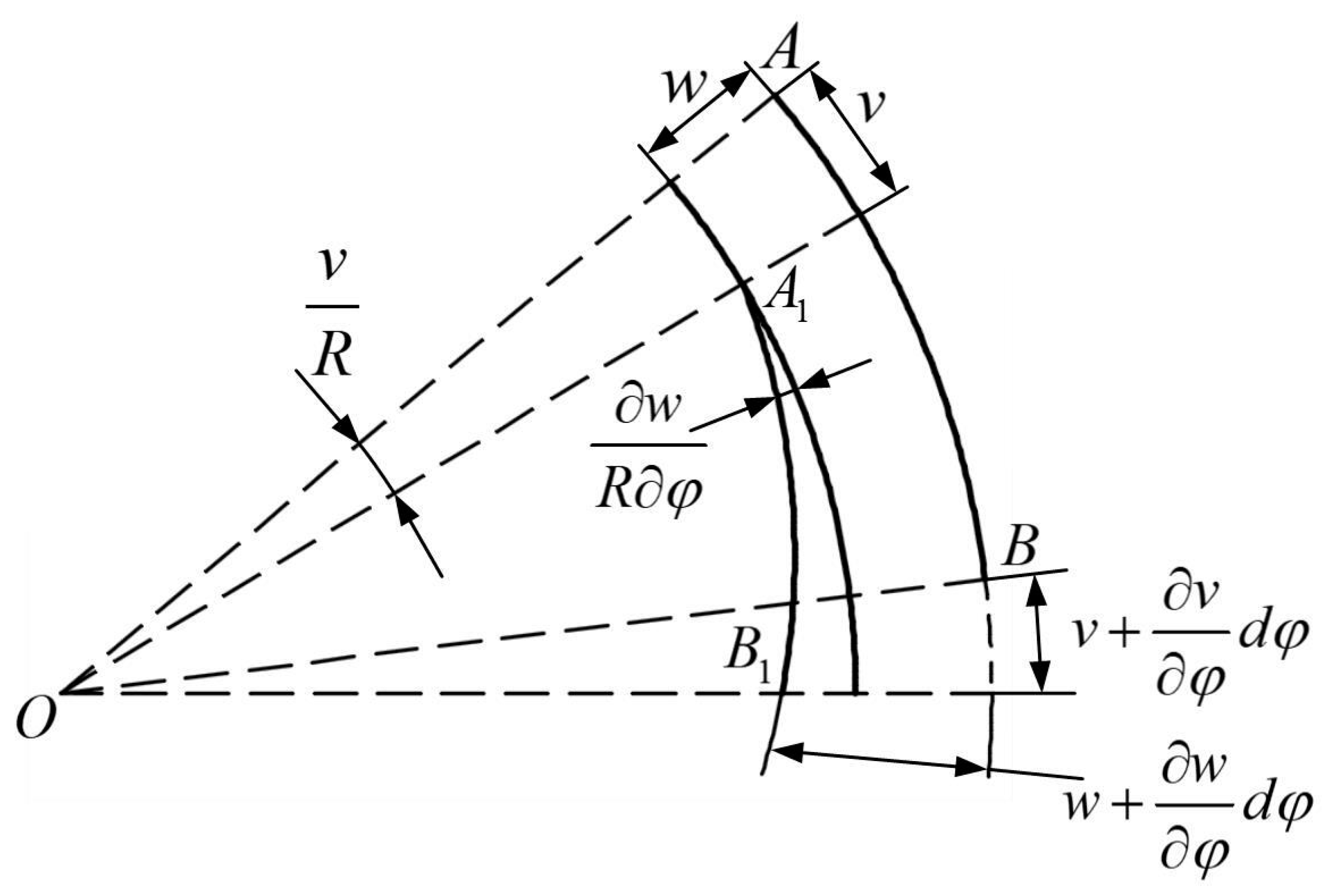
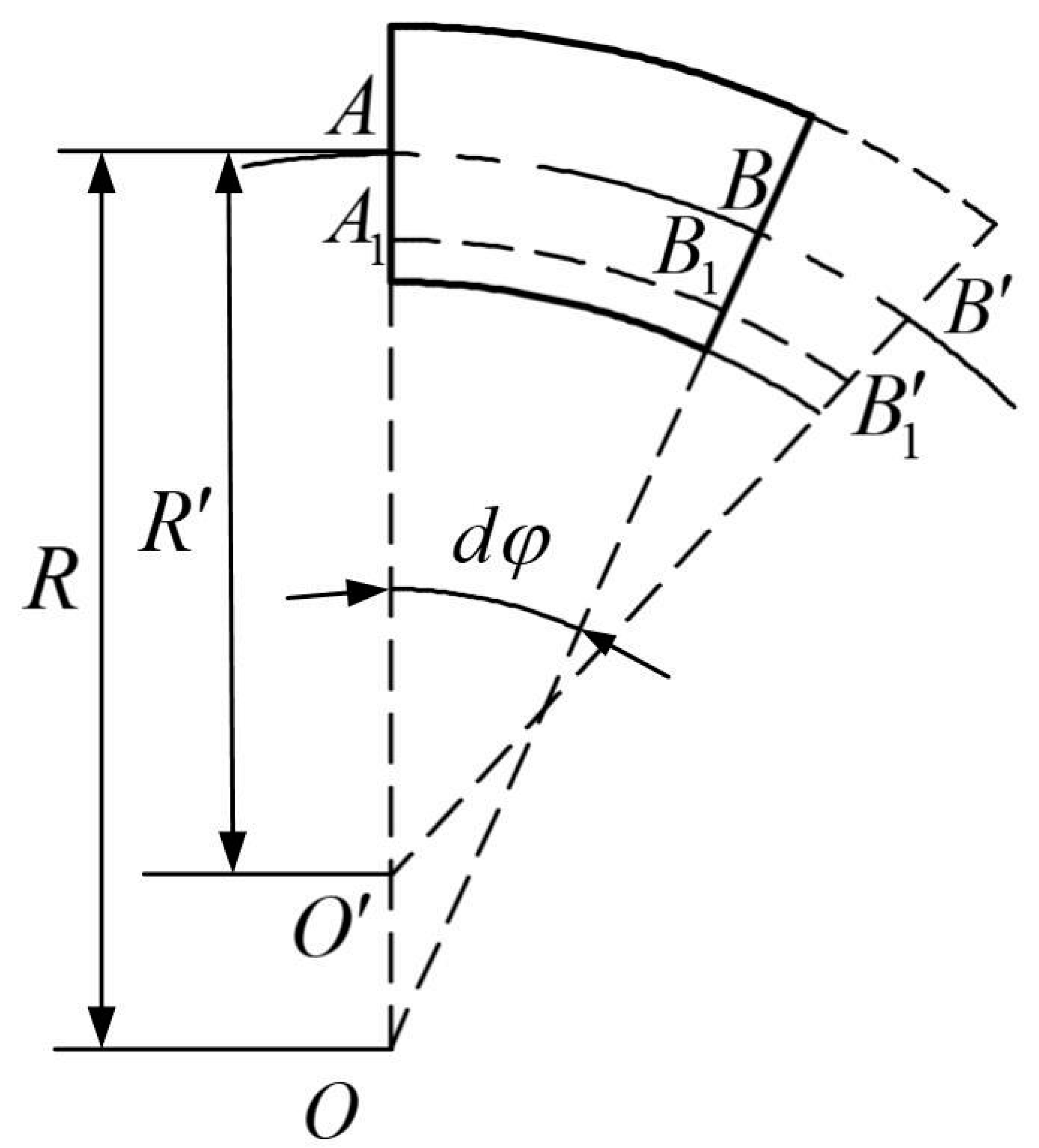
3.2. Calculation Model of Deformation under External Pressure
3.3. Calculation Model of Deformation Casued by Temperature Reduction
3.4. Calculation Model of the Pressure Hull Mass
4. Strength and Stability Constraint Models
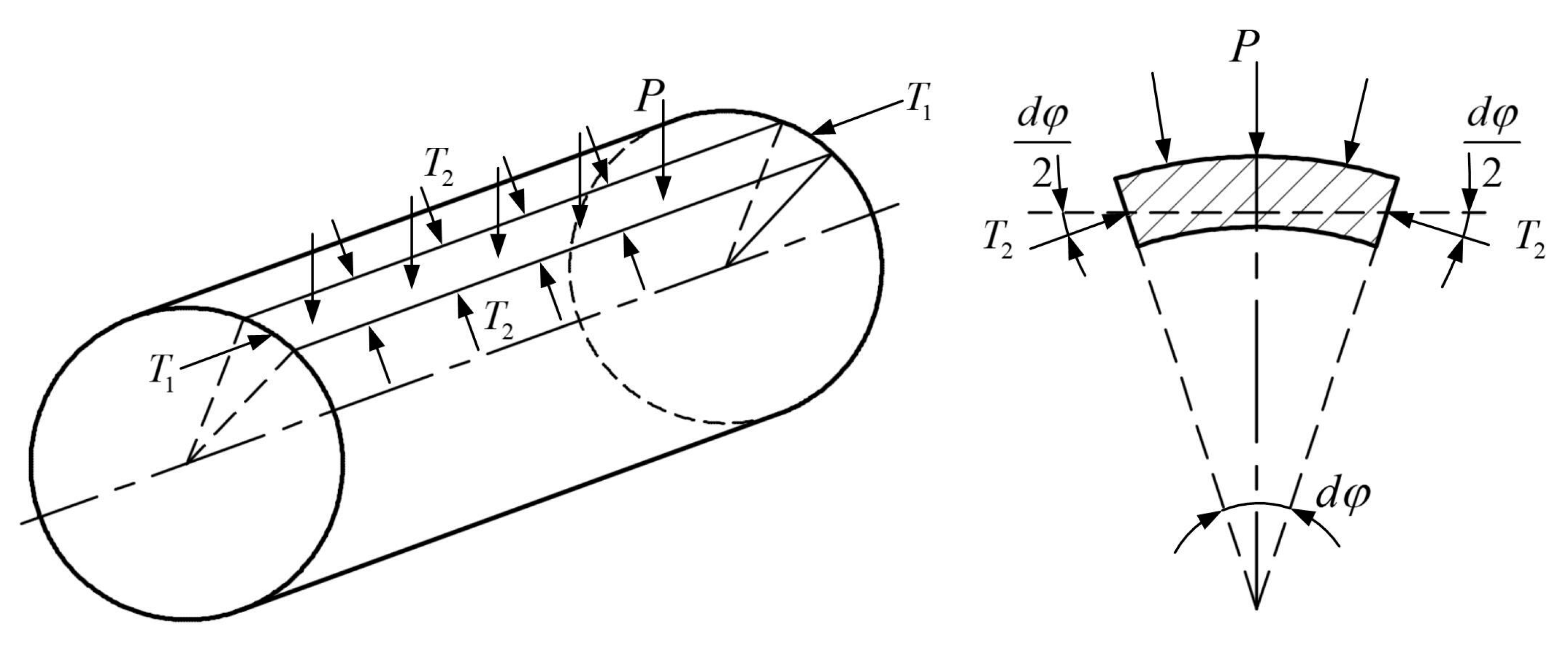
4.1. Strength Calculation Model for the Pressure Hull
4.1.1. Axial Normal Stress on the Shell Plate
4.1.2. Circumferential Stress on the Shell Plate
4.1.3. Axial Normal Stress on the Ribs
4.1.4. Strength Constraint Conditions
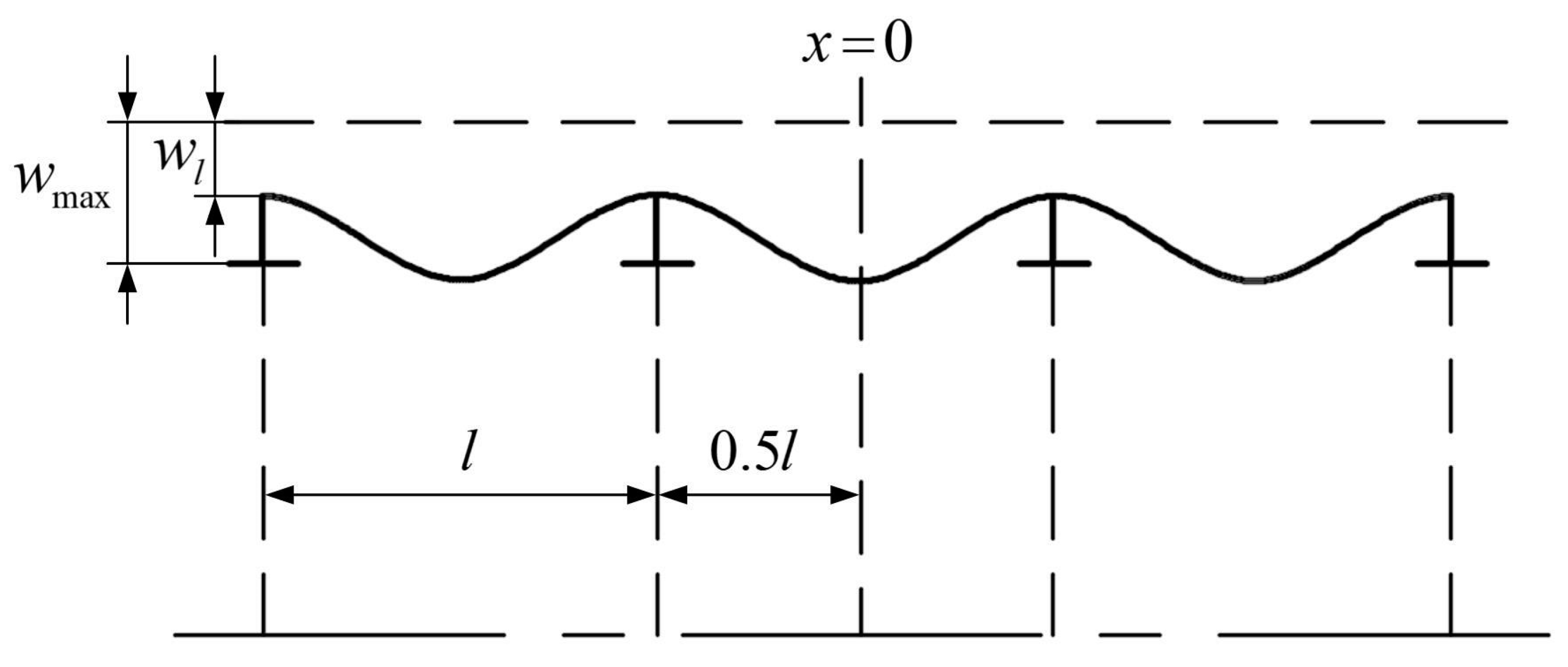
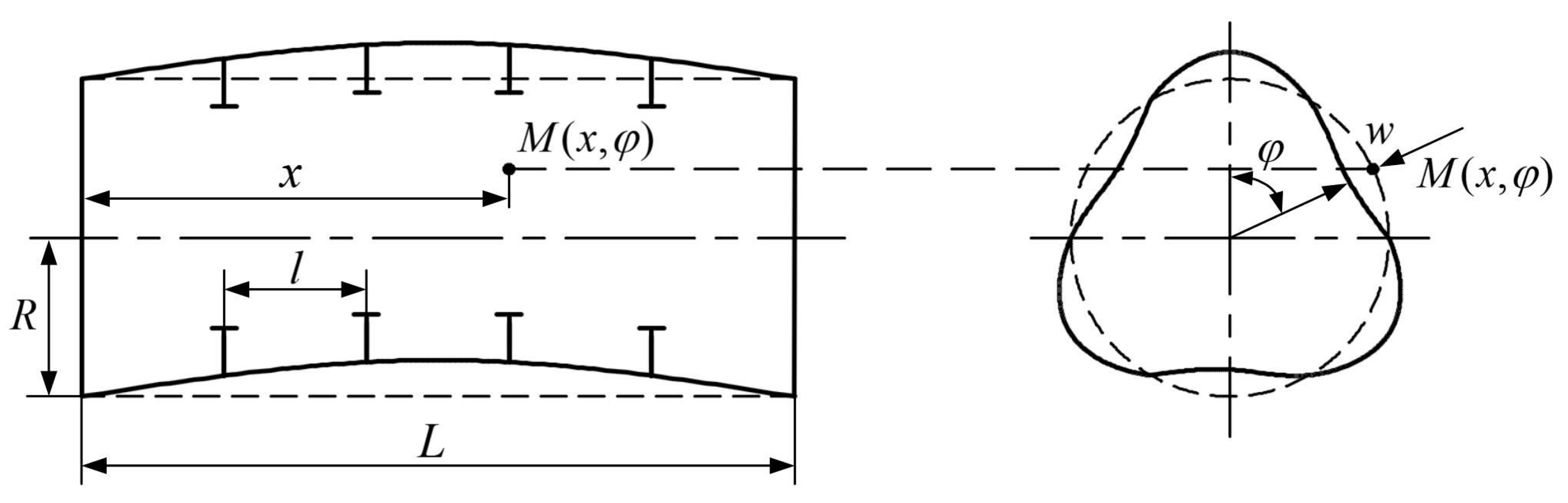
4.2. Stability Calculation Model for the Pressure Hull
4.2.1. Strain Energy of Pressure Hull
- According to Kirchhoff’s assumption [23], there is the expression . The shell is in a bi-directional stress condition, and its stress–strain relationship as shown in Equation (33).
4.2.2. External Work on Pressure Hull
4.2.3. Stability Constraint Conditions
5. Optimization Process and Results
5.1. Optimization Function
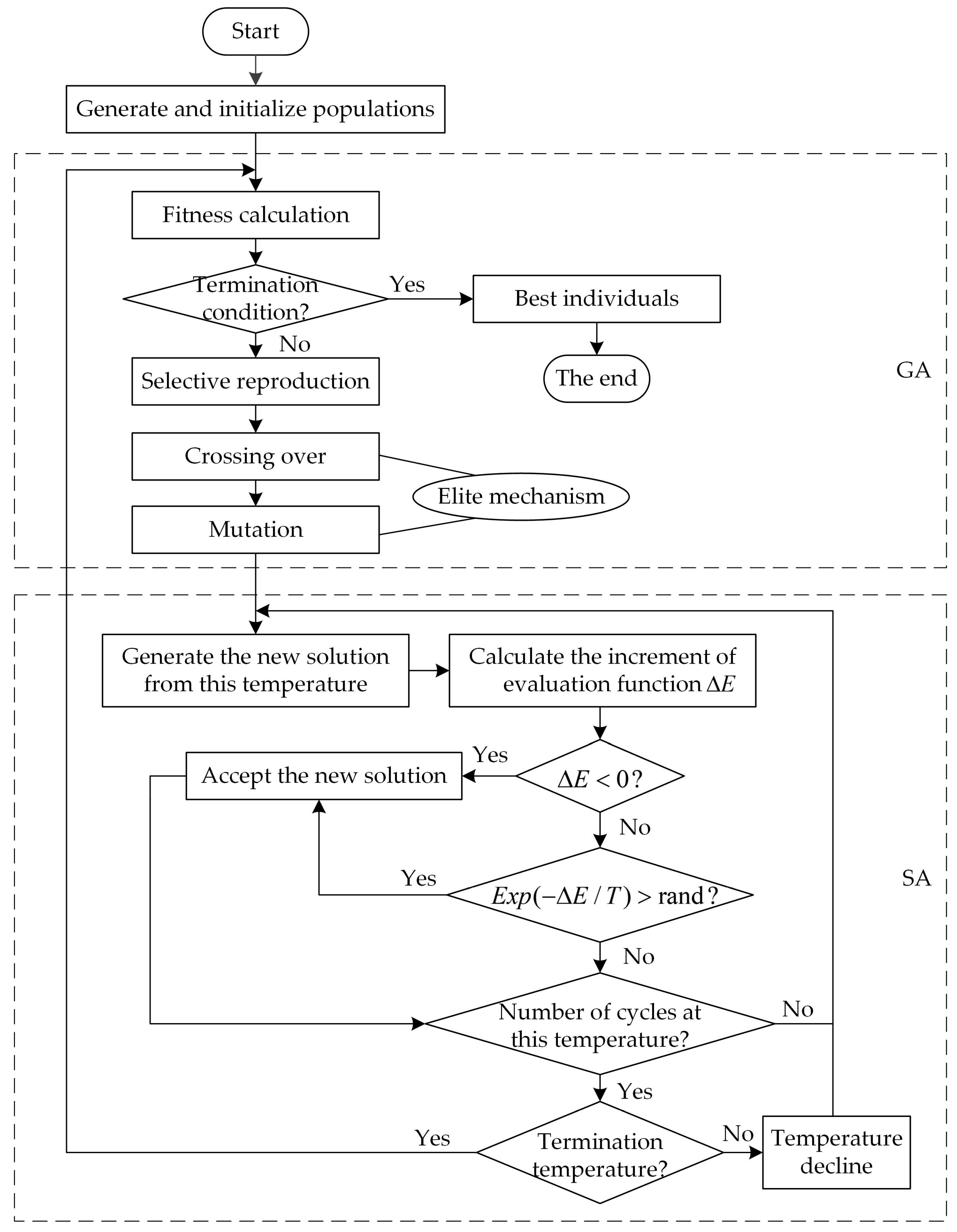
5.2. Optimization Algorithm
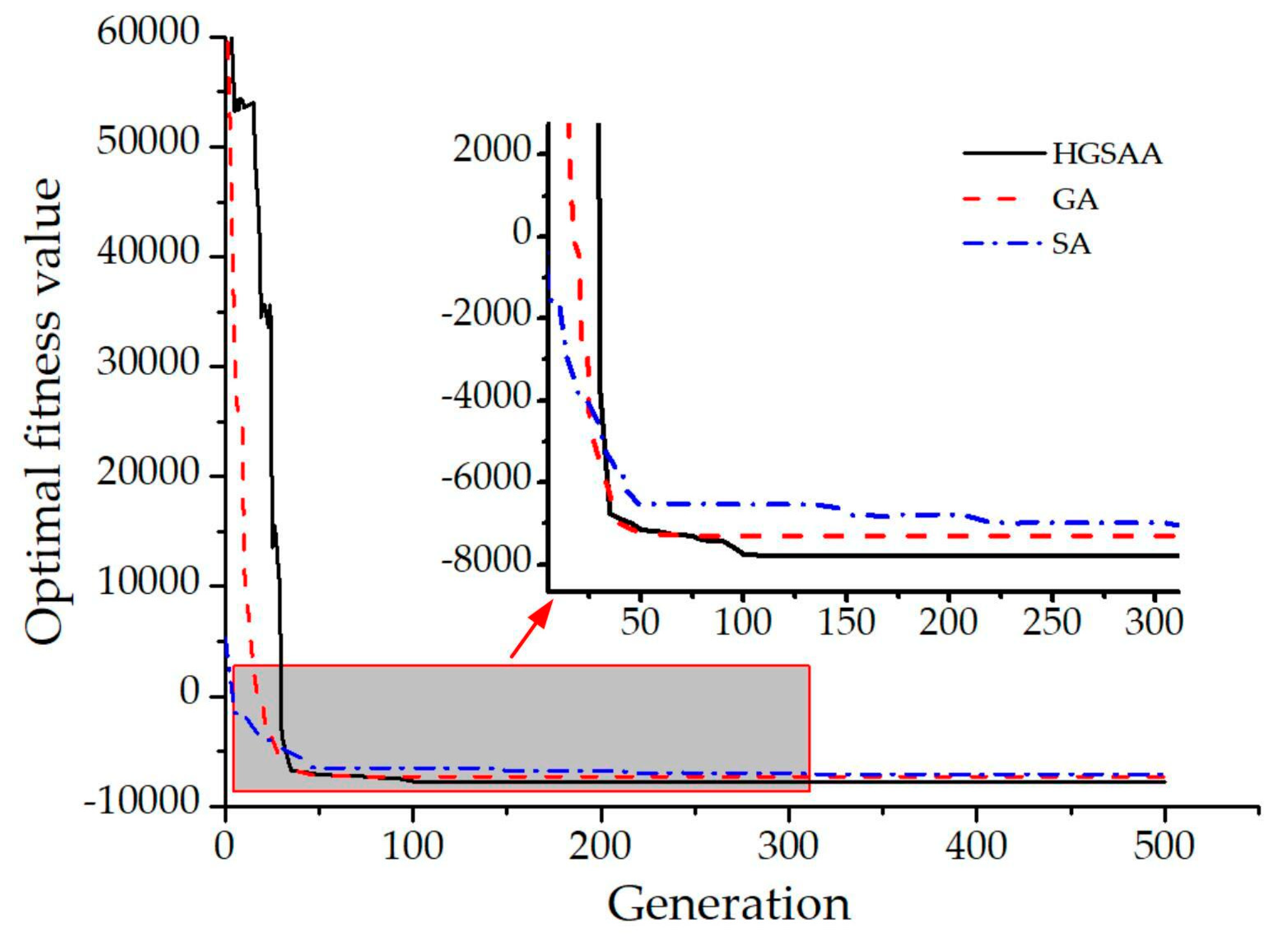
5.3. Analysis Optimization Results
6. Test Verification
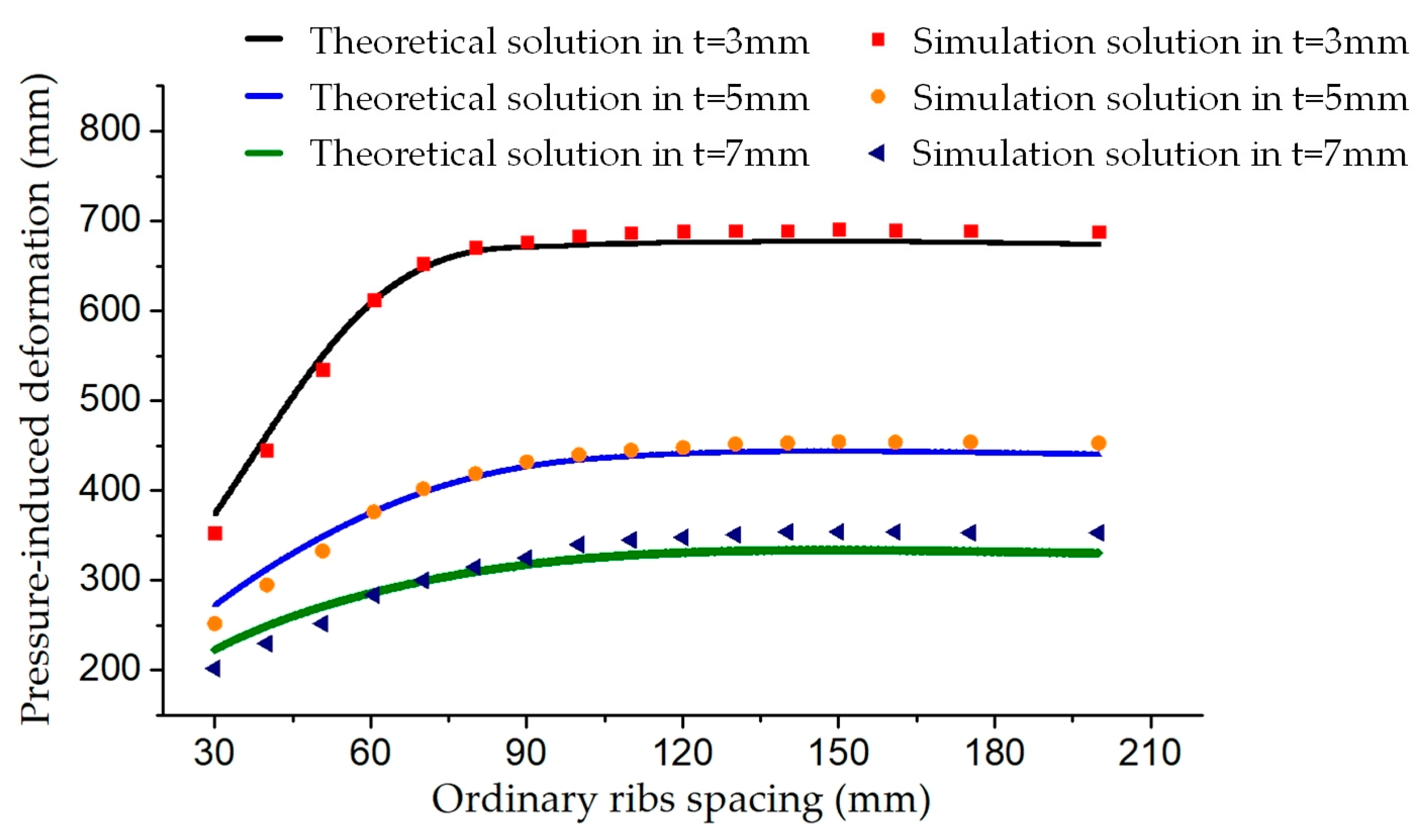
6.1. Finite Element Simulation Test Verification
6.2. Sea Trials Verification
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Bender, A.; Steinberg, D.M.; Friedman, A.L.; Williams, S.B. Analysis of an autonomous underwater glider. In Proceedings of the Australasian Conference on Robotics and Automation, Canberra, Australia, 3–5 December 2008; pp. 1–10. [Google Scholar]
- Rudnick, D.L.; Davis, R.E.; Eriksen, C.C.; Fratantoni, D.M.; Perry, M.J. Underwater gliders for ocean research. Mar. Technol. Soc. J. 2004, 38, 73–84. [Google Scholar] [CrossRef]
- Leonard, N.; Paley, D.; Davis, R.; Fratantoni, D.; Lekien, F.; Zhang, F. Coordinated control of an underwater glider fleet in an adaptive ocean sampling field experiment in Monterey Bay. J. Field Robot. 2010, 27, 718–740. [Google Scholar] [CrossRef]
- Eriksen, C.C.; Osse, T.J.; Light, R.D.; Wen, T.; Lehman, T.W.; Sabin, P.L.; Ballard, J.W.; Chiodi, A.M. Seaglider: A long-range autonomous underwater vehicle for oceanographic research. IEEE J. Ocean. Eng. 2001, 26, 424–436. [Google Scholar] [CrossRef]
- Sherman, J.; Davis, R.E.; Owens, W.B.; Valdes, J. The autonomous underwater glider “Spray”. IEEE J. Ocean. Eng. 2001, 26, 437–446. [Google Scholar] [CrossRef]
- Webb, D.C.; Simonetti, P.J.; Jones, C.P. SLOCUM: An underwater glider propelled by environmental energy. IEEE J. Ocean. Eng. 2001, 26, 447–452. [Google Scholar] [CrossRef]
- Claustre, H.; Beguery, L.; Pla, P. SeaExplorer glider breaks two world records. Sea Technol. 2014, 55, 19–21. [Google Scholar]
- Yang, M.; Wang, Y.; Wang, S.; Yang, S.; Zhang, L. Motion parameter optimization for gliding strategy analysis of underwater gliders. Ocean Eng. 2019, 191, 106502. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Y.; Yang, S.; Wang, S.; Yang, M. Sensitivity Analysis and Parameter Optimization of Energy Consumption for Underwater Gliders. Energy 2019, 191, 116506. [Google Scholar] [CrossRef]
- Osse, T.J.; Lee, T.J. Composite Pressure Hulls for Autonomous Underwater Vehicles. In Proceedings of the OCEANS 2007, Vancouver, BC, Canada, 29 September–4 October 2007; pp. 1–14. [Google Scholar]
- Simitses, G.J.; Aswani, M. Minimum-Weight Design of Stiffened Cylinders Under Hydrostatic Pressure. J. Ship Res. 1977, 21, 217–224. [Google Scholar] [CrossRef]
- Mehrabani, M.M.; Jafari, A.A.; Azadi, M. Multidisciplinary optimization of a stiffened shell by genetic algorithm. J. Mech. Sci. Technol. 2012, 26, 517–530. [Google Scholar] [CrossRef]
- Akl, W.; Ruzzene, M.; Baz, A. Optimal design of underwater stiffened shells. Struct. Multidiscip. Optim. 2002, 23, 297–310. [Google Scholar] [CrossRef]
- Shimoda, M.; Okada, T.; Nagano, T.; Shi, J. Free-form optimization method for buckling of shell structures under out-of-plane and in-plane shape variations. Struct. Multidiscip. Optim. 2016, 54, 275–288. [Google Scholar] [CrossRef]
- Liang, C.; Hsu, C.; Tsai, H. Minimum weight design of submersible pressure hull under hydrostatic pressure. Comput. Struct. 1997, 63, 187–201. [Google Scholar] [CrossRef]
- Barski, M.; Krużelecki, J. Optimal design of shells against buckling by means of the simulated annealing method. Struct. Multidiscip. Optim. 2005, 29, 61–72. [Google Scholar] [CrossRef]
- Hao, P.; Wang, B.; Li, G.; Tian, K.; Du, K.; Wang, X.; Tang, X. Surrogate-based optimization of stiffened shells including load-carrying capacity and imperfection sensitivity. Thin-Walled Struct. 2013, 72, 164–174. [Google Scholar] [CrossRef]
- Tang, T.; Li, B.; Fu, X.; Xi, Y.; Yang, G. Bi-directional evolutionary topology optimization for designing a neutrally buoyant underwater glider. Eng. Optimiz. 2018, 50, 1270–1286. [Google Scholar] [CrossRef]
- Foryś, P. Optimization of cylindrical shells stiffened by rings under external pressure including their post-buckling behaviour. Thin-Walled Struct. 2015, 95, 231–243. [Google Scholar] [CrossRef]
- Yang, M.; Yang, S.; Wang, Y.; Liang, Y.; Wang, S.; Zhang, L. Optimization design of neutrally buoyant hull for underwater gliders. Ocean Eng. 2020, 209, 107512. [Google Scholar] [CrossRef]
- Liu, J.; He, B.; Yan, T.; Yu, F.; Shen, Y. Study on carbon fiber composite hull for AUV based on response surface model and experiments. Ocean Eng. 2021, 239, 109850. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Wang, Y.; Zhang, H.; Zhang, L. Dynamic modeling and motion control strategy for deep-sea hybrid-driven underwater gliders considering hull deformation and seawater density variation. Ocean Eng. 2017, 143, 66–78. [Google Scholar] [CrossRef]
- Motygin, O.V.; Nazarov, S.A. Justification of the Kirchhoff hypotheses and error estimation for two-dimensional models of anisotropic and inhomogeneous plates, including laminated plates. IMA J. Appl. Math. 2000, 65, 1–28. [Google Scholar] [CrossRef]
- China, C.S. China Classification Society Rules for Classification of Diving Systems and Submersibles; China Communications Press: Beijing, China, 2018; pp. 1–127. [Google Scholar]
- Tian, J.; Wang, C.M.; Swaddiwudhipong, S. Elastic buckling analysis of ring-stiffened cylindrical shells under general pressure loading via the Ritz method. Thin-Walled Struct. 1999, 35, 1–24. [Google Scholar] [CrossRef]
- Libai, A.; Simmonds, J.G. Nonlinear Elastic Shell Theory. In Advances in Applied Mechanics; Hutchinson, J.W., Wu, T.Y., Eds.; Elsevier: Amsterdam, The Netherlands, 1983; Volume 23, pp. 271–371. [Google Scholar]
- Yu, J.; Zhang, F.; Zhang, A.; Jin, W.; Tian, J. Motion Parameter Optimization and Sensor Scheduling for the Sea-Wing Underwater Glider. IEEE J. Ocean. Eng. 2013, 38, 243–254. [Google Scholar] [CrossRef]





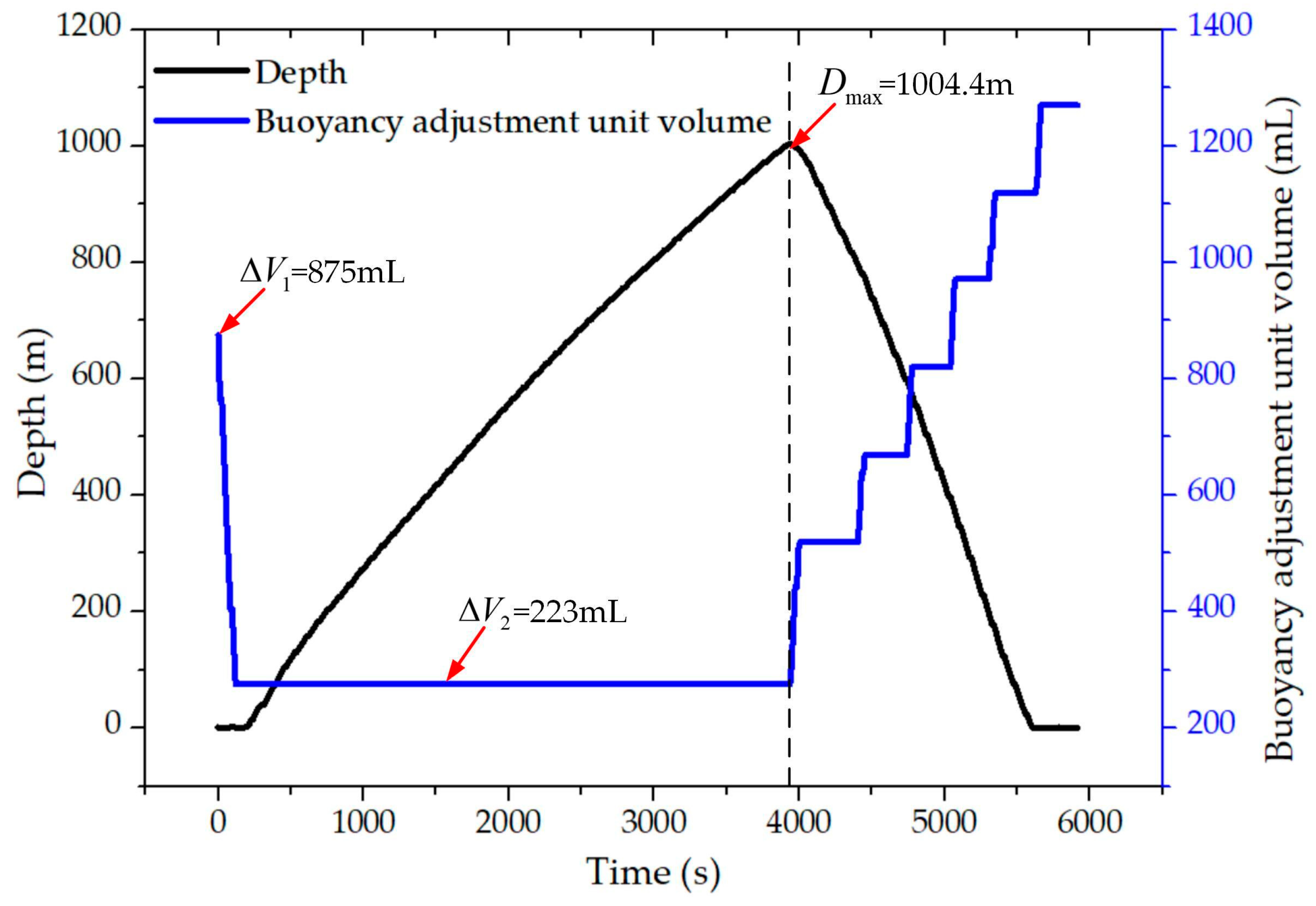

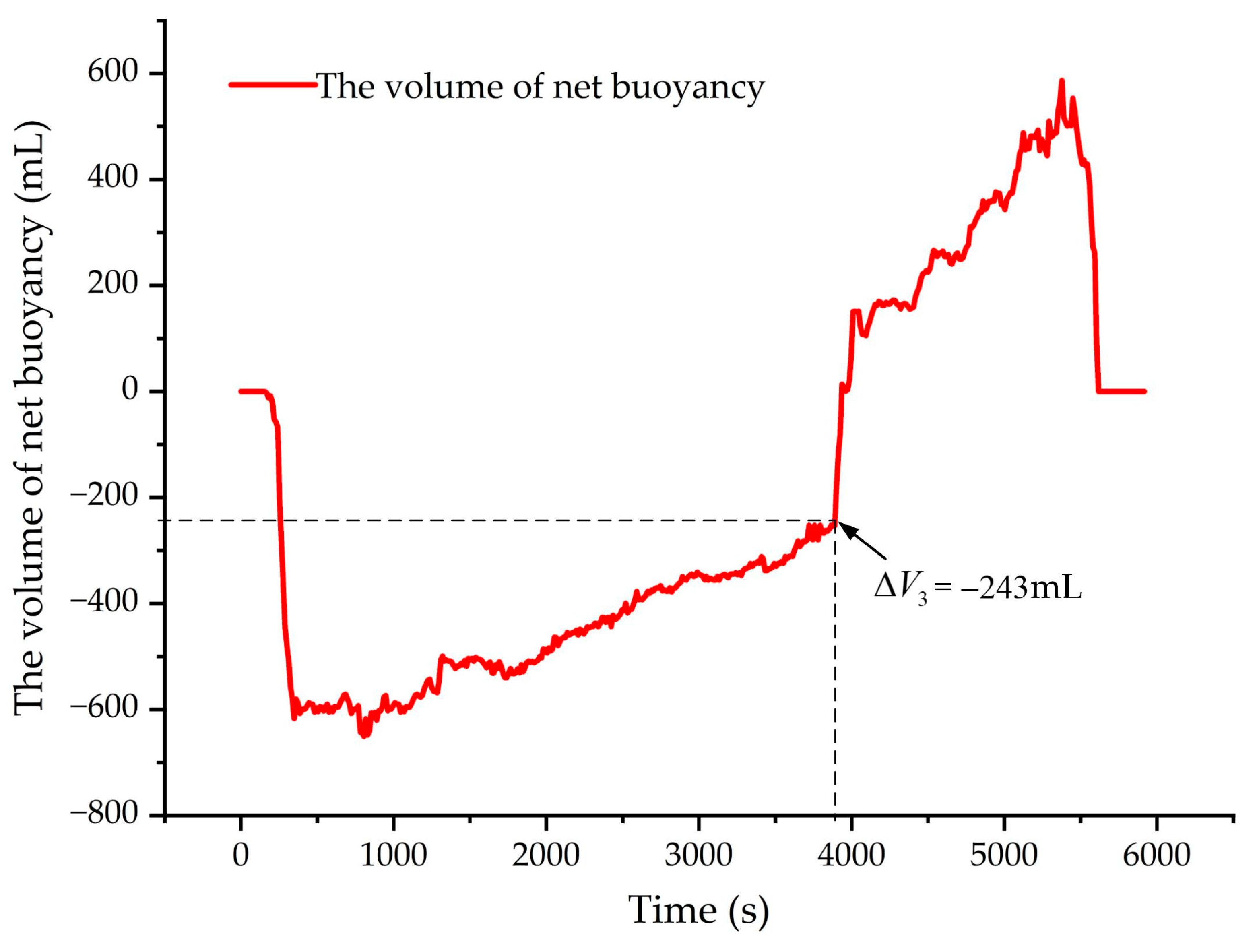
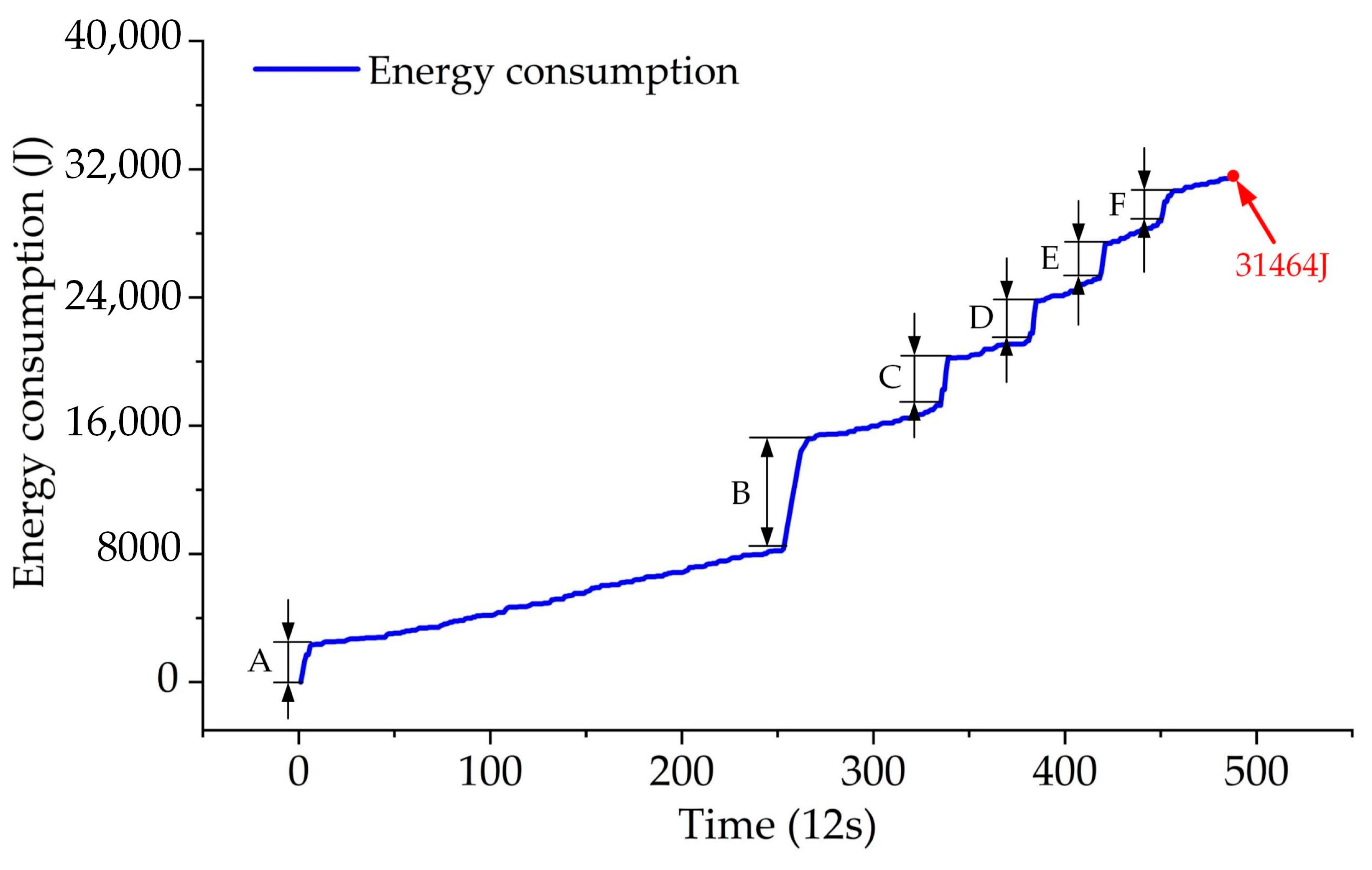
| Underwater Glider Subsystems | Average Energy Consumption (J) | Proportion of Energy Consumption |
|---|---|---|
| Buoyancy adjustment unit | 19,008 | 45.36% |
| Pitch adjustment unit | 2376 | 5.67% |
| Rudder unit | 2844 | 6.79% |
| Control board unit | 9288 | 22.16% |
| Sensors unit | 5832 | 13.92% |
| Communication unit | 2556 | 6.1% |
| Parameters | Values |
|---|---|
| Yield strength | 505 MPa |
| Modulus of elasticity | 72 GPa |
| Passion’s ratio | 0.33 |
| Coefficient of thermal expansion | /K |
| Density | 2.81 g/cm3 |
| Parameters | Original Values (mm) | HGSAA Results (mm) | Percentage of Change |
|---|---|---|---|
| 5 | 4.8 | 4% decrease | |
| 120 | 96.6 | 19.5% decrease | |
| 20 | 19.2 | 4% decrease | |
| 10 | 12.7 | 27% increase | |
| 40 | 58.3 | 45.75% increase | |
| 20 | 14.8 | 26% decrease |
| Parameters | Original Values | HGSAA Results | Percentage of Change |
|---|---|---|---|
| 27,571 g | 24,877 g | 9.77% decrease | |
| 521 mL | 603 mL | 15.74% increase | |
| 19,008 J | 16,664 J | 12.33% decrease | |
| 33.12 MJ | 38.36 MJ | 15.82% increase |
| Volume Compression | Theoretical Results (mL) | Simulation Results (mL) | Error |
|---|---|---|---|
| 457 | 483 | 5.69% | |
| 146 | 149 | 2.05% | |
| 603 | 632 | 4.81% |
| Parameters | Original Values | Actual Optimized Results | Percentage of Change |
|---|---|---|---|
| m | 27,571 g | 25,147 g | 8.8% decrease |
| 521 mL | 662 mL | 27.1% increase | |
| 19,008 J | 14,835 J | 21.9% decrease | |
| 33.12 MJ | 37.22 MJ | 12.4% increase |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Li, B.; Peng, Y.; Zou, D.; Yang, G. Optimization Design of Pressure Hull for Long-Range Underwater Glider Based on Energy Consumption Constraints. J. Mar. Sci. Eng. 2023, 11, 202. https://doi.org/10.3390/jmse11010202
Zhang J, Li B, Peng Y, Zou D, Yang G. Optimization Design of Pressure Hull for Long-Range Underwater Glider Based on Energy Consumption Constraints. Journal of Marine Science and Engineering. 2023; 11(1):202. https://doi.org/10.3390/jmse11010202
Chicago/Turabian StyleZhang, Jianxing, Baoren Li, Yuxuan Peng, Daming Zou, and Gang Yang. 2023. "Optimization Design of Pressure Hull for Long-Range Underwater Glider Based on Energy Consumption Constraints" Journal of Marine Science and Engineering 11, no. 1: 202. https://doi.org/10.3390/jmse11010202
APA StyleZhang, J., Li, B., Peng, Y., Zou, D., & Yang, G. (2023). Optimization Design of Pressure Hull for Long-Range Underwater Glider Based on Energy Consumption Constraints. Journal of Marine Science and Engineering, 11(1), 202. https://doi.org/10.3390/jmse11010202






