Simulating Ship Manoeuvrability with Artificial Neural Networks Trained by a Short Noisy Data Set
Abstract
1. Introduction
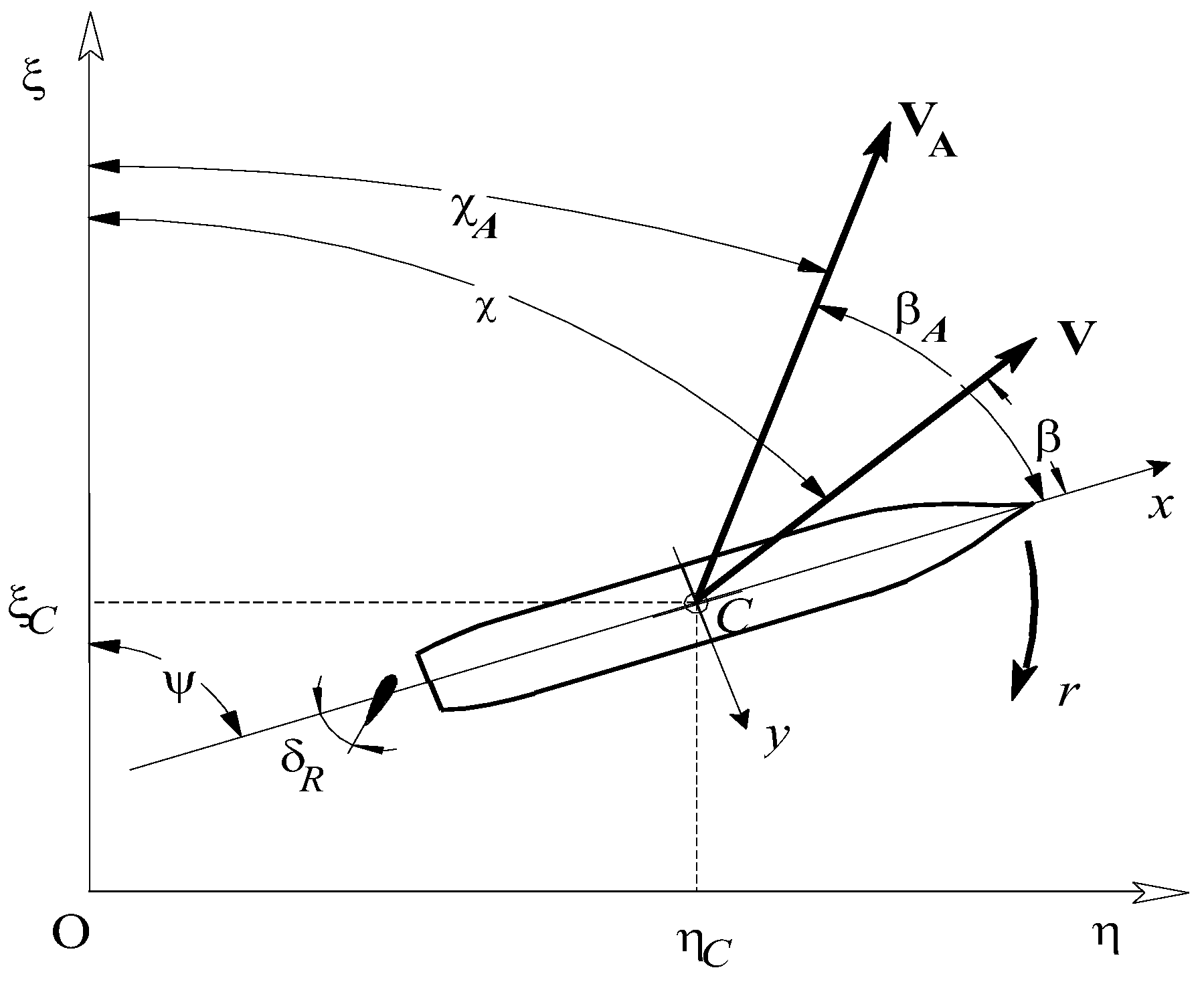
2. Description of the Manoeuvring Tests
3. Neural Network Training
- Rudder angle θ(k);
- RPM(k);
- Sway velocity at previous time step v(k − 1);
- Heading angle at previous time step (k − 1);
- x position at previous time step x(k − 1);
- y position at previous time step y(k − 1);
- Heading angle at current time step (k);
- x position at current time step x(k);
- y position at current time step y(k).
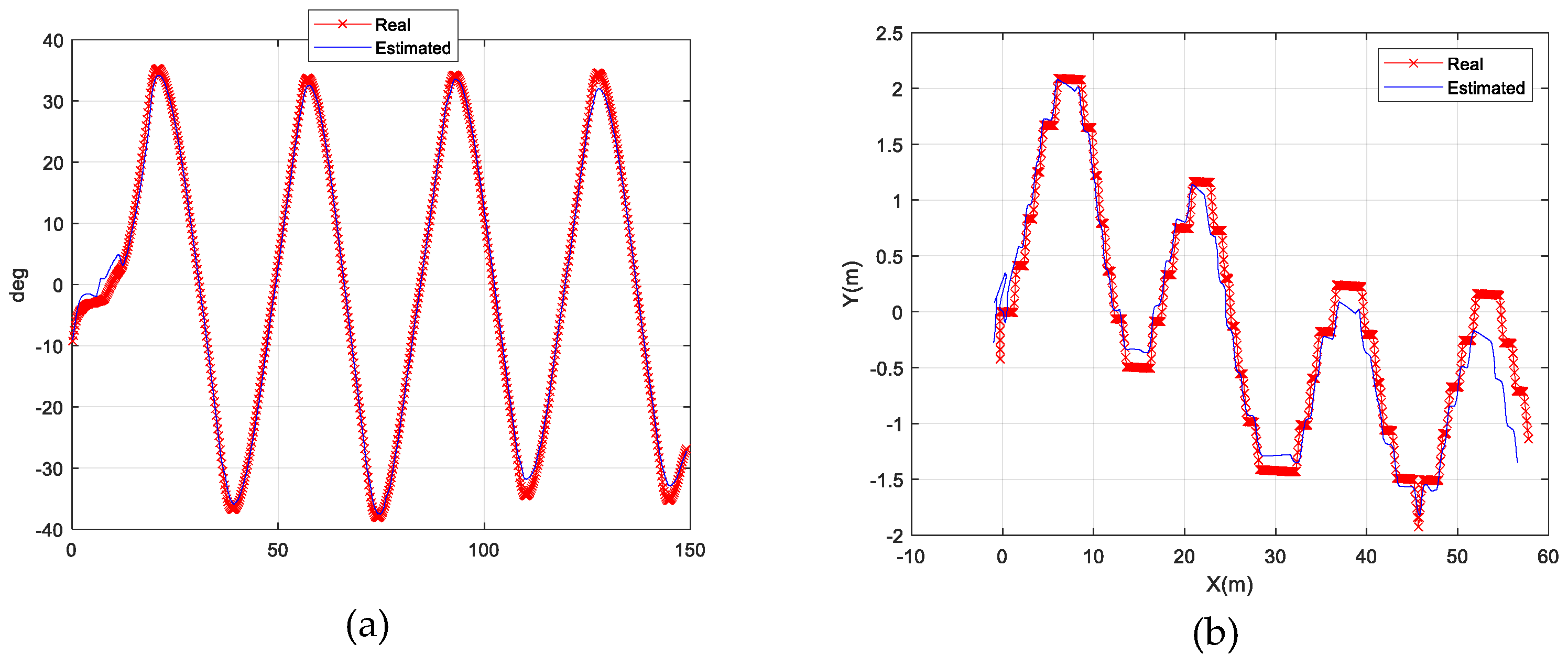
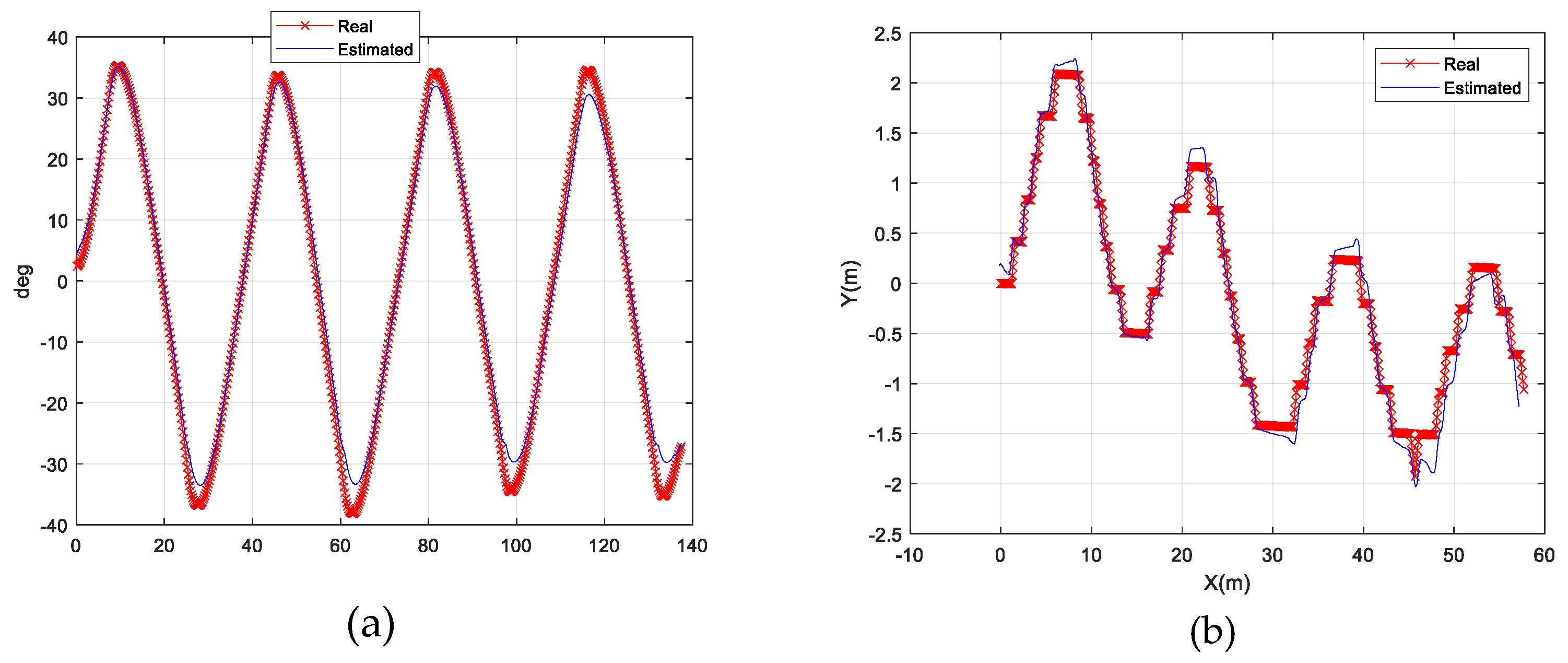
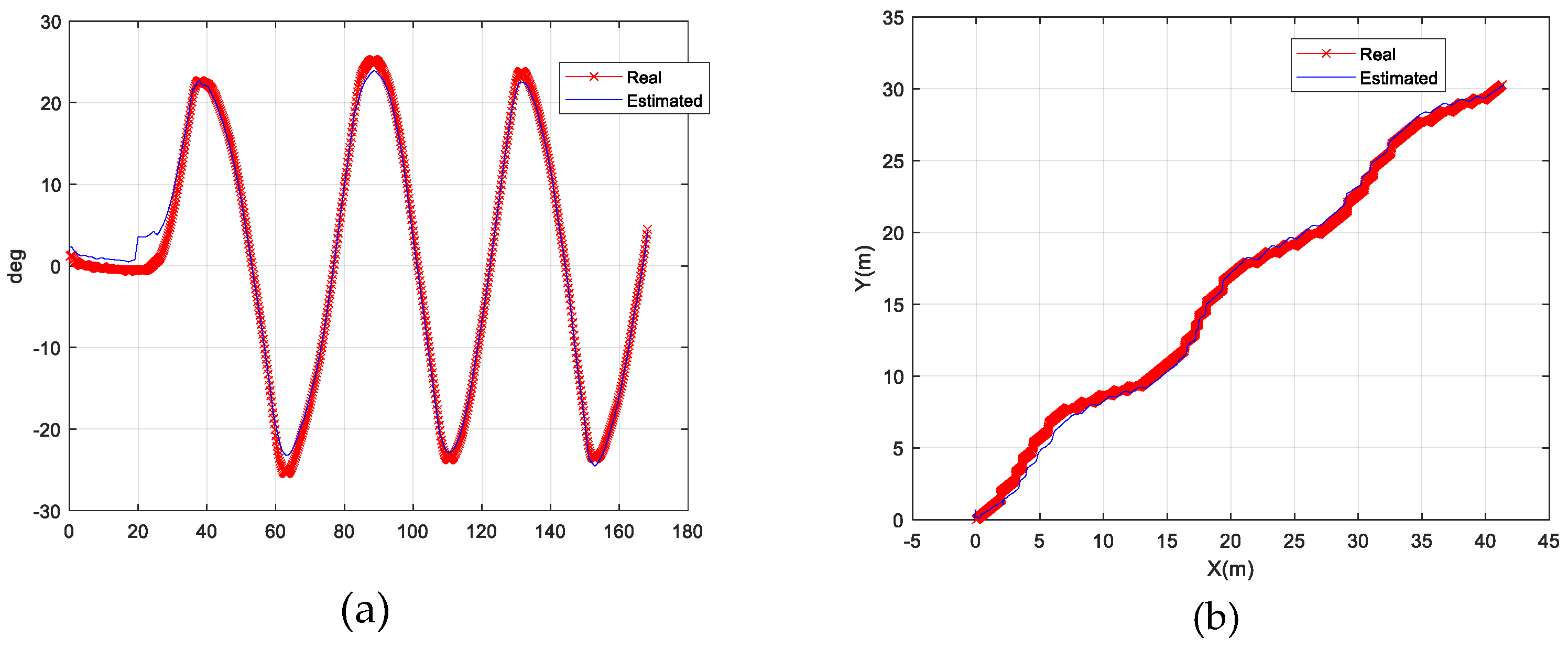
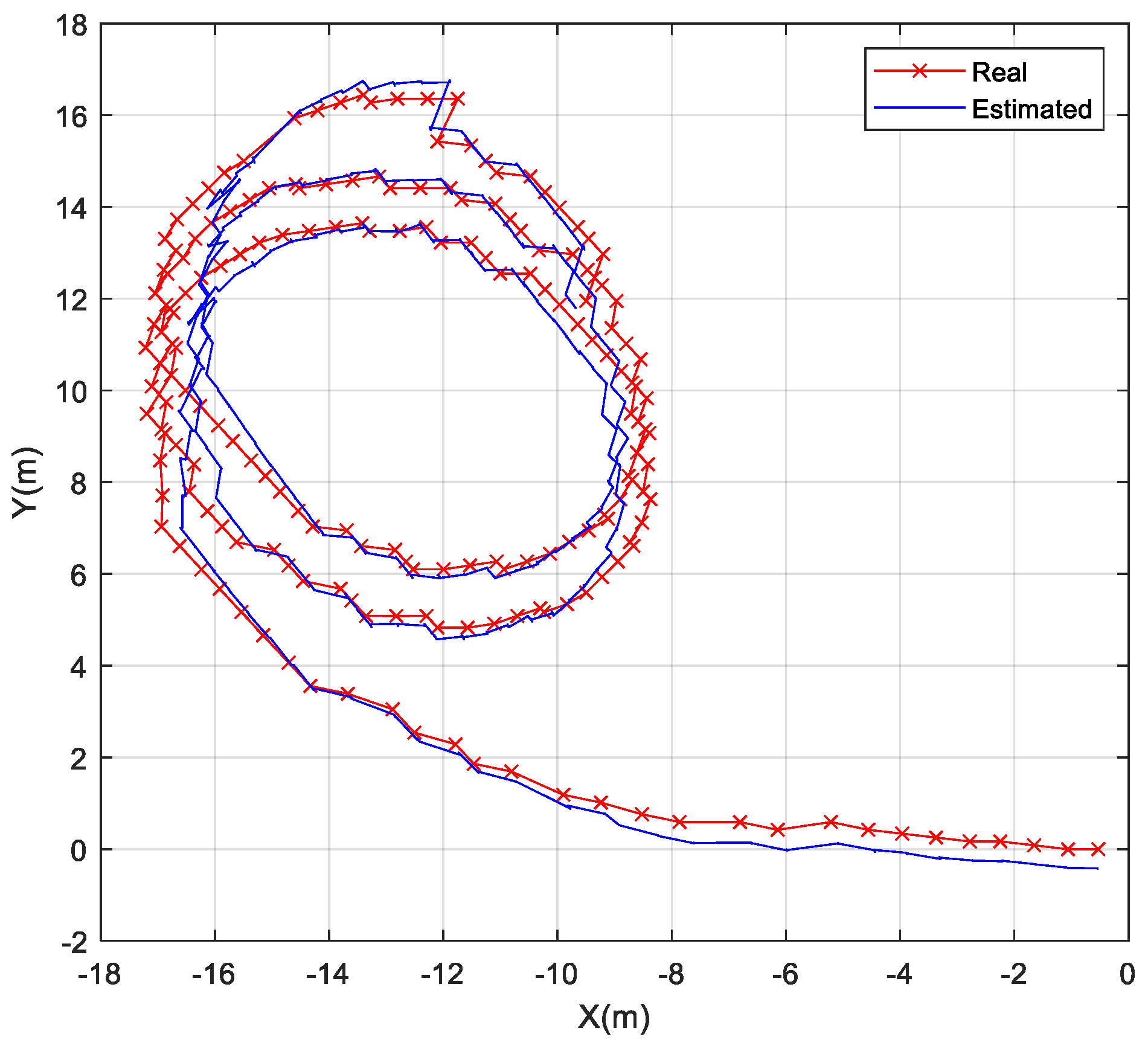
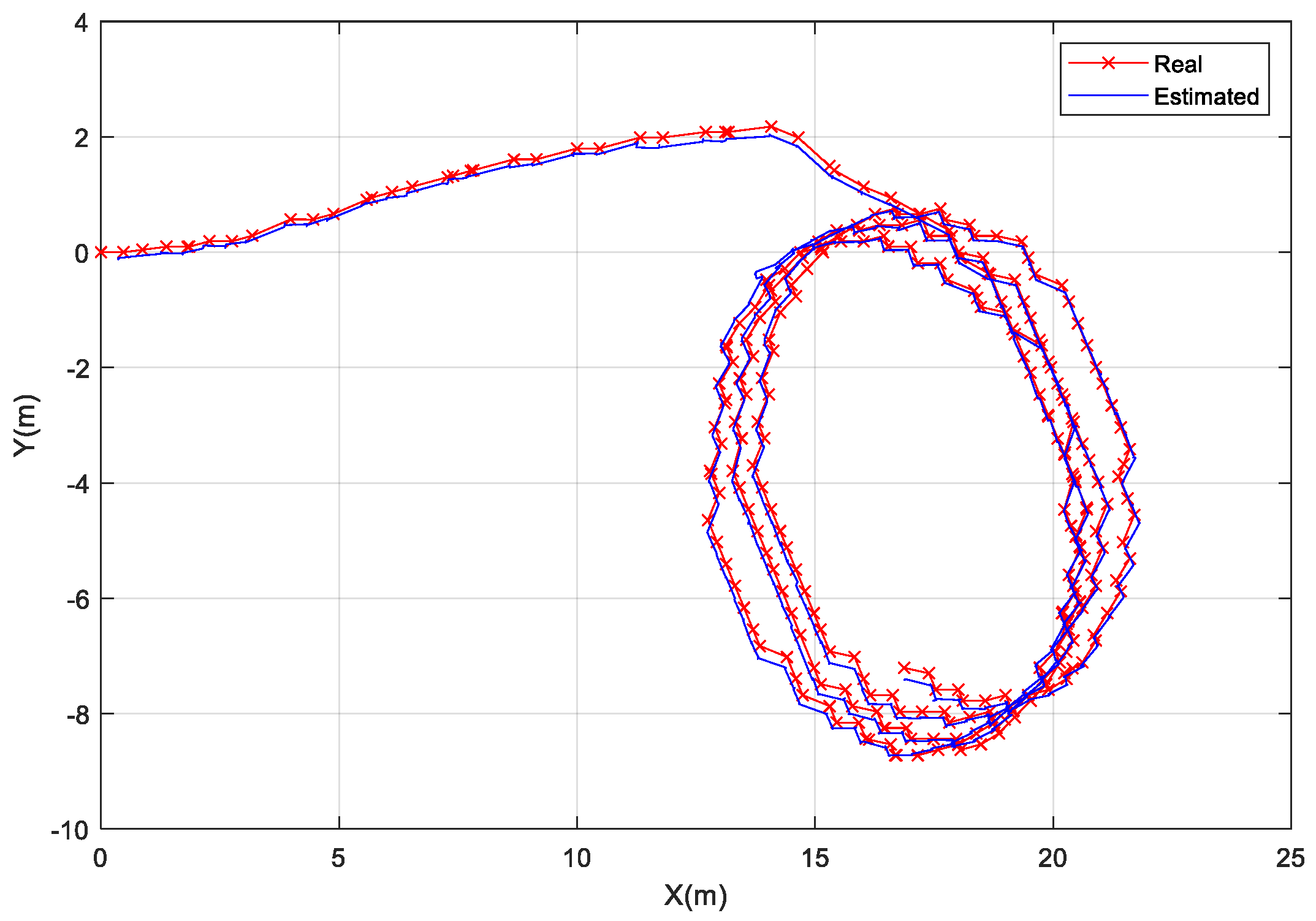
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network |
| RNN | Recursive neural network |
| MMG | Manoeuvring Mathematical Group |
| LSTM | Long short-term memory |
| SVM | Support vector machine |
| CMU | Command and monitoring unit |
| CCU | Communication and control unit |
| HMI | Human–machine interface |
| IES | Industrial Ethernet switch |
| MLP | Multilayer perceptron |
| RPM | Revolutions per minute |
References
- Crane, C.L.; Eda, H.; Landsburg, A.C. Controllability. In Principles of Naval Architecture; Lewis, E.V., Ed.; SNAME: Jersey City, NJ, USA, 1989; Volume 3, pp. 191–422. [Google Scholar]
- Abkowitz, M.A. Measurement of hydrodynamic characteristics from ship maneuvring trials by system identification. SNAME Trans. 1980, 88, 283–318. [Google Scholar]
- Abkowitz, M.A. Measurements of ship resistance, powering and maneuvering coefficients from simple trials during a regular voyage. Trans. SNAME 1988, 96, 97–128. [Google Scholar]
- Ogawa, A.; Kasai, H. On the mathematical model of manoeuvring motion of ships. Int. Shipbuild. Prog. 1978, 25, 306–319. [Google Scholar] [CrossRef]
- Nomoto, K.; Taguchi, T.; Honda, K.; Hirano, S. On the steering qualities of ships. Int. Shipbuild. Prog. 1957, 4, 354–370. [Google Scholar] [CrossRef]
- Sutulo, S.; Guedes Soares, C. Development of a core mathematical model for arbitrary manoeuvres of a shuttle tanker. Appl. Ocean. Res. 2015, 51, 293–308. [Google Scholar] [CrossRef]
- Sutulo, S.; Guedes Soares, C. Mathematical models for simulation of manoeuvring performance of ships. In Marine Technology and Engineering; Guedes Soares, C., Garbatov, Y., Fonseca, N., Teixeira, A.P., Eds.; Taylor & Francis Group: London, UK, 2011; pp. 661–698. [Google Scholar]
- Sutulo, S.; Guedes Soares, C. Review on ship manoeuvrability criteria and standards. J. Mar. Sci. Eng. 2021, 9, 904. [Google Scholar] [CrossRef]
- Sutulo, S.; Guedes Soares, C. On the application of empiric methods for prediction of ship manoeuvring properties and associated uncertainties. Ocean Eng. 2019, 186, 106111. [Google Scholar] [CrossRef]
- Sutulo, S.; Guedes Soares, C. Synthesis of experimental designs of manoeuvring captive-model tests with large number of factors. J. Mar. Sci. Technol. 2004, 9, 32–42. [Google Scholar] [CrossRef]
- Sutulo, S.; Guedes Soares, C. Development of a multifactor regression model of ship manoeuvring forces based on optimized captive-model tests. J. Ship Res. 2006, 50, 311–333. [Google Scholar] [CrossRef]
- Guedes Soares, C.; Sutulo, S.; Francisco, R.A.; Santos, F.M.; Moreira, L. Full-scale measurements of the manoeuvring capabilities of a catamaran. In Proceedings of the International Conference on Hydrodynamics of High Speed Craft, London, UK, 24–25 November 1999; RINA: London, UK, 1999; pp. 1–12. [Google Scholar]
- Guedes Soares, C.; Francisco, R.A.; Moreira, L.; Laranjinha, M. Full-scale measurements of the manoeuvering capabilities of fast patrol vessels, Argos class. Mar. Technol. 2004, 41, 7–16. [Google Scholar]
- Sutulo, S.; Guedes Soares, C. An algorithm for offline identification of ship manoeuvring mathematical models after free-running tests. Ocean Eng. 2014, 79, 10–25. [Google Scholar] [CrossRef]
- Perera, L.P.; Oliveira, P.; Guedes Soares, C. System identification of vessel steering with unstructured uncertainties by persistent excitation maneuvers. IEEE J. Ocean Eng. 2016, 41, 515–528. [Google Scholar] [CrossRef]
- Xu, H.; Hinostroza, M.A.; Hassani, V.; Guedes Soares, C. Real-time parameter estimation of nonlinear vessel steering model using support vector machine. J. Offshore Mech. Arct. Eng. 2019, 141, 061606. [Google Scholar] [CrossRef]
- Wang, Z.; Zou, Z.; Guedes Soares, C. Identification of ship manoeuvring motion based on nu-support vector machine. Ocean Eng. 2019, 183, 270–281. [Google Scholar] [CrossRef]
- Costa, A.C.; Xu, H.T.; Guedes Soares, C. Robust parameter estimation of an empirical manoeuvring model using free-running model test. J. Marit. Sci. Eng. 2021, 9, 1302. [Google Scholar] [CrossRef]
- Sutulo, S.; Moreira, L.; Guedes Soares, C. Mathematical models for ship path prediction in manoeuvring simulation systems. Ocean Eng. 2002, 29, 1–19. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, X.; Cao, X.; Huang, C.; Liu, E.; Qian, S.; Liu, X.; Wu, Y.; Dong, F.; Qiu, C.-W.; et al. Artificial intelligence: A powerful paradigm for scientific research. Innovation 2021, 2, 100179. [Google Scholar] [CrossRef]
- Atluri, G.; Karpatne, A.; Kumar, V. Spatio-temporal data mining: A survey of problems and methods. ACM Comput. Surv. 2017, 51, 1–41. [Google Scholar] [CrossRef]
- Moreira, L.; Guedes Soares, C. Dynamic model of manoeuvrability using recursive neural networks. Ocean Eng. 2003, 30, 1669–1697. [Google Scholar] [CrossRef]
- Mizuno, N.; Kuroda, M.; Okazaki, T.; Ohtsu, K. Minimum time ship maneuvering method using neural network and nonlinear model predictive compensator. Control Eng. Pract. 2007, 15, 757–765. [Google Scholar] [CrossRef]
- Ahmed, Y.A.; Hannan, M.A.; Kamal, I.M. Minimum time ship manoeuvring in narrow water ways under wind disturbances. In Proceedings of the ASME 37th International Conference on Ocean, Offshore and Artic Engineering 2018, Madrid, Spain, 17–22 June 2018. OMAE2018-78435. [Google Scholar]
- Ahmed, Y.A.; Kamal, I.Z.M.; Hannan, M.A. An artificial neural network controller for course changing manoeuvring. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 5714–5719. [Google Scholar] [CrossRef]
- Chen, X.; Meng, X.; Zhao, Y. Genetic algorithm to improve backpropagation neural network ship track prediction. J. Phys. Conf. Ser. 2020, 1650, 032133. [Google Scholar] [CrossRef]
- Theodoropoulos, P.; Spandonidis, C.; Themelis, N.; Giordamlis, C.; Fassois, S. Evaluation of different deep-learning models for the prediction of a ship’s propulsion power. J. Mar. Sci. Eng. 2021, 9, 116. [Google Scholar] [CrossRef]
- Su, Y.; Lin, J.; Zhao, D.; Guo, C.; Wang, C.; Guo, H. Real-time prediction of large-scale ship model vertical acceleration based on recurrent neural network. J. Mar. Sci. Eng. 2020, 8, 777. [Google Scholar] [CrossRef]
- Moreira, L.; Guedes Soares, C. Analysis of recursive neural networks performance trained with noisy manoeuvring data. In Maritime Transportation and Exploitation of Ocean and Coastal Resources; Guedes Soares, C., Garbatov, Y., Fonseca, N., Eds.; Taylor & Francis Group: Oxfordshire, UK, 2005; pp. 733–744. [Google Scholar]
- Moreira, L.; Guedes Soares, C. Recursive neural network model of catamaran manoeuvring. Int. J. Marit. Eng. 2012, 154, A-121–A-130. [Google Scholar] [CrossRef]
- IMO. Interim standards for ship manoeuvrability. IMO Resolut. A 1993, 751. [Google Scholar]
- Woo, J.; Park, J.; Yu, C.; Kim, N. Dynamic model identification of unmanned surface vehicles using deep learning network. Appl. Ocean Res. 2018, 78, 123–133. [Google Scholar] [CrossRef]
- Luo, W.; Moreira, L.; Guedes Soares, C. Manoeuvring simulation of catamaran by using implicit models based on support vector machines. Ocean Eng. 2014, 82, 150–159. [Google Scholar] [CrossRef]
- Wang, Z.; Guedes Soares, C.; Zou, Z.J. Optimal design of excitation signal for identification of nonlinear ship manoeuvring model. Ocean Eng. 2020, 196, 106778. [Google Scholar] [CrossRef]
- Xu, H.; Guedes Soares, C. Manoeuvring modelling of a containership in shallow water based on optimal truncated nonlinear kernel-based least square support vector machine and quantum-inspired evolutionary algorithm. Ocean Eng. 2020, 195, 106676. [Google Scholar] [CrossRef]
- Araújo, J.P.; Moreira, L.; Guedes Soares, C. Modelling ship manoeuvrability using recurrent neural networks. In Developments in Maritime Technology and Engineering; Guedes Soares, C., Santos, T.A., Eds.; Taylor and Francis: London, UK, 2021; Volume 2, pp. 131–140. [Google Scholar]
- Luo, W.; Zhang, Z. Modeling of ship maneuvering motion using neural networks. J. Mar. Sci. Appl. 2016, 15, 426–432. [Google Scholar] [CrossRef]
- Rajesh, G.; Bhattacharyya, S. System identification for nonlinear maneuvering of large tankers using artificial neural network. Appl. Ocean Res. 2008, 30, 256–263. [Google Scholar] [CrossRef]
- Hess, D.; Faller, W. Simulation of ship maneuvers using recursive neural networks. In Proceedings of the 23rd Symposium on Naval Hydrodynamics, Val de Reuil, France, 17–22 September 2000; pp. 17–22. [Google Scholar]
- Xu, H.; Hinostroza, M.A.; Guedes Soares, C. Estimation of hydrodynamic coefficients of a nonlinear manoeuvring mathematical model with free-running ship model tests. Int. J. Marit. Eng. RINA Trans. Part A 2018, 160, A-213–A-215. [Google Scholar] [CrossRef]
- Hinostroza, M.; Xu, H.; Guedes Soares, C. Path-planning and path-following control system for autonomous surface vessel. In Maritime Transportation and Harvesting of Sea Resources; Guedes Soares, C., Teixeira, A.P., Eds.; Taylor & Francis Group: London, UK, 2018; pp. 991–998. [Google Scholar]
- Hinostroza, M.; Xu, H.; Guedes Soares, C. Motion-planning, guidance and control system for autonomous surface vessel. ASME J. Offshore Mech Arct. Eng. 2021, 143, 041202. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2006. [Google Scholar]
- Tiwari, S.; Naresh, R.; Jha, R. Comparative study of backpropagation algorithms in neural network based identification of power system. Int. J. Comput. Sci. Inf. Technol. 2013, 5, 93–107. [Google Scholar] [CrossRef]



| Chemical Tanker | Real Ship | Model |
|---|---|---|
| Length (m) | 170 | 2.588 |
| Breadth (m) | 28 | 0.426 |
| Draft (estimated at the tests) (m) | 6.7 | 0.102 |
| Propeller diameter (m) | 5.4 | 0.082 |
| Design speed (m/s) | 8 | 0.984 |
| Scaling coefficient | - | 65.7 |
| # | Parameter | Unit | Equipment |
|---|---|---|---|
| 1 | Geographical coordinates | deg | Real-time kinematic GPS |
| 2 | Surge and sway | m | IXSEA inertial sensor |
| 3 | Roll and pitch angles | deg | IXSEA inertial sensor |
| 4 | Heading angle | deg | IXSEA inertial sensor |
| 5 | Relative wind speed | m/s | Ultrasonic anemometer |
| 6 | Relative wind direction | deg | Ultrasonic anemometer |
| 7 | Rudder angle | deg | Incremental encoder |
| 8 | Propeller rev. | rpm | Incremental encoder |
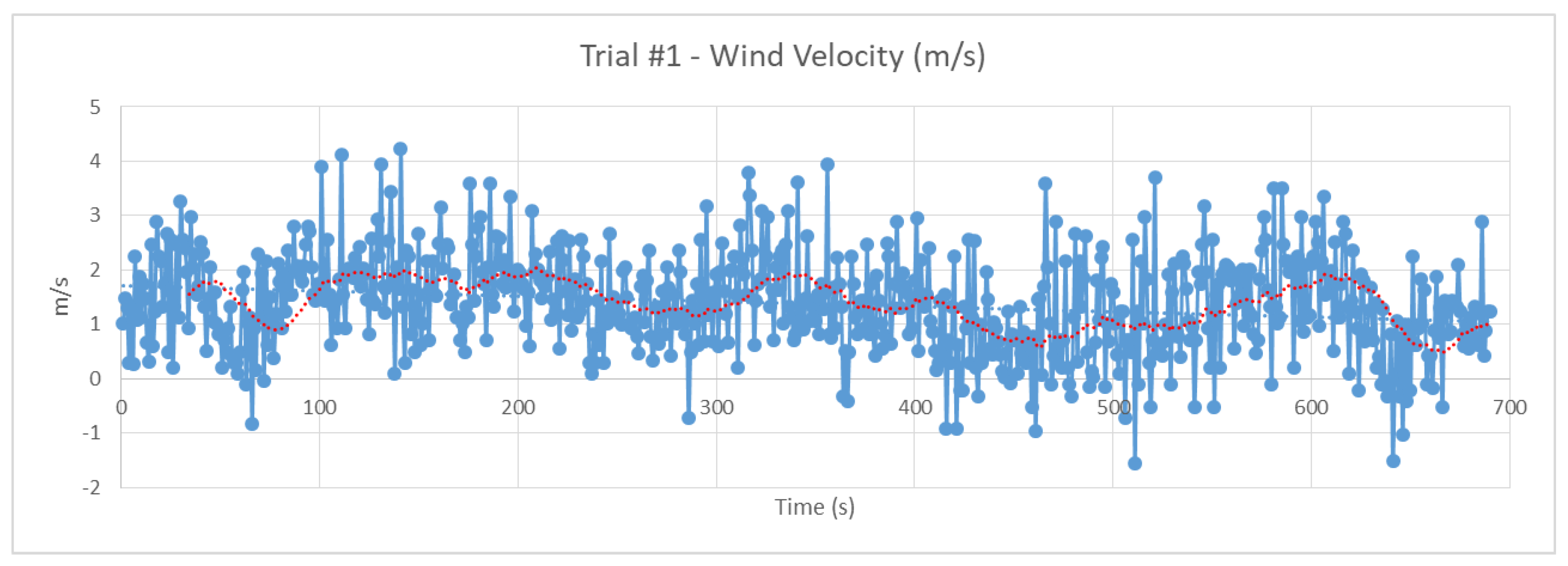
| Maneuvere | Data Points Available | Rudder Angle Range (Degrees) | Average RPM | Average Realwind Speed (Knots) | Wind Conditions |
|---|---|---|---|---|---|
| ZigZag1 | 748 | [−30, 30] | 856 | 2.7 (max 8.6) | Light Air to Gentle Breeze |
| ZigZag2 | 614 | [−30, 30] | 873 | 2.2 (max 7.9) | Light Air to Gentle Breeze |
| ZigZag3 | 565 | [−20, 20] | 844 | 2.1 (max 8.3) | Light Air to Gentle Breeze |
| ZigZag4 | 954 | [−20, 20] | 669 | 3.0 (max 10.4) | Light Air to Gentle Breeze |
| Turning1 | 992 | [0, 20] | 487 | 1.3 (max 11.4) | Light Air to Moderate Breeze |
| Turning2 | 1356 | [0, 26] | 492 | 1.2 (max 11.8) | Light Air to Moderate Breeze |
| Set | ||||
|---|---|---|---|---|
| Method | Training | Validation | Test | All |
| Levenberg–Marquardt | 0.99332 | 0.994538 | 0.99202 | 0.99333 |
| Scaled Conjugate Gradient | 0.99339 | 0.990813 | 0.9961 | 0.9934 |
| Bayesian Regularization | 0.99259 | 0.993147 | 0.99753 | 0.99314 |
| Set | ||||
|---|---|---|---|---|
| Method | Training | Validation | Test | All |
| Levenberg–Marquardt | 0.99998 | 0.999978 | 0.99998 | 0.99998 |
| Scaled Conjugate Gradient | 0.99998 | 0.999981 | 0.99998 | 0.99998 |
| Bayesian Regularization | 0.99998 | 0.99998 | 0.99998 | 0.99998 |
| Set | ||||
|---|---|---|---|---|
| Method | Training | Validation | Test | All |
| Levenberg–Marquardt | 0.99995 | 0.999954 | 0.99995 | 0.99995 |
| Scaled Conjugate Gradient | 0.99995 | 0.999949 | 0.99995 | 0.99995 |
| Bayesian Regularization | 0.99995 | 0.999948 | 0.99995 | 0.99995 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreira, L.; Guedes Soares, C. Simulating Ship Manoeuvrability with Artificial Neural Networks Trained by a Short Noisy Data Set. J. Mar. Sci. Eng. 2023, 11, 15. https://doi.org/10.3390/jmse11010015
Moreira L, Guedes Soares C. Simulating Ship Manoeuvrability with Artificial Neural Networks Trained by a Short Noisy Data Set. Journal of Marine Science and Engineering. 2023; 11(1):15. https://doi.org/10.3390/jmse11010015
Chicago/Turabian StyleMoreira, Lúcia, and C. Guedes Soares. 2023. "Simulating Ship Manoeuvrability with Artificial Neural Networks Trained by a Short Noisy Data Set" Journal of Marine Science and Engineering 11, no. 1: 15. https://doi.org/10.3390/jmse11010015
APA StyleMoreira, L., & Guedes Soares, C. (2023). Simulating Ship Manoeuvrability with Artificial Neural Networks Trained by a Short Noisy Data Set. Journal of Marine Science and Engineering, 11(1), 15. https://doi.org/10.3390/jmse11010015







