Power Tracking Control of Marine Boiler-Turbine System Based on Fractional Order Model Predictive Control Algorithm
Abstract
:1. Introduction
2. Boiler-Turbine System
3. Nonlinear Distributed MPC for the Boiler-Turbine System
3.1. The Basic of the EPSAC
3.2. The Fractional Order MPC
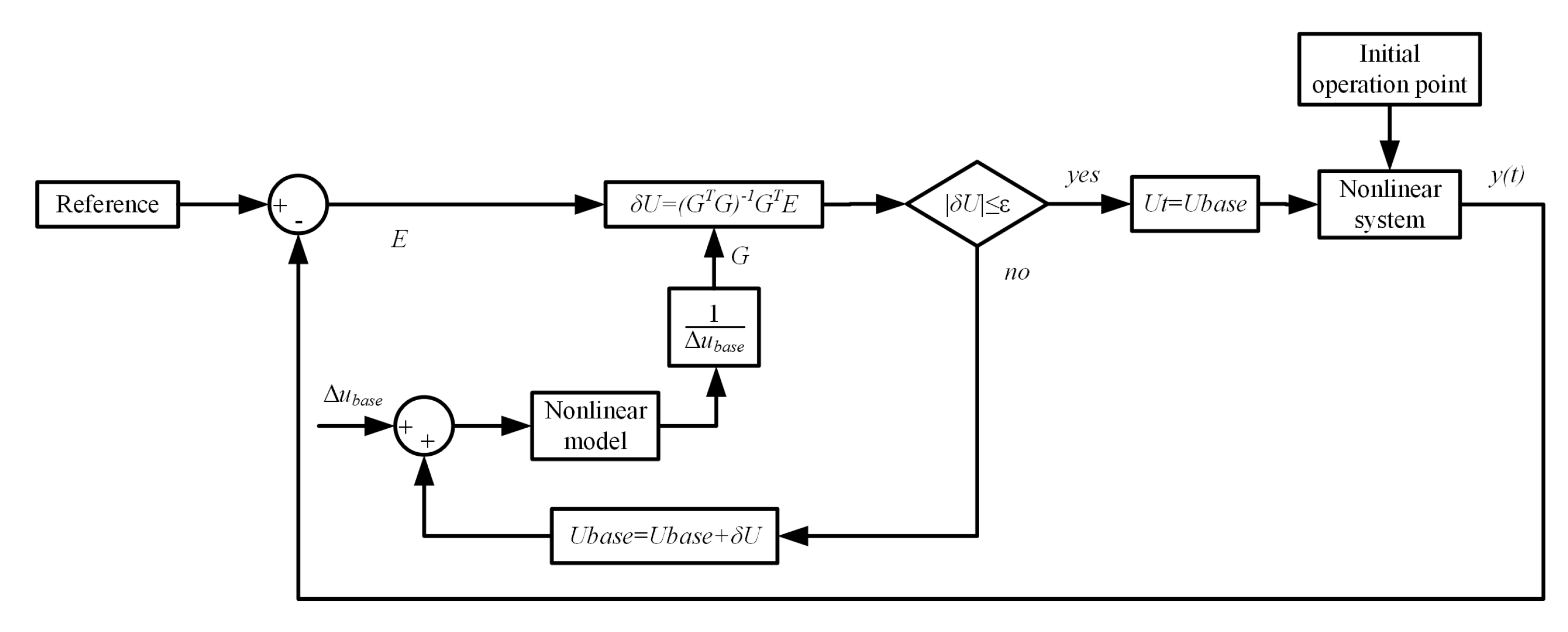
3.3. Application of the Fractional Order EPSAC to the Nonlinear MIMO System with Distributed Structure
- Choose an initial base input sequence , this part should be as close as possible to the optimal input to make the close to zero, which means that the term equals to zero;
- After chooseing the base future input, the can be calculated. The is not close to zero at the moment;
- Take the from the second step as the new , and calculate again.
- Repeat step 2 and 3 until the is as close as possible to zero, then the can be applied to the system at the time .
| Algorithm 1 Algorithm for the distributed MPC |
|
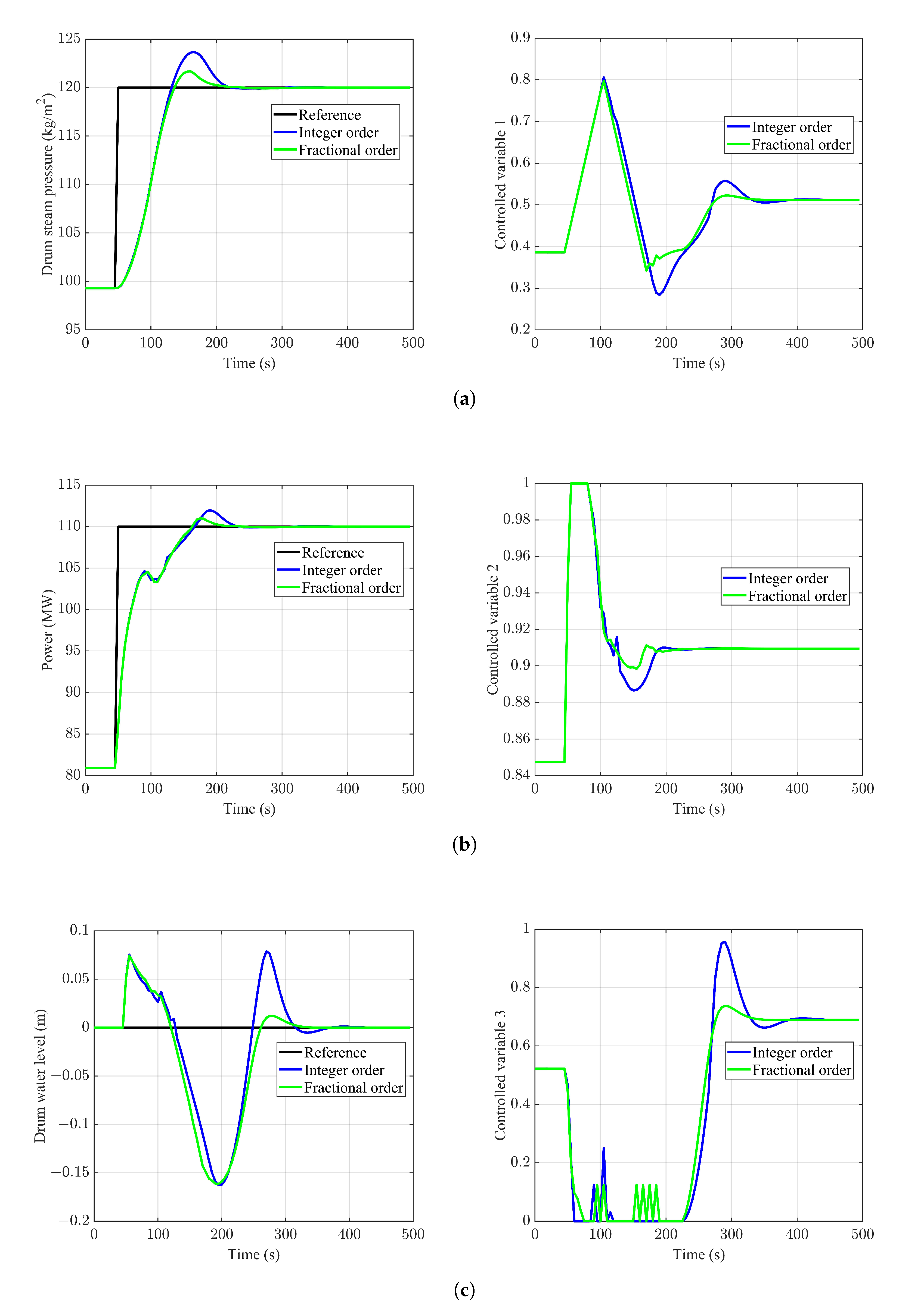
4. Simulation of the Fractional Order MPC on Boiler-Turbine System
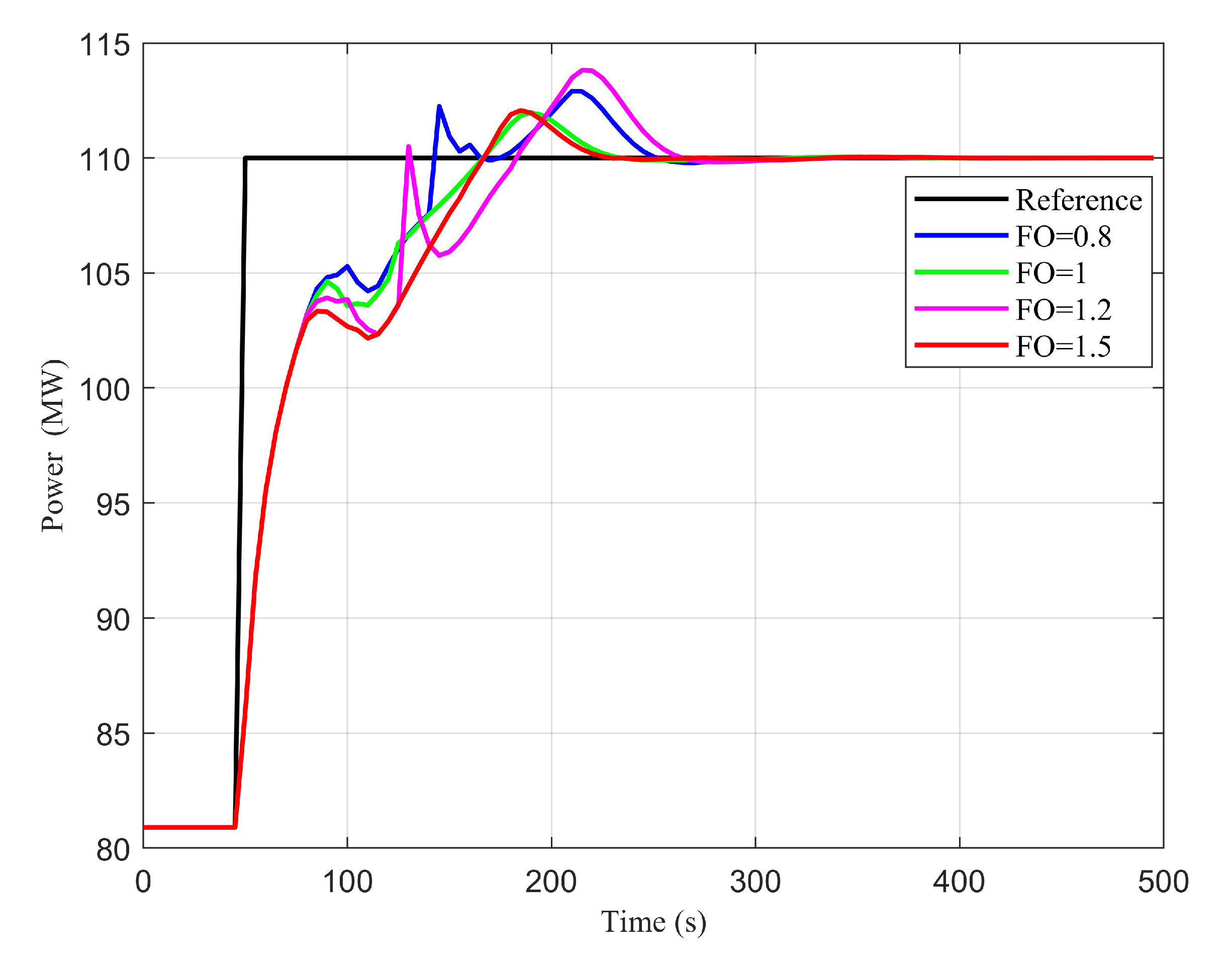
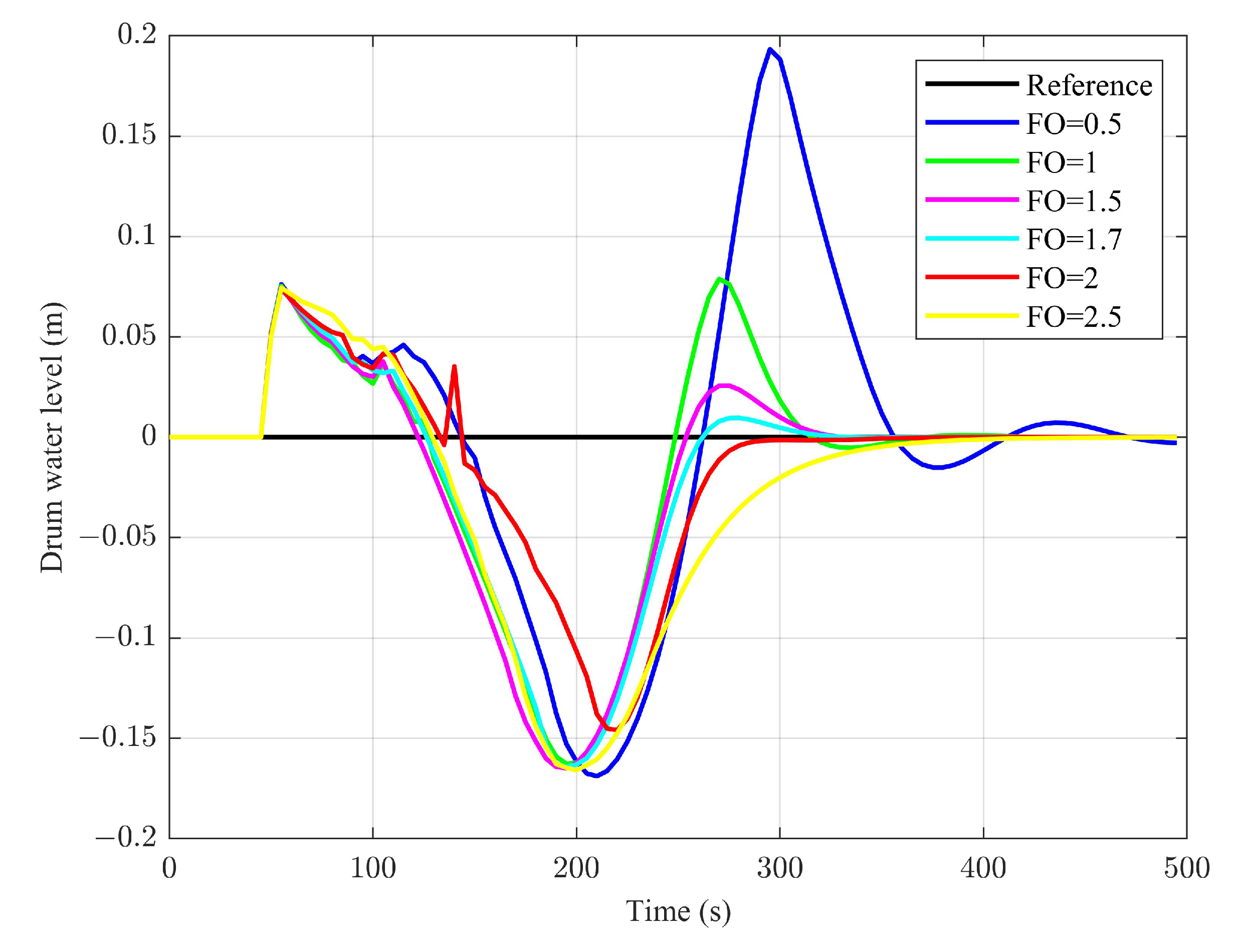
4.1. The Influence of Fractional Order Terms to the Different Loops
4.2. The Influence of Fractional Order Terms to the Different Loops
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, F.; Tang, C.; Antonietti, M. Natural and artificial humic substances to manage minerals, ions, water, and soil microorganisms. Chem. Soc. Rev. 2021, 50, 6221–6239. [Google Scholar] [CrossRef] [PubMed]
- Zeńczak, W.; Gromadzińska, A.K. Preliminary Analysis of the Use of Solid Biofuels in a Ship’s Power System. Pol. Marit. Res. 2020, 27, 67–79. [Google Scholar] [CrossRef]
- Başhan, V.; Demirel, H. Application of Fuzzy Dematel Technique to Assess Most Common Critical Operational Faults of Marine Boilers. Politek. Derg. 2019, 22, 545–555. [Google Scholar] [CrossRef]
- Luschtinetz, T.; Zeńczak, W.; Łuszczyński, D. The Selected Results of the Experimental Research of Solid Fuel Pneumatic Transportation to Ship’s Boiler. Manag. Syst. Prod. Eng. 2019, 27, 144–148. [Google Scholar] [CrossRef]
- Taler, J.; Zima, W.; Ocłoń, P.; Grądziel, S.; Taler, D.; Cebula, A.; Jaremkiewicz, M.; Korzeń, A.; Cisek, P.; Kaczmarski, K.; et al. Mathematical model of a supercritical power boiler for simulating rapid changes in boiler thermal loading. Energy 2019, 175, 580–592. [Google Scholar] [CrossRef]
- Lu, X.; Liu, Z.; Ma, L.; Wang, L.; Zhou, K.; Feng, N. A robust optimization approach for optimal load dispatch of community energy hub. Appl. Energy 2020, 259, 114195. [Google Scholar] [CrossRef]
- Piraisoodi, T.; Iruthayarajan, M.W.; Kadhar, K.M.A. An Optimized Nonlinear Controller Design for Boiler–Turbine System Using Evolutionary Algorithms. IETE J. Res. 2018, 64, 451–462. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, Y.; Li, X. A dynamic model used for controller design for fast cut back of coal-fired boiler-turbine plant. Energy 2018, 144, 526–534. [Google Scholar] [CrossRef]
- Su, Z.g.; Zhao, G.; Yang, J.; Li, Y.g. Disturbance Rejection of Nonlinear Boiler–Turbine Unit Using High-Order Sliding Mode Observer. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 5432–5443. [Google Scholar] [CrossRef]
- Liu, X.; Cui, J. Economic model predictive control of boiler-turbine system. J. Process. Control. 2018, 66, 59–67. [Google Scholar] [CrossRef]
- Tian, Z.; Yuan, J.; Xu, L.; Zhang, X.; Wang, J. Model-based adaptive sliding mode control of the subcritical boiler-turbine system with uncertainties. ISA Trans. 2018, 79, 161–171. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Liu, Y.; Lu, J.; Ling, J.; Luan, Z.; Chen, M. A New Integral Critic Learning for Optimal Tracking Control with Applications to Boiler-Turbine Systems. Optim. Control Appl. Methods 2021. [Google Scholar] [CrossRef]
- Köhler, J.; Soloperto, R.; Müller, M.A.; Allgöwer, F. A computationally efficient robust model predictive control framework for uncertain nonlinear systems. IEEE Trans. Autom. Control 2020, 66, 794–801. [Google Scholar] [CrossRef]
- Reynolds, J.; Rezgui, Y.; Kwan, A.; Piriou, S. A zone-level, building energy optimisation combining an artificial neural network, a genetic algorithm, and model predictive control. Energy 2018, 151, 729–739. [Google Scholar] [CrossRef]
- Chi, C.; Cajo, R.; Zhao, S.; Liu, G.P.; Ionescu, C.M. Fractional Order Distributed Model Predictive Control of Fast and Strong Interacting Systems. Fractal Fract. 2022, 6, 179. [Google Scholar] [CrossRef]
- Ghita, M.; Cajo Diaz, R.A.; Birs, I.R.; Copot, D.; Ionescu, C.M. Ergonomic and economic office light level control. Energies 2022, 15, 734. [Google Scholar] [CrossRef]
- Song, D.; Chang, Q.; Zheng, S.; Yang, S.; Yang, J.; Joo, Y.H. Adaptive model predictive control for yaw system of variable-speed wind turbines. J. Mod. Power Syst. Clean Energy 2020, 9, 219–224. [Google Scholar] [CrossRef]
- Sorcia-Vázquez, F.; Garcia-Beltran, C.; Valencia-Palomo, G.; Brizuela-Mendoza, J.; Rumbo-Morales, J. Decentralized robust tube-based model predictive control: Application to a four-tank-system. Rev. Mex. Ingeniería Química 2020, 19, 1135–1151. [Google Scholar] [CrossRef]
- Rumbo Morales, J.Y.; López López, G.; Alvarado, V.M.; Torres Cantero, C.A.; Azcaray Rivera, H.R. Optimal Predictive Control for a Pressure Oscillation Adsorption Process for Producing Bioethanol. Comput. Sist. 2019, 23, 1593–1617. [Google Scholar]
- Morales, J.Y.R.; López, G.L.; Martínez, V.M.A.; Vázquez, F.d.J.S.; Mendoza, J.A.B.; García, M.M. Parametric study and control of a pressure swing adsorption process to separate the water-ethanol mixture under disturbances. Sep. Purif. Technol. 2020, 236, 116214. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Zhang, Y. Model predictive current control for PMSM drives with parameter robustness improvement. IEEE Trans. Power Electron. 2018, 34, 1645–1657. [Google Scholar] [CrossRef]
- Shen, C.; Shi, Y.; Buckham, B. Trajectory tracking control of an autonomous underwater vehicle using Lyapunov-based model predictive control. IEEE Trans. Ind. Electron. 2017, 65, 5796–5805. [Google Scholar] [CrossRef]
- Zhu, H.; Zhao, G.; Sun, L.; Lee, K.Y. Nonlinear predictive control for a boiler–turbine unit based on a local model network and immune genetic algorithm. Sustainability 2019, 11, 5102. [Google Scholar] [CrossRef]
- Zhang, Y.; Decardi-Nelson, B.; Liu, J.; Shen, J.; Liu, J. Zone economic model predictive control of a coal-fired boiler-turbine generating system. Chem. Eng. Res. Des. 2020, 153, 246–256. [Google Scholar] [CrossRef]
- Liu, X.; Cui, J. Fuzzy economic model predictive control for thermal power plant. IET Control Theory Appl. 2019, 13, 1113–1120. [Google Scholar] [CrossRef]
- Wang, G.; Wu, J.; Ma, X. A nonlinear state-feedback state-feedforward tracking control strategy for a boiler-turbine unit. Asian J. Control 2020, 22, 2004–2016. [Google Scholar] [CrossRef]
- Kong, L.; Yuan, J. Disturbance-observer-based fuzzy model predictive control for nonlinear processes with disturbances and input constraints. ISA Trans. 2019, 90, 74–88. [Google Scholar] [CrossRef]
- Cui, J.; Chai, T.; Liu, X. Deep-neural-network-based economic model predictive control for ultrasupercritical power plant. IEEE Trans. Ind. Inform. 2020, 16, 5905–5913. [Google Scholar] [CrossRef]
- Sanchez, R.O.; Rumbo Morales, J.Y.; Ortiz Torres, G.; Pérez Vidal, A.F.; Valdez Resendiz, J.E.; Sorcia Vázquez, F.d.J.; Nava, N.V. Discrete State-Feedback Control Design with D-Stability and Genetic Algorithm for LED Driver Using a Buck Converter. Int. Trans. Electr. Energy Syst. 2022, 2022, 8165149. [Google Scholar] [CrossRef]
- Nedić, A.; Liu, J. Distributed optimization for control. Annu. Rev. Control Robot. Auton. Syst. 2018, 1, 77–103. [Google Scholar] [CrossRef]
- Bell, R.; Åström, K.J. Dynamic Models for Boiler-Turbine-Alternator Units: Data Logs and Parameter Estimation for a 160 MW Unit; Technical Reports; Lund Institute of Technology: Lund, Sweden, 1987; TRFT-3192. [Google Scholar]
- De Keyser, R. Model based predictive control for linear systems. In UNESCO Encyclopaedia of Life Support Systems, Robotics and Automation; Article Contribution 6.43.16.1; Eolss Publishers Co., Ltd.: Oxford, UK, 2003; Volume XI. [Google Scholar]
- De Keyser, R.; Ionescu, C.M. The disturbance model in model based predictive control. In Proceedings of the Proceedings of 2003 IEEE Conference on Control Applications, Istanbul, Turkey, 25 June 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 1, pp. 446–451. [Google Scholar]
- Fernandez, E.; Ipanaque, W.; Cajo, R.; De Keyser, R. Classical and advanced control methods applied to an anaerobic digestion reactor model. In Proceedings of the 2019 IEEE CHILEAN Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), Valparaiso, Chile, 13–27 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–7. [Google Scholar]
- Romero, M.; de Madrid, A.P.; Vinagre, B.M. Arbitrary real-order cost functions for signals and systems. Signal Process. 2011, 91, 372–378. [Google Scholar] [CrossRef]
- Zhao, S.; Cajo, R.; De Keyser, R.; Liu, S.; Ionescu, C.M. Nonlinear predictive control applied to steam/water loop in large scale ships. IFAC-PapersOnLine 2019, 52, 868–873. [Google Scholar] [CrossRef]
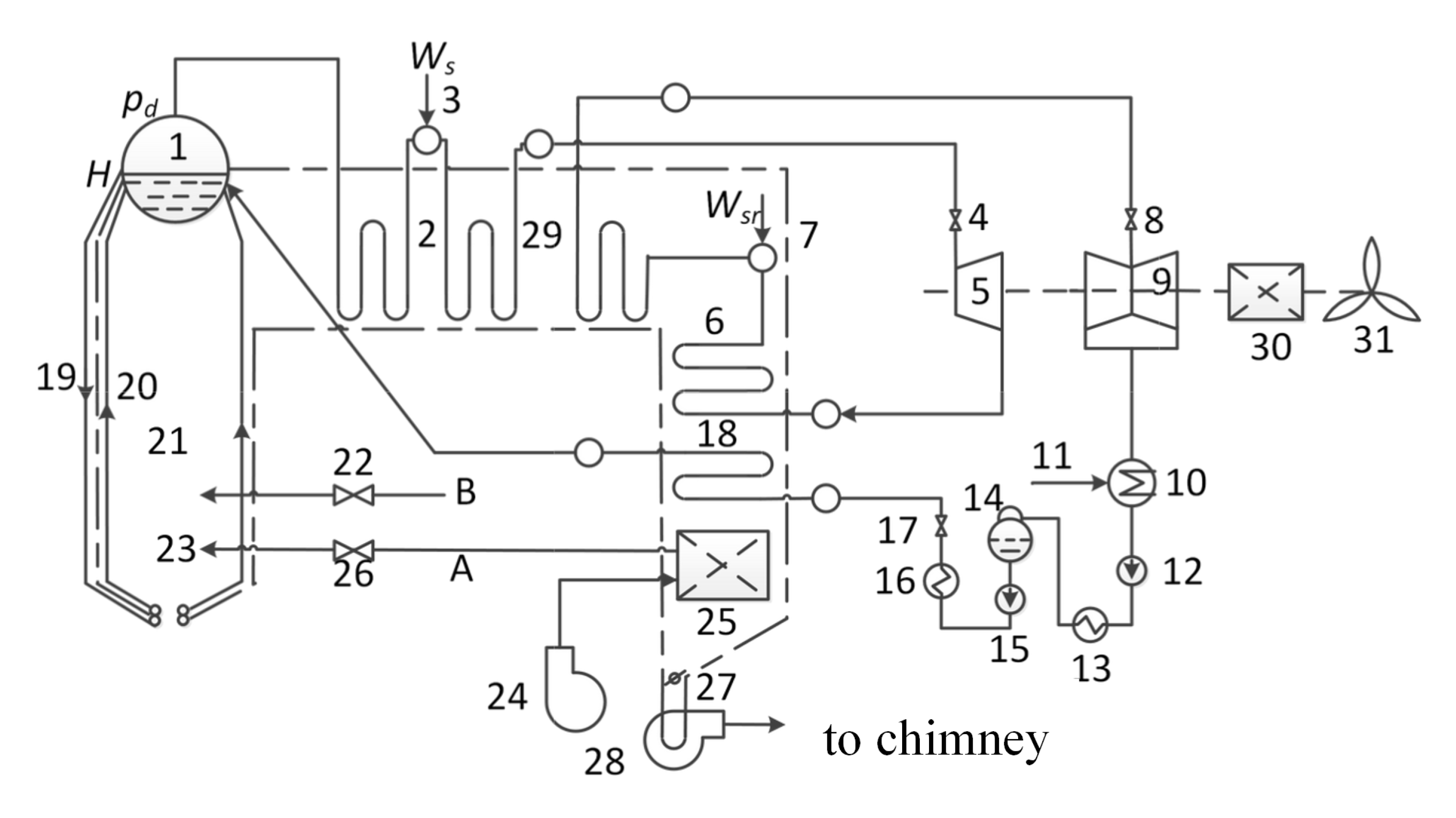

| Operating Point | Pressure | Power | Density |
|---|---|---|---|
| 1 | kg/m2 | MW | 396 |
| 2 | 120 kg/m2 | 110 MW | 331 |
| Parameters | |||||
|---|---|---|---|---|---|
| Values | , , samples | 5s | , , samples | 1 | 100 |
| Loops | Fractional Order Terms |
|---|---|
| Drum steam pressure loop | [0.5, 1, 1.5, 3] |
| Power loop | [0.8, 1, 1.2, 1.5] |
| Drum water level loop | [0.5, 1, 1.7, 2, 2.5] |
| Index | Drum Steam Pressure | Power | Drum Water Level | |
|---|---|---|---|---|
| MPC | 2.0072 | 1.5837 | 3.5389 | |
| FOMPC | 1.8342 | 1.4955 | 3.4534 | |
| MPC | 1.1961 | 0.1068 | 18.8118 | |
| FOMPC | 0.9444 | 0.1042 | 17.1870 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Wang, S.; Cajo, R.; Ren, W.; Li, B. Power Tracking Control of Marine Boiler-Turbine System Based on Fractional Order Model Predictive Control Algorithm. J. Mar. Sci. Eng. 2022, 10, 1307. https://doi.org/10.3390/jmse10091307
Zhao S, Wang S, Cajo R, Ren W, Li B. Power Tracking Control of Marine Boiler-Turbine System Based on Fractional Order Model Predictive Control Algorithm. Journal of Marine Science and Engineering. 2022; 10(9):1307. https://doi.org/10.3390/jmse10091307
Chicago/Turabian StyleZhao, Shiquan, Sizhe Wang, Ricardo Cajo, Weijie Ren, and Bing Li. 2022. "Power Tracking Control of Marine Boiler-Turbine System Based on Fractional Order Model Predictive Control Algorithm" Journal of Marine Science and Engineering 10, no. 9: 1307. https://doi.org/10.3390/jmse10091307
APA StyleZhao, S., Wang, S., Cajo, R., Ren, W., & Li, B. (2022). Power Tracking Control of Marine Boiler-Turbine System Based on Fractional Order Model Predictive Control Algorithm. Journal of Marine Science and Engineering, 10(9), 1307. https://doi.org/10.3390/jmse10091307











