Abstract
Focusing on dynamic positioning (DP) systems for ships, which are subject to environmental disturbances and actuator constraints, this paper presents a finite-time controller that uses a disturbance observer with the aid of a backstepping technique. First, to estimate the time-varying and unknown environmental disturbances in finite time, two sliding-mode disturbance observers are constructed. Specifically, an adaptive disturbance observer (ADO) effectively decreases undesired chattering without the need for prior information on environmental disturbances. Then, to handle the actuator constraints, the designed control forces are distributed into multiple actuators using a control allocation algorithm to obtain the actual forces. Next, an auxiliary dynamic system is built to compensate for velocity tracking errors induced by the mismatch of the DP control law and thruster forces. Then, with the designed ADO and the auxiliary dynamic system, a finite-time controller with a fast exponential-reaching law is designed; this ensures that the positioning errors and the sliding surface converge to zero at a fast convergence rate. Finally, numerical simulations are presented: these present a cable-laying ship experiencing wind, currents, and waves in different sea states. The results show the effectiveness of the presented control scheme.
1. Introduction
A dynamic positioning (DP) system maintains a ship’s position and heading or moves a ship along a predetermined trajectory by employing its thruster system [1]. In the 1960s, DP controllers were presented using conventional control methods [2]. Additionally, research into DP nonlinear control design gained more attention in the 1990s. In [3], a nonlinear observer backstepping controller was presented for DP systems, and its globally exponentially stable (GES) quality was illustrated via the Lyapunov stability theory. In [4], a passive and GES nonlinear observer was developed using the nonlinear kinematic equation of motion to estimate low-frequency position, the velocities of ships, and environmental disturbances, where environmental disturbances were defined as slowly varying biases induced by wind, currents, and waves. By using the observers in [4], a proportional derivative control law with estimates of environmental disturbances was presented; the designed controller achieves a GES position and heading tracking, and the performance of the control system was demonstrated by an experiment with a scaled ship model in [5]. Thus far, disturbance observers [4,5,6] have been applied to the designed DP controllers and can considerably attenuate the effects of environmental disturbances. To further improve control performance, some nonlinear techniques with various disturbance observers and adaptive strategies, such as the adaptive method [6], backstepping [7,8], fuzzy logic [9], and sliding mode control scheme [10], have been introduced to the control design for DP ships with external disturbances. In [6], a global output-feedback control scheme was proposed, whereby disturbances that act on DP for ships were taken as unknown constant disturbances and estimated by an adaptive algorithm. The approach presented in [7] was similar in that it assumes that the disturbances are constant; however, this robust adaptive controller presented for DP systems requires the known upper bound of the disturbances.
In the above analyses, external disturbances are generally treated as invariants, or else knowledge about the nature of the disturbances is needed for control design. However, in practice, sea states are constantly changing and have limited energy, which determines that the disturbances acting on the DP systems of ships are unknown, time-varying, and bounded, and their boundedness cannot be calculated exactly. Taking into account unknown time-varying environmental disturbances, Du et al. [8] developed an output-feedback control law for the DP system of a ship, which can achieve disturbance suppression using a high gain observer; however, during the design process, the system must be given prior information on the upper bounds of the disturbances. In [9], a fuzzy DP control law was developed for a ship DP system with unmodeled dynamics and external disturbances, where the first derivative of the disturbance is not required to be close to zero. In [10], a finite-time controller with a nonlinear disturbance observer was presented, where the proposed nonlinear disturbance observer did not require prior information on the disturbances and accurately determined the boundedness of the disturbance estimation errors.
As we can see from the examples given above, actuator dynamics tend not to be considered in control design [8,9,10]. In practice, the control design for a ship DP system with unknown time-varying disturbances and actuator dynamics makes DP control more complicated. Therefore, in recent years, more research has focused on improving the dynamic characteristics and stability of DP control systems.
Other factors to consider relate to extreme sea states and input saturation. In [11], a fuzzy control law was developed for a DP system with multiplicative noise, where the controller can achieve asymptotic state tracking by seeking the stability condition for the closed-loop system, subject to actuator saturation. In [12], a guaranteed cost controller was proposed for the DP system of a marine surface vessel with external disturbances and input saturation; the magnitude constraints of the control inputs were transformed into linear matrix inequalities, which were achieved by seeking a feasible control objective. In [13], a robust DP controller with a nonlinear disturbance observer was presented; here, input saturation was handled by the auxiliary system. Similarly, control schemes with the aid of an auxiliary system were proposed in [14,15,16,17]. In addition, Qiu et al. [14] proposed a practical adaptive sliding-mode control scheme for an unmanned surface vehicle; however, the basic sliding mode controller only achieved asymptotic stability. In [15], a finite-time control scheme was proposed to guarantee the boundedness of the position error, where the unknown varying-time disturbances were treated by an adaptive scheme with no prior information on the disturbances. The authors of [13,17] assumed both the maximum and the minimum generalized forces to be constant throughout the control process; however, the bound of generalized forces produced by the propulsion system is, in practice, time-varying because each actuator command is constrained by its thrust magnitude, the turning rate of the thrusters, and azimuth angles. Therefore, considering the effect of known magnitude, rate, or bandwidth constraints, Li et al. [17] proposed an auxiliary system to handle input magnitude limitations and rate constraints; however, the magnitude and rate saturation limitations of thruster forces are considered constant in this simulation. Farrell et al. [18] proposed a new backstepping controller, which used an online system to approximate the original system with physical limitations.
Therefore, to better reflect the physical characteristics of the thrusters, Fossen [19] proposed actuator dynamics, which were widely applied in the design of controls [16,20,21]. In [20], a nonlinear vectorial backstepping control law was designed for ship DP systems using actuator dynamics, and the global exponential stability of the control system was demonstrated according to Lyapunov stability analysis. In [21], an adaptive controller was designed to address uncertain parameters, and actuator dynamics were introduced to handle the input constraints.
The above-mentioned sources make the unreasonable assumption that the thruster saturation is a prior constant. Taking the thrust magnitude as an example: if the assumed constraint thrust magnitude is too large or too small, the performance of the system will be degraded, and instability could arise. Therefore, a joint-control scheme with control allocation was proposed in [22,23,24,25]; this system was applied to obtain information about whether or not the actuator is saturated. In [22], an anti-wind-up PI strategy with control allocation was proposed for the DP system of a vehicle. Perez [23] extended the work of [22] and proved its closed-loop asymptotic stability for position regulation. However, environmental disturbance suppression was not considered. The research of [24] proposed a model predictive control algorithm and yielded a near-optimal controller output for vehicle DP by solving the problem of continuous-time numerical optimization. In [25], an output-feedback fault-tolerant controller was developed for vessel DP, where an auxiliary dynamic system was introduced to handle the effect of thruster faults and saturation constraints; however, the bound of each thruster saturation constraint was considered a known constant.
Furthermore, the DP control systems above are all asymptotically stable, which implies that the DP system achieves its control goal with infinite time. Finite-time control using the terminal sliding mode (TSM) method can speed convergence to equilibrium. Moreover, a closed-loop system with a finite-time controller generally shows better anti-disturbance and higher-accuracy performance. Therefore, due to its inherent robustness, finite-time DP control has been gradually gaining popularity [10,26,27]. In [26], a passive fault-tolerant controller was developed using a nonsingular integral terminal sliding mode, which achieves global finite-time convergence of tracking errors. In [27], an adaptive nonsingular fast terminal sliding-mode control was proposed for a nonlinear system with external disturbances, which achieves finite-time tracking control at a fast convergence rate and ensures chattering-free dynamics.
In summary, we can see that there exist two important issues for DP control design: namely, disturbance suppression and actuator constraint. With regard to the first issue, sea states are known to be constantly changing and have limited energy. Previous research does not sufficiently reflect the time-varying of environmental disturbances because it either assumes that the upper bound of environmental disturbance is known or uses constant disturbances in simulation and only achieves asymptotic disturbance suppression. Concerning the second issue, actuator constraints are, in practice, undoubtedly important for DP control design. However, the time-varying nature of actuator saturation is ignored in many previous studies, such as [13,15,18]. In other studies, such as [19,20,21,22,23,24,25], the physical properties of the thruster are not fully considered. Therefore, focusing on unknown time-varying disturbances and actuator constraints in this paper. We present a disturbance observer-based finite-time control scheme with control allocation for DP systems for ships. The finite-time disturbance observer is used to estimate the unknown time-varying disturbances, the control allocation is applied online to inform the controller about actuator saturation, and the auxiliary system dynamic is constructed to handle velocity deviation. Furthermore, the closed-loop system has finite-time stability. To the best of the authors’ knowledge, this is the first published study of DP control design that both considers finite-time disturbance suppression and presents an auxiliary dynamic system designed for a joint system. The main contributions of this paper are as follows:
- (i)
- An adaptive finite-time disturbance observer is constructed to estimate unknown time-varying disturbances. It does not require prior information about the disturbances and can eliminate undesired chattering.
- (ii)
- An auxiliary dynamic system is constructed to handle the input constraints. It reduces the tracking deviation caused by the mismatch between the forces produced by the thruster system and the desired control law.
- (iii)
- By combining control design and control allocation, a finite-time control scheme with a disturbance observer and an auxiliary dynamic system is presented; this scheme can achieve disturbance suppression and handle actuator constraints. Due to the fast exponential reaching law, the controller reduces undesired chattering.
The paper is organized as follows. Preliminaries and problem formulations are described in Section 2. The two finite-time disturbance observers, the control design, and the control allocation are given in Section 3; in this section, we also propose the finite-time controller with a disturbance observer and an auxiliary dynamic system for ship DP systems. The results and discussion are presented in Section 4. Conclusions are drawn in Section 5.
2. Problem Formulation and Preliminaries
2.1. DP Ship Dynamics
The three degree of freedom DP system for ships is only concerned with low-frequency horizontal motions where two coordinate systems are defined, as shown in Figure 1. We denote the position vector in the Earth-fixed frame OEXEYE, and the velocity vector in the body-fixed frame OXY. Here, the relative direction of the wind, the currents, and the waves (, , and ) are defined according to OEXE:
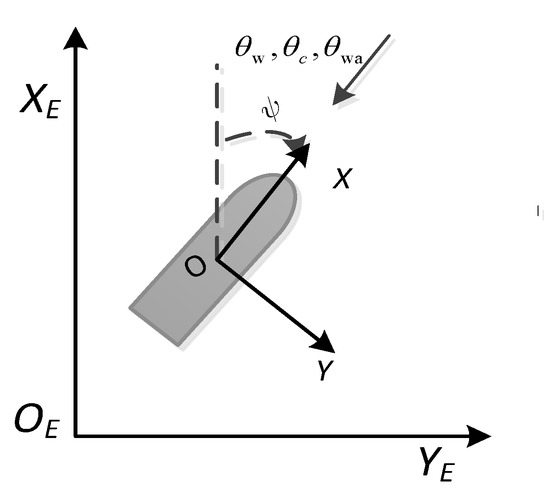
Figure 1.
Coordinate definition in horizontal planes.
The damping force can be approximated as linear at low speed, so the DP’s dynamic model of ships with environmental disturbances is expressed as:
where the rotation matrix is:
denotes the invertible and positive definite inertia matrix. is the damping matrix. is the thruster system’s actual control vector.
The compound environmental disturbance vector is defined as ; that is:
where is the wind force and moment, is the second-order wave force and moment, and is the current force and moment.
Let be the command control law consisting of forces and moment, as calculated by the DP controller.
Remark 1.
Sea states are constantly changing and have limited energy, so environmental disturbances that act on the ship are time-varying and bounded. Additionally, the upper bound of the disturbances can be roughly calculated using the wind and current load coefficients obtained from the wind tunnel test and the second-order wave force transfer functions obtained by numeral calculations. Therefore, we arrive at the following assumption:
Assumption 1.
The environmental disturbance terms are unknown, bounded, and time-varying. The upper bound of the disturbancescan be roughly calculated and satisfy.
2.2. Preliminaries
In this subsection, some lemmas are recalled that will be used in the control design.
For two same-size vectors and , the Hadamard product of and is defined as . For , is the signum function, denoting that and .
The notation refers to the Euclidean norm of a vector. and denote the maximum and minimum eigenvalues of a matrix, respectively.
Lemma 1.
(Hardy et al. [28]) Forand , the following inequality is satisfied:
Lemma 2.
(Yu et al. [29]) For a system: if there exist , and , the continuous function(defined on ) satisfies the following inequality:
Then, with the initial value can reach in finite time, and the trajectory of the system is finite-time stable. The setting time is bounded as:
Lemma 3.
(Zhu et al. [30]) For a system, the solution is finite-time stable if is constantly established for all . Then, if there exist and with , such that , for all , the solution is practical finite-time stable (PFS). Suppose that there exists a positive definite function , for , , and , such that . The solution trajectory is PFS. The setting time is bounded as:
2.3. Control Objective
Taking into account the DP system given by (1), with unknown time-varying disturbances and actuator constraints, under Assumption 1, a finite-time control law is designed such that the DP system for ships can track the predetermined trajectories .
The benefits of the designed controller are as follows: (1) it achieves disturbance suppression in finite time without any prior knowledge of the disturbances; (2) the controller receives information online about actuator saturation and compensates for the tracking errors caused by the actuator constraints; (3) it guarantees that the position and heading tracking errors converge to zero in finite time; (4) it reduces undesired chattering.
3. Finite-Time Control Design
In this section, a finite-time DP control law is developed by combining the control design and the control allocation algorithm with the aid of TSM. Two finite-time disturbance observers are designed to estimate the unknown time-varying yet bounded disturbances, and the auxiliary dynamic system is proposed to compensate for errors caused by the mismatch of forces produced by the thruster system and the DP control law.
3.1. Disturbance Observer Design
3.1.1. SMDO Design
In this subsection, to estimate the disturbances , a sliding-mode disturbance observer (SMDO) is designed. First, an auxiliary sliding variable is selected as:
where , are vectors of the sliding surface and the auxiliary variable, respectively; the design matrix is a positive definite diagonal, ; and is defined by the upper bound of environmental disturbances.
The estimated vector is proposed to be:
Because of (1), (7), and (8), we obtain:
where is the disturbance estimate error vector. From (9), we can conclude that, if the auxiliary sliding variable dynamic , then .
The Lyapunov function candidate is selected as:
Using (7), (8), and (9), the derivative of (10) is:
Note that, in Assumption 1, the environmental disturbances are bounded. It is known that the upper bound can be roughly obtained through experiments and calculations. Thus, the following inequalities hold:
Using (12), and according to Lemma 1, we obtain the following:
From (10), holds, so we obtain:
where .
Clearly, , according to Lemma 2; thus, it can be determined that the decrease in the Lyapunov function can drive the trajectories of the SMDO onto the sliding surface in finite time, which implies that can effectively estimate the bounded disturbances in finite time. Furthermore, the parameter to be designed determines the setting time. It can be shown that the setting time satisfies:
We note that and is then to be kept zero, which leads to . Thus, from (9), the disturbance estimate error vector holds, and the convergence rate can be made as fast as possible by selecting the appropriate parameter . Therefore, the following theorem holds:
Theorem 1.
Considering the DP system given by (1) with Assumption 1, the disturbance estimation error vectorof the SMDO constructed by (7) and (8) can converge to zero in finite time, as quickly as possible, by selecting the appropriate parameter.
3.1.2. ADO Design
We know that the disturbances can be effectively estimated in finite time using (7) and (8). However, the upper bound of the disturbances can only be calculated roughly. Moreover, the high-frequency switching value given by (8) may degrade the performance of the DP control system. Therefore, in order to modify the SMDO, an adaptive scheme is proposed to estimate the upper bound of disturbances . As such, we obtain the adaptive disturbance observer (ADO).
The adaptation update law is defined as:
where is a positive definite design matrix, is a vector defined by the estimates of the upper bound of the disturbances, and . Therefore, the designed ADO is, practically, finite-time stable.
Considering the Lyapunov function candidate as:
where , its time derivative is:
As has been established, the following inequality holds:
Using (12) and (19), Equation (18) can be expressed as:
where . Furthermore, consider the following two cases:
- (i)
- When , , we have:
- (ii)
- When , we have:
Therefore, from (21) and (22), according to Lemma 1, we obtain:
where and . According to Lemma 3, the decrease in can drive the trajectories of the SMDO into in finite time, and the trajectories of the SMDO are bounded as:
Furthermore, in light of (17), we know that is bounded. Furthermore, we can see from (7)–(9) that and are bounded.
3.2. Finite-Time Control Design
In this section, a finite-time control law is developed for the ship DP system; this law is combined with the designed system, the disturbance observer, and the auxiliary dynamic system. The structure of the DP system is shown in Figure 2.
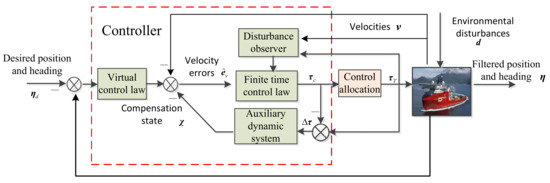
Figure 2.
The structure of the DP system.
Based on the backstepping technique, the design process is given as follows:
Step 1:
Define the position error vector as:
Its time derivative is:
Let be a virtual control input, and design an intermediate control vector as:
where and are positive definite design matrices, and .
Define the velocity error vector as . Then, (26) can be written as:
Step 2:
Here, for the second subsystem of (1), the control law will be defined to make track its command even when the actuator constraints are in effect. Note that, considering the actuator constraints, there may be deviations between the defined control law and the forces produced by the thrusters, which will result in an increase in velocity tracking errors. In order to compensate for these errors, an auxiliary dynamic system is constructed as follows:
Define the compensated tracking error vector as:
From (1) and (29), the time derivative of is:
Then, for finite-time convergence of the DP control system, a TSM surface is chosen as:
where is a positive definite design matrix, and the design constant .
Define a fast exponential reaching law:
where and are positive definite design matrices.
The finite-time control law, consisting of the disturbance observer and the auxiliary dynamic system, is as follows:
where .
From (31), and substituting (34) into the time derivative of , we have:
We note that, in (9), , and then we have:
Theorem 2.
For the ship DP system (1) with Assumption 1: choose the appropriate design matrices , , , , , , and , and the design constants , and , such that the designed controller can guarantee , , and the boundedness of other signals in finite time, where the controller includes the virtual law (27); actual control law (34); the ADO given by (7), (8), and (16); and the auxiliary dynamic system given by (29).
Proof of Theorem 2.
From (35) and (36), it is determined that the time derivative of is not affected by the bounded ADO. Furthermore, to better simplify the parameter design, we try our best to choose the Lyapunov function based on the original dynamic model. Therefore, according to the form of Equation (36), the Lyapunov function is selected as:
According to (29) and (36), the time derivative of (37) yields:
where and .
According to Lemma 2, the decrease in the Lyapunov function can drive the sliding surface vector and the tracking error vector in finite time. The setting time is:
Therefore, the DP ship can track the desired trajectories in finite time under the designed control law.
Now, we have obtained . Furthermore, in light of (32), the compensated velocity errors reach the sliding surface and stay on it forever; we integrate both sides of Equation (32) and we have . Moreover, taking into account the results of Lemma 3 and Theorem 1, we can deduce that the compensated tracking errors are bounded, and the band of the bounded region is determined by the range of . This concludes the proof. □
Remark 2.
The compensation application technique has been used in the input constraint control systems in [14,15,16,17]. However, this present study represents the first time in the literature where both the auxiliary dynamic system has been employed to compensate for errors induced by the mismatch betweenandin DP control design, and that the state vectoris bounded.
To prove that the state vector is bounded, consider another Lyapunov function candidate as , whereby the derivative of is:
Let . Here, is a positive constant vector. Then, (40) can be written as:
By the selections of , we can make , then . Therefore, is bounded. Clearly, is bounded due to . Furthermore, if , we can determine that is a particular solution of (29); then, , and is still bounded.
Remark 3.
The constant in (7), (27), and (33) can be different, depending on the performance of the DP control system. According to Theorems 1 and 2, we can see that the design parameteris related to the convergence rate of the system directly from (15) and (39). Taking as an example the finite-time control, it can be seen from the given reaching law (33) that the approach rate is mainly determined by the exponential term when the sliding surface vector is small. Therefore, the parameter is usually chosen to be small enough to speed up the convergence of the system; however, if is too small, it will increase the control input chattering and easily cause system instability.
3.3. Control Allocation
The control allocation is used to find the optimal thruster forces and direction corresponding to the controller, which can be taken as an optimization problem with cost functions and constraints. The previously presented methods for control allocation can be found in [19,31]. The unconstrained nonlinear optimization problems are formulated using Lagrange multipliers in [31,32]. However, this solution is not optimal when considering time-varying thrust directions. In this paper, the control allocation problems can be solved as nonlinearly constrained problems by considering physical limitations to the thrusters that restrict the set of admissible thrusts and azimuth angles [31,33,34].
The cost functions are formulated as follows [34]:
where is a cost function, is a thrust vector, and are, respectively, the thrust and azimuth angle at the previous sample time, is the azimuth angle vector at the current sample time, and is a vector of slack variables, which is introduced to ensure the existence of a solution. and are weighting matrices, and the matrix is significantly larger to force the optimal solution .
The equality constraint ensures that the controlled forces and moments are produced. It should be taken into consideration that there are physical limitations on the thrust and turning rate of the azimuth angle, which can be expressed as follows [34,35]:
where denotes the thruster configuration matrix, denotes the maximum thrust vector, denotes the minimum thrust vector, maximum and minimum are turning rates of the thrusters, and maximum and minimum are rates of change of azimuth angles. The optimization problem described above can be solved by sequential quadratic programming (SQP) [36,37].
In the following simulation, the control allocation algorithm (42)–(44) is applied.
4. Results and Discussions
To evaluate the effectiveness of the control scheme proposed in Section 3, we present simulations of a cable-laying ship with a DP system. The main information about the ship is listed in Table 1.

Table 1.
Overview of the ship.
The ship is equipped with four same-type azimuth thrusters (two located aft and two in the fore). The four azimuth thrusters are fixed-pitch, with a maximum thrust of 65 kN in open water, and are symmetric along the longitudinal and transverse middle sections. The sketch of thruster positions is shown in Figure 3.
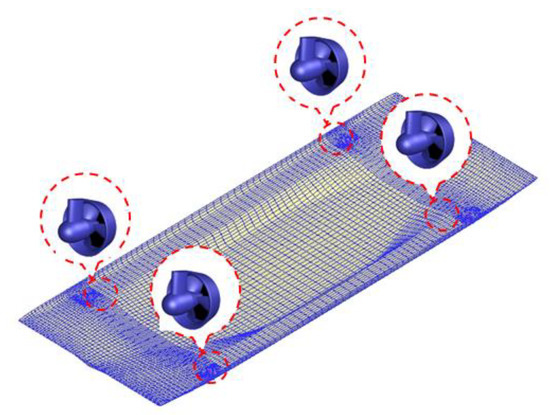
Figure 3.
Sketch of thruster positions.
In order to obtain the inertia matrix and the damping matrix , a 1/25 captive model test was carried out at the China Ship Scientific Research Center (CSSRC). The test photo is shown in Figure 4.

Figure 4.
Photo of a 1/25 captive model test.
Additionally, the parameters of the ship’s dynamic model are given as follows:
The marine environmental parameters are given in Table 2.

Table 2.
Marine environmental parameters.
Wind, second-order wave, and current loads in the surge, sway, and yaw directions are defined as follows:
where denotes the overall length of the ship, is the air density, and is the wind speed. The non-dimensional wind load coefficients , , and are functions of the relative wind direction . and are the water density and the current speed, respectively. The non-dimensional current load coefficients , , and are functions of the relative current direction . is the wave spectral density function, and is the wave frequency. The second-order wave force transfer functions , , and are functions of relative wave direction and wave frequency .
Wind and current load coefficients were obtained by a wind tunnel test in CSSRC. Second-order wave force transfer functions were obtained by numerical calculation using the software Advanced Quantitative Wave Analysis (AQWA). The results are shown in Figure 5, Figure 6 and Figure 7.
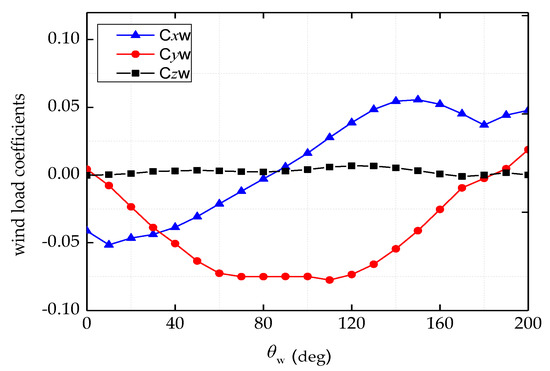
Figure 5.
Wind load coefficients.
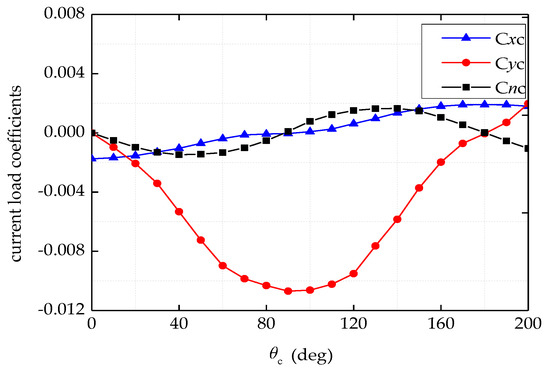
Figure 6.
Current load coefficients.
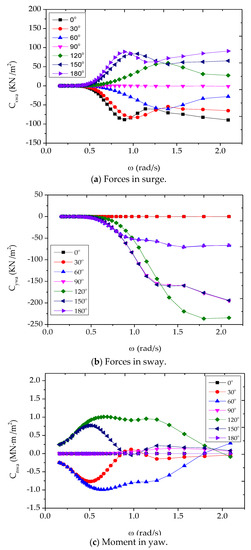
Figure 7.
Second-order wave force transfer function. (a) Forces in surge, (b) forces in sway, (c) moment in yaw.
The desired position and heading were set as . The initial states , , , and were selected.
In a simulation, the design parameters should be large in order to speed up the convergence rate; however, parameters that are too large will cause great fluctuation. The design parameters , , , and cannot be too large, because they play an important role when the errors are close to equilibrium. The parameter should satisfy , and its adjustment method is the same as that of , as shown in Remark 3.
Therefore, the disturbance observer parameters were chosen as
, , and .
The adaption update law parameter was chosen as .
The controller parameters were selected as , , , , , and .
The following simulations are performed in two parts. In Section 4.1, the performance of the developed finite-time control law and the effectiveness of the designed disturbance observer are specifically evaluated, and the advantages of the ADO for unknown environmental disturbances are verified. In Section 4.2, we evaluate the performance of the proposed controller with the ADO and the auxiliary dynamic system for the cable laying ship, subject to unknown environmental disturbances and actuator saturation.
4.1. DP System with Environmental Disturbance
Here, we assume that the control law is executed completely; that is, and . As such, the simplified finite-time control (SFTC) law is given by
In order to illustrate the performance of the SFTC scheme, a simulation comparison is presented by applying the nonsingular integral terminal sliding mode (NITSM) surface in [10], where the NITSM control law is given by:
where . A detailed description of this control law can be found in [10]. The design matrices satisfy ; in simulation, the control gain should be increased to ensure the desired convergence speed of the system. Correspondingly, the control gain of the switching function needs to be as small as possible to ensure chattering reduction; however, a value that is too small cannot guarantee a fast convergence rate of the state when the system is close to a steady state. Therefore, the control parameters were selected as , , , .
First, considering the ship DP without environmental action, i.e., , the comparison of the desired and actual position and heading of the ship are shown in Figure 8a. It is obvious that both control schemes have satisfactory control performance, and the position and heading can track the predetermined trajectories at a fast convergence rate. Moreover, the control inputs, as shown in Figure 8b, are all smooth, and the control inputs of the proposed SFTC scheme are much smaller than those of the NITSM control scheme.
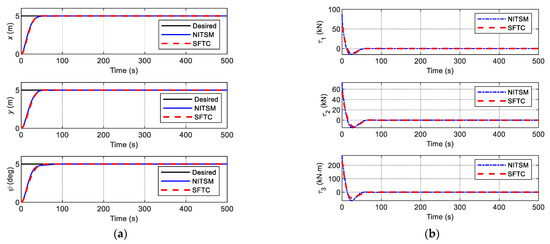
Figure 8.
Comparison of simulation results. (a) Position and heading , (b) control inputs.
In order to better observe the dynamic response of trajectory tracking, time responses for the tracking errors are given in Figure 9; this shows that the tracking errors converge to zero in finite time for the proposed SFTC scheme and the NITSM control scheme in [10]. In the first 30 s, the convergence rate of tracking errors for the proposed SFTC scheme is slower than that of the NITSM control scheme, but as time progresses, it is obvious that the convergence rate for the SFTC scheme becomes faster. The reason for this is that the SFTC scheme with the exponential item can guarantee a fast convergence rate when the tracking errors are close to zero. However, the NITSM control scheme adopts a switching function approach law. Thus, if the tracking errors are required to converge to zero at a fast convergence rate, the selected design parameter must be large enough; however, if the parameter is too large, it will induce a chattering phenomenon in the control inputs. In summary, Figure 8 and Figure 9 verify that the proposed SFTC scheme achieves its aims of having a fast convergence rate and decreasing undesired chattering.
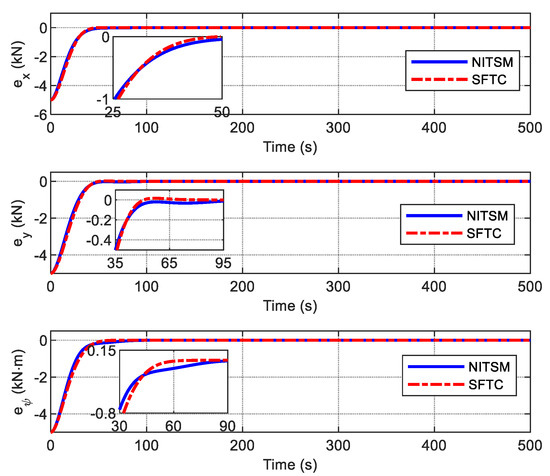
Figure 9.
Comparison of tracking errors.
Then, taking into account the environmental parameters of Case 1, as shown in Table 2, a comparison simulation is provided to evaluate the effectiveness of the two designed disturbance observers. The positioning results for the DP system under the proposed SFTC scheme are shown in Figure 10. It is observed that the SFTC scheme with ADO achieves rapid convergence of position and heading tracking. However, the disturbance-suppression performance of the SFTC scheme with SMDO is poor; there exists significant heading-tracking steady-state errors of about 0.09 deg. This is because the upper bound value selected in SMDO is much smaller than the actual disturbance , as shown in Figure 11, meaning that the environmental disturbances acting on the heading have not been effectively offset.
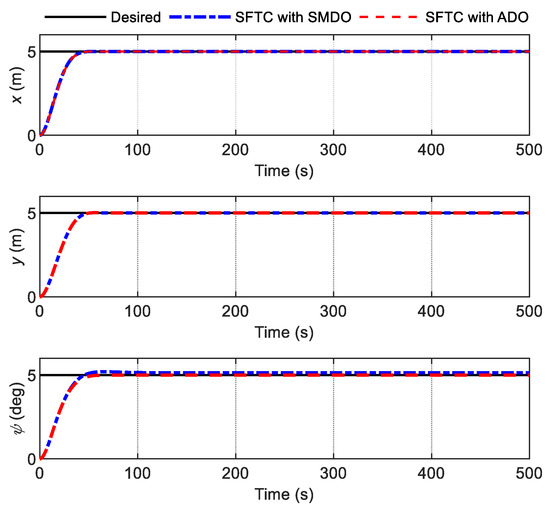
Figure 10.
Position and heading (with environmental disturbances).
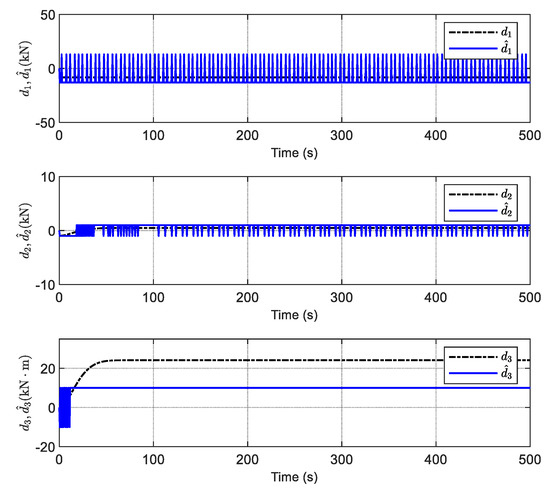
Figure 11.
Estimation of disturbances via SMDO.
The estimation of disturbances via SMDO is given in Figure 11, which shows that the high-frequency-switching observed values lead to undesired chattering. As has been established, the upper bound of the environmental disturbance required for the SMDO design cannot be calculated exactly, and if the selected upper bound is too large, it will lead to the chattering of the control inputs. However, if the selected upper bound is too small, it cannot effectively compensate for the disturbances. As shown in Figure 11, it is obvious that the chosen values are too large to cause chattering; however, the chosen is too small to result in a large estimation error. All the analyses mentioned above will eventually lead to the degradation of the performance of the DP system under the SFTC scheme with SMDO, as shown by the blue dotted line in Figure 10.
In order to eliminate the chattering, an adaptive scheme (namely, ADO) is introduced to modify the SMDO. The estimations of a disturbance generated using the ADO are shown in Figure 12, achieving a decrease in chattering compared with the results shown in Figure 11. Figure 13 shows the estimation of the upper bounds of unknown disturbances. From Figure 12 and Figure 13, it is observed that the estimation of the upper bound is highly consistent with the absolute value of the estimation of disturbances; thus, the effectiveness of the ADO is verified. The command control inputs are shown in Figure 14, which shows that the control inputs of the SFTC with ADO are much smoother than those of the SFTC with SMDO, and chattering is reduced. The above simulation results show that the proposed SFTC scheme with ADO is more effective for the DP system for ships in the presence of unknown time-varying disturbance.
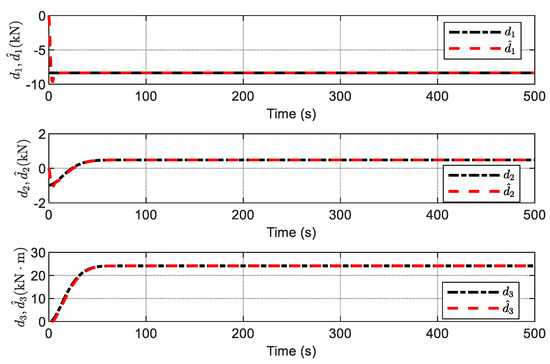
Figure 12.
Estimation of disturbances via ADO.
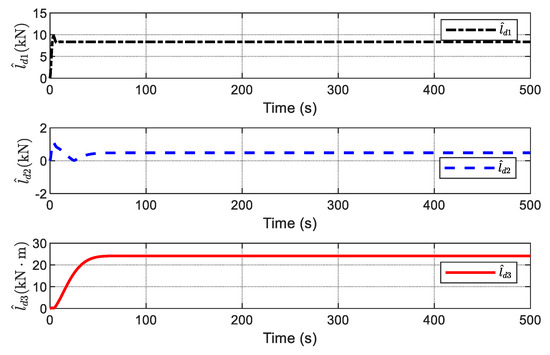
Figure 13.
Estimation of the upper bound of the disturbances via ADO.
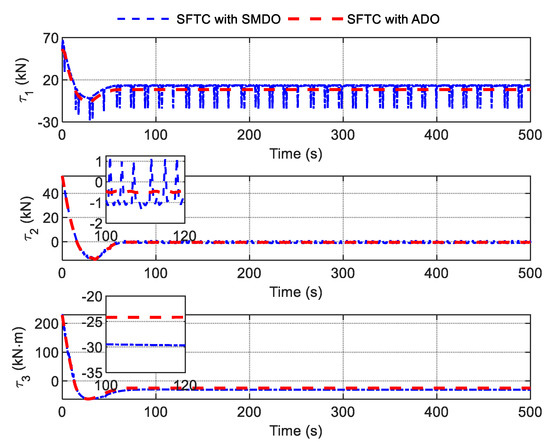
Figure 14.
Comparison of control inputs.
4.2. DP System with Environmental Disturbances and Actuator Constraints
The objective of this subsection is to demonstrate the effectiveness of the proposed finite-time control scheme, which includes the designed ADO and the auxiliary dynamic system (29). Here, using the marine environmental parameters of Case 2, which are given in Table 2, the system’s initial states and the parameters needed for the disturbance observer and controller are all the same as mentioned above. The DP system for ships has four actuators. The designed control law is distributed into each actuator. According to whether the proposed control scheme has the ADS, the simulations are carried out in the following two cases.
For simplicity, finite-time control is noted as FTC, and auxiliary dynamic system is noted as ADS in the following simulations.
Case 1: FTC with ADO.
Using the proposed FTC with ADO alone, the simulation results are shown in Figure 15, Figure 16 and Figure 17. In Figure 15, it can be observed that the curves of the actual position and heading of the ship fluctuate greatly; the time taken to reach the steady state (about 100 s) is much longer than the time (about 50 s) shown by the red dotted line in Figure 10. The reason for this is that the errors between the actual and desired trajectories are too large in the initial stage; control inputs try to reduce these differences by responding quickly. However, the calculated command control inputs have not been exactly executed by the thrusters due to the physical limitations of the actuators, as shown in Figure 16. The forces of each thruster are shown in Figure 17, and it is observed that the forces required for each thruster cannot be produced due to the amplitude limitations of the turning rate of the thrusters in practice.

Figure 15.
Position and heading .
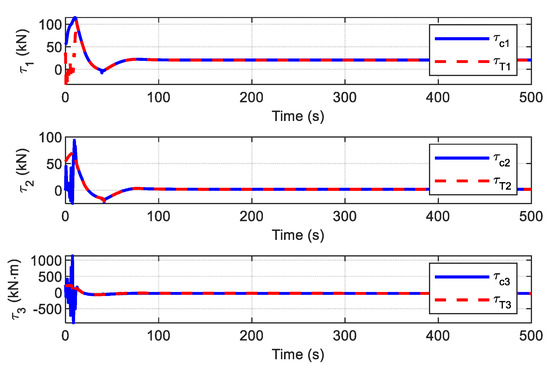
Figure 16.
Control inputs and thruster forces .
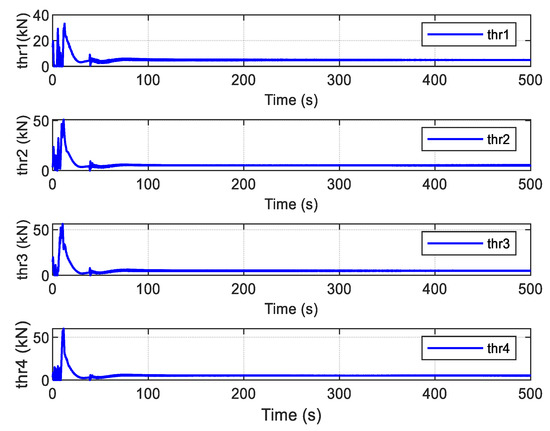
Figure 17.
The forces of each thruster.
Case 2: FTC with ADO and ADS
The performance of the proposed FTC with ADO and ADS is evaluated, where the ADS is applied to deal with the actuator constraints, and its design parameter is selected as . The curves of the position and heading of the ship are depicted in Figure 18; the position performance is found to be improved, in terms of convergence time, compared with that of FTC with ADO alone. Furthermore, the original velocity tracking errors are iteratively compensated using the ADS so that the modified velocity tracking errors are closer to zero, as shown in Figure 19. Moreover, the deviations between and (that is, the state vector of ADS) are bounded, and the theoretical analysis is verified.
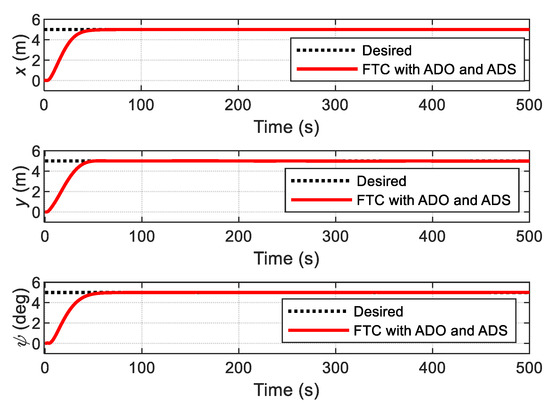
Figure 18.
Position and heading .
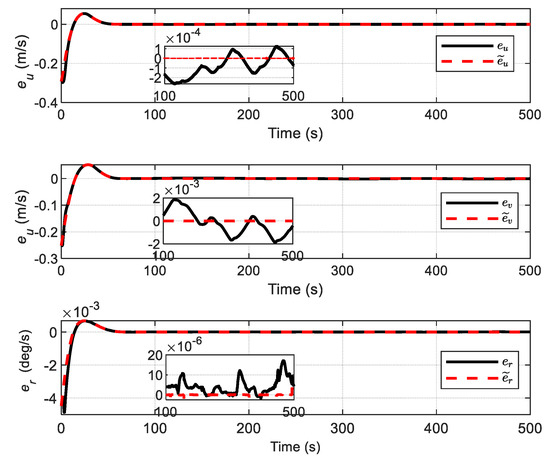
Figure 19.
The velocity errors and the compensated velocity errors.
The command control law and the actual forces provided by the thrusters are shown in Figure 20. Compared with the FTC with ADO, it can be observed that the curves of the control law with the auxiliary term are much smoother in the initial stage and more easily executed by the thruster system. The forces of each thruster are given in Figure 21, which shows that iterative compensation using the auxiliary dynamic system significantly modifies the control inputs and reduces the effect of actuator saturation.
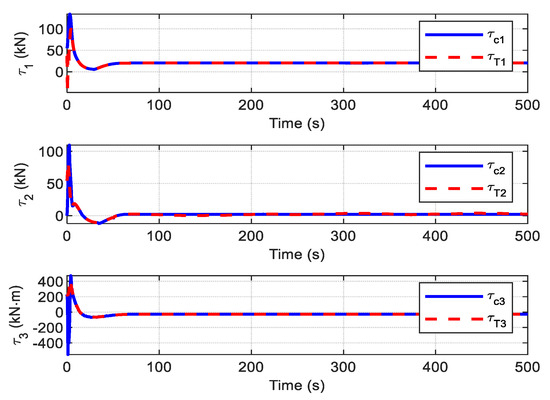
Figure 20.
Control inputs and thruster forces .
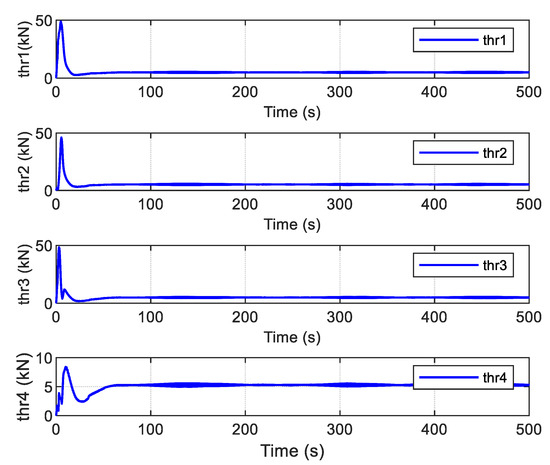
Figure 21.
The force of each thruster.
In order to quantitatively evaluate the performance of the proposed FTC with ADO and ADS, the performance indices are summarized in Table 3, where the performance indices and are used to evaluate the transient and steady-state performance of position errors, respectively. is used to evaluate the response speed and fluctuation range of the control law. From Table 3, it can be observed that the performance indices are much lower for the proposed control technique compared with the other method mentioned in Case 1; namely, FTC with ADO. Then, by comparing the simulation results, it can be concluded that the ADS is effective for handling the actuator constraints, and the performance of the proposed FTC with ADO and ADS is superior to that of the FTC with ADO.

Table 3.
Comparison of performance indices.
The estimation of disturbances, and the upper bound of the disturbances using the ADO, are given in Figure 22 and Figure 23, respectively. It is observed that the unknown varying-time disturbances can be accurately estimated by the ADO without readjusting its design parameters, and no prior information on the time-varying disturbances is required.
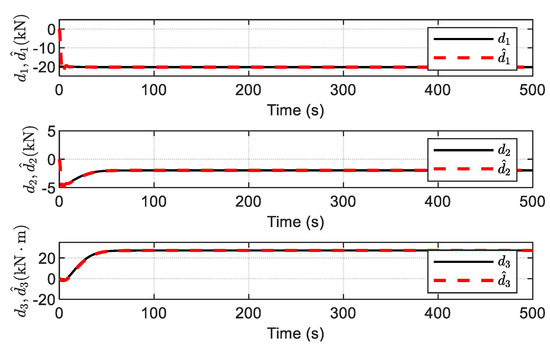
Figure 22.
Estimation of disturbances via ADO.
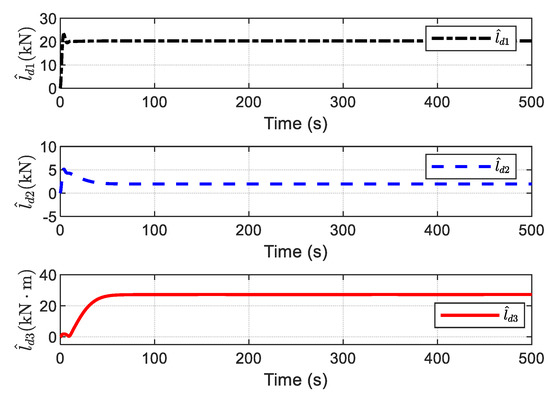
Figure 23.
Estimation of the upper bound of the disturbances via ADO.
Furthermore, because the derivative of is not strictly negative, the auxiliary sliding surface of the ADO is bounded and converges into a region of origin, as is demonstrated in Figure 24. The sliding surface is given in Figure 25, and it is observed that the sliding surface converges to zero within about 50 s. This is because the exponential reaching law guarantees that the sliding surface is reachable at high speed.
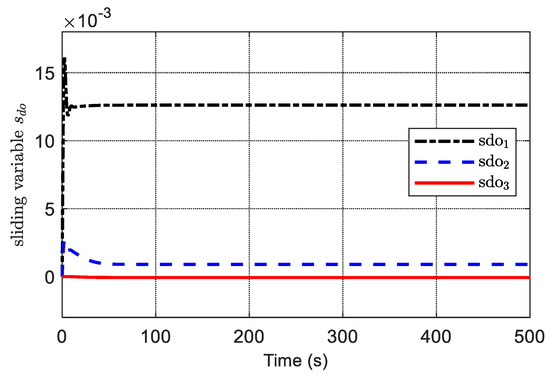
Figure 24.
The sliding surface of the ADO.
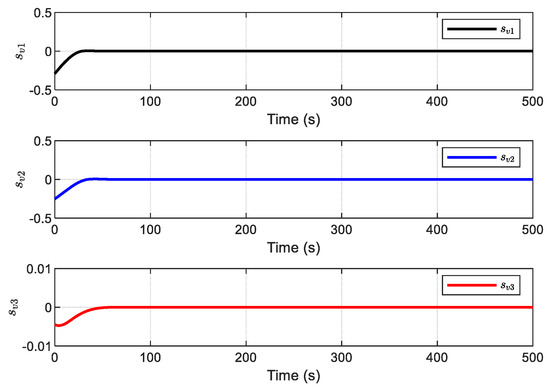
Figure 25.
The TSM surface of the controller.
5. Conclusions
In this paper, we present the design of a finite-time control law for DP systems for ships with unknown time-varying disturbances and actuator constraints. First, to achieve disturbance suppression, the SMDO was designed to estimate the disturbances and to force the estimation errors to converge to zero in finite time. Furthermore, an ADO was presented by introducing an adaptive scheme to modify the SMDO such that undesired chattering is effectively decreased, and no prior information is required to achieve the estimate of the disturbance; however, this only guarantees the boundedness of the estimation errors. Second, to reduce the effect of actuator constraints, a joint control scheme with control allocation was presented, where the control allocation is proposed to directly inform the controller of the actuator-saturation event. The deviations of the command control inputs and the actual forces are handled using the auxiliary dynamic system. Additionally, a finite-time controller was provided, which comprises a disturbance observer and an auxiliary dynamic system, and it was proven that all closed-loop system signals are finite-time convergent. Specifically, the position tracking errors can converge to zero in finite time. Finally, numerical simulations demonstrated that the designed controller achieves the finite-time convergence of position and heading tracking and that the estimates of the ADO and the velocity errors are bounded. In the future, disturbance observers with asymptotic stability in finite time will be considered. Additionally, actuator constraints will also be considered in order to enhance the control performance of the DP system. In particular, further research will focus on how to deal with the mismatch of the DP control law and thruster forces caused by the physical limitations of the thrusters.
Author Contributions
Conceptualization, Y.Z. and C.L.; methodology, Y.Z.; software, Y.Z.; validation, Y.Z. and C.L.; resources, C.L. and Y.Z.; data curation, C.L., N.Z.; writing—original draft preparation, Y.Z. and C.L.; writing—review and editing, Y.Z. and Q.Y.; visualization, Y.Z.; supervision, W.S.; project administration, W.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Jiangsu Province (Grants No BK20180953).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
List of Acronyms
| Acronym | Full Name |
| DP | dynamic positioning |
| ADO | adaptive disturbance observer |
| GES | globally exponentially stable |
| SMDO | sliding-mode disturbance observer |
| TSM | sterminal sliding mode |
| FTC | finite-time control |
| SFTC | simplified finite-time control |
| ADS | auxiliary dynamic system |
| signum function |
References
- Sargent, J.S.; Cowgill, P.N. Design considerations for dynamically positioned utility vessels. In Proceedings of the 8th Offshore Technology Conference, Houston, TX, USA, 3–6 May 1976; pp. 175–196. [Google Scholar]
- Salid, S.; Jenssen, N.A.; Balchen, J.G. Design and analysis of a dynamic positioning system based on the Kalman filtering and optimal control. IEEE Trans. Autom. Control 1983, 28, 331–339. [Google Scholar] [CrossRef]
- Fossen, T.I.; Grøvlen, Å. Nonlinear output feedback control of dynamically positioned ships using vectorial observer backstepping. IEEE Trans. Control Syst. Technol. 1998, 6, 121–128. [Google Scholar] [CrossRef]
- Fossen, T.I.; Strand, J.P. Passive nonlinear observer design for ships using Lyapunov Methods: Full-scale experiments with a supply vessel. Automatica 1999, 35, 3–16. [Google Scholar] [CrossRef]
- Loria, A.; Fossen, T.I.; Panteley, E. A separation principle for dynamic positioning of ships: Theoretical and experimental results. IEEE Trans. Control Syst. Technol. 2000, 8, 332–343. [Google Scholar] [CrossRef]
- Du, J.L.; Li, W.H.; Zheng, K.; Yu, S. Nonlinear output feedback control of dynamic positioning system of ships. J. South China Univ. Technol. Nat. Sci. Ed. 2012, 40, 70–75. [Google Scholar]
- Do, K.D. Global robust and adaptive output feedback dynamic positioning of surface ships. J. Mar. Sci. Appl. 2011, 10, 325–332. [Google Scholar] [CrossRef]
- Du, J.L.; Yang, Y.; Guo, C.; Li, G.Q. Output feedback control for dynamic positioning system of a ship based on a high gain observer. Control Theory Appl. 2013, 30, 1486–1491. [Google Scholar]
- Hu, X.; Du, J.; Shi, J. Adaptive fuzzy controller design for dynamic positioning system of vessels. Appl. Ocean. Res. 2015, 53, 46–53. [Google Scholar] [CrossRef]
- Liu, S.; Liu, Y.; Wang, N. Nonlinear disturbance observer-based backstepping finite-time sliding mode tracking control of underwater vehicles with system uncertainties and external disturbances. Nonlinear Dyn. 2017, 88, 465–476. [Google Scholar] [CrossRef]
- Chang, W.J.; Liang, H.J.; Ku, C.C. Fuzzy controller design subject to actuator saturation for dynamic ship positioning systems with multiplicative noises. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2010, 224, 725–736. [Google Scholar] [CrossRef]
- Liu, T.; Xiao, Y.; Yuan, F.; Jun, L.; Bing, H. Guaranteed cost control for dynamic positioning of marine surface vessels with input saturation. Appl. Ocean Res. 2021, 116, 102868. [Google Scholar] [CrossRef]
- Du, J.L.; Hu, X.; Krstić, M.; Sun, Y.Q. Robust dynamic positioning of ships with disturbances under input saturation. Automatica 2016, 73, 207–214. [Google Scholar] [CrossRef]
- Qiu, B.; Wang, G.; Fan, Y.; Mu, D.; Sun, X. Adaptive sliding mode trajectory tracking control for unmanned surface vehicle with modeling uncertainties and input saturation. Appl. Sci. 2019, 9, 1240. [Google Scholar] [CrossRef]
- Liang, K.; Lin, X.; Chen, Y.; Li, J.; Ding, F. Adaptive sliding mode output feedback control for dynamic positioning ships with input saturation. Ocean Eng. 2020, 206, 107245. [Google Scholar] [CrossRef]
- Hu, X.; Du, J.L. Robust nonlinear control design for dynamic positioning of marine vessels with thruster system dynamics. Nonlinear Dyn. 2018, 94, 365–376. [Google Scholar] [CrossRef]
- Li, J.; Du, J.L.; Hu, X. Robust adaptive prescribed performance control for dynamic positioning of ships under unknown disturbances and input constraints. Ocean Eng. 2020, 206, 107254. [Google Scholar] [CrossRef]
- Farrell, J.; Polycarpou, M.; Sharma, M. On-line approximation based control of uncertain nonlinear systems with magnitude, rate and bandwidth constraints on the states and actuators. In Proceedings of the 2004 American control conference, Boston, MA, USA, 30 June–2 July 2004. [Google Scholar]
- Fossen, T.I. Guidance and Control of Ocean Vehicles; John Wiley & Sons Inc.: Chichester, UK, 1994. [Google Scholar]
- Fossen, T.I.; Berge, S.P. Nonlinear vectorial backstepping design for global exponential tracking of marine vessels in the Presence of Actuator Dynamics. In Proceedings of the 36th IEEE Conference on Decision and Control, San Diego, CA, USA, 10–12 December 1997; pp. 4237–4242. [Google Scholar]
- Baris, B. An adaptive control design for dynamic positioning of unmanned surface vessels having actuator dynamics. Ocean Eng. 2021, 229, 108948. [Google Scholar]
- Perez, T. Anti-wind-up designs for dynamic positioning of marine vehicles with control allocation. IFAC Proc. Vol. 2009, 42, 243–248. [Google Scholar] [CrossRef]
- Perez, T.; Donaire, A. Constrained control design for dynamic positioning of marine vehicles with control allocation. Model Ident. Control 2009, 30, 57–70. [Google Scholar] [CrossRef]
- Veksler, A.; Johansen, T.A.; Borrelli, F.; Realfsen, B. Dynamic positioning with model predictive control. IEEE Trans. Control Syst. Technol. 2016, 24, 1340–1353. [Google Scholar] [CrossRef]
- Lin, Y.Y.; Du, J.L.; Zhu, G.B.; Li, J. Output feedback thruster fault-tolerant control for dynamic positioning of vessels under input saturation. IEEE Access 2018, 6, 76271–76281. [Google Scholar] [CrossRef]
- Li, H.; Lin, X. Robust finite-time fault-tolerant control for dynamic positioning of ships via nonsingular fast integral terminal sliding mode control. Appl. Ocean Res. 2022, 122, 103126. [Google Scholar] [CrossRef]
- Ianagui, A.S.S.; de Mello, P.C.; Tannuri, E.A. Robust output-feedback control in a dynamic positioning system via high order sliding modes: Theoretical framework and experimental evaluation. IEEE Access 2020, 8, 91701–91724. [Google Scholar] [CrossRef]
- Hardy, G.H.; Littlewood, J.E.; Polya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Zhu, Z.; Xia, Y.; Fu, M.Y. Attitude stabilization of rigid spacecraft with finite time convergence. Int. J. Robust Nonlinear 2011, 21, 686–702. [Google Scholar] [CrossRef]
- Fossen, T.I.; Johansen, T.A. A Survey of Control Allocation Methods for Ships and Underwater Vehicles. In Proceedings of the 14th Mediterranean Conference on Control and Automation, Ancona, Italy, 28–30 June 2006; pp. 110–128. [Google Scholar]
- Vu, M.T.; Thanh, H.L.N.N.; Huynh, T.T.; Do, Q.T.; Do, T.D.; Hoang, Q.D.; Le, T.H. Station-keeping control of a hovering overactuated autonomous underwater vehicle under ocean current effects and model uncertainties in the horizontal plane. IEEE Access 2021, 9, 6855–6867. [Google Scholar] [CrossRef]
- Vu, M.T.; Le, T.-H.; Thanh, H.L.N.N.; Huynh, T.-T.; Van, M.; Hoang, Q.-D.; Do, T.D. Robust position control of an over-actuated underwater vehicle under model uncertainties and ocean current effects using dynamic sliding mode surface and optimal allocation control. Sensors 2021, 21, 7474. [Google Scholar] [CrossRef]
- Johansen, T.A.; Fossen, T.I.; Berge, S.P. Constrained nonlinear control allocation with singularity avoidance using sequential quadratic programming. IEEE Trans. Control Syst. Technol. 2004, 12, 211–216. [Google Scholar] [CrossRef]
- Wu, D.F.; Ren, F.K.; Zhang, W.D. An energy optimal thrust allocation method for the marine dynamic positioning system based on adaptive hybrid artificial bee colony algorithm. Ocean Eng. 2016, 118, 216–226. [Google Scholar] [CrossRef]
- Alireza, A.; Mohammad, J.K. Alternative approach for dynamic-positioning thrust allocation using linear pseudo-inverse model. Appl. Ocean Res. 2019, 90, 101854. [Google Scholar]
- Curtis, F.E.; Gould, N.I.M.; Robinson, D.P.; Toint, P.L. An interior-point trust-funnel algorithm for nonlinear optimization. Math. Program. 2017, 161, 73–134. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).