A SOM−RBFnn-Based Calibration Algorithm of Modeled Significant Wave Height for Nearshore Areas
Abstract
:1. Introduction
2. Data and Methodology
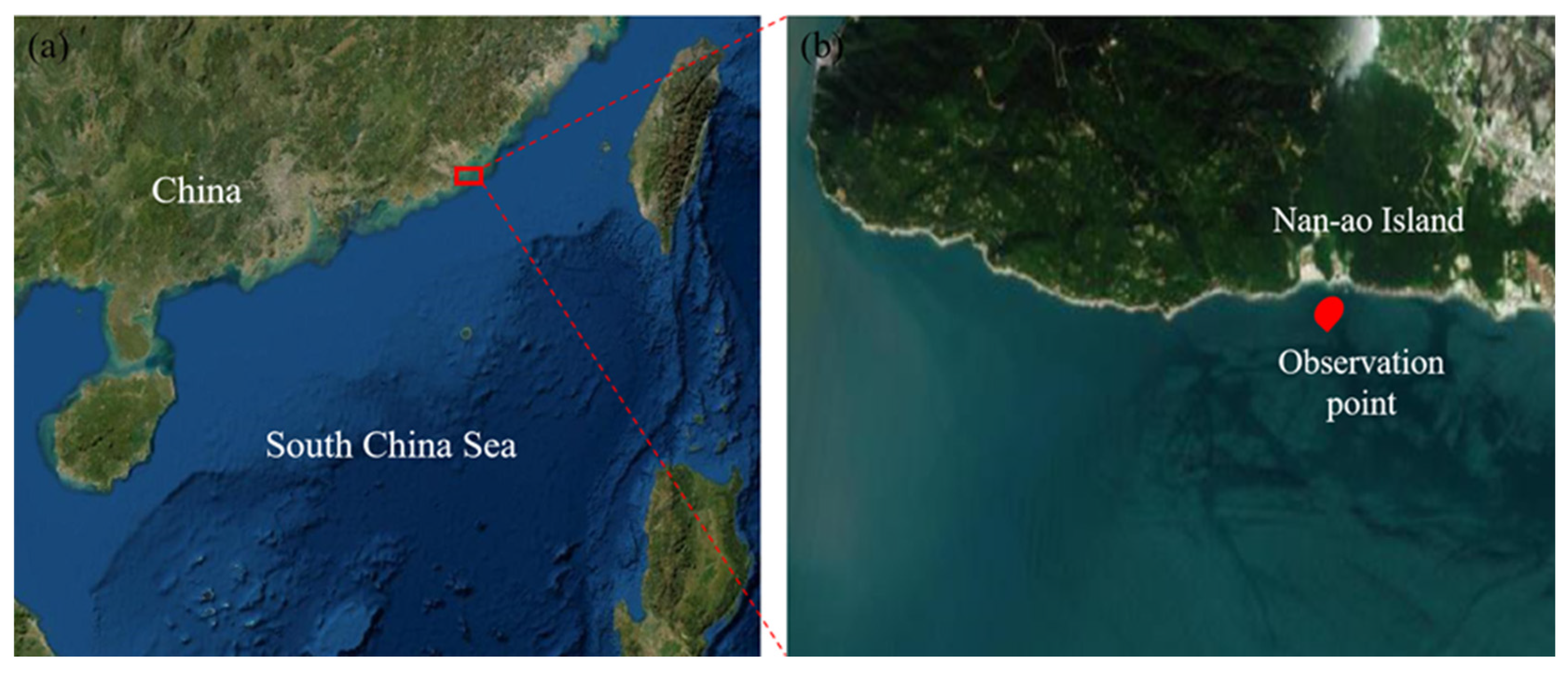
2.1. Data Used for Case Study
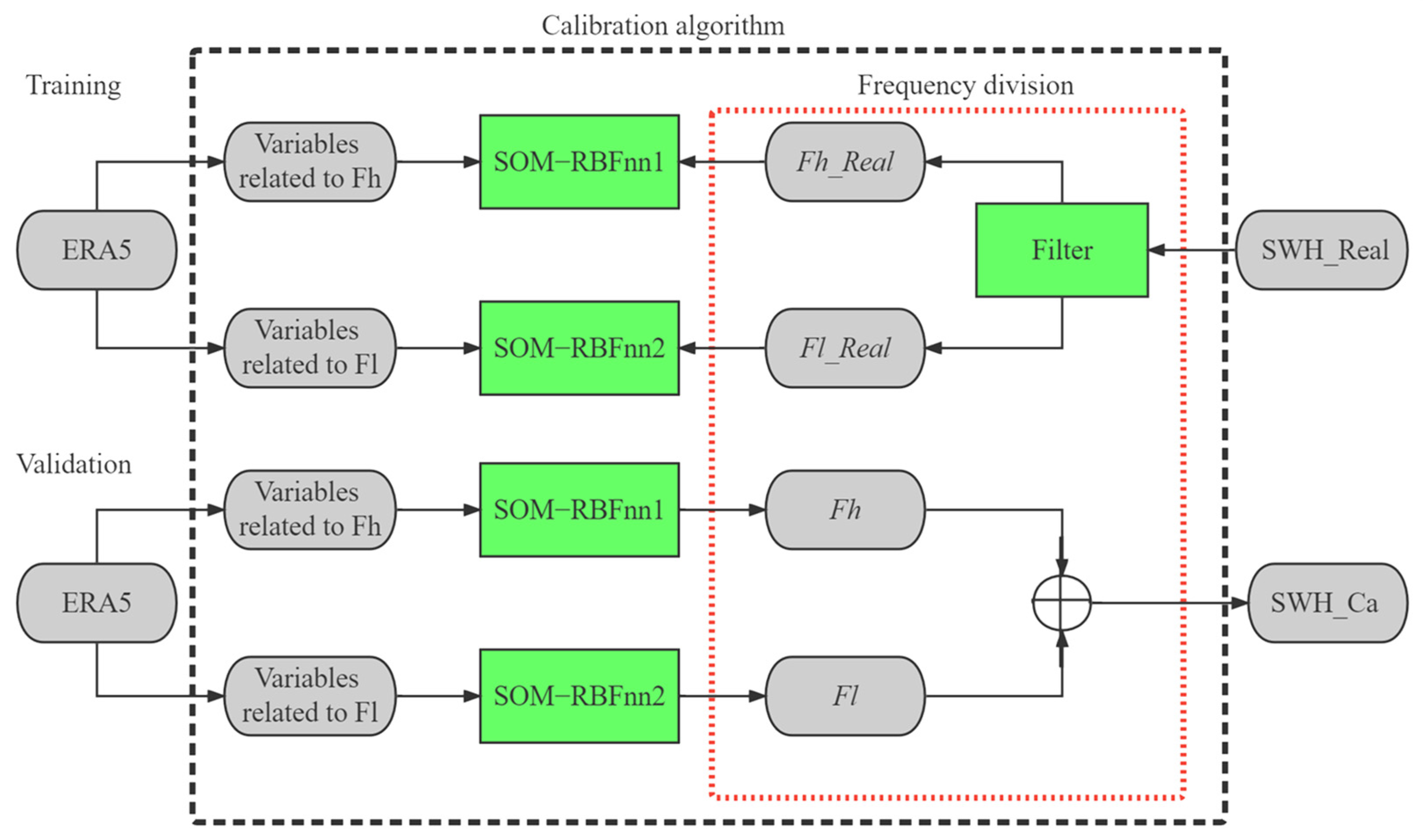
2.2. Calibration Algorithm for the Nearshore SWH
2.2.1. The Frequency Division
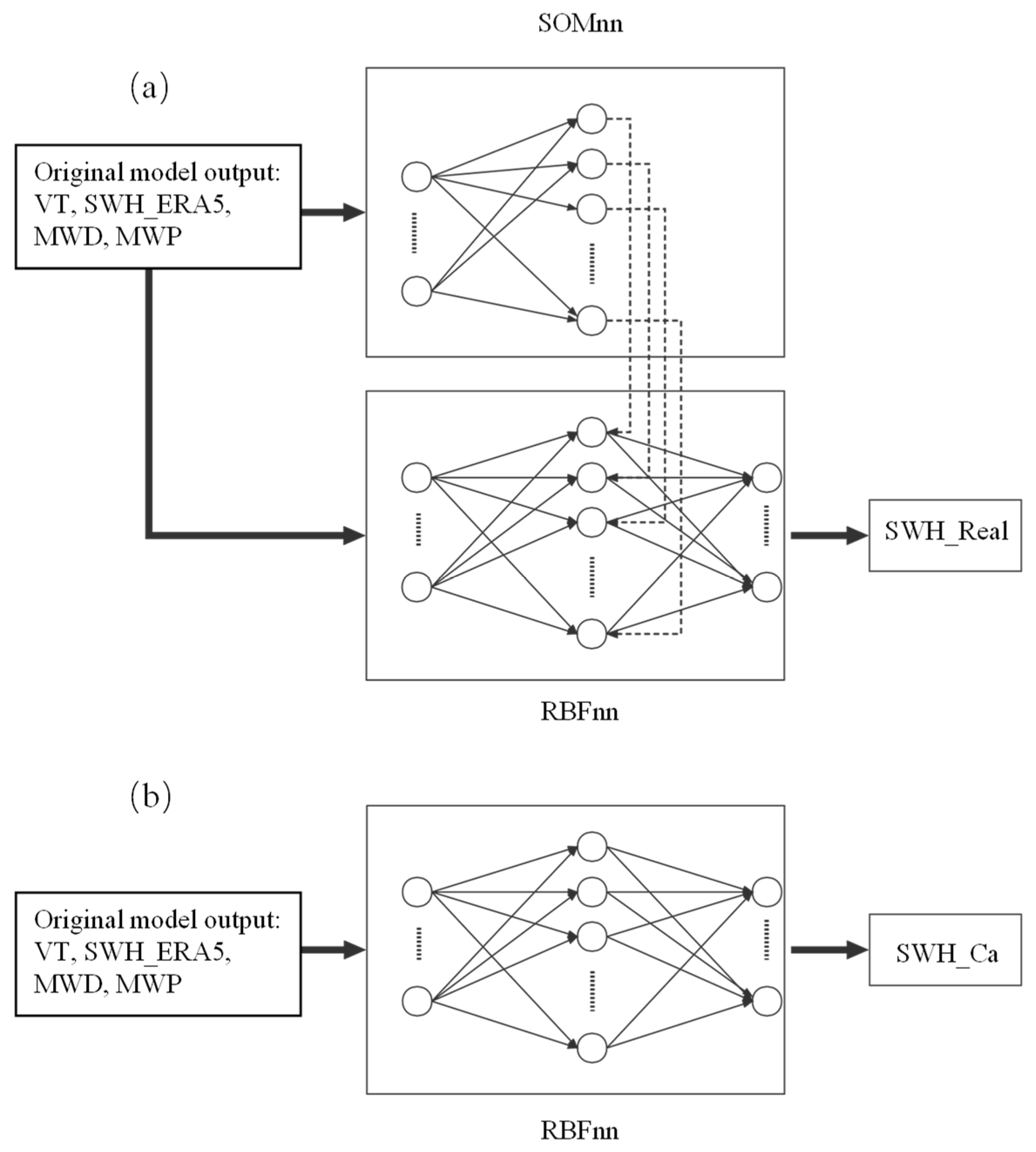
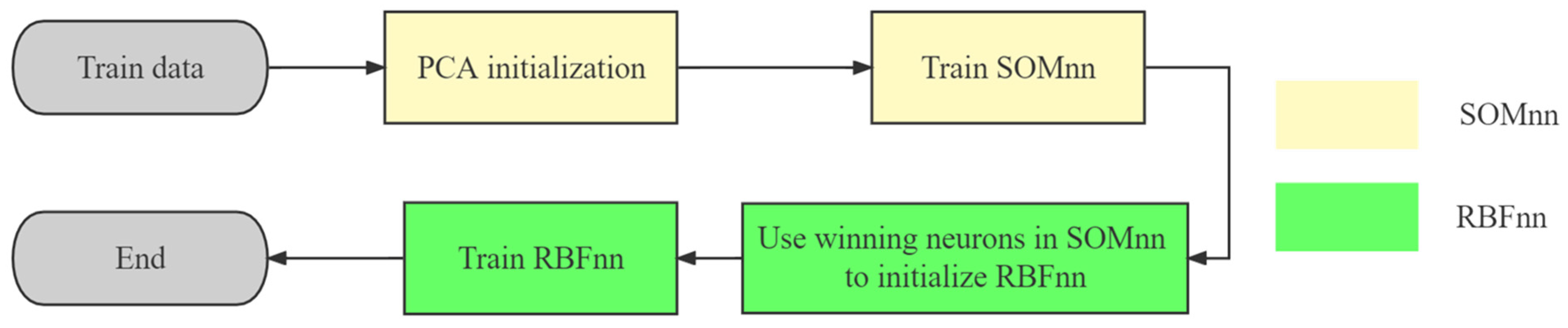
2.2.2. The SOM−RBFnn
- The node structure and scale of the SOMnn competition layer are specified. The rectangular competition layer structure is selected, and the number of nodes in the competition layer is determined to be 200 according to the data scale.
- Competitive layer node weight initialization via principal component analysis.
- Select xi as a sample, calculate the Euclidean distance between the sample and all nodes, and locate the node with the smallest distance from it,where wt(dj) = wj,t representing the weight of node dj at the t-th iteration.
- Update node weights by:where η(dj, di) is a neighborhood function, the size of which depends on the distance between node di and node dj, and it is used to characterize the influence of the BMU on its neighbors.
- If the number of iterations t does not reach the set number of times tend, repeat steps 3 and 4; otherwise, define an active node-set A, which includes all active nodes when the iteration is completed, and proceed to the step.
- Use the number and weight of SOMnn active nodes to initialize the hidden layer center ck = dk, dk ∈ A of the RBFnn, and the total number of hidden layer nodes N = crad(A).
- The RBF hidden layer outputs hij = ϕ (||xi − cj||) correspond to the sample xi input. In this study, the radial basis function is selected as the Gaussian function:
- Define the hidden layer output matrix H = [hij], and the weight matrix between the hidden layer to the output layer is WRBF = [w1RBF, w2RBF, …, wNRBF]T. The output of the RBFnn is Y = HWRBF. In the training phase, the output matrix Y is clamped, and the hidden layer output matrix H has been calculated through the above steps. Use the pseudo-inverse method to solve the weight matrix: WRBF = H−1Y.
2.3. Performance Indicators
3. Results
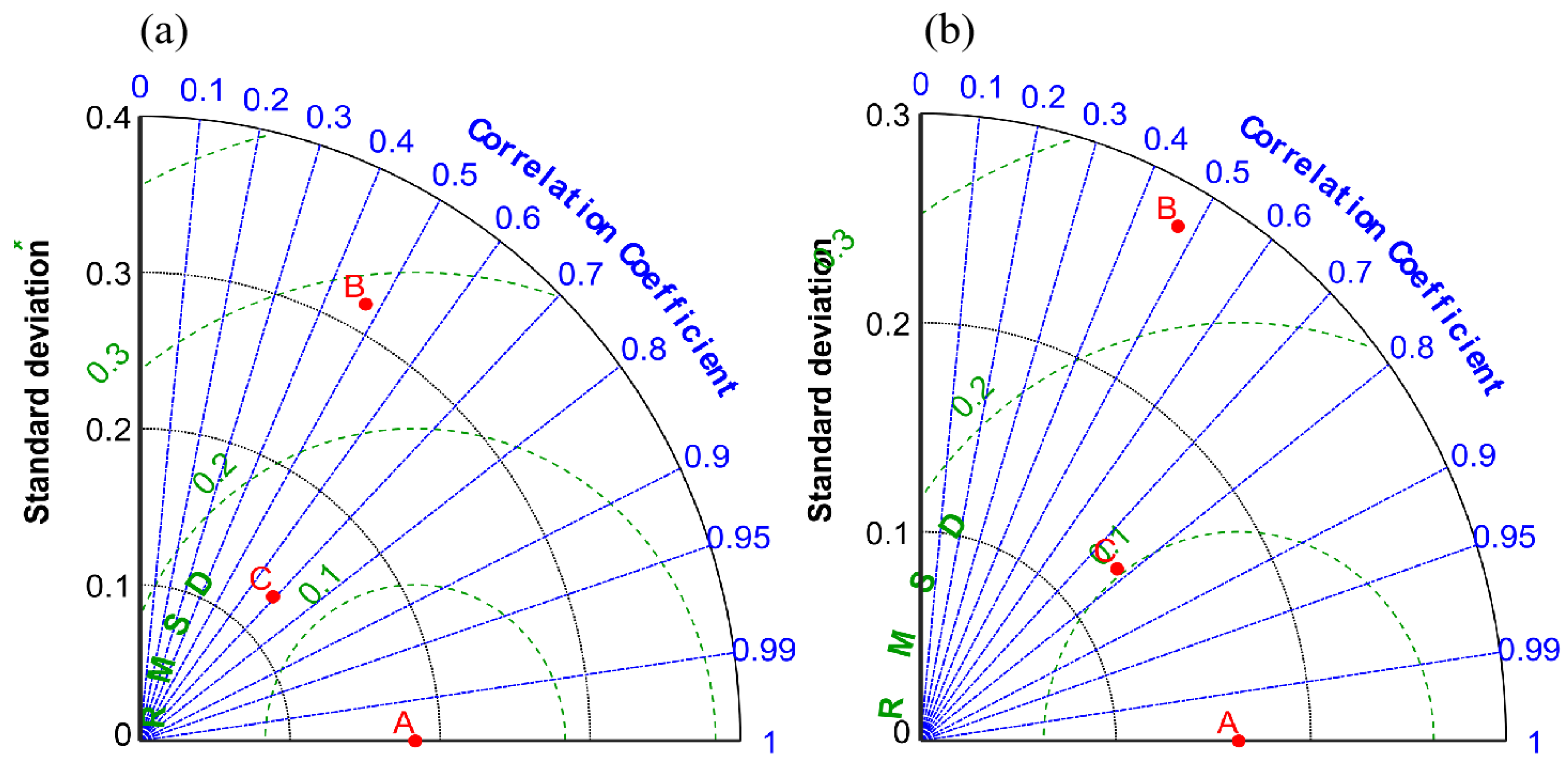
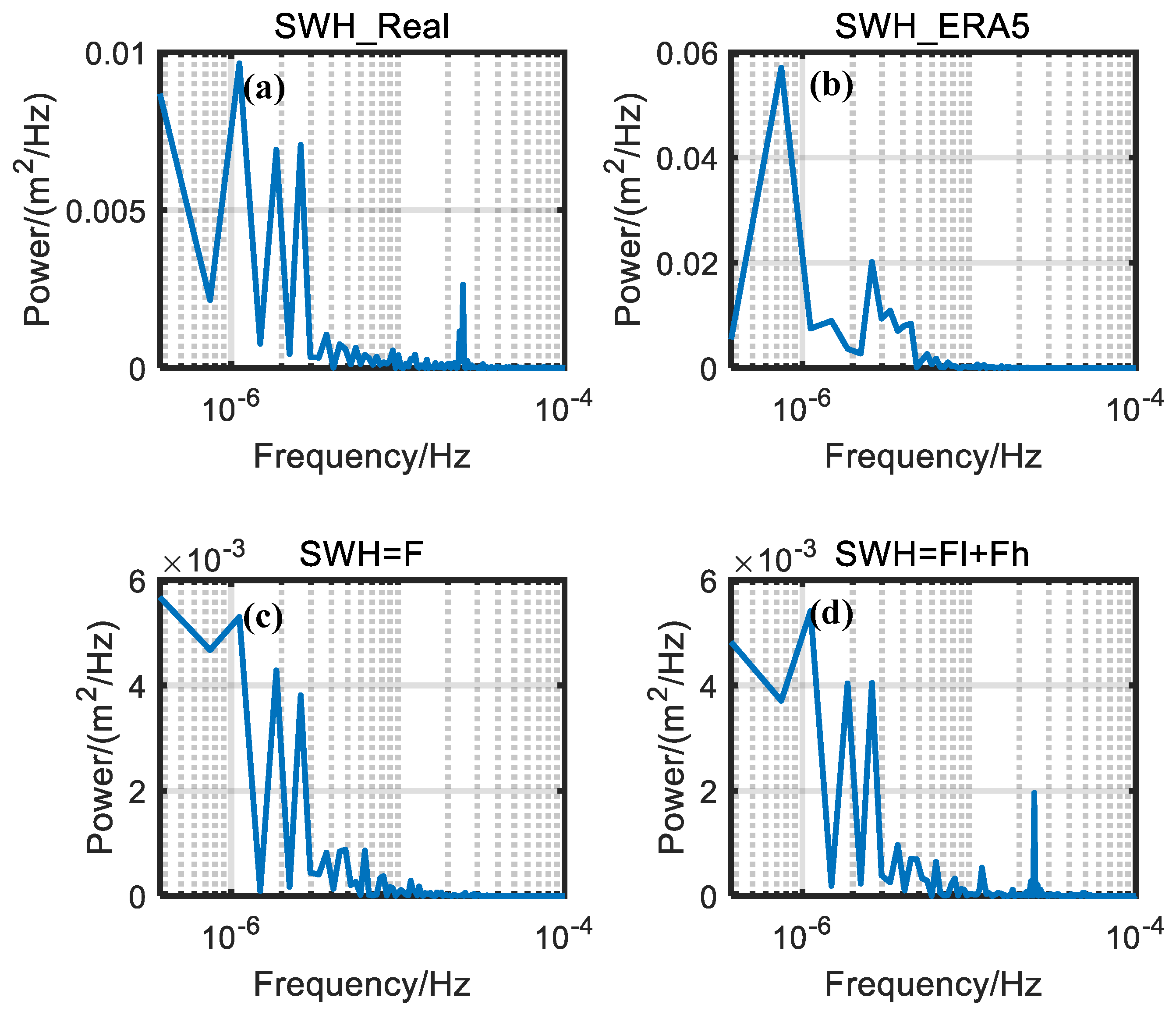
3.1. The Applicability of This Algorithm to the Study Case
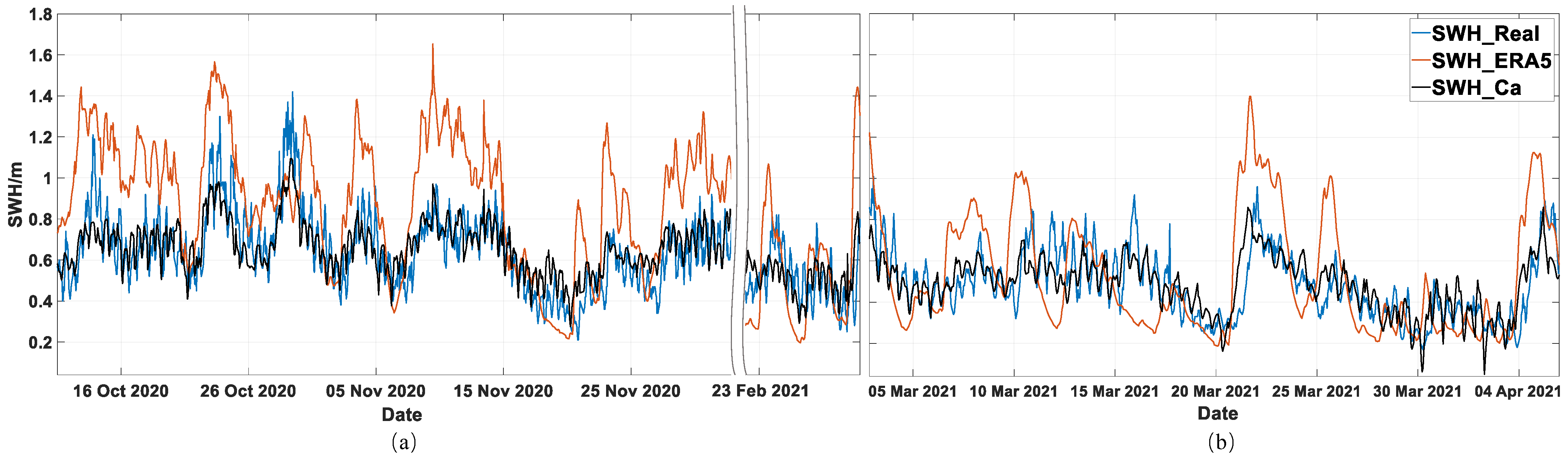
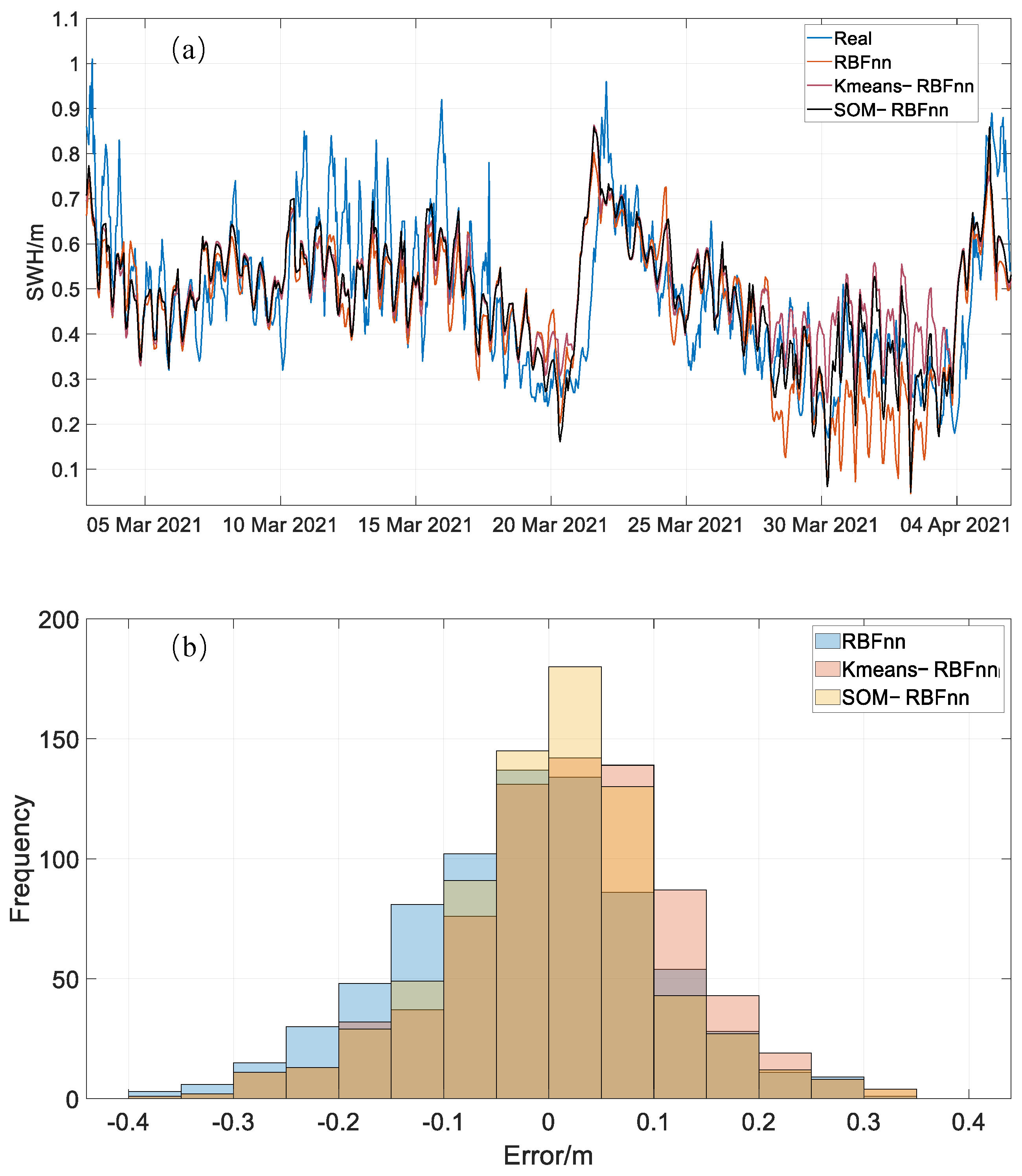
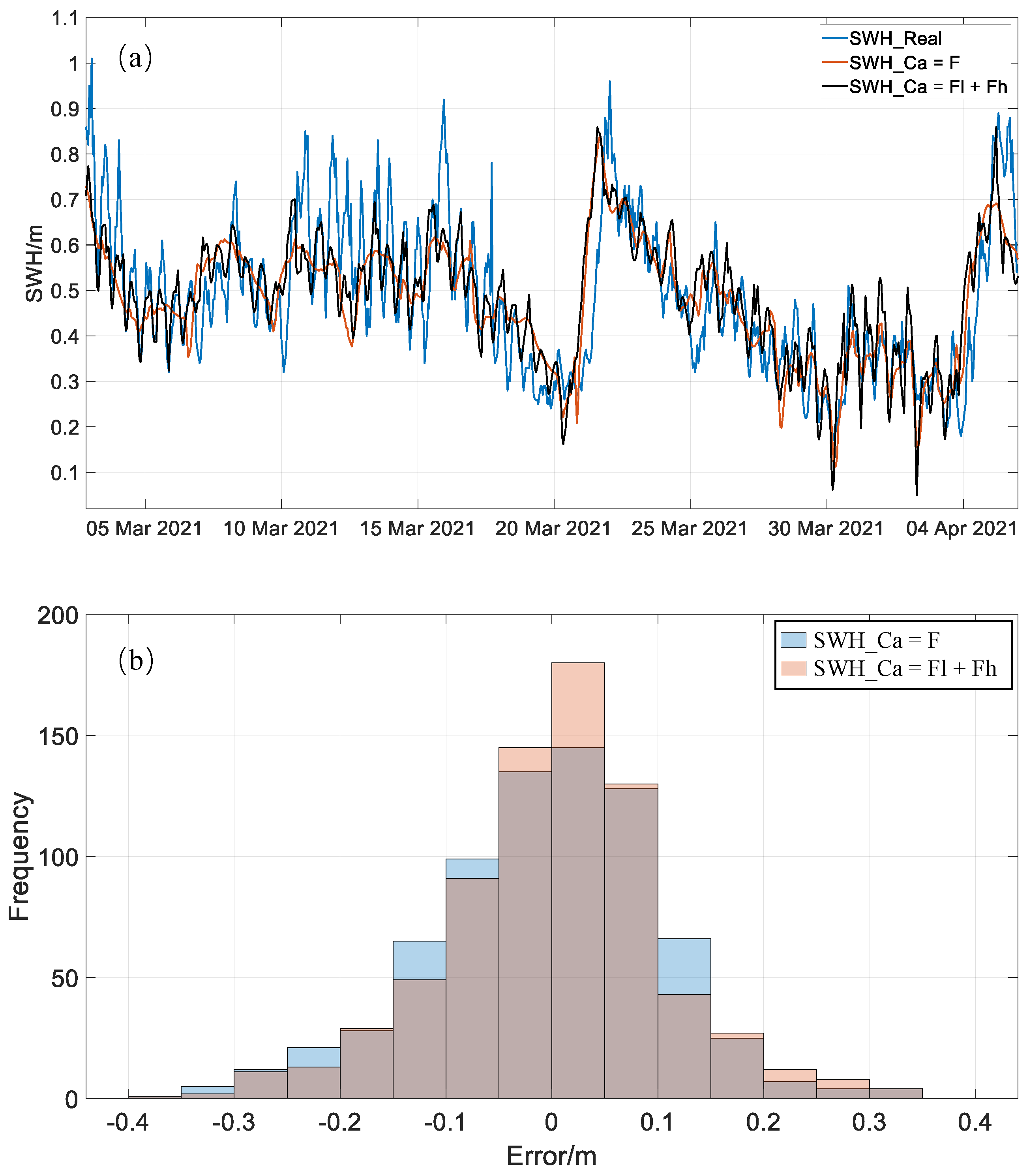
3.2. Calibration Results of the Case Study
4. Discussion
4.1. Advantages of SOM−RBFnn
4.2. Efficacy of Frequency Division Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adytia, D.; Saepudin, D.; Pudjaprasetya, S.R.; Husrin, S.; Sopaheluwakan, A. A deep learning approach for wave forecasting based on a spatially correlated wind feature, with a case study in the Java Sea, Indonesia. Fluids 2022, 7, 39. [Google Scholar] [CrossRef]
- Brus, S.R.; Wolfram, P.J.; Van Roekel, L.P.; Meixner, J.D. Unstructured global to coastal wave modeling for the Energy Exascale Earth System Model using WAVEWATCH III version 6.07. Geosci. Model. Dev. 2021, 14, 2917–2938. [Google Scholar] [CrossRef]
- Inghilesi, R.; Orasi, A.; Catini, F. The ISPRA Mediterranean coastal wave forecasting system: Evaluation and perspectives. J. Oper. Oceanogr. 2016, 9, s89–s98. [Google Scholar] [CrossRef]
- Deo, M.C.; Jha, A.; Chaphekar, A.S.; Ravikant, K. Neural networks for wave forecasting. Ocean Eng. 2001, 28, 889–898. [Google Scholar] [CrossRef]
- Deshmukh, A.N.; Deo, M.C.; Bhaskaran, P.K.; Nair, T.M.B.; Sandhya, K.G. Neural-network-based data assimilation to improve numerical ocean wave forecast. IEEE J. Oceanic 2016, 41, 944–953. [Google Scholar] [CrossRef]
- Li, B.; Li, J.; Li, Y.; Zhang, Z.; Shi, P.; Liu, J.; Chen, W. Application of artificial neural network to numerical wave simulation in the coastal region of island. J. Xiamen Univ. (Nat. Sci.) 2020, 59, 420–427. (In Chinese) [Google Scholar] [CrossRef]
- Chen, D.; Liu, F.; Zhang, Z.; Lu, X.; Li, Z. Significant wave height prediction based on wavelet graph neural network. In Proceedings of the 2021 IEEE 4th International Conference on Big Data and Artificial Intelligence (BDAI), Qingdao, China, 2–4 July 2021; pp. 80–85. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Yang, J. Forecasting of significant wave height based on gated recurrent unit network in the Taiwan Strait and its adjacent waters. Water 2021, 13, 86. [Google Scholar] [CrossRef]
- Zhou, S.; Bethel, B.J.; Sun, W.; Zhao, Y.; Xie, W.; Dong, C. Improving significant wave height forecasts using a joint empirical mode decomposition–long short-term memory network. J. Mar. Sci. Eng. 2021, 9, 744. [Google Scholar] [CrossRef]
- Namigtle-Jiménez, A.; Escobar-Jiménez, R.F.; Gómez-Aguilar, J.F.; García-Beltrán, C.D.; Téllez-Anguiano, A.C. Online ANN-based fault diagnosis implementation using an FPGA: Application in the EFI system of a vehicle. ISA Trans. 2020, 100, 358–372. [Google Scholar] [CrossRef]
- Carbot-Rojas, D.A.; Escobar-Jiménez, R.F.; Gómez-Aguilar, J.F.; García-Morales, J.; Téllez-Anguiano, A.C. Modelling and control of the spark timing of an internal combustion engine based on an ANN. Combust. Theory Model. 2020, 24, 510–529. [Google Scholar] [CrossRef]
- Qasem, S.N.; Shamsuddin, S.M.; Zain, A.M. Multi-objective hybrid evolutionary algorithms for radial basis function neural network design. Knowl. Based Syst. 2012, 27, 475–497. [Google Scholar] [CrossRef]
- Kamel, A.H.; Afan, H.A.; Sherif, M.; Ahmed, A.N.; El-Shafie, A. RBFNN versus GRNN modeling approach for sub-surface evaporation rate prediction in arid region. Sustain. Comput. Inform. Syst. 2021, 30, 100514. [Google Scholar] [CrossRef]
- Guo, X.-G.; Tian, M.-E.; Li, Q.; Ahn, C.K.; Yang, Y.-H. Multiple-fault diagnosis for spacecraft attitude control systems using RBFNN-based observers. Aerosp. Sci. Technol. 2020, 106, 106195. [Google Scholar] [CrossRef]
- Lv, Z.; Xiao, F.; Wu, Z.; Liu, Z.; Wang, Y. Hand gestures recognition from surface electromyogram signal based on self-organizing mapping and radial basis function network. Biomed. Signal. Proces. 2021, 68, 102629. [Google Scholar] [CrossRef]
- Fu, H.; Liu, T.; Zhang, S.; Zhao, D.; Ding, G. Gas emission quantity dynamic prediction model of coal mine based on SOM-RBF algorithm. Chin. J. Sens. Actuators 2015, 28, 1255–1261. (In Chinese) [Google Scholar] [CrossRef]
- Rumbell, T.; Denham, S.L.; Wennekers, T. A spiking self-organizing map combining STDP, oscillations, and continuous learning. IEEE Trans. Neural Netw. Learn. 2014, 25, 894–907. [Google Scholar] [CrossRef] [Green Version]
- Song, H.; Kuang, C.; Gu, J.; Zou, Q.; Liang, H.; Sun, X.; Ma, Z. Nonlinear tide-surge-wave interaction at a shallow coast with large scale sequential harbor constructions. Estuar. Coast. Shelf Sci. 2020, 233, 106543. [Google Scholar] [CrossRef]
- Uchiyama, Y.; McWilliams, J.C.; Shchepetkin, A.F. Wave–current interaction in an oceanic circulation model with a vortex-force formalism: Application to the surf zone. Ocean Model. 2010, 34, 16–35. [Google Scholar] [CrossRef]
- Liu, W.-C.; Huang, W.-C. Investigating typhoon-induced storm surge and waves in the coast of Taiwan using an integrally-coupled tide-surge-wave model. Ocean Eng. 2020, 212, 107571. [Google Scholar] [CrossRef]
- Qi, W.-G.; Li, C.-F.; Jeng, D.-S.; Gao, F.-P.; Liang, Z. Combined wave-current induced excess pore-pressure in a sandy seabed: Flume observations and comparisons with theoretical models. Coast. Eng. 2019, 147, 89–98. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.; Ou, J.; Li, Y.; Huang, N. Effects of tidal-current and tidal-level changes on waves in the Yangtze River estuary. J. Trop. Oceanogr. 2015, 34, 19–26. (In Chinese) [Google Scholar] [CrossRef]
- Wu, Z.; Jing, C.; Deng, B.; Cao, Y. SWAN-ROMS coupling model and its application in idealized tidal inlets. J. Harbin Eng. Univ. 2019, 40, 1420–1426. [Google Scholar] [CrossRef]
- Li, B.; Chen, W.; Liu, J.; Li, J.; Wang, S.; Xing, H. Construction and application of nearshore hydrodynamic monitoring system for uninhabited islands. J. Coast. Res. 2020, 99, 131–136. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Wang, Y.; Liao, Z.; Sun, P. Spatiotemporal variations and extreme value analysis of significant wave height in the South China Sea based on 71-year long ERA5 wave reanalysis. Appl. Ocean Res. 2021, 113, 102750. [Google Scholar] [CrossRef]
- Li, B.; Chen, W.; Li, J.; Liu, J.; Shi, P.; Xing, H. Wave energy assessment based on reanalysis data calibrated by buoy observations in the southern South China Sea. Energy Rep. 2022, 8, 5067–5079. [Google Scholar] [CrossRef]
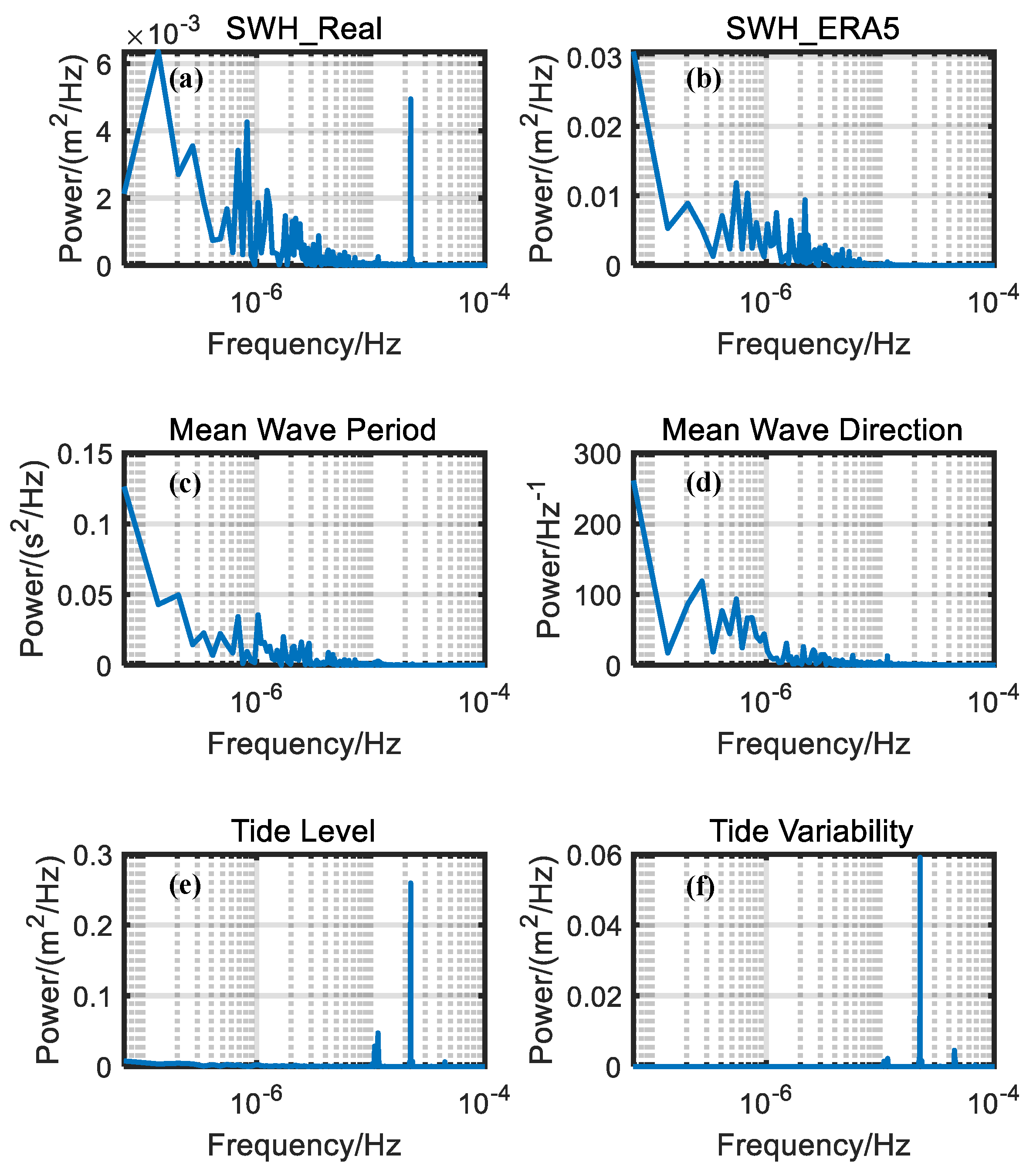
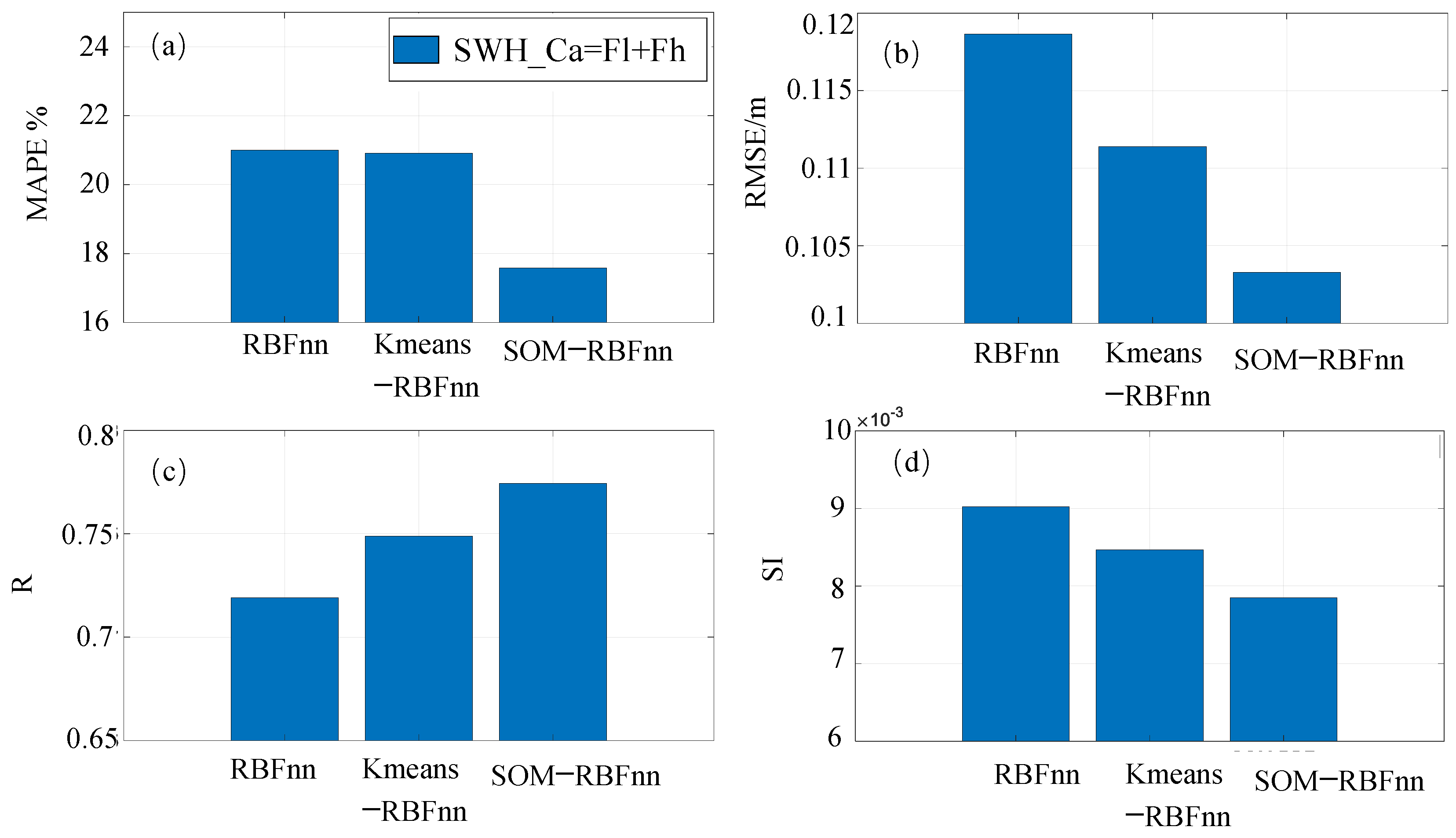
| SWH_ERA5 | MWP | MWD | TL | VT | |
|---|---|---|---|---|---|
| Fl_Real | 0.566 * | 0.700 * | −0.337 * | 0.223 * | 0.0731 * |
| Fh_Real | 0.0299 | 0.0529 * | −0.0127 | 0.287 * | 0.598 * |
| SWH_Real | 0.523 * | 0.653 * | −0.310 * | 0.298 * | 0.267 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; He, Z.; Ling, Y.; Li, J.; Sun, L.; Li, B.; Liu, J.; Chen, W. A SOM−RBFnn-Based Calibration Algorithm of Modeled Significant Wave Height for Nearshore Areas. J. Mar. Sci. Eng. 2022, 10, 706. https://doi.org/10.3390/jmse10050706
Hu H, He Z, Ling Y, Li J, Sun L, Li B, Liu J, Chen W. A SOM−RBFnn-Based Calibration Algorithm of Modeled Significant Wave Height for Nearshore Areas. Journal of Marine Science and Engineering. 2022; 10(5):706. https://doi.org/10.3390/jmse10050706
Chicago/Turabian StyleHu, Hengyu, Zhengwei He, Yanfang Ling, Junmin Li, Lu Sun, Bo Li, Junliang Liu, and Wuyang Chen. 2022. "A SOM−RBFnn-Based Calibration Algorithm of Modeled Significant Wave Height for Nearshore Areas" Journal of Marine Science and Engineering 10, no. 5: 706. https://doi.org/10.3390/jmse10050706
APA StyleHu, H., He, Z., Ling, Y., Li, J., Sun, L., Li, B., Liu, J., & Chen, W. (2022). A SOM−RBFnn-Based Calibration Algorithm of Modeled Significant Wave Height for Nearshore Areas. Journal of Marine Science and Engineering, 10(5), 706. https://doi.org/10.3390/jmse10050706







