Ship Path Planning Based on Buoy Offset Historical Trajectory Data
Abstract
:1. Introduction
2. Multiplication Seasonal SARIMA Model
2.1. ARIMA Model
2.2. Stochastic Seasonal Model
2.3. Multiplication Seasonal Model
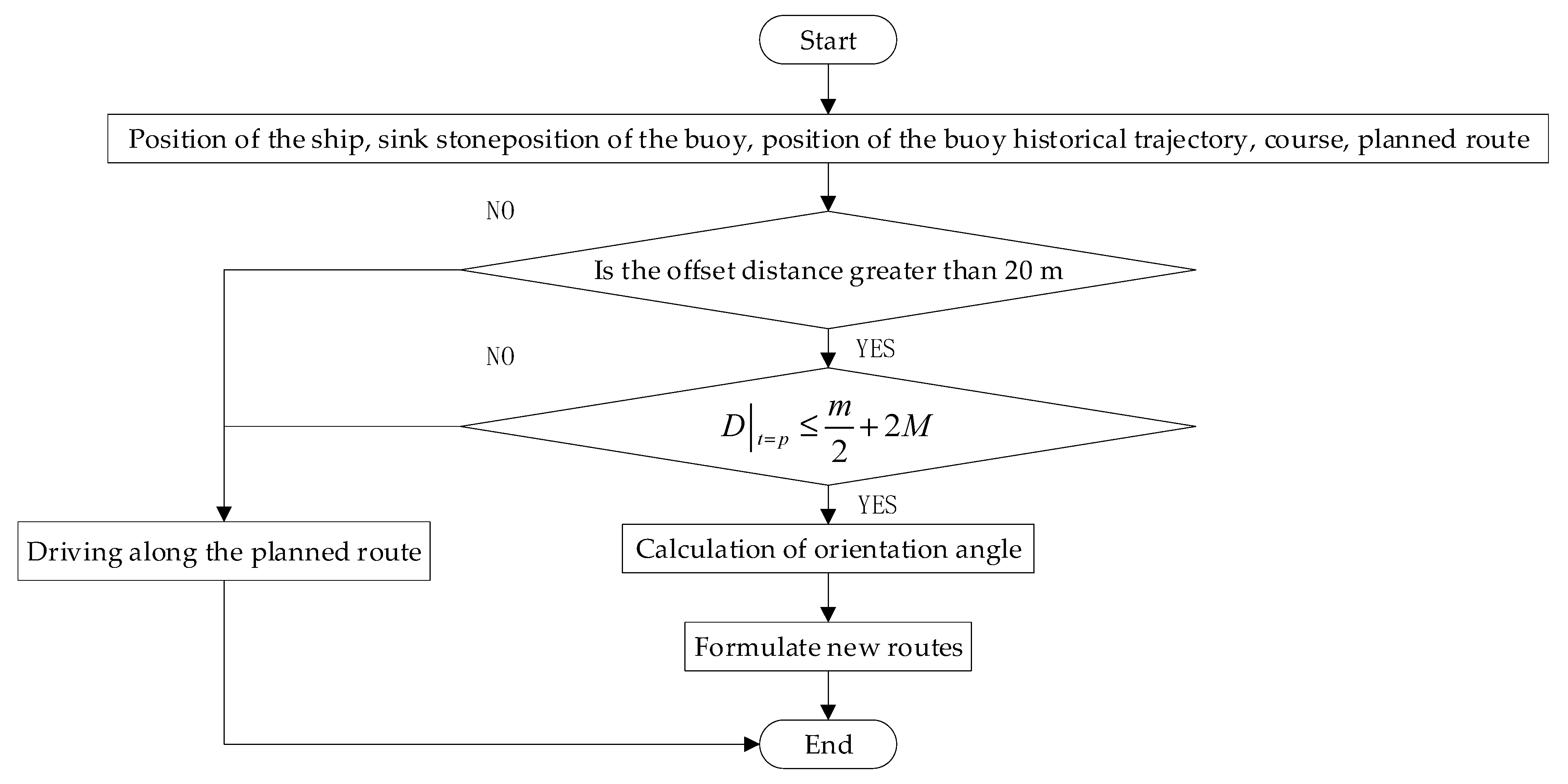
3. Ship Path-Planning Method for Random Motion of Buoy
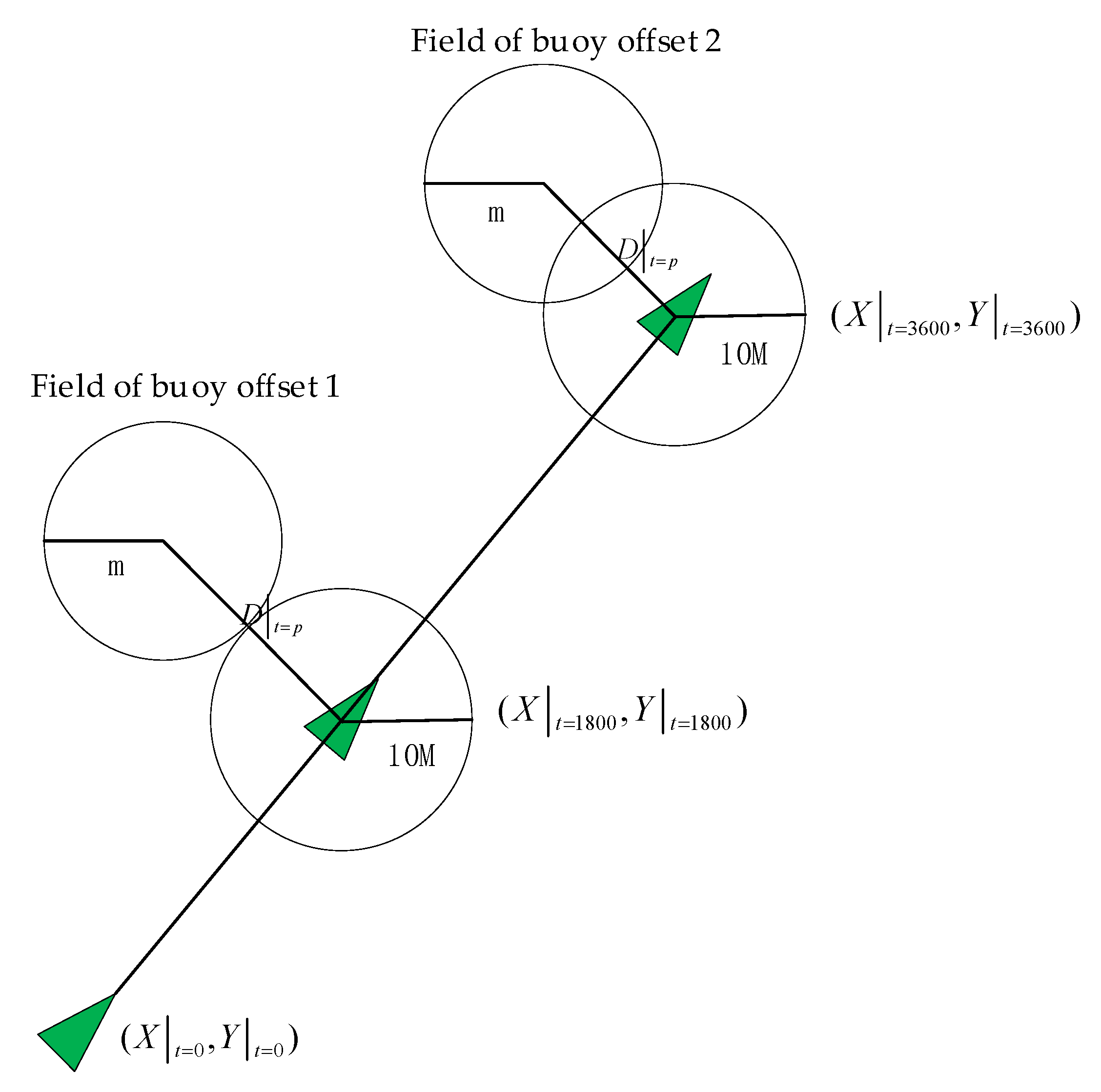
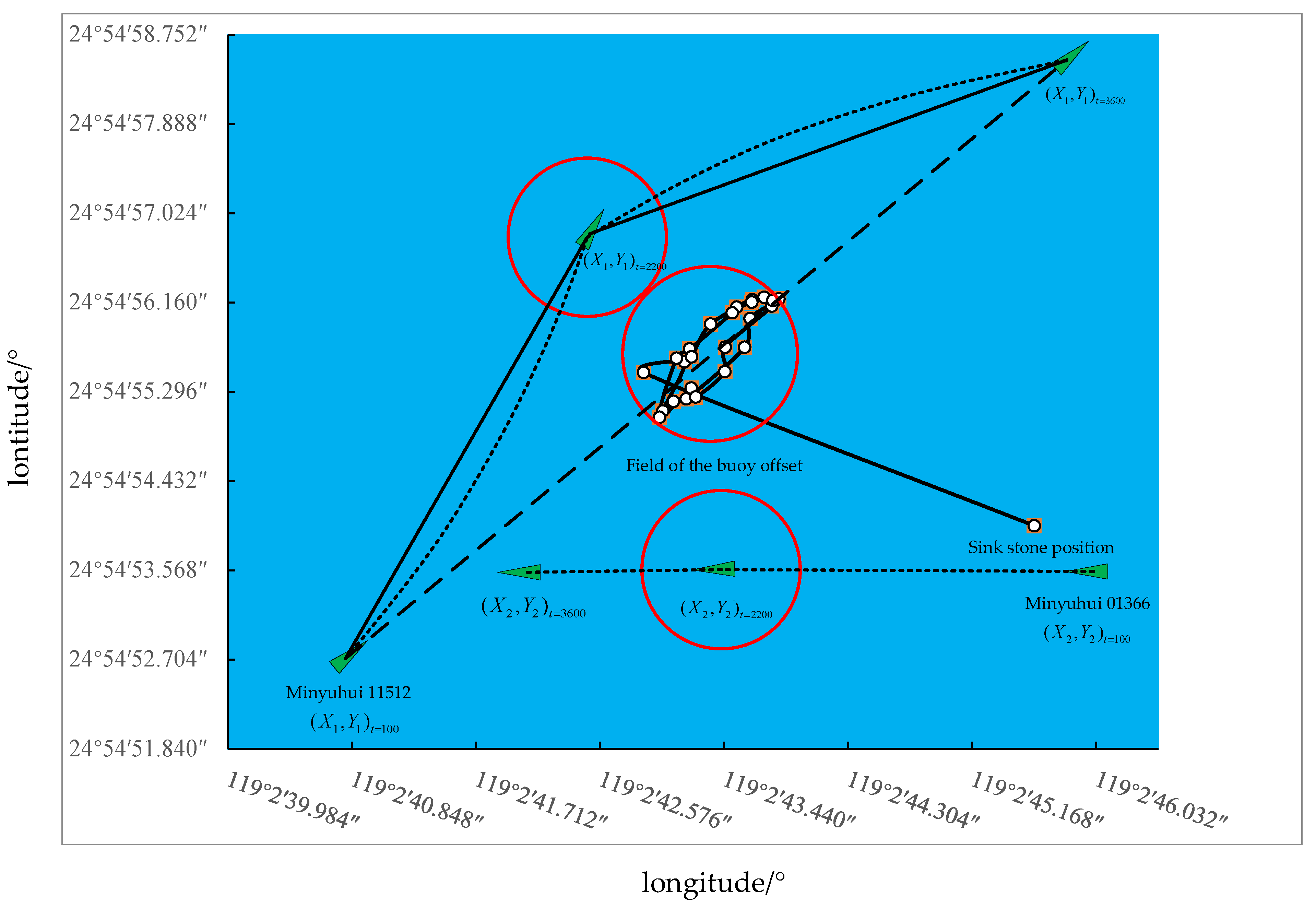
3.1. Field of Buoy Offset
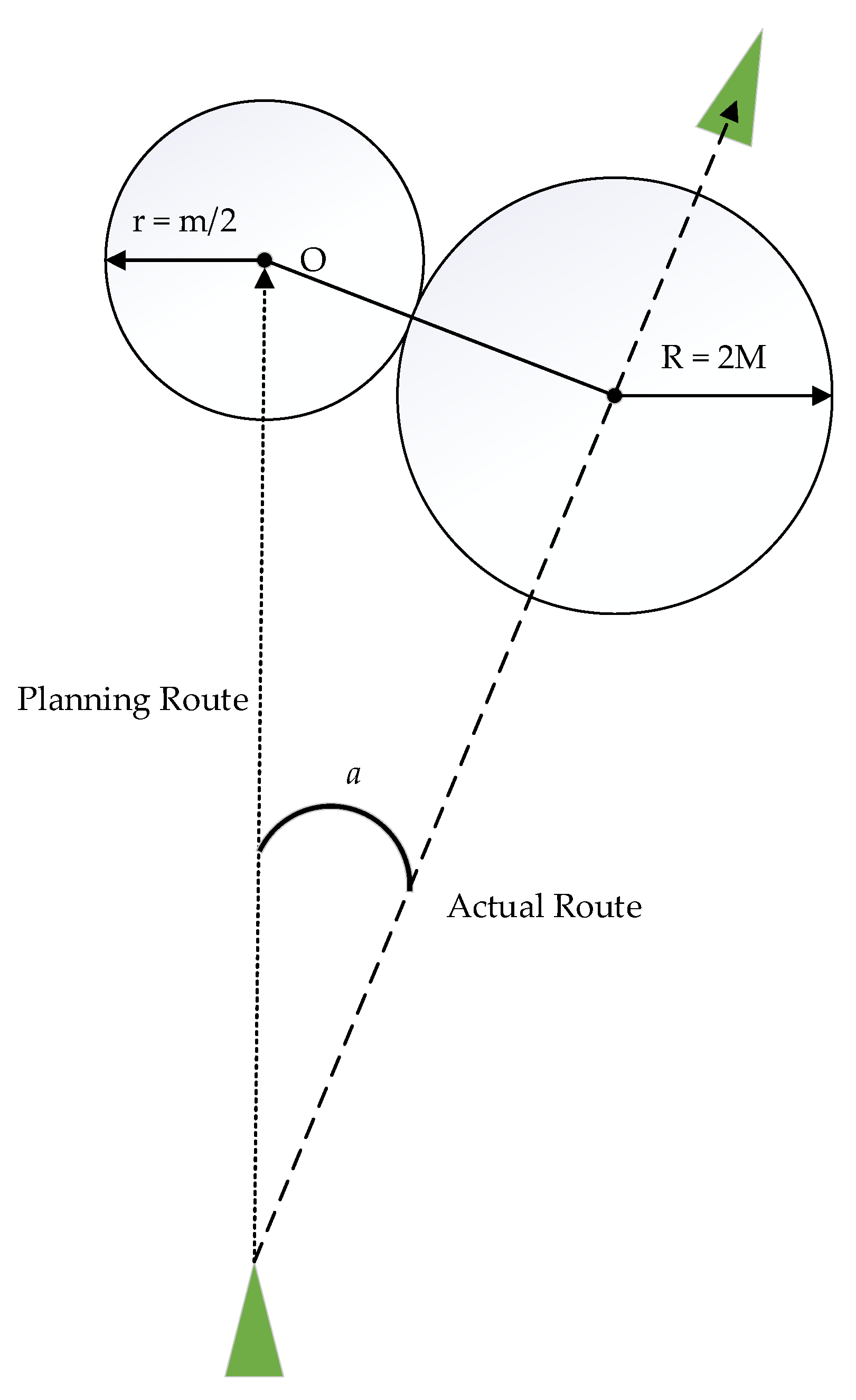
3.2. Risk Field of Ship Collision
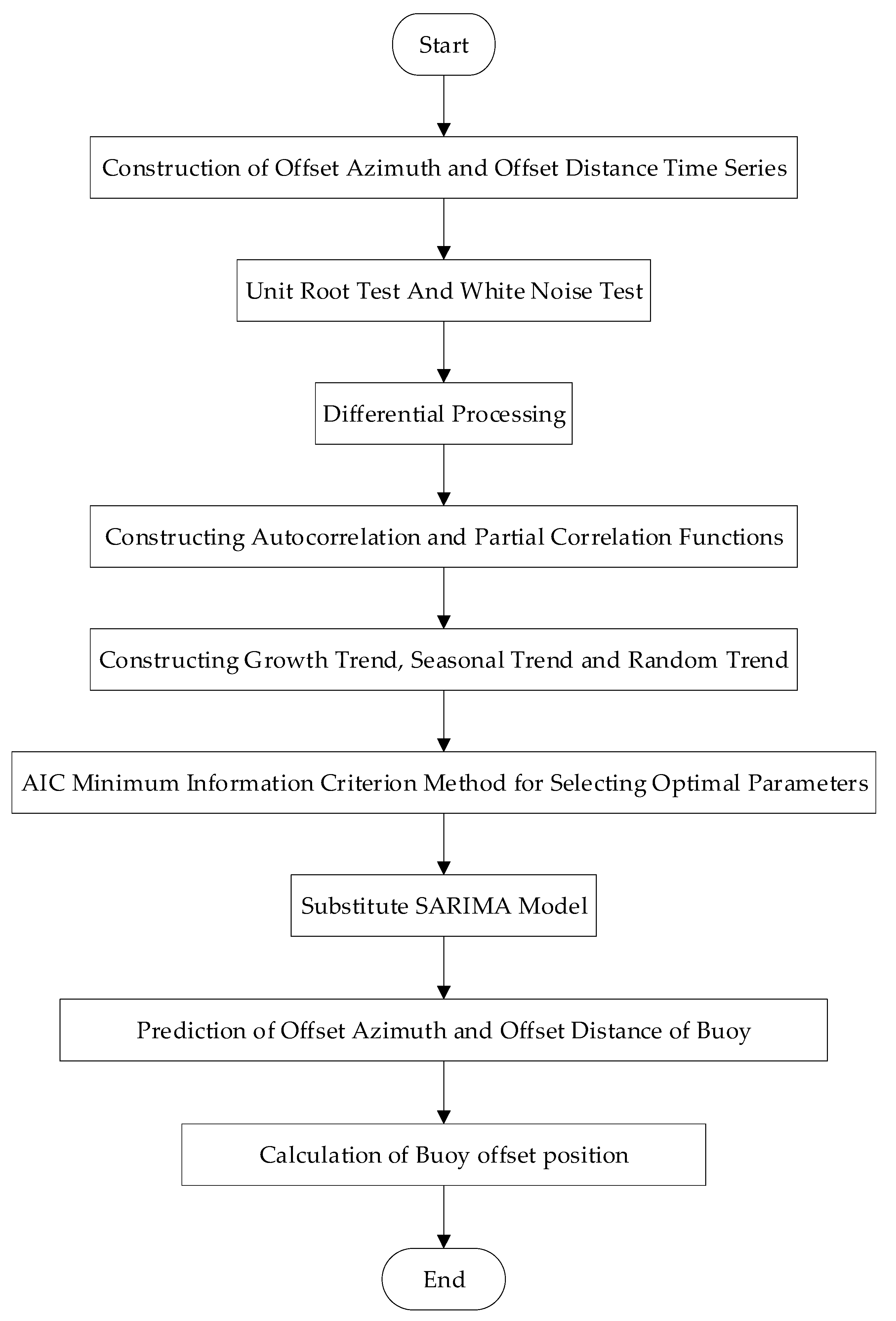
4. Buoy Offset Position Prediction
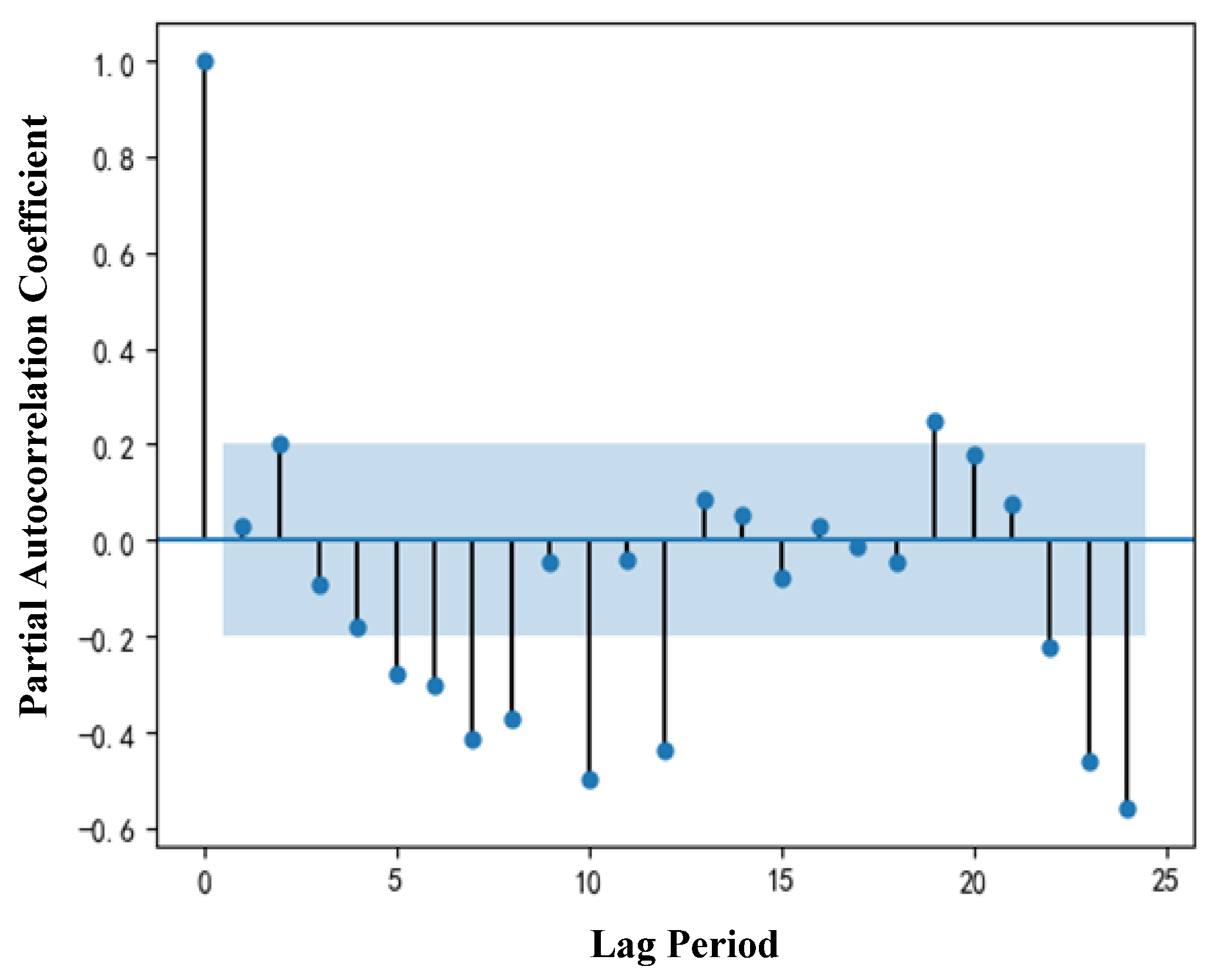
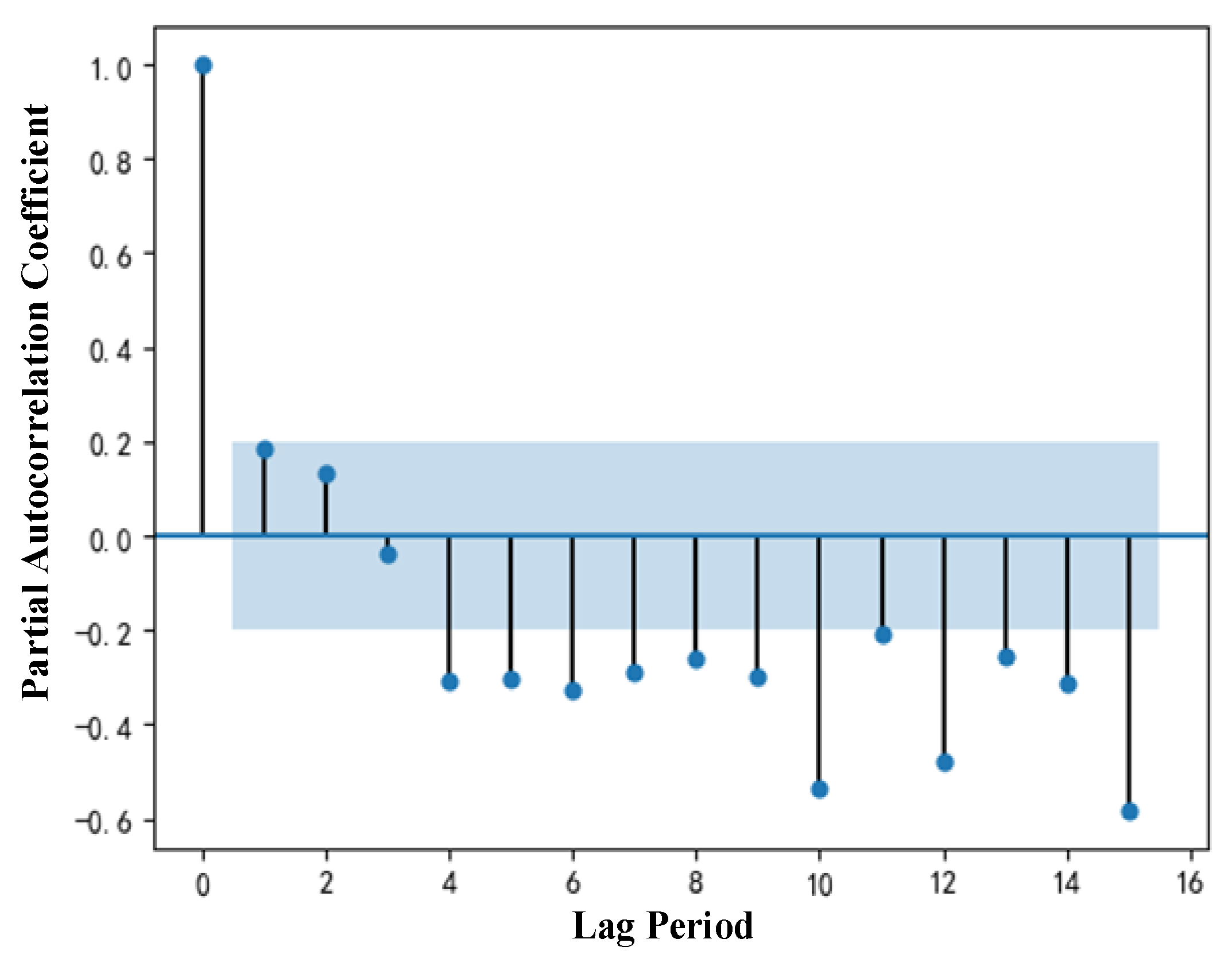
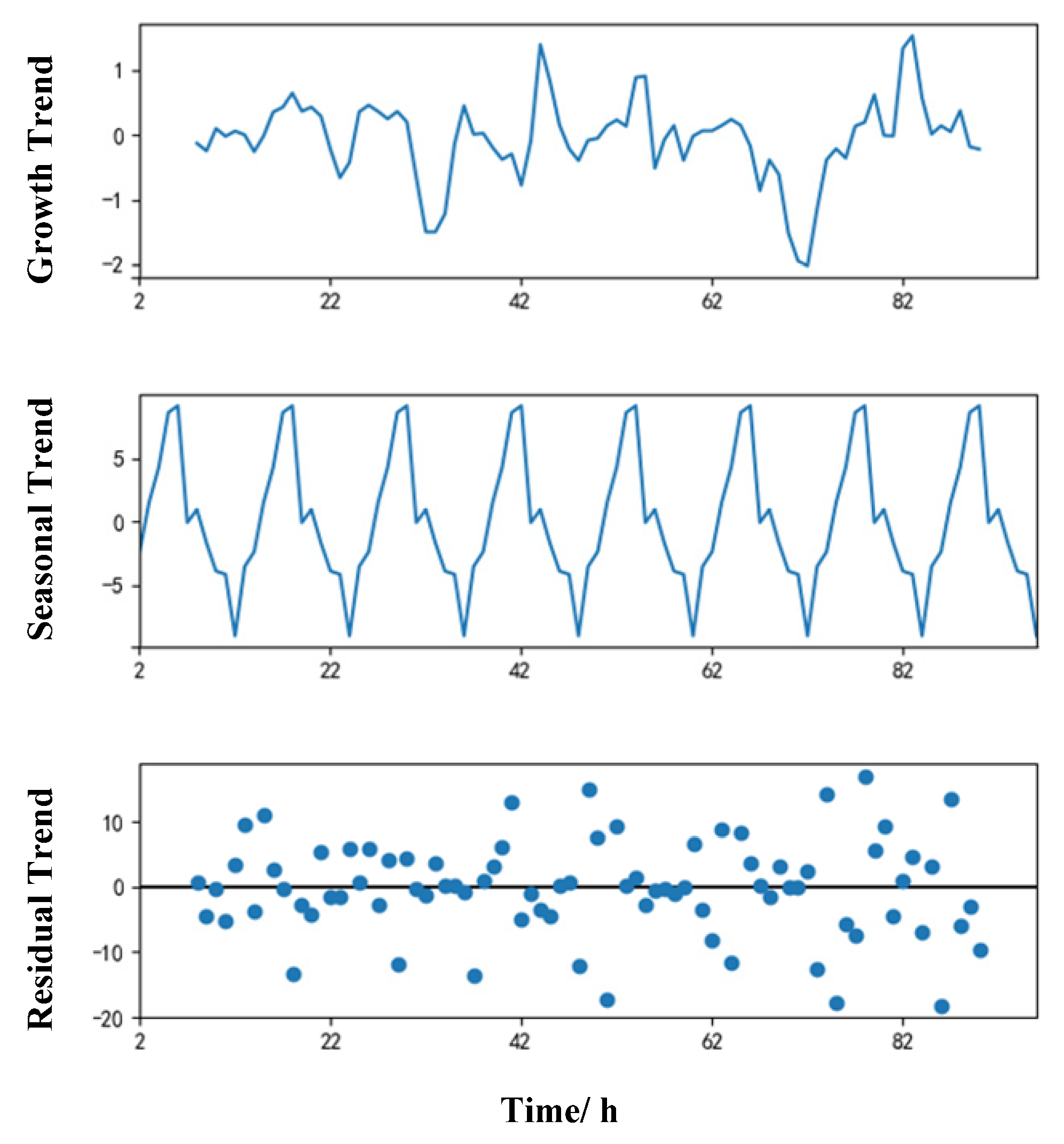
4.1. Data Verification and Processing
4.2. Parameter Selection
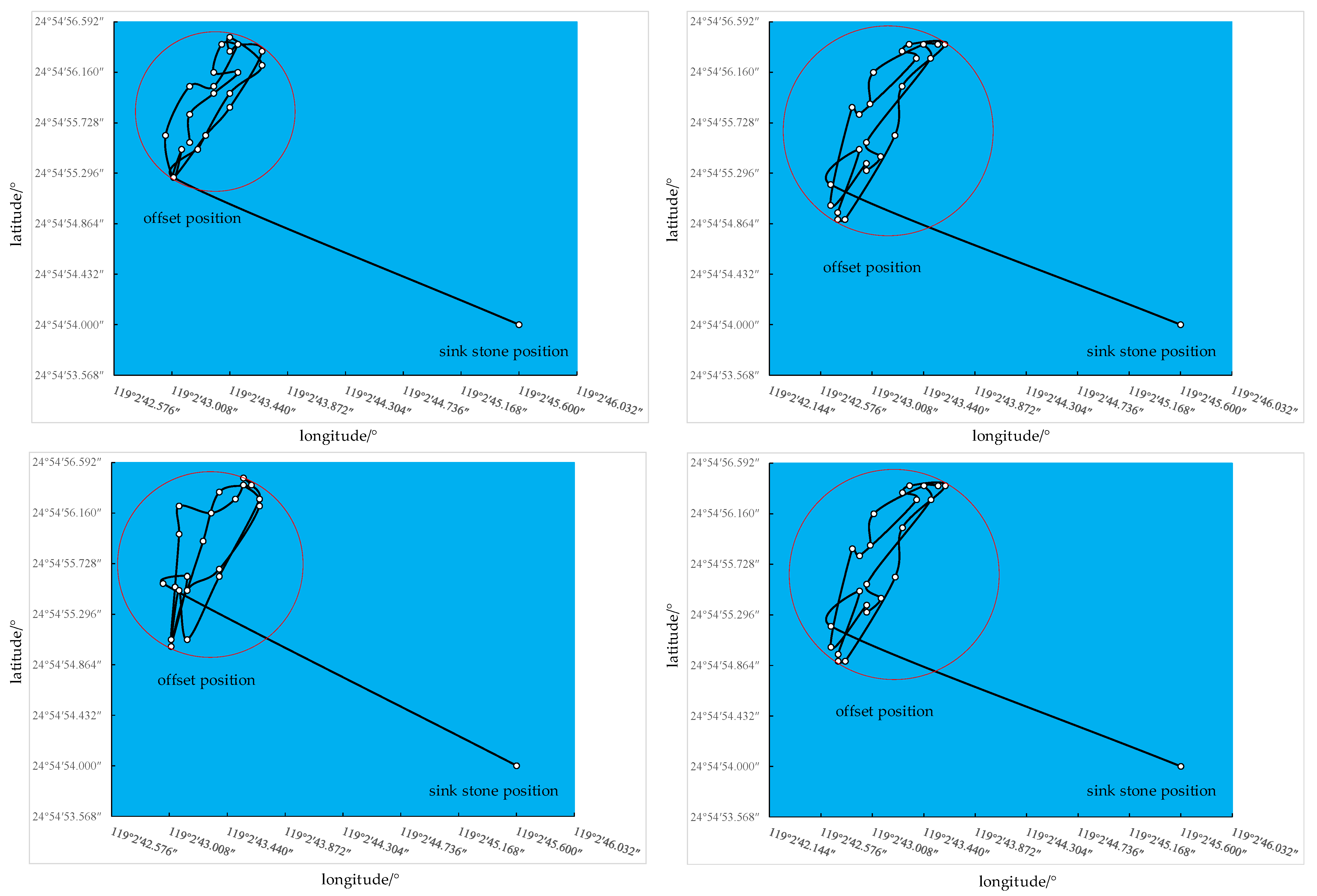
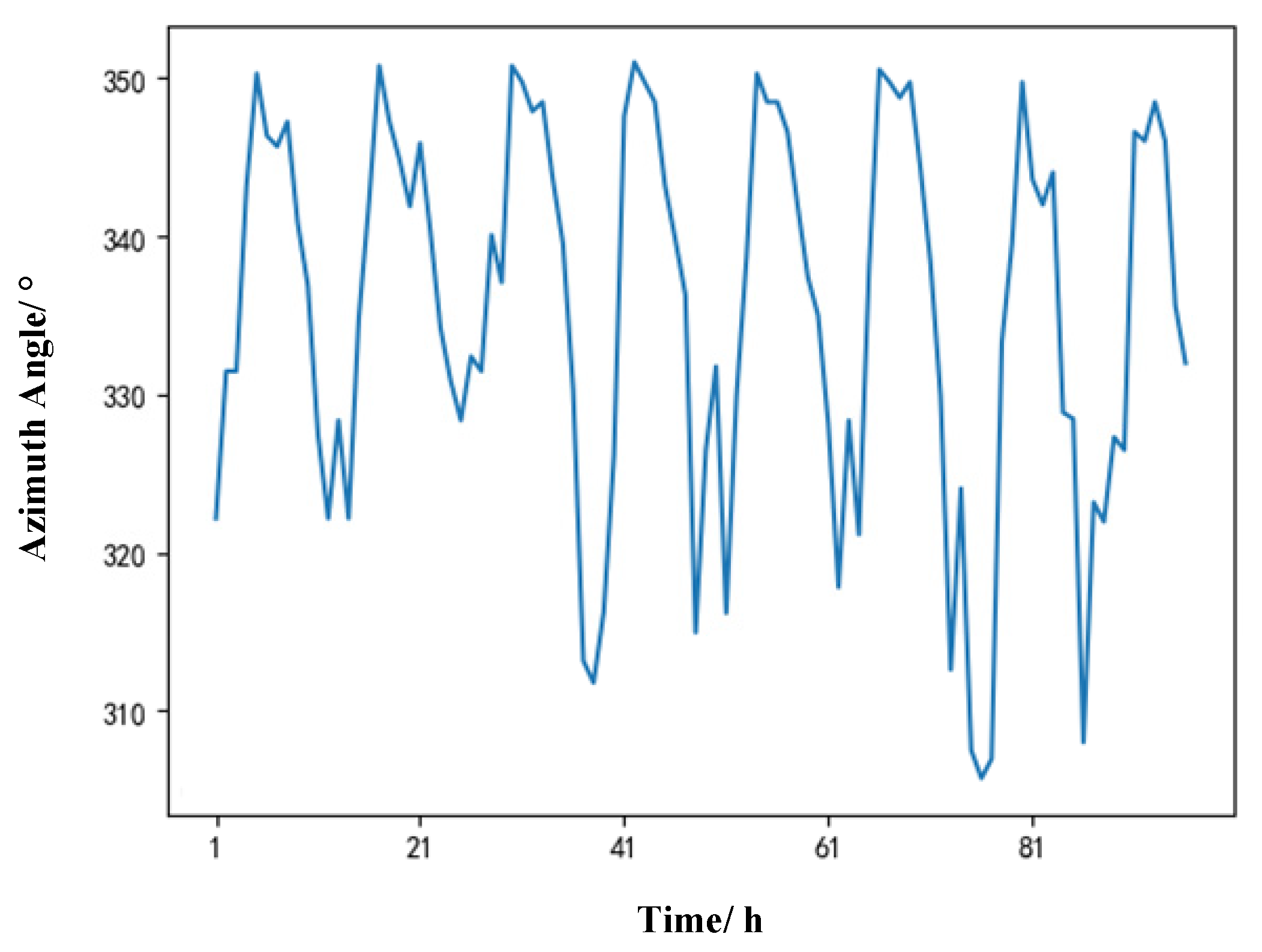
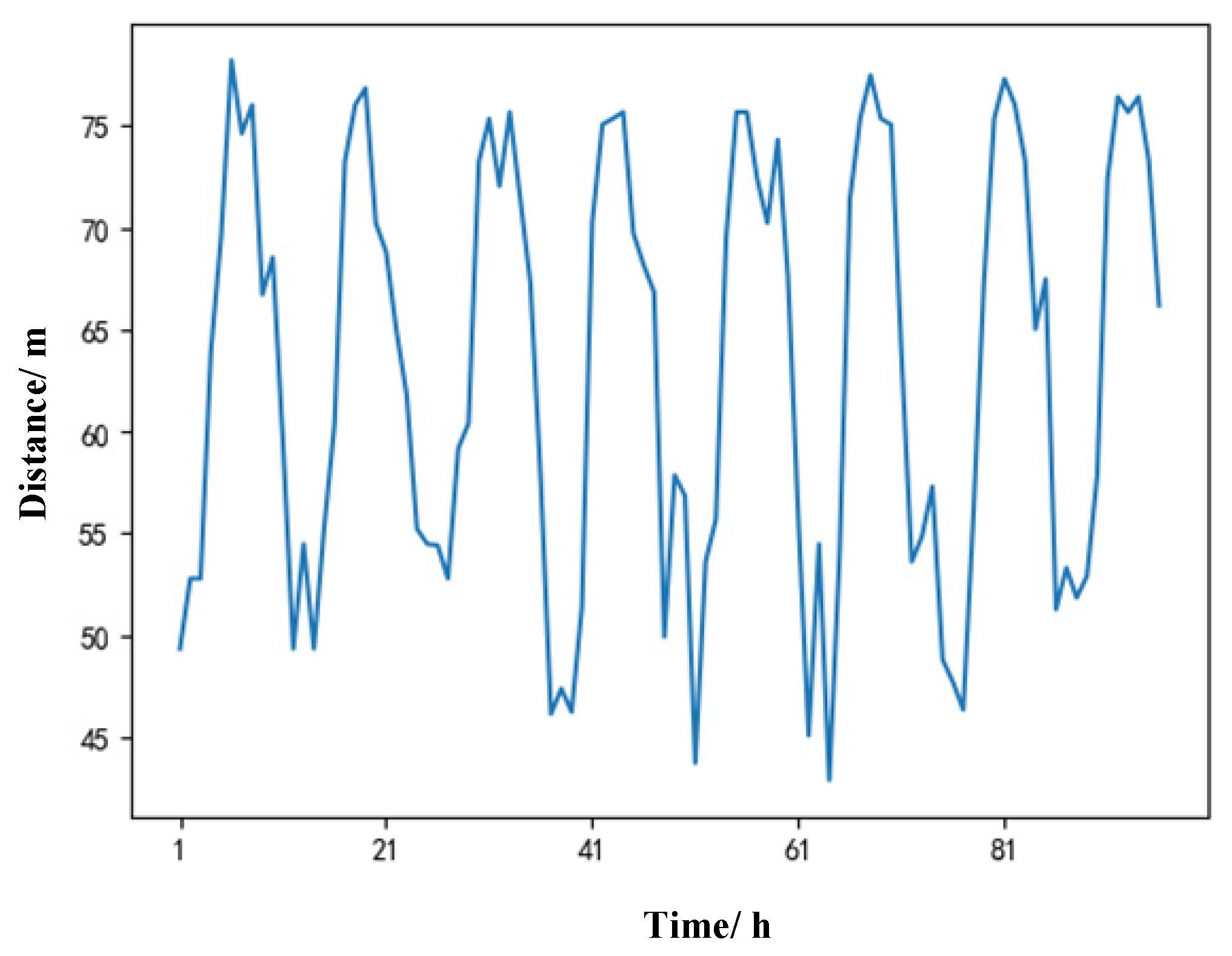
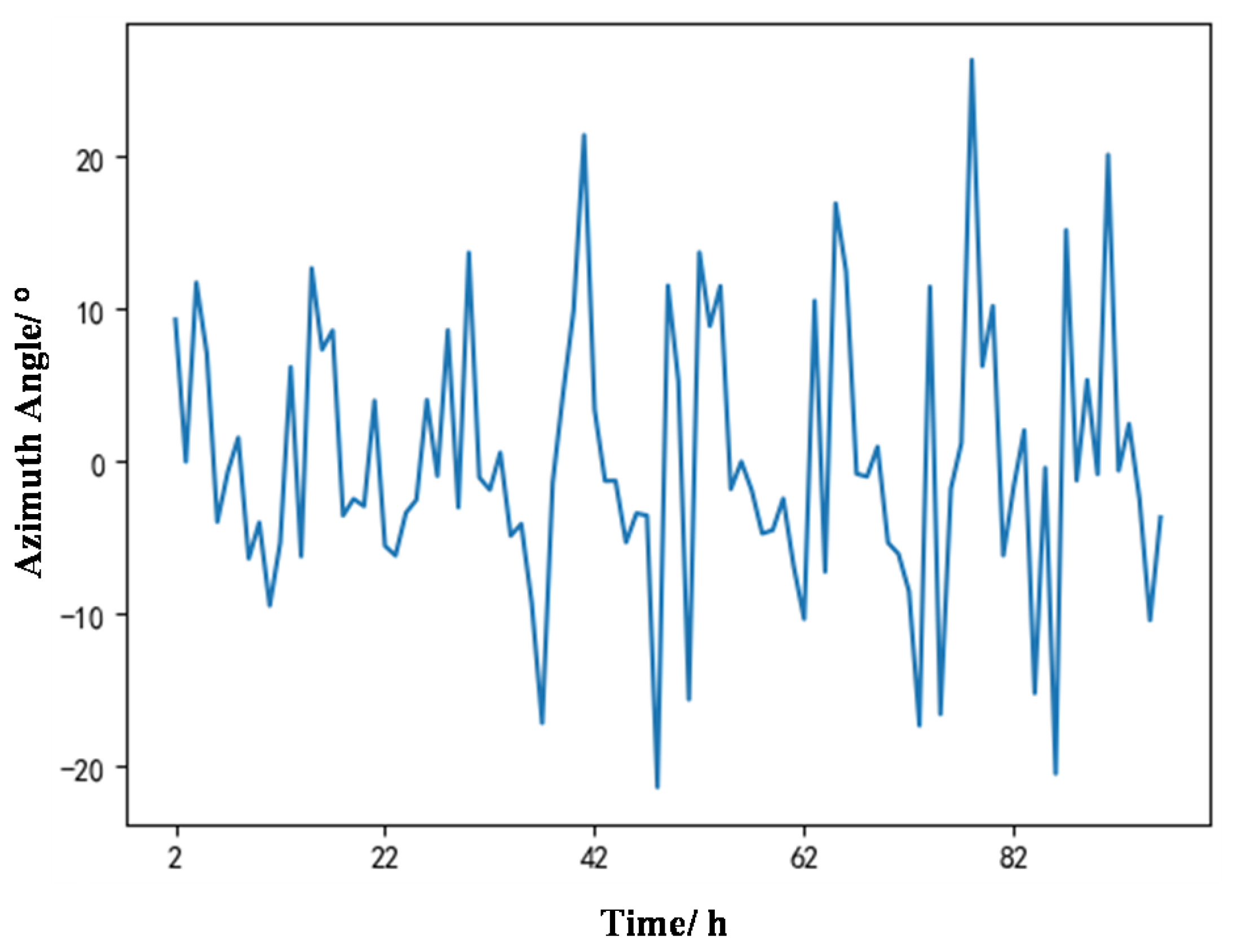
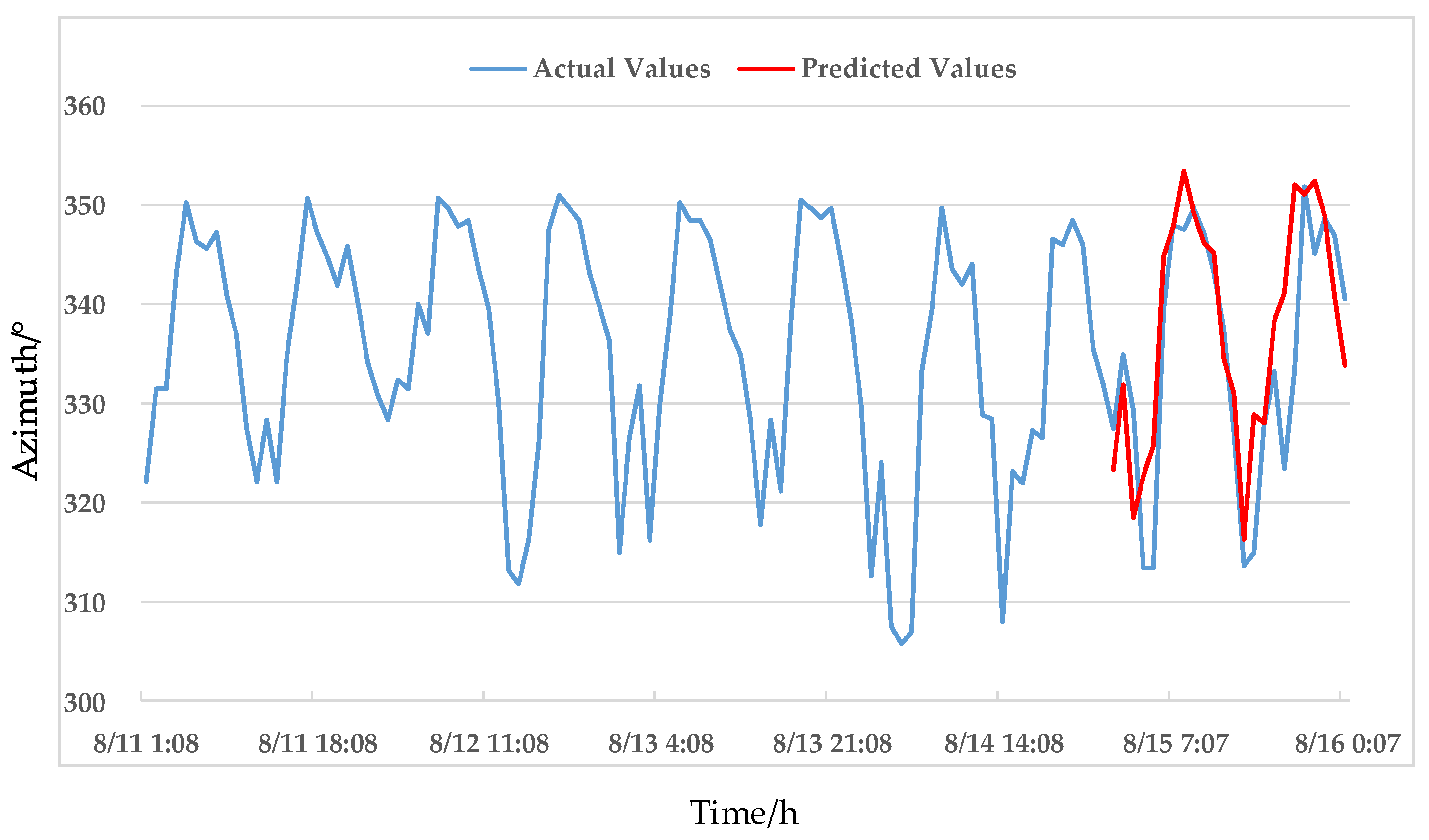
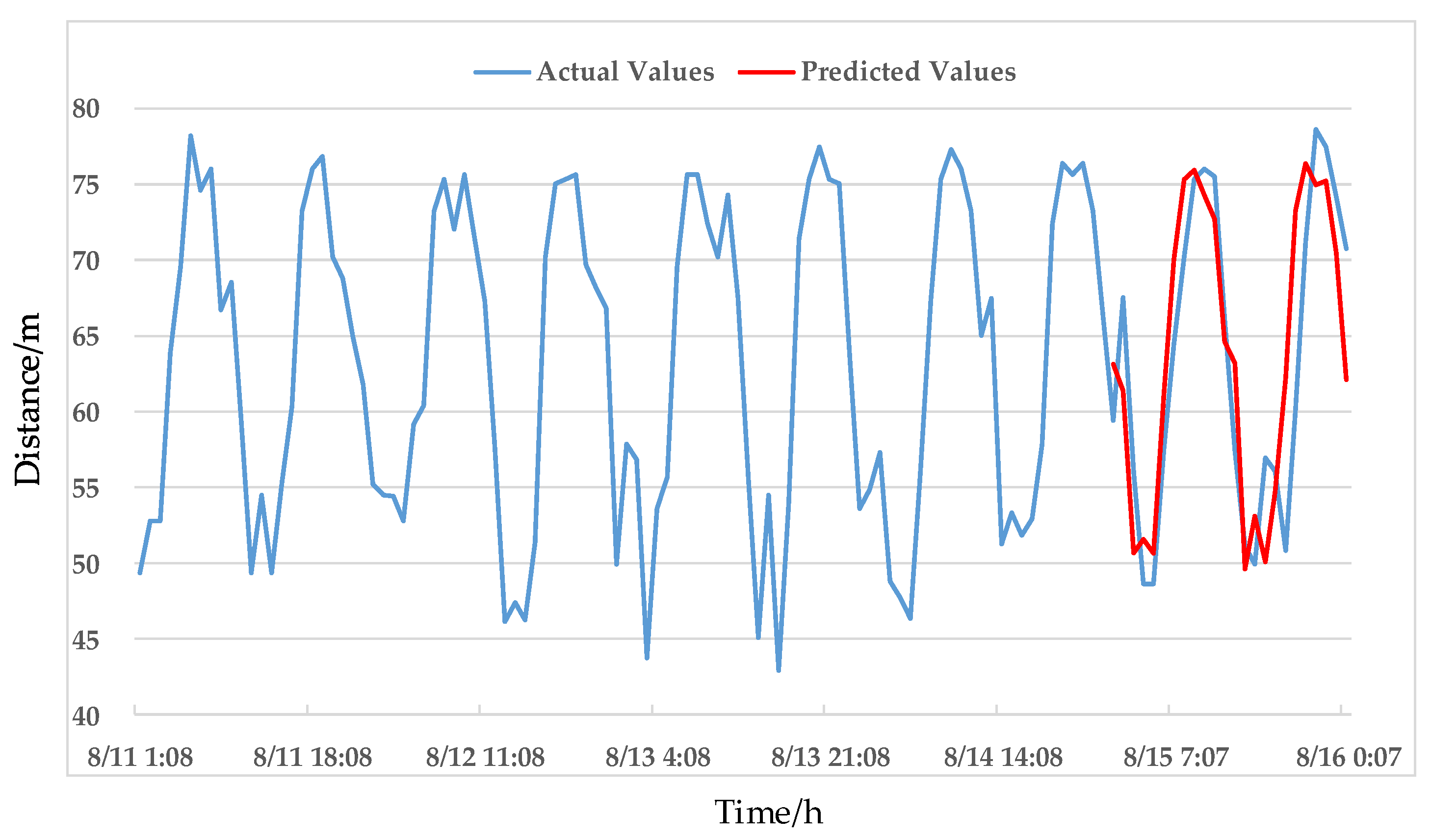
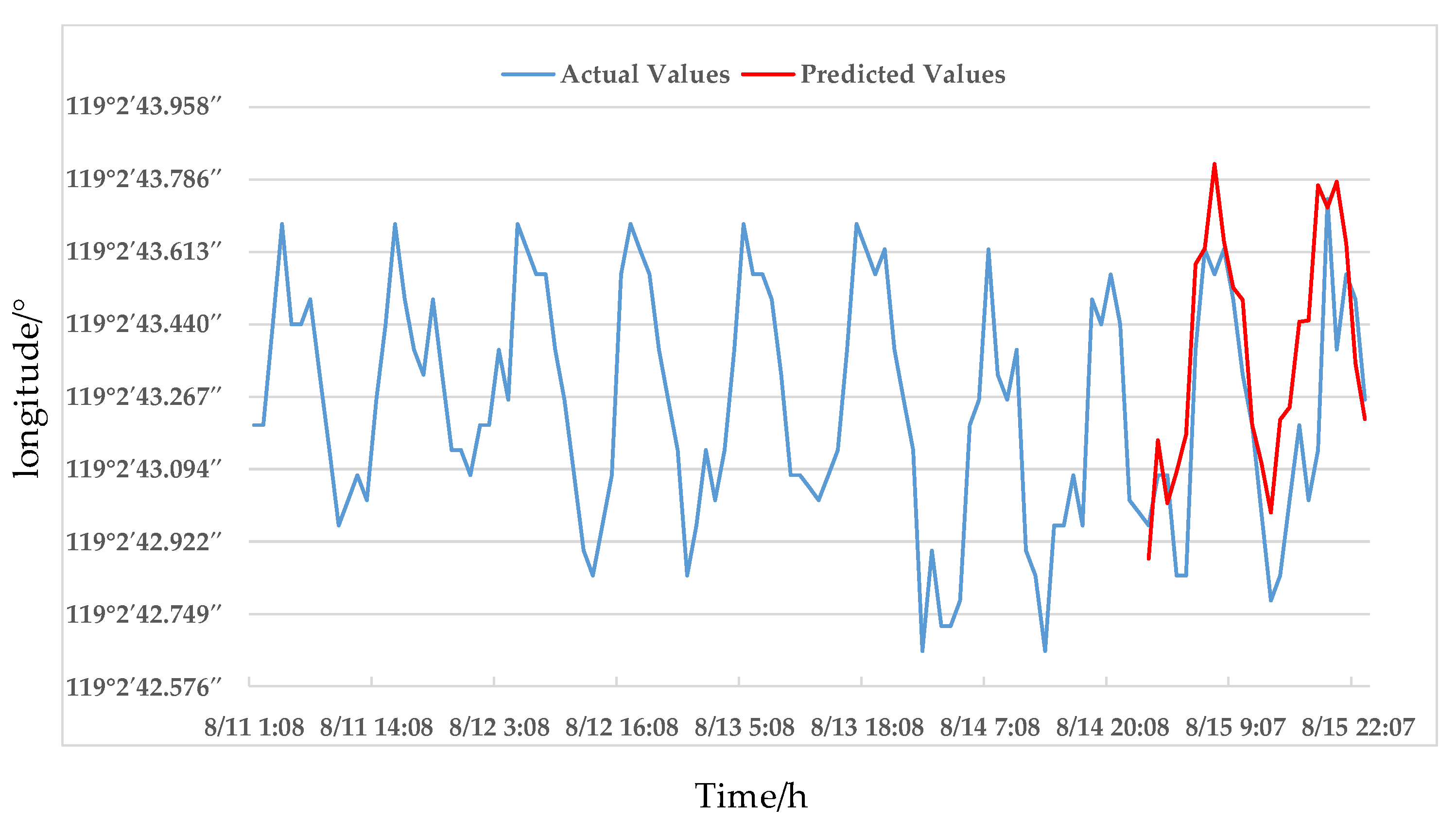
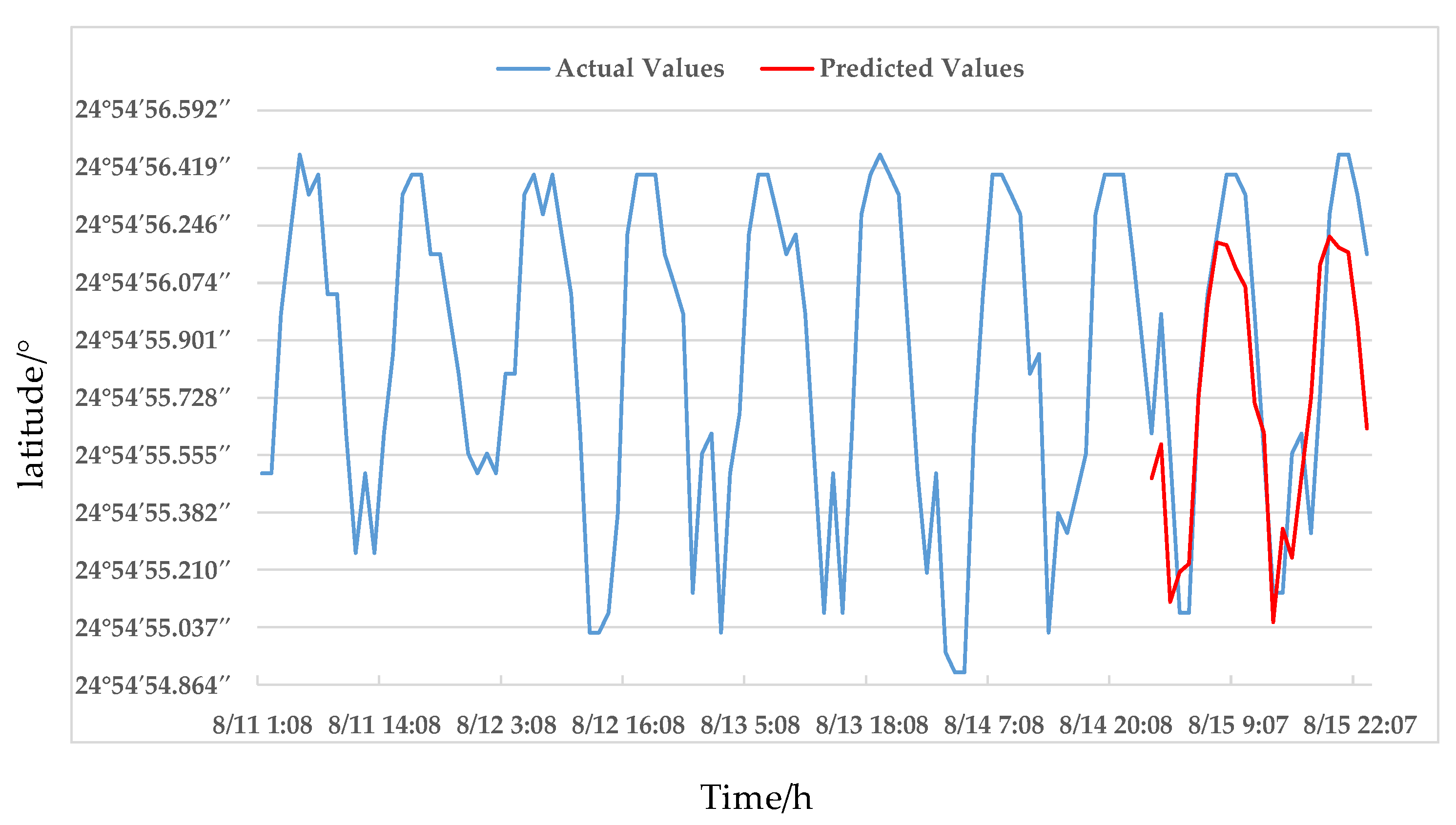
4.3. Offset Position Prediction
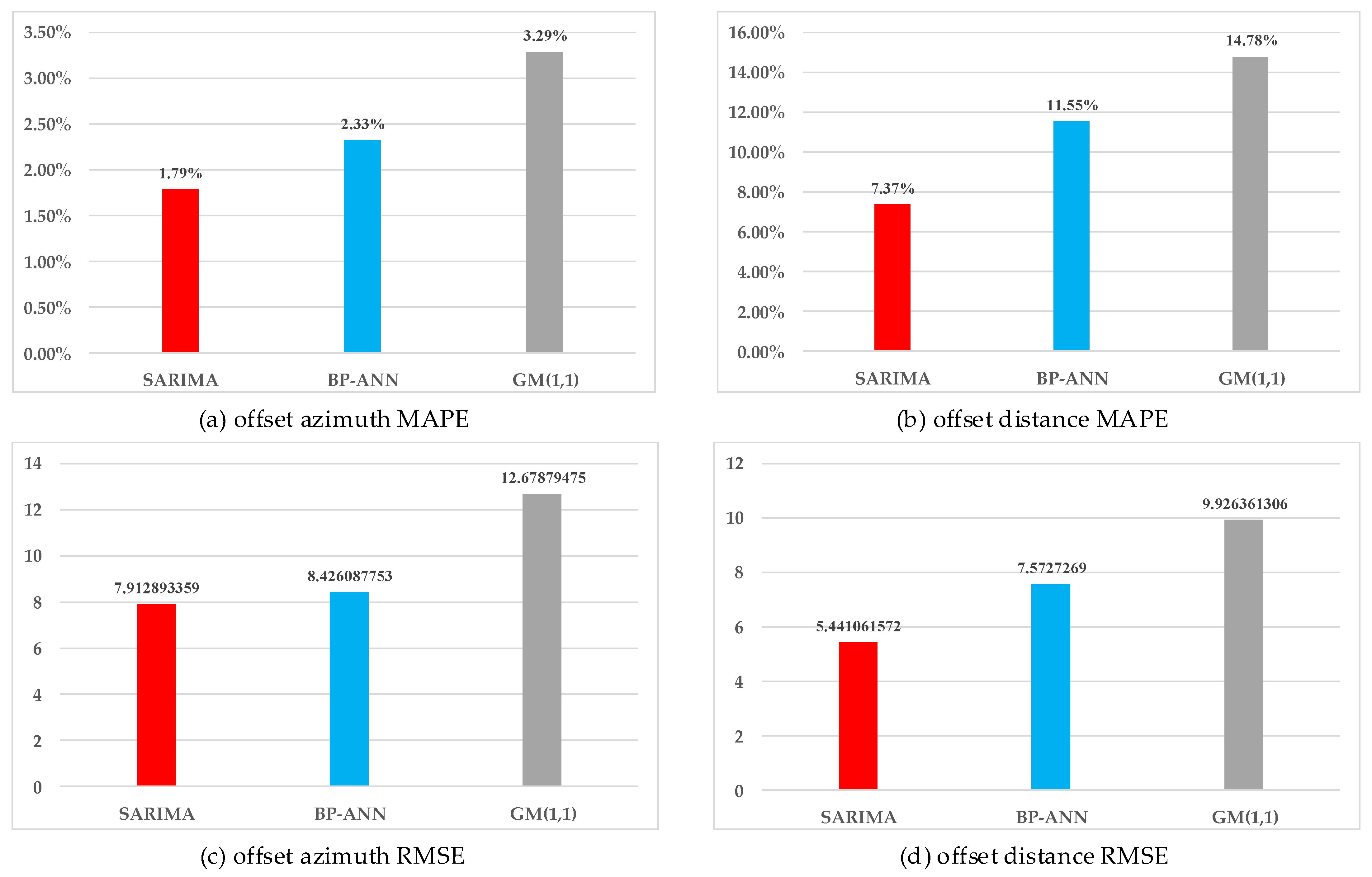
4.4. Error Analysis
5. Path-Planning Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yoo, Y.; Lee, J.S. Collision Risk Assessment Support System for MASS RO and VTSO Support in Multi-Ship Environment of Vessel Traffic Service Area. J. Mar. Sci. Eng. 2021, 9, 1143. [Google Scholar] [CrossRef]
- Rong, H.; Teixeira, A.P.; Soares, C.G. Spatial correlation analysis of near ship collision hotspots with local maritime traffic characteristics. Reliab. Eng. Syst. Saf. 2021, 209, 107463. [Google Scholar] [CrossRef]
- Luong, T.N.; Hwang, S.; Im, N. Harbour Traffic Hazard Map for real-time assessing waterway risk using Marine Traffic Hazard Index. Ocean Eng. 2021, 239, 109884. [Google Scholar] [CrossRef]
- Kim, J.K. Semi-Continuous Spatial Statistical Analysis Using AIS Data for Vessel Traffic Flow Characteristics in Fairway. J. Mar. Sci. Eng. 2021, 9, 4–378. [Google Scholar] [CrossRef]
- Piao, Z.; Guo, C.; Sun, S. Research into the Automatic Berthing of under actuated Unmanned Ships under Wind Loads Based on Experiment and Numerical Analysis. J. Mar. Sci. Eng. 2019, 7, 300. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.W.; Roh, M.I.; Kim, K.S. Ship route planning in Arctic Ocean based on POLARIS. Ocean Eng. 2021, 234, 109297. [Google Scholar] [CrossRef]
- Lazarowska, A. Ship’s trajectory planning for collision avoidance at sea based on ant colony optimization. J. Navig. 2015, 68, 291–307. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Feng, W.; Mao, Z.Y. Path planning of UUV based on HQPSO algorithm with considering the navigation error. Ocean Eng. 2021, 244, 110048. [Google Scholar] [CrossRef]
- MahmoudZadeh, S.; Yazdani, A.M.; Sammut, K.; Powers, D. Online path planning for AUV rendezvous in dynamic cluttered undersea environment using evolutionary algorithms. Appl. Soft Comput. 2018, 70, 929–945. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; Hao, C.; Su, J.C. Path planning for unmanned surface vehicle based on predictive artificial potential field. Int. J. Adv. Robot. Syst. 2020, 17, 2. [Google Scholar] [CrossRef] [Green Version]
- Lyh, H.G.; Yin, Y. COLREGS-Constrained Real-time Path Planning for Autonomous Ships Using Modified Artificial Potential Fields. J. Navig. 2019, 72, 588–608. [Google Scholar]
- Luis, S.Y.; Reina, D.G.; Marin, S.L.T. A Multiagent Deep Reinforcement Learning Approach for Path Planning in Autonomous Surface Vehicles: The Ypacarai Lake Patrolling Case. IEEE Access 2021, 9, 17084–17099. [Google Scholar] [CrossRef]
- Da Silva, A.G.; Dos Santos, D.H.; De Negreiros, A.P.F.; Silva, J.M.V.B.D.S.; Gonçalves, L.M.G. High-Level Path Planning for an Autonomous Sailboat Robot Using Q-Learning. Sensors 2020, 20, 6. [Google Scholar]
- Luis, S.Y.; Reina, D.G.; Marin, S.L.T. A Deep Reinforcement Learning Approach for the Patrolling Problem of Water Resources Through Autonomous Surface Vehicles: The Ypacarai Lake Case. IEEE Access 2020, 8, 204076–204093. [Google Scholar] [CrossRef]
- Guo, S.Y.; Zhang, X.G.; Zheng, Y.S.; Du, Y. An Autonomous Path Planning Model for Unmanned Ships Based on Deep Reinforcement Learning. Sensors 2020, 20, 426. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lazarowska, A. Comparison of Discrete Artificial Potential Field Algorithm and Wave-Front Algorithm for Autonomous Ship Trajectory Planning. IEEE Access 2021, 8, 221013–221026. [Google Scholar] [CrossRef]
- Carlucho, I.; De Paula, M.; Wang, S.; Petillot, Y.; Acosta, G.G. Adaptive low-level control of autonomous underwater vehicles using deep reinforcement learning. Robot. Auton. Syst. 2018, 107, 71–86. [Google Scholar] [CrossRef] [Green Version]
- Meyer, E.; Heiberg, A.; Rasheed, A.; San, O. COLREG-Compliant Collision Avoidance for Unmanned Surface Vehicle Using Deep Reinforcement Learning. IEEE Access 2020, 8, 165344–165364. [Google Scholar] [CrossRef]
- Zaccone, R. COLREG-Compliant Optimal Path Planning for Real-Time Guidance and Control of Autonomous Ships. J. Mar. Sci. Eng. 2021, 9, 405. [Google Scholar] [CrossRef]
- Shah, B.C.; Gupta, S.K. Long-Distance Path Planning for Unmanned Surface Vehicles in Complex Marine Environment. IEEE J. Ocean. Eng. 2020, 45, 813–830. [Google Scholar] [CrossRef]
- Lyridis, D.V. An improved ant colony optimization algorithm for unmanned surface vehicle local path planning with multi-modality constraints. Ocean Eng. 2021, 241, 109890. [Google Scholar] [CrossRef]
- Ahmed, B.; Mangalathu, S.; Jeon, J.S. Seismic damage state predictions of reinforced concrete structures using stacked long short-term memory neural networks. J. Build. Eng. 2022, 46, 103737. [Google Scholar] [CrossRef]
- Matic, P.; Bego, O.; Males, M. Complex Hydrological System Inflow Prediction using Artificial Neural Network. Teh. Vjesn. Tech. Gaz. 2022, 29, 172–177. [Google Scholar]
- Yang, Y.; Fan, C.J.; Chen, L. IPMOD: An efficient outlier detection model for high-dimensional medical data streams. Expert Syst. Appl. 2022, 191, 116212. [Google Scholar] [CrossRef]
- Bhanja, S.; Das, A. A Black Swan event-based hybrid model for Indian stock markets’ trends prediction. Innov. Syst. Softw. Eng. 2022, 1–15. [Google Scholar] [CrossRef]
- Yu, W.W.; Xing, J.M. Sports Event Model Evaluation and Prediction Method Using Principal Component Analysis. Wirel. Commun. Mob. Comput. 2022, 2022, 9351522. [Google Scholar] [CrossRef]
- Li, J.X.; Zhou, A.J.; Liao, Y.F. Forest Ecological Diversity Change Prediction Discrete Dynamic Model. Discret. Dyn. Nat. Soc. 2022, 2022, 4869363. [Google Scholar] [CrossRef]
- Liu, L.; Chen, W.Z.; Li, Y.B. Comprehensive Analysis of Pyroptosis-Related Long Noncoding RNA Immune Infiltration and Prediction of Prognosis in Patients with Colon Cancer. J. Oncol. 2022, 2022, 2035808. [Google Scholar] [CrossRef]
- Zeng, Z.; Yan, H.; Fu, A.M.N. Time-series prediction based on pattern classification. Artif. Intell. Eng. 2001, 15, 61–69. [Google Scholar] [CrossRef]
- Yuan, K.X.; Liu, J.; Yang, S.C. Time series forecasting based on kernel mapping and high-order fuzzy cognitive maps. Knowl.-Based Syst. 2020, 206, 106359. [Google Scholar] [CrossRef]
- Sebastian, R.; Thomas, N. A fractal interpolation approach to improve neural network predictions for difficult time series data. Expert Syst. Appl. 2021, 169, 114474. [Google Scholar]
- Her, M.T.; Chung, C.C.; Lin, C.T. Ship Price Predictions of Panamax Second-Hand Bulk Carriers Using Grey Models. J. Mar. Sci. Technol. Taiwan 2019, 27, 229–234. [Google Scholar]
- Sahoo, A.; Samantatay, S.; Ghose, D.K. Multilayer perceptron and support vector machine trained with grey wolf optimiser for predicting floods in Barak river, India. J. Earth Syst. Sci. 2022, 131, 85. [Google Scholar] [CrossRef]
- Paquet, E.; Soleymani, F. QuantumLeap: Hybrid quantum neural network for financial predictions. Expert Syst. Appl. 2022, 195, 116583. [Google Scholar] [CrossRef]
- Oztunc, K.; Oznur Kaymak, Y. Prediction of crude oil prices in COVID-19 outbreak using real data. Chaos Solitons Fractals 2022, 158, 111990. [Google Scholar] [CrossRef]
- Thiruchelvam, L.; Dass, S.C.; Asirvadam, S.; Daud, H.; Gill, B.S. Determine neighboring region spatial effect on dengue cases using ensemble ARIMA models. Sci. Rep. 2021, 11, 5873. [Google Scholar] [CrossRef]
- Wu, Z.Z.; Ren, L.Z.; Zhou, S.B.; Zhang, Y.; Xu, W.; Zhang, H. The Offset Azimuth Prediction of Light Buoy Based on Markov Chain Optimization Multiplicative Seasonal Model. Math. Probl. Eng. 2022, 2022, 1250206. [Google Scholar] [CrossRef]
- Koyuncu, K.; Tavacioglu, L.; Gokmen, N.; Arican, U. Forecasting COVID-19 impact on RWI/ISL container throughput index by using SARIMA models. Marit. Policy Manag. 2021, 48, 1096–1108. [Google Scholar] [CrossRef]
- Zhou, D. Research on a Novel Dynamic and Fuzzy Ship Domain; Dalian Maritime University: Dalian, China, 2017. [Google Scholar]
- Dorta, M.; Sanchez, G. Bootstrap unit-root test for random walk with drift: The bsrwalkdrift command. Stata J. 2021, 21, 39–50. [Google Scholar] [CrossRef]
- Adib, A.; Sheydaei, F.; Shoushtari, M.M.; Ashrafi, S.M. Using of gene expression programming method for prediction of daily components of tidal cycle in tidal rivers. Arab. J. Geosci. 2021, 14, 5. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Qie, Z.H.; Han, W.M. Fitting model optimization test curve based on the AIC criterion. J. Hebei Agric. Univ. 2017, 40, 120–124. [Google Scholar]
- Rahmanian, V.; Bokaie, S.; Haghdoost, A. Predicting cutaneous leishmaniasis using SARIMA and Markov switching models in Isfahan, Iran: A time-series study. Asian Pac. J. Trop. Med. 2021, 14, 83–93. [Google Scholar]





| Augmented Dickey–Fuller Test Statistic | t-Statistic | Prob | |
|---|---|---|---|
| −4.16208806 | 0.000763 | ||
| Test Critical Values: | 1% Level | −3.51273806 | - |
| 5% Level | −2.89748987 | - | |
| 10% Level | −2.58594873 | - | |
| Augmented Dickey–Fuller Test Statistic | t-Statistic | Prob | |
|---|---|---|---|
| −8.3298612 | 3.39 × 10−13 | ||
| Test Critical Values: | 1% Level | −3.5117123 | - |
| 5% Level | −2.8970475 | - | |
| 10% Level | −2.5857126 | - | |
| Model Parameter | AIC Results |
|---|---|
| SARIMA (0,1,0) × (0,1,0,24) | AIC = 570.04 |
| SARIMA (0,1,0) × (0,1,1,24) | AIC = 360.00 |
| SARIMA (0,1,0) × (1,1,0,24) | AIC = 371.57 |
| SARIMA (0,1,0) × (1,1,1,24) | AIC = 365.49 |
| SARIMA (0,1,1) × (0,1,0,24) | AIC = 505.78 |
| SARIMA (0,1,1) × (0,1,1,24) | AIC = 320.37 |
| SARIMA (0,1,1) × (1,1,0,24) | AIC = 338.86 |
| SARIMA (0,1,1) × (1,1,1,24) | AIC = 324.48 |
| SARIMA (1,1,0) × (0,1,0,24) | AIC = 548.06 |
| SARIMA (1,1,0) × (0,1,1,24) | AIC = 346.20 |
| SARIMA (1,1,0) × (1,1,0,24) | AIC = 348.26 |
| SARIMA (1,1,0) × (1,1,1,24) | AIC = 350.24 |
| SARIMA (1,1,1) × (0,1,0,24) | AIC = 503.45 |
| SARIMA (1,1,1) × (0,1,1,24) | AIC = 321.42 |
| SARIMA (1,1,1) × (1,1,0,24) | AIC = 331.35 |
| SARIMA (1,1,1) × (1,1,1,24) | AIC = 325.29 |
| Model Parameter | AIC Results |
|---|---|
| SARIMA (0,1,0) × (0,1,0,24) | AIC = 532.17 |
| SARIMA (0,1,0) × (0,1,1,24) | AIC = 329.45 |
| SARIMA (0,1,0) × (1,1,0,24) | AIC = 344.67 |
| SARIMA (0,1,0) × (1,1,1,24) | AIC = 338.06 |
| SARIMA (0,1,1) × (0,1,0,24) | AIC = 467.86 |
| SARIMA (0,1,1) × (0,1,1,24) | AIC = 299.24 |
| SARIMA (0,1,1) × (1,1,0,24) | AIC = 318.07 |
| SARIMA (0,1,1) × (1,1,1,24) | AIC = 305.10 |
| SARIMA (1,1,0) × (0,1,0,24) | AIC = 510.44 |
| SARIMA (1,1,0) × (0,1,1,24) | AIC = 324.85 |
| SARIMA (1,1,0) × (1,1,0,24) | AIC = 330.63 |
| SARIMA (1,1,0) × (1,1,1,24) | AIC = 331.37 |
| SARIMA (1,1,1) × (0,1,0,24) | AIC = 465.20 |
| SARIMA (1,1,1) × (0,1,1,24) | AIC = 301.17 |
| SARIMA (1,1,1) × (1,1,0,24) | AIC = 312.63 |
| SARIMA (1,1,1) × (1,1,1,24) | AIC = 307.10 |
| Name | MMSI | Coordinate | Course | Diameter of the Ship |
|---|---|---|---|---|
| Minhuiyu 11512 | 880011590 | (119°2′40.848″ E, 24°54′52.704″ N) | 65 | 23 m |
| Minhuiyu 01366 | 412452752 | (119°2′46.032″ E, 24°54′53.568″ N) | 270° | 23 m |
| Name | Sink Stone Position | Diameter (L) | Watermarking | Free-Board Depth |
|---|---|---|---|---|
| Meizhou Bay No.1 | (119°2′45.420″ E, 24°54′54.120″ N) | 2.4 m | >3.0 m | 0.9 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Wu, Z.; Ren, L. Ship Path Planning Based on Buoy Offset Historical Trajectory Data. J. Mar. Sci. Eng. 2022, 10, 674. https://doi.org/10.3390/jmse10050674
Zhou S, Wu Z, Ren L. Ship Path Planning Based on Buoy Offset Historical Trajectory Data. Journal of Marine Science and Engineering. 2022; 10(5):674. https://doi.org/10.3390/jmse10050674
Chicago/Turabian StyleZhou, Shibo, Zhizheng Wu, and Lüzhen Ren. 2022. "Ship Path Planning Based on Buoy Offset Historical Trajectory Data" Journal of Marine Science and Engineering 10, no. 5: 674. https://doi.org/10.3390/jmse10050674
APA StyleZhou, S., Wu, Z., & Ren, L. (2022). Ship Path Planning Based on Buoy Offset Historical Trajectory Data. Journal of Marine Science and Engineering, 10(5), 674. https://doi.org/10.3390/jmse10050674





