Abstract
In the existing research on the intelligent navigation of ships, navigation route planning often regards light buoys as fixed obstructions. However, due to factors such as water ripples, the position of the buoys keeps periodically changing. If the buoys are set to a fixed range of avoidance areas in the process of ship navigation, it is easy to allow a collision between the ship and the light buoys. Therefore, based on historical motion trajectory data of the buoys, a SARIMA-based time-series prediction model is proposed to estimate the offset position of a given buoy in a specified time. Furthermore, the collision-free path planning approach is presented to dynamically recommend an accurate sailing path. The results of the simulation experiment show that this method can effectively deal with collisions of ships caused by the offset position of the light buoys during the navigation of the large and low-speed autonomous ships.
1. Introduction
Research on marine traffic safety and efficiency has always been a challenging task in the marine traffic transportation field. Various maritime accidents occur frequently, which seriously affect the safety of life, property, and the ocean environment [1,2,3,4].
In recent years, with the rapid growth of artificial intelligence, cloud computing and the Internet of Things (IoT), the applications of intelligent systems have been widely integrated into people’s social lives. Similarly, artificial intelligence technologies have been employed into the marine traffic field to help improve economic efficiency. Thereby, autonomous navigation technology has become an important research topic. In intelligent navigation systems, automatic route optimization based on electric nautical chart (ENC) and weather forecast data is an intelligent navigation function which effectively helps to improve the efficiency of the route plan [5].
However, during voyage optimization, some uncertainties are usually neglected. For instance, light buoys are always regarded as fixed objects in the ENCs, but the positions of the light buoys periodically change due to the wind and currents, which is not considered in the automatic route plan. Therefore, exploring the position offset of the buoy is an important and significant task in the route planning of autonomous ships.
There are many methods for ship path planning, such as the genetic algorithm [6,7], particle swarm optimization algorithm [8,9], artificial potential field method [10,11], and deep learning [12,13,14]. These methods can effectively enhance the navigation safety of ships. GUO et al. [15] proposed an autonomous path-planning model based on DRL to realize the intelligent path planning of unmanned ships in an unknown environment. The model has good convergence speed and stability, but does not consider the ship motion model and the actual verification environment. LAZAROWSKA et al. [16] employed the discrete artificial potential field algorithm, which can generate a collision-free path in an environment containing static and dynamic obstacles. However, in the simulation, the obstacles in reality are often irregular. Carlucho et al. [17] proposed a deep RL framework for adaptive control applications of AUVs based on an actor–critic goal-oriented deep RL architecture, which takes the available raw sensory information as input for the continuous control actions, which are the low-level commands for the AUV’s thrusters. MEYER et al. [18] proposed a deep reinforcement learning algorithm. It follows a desired path known a priori while avoiding collisions with other ships along the way. ZACCONE [19] proposed an optimal path-planning algorithm based on RRT *, and discussed collision avoidance, compliance with COLREG regulations, path feasibility, and optimality in detail. However, in terms of simulation, the Motion-Planning, Guidance and Control (MPGC) system can be regarded as a medium-range or short-range collision-avoidance system, which should be integrated with a higher-level offline path-planning system in order to manage remote routes. SHAH et al. [20] developed an acceptable heuristic that takes into account large islands while estimating costs and provides better estimates than Euclidean distance-based heuristics. However, the algorithm has some drawbacks in solving some time-varying obstacles. LYRIDIS et al. [21] proposed an improved ant colony optimization algorithm to deal with the local path planning of obstacle avoidance by considering wind, waves, and obstacles. However, only obstacles with elliptical trajectories are considered in this paper, which does not have universality.
In recent years, more and more scholars have been using the time-series prediction model to solve problems in natural disasters, hydrology, medicine, chemistry, transportation, economy, etc. [22,23,24,25]. YU et al. [26] proposed a PCA prediction method for sports event model evaluation, aiming at the problems of poor average fitness and low accuracy of risk prediction of traditional methods. The results show that the method has good average fitness. LI et al. [27] constructed a WebGIS scheme of a forest information system and open-source network geographic information system oriented to spatial information field and supported OGC, and used the grey model to predict the development trend. The results showed that the method realized the double growth of forest area and forest volume, and the forest coverage rate reached a new level. LIU et al. [28] used the data from TCGA to create multi-gene features, and evaluated the predictive significance of each lncRNA related to cell proptosis for survival. ZENG et al. [29] proposed a time-series prediction method based on pattern analysis, and used the probability relaxation method to classify the probability vectors of the basic pattern. YUAN et al. [30] proposed a Kernel-HFCM model based on kernel mapping and HFFCM to predict time series inspired by the kernel method and SVR. SEBASTIAN et al. [31] proposed a fractal interpolation method which can generate finer-grained time series from insufficient data sets. HER et al. [32] applied the grey theory model GM (1,1) to the prediction of the price of Panama-type two-wheeled ships, in order to deal with bulk carriers with different periods and different sample sizes. SAHOO et al. [33] proposed the MLP-GWO model and the SVM-GWO model, and compared them with the traditional support vector machine (SVM) model and multilayer perceptron (MLP) model, respectively. The research results show that the model can effectively predict floods. PAQUET et al. [34] proposed a QuantumLeap system for financial forecasting, and studies have shown that this method has better forecasting results. OZTUNC et al. [35] proposed a crude oil price-prediction model combining fuzzy time series and a maximum integer function. The research results show that this method can accurately predict crude oil prices.
The above research methods can effectively predict the target to some extent, but there are also some shortcomings. In the sports events evaluation model, only a certain area was to collect samples and it did not expand the collection area, so it has a certain one-sidedness. LI et al. [27] did not study the explanation of the dynamic economic model of sustainable development of forest resources. It is not enough to rely on these qualitative discussions or simple quantitative research. LIU [28] did not carry out experiments to prove the difference in molecular transcription and expression levels, the data of this study are based only on TCGA data, and the data source is relatively singlular. The pattern analysis method proposed by ZENG [29] has limitations in predicting the trend of time-series signals, and it is difficult to predict the value of time-series signals. The Kernel-HFCM model has no suitable method to evaluate KFTS. The grey GM (1,1) model has a strong dependence on historical data and cannot consider the relationship between various factors. The BP-ANN model easily falls into the local optimum and converges too slowly. The Bayesian model needs to know the prior probability in advance, and in most cases, the prior probability is taken from the assumption. Therefore, in the case of the assumed prior model, it easily leads to poor prediction accuracy and high requirements for the form of input data.
In this paper, the SARIMA (Seasonal Autoregressive Integrated Moving Average, SARIMA) model is introduced to predict the motion of the light float, which is used for the path planning of the ship. The main reason for this is that the SARIMA model is an important time-series analysis method, and it can effectively deal with the seasonal tendency, random interference characteristics, and the correlation of the data to establish the time-series prediction motion model of the buoys. Due to the regularity and seasonality of the offset position of the buoys, this paper proposes a ship path-planning method based on the fusion of the historical trajectory data of the buoys and the SARIMA model, to deal with the ship collision caused by the offset of the buoys during the navigation of a broad low-speed ship.
2. Multiplication Seasonal SARIMA Model
2.1. ARIMA Model
The ARIMA [36,37] model is a time-series prediction method proposed by Jenkins and Box, which is mainly used to study both trend and seasonal time series. The basic form is ARIMA (p, d, q), where p, d, and q represent the non-seasonal regression order, moving average order, and non-seasonal moving average order, respectively. The ARIMA (p, d, q) model is composed of an autoregressive model AR (p) and moving average model MA (q), and the formula is shown in Equation (1).
where is a delay operator; is zero mean white noise sequence; is time series; is a polynomial of self-regression coefficients; is a moving average coefficient polynomial; and are the corresponding coefficients, respectively.
After the integration of AR (p) and MA (q), the ARIMA (p, d, q) model is obtained after the d-order difference of its trend, as shown in Equation (2).
where is a difference operator; is trend difference; .
2.2. Stochastic Seasonal Model
The stochastic seasonal model ARIMA (P, D, Q) is a time series that only contains periodicity and trend after the integration of AR (P) seasonal autoregressive model and MA (Q) seasonal moving average model through seasonal periodic difference. The general forms of AR (P) and MA (Q) are shown in Equation (3).
where is a polynomial of seasonal autoregressive coefficients; is a polynomial of seasonal moving average coefficients; and are the corresponding coefficients, respectively.
After the integration of AR (P) and MA (Q), the seasonal and periodic parts of AR (P) and MA (Q) are processed by S and D order difference, and the ARIMA (P, D, Q) S model is obtained. The formula is shown in Equation (4).
where is the periodic difference; is seasonal difference.
2.3. Multiplication Seasonal Model
The multiplication seasonal model [38] refers to the multiplication of the difference between the autoregressive moving average model and the stochastic seasonal model. It is an important method to deal with time series with seasonality and trend. The general form is SARIMA (p, d, q) × (P, D, Q) s. The parameters p, d, q, P, D, Q, and S represent the non-seasonal regression order, the moving average order, the non-seasonal moving average order, the seasonal autoregressive order, the seasonal difference order, the seasonal average moving order, and the unit cycle, respectively. The general form is shown in Equation (5).
where .
3. Ship Path-Planning Method for Random Motion of Buoy
The buoy is a navigational aid sign that indicates the navigation channel, and the marker to float and avoid danger. It plays an important role in ensuring the safety of a ship’s navigation. However, due to external forces such as wind, current, and ship traveling waves, the position of the buoy moves randomly. Therefore, the ship cannot rely on the buoy for navigation. In general, the navigator uses the chart to determine the position of the buoy. Because the position of the buoy marked on the chart is the position of the sinking rock of the buoy issued by the aviation security department, and the navigator sees the position of the floating body, the floating position moves randomly under the action of external force, which is not consistent with the position of the sinking rock. Therefore, when the ship approaches the buoy, the position of the buoy is generally seen as not the position marked on the chart, which will cause certain interference for the ship to avoid the buoy. In the context of the rapid development of unmanned ships, how to help ships predict the movement of buoys during autonomous route planning and effectively avoid them is an important task to ensure the safety of unmanned ships. In this section, an autonomous route planning model for unmanned ships based on the random motion of buoys is proposed to solve this problem.
This method is a combination of the SARIMA model, the ship domain model, and the historical trajectory data of the light buoy. By decomposing the historical offset longitude and latitude data of the buoy into offset distance data and offset azimuth data, the time series based on offset azimuth and offset distance is constructed, respectively, and the time series are input into the SARIMA model. The stability of the time series is tested by the unit root test method, and the requirements for the stability of the time series are solved by differential processing. The optimal parameters are selected according to the autocorrelation function, offset autocorrelation function, seasonal trend, random trend, growth trend, and AIC minimum information criterion. After predicting the offset azimuth and offset distance over the next 24 h, the offset coordinates of the buoy are inversed by the Mercator projection coordinates, and the position range of the buoy offset in the future is determined.
3.1. Field of Buoy Offset
As an indicator of ship navigation, the buoy plays an important role in the navigational safety of the ship. However, due to factors such as tides, ripple waves, and human collisions, the actual position of the buoy often deviates from the position of the sunken stone. Therefore, in the path planning process of the ship, if the offset problem of the buoy cannot be effectively dealt with, it will greatly affect the navigation safety of the ship. How to accurately calculate the offset position of the buoy is the content introduced in this section. The prediction process of the buoy offset is shown in Figure 1.
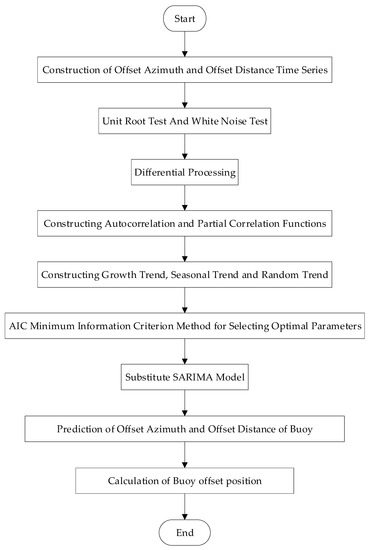
Figure 1.
Buoy offset position-prediction process.
According to the multiplication seasonal prediction model, the offset position of the buoys over the next 24 h is predicted in order to delineate the area where the ship may collide during navigation. The offset fields of some buoys are shown in Figure 2.
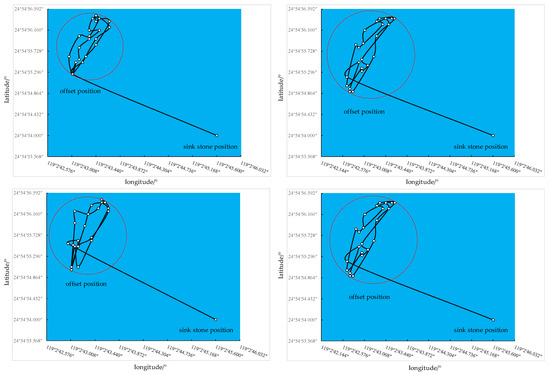
Figure 2.
Field of buoy offset.
3.2. Risk Field of Ship Collision
As a field used to measure whether the ship’s navigation route is safe, the field of collision risk [39] is an important condition for judging whether the ship’s navigation route collides with a target. The ship safety field is divided into the left eccentric ellipse field, left eccentric circular field, and circular field. Because the target collision avoidance object in this paper needs the ship to pass the target object from a certain distance, this paper will use the circular field.
According to the field of ship safety, set , according to Formula (6), to determine whether there is a collision risk on the navigation path at this time. When satisfied, there is a collision risk; otherwise, there is no collision risk.
where represents the distance between the ship and the buoy area center at p; represents a ship collision avoidance orientation; m is the diameter of the buoy offset field.
It can be seen from Figure 3 that when the ship navigation parameter t = 1800, the distance between the ship domain center and the buoy domain center is greater than or equal to m/2 + 2M, so there is no collision risk. When the navigation parameter t = 3600, the distance between the ship domain center and the buoy domain center is less than m/2 + 2M, so there is a collision risk.
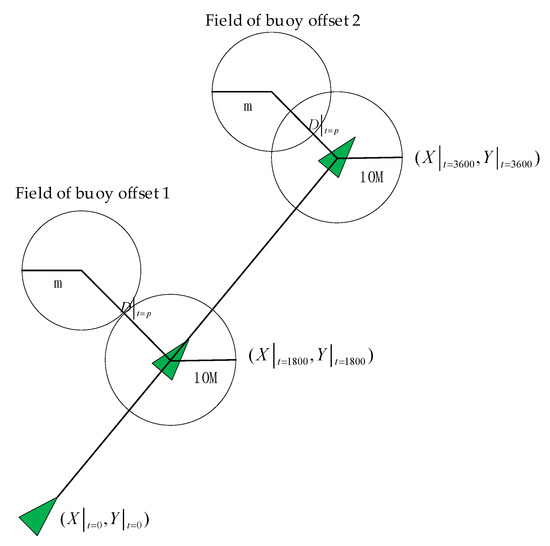
Figure 3.
Ship navigation risk determination.
It can be seen from the Figure 4; the a is the collision avoidance steering angle; O is the buoy field center; r is the radius of the buoy field. The path planning process is shown in Figure 5.
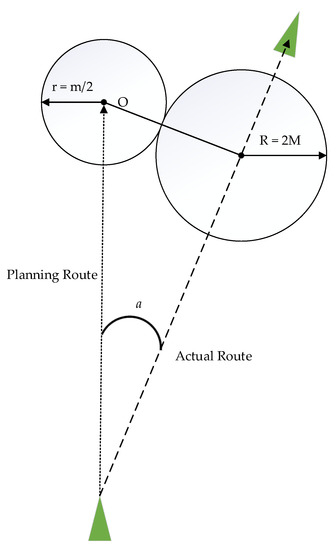
Figure 4.
Ships avoid navigation.
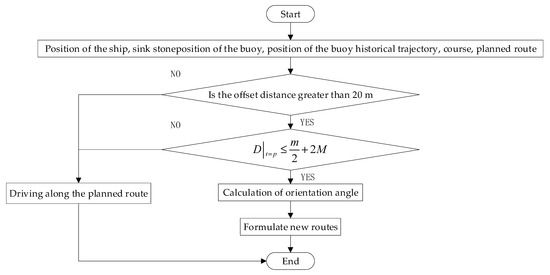
Figure 5.
Ship path-planning process.
4. Buoy Offset Position Prediction
In this section, 96 h of continuous data from 11 to 15 August 2018 of the No. 1 buoy of Meizhou Bay are taken as the initial data. The data of the longitude and latitude position of the buoy offset are decomposed into the historical trajectory data of the offset distance and the offset azimuth angle, and the time-series data are tested and analyzed to establish a mathematical model to predict the longitude and latitude position of the buoy offset for 24 h on 16 August 2018. The sink stone position is (119°2′45.420′′ E, 24°54′54.120′′ N).
4.1. Data Verification and Processing
The stability of data is an important prerequisite for the use of the multiplication seasonal model. It is necessary to carry out difference processing on the time series and to carry out unit root test on the processed time series. If the test requirements are met, the data are stable, and if the test requirements are not met, further difference processing is needed. The offset azimuth and offset distance trend are shown in Figure 6 and Figure 7, and the first-order difference is shown in Figure 8 and Figure 9.
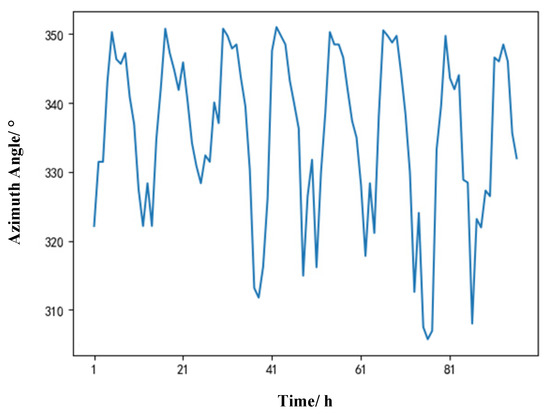
Figure 6.
Offset azimuth trend.
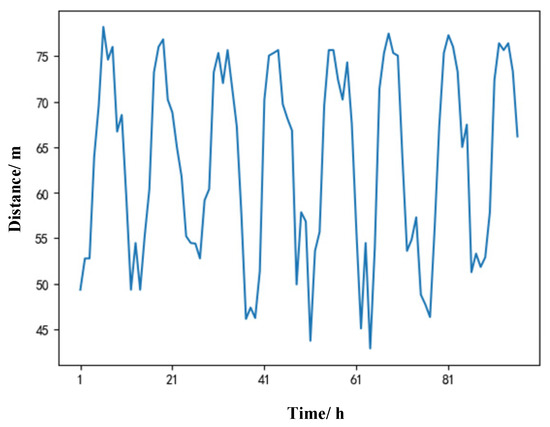
Figure 7.
Offset distance trend.
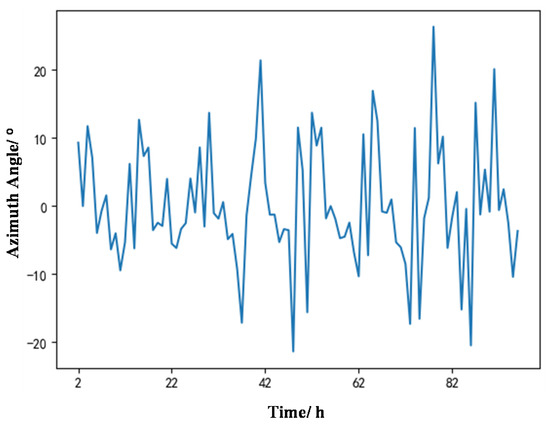
Figure 8.
The first-order difference of offset azimuth.
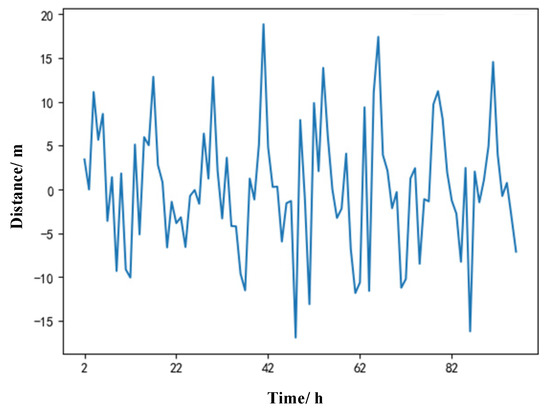
Figure 9.
The first-order difference of offset distance.
It can be seen from Figure 6 and Figure 7 that the offset azimuth trend and offset distance trend have very obvious instability, so it is necessary to carry out differential processing on the time series. The results of differential processing are shown in Figure 8 and Figure 9. To accurately test whether the processing results meet the requirements of the multiplication seasonal model for data stability, it is necessary to conduct a unit root test on time series. The Augmented Dickey–Fuller test statistic (ADF) [40] is one of the most important methods for testing whether the time series are stationary and contain white noise sequences. The test results are shown in Table 1.

Table 1.
ADF test results of offset azimuth.
According to Table 1 and Table 2, the ADF test statistics of the offset azimuth time series and the offset distance time series are lower than the corresponding critical values of 1%, 5% and 10%, and the probability is p < 0.05. Therefore, the time series meet the test requirements and are stable.

Table 2.
ADF test results of offset distance.
4.2. Parameter Selection
The parameter d = 1 can be determined when the trend of the time series of offset azimuth and offset distance disappear after the first-order difference. The parameter D = 1 can be determined when the time series of offset azimuth and offset distance disappear seasonally. However, to determine the optimal combination model, the final values of parameters p and q must be determined by combining autocorrelation function (ACF) and partial autocorrelation function (PACF) [41]. The ranges of parameters p and q in the multiplicative seasonal model are [0,2]. The ACF and PACF analysis of offset azimuth and offset distance are shown in Figure 10, Figure 11, Figure 12 and Figure 13.
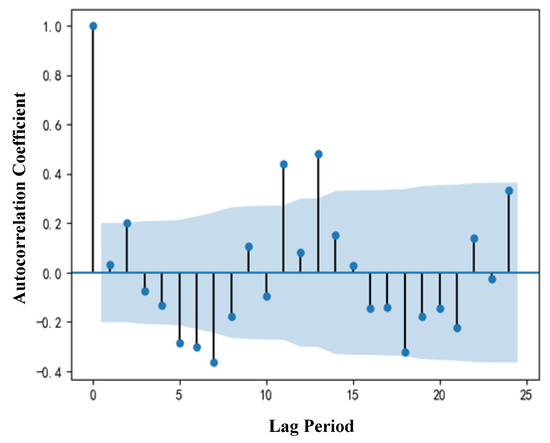
Figure 10.
Offset azimuth ACF analysis.
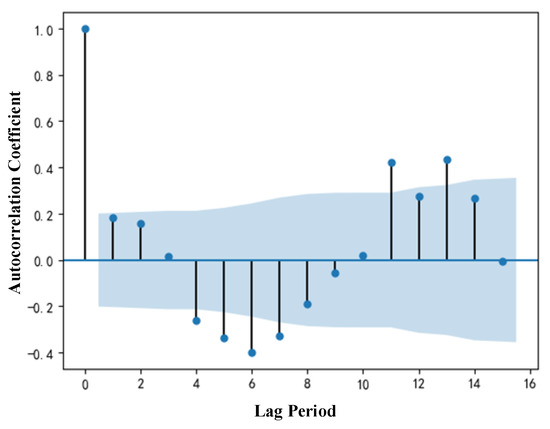
Figure 11.
Offset distance ACF analysis.
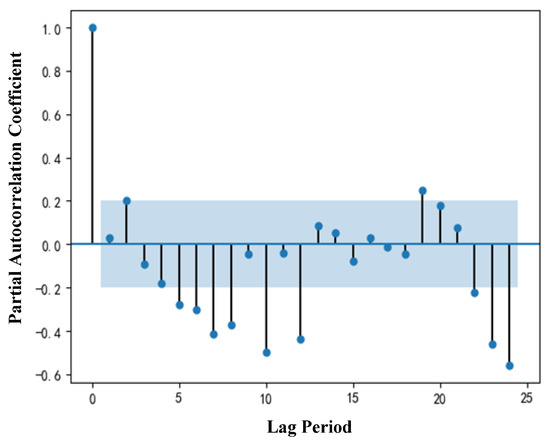
Figure 12.
Offset azimuth PACF analysis.
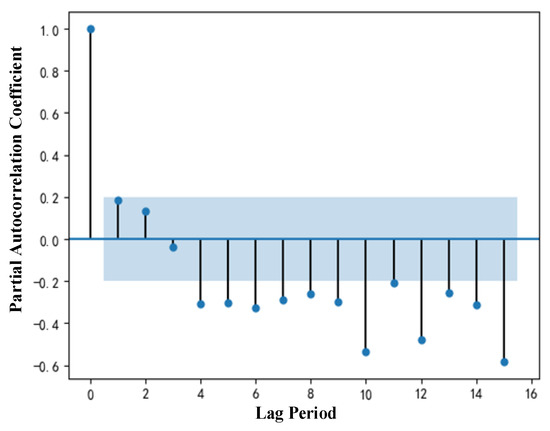
Figure 13.
Offset distance PACF analysis.
It can be seen from the ACF and PACF graphs of offset azimuth and offset distance that there is no obvious tailing or truncation. Therefore, it is necessary to separate the time-series data of offset azimuth and offset distance. The time-series data are divided into seasonal trend, random fluctuation trend and growth trend. The analysis results are shown in Figure 14 and Figure 15.
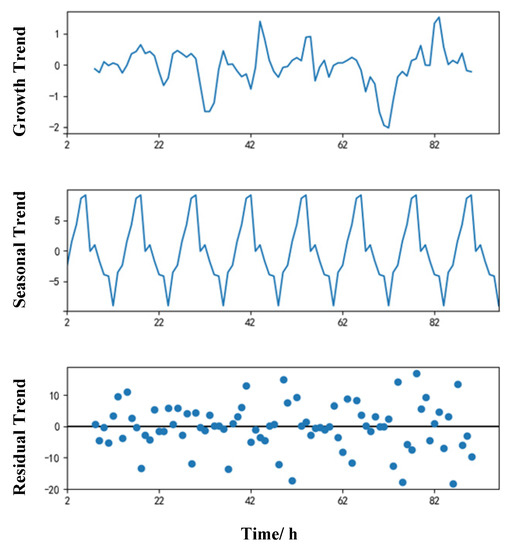
Figure 14.
Analysis of offset azimuth trend.
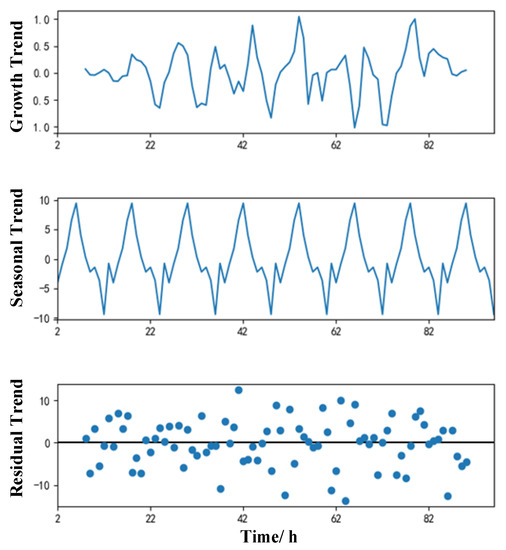
Figure 15.
Analysis of offset distance trend.
It can be seen from Figure 14 and Figure 15 that the time-series data of offset azimuth and offset distance have very obvious periodicity and seasonality. Therefore, the periodic parameter S = 24 can be determined, and there is no obvious change in the trend of random fluctuation and the trend of growth. To establish the multiplication seasonal model of optimal parameter combinations, it is necessary to optimize the combination of various parameters and select the optimal parameters according to the AIC minimum information criterion method [42]. The smaller the value obtained by AIC, the better the prediction model. The AIC calculation results of the offset azimuth and offset distance are shown in Table 3 and Table 4.

Table 3.
AIC calculation results of offset azimuth.

Table 4.
AIC calculation results of offset distance.
Table 3 and Table 4 shows that the minimum AIC value of offset azimuth is 320.38 and the minimum AIC value of offset distance is 299.25. Therefore, the parameters of offset azimuth can be determined as p = 0, q = 1, p = 0, Q = 1. The parameters of offset distance p = 0, q = 1, P = 0, Q = 1, so the offset azimuth and offset distance should choose SARIMA (0,1,1) × (0,1,1) 24 as the optimal parameter combination of the SARIMA model.
4.3. Offset Position Prediction
According to the multiplication seasonal model of the optimal parameter combinations, the offset azimuth and offset distance from 1:00 to 24:00 on 15 August 2018 are predicted, and the predicted values are compared with the actual values. The predicted results are compared in Figure 16 and Figure 17.
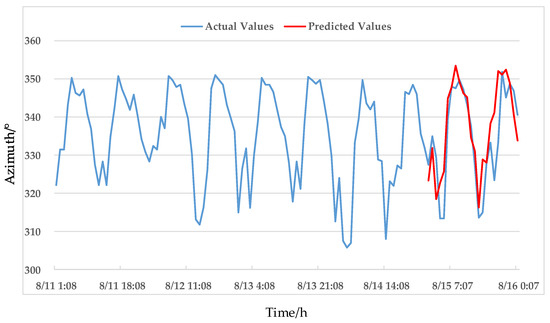
Figure 16.
Comparison of offset azimuth prediction.
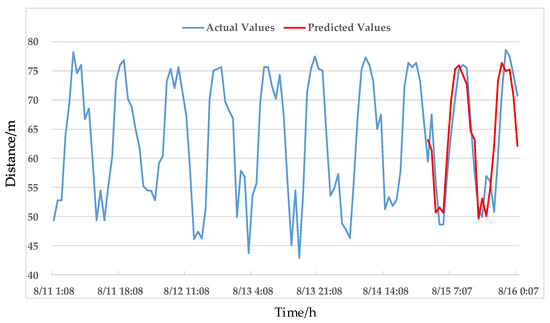
Figure 17.
Comparison of offset distance prediction.
After calculating the predicted values of the offset azimuth and predicted values of the offset distance, the Mercator projection coordinates of the known sink stone position are (13252140.099131335,2865307.8948890963), and the Mercator projection coordinates of the predicted point are calculated according to Formula (8).
where is the Mercator projection coordinate of the prediction position; is the Mercator projection coordinates of the buoy position; are the longitude and latitude coordinates of the prediction position; represents predicted offset distance; represents the predicted azimuth.
After calculating the Mercator projection coordinates of the prediction position, the latitude and longitude coordinates of the prediction position are calculated according to Formula (9) and the actual values are compared with the predicted values, see Figure 18 and Figure 19.
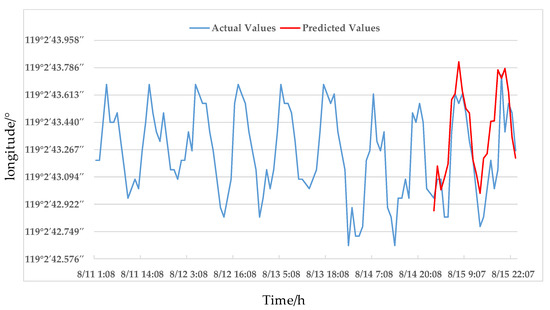
Figure 18.
Comparison of longitude prediction.
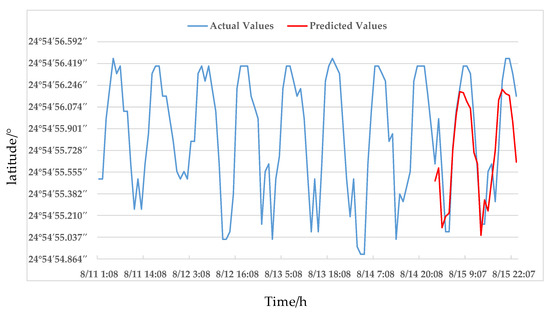
Figure 19.
Comparison of latitude prediction.
4.4. Error Analysis
According to the mean absolute percentage error (MAPE) and root-mean-squared error (RMSE) [43], the error tests of predicted offset azimuth and predicted offset distance are carried out. The formulas are shown in Formulas (10) and (11).
The predicted offset azimuth MAPE = 1.79%, RMSE = 7.912893, predicted offset distance MAPE = 7.37%, and RMSE = 5.441061 of the SARIMA models are calculated. To reflect the advantages of the model, the prediction results of the SARIMA model, BP neural network prediction model, and grey GM (1,1) prediction model are compared, and this comparison is shown in Figure 20.
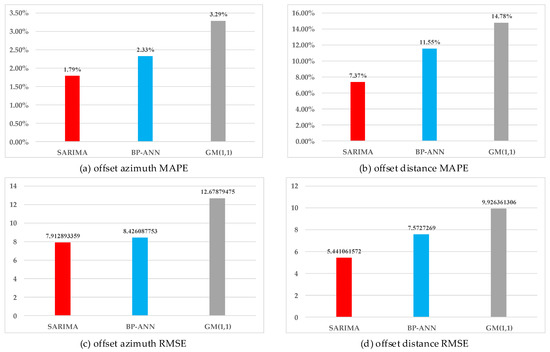
Figure 20.
Error analysis.
According to Figure 20, compared to BP neural network prediction model and grey GM (1,1) prediction model, the prediction error of the multiplication seasonal model is lower, and it is more effective for predicting the offset position of the buoy.
5. Path-Planning Simulation
This paper takes Minhuiyu 11,512 and Minhuiyu 01,366 boats as the simulation ships and Meizhou Bay No.1 buoy as the avoidance object to simulate the path planning of the ship. The parameters of the ship and the buoy are shown in Table 5 and Table 6.

Table 5.
Simulation of ship parameters.

Table 6.
Simulation of buoy parameters.
The multiplication seasonal model is used as the prediction model to predict the future offset position, and then the predicted offset trajectory is made according to the predicted offset value of the next 24 h. According to Formula (7), the parameter m of the buoy offset field is calculated, and the buoy offset field is made. Figure 21 is used to calculate the buoy field parameter m = 46.8, and the center coordinate of the buoy offset field is (119°2′41.760′′ E, 24°54′56.520′′ N).
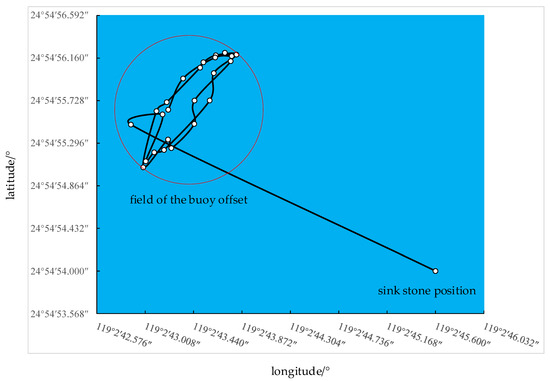
Figure 21.
Field of Meizhou bay No.1 buoy offset.
Taking Minyuhui 11512, Minyuhui 01,366 and Meizhou Bay 1 # buoy as simulation objects, the circular ship domain # 1, circular ship domain # 2 and buoy offset domain # 1 are constructed, respectively. The simulation results are shown in Figure 22.
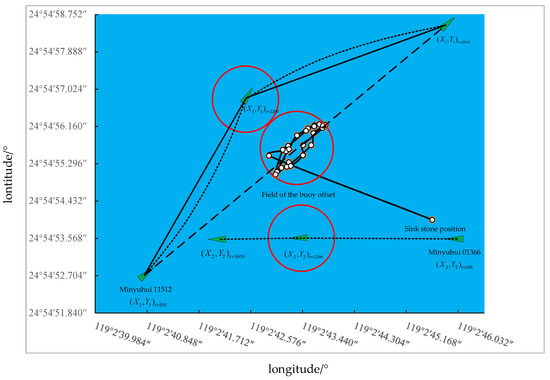
Figure 22.
Ship path planning.
When the navigation parameter t = 100 s, Minyuhui 11,512 is 0.065 nautical miles from the center of the buoy field, with a heading of 65°, there is a risk of collision, and the collision avoidance angle is 22°. Minyuhui 01,366 is 0.058 nautical miles from the buoy field center, heading 270°, with no risk of collision, and no need to change direction.
When the navigation parameter t = 2200 s, Minyuhui 11,512 is 0.037 nautical miles from the center of the buoy, with a heading of 43°, and the absolute difference between the actual route and the planned route is greater than 1°. Therefore, it is necessary to perform re-navigation, and the re-navigation angle is 47°. Minyuhui 01,366 is more than 0.037 nautical miles away from the buoy field center, with a heading of 270°, no risk of collision, and no need to change direction.
When the navigation parameter t = 3600 s, Minyuhui 11,512 is 0.057 nautical miles from the center of the buoy area, with a heading of 65°, the heading and planned route angle are the same, and the re-navigation is successful. Minyuhui 01,366 is 0.041 nautical miles from the buoy field center, with a heading of 270°, no risk of collision, and no need to change direction.
6. Conclusions
In view of the traditional path-planning method, it is difficult to solve the problem of ship collision caused by marine buoy offset, and this paper proposes a ship path-planning method based on historical trajectory data and the SARIMA model. By predicting the offset trajectory of the buoy, this party delimits the circular offset field and plans the navigation path of an unmanned ship in combination with the dangerous field of the ship. The SARIMA prediction model is compared with the BP neural network prediction model and GM (1,1) model. Compared to the BP neural network prediction model, the prediction offset azimuth MAPE of the SARIMA model is reduced by 0.54%, the RMSE is reduced by 0.51, the offset distance MAPE is decreased by 4.18%, and RMSE is decreased by 2.13. Compared to the GM (1,1) prediction model, the predicted offset azimuth MAPE of the SARIMA model is reduced by 1.50%, the RMSE is reduced by 4.77, the offset distance MAPE is reduced by 7.41%, and the RMSE is reduced by 4.49. These research results show that this method can accurately predict the offset position of a buoy, and can effectively plan the navigation path of unmanned ships. However, this paper is too simple regarding the area division of the offset of the buoy, and only uses the circular area to divide it. Furthermore, some natural factors are not taken into account in the prediction model. In the follow-up, the field division of the offset position of the buoy will be further studied to minimize the offset field of the buoy, and further, we will consider the influence of natural factors such as flow and typhoons on the offset prediction of a light buoy.
Author Contributions
Conceptualization, S.Z. and Z.W.; methodology, L.R.; software, L.R.; validation, S.Z. and Z.W.; formal analysis, Z.W.; investigation, S.Z.; resources, Z.W.; data curation, S.Z.; writing—original draft preparation, L.R.; writing—review and editing, Z.W.; visualization, S.Z.; supervision, Z.W.; project administration, L.R.; funding acquisition, L.R. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of Fujian Province (Grant no. 2020J01658, 2019J01325), Open Project Fund of National Local Joint Engineering Research Center for Ship Assisted Navigation Technology (Grant no. HHXY2020002), Doctoral Start-up Fund of Jimei University (Grant no. ZQ2019012).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yoo, Y.; Lee, J.S. Collision Risk Assessment Support System for MASS RO and VTSO Support in Multi-Ship Environment of Vessel Traffic Service Area. J. Mar. Sci. Eng. 2021, 9, 1143. [Google Scholar] [CrossRef]
- Rong, H.; Teixeira, A.P.; Soares, C.G. Spatial correlation analysis of near ship collision hotspots with local maritime traffic characteristics. Reliab. Eng. Syst. Saf. 2021, 209, 107463. [Google Scholar] [CrossRef]
- Luong, T.N.; Hwang, S.; Im, N. Harbour Traffic Hazard Map for real-time assessing waterway risk using Marine Traffic Hazard Index. Ocean Eng. 2021, 239, 109884. [Google Scholar] [CrossRef]
- Kim, J.K. Semi-Continuous Spatial Statistical Analysis Using AIS Data for Vessel Traffic Flow Characteristics in Fairway. J. Mar. Sci. Eng. 2021, 9, 4–378. [Google Scholar] [CrossRef]
- Piao, Z.; Guo, C.; Sun, S. Research into the Automatic Berthing of under actuated Unmanned Ships under Wind Loads Based on Experiment and Numerical Analysis. J. Mar. Sci. Eng. 2019, 7, 300. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.W.; Roh, M.I.; Kim, K.S. Ship route planning in Arctic Ocean based on POLARIS. Ocean Eng. 2021, 234, 109297. [Google Scholar] [CrossRef]
- Lazarowska, A. Ship’s trajectory planning for collision avoidance at sea based on ant colony optimization. J. Navig. 2015, 68, 291–307. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Feng, W.; Mao, Z.Y. Path planning of UUV based on HQPSO algorithm with considering the navigation error. Ocean Eng. 2021, 244, 110048. [Google Scholar] [CrossRef]
- MahmoudZadeh, S.; Yazdani, A.M.; Sammut, K.; Powers, D. Online path planning for AUV rendezvous in dynamic cluttered undersea environment using evolutionary algorithms. Appl. Soft Comput. 2018, 70, 929–945. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; Hao, C.; Su, J.C. Path planning for unmanned surface vehicle based on predictive artificial potential field. Int. J. Adv. Robot. Syst. 2020, 17, 2. [Google Scholar] [CrossRef] [Green Version]
- Lyh, H.G.; Yin, Y. COLREGS-Constrained Real-time Path Planning for Autonomous Ships Using Modified Artificial Potential Fields. J. Navig. 2019, 72, 588–608. [Google Scholar]
- Luis, S.Y.; Reina, D.G.; Marin, S.L.T. A Multiagent Deep Reinforcement Learning Approach for Path Planning in Autonomous Surface Vehicles: The Ypacarai Lake Patrolling Case. IEEE Access 2021, 9, 17084–17099. [Google Scholar] [CrossRef]
- Da Silva, A.G.; Dos Santos, D.H.; De Negreiros, A.P.F.; Silva, J.M.V.B.D.S.; Gonçalves, L.M.G. High-Level Path Planning for an Autonomous Sailboat Robot Using Q-Learning. Sensors 2020, 20, 6. [Google Scholar]
- Luis, S.Y.; Reina, D.G.; Marin, S.L.T. A Deep Reinforcement Learning Approach for the Patrolling Problem of Water Resources Through Autonomous Surface Vehicles: The Ypacarai Lake Case. IEEE Access 2020, 8, 204076–204093. [Google Scholar] [CrossRef]
- Guo, S.Y.; Zhang, X.G.; Zheng, Y.S.; Du, Y. An Autonomous Path Planning Model for Unmanned Ships Based on Deep Reinforcement Learning. Sensors 2020, 20, 426. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lazarowska, A. Comparison of Discrete Artificial Potential Field Algorithm and Wave-Front Algorithm for Autonomous Ship Trajectory Planning. IEEE Access 2021, 8, 221013–221026. [Google Scholar] [CrossRef]
- Carlucho, I.; De Paula, M.; Wang, S.; Petillot, Y.; Acosta, G.G. Adaptive low-level control of autonomous underwater vehicles using deep reinforcement learning. Robot. Auton. Syst. 2018, 107, 71–86. [Google Scholar] [CrossRef] [Green Version]
- Meyer, E.; Heiberg, A.; Rasheed, A.; San, O. COLREG-Compliant Collision Avoidance for Unmanned Surface Vehicle Using Deep Reinforcement Learning. IEEE Access 2020, 8, 165344–165364. [Google Scholar] [CrossRef]
- Zaccone, R. COLREG-Compliant Optimal Path Planning for Real-Time Guidance and Control of Autonomous Ships. J. Mar. Sci. Eng. 2021, 9, 405. [Google Scholar] [CrossRef]
- Shah, B.C.; Gupta, S.K. Long-Distance Path Planning for Unmanned Surface Vehicles in Complex Marine Environment. IEEE J. Ocean. Eng. 2020, 45, 813–830. [Google Scholar] [CrossRef]
- Lyridis, D.V. An improved ant colony optimization algorithm for unmanned surface vehicle local path planning with multi-modality constraints. Ocean Eng. 2021, 241, 109890. [Google Scholar] [CrossRef]
- Ahmed, B.; Mangalathu, S.; Jeon, J.S. Seismic damage state predictions of reinforced concrete structures using stacked long short-term memory neural networks. J. Build. Eng. 2022, 46, 103737. [Google Scholar] [CrossRef]
- Matic, P.; Bego, O.; Males, M. Complex Hydrological System Inflow Prediction using Artificial Neural Network. Teh. Vjesn. Tech. Gaz. 2022, 29, 172–177. [Google Scholar]
- Yang, Y.; Fan, C.J.; Chen, L. IPMOD: An efficient outlier detection model for high-dimensional medical data streams. Expert Syst. Appl. 2022, 191, 116212. [Google Scholar] [CrossRef]
- Bhanja, S.; Das, A. A Black Swan event-based hybrid model for Indian stock markets’ trends prediction. Innov. Syst. Softw. Eng. 2022, 1–15. [Google Scholar] [CrossRef]
- Yu, W.W.; Xing, J.M. Sports Event Model Evaluation and Prediction Method Using Principal Component Analysis. Wirel. Commun. Mob. Comput. 2022, 2022, 9351522. [Google Scholar] [CrossRef]
- Li, J.X.; Zhou, A.J.; Liao, Y.F. Forest Ecological Diversity Change Prediction Discrete Dynamic Model. Discret. Dyn. Nat. Soc. 2022, 2022, 4869363. [Google Scholar] [CrossRef]
- Liu, L.; Chen, W.Z.; Li, Y.B. Comprehensive Analysis of Pyroptosis-Related Long Noncoding RNA Immune Infiltration and Prediction of Prognosis in Patients with Colon Cancer. J. Oncol. 2022, 2022, 2035808. [Google Scholar] [CrossRef]
- Zeng, Z.; Yan, H.; Fu, A.M.N. Time-series prediction based on pattern classification. Artif. Intell. Eng. 2001, 15, 61–69. [Google Scholar] [CrossRef]
- Yuan, K.X.; Liu, J.; Yang, S.C. Time series forecasting based on kernel mapping and high-order fuzzy cognitive maps. Knowl.-Based Syst. 2020, 206, 106359. [Google Scholar] [CrossRef]
- Sebastian, R.; Thomas, N. A fractal interpolation approach to improve neural network predictions for difficult time series data. Expert Syst. Appl. 2021, 169, 114474. [Google Scholar]
- Her, M.T.; Chung, C.C.; Lin, C.T. Ship Price Predictions of Panamax Second-Hand Bulk Carriers Using Grey Models. J. Mar. Sci. Technol. Taiwan 2019, 27, 229–234. [Google Scholar]
- Sahoo, A.; Samantatay, S.; Ghose, D.K. Multilayer perceptron and support vector machine trained with grey wolf optimiser for predicting floods in Barak river, India. J. Earth Syst. Sci. 2022, 131, 85. [Google Scholar] [CrossRef]
- Paquet, E.; Soleymani, F. QuantumLeap: Hybrid quantum neural network for financial predictions. Expert Syst. Appl. 2022, 195, 116583. [Google Scholar] [CrossRef]
- Oztunc, K.; Oznur Kaymak, Y. Prediction of crude oil prices in COVID-19 outbreak using real data. Chaos Solitons Fractals 2022, 158, 111990. [Google Scholar] [CrossRef]
- Thiruchelvam, L.; Dass, S.C.; Asirvadam, S.; Daud, H.; Gill, B.S. Determine neighboring region spatial effect on dengue cases using ensemble ARIMA models. Sci. Rep. 2021, 11, 5873. [Google Scholar] [CrossRef]
- Wu, Z.Z.; Ren, L.Z.; Zhou, S.B.; Zhang, Y.; Xu, W.; Zhang, H. The Offset Azimuth Prediction of Light Buoy Based on Markov Chain Optimization Multiplicative Seasonal Model. Math. Probl. Eng. 2022, 2022, 1250206. [Google Scholar] [CrossRef]
- Koyuncu, K.; Tavacioglu, L.; Gokmen, N.; Arican, U. Forecasting COVID-19 impact on RWI/ISL container throughput index by using SARIMA models. Marit. Policy Manag. 2021, 48, 1096–1108. [Google Scholar] [CrossRef]
- Zhou, D. Research on a Novel Dynamic and Fuzzy Ship Domain; Dalian Maritime University: Dalian, China, 2017. [Google Scholar]
- Dorta, M.; Sanchez, G. Bootstrap unit-root test for random walk with drift: The bsrwalkdrift command. Stata J. 2021, 21, 39–50. [Google Scholar] [CrossRef]
- Adib, A.; Sheydaei, F.; Shoushtari, M.M.; Ashrafi, S.M. Using of gene expression programming method for prediction of daily components of tidal cycle in tidal rivers. Arab. J. Geosci. 2021, 14, 5. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Qie, Z.H.; Han, W.M. Fitting model optimization test curve based on the AIC criterion. J. Hebei Agric. Univ. 2017, 40, 120–124. [Google Scholar]
- Rahmanian, V.; Bokaie, S.; Haghdoost, A. Predicting cutaneous leishmaniasis using SARIMA and Markov switching models in Isfahan, Iran: A time-series study. Asian Pac. J. Trop. Med. 2021, 14, 83–93. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).