Numerical Study on the Turbulent Structure of Tsunami Bottom Boundary Layer Using the 2011 Tohoku Tsunami Waveform
Abstract
:1. Introduction
2. Materials and Methods
2.1. GPS Wave Gauge Data
2.2. Numerical Analysis Using the k-ω Turbulence Model
3. Results and Discussion
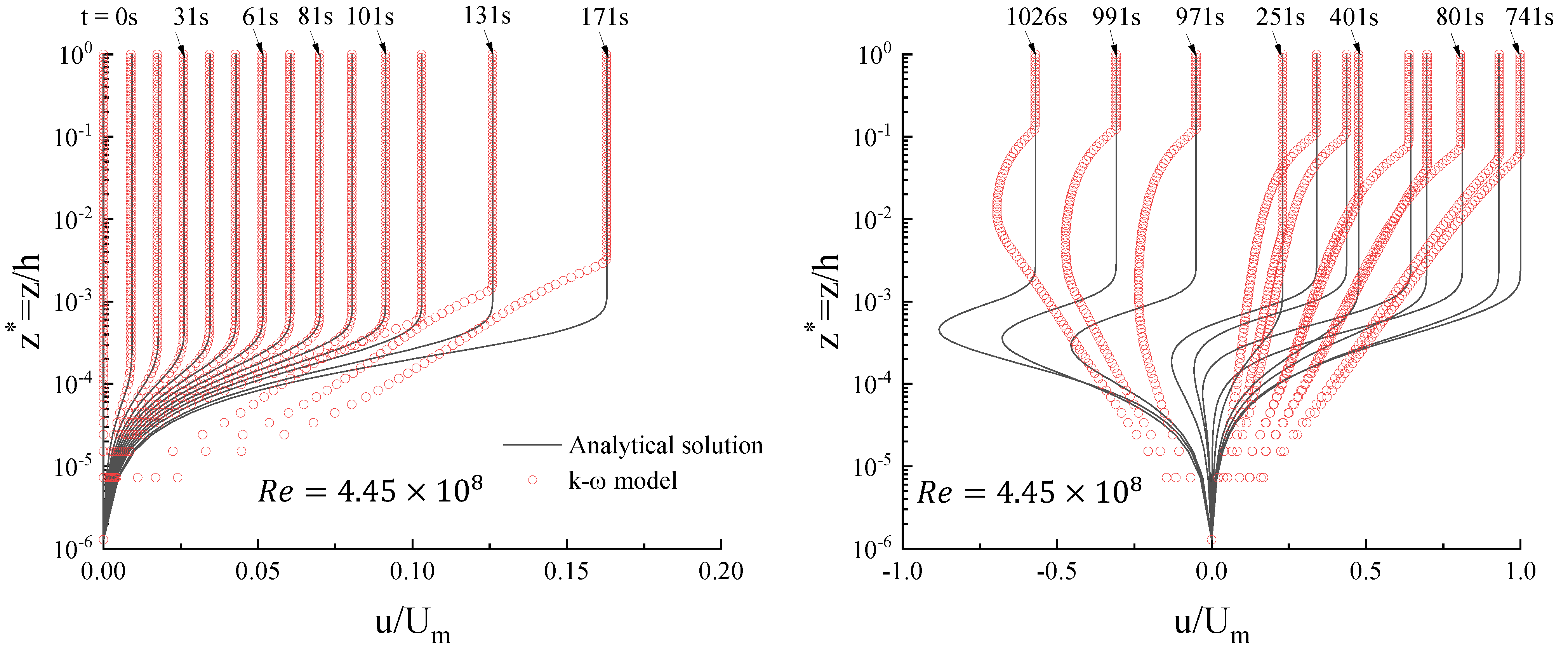
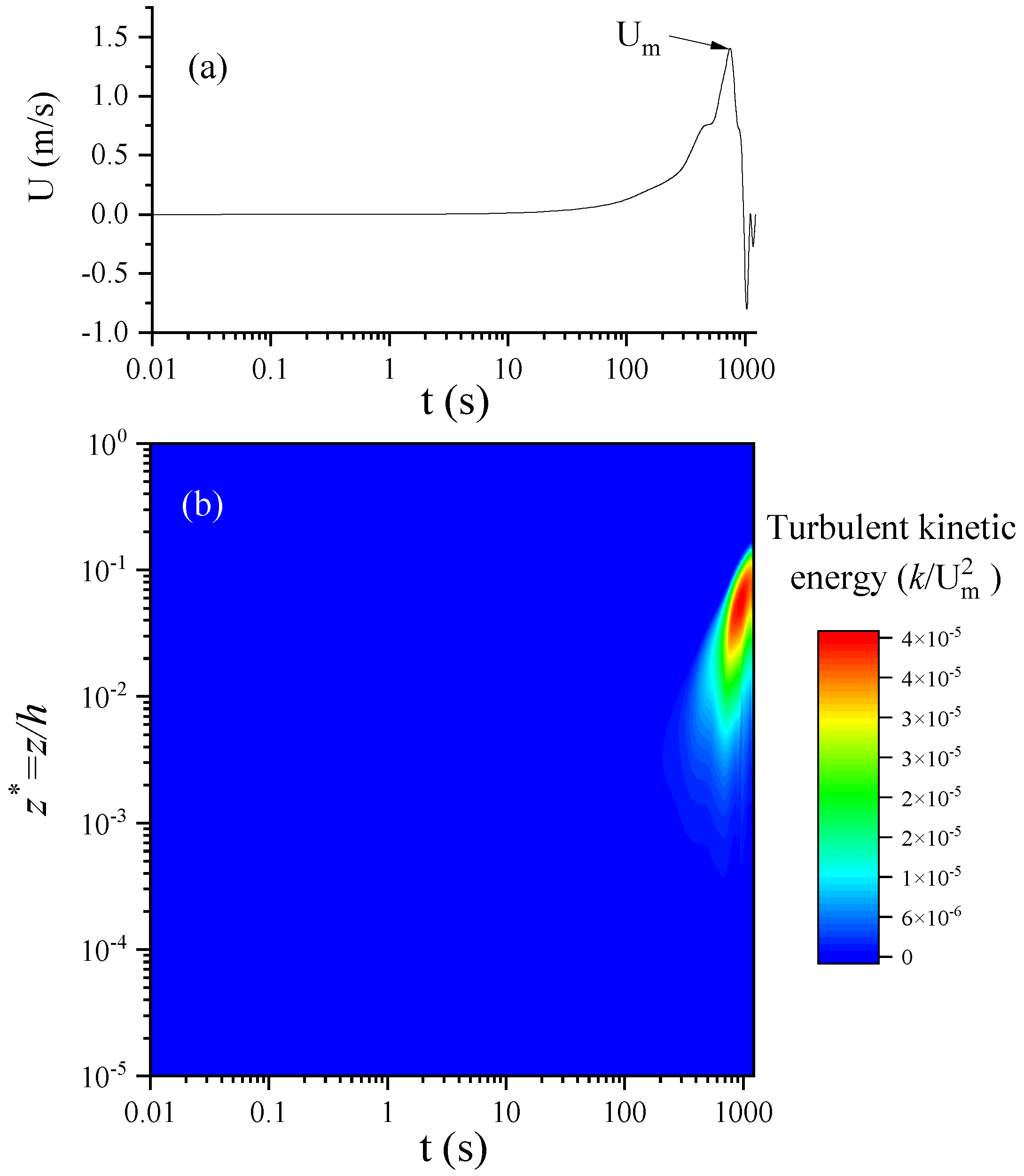
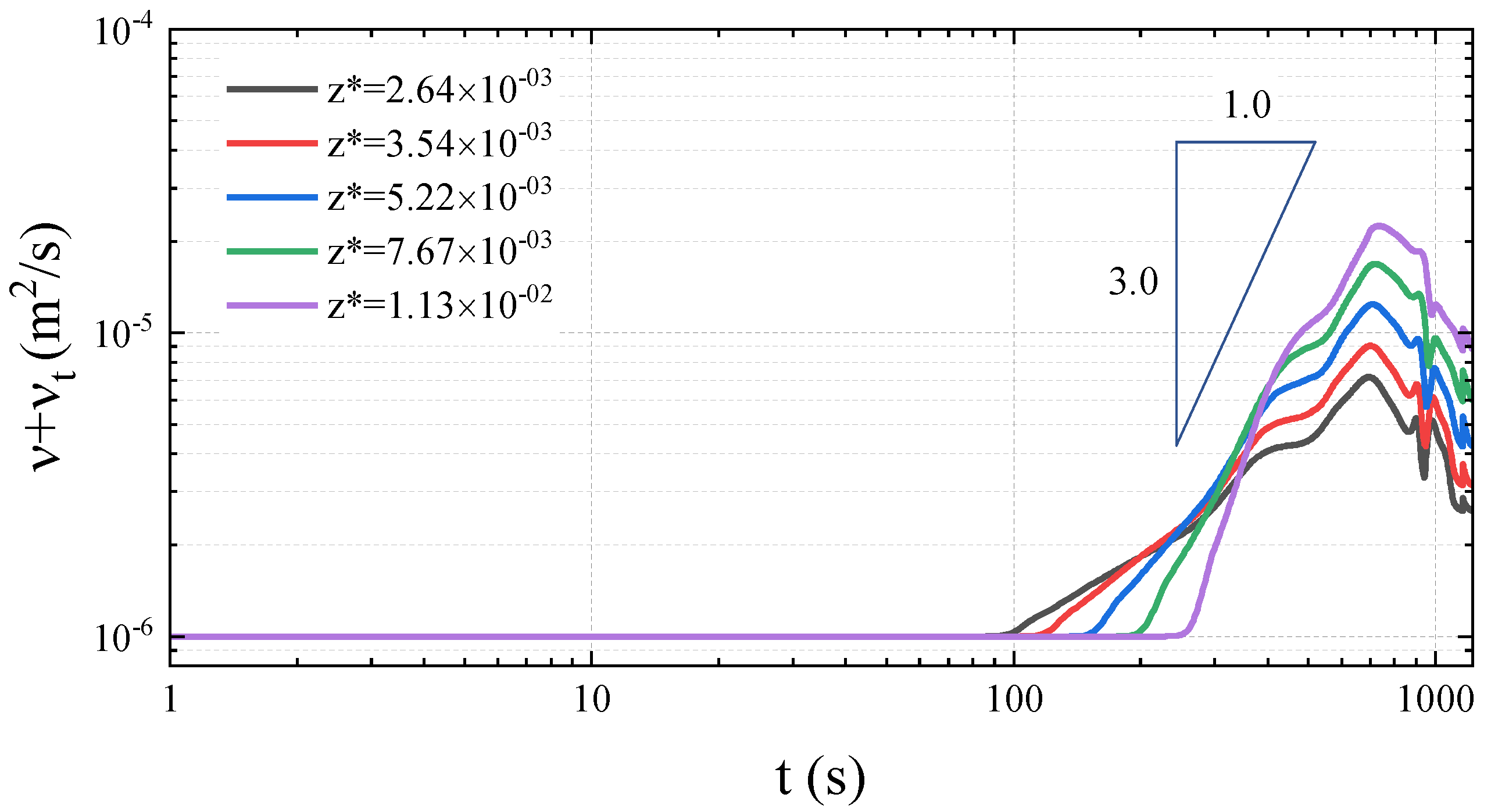
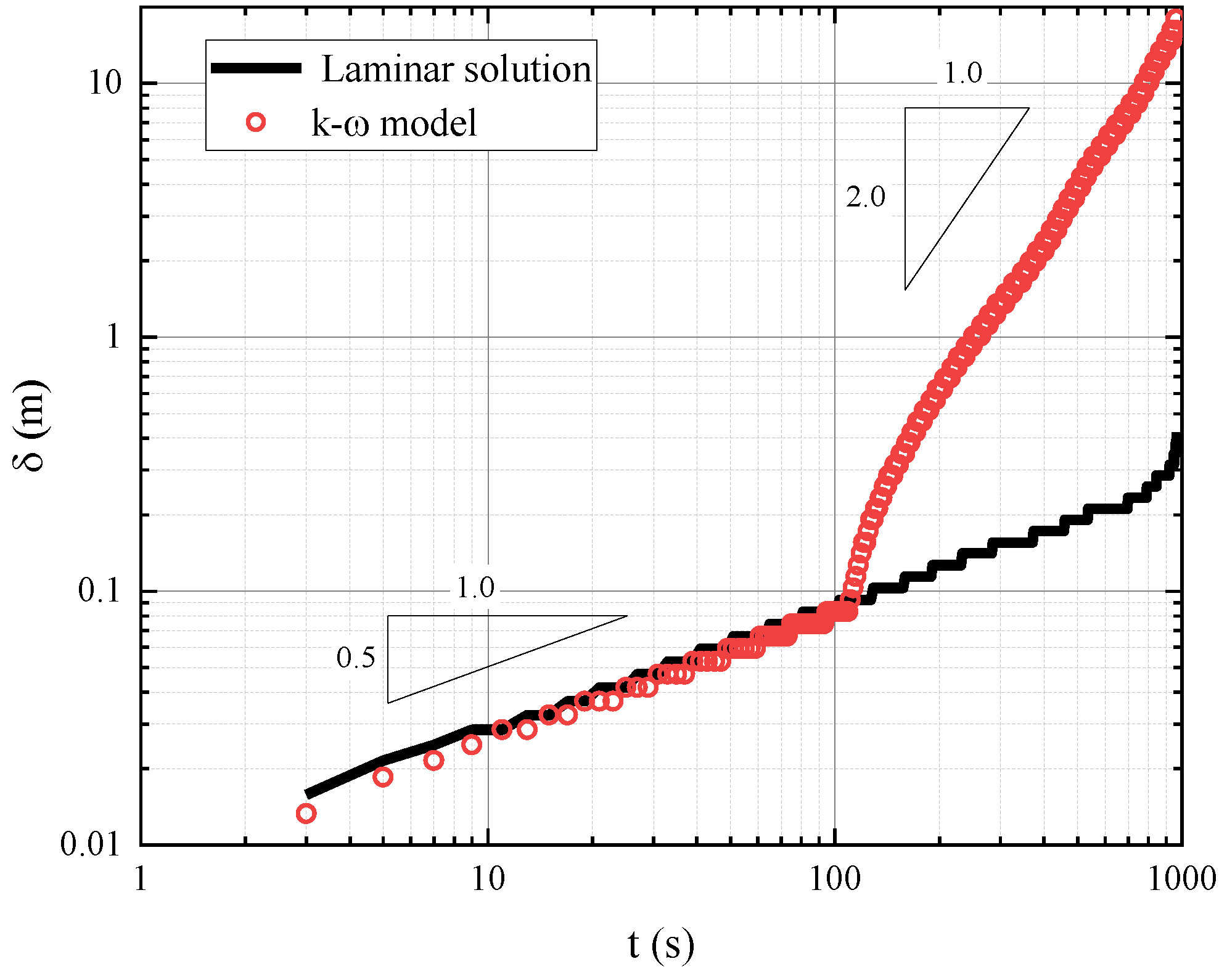
3.1. Transition from Laminar to Turbulence in the Tsunami Boundary Layer
3.2. Characteristics of the Turbulent Structure of Tsunami Bottom Boundary Layer Using the 2011 Tohoku Tsunami Waveform
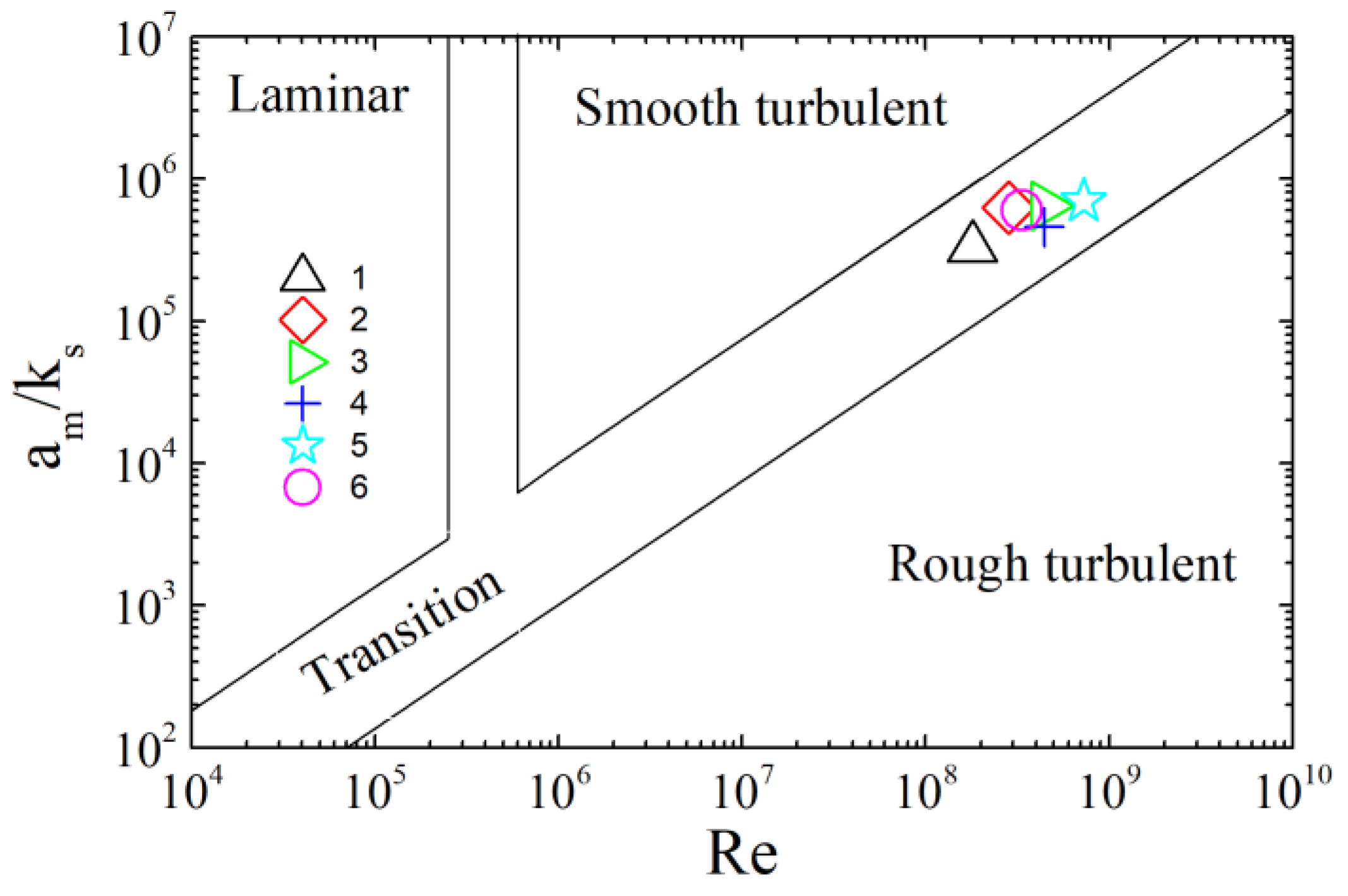
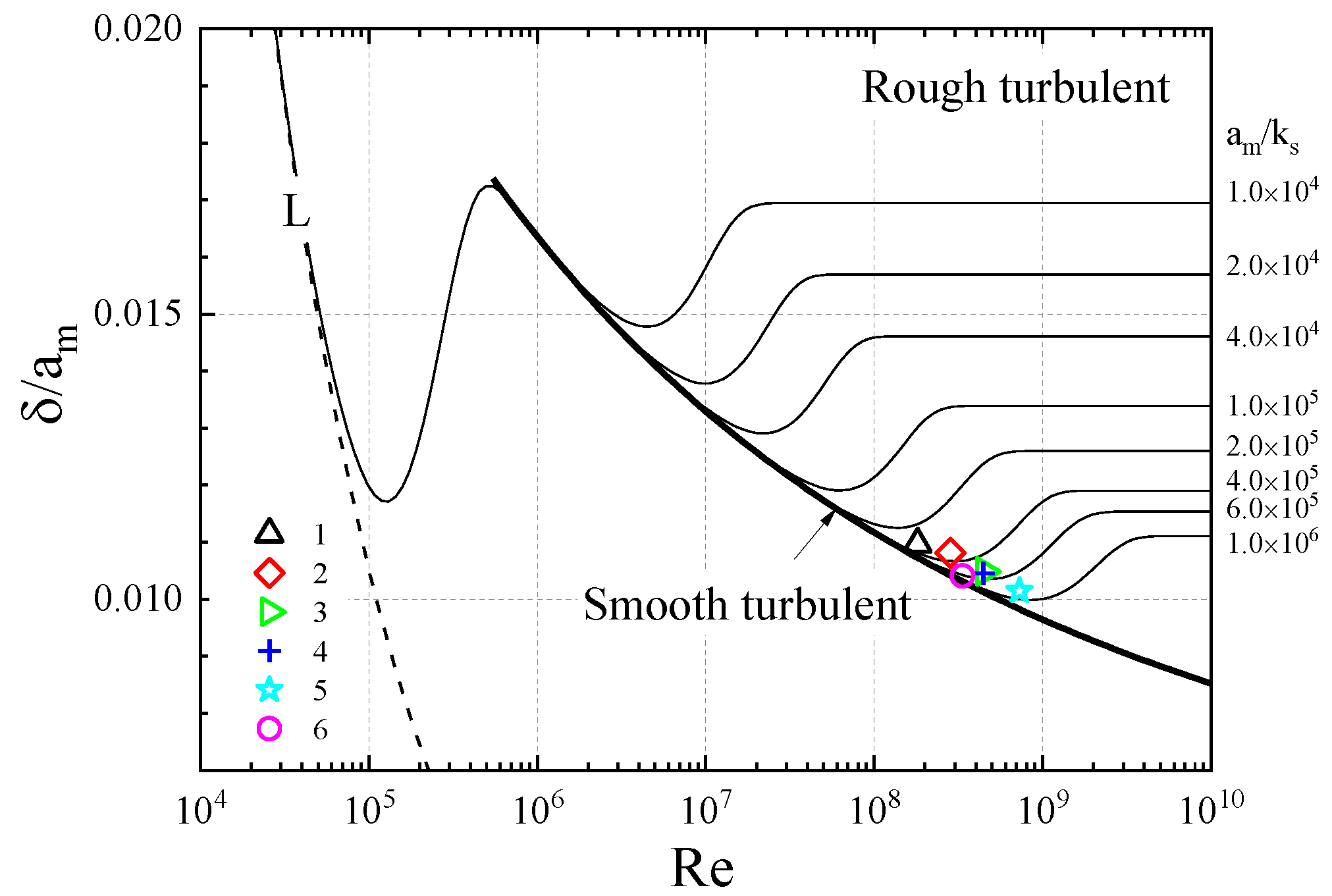
3.2.1. Inspection of the Depth-Limitation Condition
3.2.2. Inspection of the Transition to Turbulence
3.2.3. Inspection of the Flow Regime of the Boundary Layer
3.2.4. Inspection of the Transitional Characteristics of the Boundary Layer Thickness and Friction Factor
3.2.5. Tsunami-Induced Velocity
3.2.6. Tsunami-Induced Bottom Shear Stress
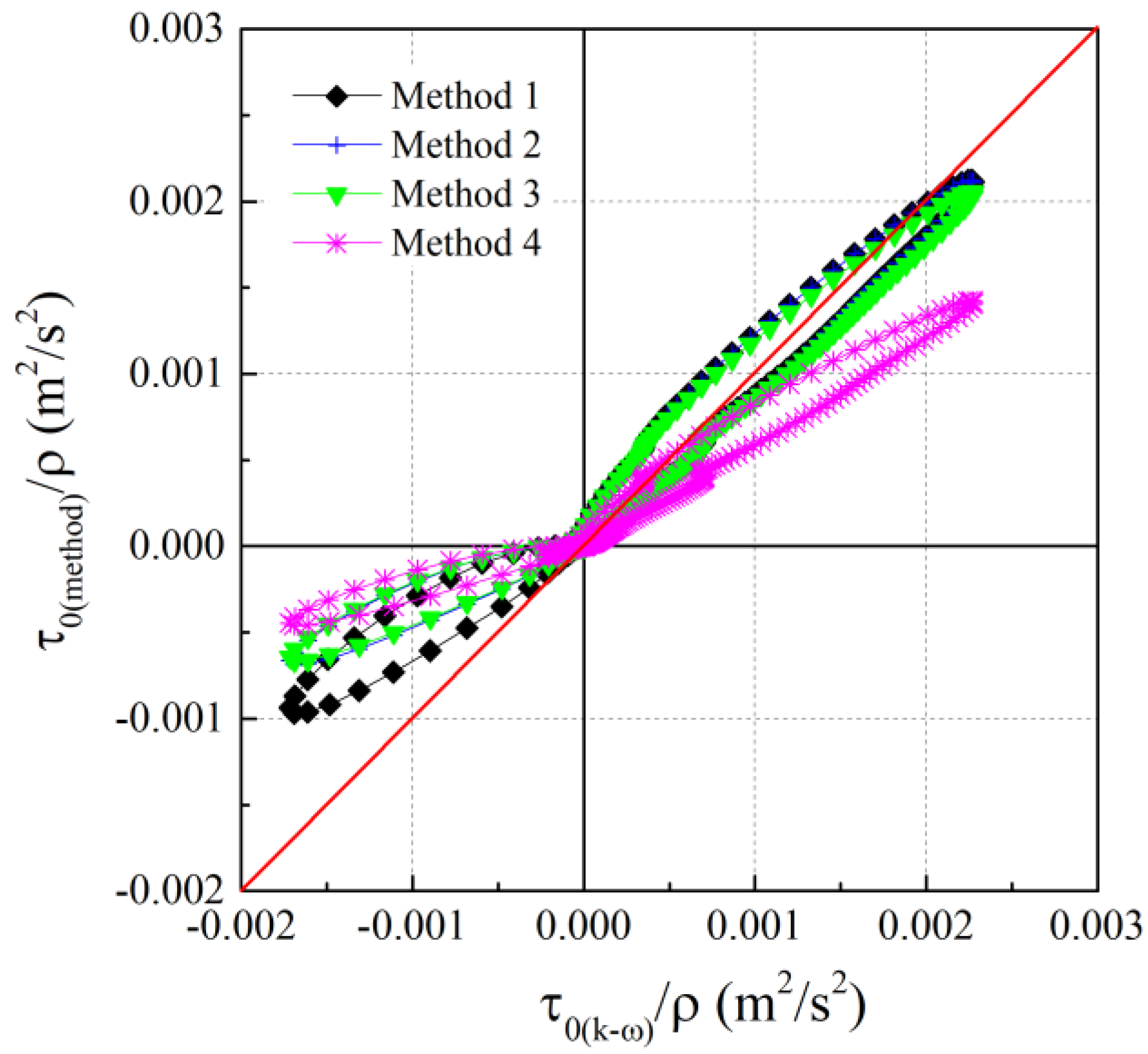
4. Simple Methods of Calculating Bottom Shear Stress
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jonsson, I.G. Wave boundary layer and friction factors. Coast. Eng. Proc. 1966, 1, 127–148. [Google Scholar]
- Tinh, N.X.; Tanaka, H. Study on boundary layer development and bottom shear stress beneath a tsunami. Coast. Eng. J. 2019, 61, 574–589. [Google Scholar] [CrossRef]
- Tanaka, H.; Tinh, N.X.; Yu, X.; Liu, G. Development of depth-limited wave boundary layers over a smooth bottom. J. Mar. Sci. Eng. 2021, 9, 27. [Google Scholar] [CrossRef]
- Lacy, J.R.; Rubin, D.M.; Buscombe, D. Currents, drag, and sediment transport induced by a tsunami. J. Geophys. Res. 2012, 117, C9. [Google Scholar] [CrossRef]
- Makris, A.; Lacy, J.R.; Fuhrman, D.R. Numerical Simulation of the Boundary Layer Flow Generated in Monterey Bay, California, by the 2010 Chilean Tsunami Case Study. J. Waterw. Port Coast. Ocean. Eng. 2021, 147, 6. [Google Scholar] [CrossRef]
- Williams, I.A.; Fuhrman, D.R. Numerical simulation of tsunami-scale wave boundary layers. Coast. Eng. 2016, 110, 17–31. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, H.; Tinh, N.X.; Sana, A. Transitional behavior of a flow regime in shoaling tsunami boundary layers. J. Mar. Sci. Eng. 2020, 8, 700. [Google Scholar] [CrossRef]
- Kawai, H.; Satoh, M.; Kawaguchi, K.; Seki, K. Characteristics of the 2011 Tohoku tsunami waveform acquired around Japan by Nowphas equipment. Coast. Eng. J. 2013, 55, 1350008. [Google Scholar] [CrossRef]
- Tinh, N.X.; Tanaka, H.; Yu, X.; Liu, G. Numerical implementation of wave friction factor into the 1D tsunami shallow water equation model. Coast. Eng. J. 2021, 63, 174–186. [Google Scholar] [CrossRef]
- Larson, M. A closed form solution for turbulent wave boundary layers. Coast. Eng. Proc. 1996, 1, 3244–3256. [Google Scholar]
- Liu, P.L.-F.; Park, Y.S.; Cowen, E.A. Boundary layer flow and bed shear stress under a solitary wave. J. Fluid Mech. 2007, 574, 449–463. [Google Scholar] [CrossRef]
- Suntoyo; Tanaka, H. Numerical modeling of boundary layer flows for a solitary wave. J. Hydro-Environ. Res. 2009, 3, 129–137. [Google Scholar]
- Vittori, G.; Blondeaux, P. The boundary layer at the bottom of a solitary wave and implications for sediment transport. Prog. Oceanogr. 2014, 120, 399–409. [Google Scholar] [CrossRef]
- Suntoyo; Tanaka, H.; Sana, A. Characteristics of turbulent boundary layers over a rough bed under saw-tooth waves and its application to sediment transport. Coast. Eng. 2008, 55, 1102–1112. [Google Scholar] [CrossRef]
- Suntoyo; Tanaka, H. Effect of bed roughness on turbulent boundary layer and net sediment transport under asymmetric waves. Coast. Eng. 2009, 56–59, 960–969. [Google Scholar]
- Sana, A.; Ghumman, A.R.; Tanaka, H. Modeling of a rough-wall oscillatory boundary layer using two-equation turbulence models. J. Hydraul. Eng. 2009, 135, 60–65. [Google Scholar] [CrossRef]
- Wilcox, D.C. Reassessment of the scale determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for Eng. applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Kamphuis, J.W. Determination of sand roughness for fixed bed. J. Hydraul. Res. 1974, 12, 193–203. [Google Scholar] [CrossRef]
- Nadaoka, K.; Yagi, H.; Nihei, Y.; Nomoto, K. Characteristics of turbulent structure in asymmetrical oscillatory flow. Proc. Coast. Eng. JSCE 1994, 41, 141–145. (In Japanese) [Google Scholar]
- Kondo, J. Operational Calculus; Baifukan: Tokyo, Japan, 1956. (In Japanese) [Google Scholar]
- Tanaka, H.; Sumer, B.M.; Lodahl, C. Theoretical and experimental investigation on laminar boundary layers under cnoidal wave motion. Coast. Eng. Japan 1998, 40, 81–89. [Google Scholar] [CrossRef]
- Tanaka, H.; Thu, A. Full-range equation of friction coefficient and phase difference in a wave-current boundary layer. Coast. Eng. 1994, 22, 237–254. [Google Scholar] [CrossRef]
- Tanaka, H.; Tinh, N.X.; Sana, A. Improvement of the full-range equation for wave boundary layer thickness. J. Mar. Sci. Eng. 2020, 8, 573. [Google Scholar] [CrossRef]
- Larsen, B.E.; Fuhrman, D.R. Full-scale CFD simulation of tsunamis. Part 2 Boundary layers and bed shear stresses. Coast. Eng. 2019, 151, 42–57. [Google Scholar] [CrossRef]
- Tanaka, H.; Shuto, N. Friction laws and flow regimes under wave and current motion. J. Hydraul. Res. 1984, 22, 245–261. [Google Scholar] [CrossRef]
- Tanaka, H.; Sana, A. Numerical study on transition to turbulence in a wave boundary layer. The EUROMECH 310 Proc. In Sediment Transport Mechanisms in Coastal Environments and Rivers; World Scientific: Singapore, 1994; pp. 14–25. [Google Scholar]
- Jensen, B.L.; Sumer, B.M.; Fredsøe, J. Turbulent oscillatory boundary layers at high Reynolds numbers. J. Fluid Mech. 1989, 206, 265–297. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, H.; Chian, S.C.; Shuto, N. Experiments on an oscillatory flow accompanied with a unidirectional motion. Coast. Eng. Japan 1983, 26, 19–37. [Google Scholar] [CrossRef]
- Sumer, B.M.; Jensen, P.M.; Sørensen, L.B.; Fredsøe, J.; Liu, P.L.-F.; Cartesen, S. Coherent structures in wave boundary layers. Part 2. Solitary motion. J. Fluid Mech. 2010, 646, 207–231. [Google Scholar] [CrossRef]
- Tanaka, H.; Winarta, B.; Suntoyo; Yamaji, H. Validation of a new generation system for bottom boundary layer beneath solitary wave. Coast. Eng. 2012, 59, 46–56. [Google Scholar] [CrossRef]
- Yuan, J. Turbulent boundary layers under irregular waves and currents Experiments and the equivalent-wave concept. J. Geophys. Res. Oceans 2016, 121, 2616–2640. [Google Scholar] [CrossRef]
- Tanaka, H.; Samad, M.A. Prediction of instantaneous bottom shear stress for turbulent plane bed condition under irregular waves. J. Hydraul. Res. 2006, 44, 94–106. [Google Scholar] [CrossRef]
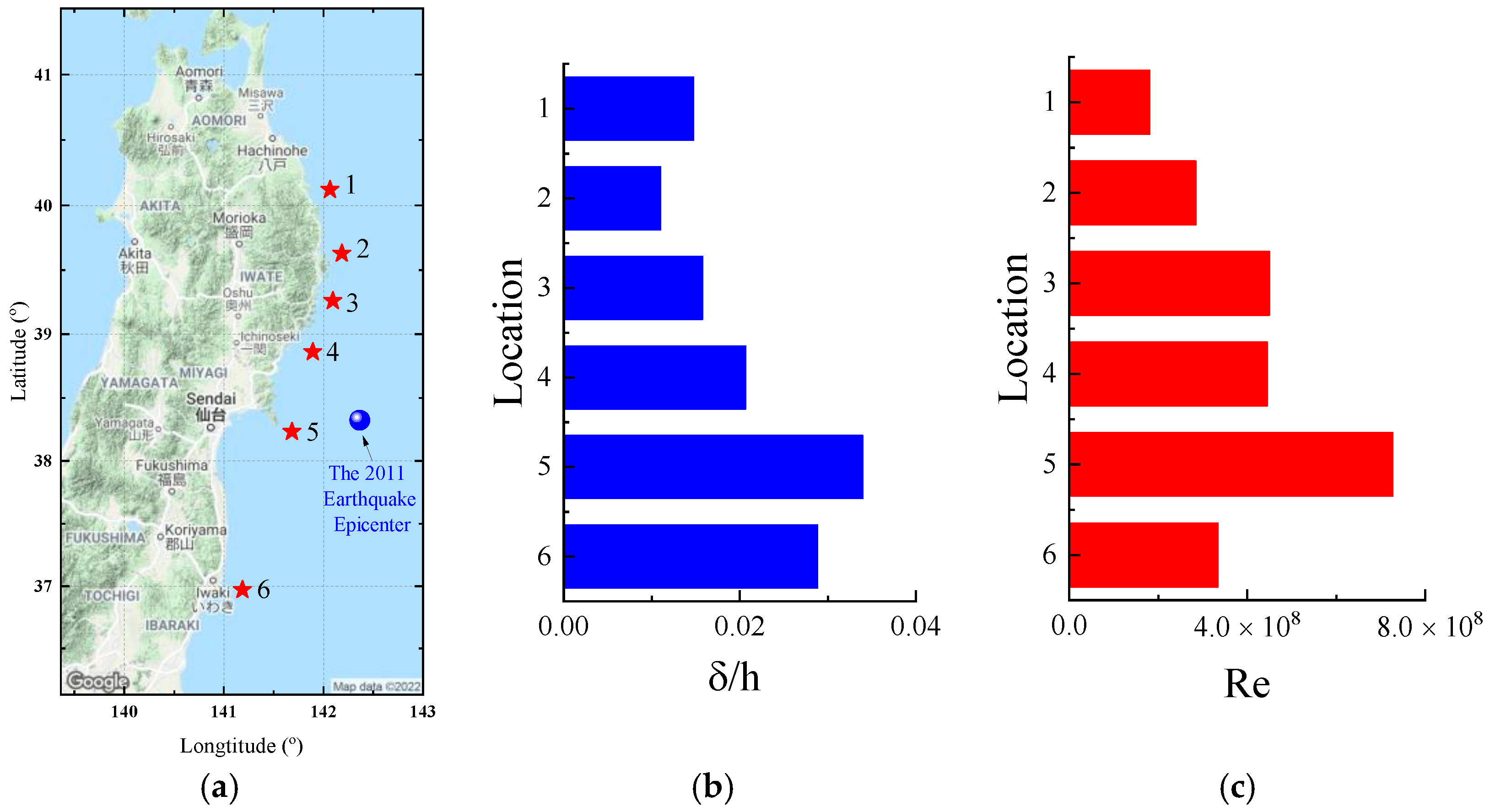
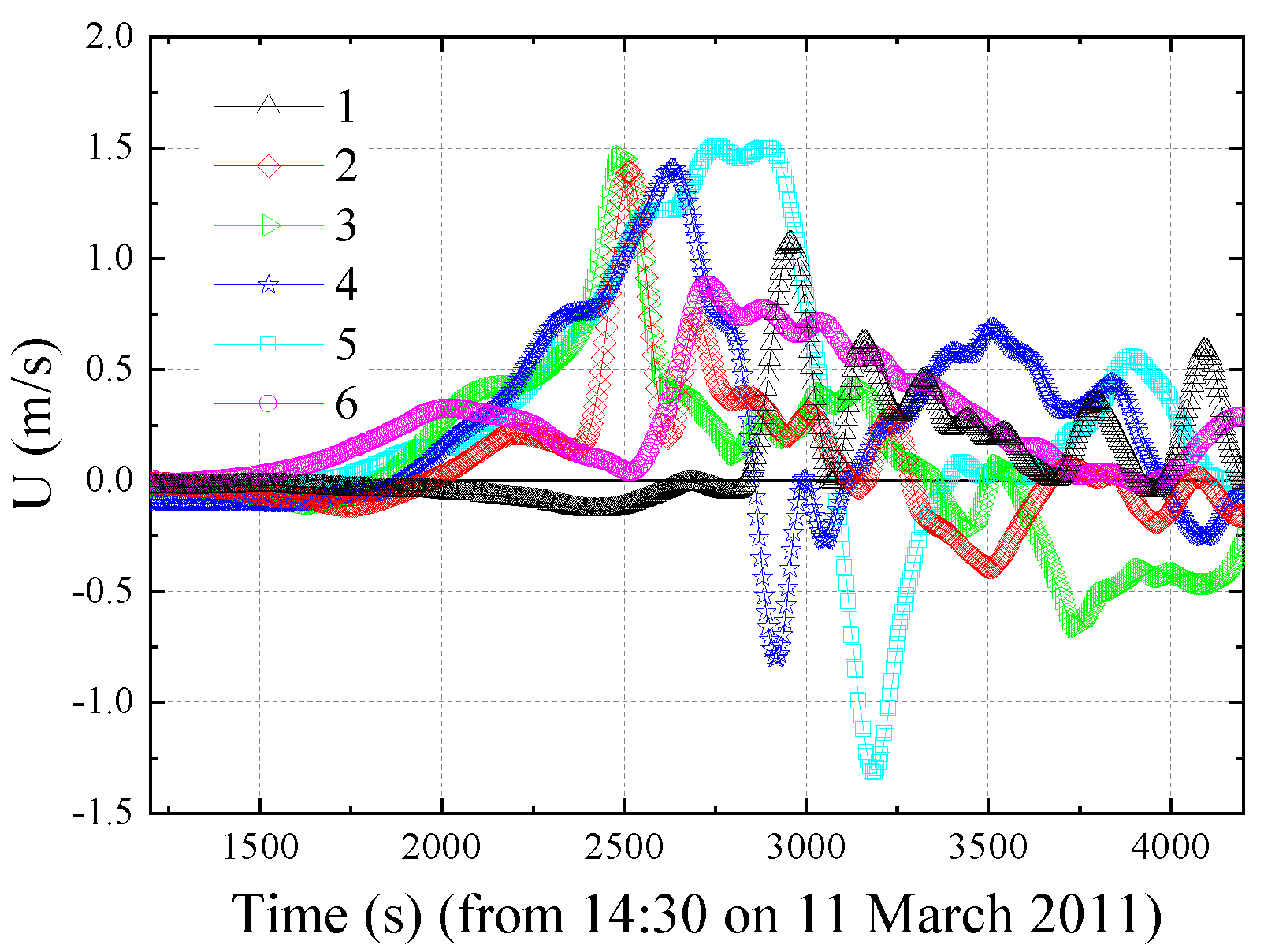

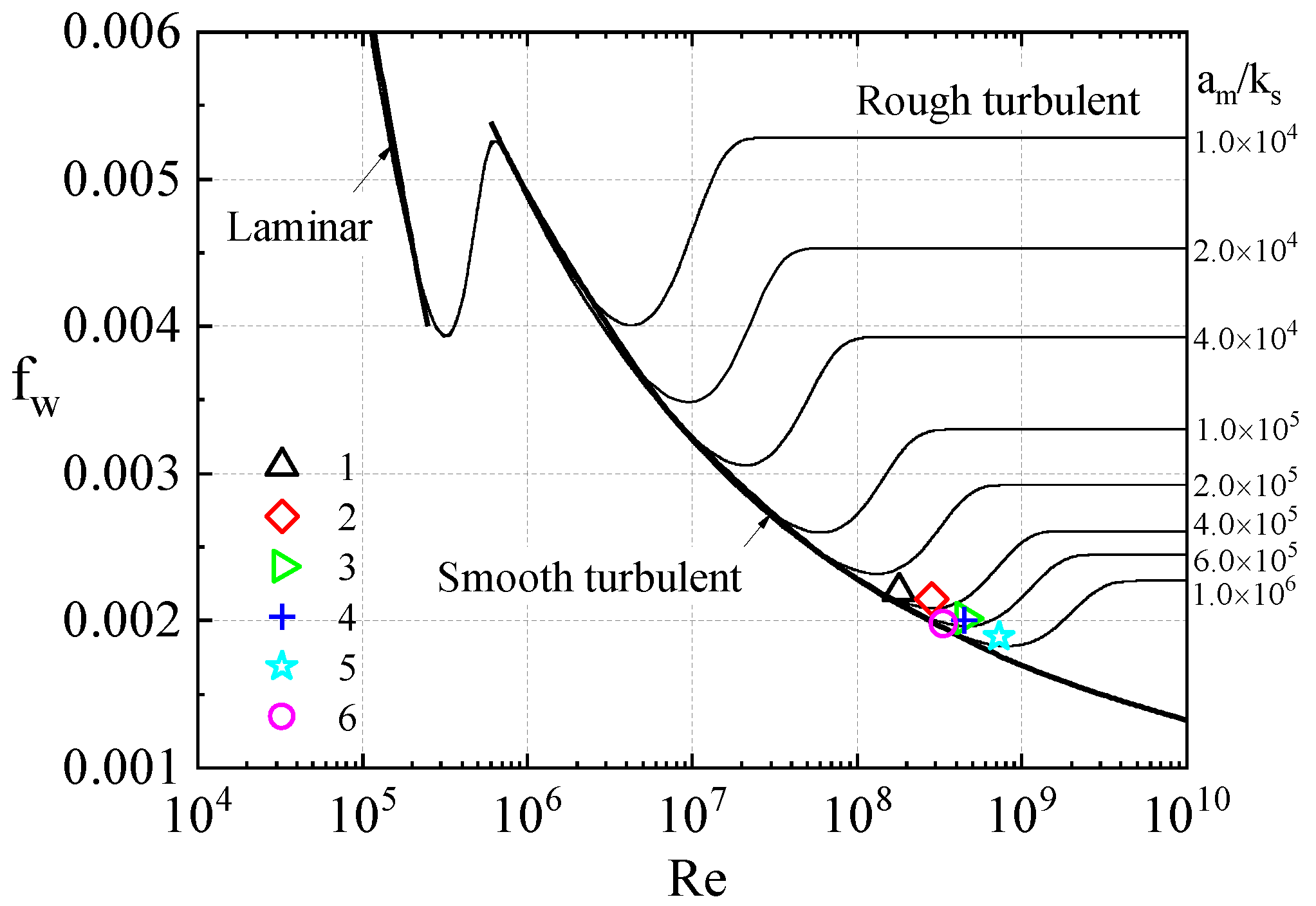
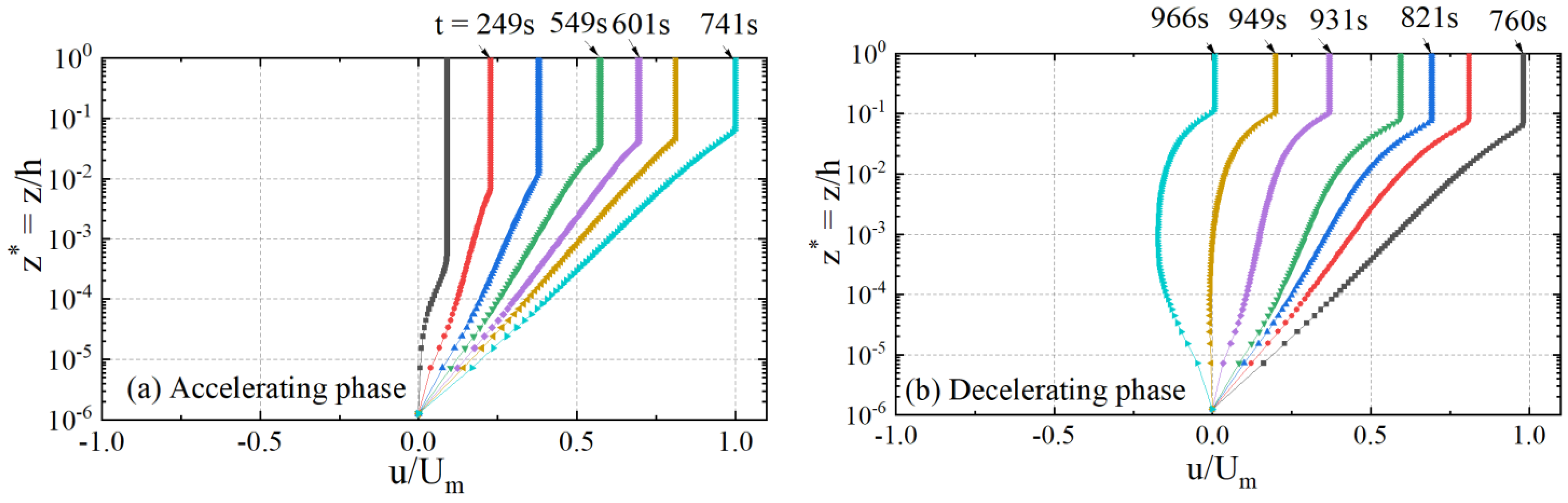
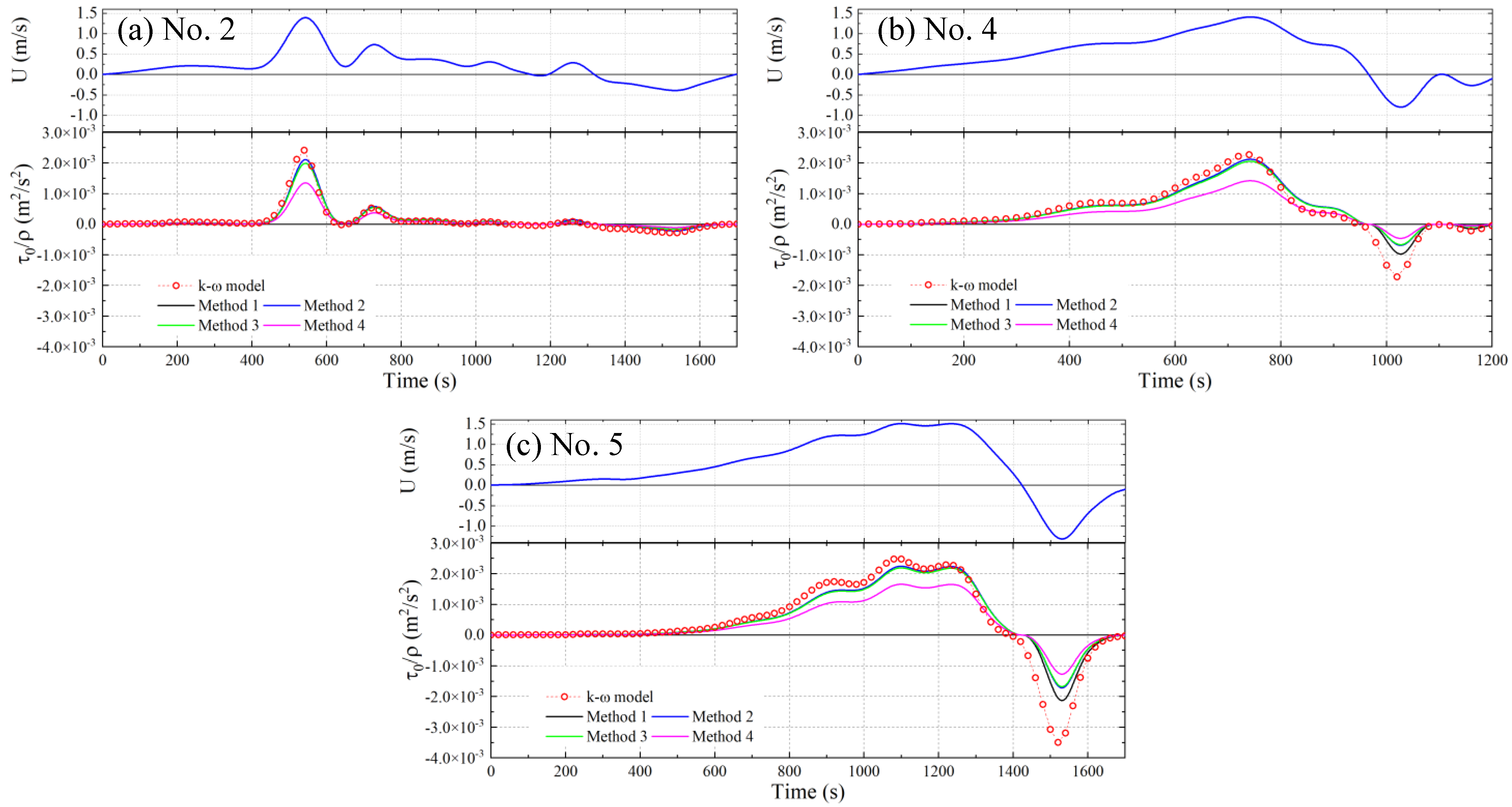
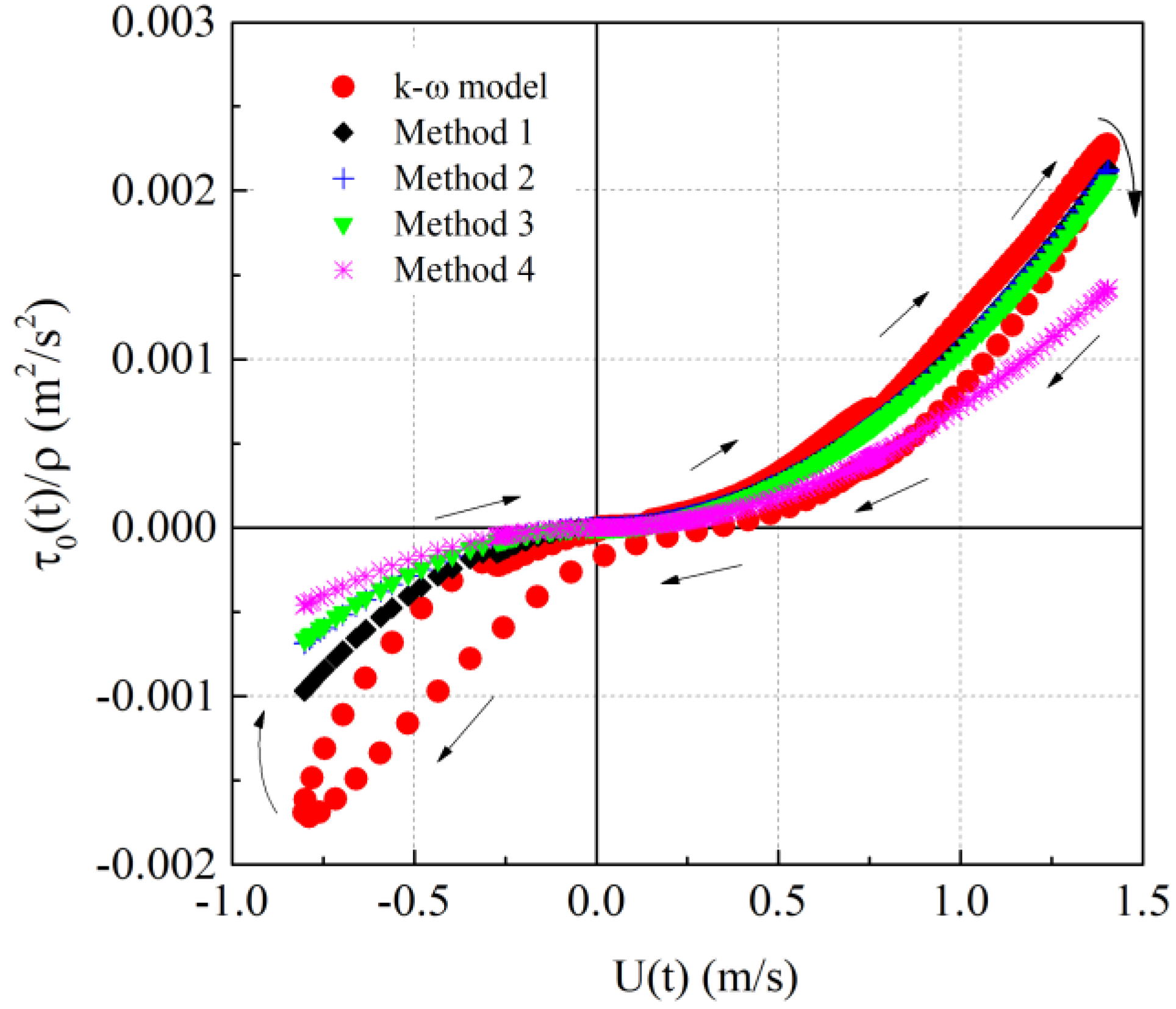

| No. | Measuring Station | Lattitude (deg.) | Longitude (deg.) | Water Depth (m) |
|---|---|---|---|---|
| 1 | North Iwate | 40.1167 | 142.0667 | 125 |
| 2 | Central Iwate | 39.6272 | 142.1867 | 200 |
| 3 | South Iwate | 39.2586 | 142.0969 | 204 |
| 4 | North Miyagi | 38.8578 | 141.8944 | 160 |
| 5 | Central Miyagi | 38.2325 | 141.6836 | 144 |
| 6 | Fukushima | 36.9714 | 141.1856 | 137 |
| Method | Explanation |
|---|---|
| k-ω model (truth) | Numerical solution using the turbulence model. |
| Method 1 | Using , … for each crest phase and trough phase from numerical integration of the velocity, calculate , … for each. |
| Method 2 | Using from the first positive wave, calculate , and use this single value for subsequent waves. |
| Method 3 | Using the and (duration of the first positive wave), calculate to obtain , and use this single value for subsequent waves. |
| Method 4 | Steady flow friction coefficient (from log law). |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tinh, N.X.; Tanaka, H.; Yu, X.; Liu, G. Numerical Study on the Turbulent Structure of Tsunami Bottom Boundary Layer Using the 2011 Tohoku Tsunami Waveform. J. Mar. Sci. Eng. 2022, 10, 173. https://doi.org/10.3390/jmse10020173
Tinh NX, Tanaka H, Yu X, Liu G. Numerical Study on the Turbulent Structure of Tsunami Bottom Boundary Layer Using the 2011 Tohoku Tsunami Waveform. Journal of Marine Science and Engineering. 2022; 10(2):173. https://doi.org/10.3390/jmse10020173
Chicago/Turabian StyleTinh, Nguyen Xuan, Hitoshi Tanaka, Xiping Yu, and Guangwei Liu. 2022. "Numerical Study on the Turbulent Structure of Tsunami Bottom Boundary Layer Using the 2011 Tohoku Tsunami Waveform" Journal of Marine Science and Engineering 10, no. 2: 173. https://doi.org/10.3390/jmse10020173
APA StyleTinh, N. X., Tanaka, H., Yu, X., & Liu, G. (2022). Numerical Study on the Turbulent Structure of Tsunami Bottom Boundary Layer Using the 2011 Tohoku Tsunami Waveform. Journal of Marine Science and Engineering, 10(2), 173. https://doi.org/10.3390/jmse10020173








