Abstract
Shipping, as an important part of the global supply chain, has always been quite sensitive to maritime accidents. Fatality and injury are important metrics indicating an accident’s severity. Understanding the driving factors of fatality and injury outcomes of maritime accidents can help to improve supply chain security. Based on maritime accident data obtained from the Lloyd’s List Intelligence, this paper identifies accident-prone sea areas through kernel density estimation (KDE) and selects two of the areas to conduct a comparative study on factors contributing to fatality and injury outcomes of maritime accidents through zero-inflated negative binomial (ZINB) and elastic analysis. The results show that collision and ship age significantly impact the number of fatalities and injuries. Specifically, collision and ship age have greater impacts on fatality and injury outcomes of accidents that occurred in the English Channel and North Sea. Whether the accident occurs in ports and whether the accident causes a total loss have more significant impacts on the fatality and injury outcomes of accidents in the Black Sea and the eastern Mediterranean Sea. The research results can potentially support the reduction of fatalities and injuries in maritime accident and help to manage maritime risk.
1. Introduction
As a primary mode of transportation in international trade, shipping undertakes approximately 80% of global trade transportation(UNCTAD) [1], playing an essential role in global supply chains [2]. International trade development has accelerated the development of the shipping industry. However, the heavy maritime traffic has also caused frequent maritime accidents, causing fatalities and injuries, environmental problems, and economic losses, undermining the sustainable development of the supply chain. For example, the Bahamian-flagged ro-ro ship MV Baltic Ace collided with the Cyprus-registered container ship Corvus J on 5 December 2012, in the North Sea and eventually sank, causing 11 deaths. The Panamanian-flagged tanker Sanchi and the Hong Kong cargo ship Changfeng Crystal collided in January 2018 in the East China Sea, which eventually caused the Sanchi to explode and catch fire, leaving 3 people dead and 29 on board missing. In addition, a large amount of oil caught fire in the surrounding sea, seriously polluting the ecological environment. According to the Lloyd’s List Intelligence Casualty Statistics, 1720 casualties were caused in maritime accidents worldwide from 2005 to 2020, accounting for 3.41% of all accidents. Fatality and injury are important metrics indicating the severity of a maritime accident. With the ship upsizing trend in recent years, the amount of cargo and passengers carried by a single ship also grows, and a single accident may lead to catastrophic consequences, creating challenges to maritime safety management. Maritime safety further affects maritime logistics in the global supply chain. Based on the above considerations, it is necessary to analyze the influencing factors of fatality and injury outcomes of maritime accidents and formulate proper preventive measures to reduce accident-caused fatalities and injuries and improve maritime logistics safety.
The characteristics and contributing factors of fatalities and injuries in maritime accidents for different ship types and different sea areas have been studied in the past decades. Using the negative binomial (NB) regression method, Yip [3] studied the characteristics of ship accidents in Hong Kong waters from 2001 to 2005. Based on the negative binomial and Poisson regression methods, Talley et al. [4] studied the determinants of the number of injuries, deaths, and missing passengers of passenger ships investigated by the U.S. Coast Guard from 1991 to 2001. Taking the fishing boat accident data in the northeastern United States from 2001 to 2008 as a research sample and based on the ordered probability model, Jin [5] explored the factors that affect the accident’s severity and found that foundered and ship stability affect the degree of fatalities and injuries. Uğurlu et al. [6] used the Bayesian network to construct a model for fishing vessels of 7 m or above in total length from 2008 to 2018 to explore the significant correlation between accident categories and vessel length, vessel age, fatalities and injuries, and vessel losses. Based on the accident data of British fishing vessels from 1948 to 2008, Roberts et al. [7] explored the influencing factors and trends of accident fatalities and injuries and ship losses. With passenger ship accidents in the northeastern United States from 2001 to 2008 as the input, Yip et al. [8] built NB and Poisson regression models to identify the determinants of the number of injuries, deaths, and missing passengers. Considering a large number of zero-injury observations in maritime accident data, Weng, et al. [9] used the zero-inflated negative binomial (ZINB) model to study the accidents causing deaths and missing persons in the South China Sea and analyze the influencing factors of the number of deaths and missing persons in accidents in the waters. Hao et al. [10] selected more than 1,500 ship accidents on the trunk routes of the Yangtze River from 2008 to 2014 as objects and used the ZINB model to explore the factors that contribute to the number of deaths and missing persons in accidents in this water area and degree of influence of these factors, as well as the reasons behind these influencing factors. Wang et al. [11] performed ZINB regression analysis of the accident data over the past 26 years and explored the degrees of influence of the eight factors contributing to tanker crew fatalities and injuries. Weng et al. [12] combined the maximum likelihood regression tree and the ZINB model and used the number of deaths and missing persons at different times in different waters as the dependent variables to analyze the causes of fatalities and missing persons in accidents and their corresponding marginal effects. Wang et al. [13] and Weng and Li [14] used association rules to explore the relevant factors that affect the number of fatalities in marine vessel accidents. Wang et al. [15] used a zero-inflated ordered probability model and identified two states, namely injury-free and injury-prone, in a maritime accident, and explored the factors affecting the severity of accident injury. Most of the above literature targeted specific vessel types, such as fishing vessels [5,6,7] and passenger ships [8], or specific sea waters [3,5,9,10]. Studies that target all vessel types and across different accident-prone sea areas can horizontally compare the differences in the influencing factors of fatalities and injuries, thereby supporting safety management decisions in different sea areas. However, such studies are relatively rare. In terms of quantitative analysis methods, the literature usually adopts association rule mining [13,14,16], Bayesian network [16,17,18,19,20,21], logit model [22,23,24,25], NB regression model [3,4], and ZINB regression model [9,10,12]. Specifically, the ZINB method is suitable where a large number of zero values exist in dependent variables and is more suitable for handling overdispersed data [26].
In recent years, some studies have analyzed the overall characteristics of global maritime accidents and their influencing factors. For example, Huang, et al. [27] used Geographic Information System (GIS) to analyze the spatial distribution of maritime accidents from 2002 to 2011. Zhang et al. [28] used the Kernel Density Estimation (KDE) and k-means clustering methods to study the spatial distribution of global maritime accidents from 2003 to 2018. Wang et al. [29] adopted density analysis and clustering analysis to probe into the spatial distribution of maritime accidents from two aspects: accident frequency and accident severity. These studies provide important references for the identification of accident-prone areas. The hotspots with high accident densities identified in these studies include part of the sea areas around the United Kingdom, the Mediterranean, east Asia, etc. In particular, as the busiest shipping area in the world, the English Channel links to the southern part of the North Sea by the Strait of Dover at its northeastern end and serves 500 ships daily. The Mediterranean Sea connects to the Atlantic by the Strait of Gibraltar and links to the red sea by the Suez Canal. The Mediterranean Sea has a number of major routes in the world. Therefore, it is essential to understand the characteristics and risk of maritime accidents in the above areas. Many scholars have investigated maritime accidents in the North Sea and the English Channel. Based on ship state information provided by the automatic identification system, van Westrenen and Ellerbroek [30] analyzed the traffic and calculated situations of near-miss collisions on the North Sea. Roberts, Jaremin and Marlow [7] investigated the circumstances and characteristics of fishing vessel accidents from 1948 to 2008 and found that most fatalities from collisions occurred in the English Channel and North Sea. MacDuff [31] assessed the probability of collisions between large ships and offshore structures in the North Sea and discussed the problem of safe navigation of the English Channel and the North Sea by the methods of probability analysis. Maritime accidents that occurred in the Mediterranean Sea have also been investigated by many scholars. Soussi et al. [32] constructed a Lagrangian-based maritime and coastal risk model to assess the risk of oil spill accidents in the Mediterranean littoral. Otay and Özkan [33] developed a physics-based mathematical model to simulate the random transit maritime traffic through the Strait of Istanbul, and estimate the probability distribution of vessel casualties. The above studies mainly focused on the exploration of circumstances related to the occurrence or risk of maritime accidents in the English Channel and the Mediterranean Sea. Very few of them have particularly explored and compared factors contributing to fatality and injury outcomes of maritime accidents in these areas.
Based on the Lloyd’s List Intelligence data, this work selects the global maritime accident data from 2005 to 2020 to analyze their characteristics and filter the influencing factors of maritime accident fatalities and injuries. With the help of GIS, the paper uses KDE to analyze the spatial characteristics of global maritime accidents. It selects accident-prone sea areas and combines the filtered maritime accident fatality and injury factors for zero-inflated negative binomial and elastic analysis. This way, the influencing factors of fatalities and injuries in the selected sea areas are compared and analyzed to help propose preventive measures. This study addressed three questions: (1) What areas are prone to maritime accidents worldwide? (2) What factors affect fatalities and injuries in accident-prone sea areas? (3) What are the differences in the influencing factors of fatalities and injuries in different sea areas? How should we take measures to avoid accident fatalities and injuries? The paper aims to analyze the influencing factors of fatality and injury outcomes of maritime accidents and formulate proper preventive measures to provide references for the formulation of safety precautions in accident-prone maritime areas and to improve maritime safety.
2. Data Sources
This article selects the maritime accident data in the global sea areas from January 2005 to December 2020 from the shipping accident database managed by Lloyd’s List Intelligence Company as research objects. Each piece of data in the objects includes the ship’s name, the ship’s IMO code, flag state, gross tonnage, accident time, accident sea area, accident cause, vessel type, number of injuries, number of missing, number of deaths, degree of hull damage, and the latitude and longitude of the accident site. In addition, by referring to the Flag of Convenience (FOC) list of the International Transport Workers’ Federation (ITF) [34], this article divides the flag states of the involved ships into FOC and non-FOC to facilitate subsequent statistical analysis.
Figure 1 shows the distribution of maritime accidents involving deaths, missing and injuries. The proportions of accidents involving deaths, missing persons, and injuries stood at 1.82% (Figure 1a), 0.8% (Figure 1b), and 1.44% (Figure 1c), respectively, and the proportion of accidents without fatalities and injuries reached 96.59% (Figure 1d). This shows that the zero values of the number of fatalities and injuries are inflated.
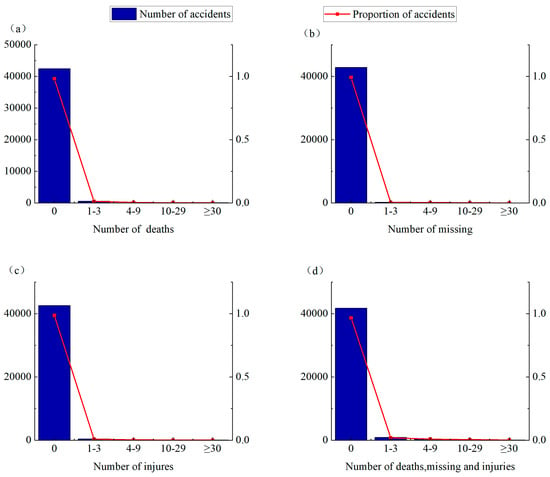
Figure 1.
Distribution of maritime accidents involving (a) deaths, (b) missing, (c) injuries and (d) deaths, missing and injuries.
Since the number of fatalities and injuries in a maritime accident can directly reflect the severity of the accident, the dependent variable used in this work was the total number of fatalities and injuries (i.e., deaths, missing and injuries) in the maritime accident. In addition, based on knowledge obtained from the investigation of the relevant literature (Table 1), flag, vessel type, loss type, pollution indicator, serious indicator, ship age, whether in port and cause of fatality and injury (machinery damage, collision, grounding, fire/explosion, contact, foundered and hull damage) were set as potential independent variables (Table 2).

Table 1.
Literature of independent variables.

Table 2.
Model variable description.
3. Methodology
3.1. Framework
The logic of model construction is shown in Figure 2. First, the paper analyzes the spatial distribution of the global maritime accident data through KDE to identify the accident-prone sea areas in the global maritime sector and select the areas for study. Then, it builds a statistical model based on the characteristics of the maritime accident fatalities and injuries in the areas for study and determined through the goodness of fit test that the ZINB model was the optimal model. Next, according to the model results, the article analyzed the factors driving the fatalities and injuries in the two areas. Finally, the driving factors of fatalities and injuries of the two areas were compared and analyzed according to the elastic analysis theory.
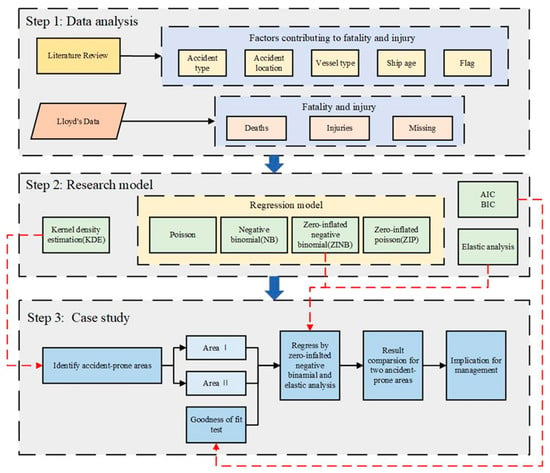
Figure 2.
Model construction logic diagram.
3.2. Kernel Density Estimation (KDE)
The KDE method can identify the sea areas with concentrated accidents to intuitively analyze the spatial agglomeration of accidents, which is conducive to a comprehensive analysis of accident characteristics. Therefore, this research adopts the kernel density theory to identify accident-prone maritime areas worldwide.
KDE reveals the frequency of accident locations in the geographic space. The denser the locations, the higher the frequency of accidents in the area, and vice versa. The kernel model of KDE is a non-parametric one, which reduces the interference by other potential factors by converting discrete data into a continuous distribution function to analyze the changing characteristics of variables. Its kernel density function is shown as Formula (1).
where is denoted as the estimation of the density function ; is denoted as the kernel function; is denoted the sample observation value, is denoted as the sample mean, and is denoted the bandwidth.
The result of KDE is subject to the collective impact of the kernel function, the bandwidth, and the cell size [48]. Commonly used kernel functions include the Gaussian kernel function and the boxcar kernel function. The Gaussian kernel function that conforms to the normal distribution is generally selected as the KDE function in the present work. Bandwidth affects the smoothness of the density surface [49], while the cell size primarily affects the coarseness of the generated surface [50]. With reference to the parameter settings in the related study [27,28,51,52], combined with the data samples of this study, this paper selects parameters with a bandwidth of 5 degrees and a cell size of 0.5 degrees.
3.3. Zero-Inflated Negative Binomial (ZINB) Model
This study ad tops the ZINB model to quantitatively analyze various factors’ influence on maritime accident fatalities and injuries. The ZINB model was improved and extended from the NB model. The NB distribution is regarded a continuous mixed Poisson distribution [53], and the probability distribution function of the Poisson regression model is shown in Formula (2).
Suppose , and we can obtain the Poisson regression model, where is the covariate vector of , that is, the various factors influencing the maritime accident fatalities and injuries , such as flag and vessel type, while is the parameter vector, and is the number of covariants.
The probability distribution function expression of the NB regression model is shown in Formula (3). In the negative binomial distribution, the variance is greater than the mean.
Suppose , and we can obtain the NB regression model, where is the covariate vector of , that is, the various factors influencing the maritime accident fatalities and injuries , such as flag and vessel type, while is the parameter vector, is the number of covariants, and is the overdispersion parameter.
The ZINB model is suitable when there are many zero values in the sample data, and the variance is greater than the mean (that is, overdispersion). The probability distribution function is a mixed distribution, including the zero-valued and non-zero-valued parts [53]. Suppose represents the proportion of zero values. If , the greater the value, the more severe the zero inflation. If , the model is a common negative binomial regression model. The probability distribution function of the zero-inflated negative binomial model is shown in Formula (4).
Suppose , and we can obtain the ZINB model. Where, is the covariate vector of , that is, the various factors influencing the maritime accident fatalities and injuries , such as flag and vessel type. is the parameter vector, is the number of covariates, and is the reciprocal of the overdispersion parameter .
This paper also uses the zero-inflated Poisson regression model, and its probability distribution function is shown in Formula (5).
Suppose , and we can obtain the Zero-inflated Poisson (ZIP) regression model, where, is the covariate vector of , that is, the various factors influencing the maritime accident fatalities and injuries , such as flag and vessel type, while is the parameter vector, and is the number of covariants.
The same sample data generally have multiple applicable models, but not all the applicable models are the best regression model. For this reason, it is necessary to perform a goodness-of-fit test to obtain the best regression model. Frequently-used model selection criteria include the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC). The specific meanings of the two criteria are shown in Formulas (6) and (7).
represents the number of parameters contained, is the log-likelihood function, and is the number of sample data observations. The AIC and BIC criteria reflect the model loss information, so the smaller the information loss, the better the fitting effect of the model.
3.4. Elastic Analysis
Elastic analysis is a quantitative index to measure the degree of influence of independent variable changes on dependent variables that originated in the field of mechanics. Elastic analysis can accurately identify the contribution of various factors to the number of fatalities and injuries so as to intuitively identify key factors and provide a quantitative basis for decision-makers to formulate preventive measures. Elastic analysis in this study is expressed as Formula (8).
where represents the elasticity coefficient of the i-th factor, represents the i-th influencing factor. , and is the coefficient of the factor in the selected regression model.
4. Results and Discussion
4.1. Identification of Accident-Prone Areas
The density of global maritime accidents is shown in Figure 3a. The kernel density values are divided into five categories. Two red areas appeared (that is, the areas with the highest accident density), namely (1) the English Channel and the North Sea, and (2) the Black Sea and the eastern Mediterranean Sea. The orange areas represent sea areas with high accident density, such as parts of the western coast of the United States, the eastern coasts of Canada and the United States, and the waters near the Strait of Malacca. The spatial distribution shows that significant differences exist in the number of maritime accidents in different sea areas. This paper selects two sea areas with high levels of accident densities and similar sizes of data samples to conduct a comparative analysis of factors influencing fatality and injury outcomes of maritime accidents. The English Channel, the Bay of Biscay, and the North Sea (Area I, Figure 3b), as well as the Black Sea and the eastern Mediterranean Sea (Area II, Figure 3c) were selected as the areas of study. Both sea areas are located in Europe and have a large number of ports. Area I has developed a shipping trade with high ship traffic. The narrower English Channel, with many shoals, connects to the open Bay of Biscay and the North Sea. Area II has a twisty coastline, with many islands in the waters connecting the eastern Mediterranean Sea and the Black Sea areas.
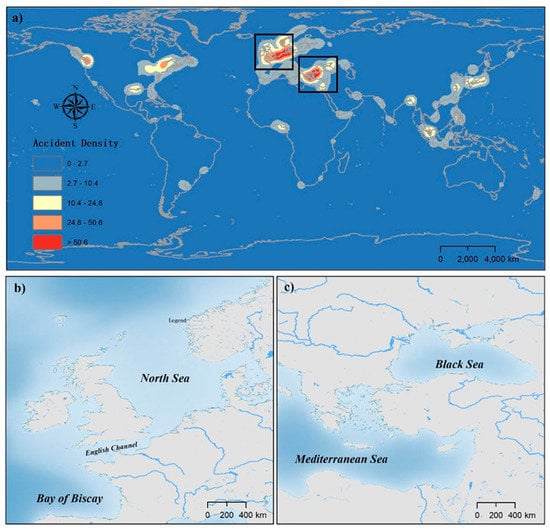
Figure 3.
Maps showing (a) density of global maritime accidents and the geographic locations of (b) Area I and (c) Area II.
4.2. Zero-Inflated Negative Binomial Model and Elastic Analysis RESULTS and Their Theoretical Implications
Areas I and II have 7864 and 6815 maritime accident records, respectively. Since the data in some fields are missing, 7637 and 6778 records were left to conduct the model fitting. To select the model with the best performance, this study uses AIC and BIC to test the goodness of fit of Poisson regression, NB regression, ZINB regression, and ZIP regression. The results are shown in Table 3. The smaller the AIC and BIC values, the less the information loss, and the better the fitting performance of the model. It is observed from Table 3 that in terms of the AIC indicator, Poisson > NB > ZIP > ZINB, while in terms of the BIC indicator, Poisson > NB > ZIP > ZINB. To sum up, the ZINB model has the best fit.

Table 3.
Goodness of fit test results for different regression models.
The regression coefficients, standard errors, and values obtained from the ZINB model are shown in Table 4. The elastic analysis results of the regression coefficients are shown in Table 5.

Table 4.
Regression parameters of the zero-inflated negative binomial models.

Table 5.
Elastic analysis results of the zero-inflated negative binomial models.
At the 95% confidence level, all variables, except hull damage and flag, significantly impact the number of fatalities and injuries in the two sea areas. Specifically, whether in port and pollution indicator have negative impacts on the number of fatalities and injuries, and the other indicators have positive impacts. In addition, the impact of hull damage on the number of fatalities and injuries is significant at a 90% confidence level in Area II only. The impact of flag on the number of fatalities and injuries is significant at a 90% confidence level in both areas and at a 95% confidence level in Area II.
Among the 14 independent variables, the three variables of loss type, pollution indicator, and serious indicator are artificially defined after the accident. Loss type and serious indicator positively correlate with the number of fatalities and injuries, indicating that accidents that result in total loss or are serious can cause a larger number of fatalities and injuries. The coefficient of pollution indicator is negative, meaning that the accident seriously pollutes the water area, and the resulting fatalities and injuries may decrease. According to the result of the elastic analysis, when the number of accidents with pollution increases by 1%, the number of fatalities and injuries in Areas I and II will decrease by 0.044% and 0.101%, respectively. These elasticity coefficients are relatively low probably because most of the ships causing pollution are oil tankers and dangerous goods carriers with few passengers on board.
The other 11 independent variables are factors that directly impact the number of fatalities and injuries in accidents and can reflect the cause of the accident. Flags in this study are divided into FOC and non-FOC. The regression coefficient of flag is positive, and the elasticity coefficients are 0.131 and 0.180, respectively, indicating that FOC ships may cause more fatalities and injuries than non-FOC ships. This may be because that the registration and supervision of flags of convenience are more relaxed, leading to a greater probability of accidents and a higher number of fatalities and injuries. The regression coefficient of vessel type is positive, and the elasticity coefficients are 0.037 and 0.083, respectively, indicating that the more passenger ship accidents, the greater the number of fatalities and injuries, which is consistent with the findings from Weng and Yang [24]. Ship age represents the service life of a ship. The elasticity coefficients of Ship age are positive, being 1.008 and 0.973, respectively, meaning that Ship age has a significant positive impact on the number of fatalities and injuries in both sea areas. This indicates that the older the ship, the poorer the ship’s performance, and the easier the accident is to cause fatalities and injuries. Whether an accident occurs in a port reflects how far the accident is from the coast. The coefficient of whether in port is negative, and the elasticity coefficients are −0.207 and −0.578, respectively, indicating that the farther away from the port area, the more fatalities and injuries in the accident. This is possibly because the closer the accident is to the coast, the more timely the rescue from the shore. Meanwhile, the coastal marine environment is relatively less harsh, which also increases the chance of survival. This conclusion is consistent with that of Wang and Yang [38] and Weng and Yang [24].
The regression coefficients of machinery damage, collision, grounding, fire/explosion, contact, and foundered are all positive, indicating that these types of accidents positively impact the number of fatalities and injuries. The elasticity coefficients of machinery damage are 0.064 and 0.107, respectively, being relatively low for the following reasons: (1) the crew can detect hull damage or mechanical failures early with the help of equipment and hence reserve sufficient time for reaction; (2) ships are equipped with increasingly well-rounded emergency rescue plans, and personnel’s self-rescue abilities are constantly improved. The regression coefficient of collision is positive, with the elasticity coefficients of 1.178 and 1.102, respectively. That is to say, when this type of accident changes by 1%, the number of fatalities and injuries in Areas I and II will change by 1.178% and 1.102%, respectively. This is possibly because that ship collision involves two or more ships, increasing the fatalities and injuries exponentially. In addition, ship collision usually takes a very short period of time, making the crews and passengers have limited time to react or escape, so the probability of fatalities and injuries is high. The elasticity coefficients of grounding are 0.261 and 0.172, respectively, possibly because a grounding accident allows sufficient time for crew members to react, so the impact of grounding on the number of fatalities and injuries is modest. The elasticity coefficients of fire/explosion are 0.201 and 0.225, respectively. Fire/explosion accidents can easily cause rescue difficulties and chaos in escape order, increasing the chance of fatalities and injuries. This conclusion is also manifested in the relevant literature [9,10]. In a serious fire/explosion, people on board have no other option but to jump into the sea with the help of life-saving equipment, but the chance of survival is very small due to the harsh sea environment. The elasticity coefficients of contact are 0.133 and 0.138, respectively. Contact refers to the failure of a ship after it hits overwater or underwater objects. A serious accident of this type may cause foundered or capsizing, so contact greatly impacts fatalities and injuries. The elasticity coefficients of foundered are 0.049 and 0.070. In general, foundering may result in capsize, making it difficult for the crew and passengers to escape quickly. When this type of accident happens, the dangerous marine environment and the lack of professional self-rescue ability of people on board may result in a small chance of survival. Hull damage with a significant impact is seen in Area II only, and its elasticity coefficient is the lowest, at 0.033. The reasons may be as follows: (1) hull damage can generally be detected through personnel inspection and equipment monitoring; and (2) hull damage requires a development period, during which personnel on board can intervene early to reduce the occurrence of such incidents and the resulting fatalities and injuries.
4.3. Result Comparison between Two Accident-Prone Areas and Its Theoretical Implications
Figure 4 shows the absolute values of the elastic coefficients of the ZINB models for the two sea areas.
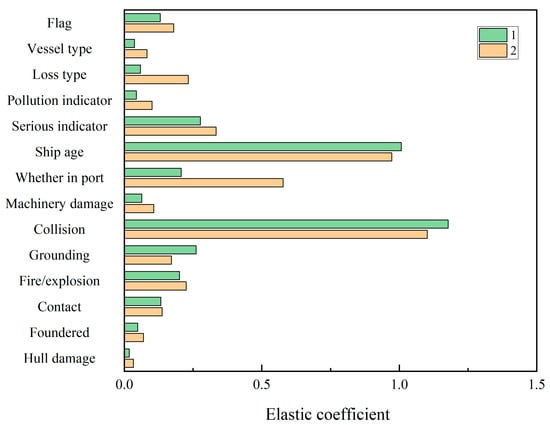
Figure 4.
Absolute values of elasticity coefficients of the zero-inflated negative binomial models represented by a bar chart.
The elasticity coefficients of collision in the two sea areas are the largest, indicating that collision is the primary factor driving fatality and injury outcomes of accidents in both areas. Specifically, the elasticity coefficient of collision in Area I is slightly higher than that of Area II, which may be related to the differences in the number of ships and the geographical environments of the two sea areas. On one hand, Area I is home to the world-famous ports of Antwerp, Rotterdam, Felixstowe, Southampton, etc. As the main passage connecting the Bay of Biscay and the North Sea, the English Channel is narrow and has a high volume of vessel traffic, increasing the possibility of collisions among ships and hence the fatality and injury outcomes caused by collision. On the other hand, the eastern Mediterranean Sea area of Area II is wider and more open, and it therefore has a lower incidence of collision accidents; the Black Sea area of Area II has less busy shipping routes compared to Area I; therefore, it is reasonable that collision is related to a smaller number of fatalities and injuries in Area II.
The elasticity coefficients of ship age are high in both sea areas, indicating that controlling ship age can significantly reduce fatalities and injuries. This conclusion is consistent with that of Wang and Yang [38] and Weng and Yang [24]. The elasticity coefficient in Area I is higher than that in Area II possibly because the geographical environment of Area I is relatively poorer, and the geographical features—more narrow and shallow shoals—of the English Channel make it easier for ships of the same age to have accidents that result in a larger number of fatalities and injuries in Area I.
The absolute value of the elasticity coefficient of whether in port in Area II is much larger than that in Area I, meaning that accidents that occurred far from the port in Area II can lead to greater fatalities and injuries compared with Area I. Total loss of a ship occurs when a ship is unlikely to be saved or recovered, or the sum of rescue, salvage, and repair, among other costs, reaches or exceeds the ship value before the collision or contact occurred. The elasticity coefficient of loss type in Area II is much higher than in Area I. These results may be explained by the following reasons: (1) The eastern Mediterranean Sea area in Area II has a large number of ships and an open space, making it difficult to obtain shore rescue when an accident occurs, particularly when a ship suffers a total loss; and (2) The countries surrounding Area I may have a higher level of risk management and rescue mechanisms for ship accidents.
The elasticity coefficient of fire/explosion in Area II is slightly higher than that in Area I, which is related to the difference in vessel types navigating in the two sea areas. Most of the oil exported from the Middle East to Europe and North America passes through the eastern Mediterranean Sea in Area II, and the number of oil tankers sailing in this area is higher than in Area I. Oil tankers are flammable and explosive compared to other ships, so the fire and explosion accidents in Area II are more likely to cause greater fatalities and injuries. The elasticity coefficient of grounding in Area I is significantly higher than that in Area II, which can be attributed to the geographical differences between the two sea areas: (1) The English Channel in Area I is narrow and has many shoals, which easily causes ship grounding; (2) The eastern Mediterranean Sea and the Black Sea in Area II have open spaces and suitable ocean depths. The elasticity coefficients of Hull damage and machinery damage are small. However, attention should be paid to the hull damage and machinery damage caused by human factors in the actual sailing process to avoid more severe marine perils. Foundered accidents in the two sea areas had a smaller impact on the number of fatalities and injuries, which was different from the conclusion of Weng, Ge and Han [9]. This may be due to the timeliness of shore rescue and the differences in marine governance levels in the surrounding countries.
The elasticity coefficient of the flag in Area II is higher than that in Area I possibly because (1) The eastern Mediterranean Sea in Area II is located on the trunk traffic routes with a great number of ships of various types passing through it, including many FOC ships; (2) The sea area is located in the Bay of Biscay, the English Channel, and the North Sea, and the surrounding countries, such as Britain, France, Spain, Germany, Belgium, the Netherlands, and Norway have all joined the Paris Memorandum of Understanding. As the first cooperation organization for port states to supervise the region, the Paris Memorandum of Understanding is unrivaled among regional memorandums in scale and expertise. Therefore, the port state supervision of Area I is more stringent than that of Area II. Even FOC ships are subject to strict port state supervision in Area I, which ensures the better performance of FOC ships in Area I than in Area II and reduces the fatalities and injuries.
4.4. Implication for Management
Maritime accidents threaten the safety and development of the shipping industry and further impact the safety of the global supply chain. Therefore, the research results can help to analyze the influencing factors of maritime accidents and propose targeted measures to avoid maritime accidents. The results show that ship collision has the greatest impact on fatalities and injuries. Therefore, effectively preventing ship collisions can potentially minimize the fatalities and injuries of maritime accidents. Ship collision can be prevented by optimizing the waterway, identifying the hidden areas of potential ship collisions, and traffic separation schemes, among other measures. Firstly, waterway authorities are expected to regularly manage the waterways to promptly eliminate hidden dangers and optimize the navigation environment of ships. Secondly, relevant countries and organizations in sea areas with high ship traffic (such as the English Channel in Area I) can set up risk-avoiding areas to create a space for ship emergency handling to avoid chain-reaction accidents. Thirdly, for sea areas with dense routes, IMO should revise existing or establish new traffic separation schemes to improve ship navigation efficiency. Fourthly, surrounding countries and regions should establish two-way routes, recommended tracks, etc., to improve ship traffic efficiency and reduce the probability of collision. Fifthly, for accident-prone sea areas, relevant countries and organizations should set up precautionary and safety areas to guide ships. Finally, when it is necessary to make a turn when the ship is sailing at high speed and enough space for operation is available, the operation with a smaller course change should be prioritized Zhou, et al. [54].
Most fire and explosion accidents occur when the ship is sailing and originate in the engine room, followed by the cargo spaces. For such accidents, the fatalities and injuries can be reduced from three aspects: prevention, supervision, and rescue Chen, et al. [55]. Firstly, the crew is expected to keep the machinery in the engine room clean, check all the pipes and fittings regularly, and prevent fuel oil leakage and short circuit of electrical equipment. Smoking and fire should be strictly prohibited in the cargo hold areas in real-time, and the International Maritime Dangerous Goods Code (IMDG) should be strictly adhered to. Secondly, the crew should ensure the normal operation of the engine room fire alarm. For flammable and explosive cargoes, the temperature, humidity, oxygen content, etc., of the cargo compartment should be monitored in real-time through professional equipment. Thirdly, the crew should regularly update the fire-fighting equipment and ensure the clearance of fire-fighting passages. In addition, they should receive regular training to improve their fire-fighting awareness and capability.
For grounding in sea areas with many shoals, relevant authorities are expected to continuously monitor and optimize the existing deep-water routes to meet the draft demand of large ships. Secondly, for ships with different draft conditions, corresponding recommended tracks should be set to meet the sailing needs. Thirdly, the management of ship enterprises should strengthen skillset training and quality training on their crew members to minimize incompliant operation during the voyage and improve crew members’ safety awareness [56]. Fourthly, before a ship sails, the route should be planned according to the ship size [57]. For hull damage, ship loss, and machinery damage, the countries and international organizations that have jurisdiction over the relevant waters should supervise ships, especially passenger ships, in addition to requiring crew members to comply with operation requirements during the sailing process to avoid such accidents. In addition, they should continuously improve the rescue system to enable the prompt rescue of ships in emergencies and reduce fatalities and injuries. As the second biggest influencing factor, ship age greatly affects the fatalities and injuries in an accident. Therefore, relevant authorities should strengthen the supervision of older ships and regularly check the navigational performance, hull structure, and mechanical equipment of such ships. Ships exceeding their service life should be forcibly banned from sailing.
For port, foundered, and flag factors, we can prevent accidents and reduce fatalities and injuries by improving accident rescue, foundered personnel positioning, and fulfillment of the responsibilities of the flag states. (1) The closer to the coast, the fewer fatalities and injuries, which fully reflects the importance of rescue. Therefore, it is necessary to strengthen the supervision over shore vessels and follow up on ships’ navigation statuses in real-time. Meanwhile, countries worldwide should strengthen emergency rescue teams in accident-prone areas so that ships can get rescued at sea and reduce fatalities and injuries as much as possible when they are far away from the coast. (2) For foundered accidents, modern technology should be employed to strengthen high-precision positioning of people on board, enable quick ship locating and help calls for rescue in case of danger, and reduce fatalities and injuries caused by blind spots of search [58]. As a matter of fact, the portable Emergency Position Indicating Radio Beacons (EPIRBs) has been mandatory for ships sailing in A3 areas: SOLAS has required that every ship engaged on voyages beyond Sea Areas A1 and A2, but remaining within Sea Area A3 should be provided with a 406 MHz EPIRB [59]. What’s more, Cospas-Sarsat is best known as the system that detects and locates emergency beacons activates by aircraft, ships and people engaged in recreational activities in remote areas, and then sends these distress alerts to search-and-rescue (SAR) authorities. Between January 2019 and December 2021 the Cospas-Sarsat System assisted in rescuing at least 8675 people [60]. (3) Concerning the impact of the flag factor, the international community should urge the flag states to fulfill their responsibilities as a supervisor, especially the states of flags of convenience. The international legislative framework usually does not cover small ships, so the port states should strengthen the management and inspection of such ships. Alternatively, other means should be adopted to inspect ships that do not fall under the legislative framework [37]. Therefore, FOC states should constantly improve the relevant domestic legal systems, such as the ship registration system and the ship management system, and appropriately improve the safety standards of ships registered in domestic to reduce the fatality and injury outcomes of maritime accidents.
For pollution caused by maritime accidents, it is possible to improve the safety performance of oil tankers, improve oil tanker registration and oil pollution compensation systems, complete the oil spill emergency response mechanisms [61], strengthen crew skillset training and quality training [62], implement full-process monitoring over navigation and operation of oil tankers [63], and improve ship pollution tracking technology [64] to reduce pollution accidents, avoid fatalities and injuries, and ensure the sustainability of supply chains.
5. Conclusions
This study uses maritime accident data obtained from the Lloyd’s List Intelligence to identify accident-prone areas through KDE. It then uses the ZINB regression and elastic analysis to quantitatively analyze and compare the factors affecting the fatality and injury outcomes of maritime accidents in accident-prone areas. The following conclusions are drawn from the study.
The accident-prone areas are identified and two of them are selected, with Area I being the English Channel, the Bay of Biscay, and the North Sea, and Area II being the Black Sea and the eastern Mediterranean Sea. The main factors affecting the number of fatalities and injuries in the two areas include the flag, vessel type, loss type, pollution indicator, serious indicator, ship age, whether in port, machinery damage, collision, grounding, fire/explosion, contact, foundered, and hull damage. Collision and ship age are the factors that show the greatest impacts, whereas hull damage and machinery damage show the least impacts on fatality and injury outcomes of maritime accidents. Specifically, collision and ship age have greater impacts on fatalities and injuries in Area I, whereas whether in port and loss type have greater impacts on the fatalities and injuries in Area II. These differences are primarily attributed to the differences in the natural environment and the governance level in the surrounding countries of the two sea areas. Finally, implications for management are proposed based on the results. Insights obtained from this paper have the potential to guide the reduction of fatalities and injuries in maritime accidents and support maritime risk management.
There are certain limitations in the present study. First, only one source of the accident data was used, which may introduce bias when some accidents are not reported or misreported. Second, there is a limited number of attributes contained in the accident data, making it unable to explore the influence of human and environmental factors on fatality and injury outcomes of maritime accidents. To overcome these limitations, in future work, we intend to: (1) collect more sources of accident data from local, regional and global datasets, compare their differences and establish a reliable methodology for the fusion of data from different sources; and (2) collect human behavior and environment data to improve the understanding of human and environmental factors affecting the number of fatality and injury of maritime accidents. Future work may also look at factors contributing to fatality and injury outcomes of maritime accidents in other regions of the world.
Author Contributions
Conceptualization, Y.Z. (Yang Zhang); data curation, Q.X.; formal analysis, Q.X.; funding acquisition, J.C. and S.F.; investigation, Y.Z. (Yujia Zhai); methodology, Y.Z. (Yang Zhang); resources, H.W.; supervision, J.C.; validation, H.W.; visualization, Y.Z. (Yujia Zhai); writing—original draft, Y.Z. (Yujia Zhai) and Q.X.; writing—review and editing, Y.Z. (Yang Zhang) and S.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Youth Innovation Team of Shaanxi Universities and Shanghai Rising-Star Program, Grant No. 22QC1400600.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the supports from the Youth Innovation Team of Shaanxi Universities and the Shanghai Rising-Star Program (Grant No. 22QC1400600). The authors also acknowledge the anonymous reviewers for their suggestions that improved the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- UNCTAD. Review of Maritime Transport 2021; UNCTAD: Geneva, Switzerland, 2021. [Google Scholar]
- Carbone, V.; Martino, M.D. The changing role of ports in supply-chain management: An empirical analysis. Marit. Policy Manag. 2003, 30, 305–320. [Google Scholar] [CrossRef]
- Yip, T.L. Port traffic risks–A study of accidents in Hong Kong waters. Transp. Res. Part E: Logist. Transp. Rev. 2008, 44, 921–931. [Google Scholar] [CrossRef]
- Talley, W.K.; Jin, D.; Kite-Powell, H. Determinants of the severity of passenger vessel accidents. Marit. Policy Manag. 2006, 33, 173–186. [Google Scholar] [CrossRef]
- Jin, D. The determinants of fishing vessel accident severity. Accid. Anal. Prev. 2014, 66, 1–7. [Google Scholar] [CrossRef]
- Uğurlu, F.; Yıldız, S.; Boran, M.; Uğurlu, Ö.; Wang, J. Analysis of fishing vessel accidents with Bayesian network and Chi-square methods. Ocean. Eng. 2020, 198, 106956. [Google Scholar] [CrossRef]
- Roberts, S.E.; Jaremin, B.; Marlow, P.B. Human and fishing vessel losses in sea accidents in the UK fishing industry from 1948 to 2008. Int. Marit. Health 2010, 62, 143–153. [Google Scholar]
- Yip, T.L.; Jin, D.; Talley, W.K. Determinants of injuries in passenger vessel accidents. Accid. Anal. Prev. 2015, 82, 112–117. [Google Scholar] [CrossRef]
- Weng, J.; Ge, Y.E.; Han, H. Evaluation of shipping accident casualties using zero-inflated negative binomial regression technique. J. Navig. 2016, 69, 433–448. [Google Scholar] [CrossRef]
- Hao, W.; Ya-dong, Y.; Yong, M. Research on the Yangtze River accident casualties using zero-inflated negative binomial regression technique. In Proceedings of the 2016 IEEE International Conference on Intelligent Transportation Engineering (ICITE), Singapore, 20–22 August 2016; pp. 72–75. [Google Scholar]
- Wang, J.; Zhou, Y.; Zhuang, L.; Shi, L.; Zhang, S. Study on the critical factors and hot spots of crude oil tanker accidents. Ocean. Coast. Manag. 2022, 217, 106010. [Google Scholar] [CrossRef]
- Weng, J.; Yang, D.; Qian, T.; Huang, Z. Combining zero-inflated negative binomial regression with MLRT techniques: An approach to evaluating shipping accident casualties. Ocean. Eng. 2018, 166, 135–144. [Google Scholar] [CrossRef]
- Wang, L.; Huang, R.; Shi, W.; Zhang, C. Domino effect in marine accidents: Evidence from temporal association rules. Transp. Policy 2021, 103, 236–244. [Google Scholar] [CrossRef]
- Weng, J.; Li, G. Exploring shipping accident contributory factors using association rules. J. Transp. Saf. Secur. 2019, 11, 36–57. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Wang, X.; Huang, D.; Cao, L.; Wang, J. Analysis of the injury-severity outcomes of maritime accidents using a zero-inflated ordered probit model. Ocean. Eng. 2022, 258, 111796. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, L.; Shu, Y.; Zhu, W. Evaluation model and management strategy for reducing pollution caused by ship collision in coastal waters. Ocean. Coast. Manag. 2021, 203, 105446. [Google Scholar] [CrossRef]
- Kamal, B.; Kutay, Ş. Assessment of causal mechanism of ship bunkering oil pollution. Ocean. Coast. Manag. 2021, 215, 105939. [Google Scholar] [CrossRef]
- Khan, R.U.; Yin, J.; Mustafa, F.S.; Anning, N. Risk assessment for berthing of hazardous cargo vessels using Bayesian networks. Ocean. Coast. Manag. 2021, 210, 105673. [Google Scholar] [CrossRef]
- Li, H.; Ren, X.; Yang, Z. Data-driven Bayesian network for risk analysis of global maritime accidents. Reliab. Eng. Syst. Saf. 2022, 230, 108938. [Google Scholar] [CrossRef]
- Liu, K.; Yu, Q.; Yuan, Z.; Yang, Z.; Shu, Y. A systematic analysis for maritime accidents causation in Chinese coastal waters using machine learning approaches. Ocean. Coast. Manag. 2021, 213, 105859. [Google Scholar] [CrossRef]
- Zhang, J.; Teixeira, Â.P.; Guedes Soares, C.; Yan, X.; Liu, K. Maritime transportation risk assessment of Tianjin Port with Bayesian belief networks. Risk Anal. 2016, 36, 1171–1187. [Google Scholar] [CrossRef]
- Çakir, E. Determinants of medical evacuations from merchant cargo ships: Evidence from Telemedical Assistance Service of Turkey data. Ocean. Coast. Manag. 2021, 211, 105797. [Google Scholar] [CrossRef]
- Chen, J.; Bian, W.; Wan, Z.; Wang, S.; Zheng, H.; Cheng, C. Factor assessment of marine casualties caused by total loss. Int. J. Disaster Risk Reduct. 2020, 47, 101560. [Google Scholar] [CrossRef]
- Weng, J.; Yang, D. Investigation of shipping accident injury severity and mortality. Accid. Anal. Prev. 2015, 76, 92–101. [Google Scholar] [CrossRef] [PubMed]
- Weng, J.; Yang, D.; Chai, T.; Fu, S. Investigation of occurrence likelihood of human errors in shipping operations. Ocean. Eng. 2019, 182, 28–37. [Google Scholar] [CrossRef]
- Ridout, M.; Hinde, J.; Demétrio, C.G. A score test for testing a zero—Inflated Poisson regression model against zero—Inflated negative binomial alternatives. Biometrics 2001, 57, 219–223. [Google Scholar] [CrossRef]
- Huang, D.-Z.; Hu, H.; Li, Y.-Z. Spatial analysis of maritime accidents using the geographic information system. Transp. Res. Rec. 2013, 2326, 39–44. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, X.; Chen, J.; Cheng, C. Spatial patterns and characteristics of global maritime accidents. Reliab. Eng. Syst. Saf. 2021, 206, 107310. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Liu, Z.; Wang, X.; Wang, J. GIS-based analysis on the spatial patterns of global maritime accidents. Ocean. Eng. 2022, 245, 110569. [Google Scholar] [CrossRef]
- van Westrenen, F.; Ellerbroek, J. The effect of traffic complexity on the development of near misses on the North Sea. IEEE Trans. Syst. Man Cybern. Syst. 2015, 47, 432–440. [Google Scholar] [CrossRef]
- MacDuff, T. The probability of vessel collisions. Ocean. Ind. 1974, 9, 144–148. [Google Scholar]
- Soussi, A.; Bersani, C.; Sacile, R.; Bouchta, D.; El Amarti, A.; Seghiouer, H.; Nachite, D.; Al Miys, J. Coastal risk modelling for oil spill in the Mediterranean Sea. Context 2020, 10, 25. [Google Scholar] [CrossRef]
- Otay, E.N.; Özkan, S. Stochastic Prediction of Maritime Accidents in the strait of Istanbul. In Proceedings of the 3rd International Conference on Oil Spills in the Mediterranean and Black Sea Regions, Istanbul, Turkey, 1 September 2003; pp. 92–104. [Google Scholar]
- ITF. International Transport Workers’ Federation. Available online: https://www.itfseafarers.org/foc-registries.cfm (accessed on 1 November 2022).
- Chen, J.; Zhang, W.; Li, S.; Zhang, F.; Zhu, Y.; Huang, X. Identifying critical factors of oil spill in the tanker shipping industry worldwide. J. Clean. Prod. 2018, 180, 1–10. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Wang, X.; Graham, T.; Wang, J. An analysis of factors affecting the severity of marine accidents. Reliab. Eng. Syst. Saf. 2021, 210, 107513. [Google Scholar] [CrossRef]
- Chen, J.; Bian, W.; Wan, Z.; Yang, Z.; Zheng, H.; Wang, P. Identifying factors influencing total-loss marine accidents in the world: Analysis and evaluation based on ship types and sea regions. Ocean. Eng. 2019, 191, 106495. [Google Scholar] [CrossRef]
- Wang, L.; Yang, Z. Bayesian network modelling and analysis of accident severity in waterborne transportation: A case study in China. Reliab. Eng. Syst. Saf. 2018, 180, 277–289. [Google Scholar] [CrossRef]
- Li, K.X.; Yin, J.; Fan, L. Ship safety index. Transp. Res. Part A Policy Pract. 2014, 66, 75–87. [Google Scholar] [CrossRef]
- Li, G.; Weng, J.; Wu, B.; Hou, Z. Incorporating multi-scenario underreporting rates into MICE for underreported maritime accident record analysis. Ocean. Eng. 2022, 246, 110620. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, F.; Yang, C.; Zhang, C.; Luo, L. Factor and trend analysis of total-loss marine casualty using a fuzzy matter element method. Int. J. Disaster Risk Reduct. 2017, 24, 383–390. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Y.; Zhang, S.; Zhuang, L.; Shi, L.; Chen, J.; Hu, D. Societal risk acceptance criteria of the global general cargo ships. Ocean. Eng. 2022, 261, 112162. [Google Scholar] [CrossRef]
- Fu, S.; Yu, Y.; Chen, J.; Han, B.; Wu, Z. Towards a probabilistic approach for risk analysis of nuclear-powered icebreakers using FMEA and FRAM. Ocean. Eng. 2022, 260, 112041. [Google Scholar] [CrossRef]
- Zhang, J.; Teixeira, Â.P.; Soares, C.G.; Yan, X. Quantitative assessment of collision risk influence factors in the Tianjin port. Saf. Sci. 2018, 110, 363–371. [Google Scholar] [CrossRef]
- Zhang, D.; Yan, X.; Yang, Z.L.; Wall, A.; Wang, J. Incorporation of formal safety assessment and Bayesian network in navigational risk estimation of the Yangtze River. Reliab. Eng. Syst. Saf. 2013, 118, 93–105. [Google Scholar] [CrossRef]
- Knapp, S.; Bijwaard, G.; Heij, C. Estimated incident cost savings in shipping due to inspections. Accid. Anal. Prev. 2011, 43, 1532–1539. [Google Scholar] [CrossRef] [PubMed]
- Balmat, J.-F.; Lafont, F.; Maifret, R.; Pessel, N. MAritime RISk Assessment (MARISA), a fuzzy approach to define an individual ship risk factor. Ocean. Eng. 2009, 36, 1278–1286. [Google Scholar] [CrossRef]
- Jones, M.C.; Marron, J.S.; Sheather, S.J. A brief survey of bandwidth selection for density estimation. J. Am. Stat. Assoc. 1996, 91, 401–407. [Google Scholar] [CrossRef]
- Park, B.U.; Marron, J.S. Comparison of data-driven bandwidth selectors. J. Am. Stat. Assoc. 1990, 85, 66–72. [Google Scholar] [CrossRef]
- Nicholson, A. Analysis of spatial distributions of accidents. Saf. Sci. 1998, 31, 71–91. [Google Scholar] [CrossRef]
- Dobbins, J.P.; Jenkins, L.M. Geographic information systems for estimating coastal maritime risk. Transp. Res. Rec. 2011, 2222, 17–24. [Google Scholar] [CrossRef]
- Ugurlu, O.; Yildirim, U.; Yuksekyildiz, E. Marine accident analysis with GIS. J. Shipp. Ocean. Eng. 2013, 3, 21. [Google Scholar]
- Zeileis, A.; Kleiber, C.; Jackman, S. Regression models for count data in R. J. Stat. Softw. 2008, 27, 1–25. [Google Scholar] [CrossRef]
- Zhou, K.; Chen, J.; Liu, X. Optimal collision-avoidance manoeuvres to minimise bunker consumption under the two-ship crossing situation. J. Navig. 2018, 71, 151–168. [Google Scholar] [CrossRef]
- Chen, J.; Zheng, H.; Wei, L.; Wan, Z.; Ren, R.; Li, J.; Li, H.; Bian, W.; Gao, M.; Bai, Y. Factor diagnosis and future governance of dangerous goods accidents in China’s ports. Env. Pollut. 2020, 257, 113582. [Google Scholar] [CrossRef] [PubMed]
- Fu, S.; Yu, Y.; Chen, J.; Xi, Y.; Zhang, M. A framework for quantitative analysis of the causation of grounding accidents in arctic shipping. Reliab. Eng. Syst. Saf. 2022, 226, 108706. [Google Scholar] [CrossRef]
- Ma, X.; Deng, W.; Qiao, W.; Lan, H. A methodology to quantify the risk propagation of hazardous events for ship grounding accidents based on directed CN. Reliab. Eng. Syst. Saf. 2022, 221, 108334. [Google Scholar] [CrossRef]
- Kum, S.; Sahin, B. A root cause analysis for Arctic Marine accidents from 1993 to 2011. Saf. Sci. 2015, 74, 206–220. [Google Scholar] [CrossRef]
- Harmonization of GMDSS Requirements for Radio Installations on Board SOLAS Ships; IMO: London, UK, 2004.
- C/S. Cospas-Sarsat System Data No 46; COSPAS-SARSAT: Montreal, QC, Canada, 2020. [Google Scholar]
- Zhang, W.; Li, C.; Chen, J.; Wan, Z.; Shu, Y.; Song, L.; Xu, L.; Di, Z. Governance of global vessel-source marine oil spills: Characteristics and refreshed strategies. Ocean. Coast. Manag. 2021, 213, 105874. [Google Scholar] [CrossRef]
- Chen, J.; Di, Z.; Shi, J.; Shu, Y.; Wan, Z.; Song, L.; Zhang, W. Marine oil spill pollution causes and governance: A case study of Sanchi tanker collision and explosion. J. Clean. Prod. 2020, 273, 122978. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, W.; Wan, Z.; Li, S.; Huang, T.; Fei, Y. Oil spills from global tankers: Status review and future governance. J. Clean. Prod. 2019, 227, 20–32. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, W.; Han, J.; Li, Y. Tracing illegal oil discharges from vessels using SAR and AIS in Bohai Sea of China. Ocean. Coast. Manag. 2021, 211, 105783. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).