On Sea-Level Change in Coastal Areas
Abstract
1. Introduction
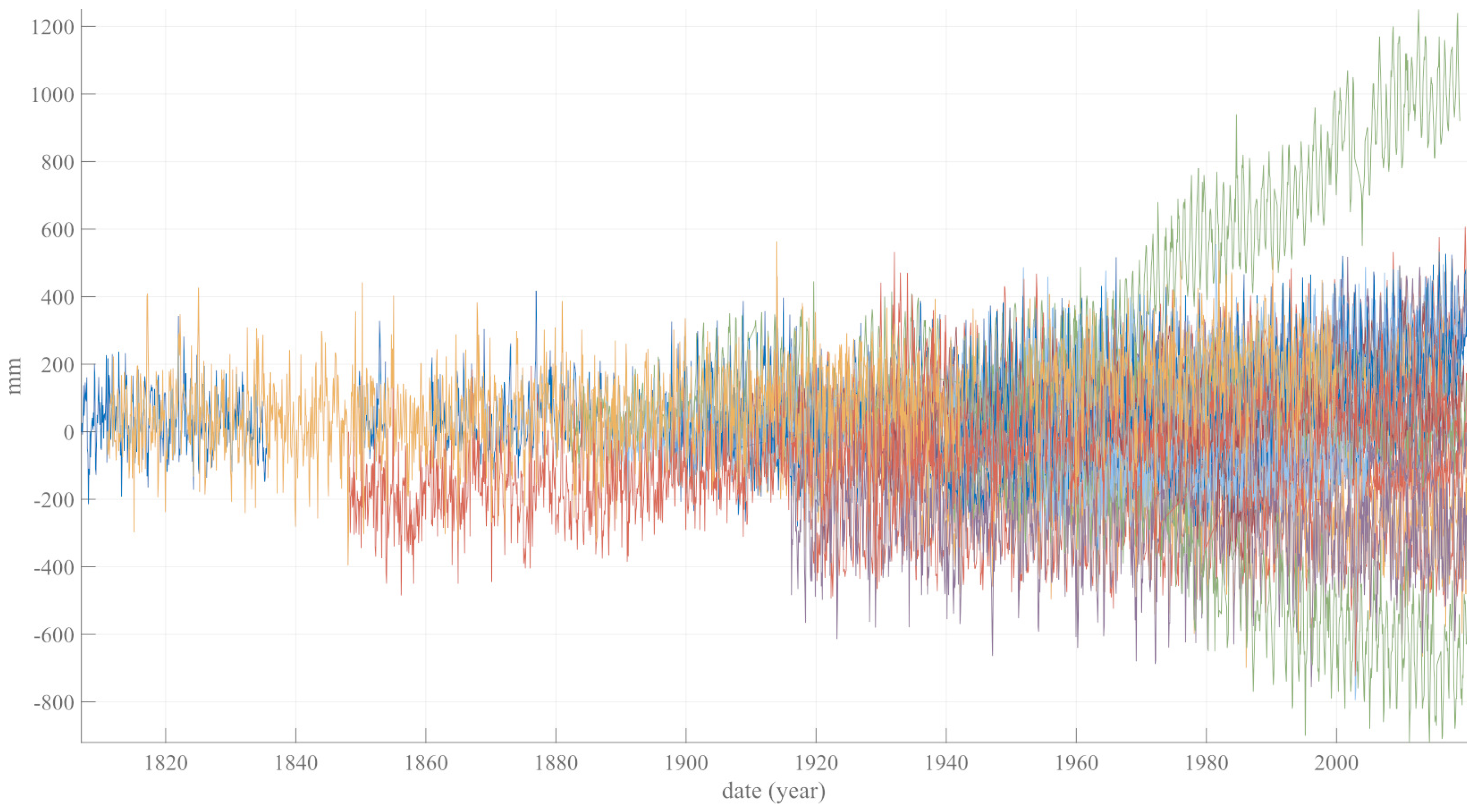
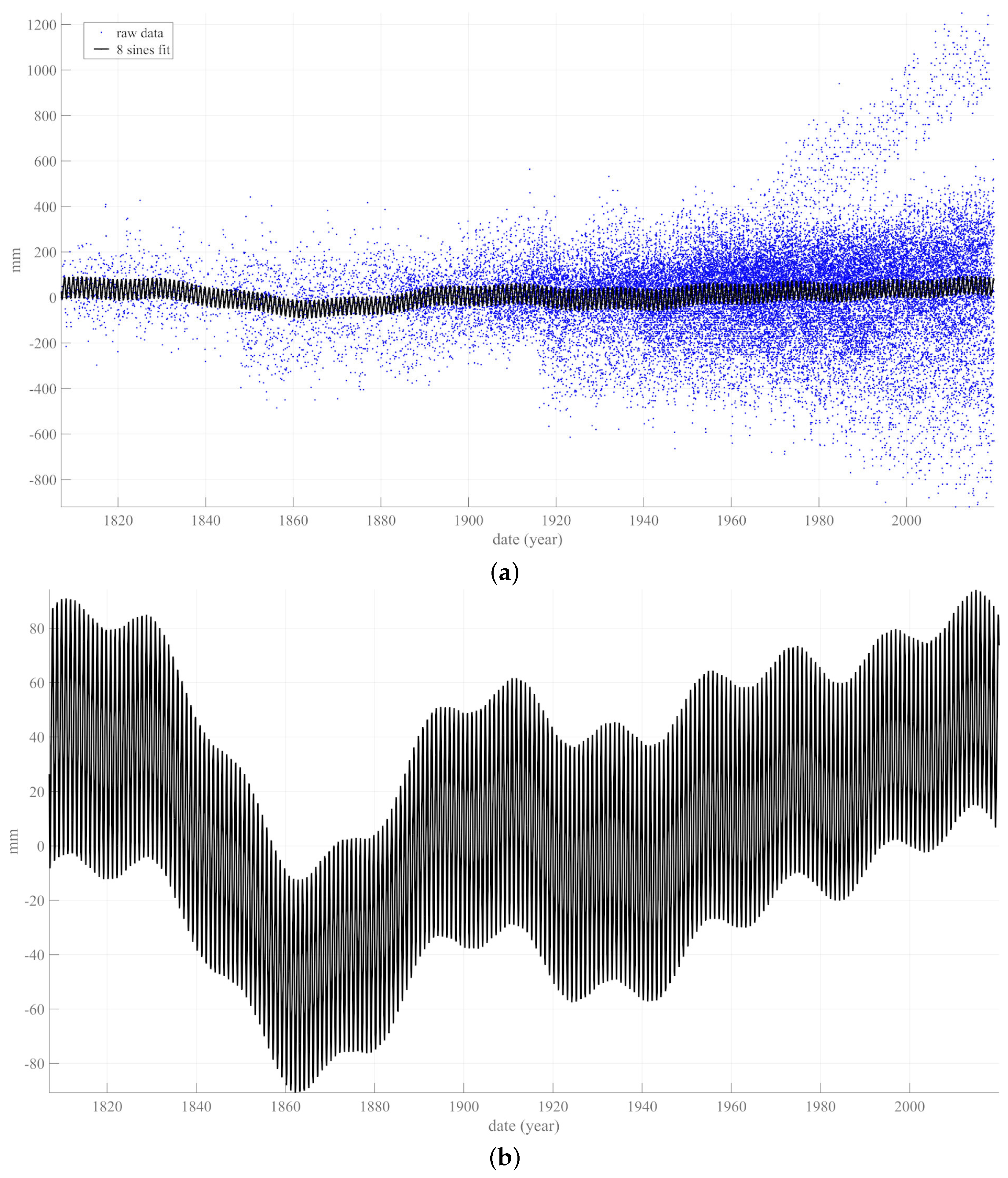
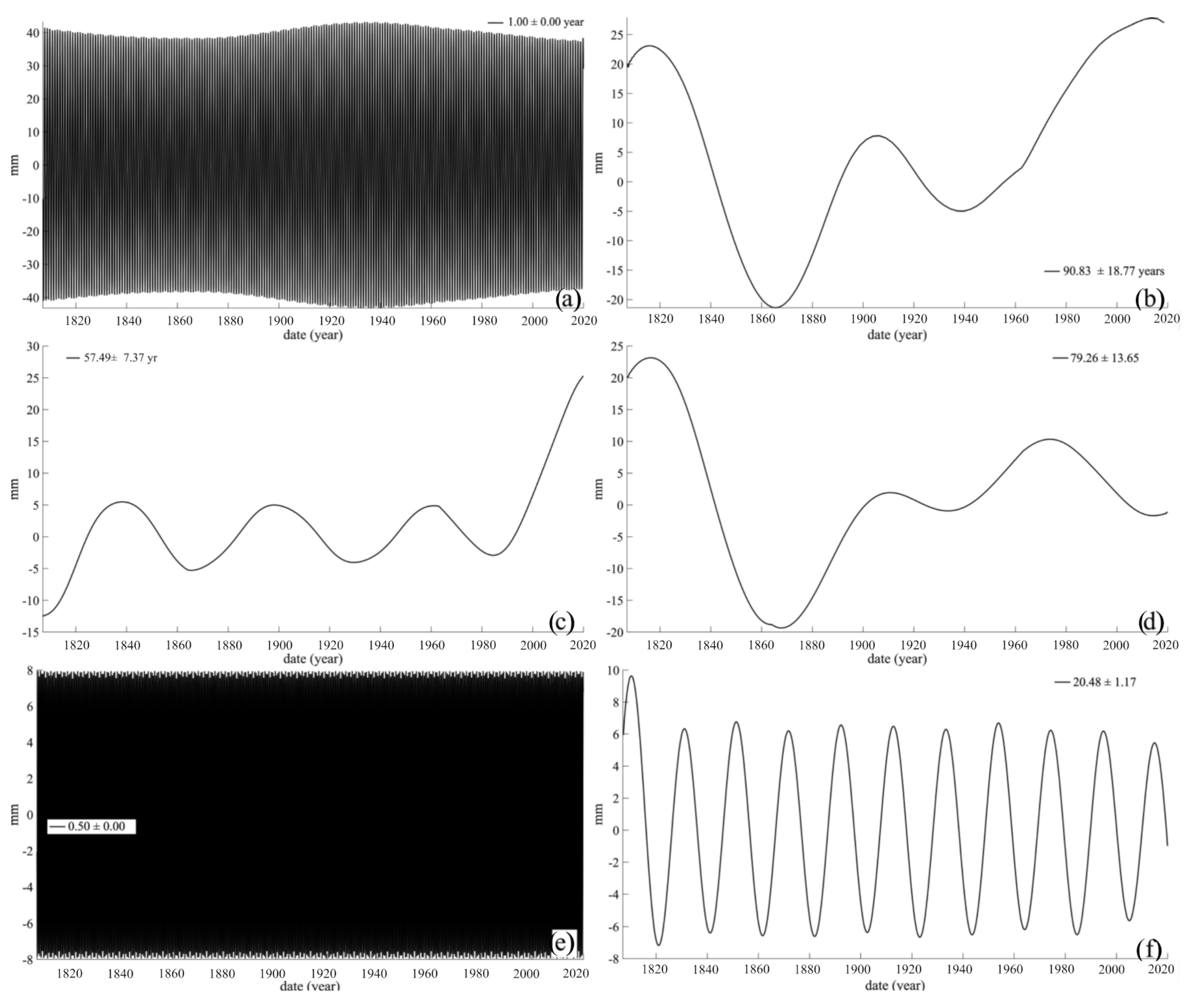
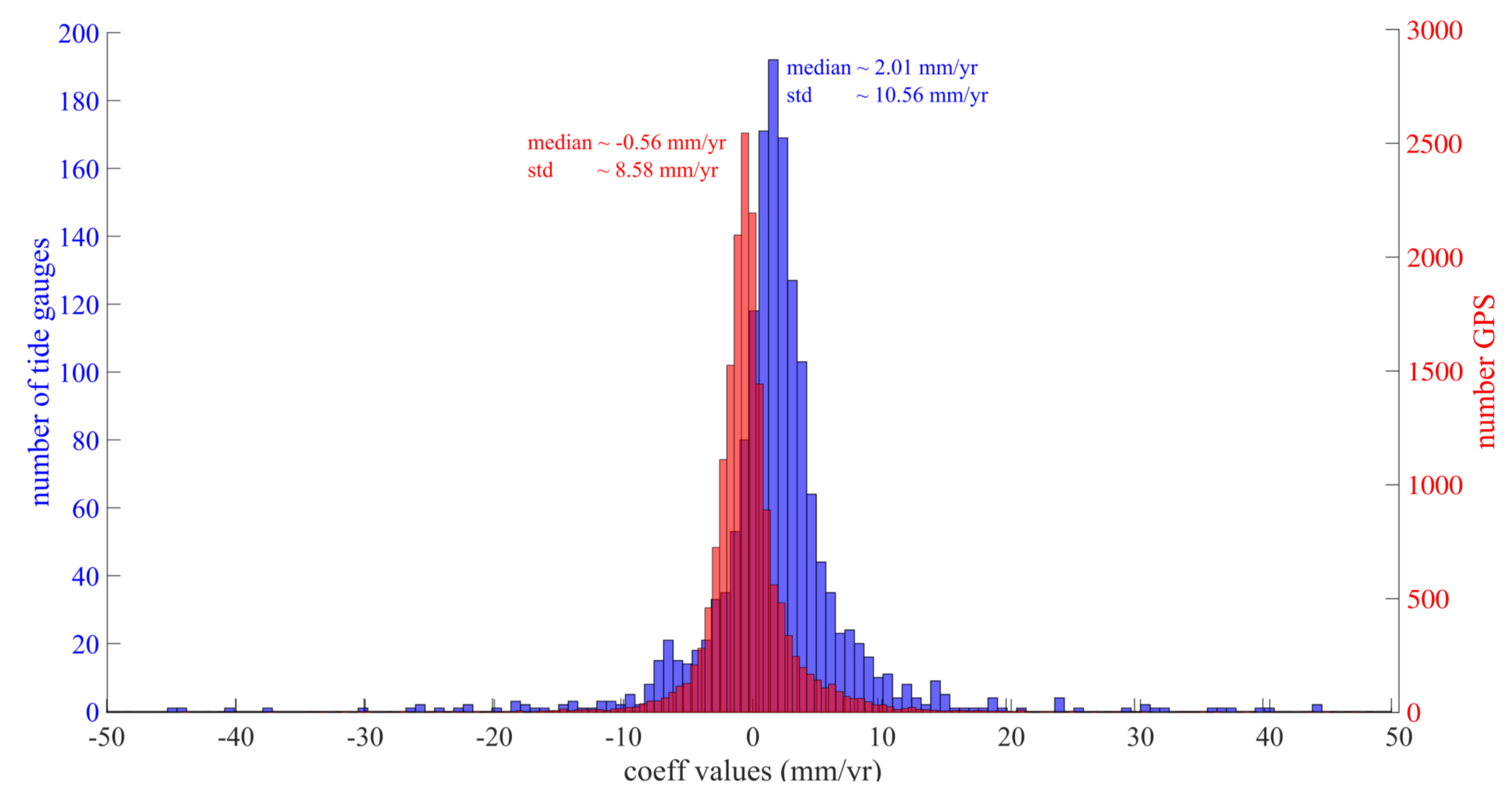
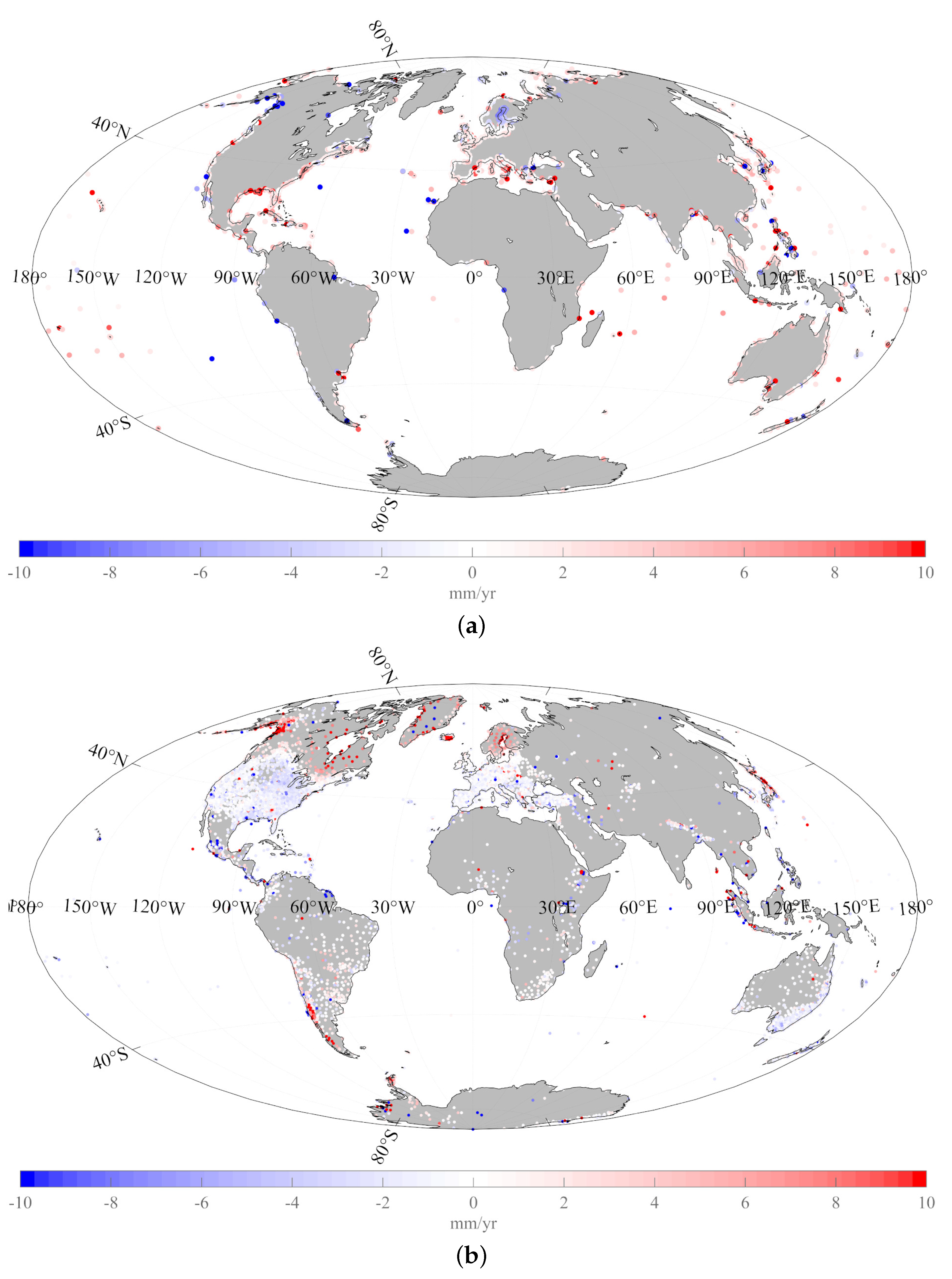
2. SSA of Tide Gauge Records Time Series (i.e.,
3. Introducing the GPS Vertical Land Motion Time Series (the
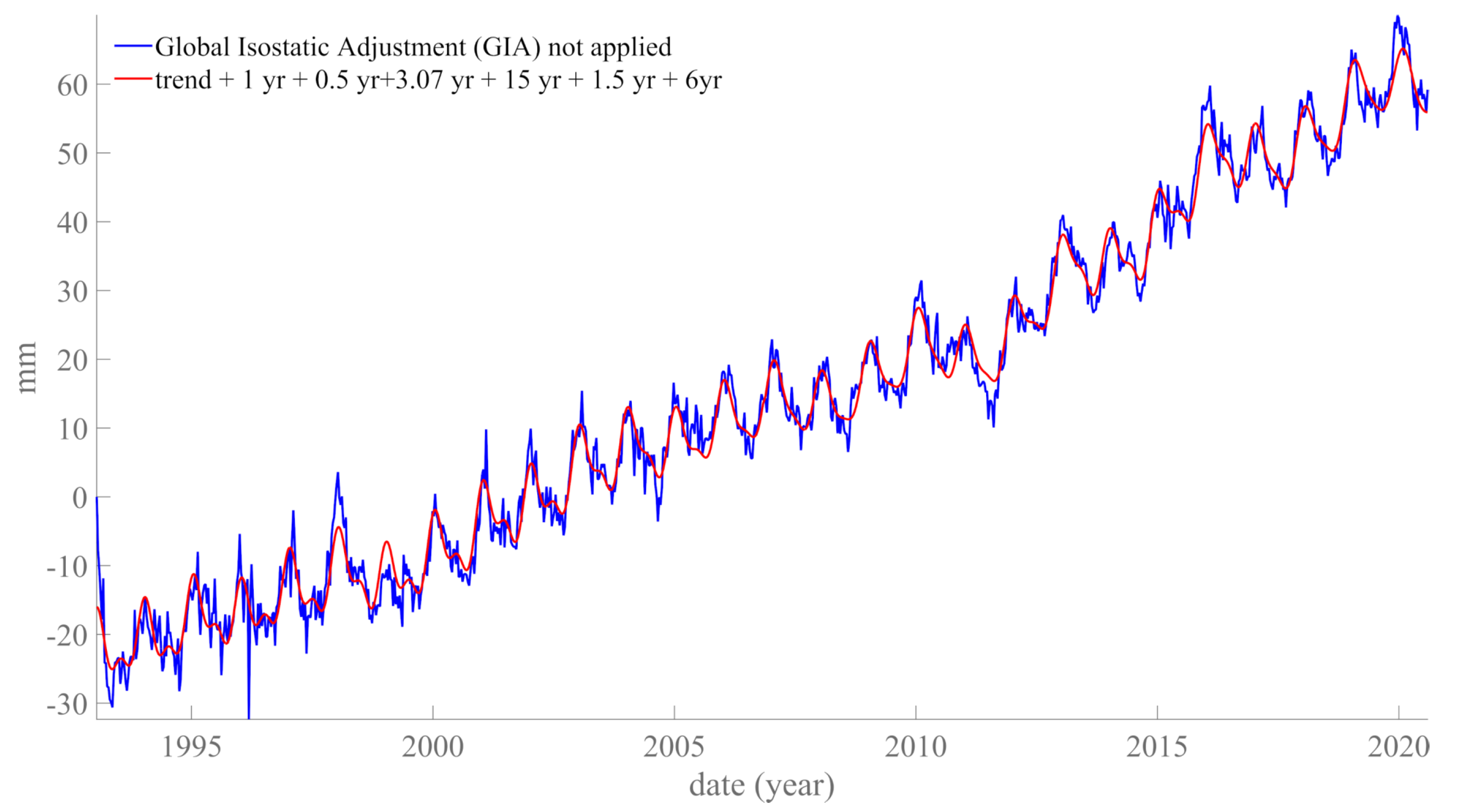
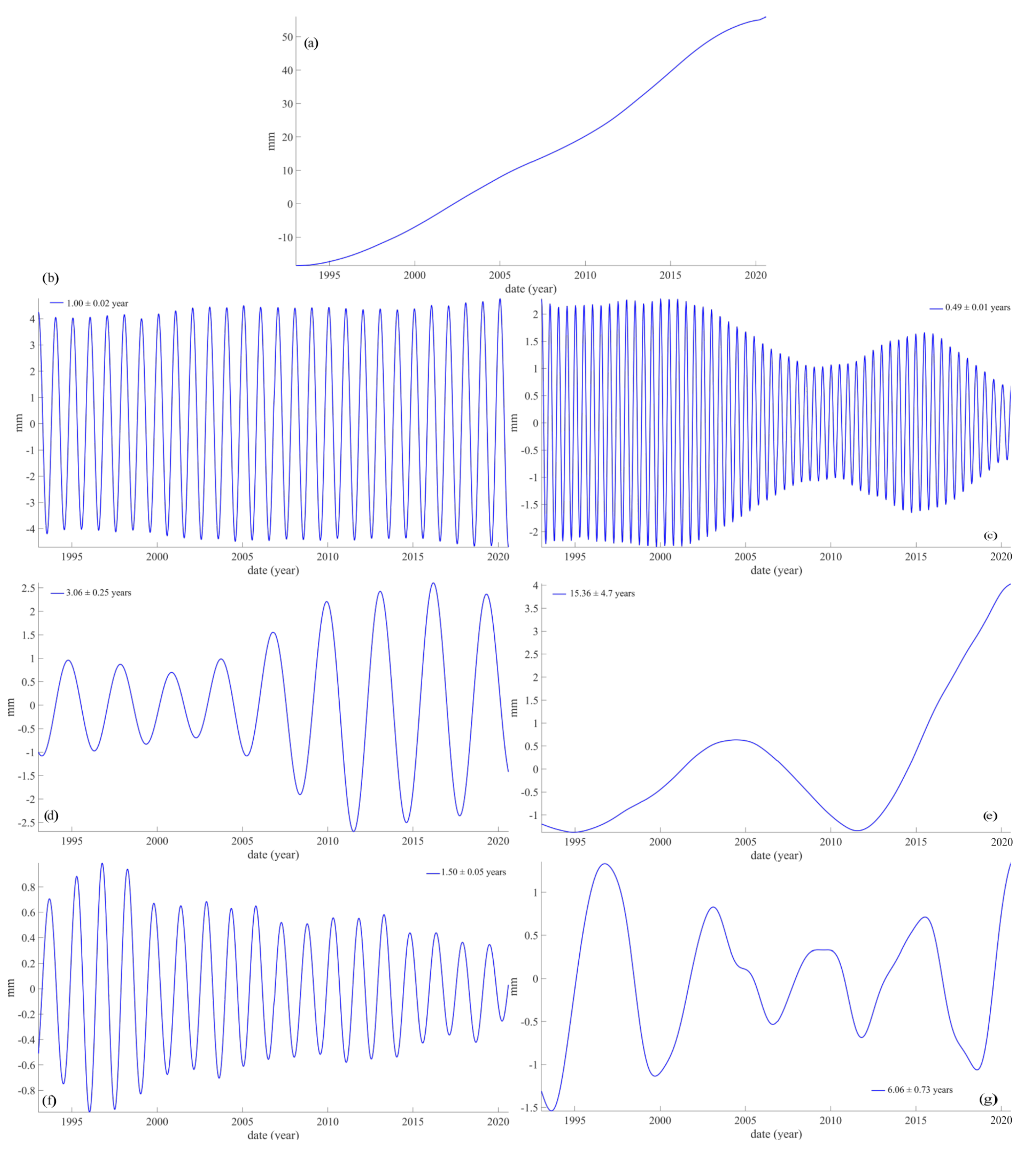
4. SSA of GSL Curves Obtained with Inclusion of Satellite Data
5. Discussion
5.1. Components Shared by GSLl, GSLTG and SSN
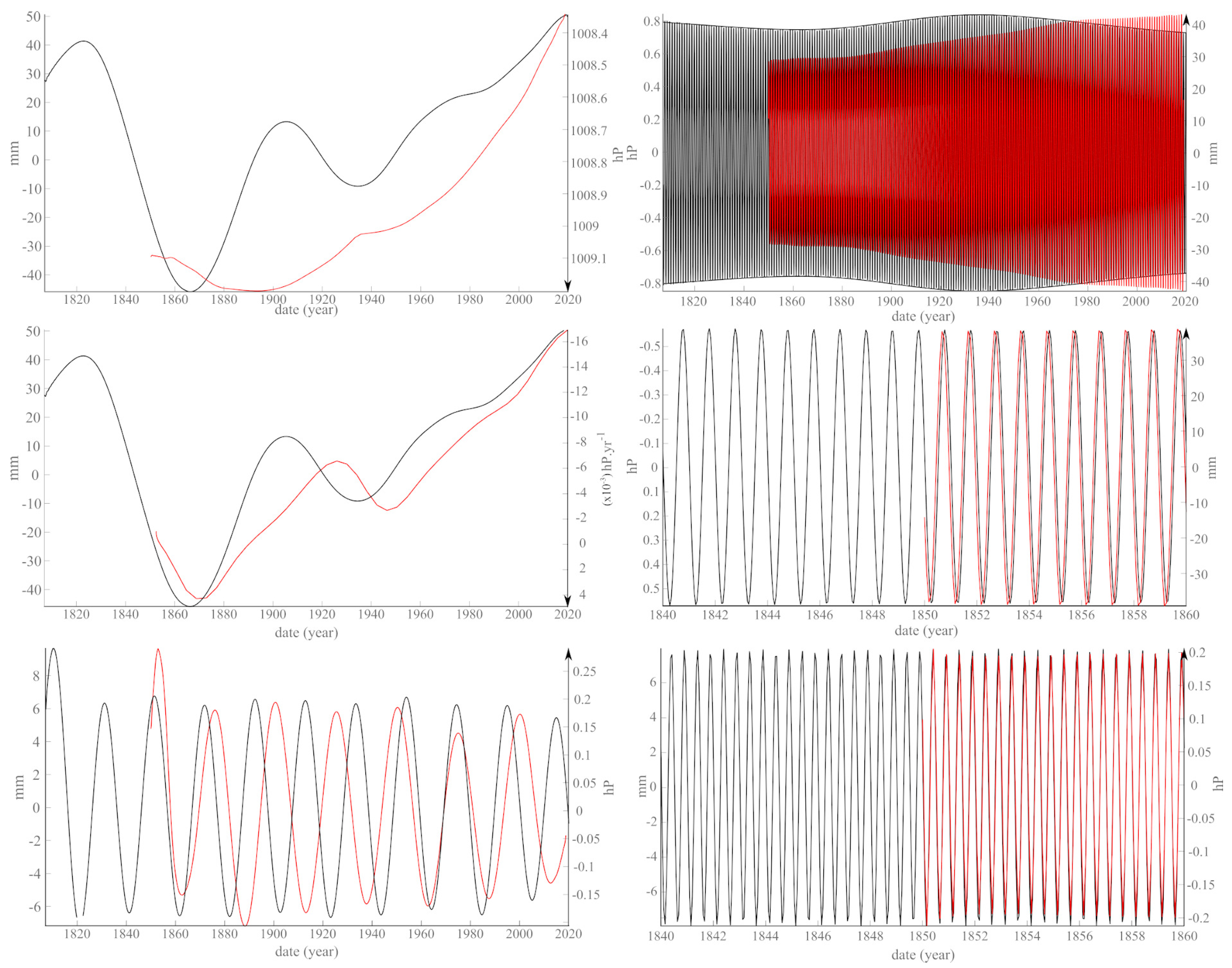
5.2. Comparison with Global Pressure GP
5.3. Comparison with the Mean Motion of the Rotation Pole (RP)
5.4. The Liouville–Euler System and Solar Components in Sea Level
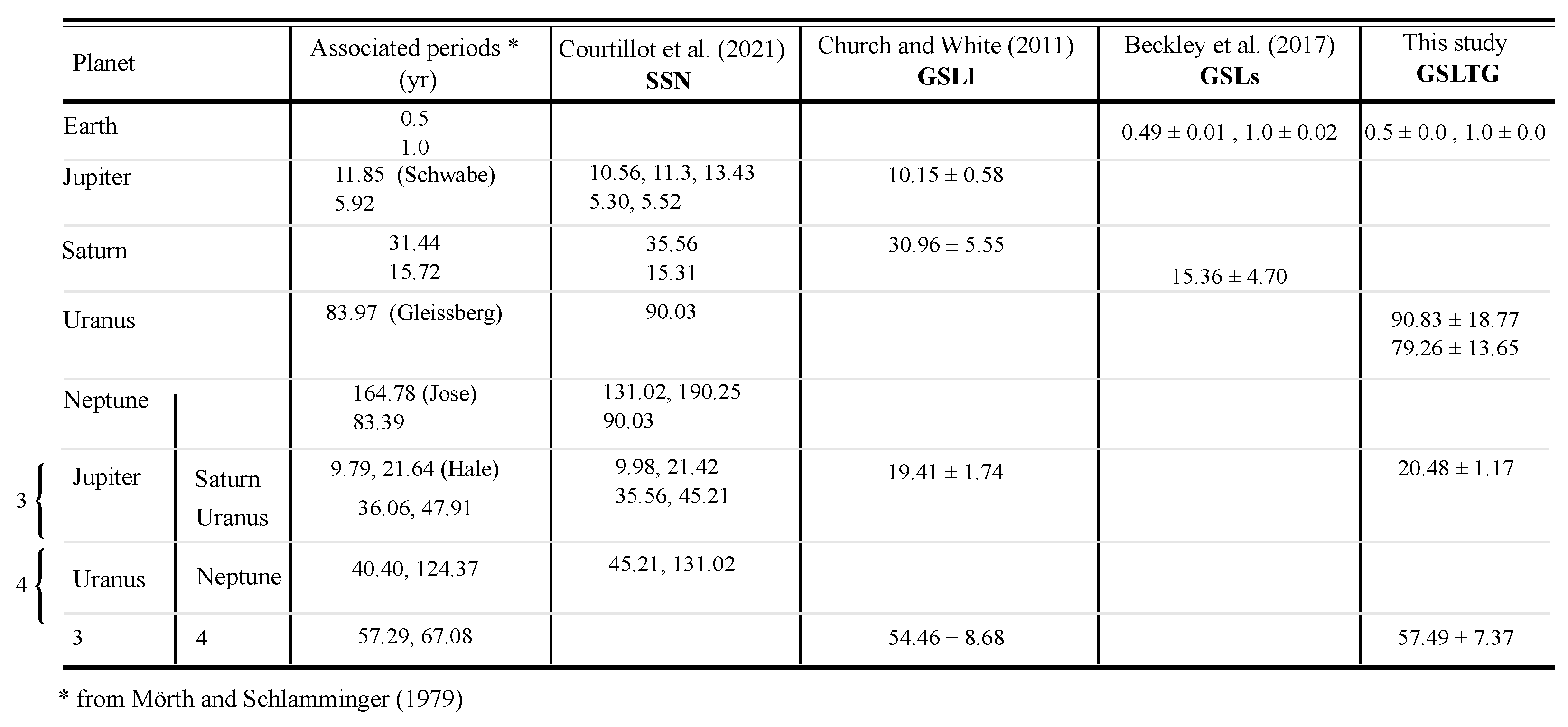
5.5. Planetary Forcings
6. Summary and Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Farrell, W.E.; Clark, J.A. On post glacial sea level. Geophys. J. Int. 1976, 46, 647–667. [Google Scholar] [CrossRef]
- Wu, P.; Peltier, W.R. Glacial isostatic adjustment and the free air gravity anomaly as a constraint on deep mantle viscosity. Geophys. J. Int. 1983, 74, 377–449. [Google Scholar] [CrossRef]
- Mitrovica, J.X.; Milne, G.A. On post-glacial sea level: I.General theory. Geophys. J. Int. 2003, 154, 253–267. [Google Scholar] [CrossRef]
- Spada, G.; Stocchi, P. The Sea Level Equation, Theory and Numerical Examples; Aracne online edition 2006; Aracne Editrice: Roma, Italy, 2006; pp. 1–96. ISBN 10 8854803847. [Google Scholar]
- Spada, G.; Stocchi, P. SELEN: A Fortran 90 program for solving the sea-level equation. Comput. Geosci. 2007, 33, 538–562. [Google Scholar] [CrossRef]
- Spada, G.; Melini, D.; Galassi, G.; Colleoni, F. Modeling sea level changes and geodetic variations by glacial isostasy: The improved SELEN code. arXiv 2012, arXiv:1212.5061. [Google Scholar] [CrossRef]
- Blewitt, G.; Kreemer, C.; Hammond, W.C.; Gazeaux, J. MIDAS robust trend estimator for accurate GPS station velocities without step detection. J. Geophys. Res. Solid Earth 2016, 121, 2054–2068. [Google Scholar] [CrossRef]
- Hammond, W.C.; Blewitt, G.; Kreemer, C.; Nerem, R.S. GPS Imaging of Global Vertical Land Motion for Studies of Sea Level Rise. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022355. [Google Scholar] [CrossRef]
- Lambeck, K. The Earth’s Variable Rotation: Geophysical Causes and Consequences; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Laplace, P.S. Traité de méCanique céLeste; de l’Imprimerie de; Crapelet: Paris, France, 1799. [Google Scholar]
- Nomitsu, T.; Okamoto, M. The causes of the annual variation of the mean sea level along the Japanese coast. Mem. Coll. Sci. Kyoto Imp. Univ. Ser. 1927, 10, 125–161. [Google Scholar]
- Marmer, H.A. Tidal Datum Planes; US Government Printing Office: Washington, DC, USA, 1927; p. 135.
- Jacobs, W.C. Sea level departures on the California coast as related to the dynamics of the atmosphere over the North Pacific Ocean. J. Mar. Res. 1939, 2, 181–194. [Google Scholar] [CrossRef]
- LaFond, E.C. Variations of sea level on the Pacific coast of the United States. J. Mar. Res. 1939, 2, 17–29. [Google Scholar] [CrossRef]
- McEwen, G.F. Some Energy Relations between the Sea Surface and the Atmosphere; Yale Univ: New Haven, CT, USA, 1937. [Google Scholar]
- Peltier, W.R.; Andrews, J.T. Glacial-isostatic adjustment—I, The forward problem. Geophys. J. Int. 1976, 46, 605–646. [Google Scholar] [CrossRef]
- Nakiboglu, S.M.; Lambeck, K. Deglaciation effects on the rotation of the Earth. Geophys. J. Int. 1980, 62, 49–58. [Google Scholar] [CrossRef]
- Etkins, R.; Epstein, E.S. The rise of global mean sea level as an indication of climate change. Science 1982, 215, 287–289. [Google Scholar] [CrossRef]
- Gornitz, V.; Lebedeff, S.; Hansen, J. Global sea level trend in the past century. Science 1982, 215, 1611–1614. [Google Scholar] [CrossRef]
- Lambeck, K.; Nakiboglu, S.M. Recent global changes in sealevel. Geophys. Res. Lett. 1984, 11, 959–961. [Google Scholar] [CrossRef]
- Meier, M.F. Contribution of small glaciers to global sea level. Science 1984, 226, 1418–1421. [Google Scholar] [CrossRef]
- Peltier, W.R.; Tushingham, A.M. Global sea level rise and the greenhouse effect: Might they be connected? Science 1989, 244, 806–810. [Google Scholar] [CrossRef] [PubMed]
- Douglas, B.C. Global sea level rise. J. Geophys. Res. Oceans 1991, 96, 6981–6992. [Google Scholar] [CrossRef]
- Douglas, B.C. Global sea level acceleration. J. Geophys. Res. Oceans 1992, 97, 12699–12706. [Google Scholar] [CrossRef]
- Douglas, B.C. Global sea rise: A redetermination. Surv. Geophys. 1997, 18, 279–292. [Google Scholar] [CrossRef]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V. Sea-Level Change at the Brest (France) Tide Gauge and the Markowitz Component of Earth’s Rotation. J. Coast. Res. 2021, 37, 683–690. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J. Sea-level rise from the late 19th to the early 21st century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef]
- Golyandina, N.; Zhigljavsky, A. Singular Spectrum Analysis for Time Series; Springer: Berlin/Heidelberg, Germany, 2013; p. 120. [Google Scholar]
- Lemmerling, P.; Van Huffel, S. Analysis of the structured total least squares problem for Hankel/Toeplitz matrices. Numer. Algorithms 2001, 27, 89–114. [Google Scholar] [CrossRef]
- Golub, G.H.; Reinsch, C. Singular value decomposition and least squares solutions. In Linear Algebra; Springer: Berlin/Heidelberg, Germany, 1971; pp. 134–151. [Google Scholar]
- Lopes, F.; Le Mouël, J.L.; Gibert, D. The mantle rotation pole position. A solar component. Comptes Rendus Geosci. 2017, 349, 159–164. [Google Scholar] [CrossRef]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V. Characteristic time scales of decadal to centennial changes in global surface temperatures over the past 150 years. Earth Space Sci. 2020, 7, e2019EA000671. [Google Scholar] [CrossRef]
- Gleissberg, W. A table of secular variations of the solar cycle. Terr. Magn. Atmos. Electr. 1944, 49, 243–244. [Google Scholar] [CrossRef]
- Jose, P.D. Sun’s motion and sunspots. Astron. J. 1965, 70, 193–200. [Google Scholar] [CrossRef]
- Coles, W.A.; Rickett, B.J.; Rumsey, V.H.; Kaufman, J.J.; Turley, D.G.; Ananthakrishnan, S.A.; Armstrong, J.W.; Harmons, K.; Scott, S.L.; Sime, D.G. Solar cycle changes in the polar solar wind. Nature 1980, 286, 239–241. [Google Scholar] [CrossRef]
- Charvatova, I.; Strestik, J. Long-term variations in duration of solar cycles. Bull. Astron. Inst. Czechoslov. 1991, 42, 90–97. [Google Scholar]
- Usoskin, I.G. A history of solar activity over millennia. Living Rev. Sol. Phys. 2017, 14, 3. [Google Scholar] [CrossRef]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V. Solar turbulence from sunspot records. Mon. Notices R. Astron. Soc. 2020, 492, 1416–1420. [Google Scholar] [CrossRef]
- Courtillot, V.; Lopes, F.; Le Mouël, J.L. On the prediction of solar cycles. Sol. Phys. 2021, 296, 1–23. [Google Scholar] [CrossRef]
- Wood, C.A.; Lovett, R.R. Rainfall, drought and the solar cycle. Nature 1974, 251, 594–596. [Google Scholar] [CrossRef]
- Mörth, H.T.; Schlamminger, L. “Planetary Motion, Sunspots and Climate”, Solar-Terrestrial Influences on Weather and Climate; Springer: Dordrecht, The Nederland, 1979; pp. 193–207. [Google Scholar]
- Schlesinger, M.E.; Ramankutty, N. An oscillation in the global climate system of period 65–70 years. Nature 1994, 367, 723–726. [Google Scholar] [CrossRef]
- Lau, K.M.; Weng, H. Climate signal detection using wavelet transform: How to maketime series sing, Bull. Am. Meteorol. Soc. 1995, 76, 2391–2402. [Google Scholar] [CrossRef]
- Scafetta, N. Empirical evidence for a celestial origin of the climate oscillations and its implications. J. Atmos. Sol. Terr. Phys. 2010, 72, 951–970. [Google Scholar] [CrossRef]
- Courtillot, V.; Le Mouël, J.L.; Kossobokov, V.; Gibert, G.; Lopes, F. Multi-Decadal Trends of Global Surface Temperature: A Broken Line with Alternating 30 yr Linear Segments? NPJ Clim. Atmos. Sci. 2013, 3, 34080. [Google Scholar] [CrossRef]
- Scafetta, N. High resolution coherence analysis between planetary and climate oscillations. Adv. Space Res. 2016, 57, 2121–2135. [Google Scholar] [CrossRef]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V. A solar signature in many climate indices. J. Geophys. Res. Atmos. 2019, 124, 2600–2619. [Google Scholar] [CrossRef]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V. Singular spectral analysis of the aa and Dst geomagnetic indices. J. Geophys. Res. Space Phys. 2019, 124, 6403–6417. [Google Scholar] [CrossRef]
- Scafetta, N.; Milani, F.; Bianchini, A. A 60-year cycle in the Meteorite fall frequency suggests a possible interplanetary dust forcing of the Earth’s climate driven by planetary oscillations. Geophys. Res. Lett. 2020, 47, e2020GL089954. [Google Scholar] [CrossRef]
- Cionco, R.G.; Kudryavtsev, S.M.; Soon, W.H.H. Possible Origin of Some Periodicities Detected in Solar Terrestrial Studies: Earth’s Orbital Movements. Earth Space Sci. 2021, 8, e2021EA001805. [Google Scholar] [CrossRef]
- Lopes, F.; Le Mouël, J.L.; Courtillot, V.; Gibert, D. On the shoulders of Laplace. Phys. Earth Planet. Inter. 2021, 316, 106693. [Google Scholar] [CrossRef]
- Scafetta, N. Reconstruction of the Interannual to Millennial Scale Patterns of the Global Surface Temperature. Atmosphere 2021, 12, 147. [Google Scholar] [CrossRef]
- Lopes, F.; Courtillot, V.; Gibert, D.; Mouël, J.-L.L. On Two Formulations of Polar Motion and Identification of Its Sources. Geosciences 2022, 12, 398. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Moore, J.C.; Grinsted, A.; Woodworth, P.L. Recent global sea level acceleration started over 200 years ago? Geophys. Res. Lett. 2008, 35, 1–4. [Google Scholar] [CrossRef]
- Chambers, D.P.; Merrifield, M.A.; Nerem, R.S. Is there a 60-year oscillation in global mean sea level? Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Chen, X.; Feng, F.; Huang, N.E. Global sea level trend during 1993–2012. Glob. Planet Change 2014, 112, 26–32. [Google Scholar] [CrossRef]
- Wahl, T.; Chambers, D.P. Evidence for multidecadal variability in US extreme sea level records. J. Geophys. Res. Oceans 2015, 120, 1527–1544. [Google Scholar] [CrossRef]
- Bank, M.J.; Scafetta, N. Scaling, mirror symmetries and musical consonances among the distances of the planets of the solar system. arXiv 2022, arXiv:2202.03939. [Google Scholar] [CrossRef]
- Menke, W. Geophysical Data Analysis: Discrete Inverse Theory; International Geophysics Series; Academic Press: Cambridge, MA, USA, 1989; Volume 45. [Google Scholar]
- Glatting, G.; Kletting, P.; Reske, S.N.; Hohl, K.; Ring, C. Choosing the optimal fit function: Comparison of the Akaike information criterion and the F test. Med. Phys. 2007, 34, 4285–4292. [Google Scholar] [CrossRef]
- Tsimplis, M.N.; Baker, T.F. Sea level drop in the Mediterranean Sea: An indicator of deep water salinity and temperature changes? Geophys. Res. Lett. 2000, 27, 1731–1734. [Google Scholar] [CrossRef]
- Marcos, M.; Tsimplis, M.N. Coastal sea level trends in Southern Europe. Geophys. J. Int. 2008, 175, 70–82. [Google Scholar] [CrossRef]
- Wahl, T.; Haigh, I.D.; Woodworth, P.L.; Albrecht, F.; Dillingh, D.; Jensen, J.; Nicholls, R.J.; Weisse, R.; Wöppelmann, G. Observed mean sea level changes around the North Sea coastline from 1800 to present. Earth Sci. Rev. 2013, 124, 51–67. [Google Scholar] [CrossRef]
- White, N.J.; Haigh, I.D.; Church, J.A.; Koen, T.; Watson, C.S.; Pritchard, T.R.; Watson, P.J.; Burgette, R.J.; McInnes, K.L.; You, Z.J. Australian sea levels-Trends, regional variability and influencing factors. Earth Sci. Rev. 2014, 136, 155–174. [Google Scholar] [CrossRef]
- Beckley, B.; Zelensky, N.P.; Holmes, S.A.; Lemoine, F.G.; Ray, R.D.; Mitchum, G.T.; Desai, S.; Brown, S.T. Global Mean Sea Level Trend from Integrated Multi-Mission Ocean Altimeters TOPEX/Poseidon Jason-1 and OSTM/Jason-2 Version 3; Ver. 3; Dataset Accessed; 2015. Available online: https://podaac.jpl.nasa.gov/dataset/MERGED_TP_J1_OSTM_OST_GMSL_ASCII_V51 (accessed on 5 July 2020).
- Beckley, B.D.; Zelensky, N.P.; Holmes, S.A.; Lemoine, F.G.; Ray, R.D.; Mitchum, G.T.; Desai, S.D.; Brown, S.T. Assessment of the Jason-2 Extension to the TOPEX/Poseidon, Jason-1 Sea-Surface Height Time Series for Global Mean Sea Level Monitoring. Mar. Geodesy 2010, 33, 447–471. [Google Scholar] [CrossRef]
- Beckley, B.D.; Callahan, P.S.; Hancock III, D.W.; Mitchum, G.T.; Ray, R.D. On the “Cal Mode” Correction to TOPEX Satellite Altimetry and Its Effect on the Global Mean Sea Level Time Series. J. Geophys. Res. Oceans 2017, 122, 8371–8384. [Google Scholar] [CrossRef]
- Allan, R.; Ansell, T. A new globally complete monthly historical gridded mean sea level pressure dataset (HadSLP2): 1850–2004. J. Clim. 2006, 19, 5816–5842. [Google Scholar] [CrossRef]
- Moreira, L.; Cazenave, A.; Palanisamy, H. Influence of interannual variability in estimating the rate and acceleration of present-day global mean sea level. Glob. Planet Chang. 2021, 199, 103450. [Google Scholar] [CrossRef]
- Lopes, F.; Courtillot, V.; Gibert, D.; Le Mouël, J.L. On pseudo-periodic perturbations of planetary orbits, and oscillations of Earth’s rotation and revolution: Lagrange’s formulation. arXiv 2022, arXiv:2209.07213. [Google Scholar] [CrossRef]
- Le Mouël, J.L.; Lopes, F.; Courtillot, V.; Gibert, D. On forcings of length of day changes: From 9-day to 18.6-year oscillations. Phys. Earth Planet. Inter. 2019, 292, 1–11. [Google Scholar] [CrossRef]
- Warrick, R.A.; Oerlemans, J. Sea Level Rise Climate Change—The IPCC Scientific Assessment; 1990. pp. 257–281. Available online: https://www.ipcc.ch/report/ar1/wg1/sea-level-rise/ (accessed on 5 July 2020).
- Merrifield, M.A.; Thompson, P.R.; Lander, M. Multidecadal sea level anomalies and trends in the western tropical Pacific. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Parker, A. Sea level trends at locations of the United States with more than 100 years of recording. Nat. Hazards 2013, 65, 1011–1021. [Google Scholar] [CrossRef]
- Parker, A.; Ollier, C.D. Coastal planning should be based on proven sea level data. Ocean Coast Manag 2016, 124, 1–9. [Google Scholar] [CrossRef]
- Dumont, S.; Petrosino, S.; Neves, M.C. On the Link Between Global Volcanic Activity and Global Mean Sea Level. Front. Earth Sci. 2022, 10, 845511. [Google Scholar] [CrossRef]

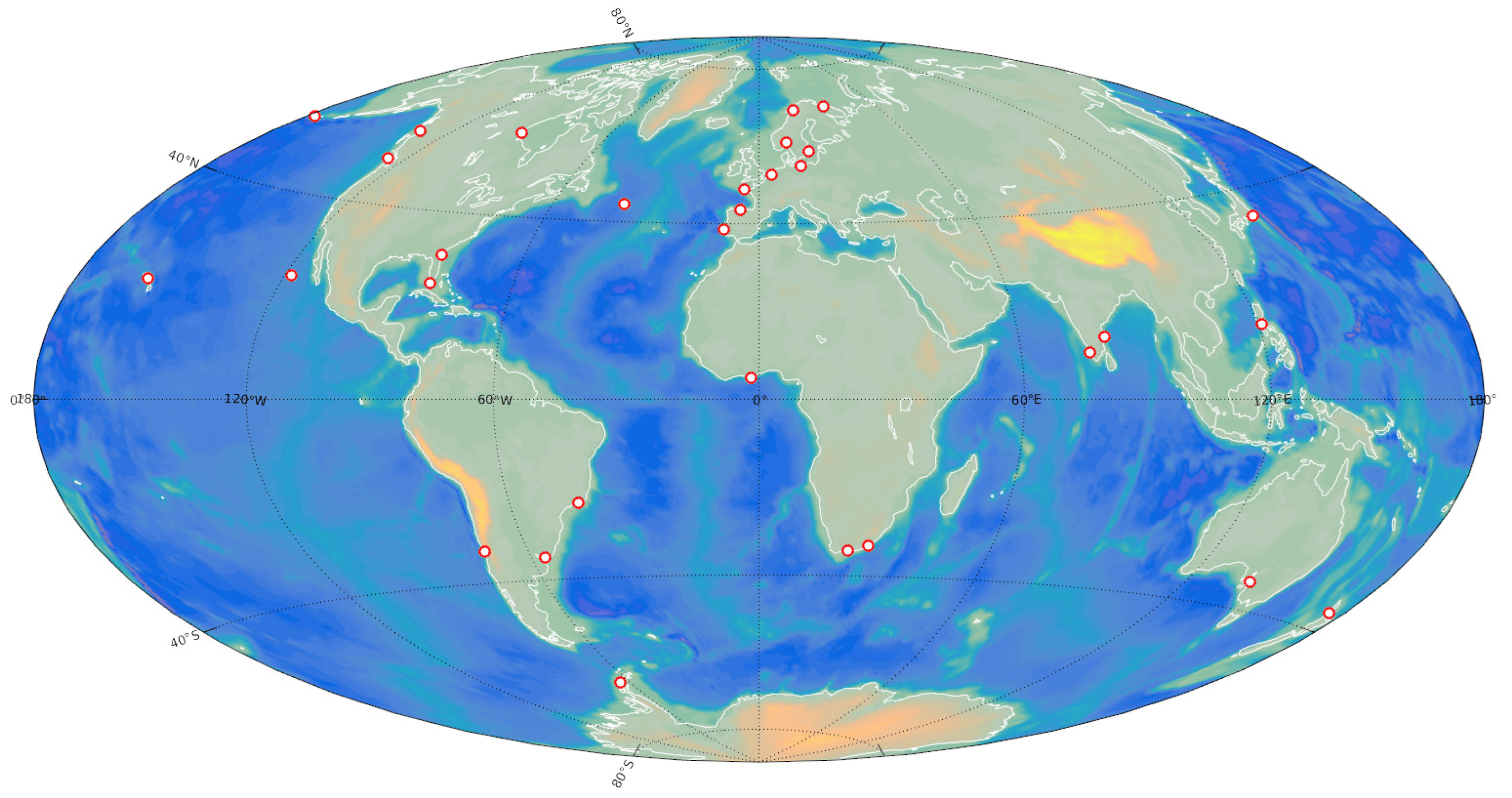



| Tide Gauge Site | Lat () | Lon () |
|---|---|---|
| Adak Sweeper Cove | 51.863 | −176.632 |
| Argentine Islands | −65.246 | −64.257 |
| Auckland | −36.843 | 174.769 |
| Brest | 48.382 | 4.494 |
| Churchill | 58.767 | −94.183 |
| Chennai | 13.100 | 80.300 |
| Cochin | 9.967 | 76.267 |
| East-London | −33.027 | 27.932 |
| Fernandina Beach | 30.672 | −81.465 |
| Honolulu | 21.307 | −157.867 |
| Ketchikan | 55.332 | −131.625 |
| Key West | 24.555 | −81.806 |
| Knysna | −34.049 | 23.046 |
| Lisbon | 38.700 | −9.133 |
| Marseille | 43.279 | 5.354 |
| Maasluis | 51.918 | 4.25 |
| Manila, S.harbor | 14.583 | 120.967 |
| Mera | 34.919 | 139.825 |
| Montevideo | −34.900 | −56.250 |
| Narvik | 68.428 | 17.426 |
| Oslo | 59.909 | 10.735 |
| Polyarny | 69.200 | 33.483 |
| Port Adelaide | −34.780 | 138.481 |
| Rio de Janeiro | −22.933 | −43.133 |
| Swinoujscie | 53.917 | 14.233 |
| Takoradi | 4.885 | −1.745 |
| Tofino | 49.150 | −125.917 |
| Tuapse | 44.100 | 39.067 |
| Valparaiso | −33.027 | −71.626 |
| Visby | 57.639 | 18.284 |
| Xiamen | 24.450 | 118.067 |
| Sea Level (mm) | Pressure (hPa) | Ratio (hPa/mm) | |
|---|---|---|---|
| Trend | 45 | 0.8 | 0.019 |
| ∼20–30 yr | 18 | 0.45 | 0.025 |
| 1 yr | 80 | 1.6 | 0.020 |
| 0.5 yr | 16 | 0.3 | 0.019 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Courtillot, V.; Le Mouël, J.-L.; Lopes, F.; Gibert, D. On Sea-Level Change in Coastal Areas. J. Mar. Sci. Eng. 2022, 10, 1871. https://doi.org/10.3390/jmse10121871
Courtillot V, Le Mouël J-L, Lopes F, Gibert D. On Sea-Level Change in Coastal Areas. Journal of Marine Science and Engineering. 2022; 10(12):1871. https://doi.org/10.3390/jmse10121871
Chicago/Turabian StyleCourtillot, Vincent, Jean-Louis Le Mouël, Fernando Lopes, and Dominique Gibert. 2022. "On Sea-Level Change in Coastal Areas" Journal of Marine Science and Engineering 10, no. 12: 1871. https://doi.org/10.3390/jmse10121871
APA StyleCourtillot, V., Le Mouël, J.-L., Lopes, F., & Gibert, D. (2022). On Sea-Level Change in Coastal Areas. Journal of Marine Science and Engineering, 10(12), 1871. https://doi.org/10.3390/jmse10121871





