Fast High-Precision Bisection Feedback Search Algorithm and Its Application in Flattening the NURBS Curve
Abstract
1. Introduction
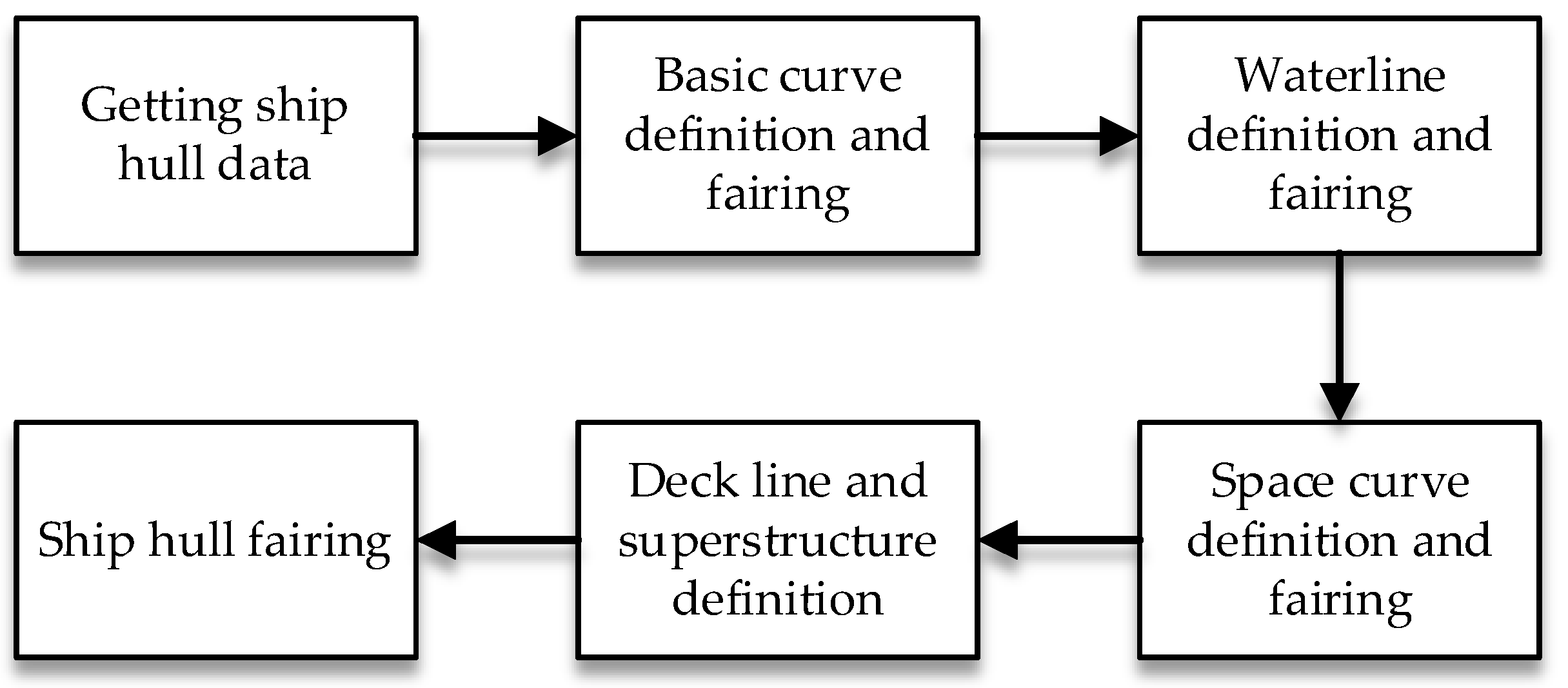
1.1. Modeling and Deformation of the Ship Hull
1.2. Inversion Algorithms of NURBS Curves
1.3. Problems with the IR-BFS Inversion Algorithm
1.4. Research Objectives and Structure
2. Mathematical Background
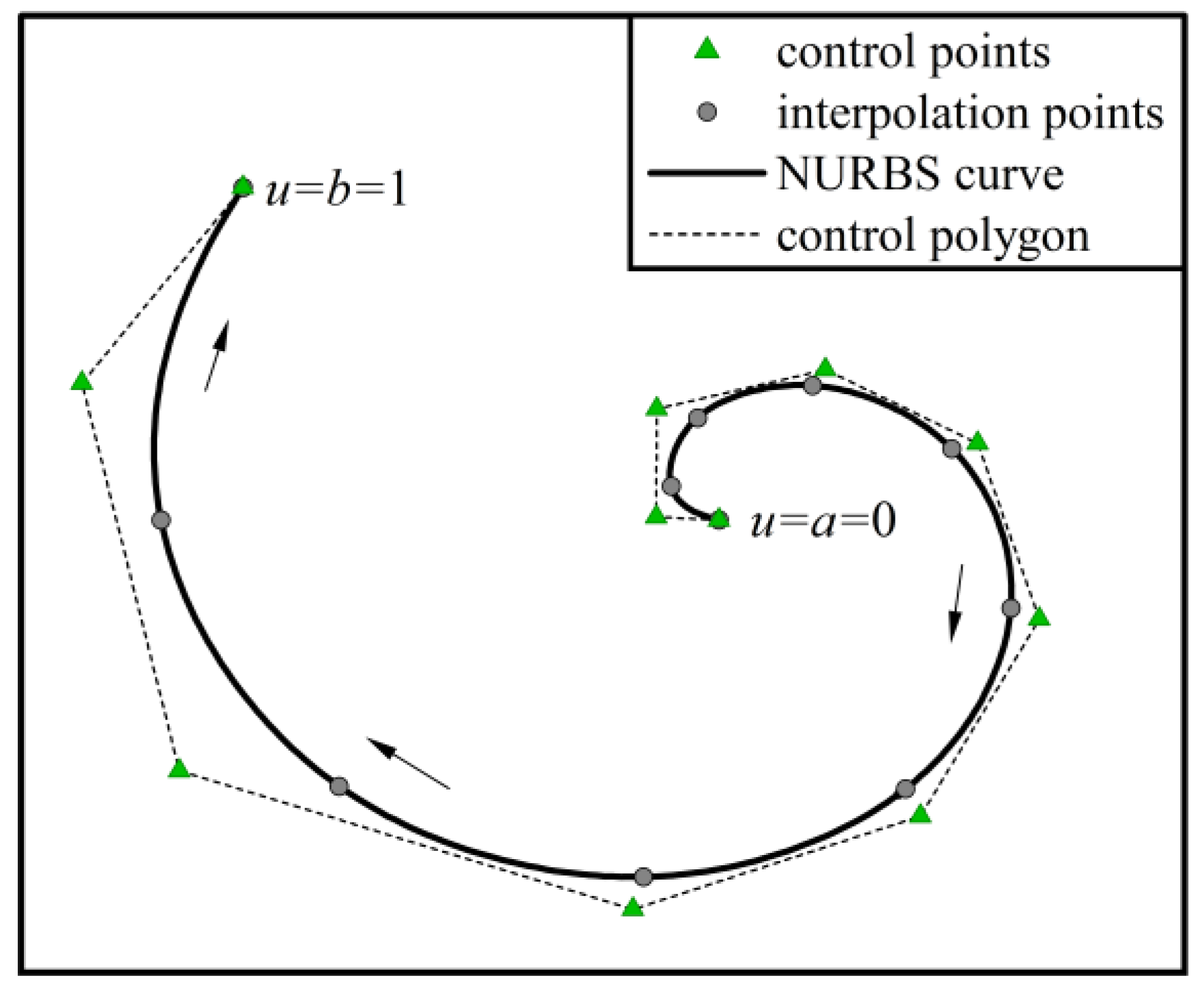
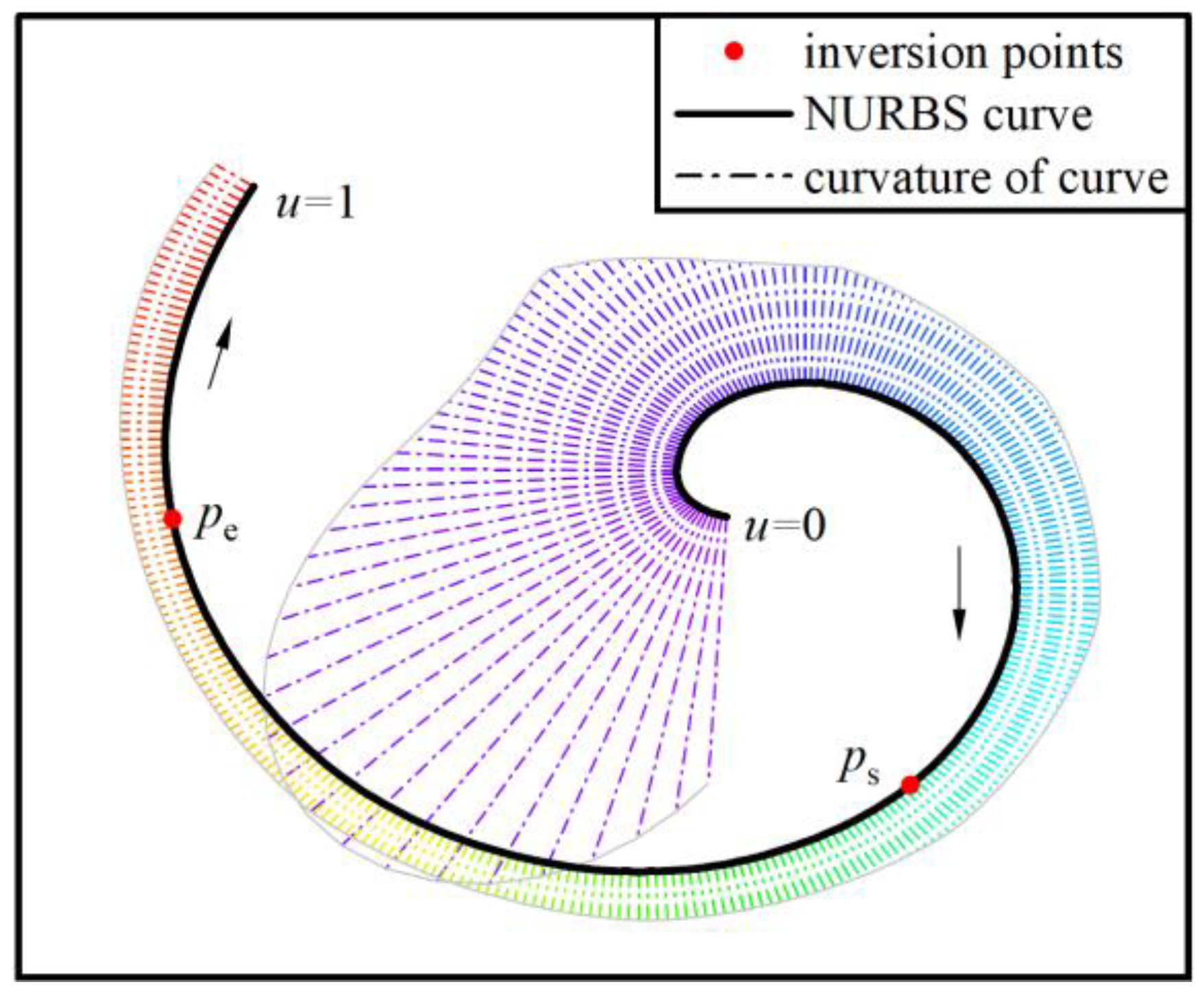
2.1. NURBS Curve
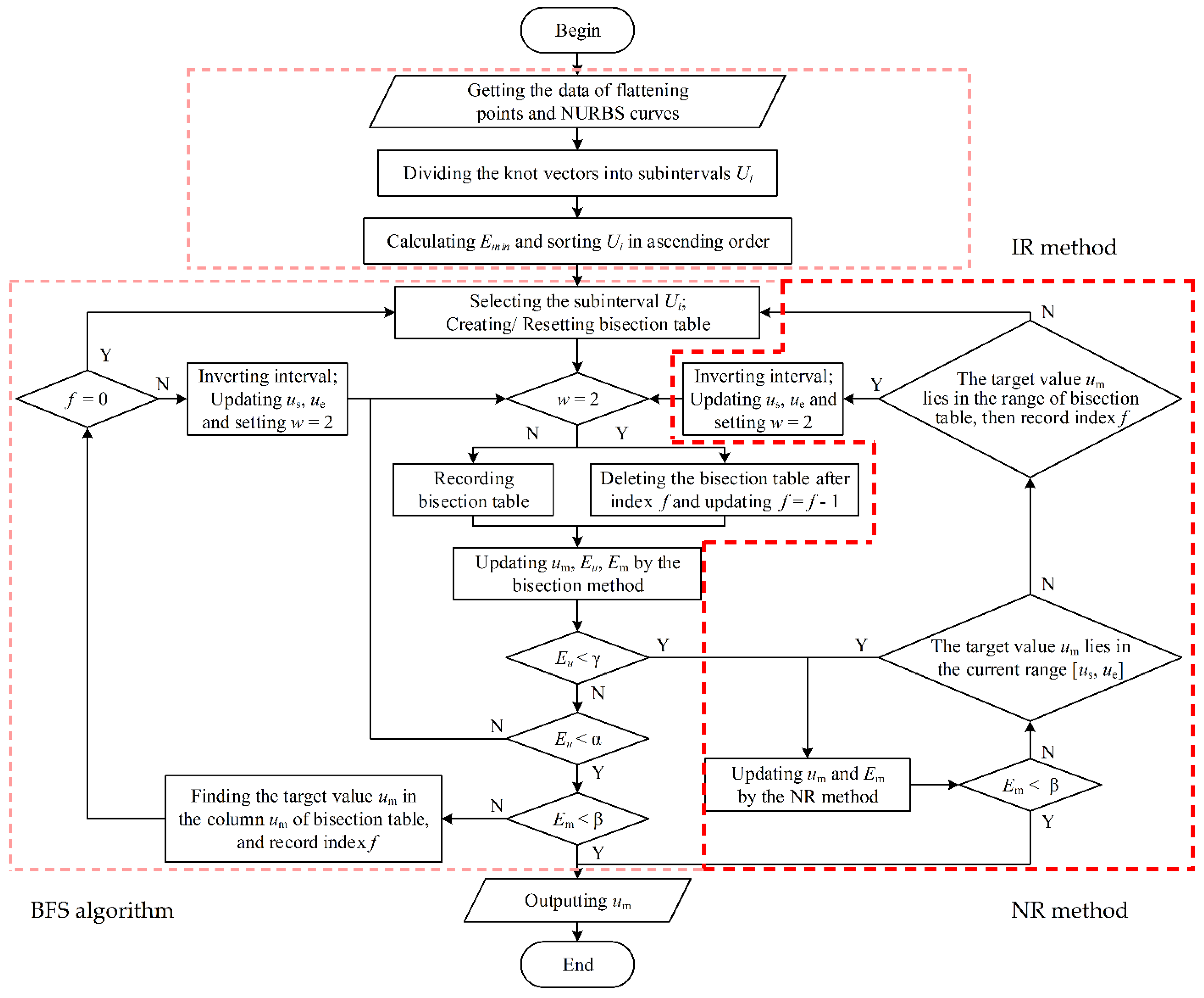
2.2. IR-BFS Inversion Algorithm
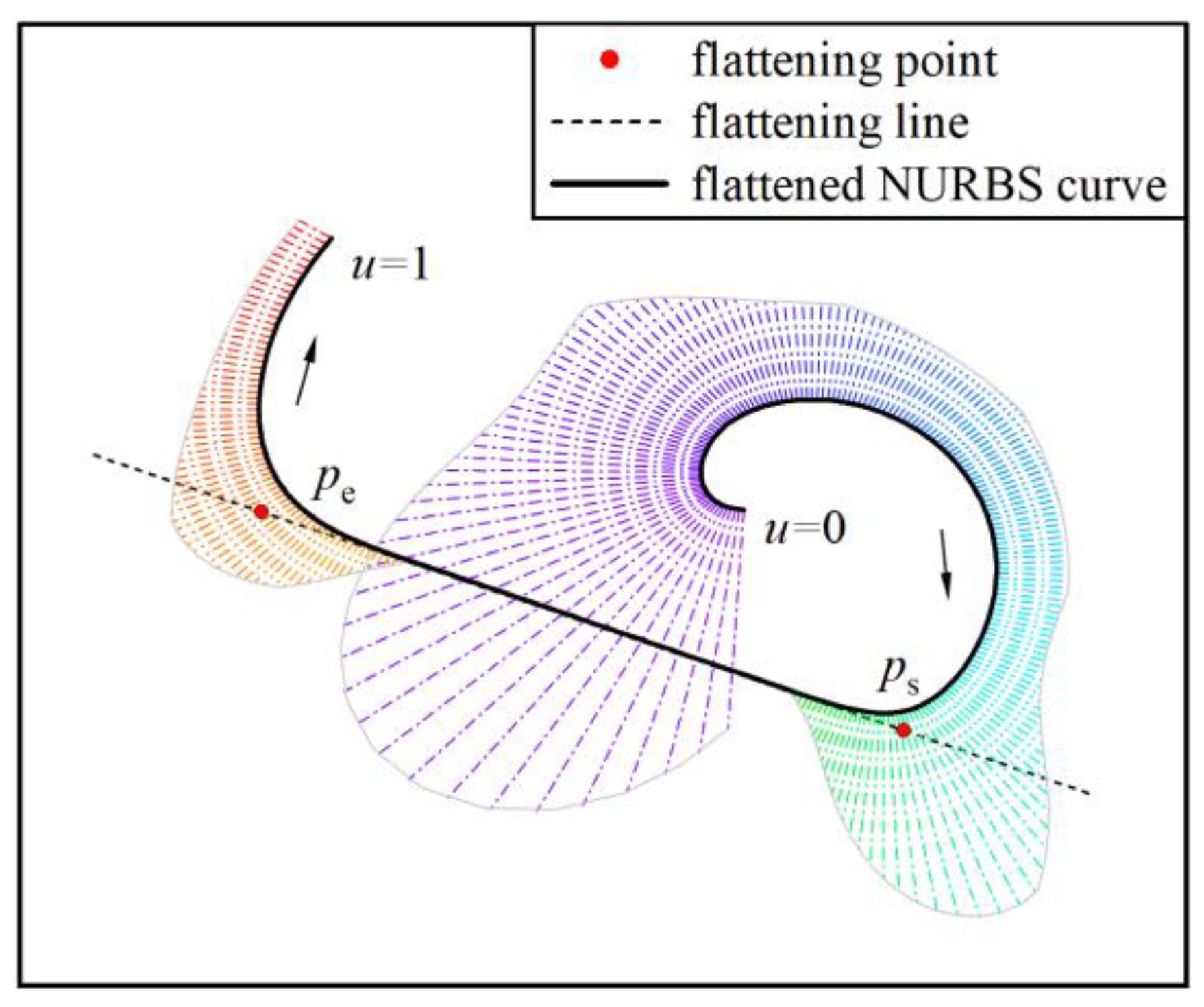
2.3. Flattening Algorithm of the NURBS Curve
3. Framework of the Proposed Methodology
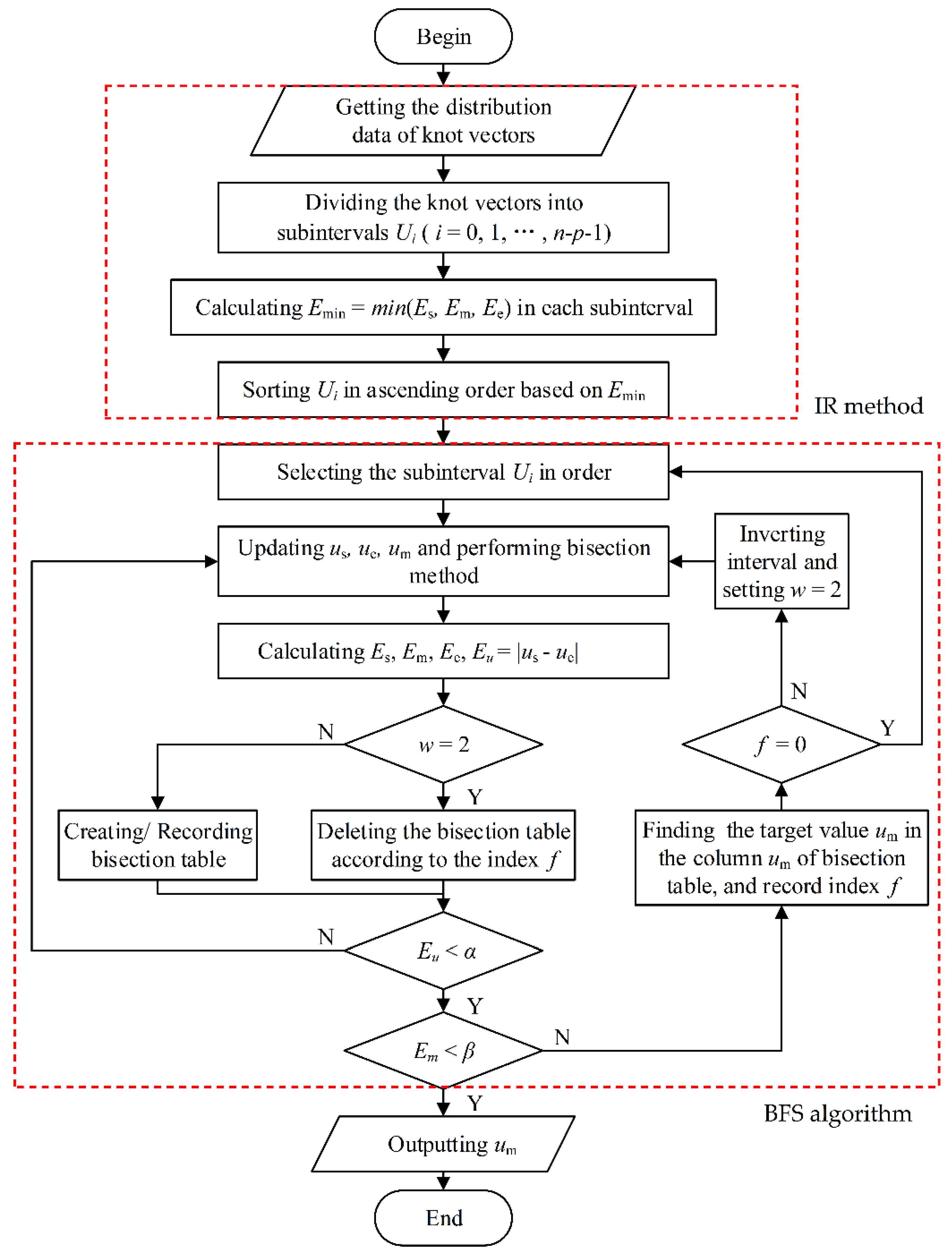
3.1. Overall Design of the FHP-BFS Algorithm
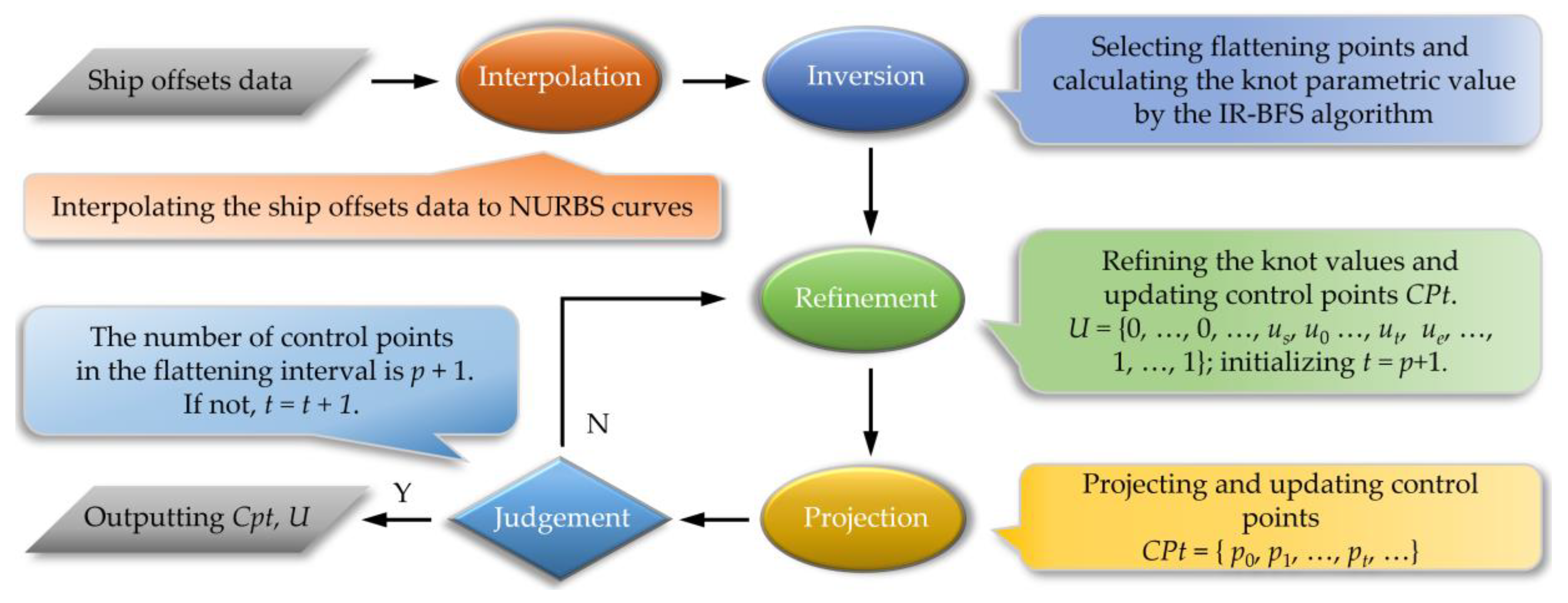
3.2. Flattening Algorithm Based on the FHP-BFS Algorithm
| Algorithm 1: Flattening algorithm based on the fast high-precision bisection feedback search (FHP-BFS) algorithm. |
| Input:—list of offsets table; —location points of flattening line segment ends; |
| —degree of the interpolated NURBS curve. |
| Output: — control point vector and knot vector of a flattened NURBS curve. |
| 1: function |
| 2: //interpolation operation of list |
| 3: // are parametric values of the endpoint of the flattening line segment |
| 4: //point inversion by the FHP-BFS algorithm |
| 5: |
| 6: // is the number of points projected successfully |
| 7: // is the knot refinement number |
| 8: |
| 9: while do |
| 10: |
| 11: //knot refinement algorithm |
| 12: Projection of the control point located on the same side of the flattening line segment |
| 13: update , s |
| 14: end while |
| 15: return |
| 16: end function |
4. Results
4.1. Comparison of Algorithms between FHP-BFS and IR-BFS
4.1.1. Validation of the Practical Effectiveness of the FHP-BFS Algorithm
4.1.2. Setting the Precision of the Threshold of the FHP-BFS Algorithm
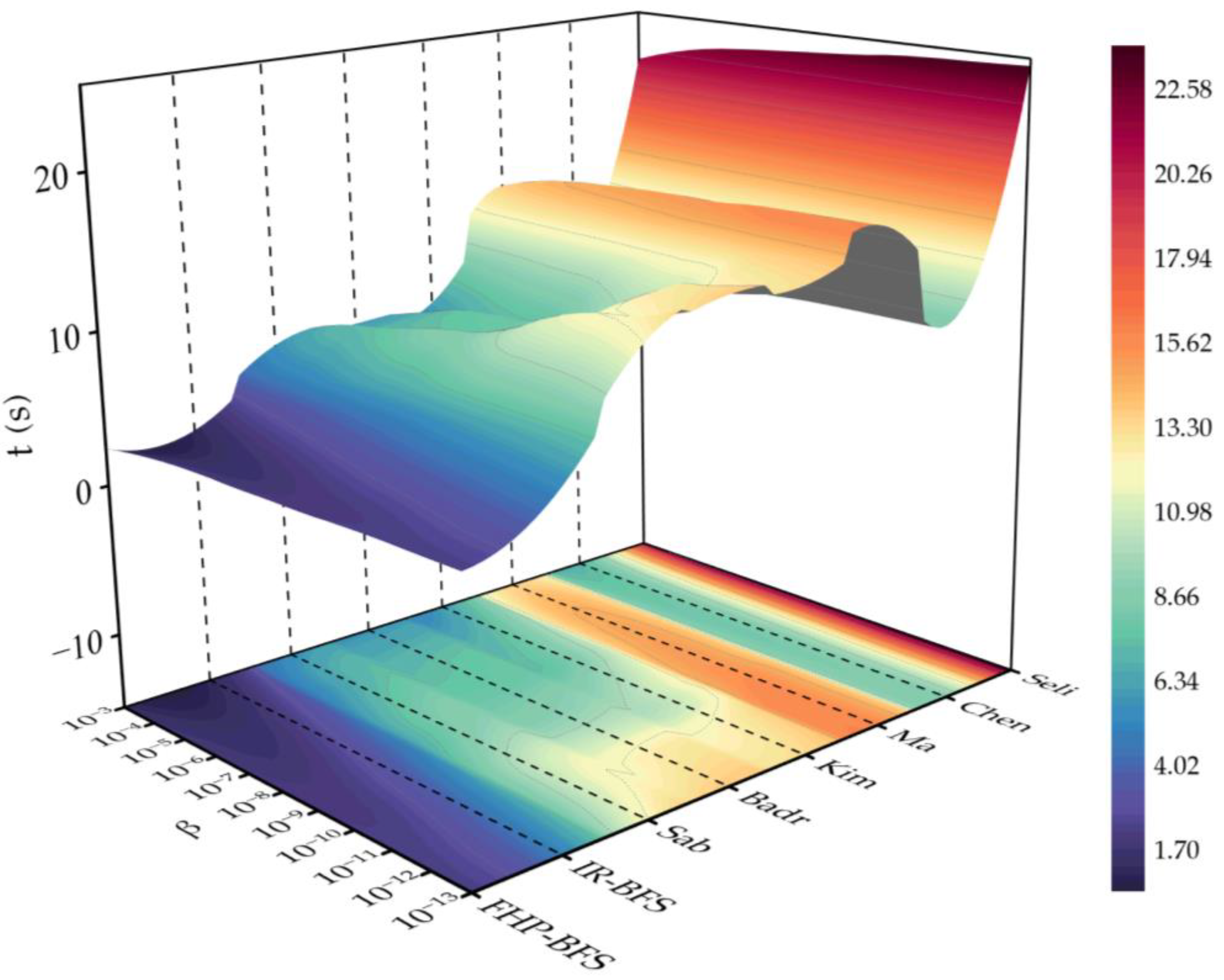
4.2. Comparison with Other Algorithms
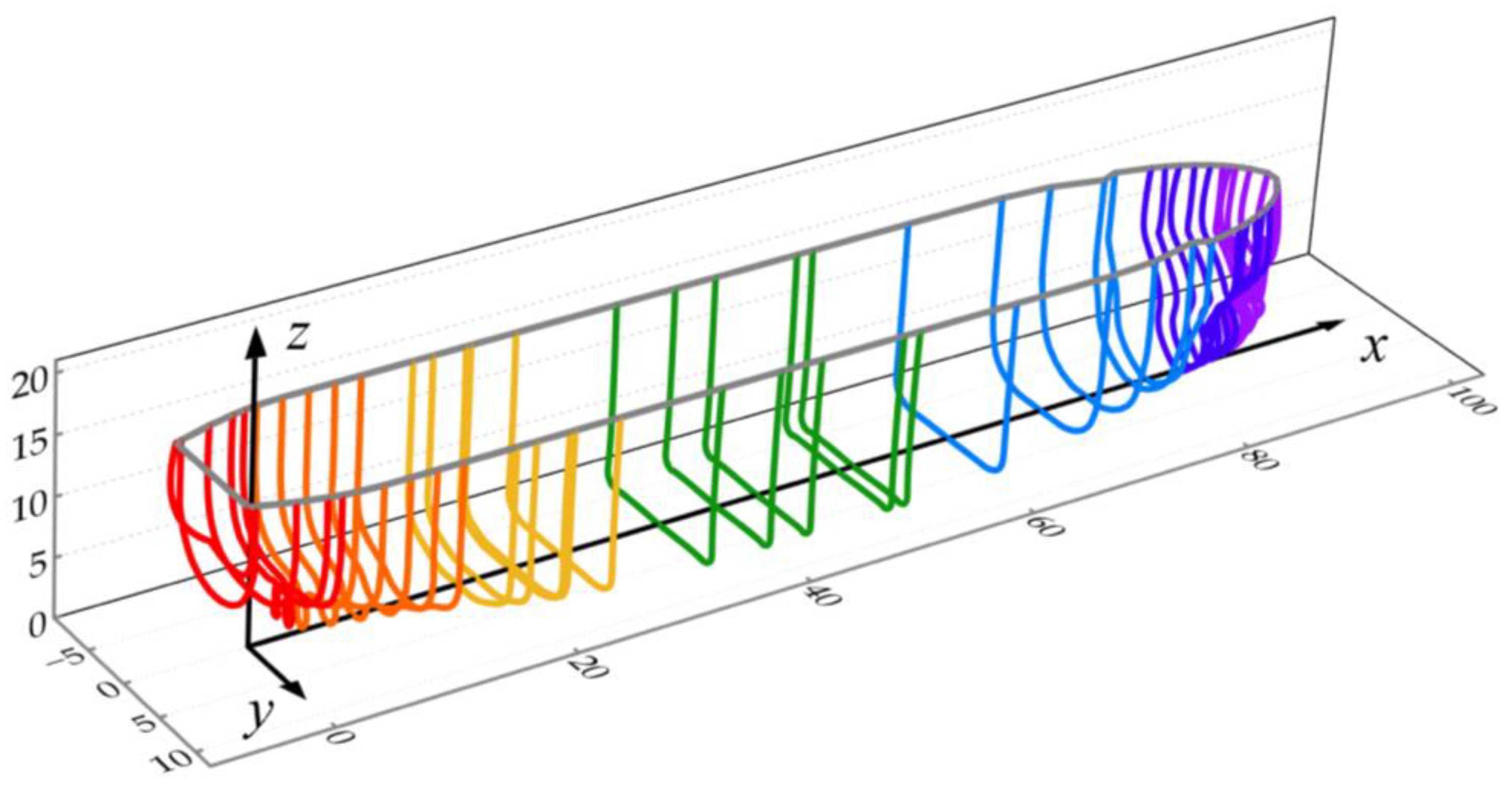
4.3. Evaluation of the Flattening Algorithm
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FHP-BFS | Fast high-precision bisection feedback search |
| IR-BFS | Interval reformation and bisection feedback search |
| NURBS | Non-uniform rational B-spline |
| NR | Newton-Raphson |
References
- Nategh, M.J.; Parvaz, H. Development of computer aided clamping system design for workpieces with freeform surfaces. Comput.-Aided Des. 2018, 95, 52–61. [Google Scholar] [CrossRef]
- Bulian, G.; Cardinale, M.; Dafermos, G.; Lindroth, D.; Zaraphonitis, G. Probabilistic assessment of damaged survivability of passenger ships in case of grounding or contact. Ocean Eng. 2020, 218, 107396. [Google Scholar] [CrossRef]
- Sun, X.; Ni, Y.; Liu, C.; Wang, Z. A practical method for stability assessment of a damaged ship. Ocean Eng. 2021, 222, 108594. [Google Scholar] [CrossRef]
- Martin, W.; Cohen, E.; Fish, R.; Shirley, P. Practical ray tracing of trimmed NURBS surfaces. J. Graph. Tools 2000, 5, 27–52. [Google Scholar] [CrossRef]
- Guthe, M.; Balázs, A.; Klein, R. GPU-based trimming and tessellation of NURBS and T-Spline surfaces. ACM Trans. Graph 2005, 24, 1016–1023. [Google Scholar] [CrossRef]
- Dokken, T. Finding intersections of B-spline represented geometries using recursive subdivision techniques. Comput.-Aided Geom. Des. 1985, 2, 189–195. [Google Scholar] [CrossRef]
- Dokken, T.; Skytt, V.; Ytrehus, A.M. Recursive subdivision and iteration in intersections and related problems. In Mathematical Methods in Computer Aided Geometric Design; Academic Press: Cambridge, MA, USA, 1989; pp. 207–214. [Google Scholar]
- Sederberg, T.W.; Nishita, T. Curve intersection using Bézier clipping. Comput. Aided Des. 1990, 22, 538–549. [Google Scholar] [CrossRef]
- Efremov, A.; Havran, V.; Seidel, H.P. Robust and numerically stable Bézier clipping method for ray tracing NURBS surfaces. In Proceedings of the 21st Spring Conference on Computer Graph, Budmerice, Slovakia, 12–14 May 2005; pp. 127–135. [Google Scholar]
- Lee, D.; Lee, S.S.; Park, B.J. 3-D geometric modeler for rapid ship safety assessment. Ocean Eng. 2004, 31, 1219–1230. [Google Scholar] [CrossRef]
- Lu, C.; Lin, Y.; Ji, Z.; Chen, M. Ship hull representation with a single NURBS surface. In Proceedings of the ISOPE-2005 Conference: International Offshore and Polar Engineering Conference, Seoul, Republic of Korea, 19–24 June 2005. [Google Scholar]
- Lu, C.; Lin, Y.; Ji, Z. Ship hull representation based on offset data with a single NURBS surface. Ship Technol. Res. 2007, 54, 81–88. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, Y.; Chen, Z.; Feng, Y. CFD-based multi-objective optimization of a waterjet- propelled trimaran. Ocean Eng. 2019, 195, 106755. [Google Scholar] [CrossRef]
- Kuznecovs, A.; Ringsberg, J.W.; Johnson, E.; Yamada, Y. Ultimate limit state analysis of a double-hull tanker subjected to biaxial bending in intact and collision-damaged conditions. Ocean Eng. 2020, 209, 107519. [Google Scholar] [CrossRef]
- Piegl, L.A.; Tiller, W. The NURBS Book, 2nd ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Johnson, D.E.; Cohen, E. A framework for efficient minimum distance computations. In Proceedings of the IEEE International Conference on Robotics & Automation (ICRA), Leuven, Belgium, 20 May 1998; pp. 3678–3684. [Google Scholar]
- Johnson, D.E.; Cohen, E. Distance extrema for spline models using tangent cones. In Proceedings of the GI’05: Proceedings of Graphics Interface 2005, Victoria, BC, Canada, 9–11 May 2005; pp. 169–175. [Google Scholar]
- Ma, Y.L.; Hewitt, W.T. Point inversion and projection for NURBS curve and surface: Control polygon approach. Comput.-Aided Geom. Des. 2003, 20, 79–99. [Google Scholar] [CrossRef]
- Selimovic, I. Improved algorithms for the projection of points on NURBS curves and surfaces. Comput.-Aided Geom. Des. 2006, 23, 439–445. [Google Scholar] [CrossRef]
- Chen, X.D.; Yong, J.H.; Wang, G.; Paul, J.C.; Xu, G. Computing the minimum distance between a point and a NURBS curve. Comput.-Aided Des. 2008, 40, 1051–1054. [Google Scholar] [CrossRef]
- Chen, X.D.; Xu, G.; Yong, J.H.; Wang, G.; Paul, J.C. Computing the minimum distance between a point and clamped B-spline surface. Graphical Models 2009, 71, 107–112. [Google Scholar] [CrossRef]
- Oh, Y.T.; Kim, Y.J.; Lee, J.; Kim, M.S.; Elber, G. Efficient point projection to freeform curves and surfaces. In Proceedings of the International Conference on Geometric Modeling and Processing, Castro Urdiales, Spain, 16–18 June 2010; pp. 192–205. [Google Scholar]
- Oh, Y.T.; Kim, Y.J.; Lee, J.; Kim, M.S.; Elber, G. Continuous point projection to planar freeform curves using spiral curves. The Visual Comp. 2012, 28, 111–123. [Google Scholar] [CrossRef]
- Li, X.W.; Wu, Z.N.; Hou, L.K.; Wang, L.; Yue, C.G.; Xin, Q. A geometric orthogonal projection strategy for computing the minimum distance between a point and a spatial parametric curve. Algorithms 2016, 9, 15. [Google Scholar] [CrossRef]
- Quinlan, S. Efficient distance computation between non-convex objects. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), San Diego, CA, USA, 8–13 May 1994; pp. 3324–3329. [Google Scholar]
- Dennis, J.E.; Schnabel, R.B. Numerical Methods for Unconstrained Optimization and Nonlinear Equations; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 1996. [Google Scholar]
- Shacham, M. Numerical solution of constrained nonlinear algebraic equations. Int. J. Numer. Methods Eng. 1986, 23, 1455–1481. [Google Scholar] [CrossRef]
- Zhu, K.G.; Shi, G.Y.; Liu, J. Improved flattening algorithm for NURBS curve based on bisection feedback search algorithm and interval reformation method. Ocean Eng. 2022, 247, 110635. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Constrained Optimization and Lagrange Multiplier Methods; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Ring, W.; Wirth, B. Optimization methods on Riemannian manifolds and their application to shape space. SIAM J. Optim. 2012, 22, 596–627. [Google Scholar] [CrossRef]
- Huang, F.; Kim, H.Y.; Yang, C. A new method of ship bulbous bow generation and modification. In Proceedings of the Twenty-Fourth International Offshore and Polar Engineering Conference, Busan, Republic of Korea, 15–20 June 2014. [Google Scholar]
- Absil, P.A.; Baker, C.G.; Gallivan, K.A. Trust-region methods on Riemannian manifolds. Found. Comput. Math. 2007, 7, 303–330. [Google Scholar] [CrossRef]
- Absil, P.A.; Mahony, R.; Sepulchre, R. Optimization Algorithms on Matrix Manifolds; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 1987. [Google Scholar]
- Deuflhard, P. Newton Methods for Nonlinear Problems; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Jiang, X.N.; Yan, L. Relevant integrals of NURBS and its application in hull line element design. Ocean Eng. 2022, 251, 111147. [Google Scholar] [CrossRef]
- Nam, J.H.; Bang, N.S. A curve based hull form variation with geometric constraints of area and centroid. Ocean Eng. 2017, 133, 1–8. [Google Scholar] [CrossRef]
- De Boor, C. A Practical Guide to Splines; Springer: New York, NY, USA, 1978. [Google Scholar]
- McCartney, J.; Hinds, B.K.; Chong, K.W. Pattern flattening for orthotropic materials. Comput.-Aided Des. 2005, 37, 631–644. [Google Scholar] [CrossRef]
- Takezawa, M.; Matsuo, K.; Maekawa, T. Control of lines of curvature for plate forming in shipbuilding. Comput.-Aided Geom. Des. 2019, 75, 101785.1–101785.14. [Google Scholar] [CrossRef]
- Badr, E.; Sultan, A.; Abdallah, E.G. A Comparative Study among New Hybrid Root Finding Algorithms and Traditional Methods. Mathematics 2021, 9, 1306. [Google Scholar] [CrossRef]
- Sabharwal, C.L. An Iterative Hybrid Algorithm for Roots of Non-Linear Equations. Eng 2021, 2, 7. [Google Scholar] [CrossRef]
- Kim, J.; Noh, T.; Oh, W. An improved hybrid algorithm to bisection method and Newton-Raphson method. Appl. Math. Sci. 2017, 11, 2789–2797. [Google Scholar] [CrossRef]
- Ye, Y. Combining Binary Search and Newton′s Method to Compute Real Roots for a Class of Real Functions. J. Complex. 1994, 10, 271–280. [Google Scholar] [CrossRef]

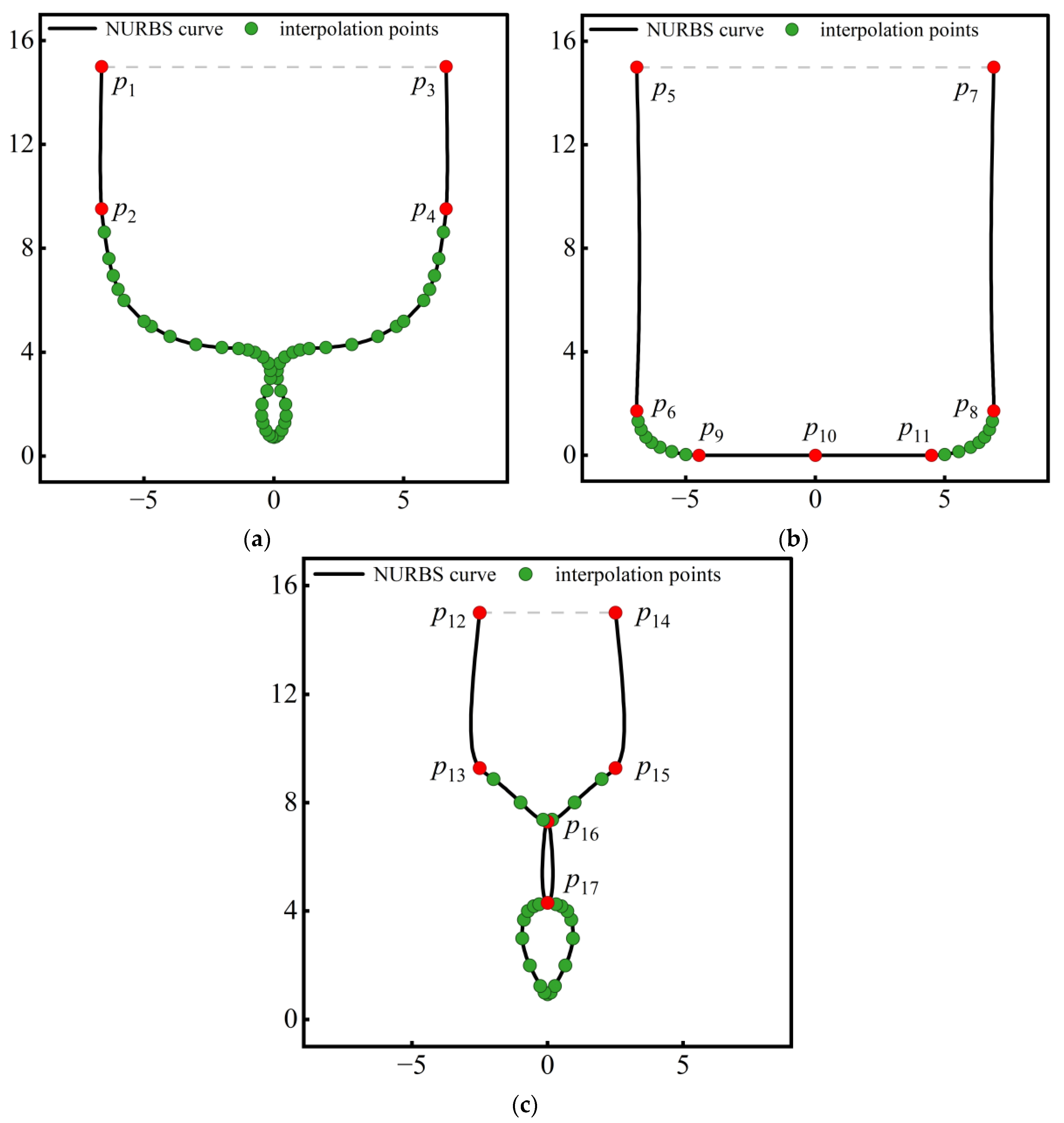

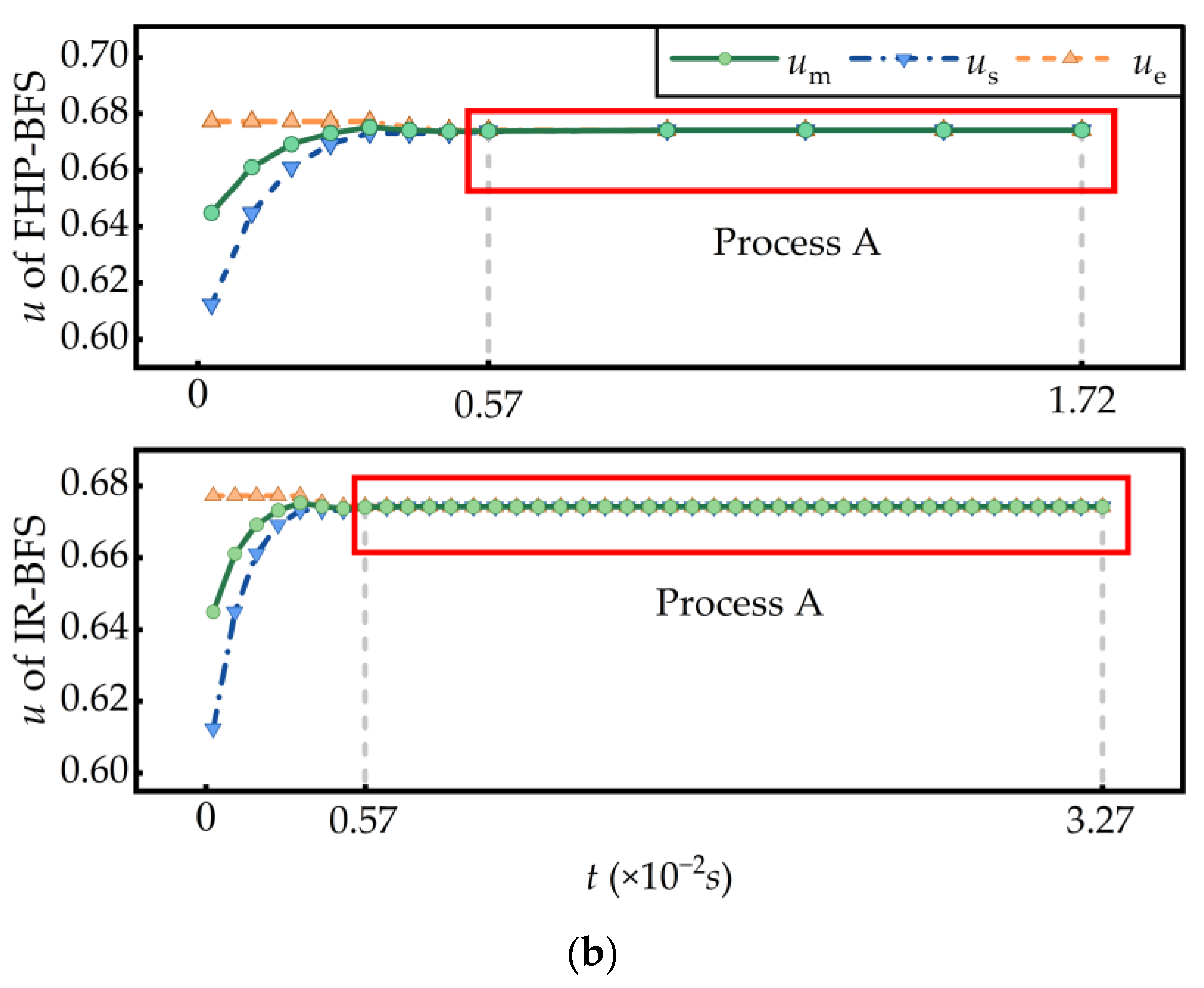
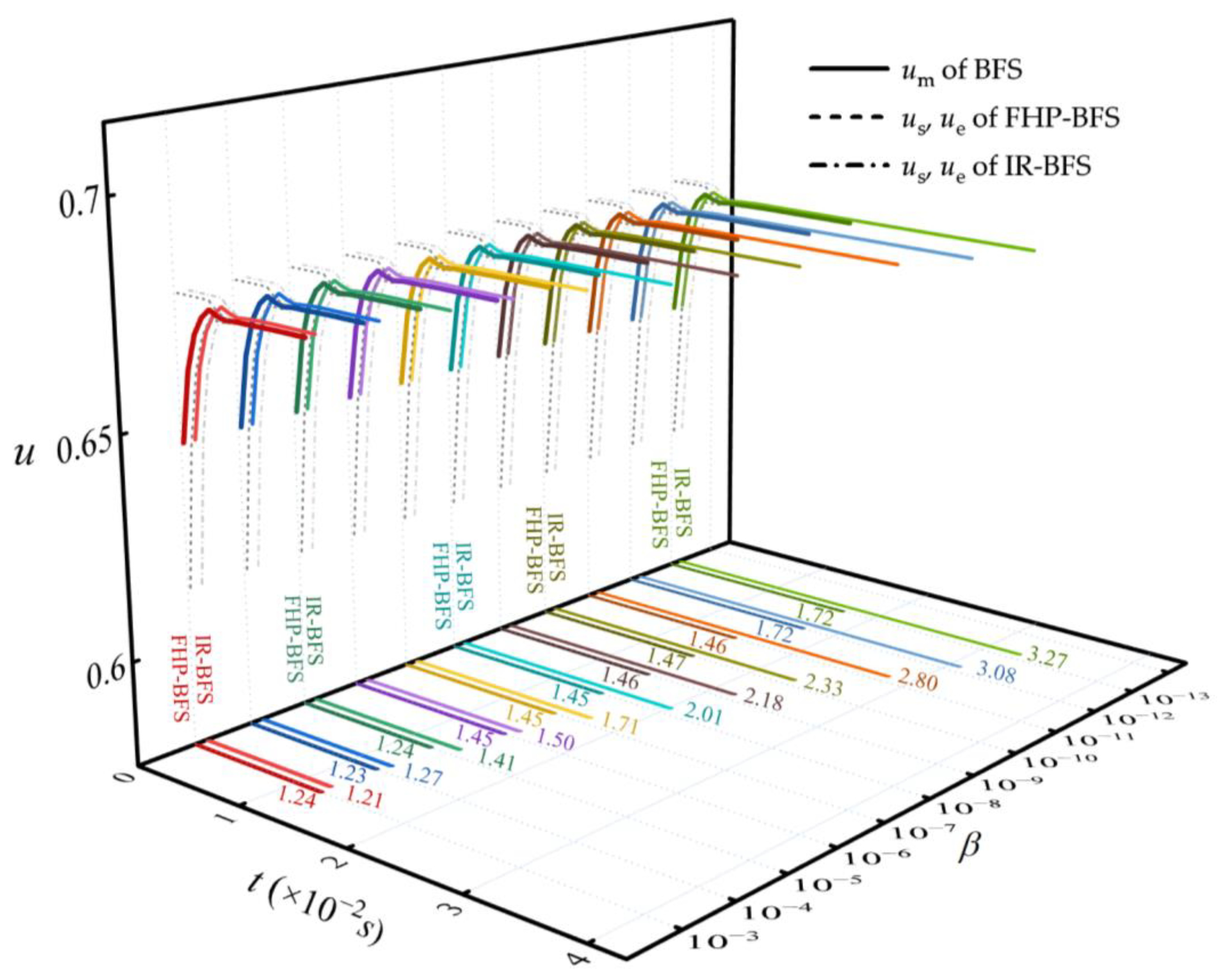
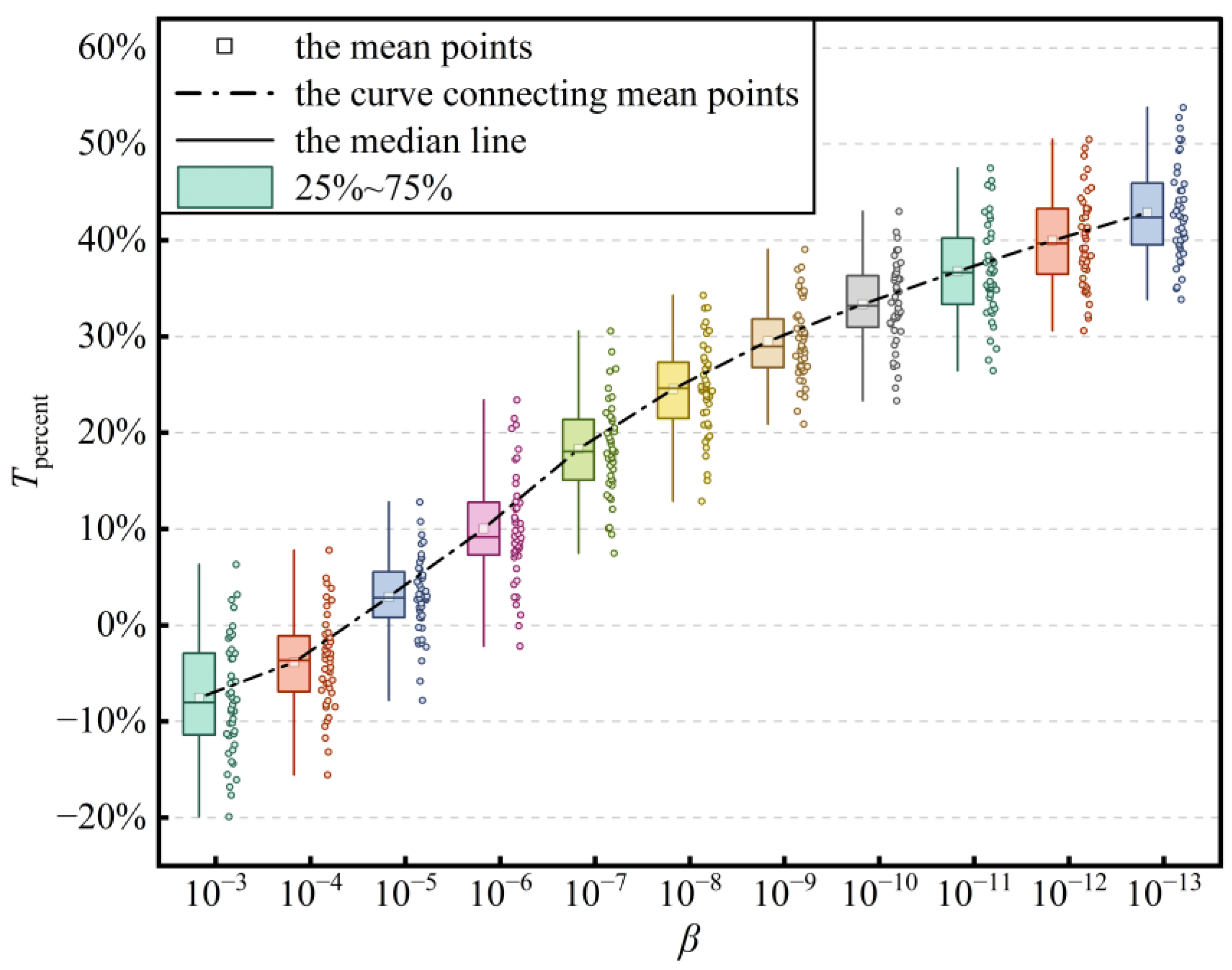



| x (Station 4) | x (Station 14) | x (Station 32) | ||||||
|---|---|---|---|---|---|---|---|---|
| Index | y | z | Index | y | z | Index | y | z |
| 1 | 0.000 | 0.731 | 1 | 0.000 | 0.000 | 1 | 0.000 | 0.932 |
| 2 | 0.082 | 0.750 | 2 | 4.490 | 0.000 | 2 | 0.115 | 1.000 |
| 3 | 0.179 | 0.821 | 3 | 5.000 | 0.035 | 3 | 0.267 | 1.241 |
| 4 | 0.303 | 1.000 | 4 | 6.000 | 0.313 | … | … | … |
| 5 | 0.426 | 1.287 | 5 | 6.322 | 0.500 | 10 | 0.000 | 4.306 |
| … | … | … | 6 | 6.541 | 0.710 | 11 | 0.000 | 7.306 |
| 23 | 6.191 | 6.953 | 7 | 6.732 | 1.000 | 12 | 0.164 | 7.371 |
| 24 | 6.359 | 7.610 | 8 | 6.850 | 1.319 | … | … | … |
| 25 | 6.531 | 8.630 | 9 | 6.900 | 1.719 | 14 | 2.000 | 8.877 |
| 26 | 6.638 | 9.520 | 10 | 6.900 | 15.00 | 15 | 2.505 | 9.284 |
| 27 | 6.638 | 15.00 | - | - | - | 16 | 2.505 | 15.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, K.; Shi, G.; Liu, J.; Shi, J. Fast High-Precision Bisection Feedback Search Algorithm and Its Application in Flattening the NURBS Curve. J. Mar. Sci. Eng. 2022, 10, 1851. https://doi.org/10.3390/jmse10121851
Zhu K, Shi G, Liu J, Shi J. Fast High-Precision Bisection Feedback Search Algorithm and Its Application in Flattening the NURBS Curve. Journal of Marine Science and Engineering. 2022; 10(12):1851. https://doi.org/10.3390/jmse10121851
Chicago/Turabian StyleZhu, Kaige, Guoyou Shi, Jiao Liu, and Jiahui Shi. 2022. "Fast High-Precision Bisection Feedback Search Algorithm and Its Application in Flattening the NURBS Curve" Journal of Marine Science and Engineering 10, no. 12: 1851. https://doi.org/10.3390/jmse10121851
APA StyleZhu, K., Shi, G., Liu, J., & Shi, J. (2022). Fast High-Precision Bisection Feedback Search Algorithm and Its Application in Flattening the NURBS Curve. Journal of Marine Science and Engineering, 10(12), 1851. https://doi.org/10.3390/jmse10121851





