Experimental Investigation on Juncture Flow Associated with a Surface-Mounted Circular Cylinder Trailed by a Backward-Facing Step
Abstract
1. Introduction
- Kubendran and Harvey [2] and Pierce and Shin [3] used fillers in the junction zone of a surface-mounted foil-section cylinder to control HSVs. Their experimental results revealed that fillers are effective in reducing the number of HSVs; however, an oversized filler is unsuitable for suppressing HSVs.
- Wei et al. [4] experimentally studied the HSVs associated with surface-mounted square-, circular-, and diamond-shaped cylinders. They found that the size and strength of the HSV and its distance from, wall shear stresses at, and pressures near the cylinder’s leading edge (LE) decreased as the cylinder’s geometry was modified from a square to a circle and a diamond with leading vertex angles of 90°, 60°, and 30°. The aforementioned authors attributed this result to the decreasing adverse pressure gradient formed in front of the cylinder because of the decreased blockage effect of superior cylinder geometries.
- Liu et al. [5] used a submarine model and examined the HSV induced by the sail, which is known to cause nonuniformities in the trailing wake flow and thus result in unwanted noise, vibration, and performance reductions. They installed a rectangular baffler on either side of the sail to generate an attached vortex that counter-rotated against the HSV to weaken it and rectify the trailing wake flow.
- Younis et al. [6] generated a vortex counter-rotating against the HSV of a surface-mounted circular cylinder by using a triangular vortex generator. They reported that with the vortex generator, the circulation of the HSV decreased to approximately 4.7% of its original value, and the pressure gradient formed in front of the circular cylinder considerably reduced.
- Huang et al. [7] studied the effects of junction fillers’ geometric parameters on the HSV upstream a surface-mounted circular cylinder. They found that as the axial length of the filler increased, the flow structure in the junction area was varied from the vortical-flow mode to the forward-flow mode when the separation of the upstream boundary layer did not occur.
2. Experimental Setup and Methods
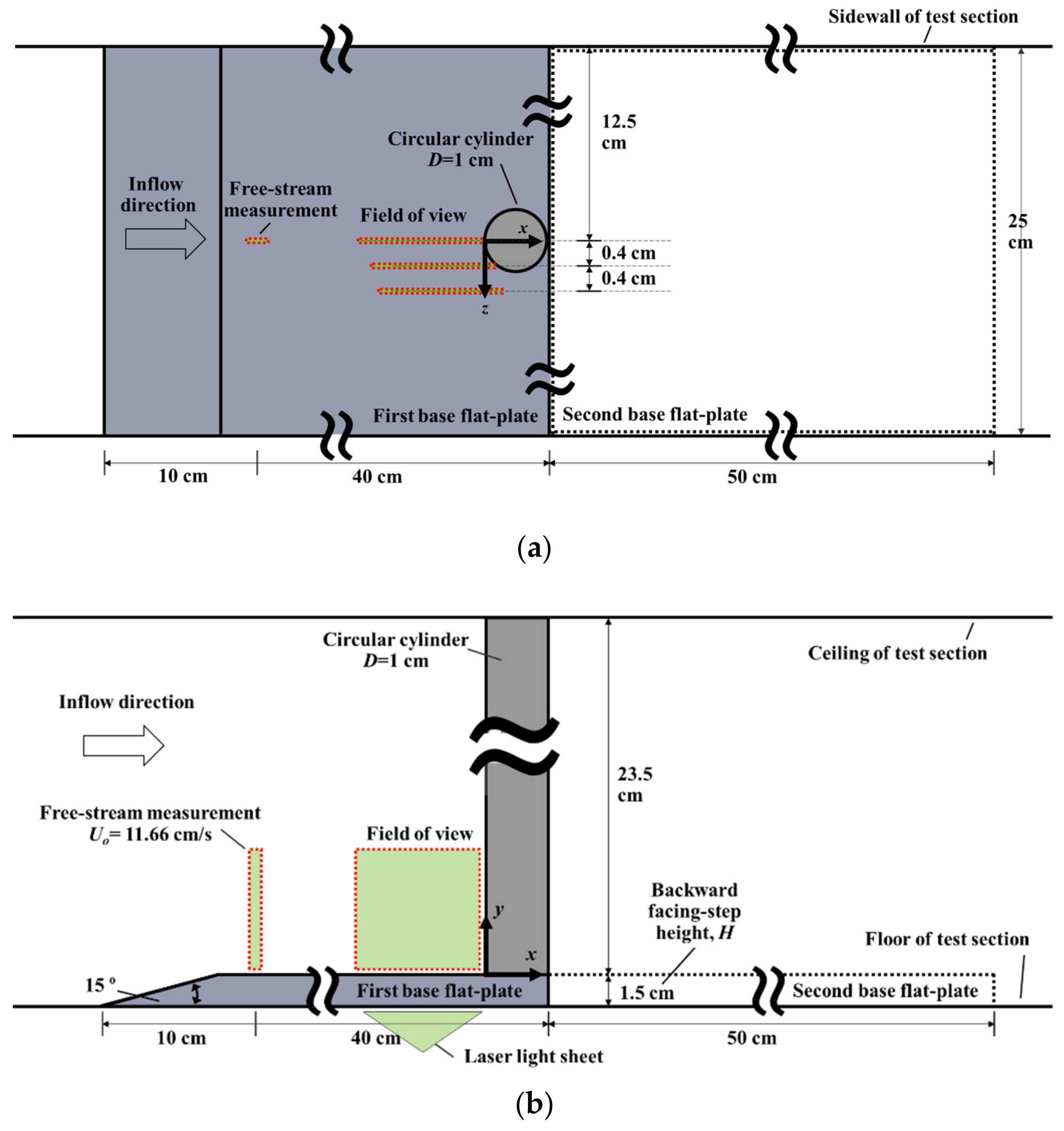
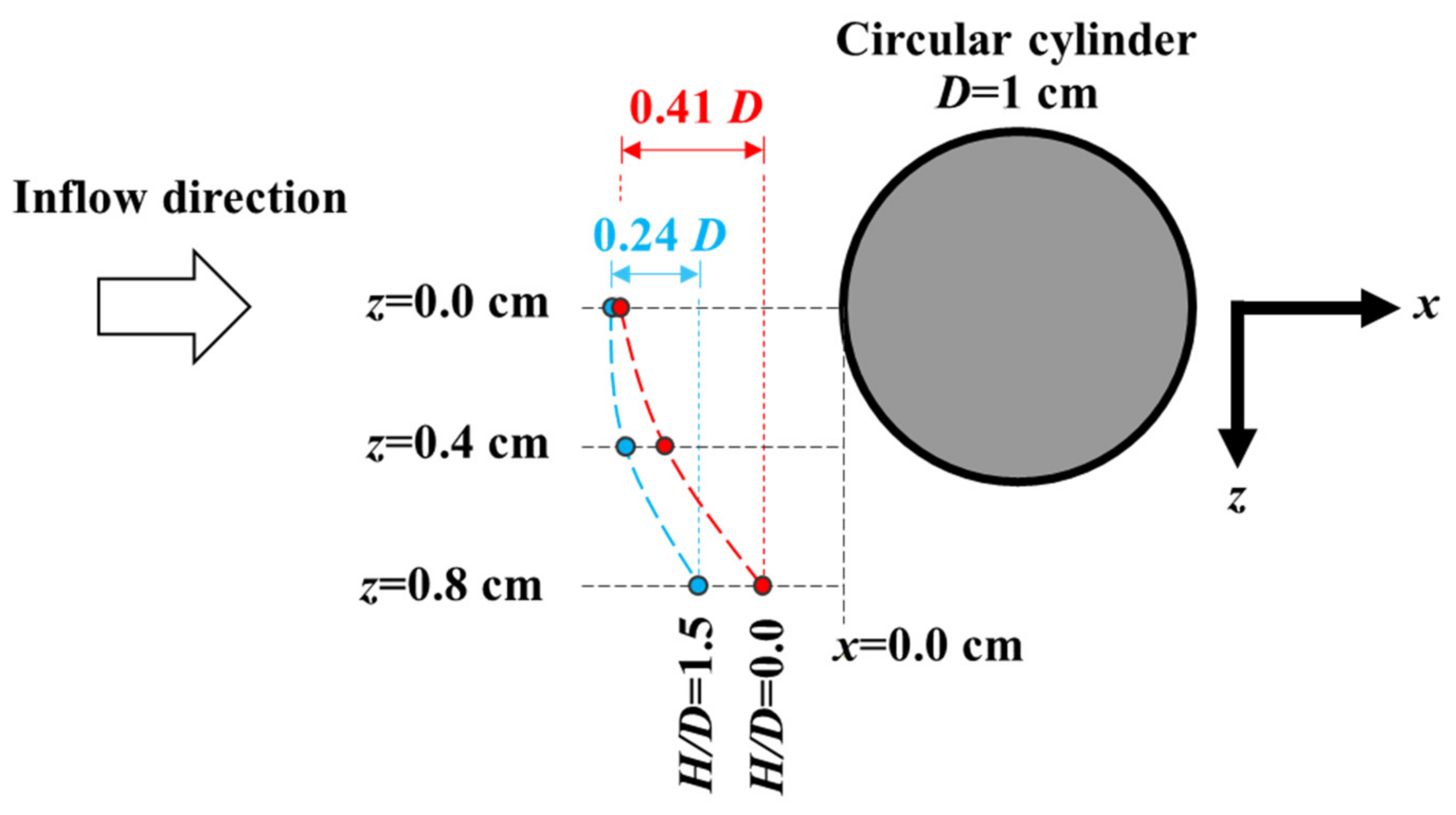
2.1. Water Tunnel and Experimental Conditions
2.2. PIV Techniques
- A.
- The qualitative PIV-based flow visualizations were used to capture the kinematic behaviors of the HSVs associated with the circular cylinder. The clear flow structures, including vortical structures, were visualized using the pathlines of the seeding particles at a prolonged exposure time of 42,000 µs. The high-speed CMOS camera captured 1440 frames at the sampling rate of 24 fps for 60 s in each plane when z = 0, 0.4, and 0.8 cm. Even though the z = 0.4 and 0.8 cm planes did not cut perpendicular to the axis of the HSV as done approximately by Praisner and Smith [16,17], the HSV’s kinematic modes and its approximate center positions to show the spanwise development could still be investigated with the flow visualizations at these three z-planes.
- B.
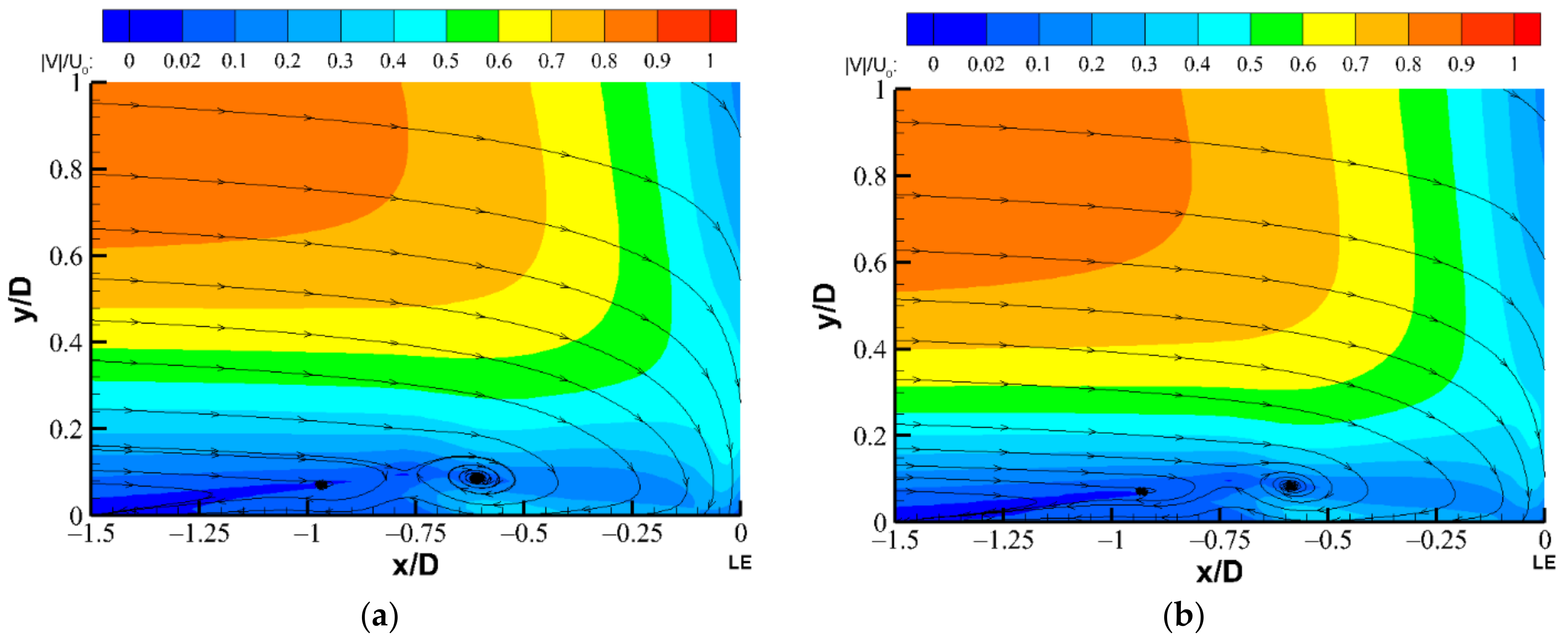
- The quantitative PIV flow measurements at the symmetric plane of z = 0 cm were performed to investigate the HSV’s flow characteristics. A sequence of 3000 frames of the particle images was recorded using a high-speed CMOS camera at a sampling rate of 170 fps with an exposure time of 125 μs. The time series of instantaneous velocity vector maps were then yielded from the consecutive particle images using the cross-correlation analysis performed with LaVision’s DaVis FlowMaster software package. The HSV’s flow characteristics, namely, its radius, core vorticity, and circulation, could be determined using the in-house vortex-fitting algorithms (details follow) with the vorticity distributions calculated from the measured velocity vector maps.
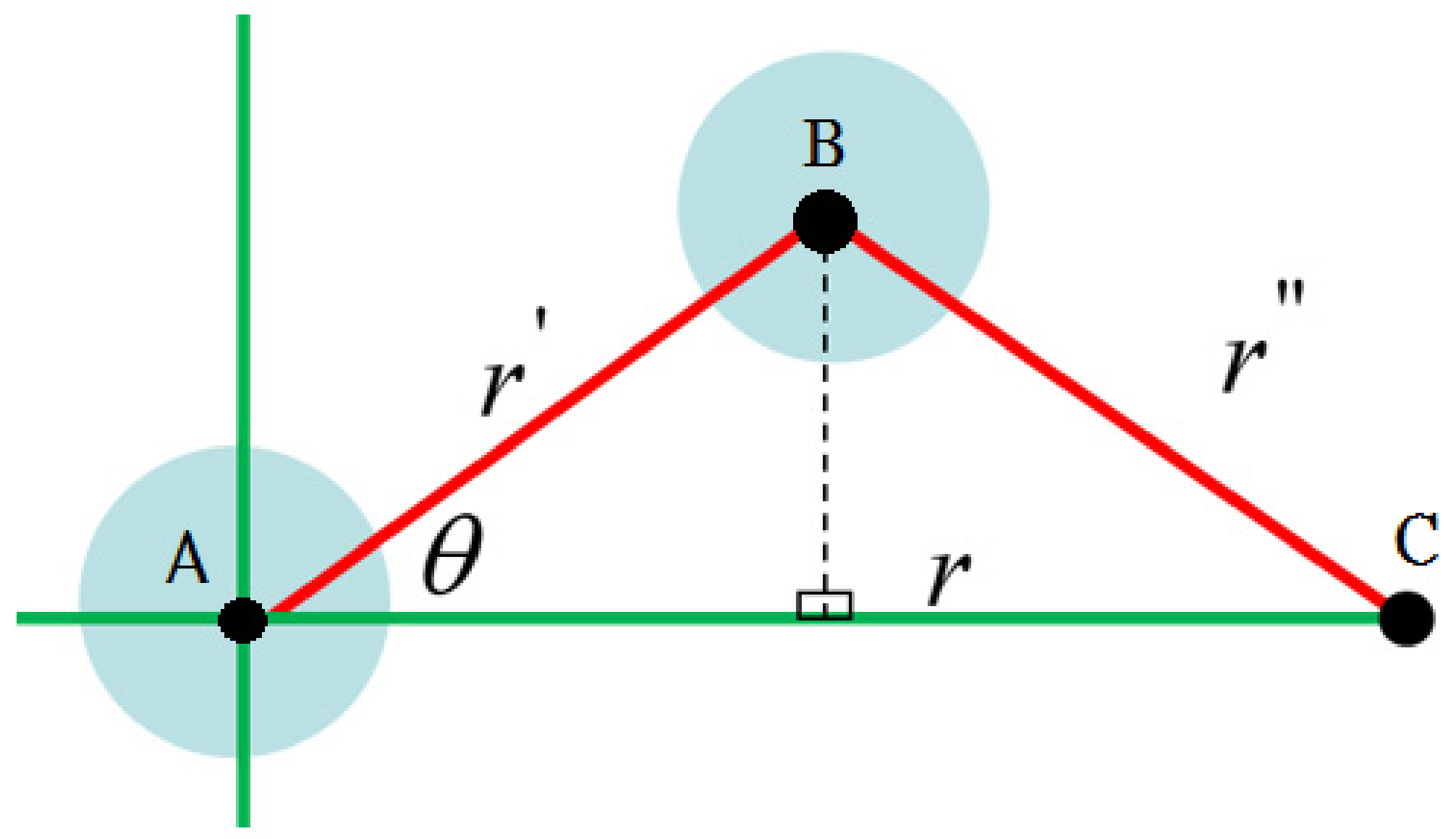
2.3. Vortex-Fitting Algorithms
- (1)
- defining the range of the search for the vortex core position as a region near an initial reference vortex core position using the particle pathlines associated with the HSV found in the PIV-based flow visualizations;
- (2)
- expanding an 11 × 11 grid centered at the reference vortex core position to compute the vorticity distribution;
- (3)
- adjusting this computed vorticity distribution using the vortex radius, standard deviation of the Gaussian distribution, and circulation strength, as shown in the equations listed below;
- (4)
- determining a suitable combination of these three parameters mentioned in (3) by minimizing the root-mean-square deviation between the actual vorticity distribution obtained in the PIV measurement and the computed vorticity distribution.
3. Results and Discussion
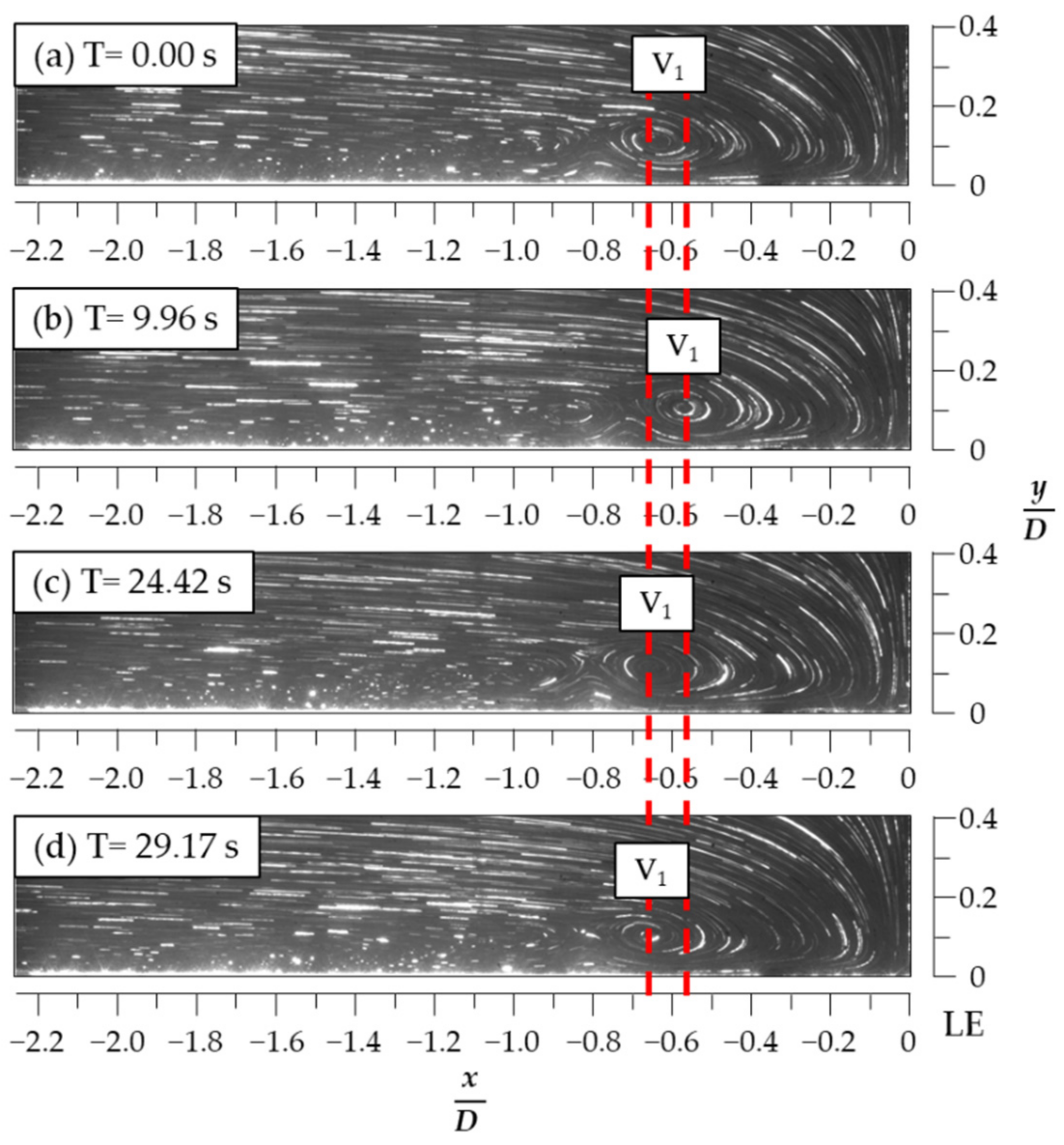
3.1. Flow Visualization for the HSVs When H/D = 0
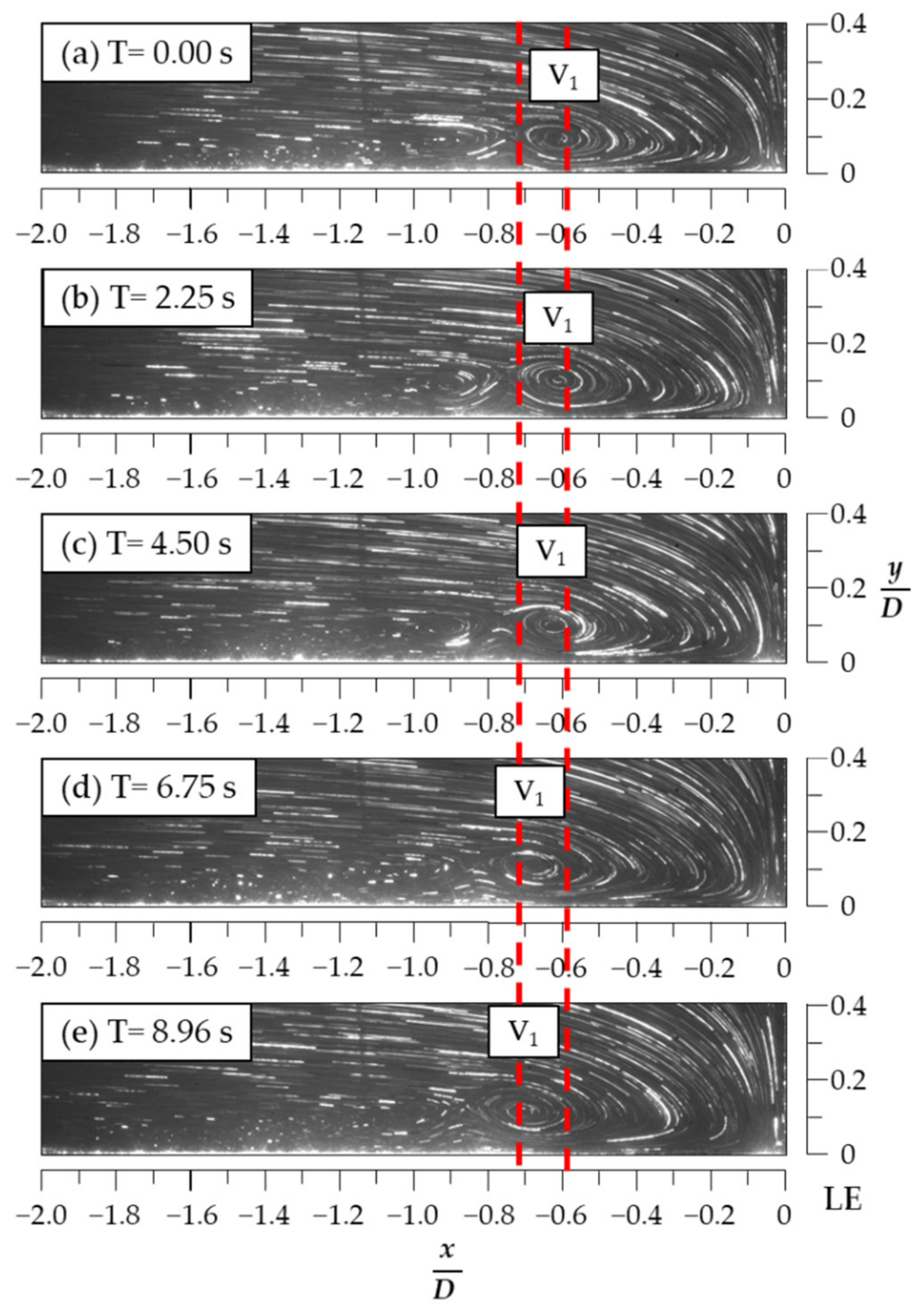
3.2. Flow Visualization for the HSVs When H/D = 1.5
3.3. Mode Duration and Spanwise Extension of the HSV
3.4. Flow Characteristics of the HSV When H/D = 0 and 1.5 (z = 0 cm Plane)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| δ0.99Uo | Boundary layer thickness |
| Re | Reynolds number |
| D | Diameter of the circular cylinder |
| Uo | Free-stream velocity |
| H | Height of the backward-facing step |
| x, y, z | Cartesian coordinate system |
| ε | Combined uncertainty for particle image displacement |
| r, θ, z | Cylindrical coordinate system |
| vθ | Circumferential velocity |
| Γ | Circulation |
| a | Radius of vortex |
| ωz | Vorticity parallel to z-direction |
| p | Probability density function |
| σ | Standard deviation |
| r′ | Distance between the averaged vortex core position |
| r″ | Distance between the discrete vortex core position and an arbitrary position |
| r | Distance between the averaged vortex core position and an arbitrary position |
| xm | Mean position of the vortex’s core in the x-direction |
| |V| | Velocity magnitude |
| du/dx | x-normal strain rate |
References
- Schwind, R. The Three Dimensional Boundary Layer Near a Strut; Gas Turbine Laboratory Report; Massachusetts Institute of Technology: Cambridge, MA, USA, 1962. [Google Scholar]
- Kubendran, L.R.; Harvey, W.D. Juncture flow control using leading-edge fillets. In Proceedings of the 3rd Applied Aerodynamics Conference, Colorado Springs, CO, USA, 14–16 October 1985; p. 4097. [Google Scholar]
- Pierce, F.J.; Shin, J. An experimental investigation of effects of leading-edge fillets on a turbulent junction vortex. In Proceedings of the 2nd International Symposium on Performance Enhancement for Marine Application, University of Rhode Island, Kingston, RI, USA, October 1990; pp. 61–71. [Google Scholar]
- Wei, Q.D.; Wang, J.M.; Chen, G.; Lu, Z.B.; Bi, W.T. Modification of junction flows by altering the section shapes of the cylinders. J. Vis. 2008, 11, 115–124. [Google Scholar] [CrossRef]
- Liu, Z.H.; Xiong, Y.; Wang, Z.Z.; Wang, S.; Tu, C.X. Experimental study on effect of a new vortex control baffler and its influencing factor. China Ocean Eng. 2011, 25, 83–96. [Google Scholar] [CrossRef]
- Younis, M.Y.; Zhang, H.; Zhu, R.; Muhammad, Z. Horseshoe vortex control using streamwise vortices. Procedia Eng. 2015, 126, 139–144. [Google Scholar] [CrossRef]
- Huang, R.F.; Hsu, C.M.; Chen, C. Effects of an upstream tetrahedron on the circular cylinder-flat plate juncture flow. Exp. Fluid 2015, 56, 146. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. Flow around Circular Cylinder; Oxford University Press: New York, NY, USA, 1997; Volume 1. [Google Scholar]
- Zdravkovich, M.M. Flow around Circular Cylinder; Oxford University Press: New York, NY, USA, 2003; Volume 2. [Google Scholar]
- Coutanceau, M.; Bouard, R. Experimental determination of the main features of the viscous flow in the wake of a circular cylinder in uniform translation. Part 1. Steady flow. J. Fluid Mech. 1977, 79, 231–256. [Google Scholar] [CrossRef]
- Coutanceau, M.; Bouard, R. Experimental determination of the main features of the viscous flow in the wake of a circular cylinder in uniform translation. Part 2. Unsteady flow. J. Fluid Mech. 1977, 79, 257–272. [Google Scholar] [CrossRef]
- Eaton, J.K.; Johnston, J.P. A review of research on subsonic turbulent flow reattachment. AIAA J. 1981, 19, 1093–1100. [Google Scholar] [CrossRef]
- Rinoie, K.; Shirai, Y.; Sunada, Y. Behavior of separated and reattaching flow formed over a backward facing step. Trans. Jpn. Soc. Aeronaut. Space Sci. 2002, 45, 20–27. [Google Scholar] [CrossRef]
- Wei, Q.D.; Chen, G.; Du, X.D. Experimental Study on the Structure of Juncture Flows. J. Vis. 2001, 3, 341–348. [Google Scholar] [CrossRef]
- Baker, C.J. The laminar horseshoe vortex. J. Fluid Mech. 1979, 95, 347–367. [Google Scholar] [CrossRef]
- Praisner, T.J.; Smith, C.R. The dynamics of the horse shoe vortex and associated endwall heat transfer, Part 1—Temporal behavior. J. Turbomach. 2005, 128, 747–754. [Google Scholar] [CrossRef]
- Praisner, T.J.; Smith, C.R. The dynamics of the horse shoe vortex and associated endwall heat transfer, Part 2—Time mean behavior. J. Turbomach. 2005, 128, 755–762. [Google Scholar] [CrossRef]
- Hada, S.; Takeishi, K.; Oda, Y.; Mori, S.; Nuta, Y. The effect of leading-edge diameter on the horse shoe vortex and endwall heat transfer. In Proceedings of the ASME Turbo Expo 2008, Berlin, Germany, 9–13 June 2008. [Google Scholar]
- 1003005_Flowmaster_D10.2. Product Manual for DaVis 10.2; LaVision GmbH: Göttingen, Germany, 2021.
- Burgers, J.M. A mathematical model illustrating the theory of turbulence. In Advances in Applied Mechanics; New York, NY, USA, 1948; Volume 1, pp. 171–199. [Google Scholar]
- Lin, C.; Chiu, P.H.; Shieh, S.J. Characteristics of horseshoe vortex system near a vertical plate-base plate juncture. Exp. Therm. Fluid Sci. 2002, 27, 25–46. [Google Scholar] [CrossRef]
- Lin, C.; Ho, T.C.; Dey, S. Characteristics of steady horseshoe vortex system near junction of square cylinder and base plate. J. Eng. Mech. 2008, 134, 184–197. [Google Scholar] [CrossRef]
- Rodriguez y Dominguez, M.M.; Romero-Mendez, R.; De Lange, D.F.; Hernández-Guerrero, A. Laminar horseshoe vortices upstream of a short cylinder normal to a flat plate. Ing. Mecánica Tecnol. Y Desarro. 2011, 3, 219–228. [Google Scholar]





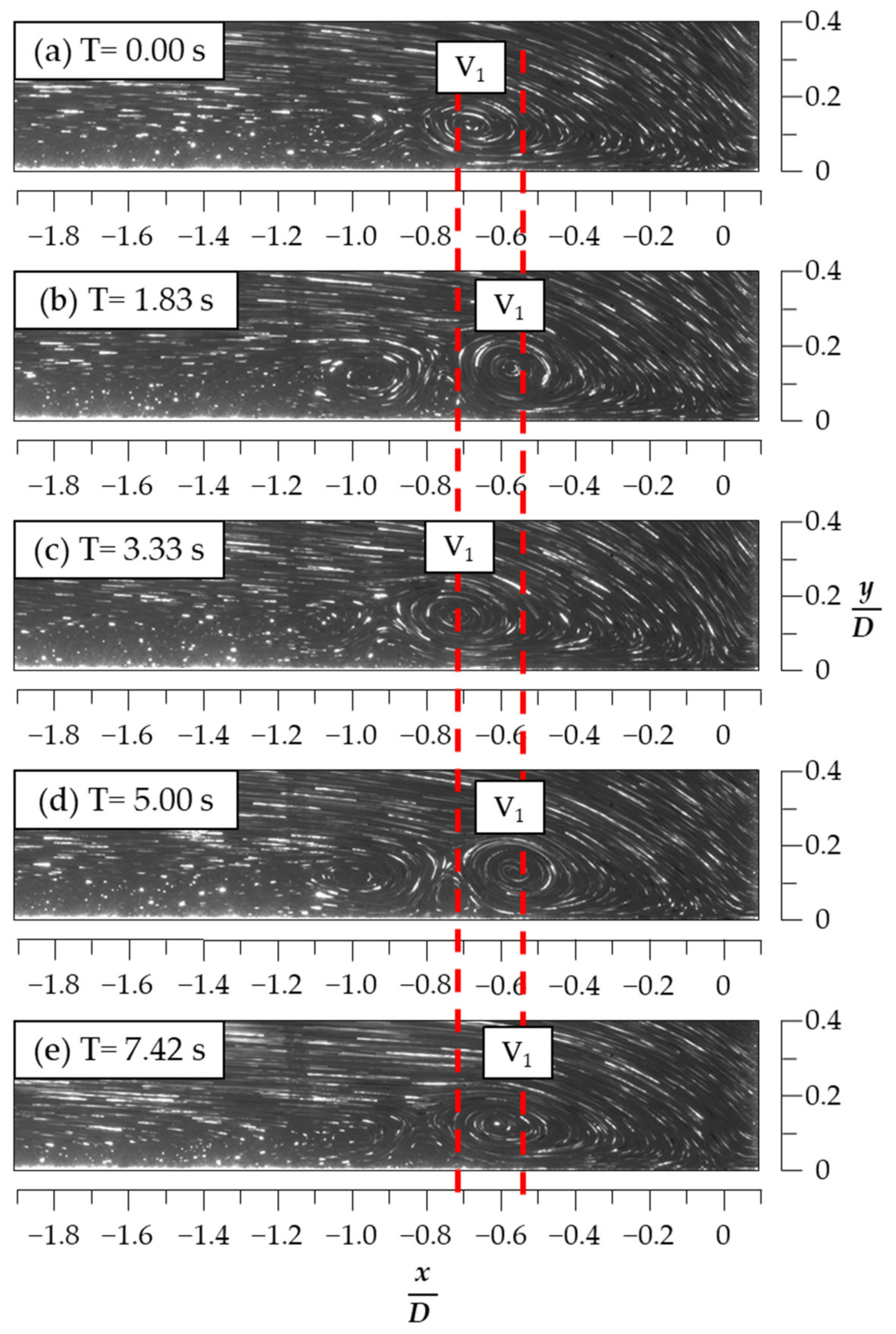
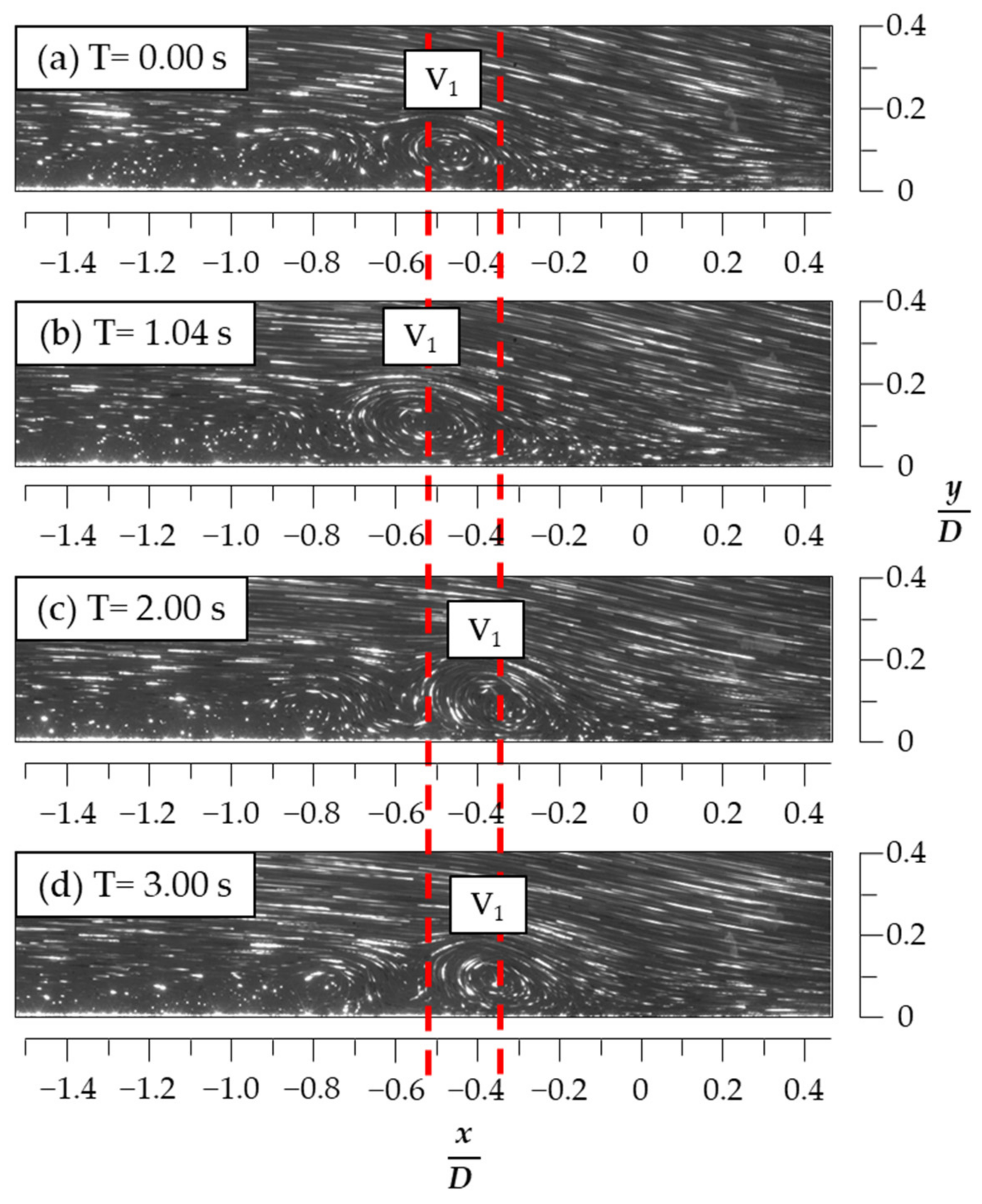


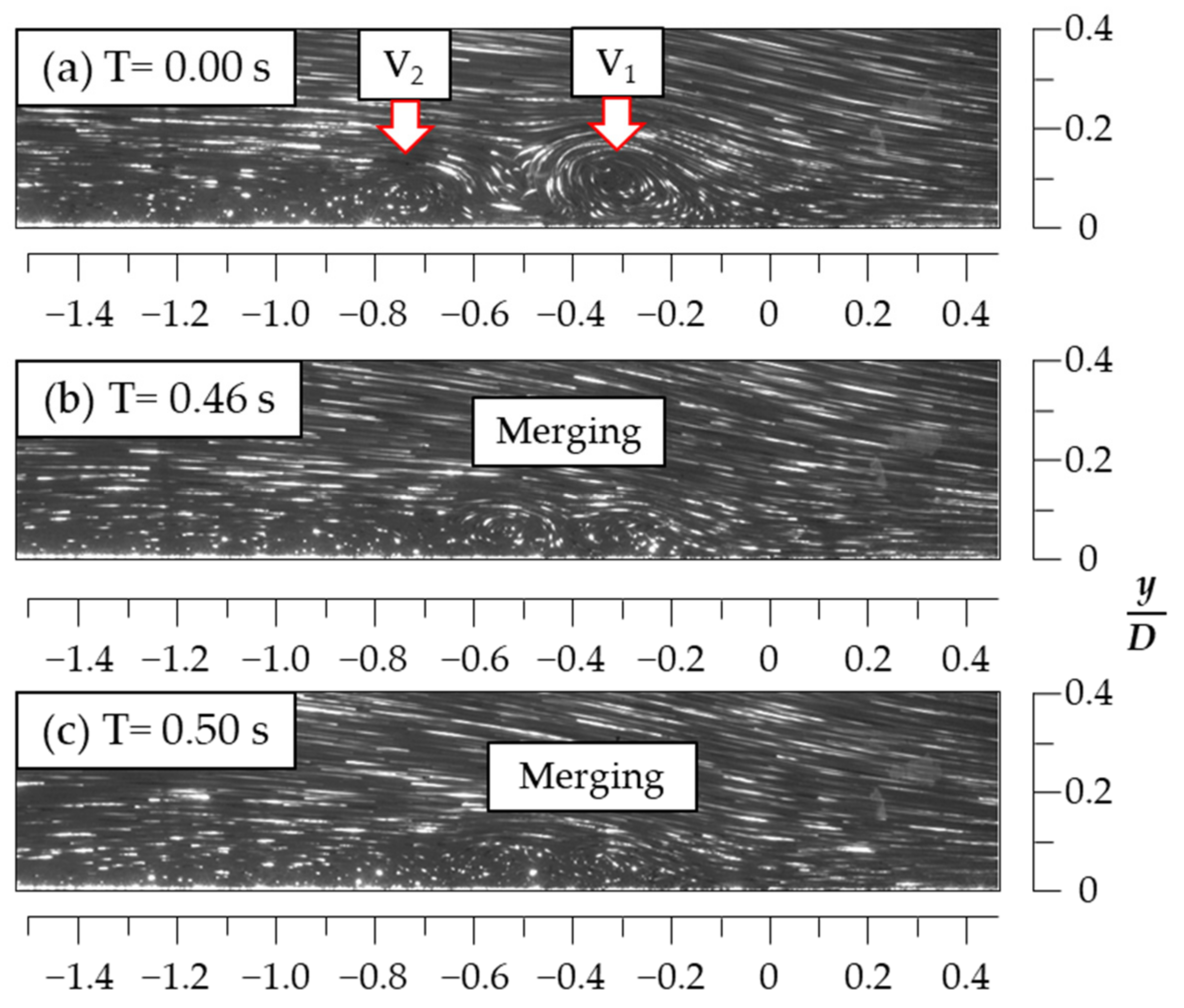
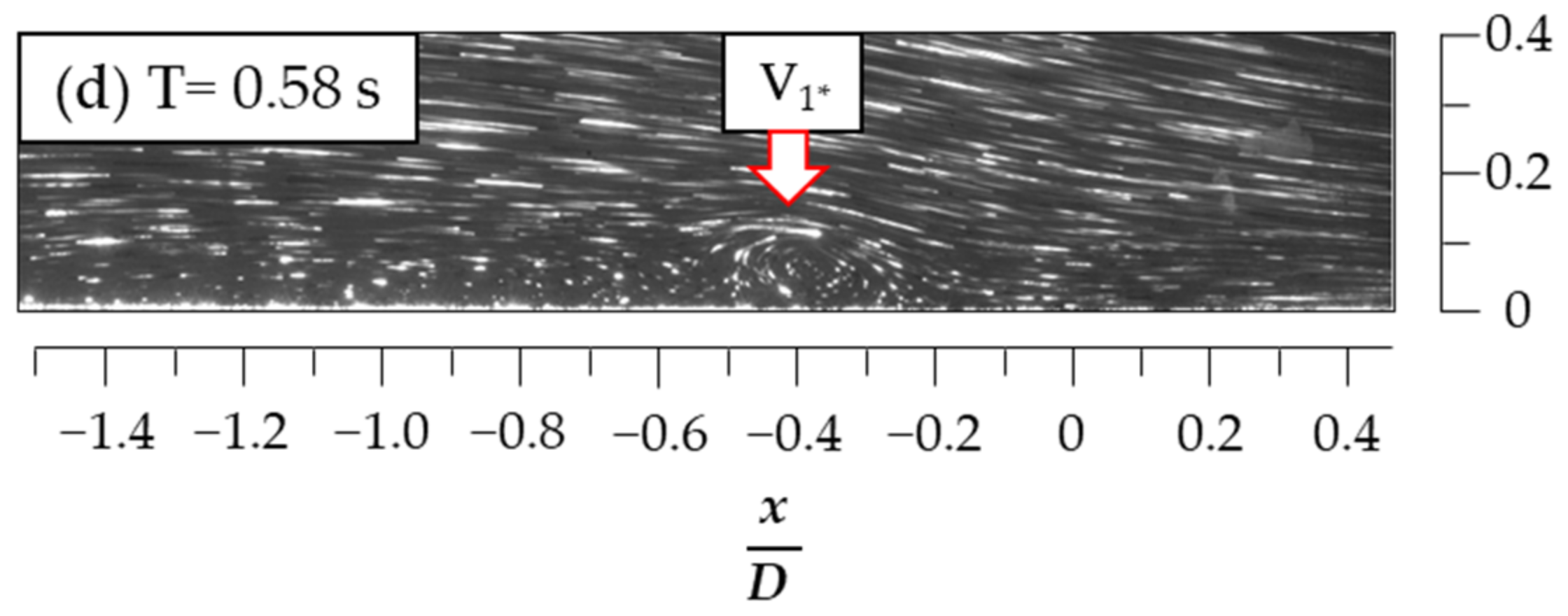

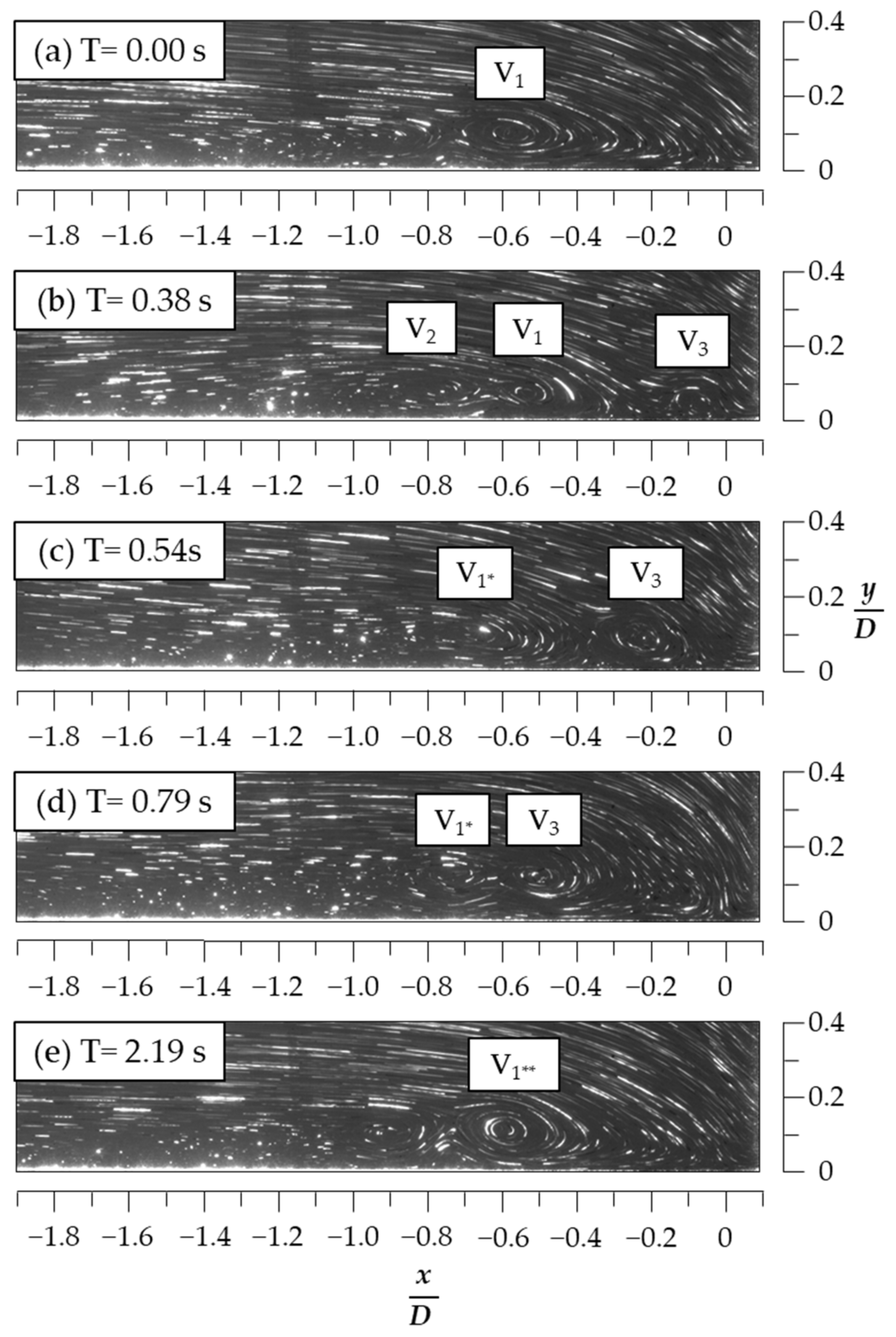
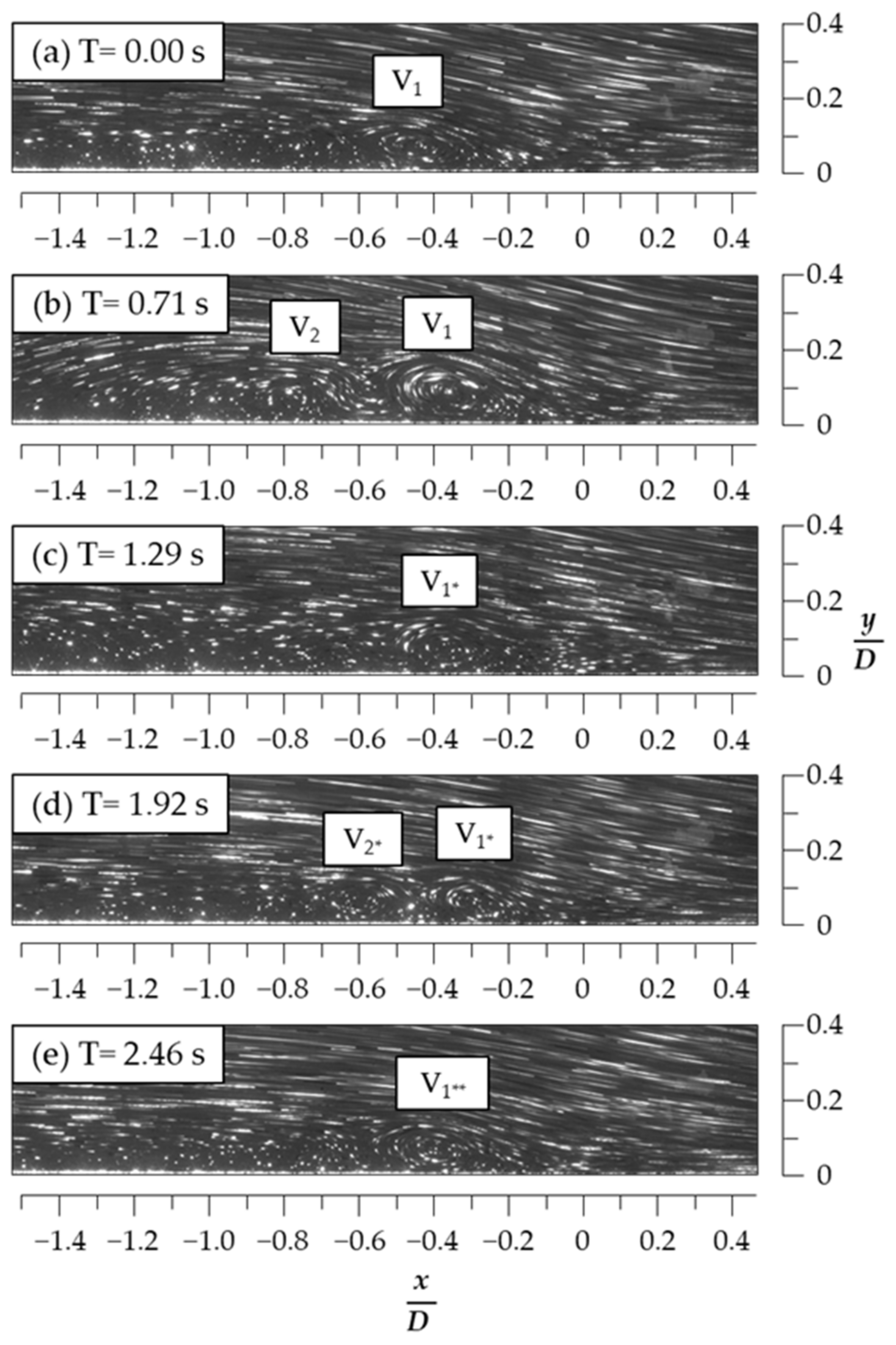

| H/D | Kinematic Modes | Duration (%) |
|---|---|---|
| 0 | Oscillations with a small displacement | 98.6 |
| Breakaway to roll-up | 1.4 | |
| 1.5 | Oscillations with a small displacement | 83.3 |
| Merging | 4.5 | |
| Mixed | 12.2 |
| H/D | z (cm) | Mean x-Position of the V1′s Core (xm/D) |
|---|---|---|
| 0 | 0 | −0.64 |
| 0.4 | −0.51 | |
| 0.8 | −0.23 | |
| 1.5 | 0 | −0.66 |
| 0.4 | −0.62 | |
| 0.8 | −0.42 |
| H/D | R/D | ωzD/Uo | Γ/Uo D |
|---|---|---|---|
| 0 | 0.085 | 9.677 | 0.251 |
| 1.5 | 0.092 | 8.966 | 0.267 |
| Differences (% with respect to H/D = 0) | 8.24 | −7.35 | 6.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.-Y.; Chow, Y.-C. Experimental Investigation on Juncture Flow Associated with a Surface-Mounted Circular Cylinder Trailed by a Backward-Facing Step. J. Mar. Sci. Eng. 2022, 10, 1494. https://doi.org/10.3390/jmse10101494
Yang C-Y, Chow Y-C. Experimental Investigation on Juncture Flow Associated with a Surface-Mounted Circular Cylinder Trailed by a Backward-Facing Step. Journal of Marine Science and Engineering. 2022; 10(10):1494. https://doi.org/10.3390/jmse10101494
Chicago/Turabian StyleYang, Chun-Yao, and Yi-Chih Chow. 2022. "Experimental Investigation on Juncture Flow Associated with a Surface-Mounted Circular Cylinder Trailed by a Backward-Facing Step" Journal of Marine Science and Engineering 10, no. 10: 1494. https://doi.org/10.3390/jmse10101494
APA StyleYang, C.-Y., & Chow, Y.-C. (2022). Experimental Investigation on Juncture Flow Associated with a Surface-Mounted Circular Cylinder Trailed by a Backward-Facing Step. Journal of Marine Science and Engineering, 10(10), 1494. https://doi.org/10.3390/jmse10101494





